A General On-Orbit Absolute Radiometric Calibration Method Compatible with Multiple Imaging Conditions
Abstract
1. Introduction
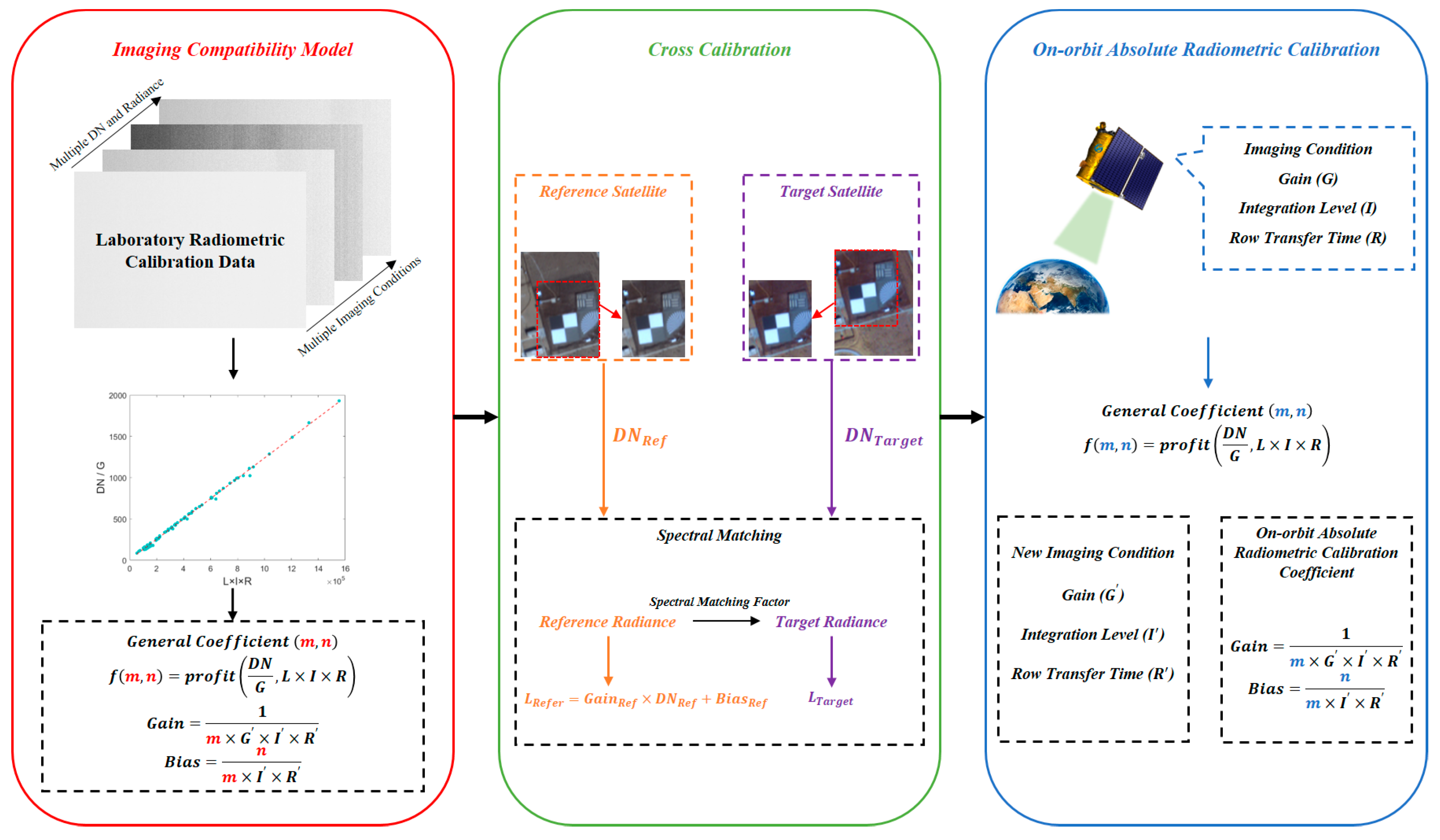
- A general on-orbit absolute radiometric calibration method compatible with multiple imaging conditions is proposed, including an imaging condition compatibility model and cross calibration. By using the proposed method, all imaging conditions of optical remote sensing satellite sensors can be calibrated in one imaging task, which greatly improve the timeliness and accuracy of on-orbit absolute radiometric calibration.
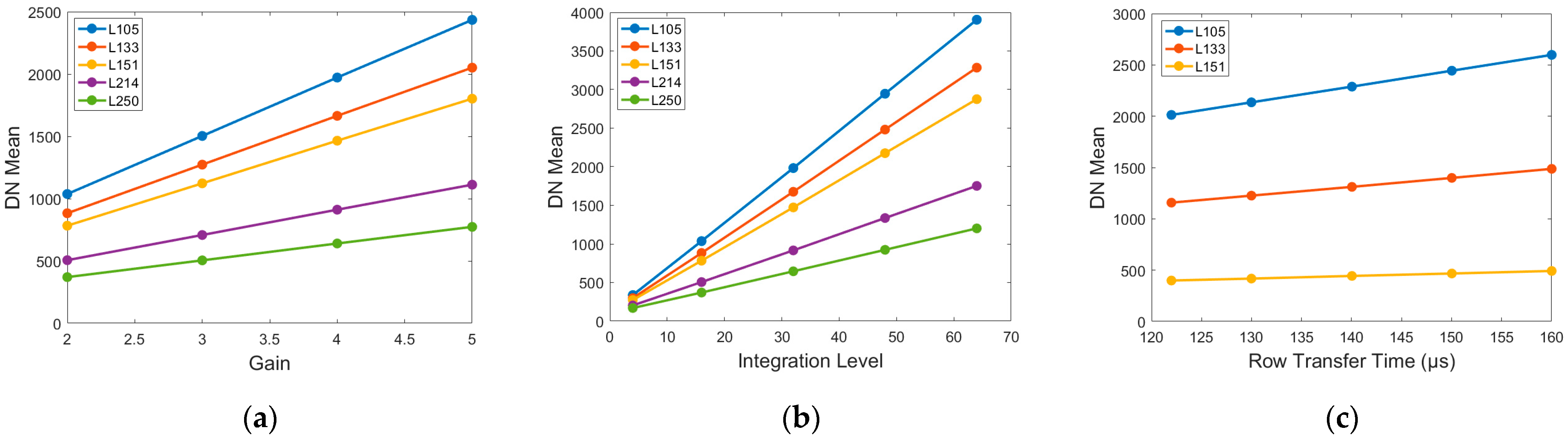
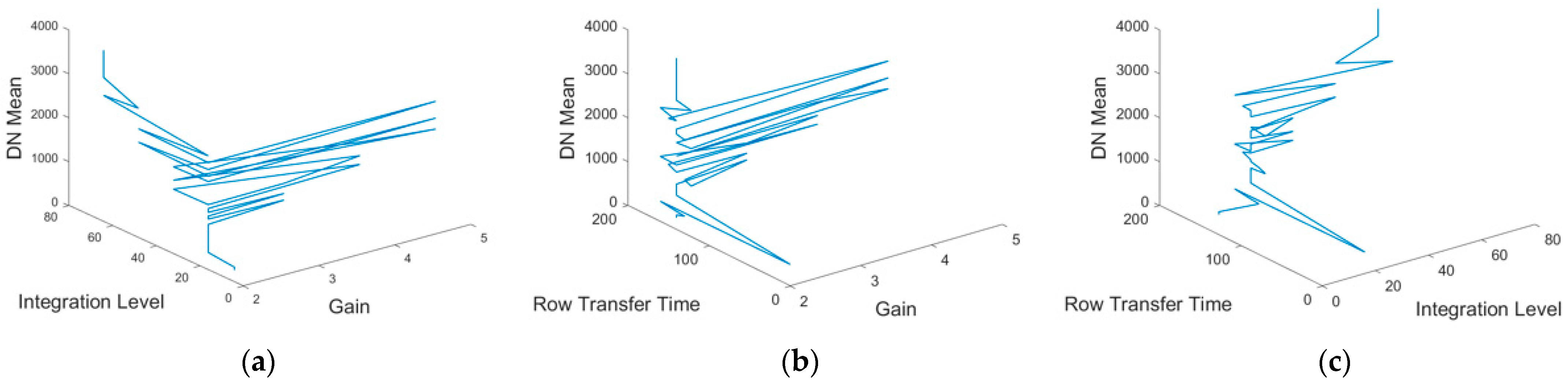
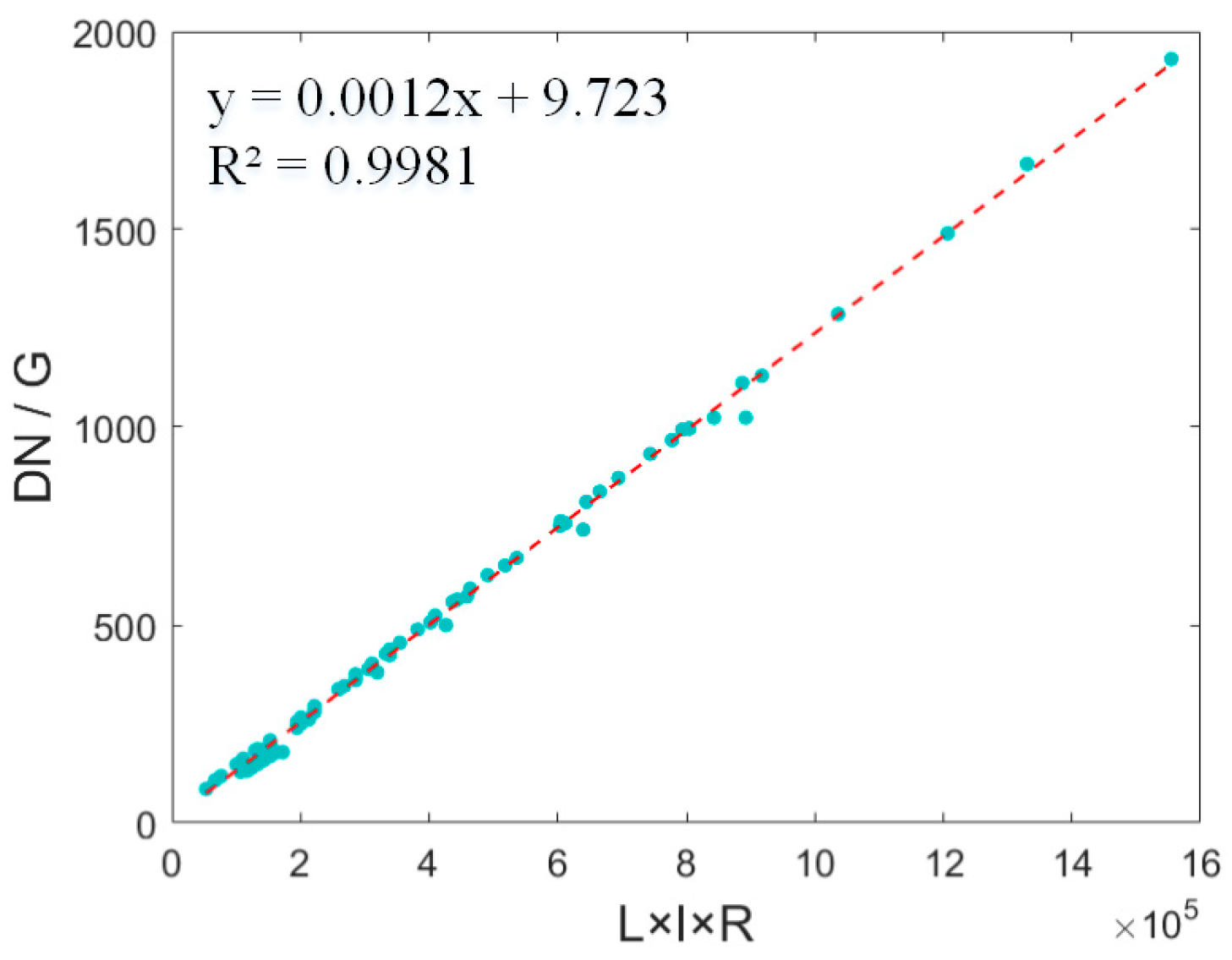
- A large amount of laboratory radiometric calibration data are used to explore the mathematical relationship between the imaging condition (row transfer time, integration level and gain), radiance, and DN to successfully build an imaging compatibility model, and we integrate row transfer time, integration level, gain, radiance, and DN into a uniform formula.
- In cross calibration, we flexibly use the corresponding points-matching method based on different surface features to ensure the accuracy and effectiveness of the corresponding points. On the other hand, a more concise and effective method is proposed for calculating the spectral-matching factor, which simplifies the calculation process and improves the effectiveness of computation.
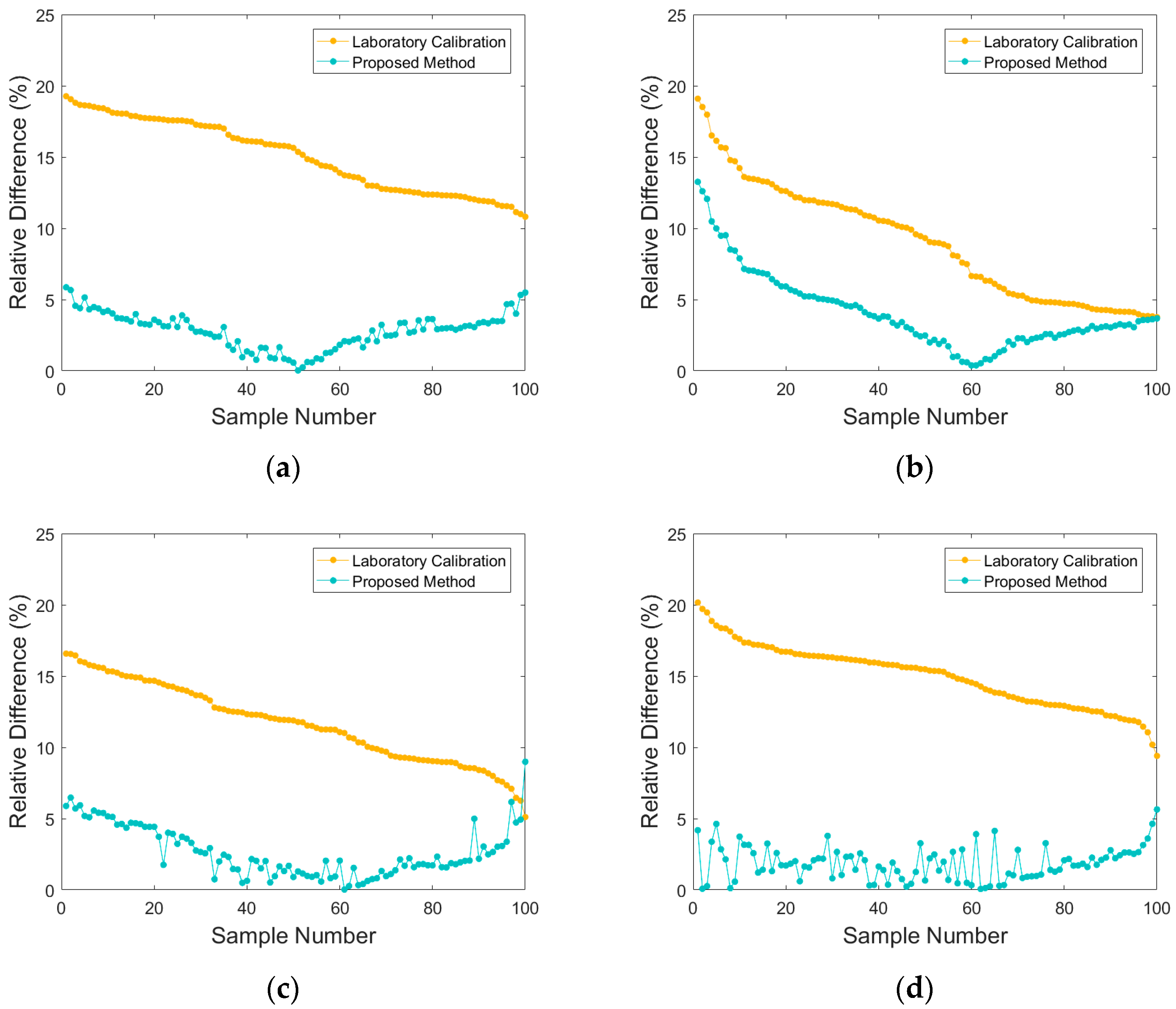
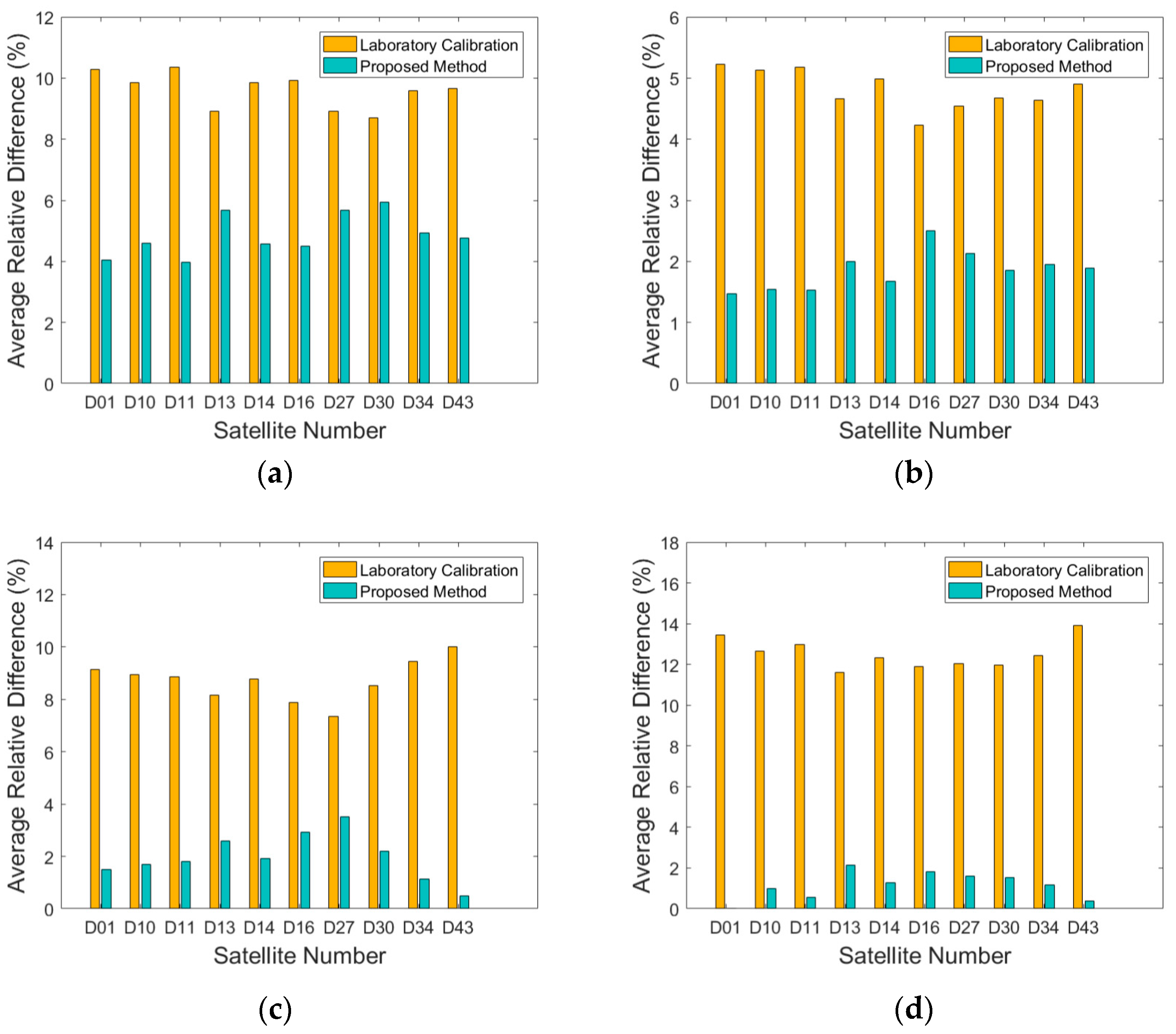
- We used Sentinel-2 series satellites as the reference satellite and Jilin-1 GF03D series satellites as the target satellites for the experiment. Specifically, five imaging tasks of the JL1GF03D11 satellites with different imaging conditions are used to verify the effectiveness of the proposed method. The experiments show that the average relative difference is reduced to 2.79% and the RMSE is reduced to 1.51 compared with the laboratory radiometric calibration method. Similarly, 20 imaging tasks of the Jilin-1 GF03D series satellites with different imaging conditions and different surface features are used to validate the generality of the proposed method. The experimental results show that the goodness of fit of the general coefficient is all greater than 95%, and the average relative difference between the reference radiance and the calibrated radiance of the proposed method is 2.46%, with an RMSE of 1.67.
2. Methods
2.1. Imaging Condition Compatibility Model
2.2. Cross Calibration
2.2.1. Calibration Field
2.2.2. Corresponding Points Matching
2.2.3. Spectral Matching
3. Results
3.1. Reference Satellite and Target Satellite
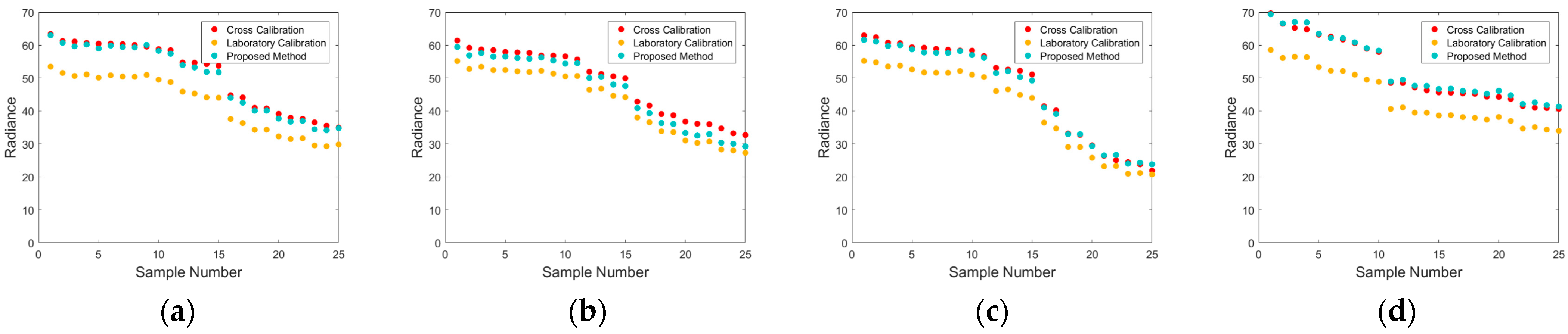
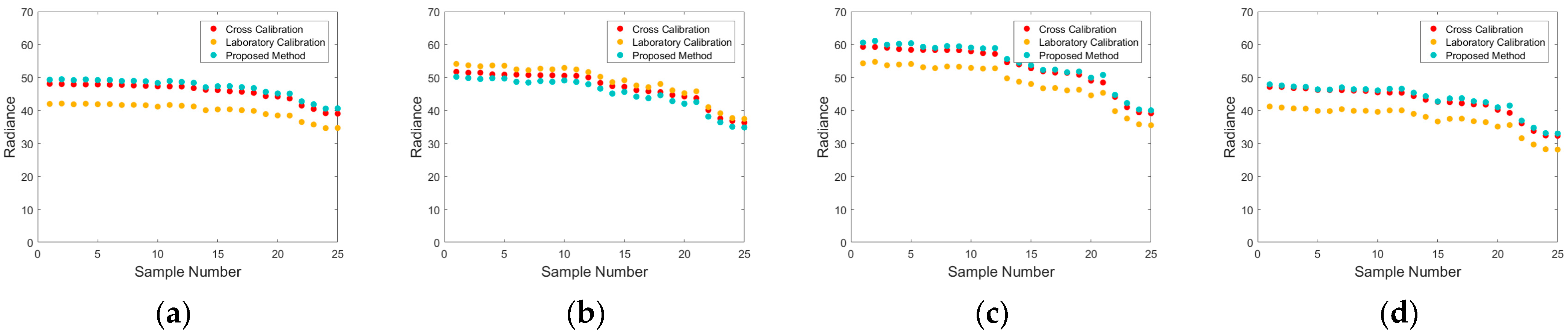
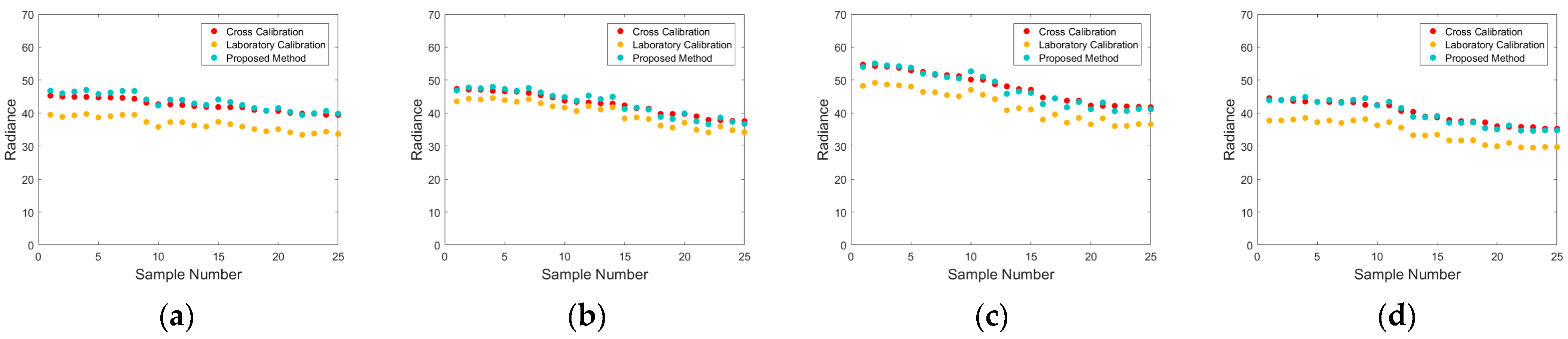
3.2. Evaluation of Effectiveness
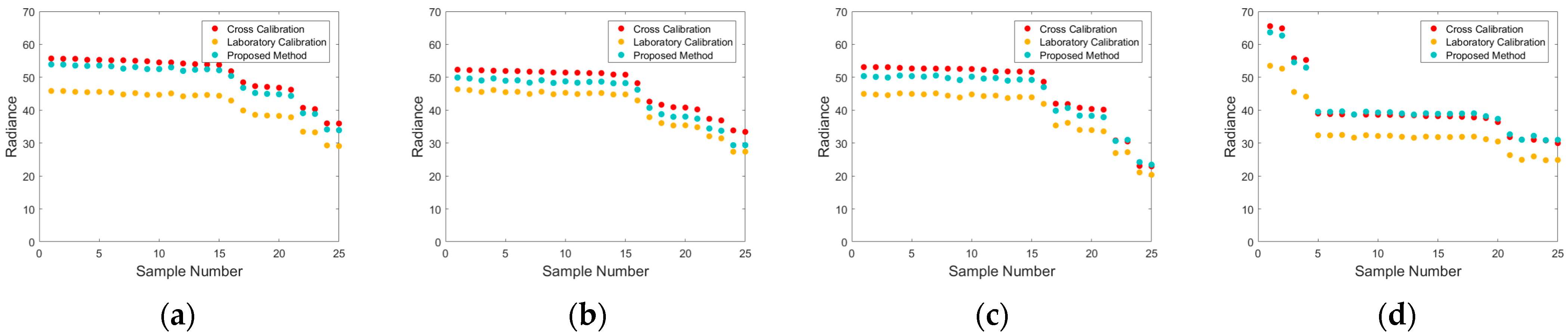
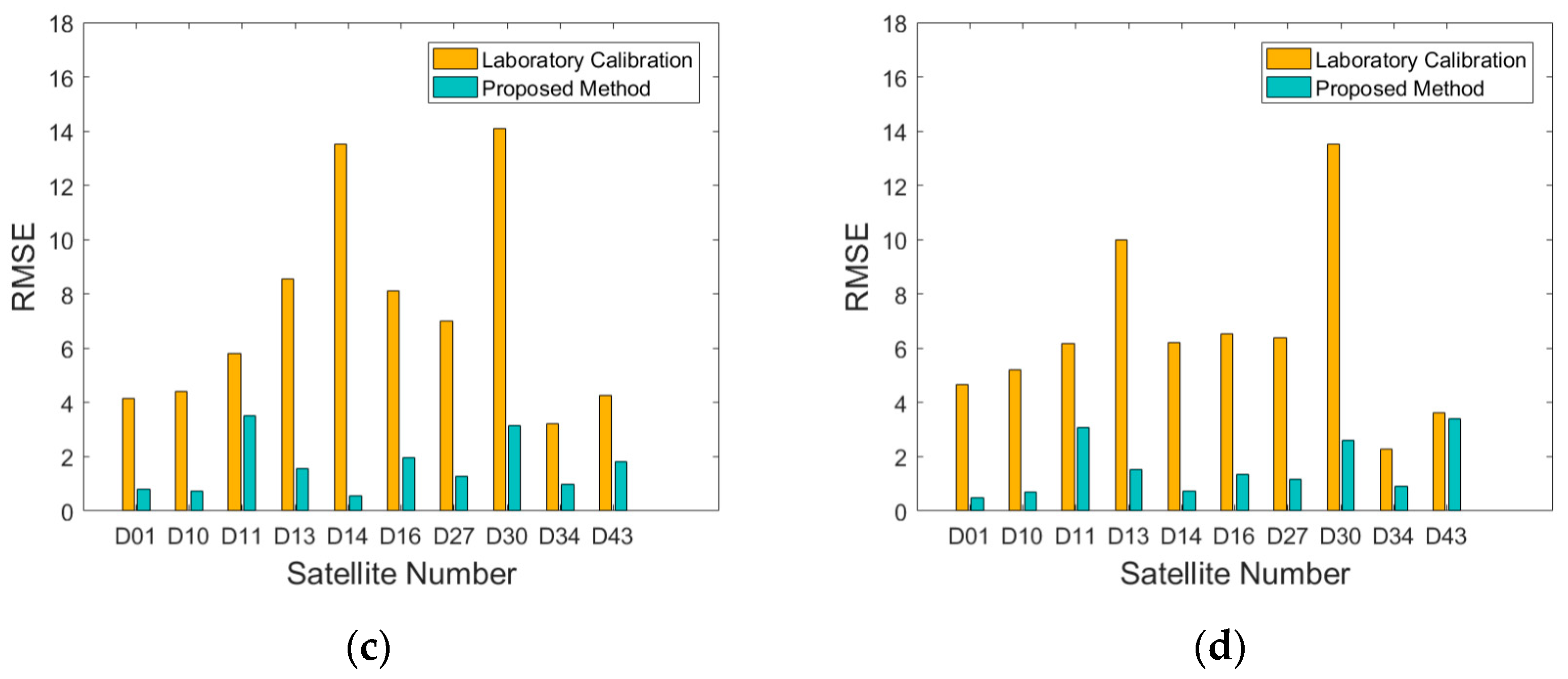
3.3. Evaluation of Generality
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, Z.; Thome, K.; Lockwood, R.; Wenny, B.N. Absolute radiometric calibration of an imaging spectroradiometer using a laboratory detector-based approach. Remote Sens. 2022, 14, 2245. [Google Scholar] [CrossRef]
- Hattori, T.; Dasai, F.; Sato, H.; Kato, R.; Sawada, K. CCD multi-ion image sensor with four 128 × 128 pixels array. Sensors 2019, 19, 1582. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Y.; Yang, T.; Wang, M.; Hong, H.; Zhang, Y.; Wang, L.; Rao, Q. Jitter Detection Method Based on Sequence CMOS Images Captured by Rolling Shutter Mode for High-Resolution Remote Sensing Satellite. Remote Sens. 2022, 14, 342. [Google Scholar] [CrossRef]
- Li, J.; Dai, Y.; Su, X.; Wu, W. Efficient Dual-Branch Bottleneck Networks of Semantic Segmentation Based on CCD Camera. Remote Sens. 2022, 14, 3925. [Google Scholar] [CrossRef]
- Xu, J.; Sun, T. Study on Super-Resolution of Images Obtained by Micro Satellite with CMOS Sensor. In Proceedings of the 2019 IEEE 4th International Conference on Signal and Image Processing (ICSIP), Wuxi, China, 19–21 July 2019. [Google Scholar]
- Xie, Y.; Han, J.; Gu, X.; Liu, Q. On-Orbit Radiometric Calibration for a Space-Borne Multi-Camera Mosaic Imaging Sensor. Remote Sens. 2017, 9, 1248. [Google Scholar] [CrossRef]
- Liu, J.; Cui, Y.; He, H.; Yin, Y. Research on the Influence of Different Factors of Micro-Vibration on the Radiation Quality of TDICCD Images. In 5th International Symposium of Space Optical Instruments and Applications; Springer: Cham, Switzerland, 2020. [Google Scholar]
- Sun, Z.; Li, Z.; Li, W.; Wang, X.; Gao, Z.; Zhao, Y.; Liu, Y.; Zhang, H.; Liu, D. Design and Implementation of TDI CCD Imaging Circuits in Space Applications. J. Phys. Conf. Ser. 2022, 2201, 012001. [Google Scholar] [CrossRef]
- Yue, Q. Multi-view imaging simulation of a space born TDI CCD camera and a 3D geometric reconstruction estimate. IOP Conf. Ser. Earth Environ. Sci. 2022, 1004, 012013. [Google Scholar]
- Zhao, Y.; Gobbi, M.; Hueso, L.E.; Samorì, P. Molecular Approach to Engineer Two-Dimensional Devices for CMOS and beyond-CMOS Applications. Chem. Rev. 2022, 122, 50–131. [Google Scholar] [CrossRef]
- Czapla-Myers, J.S.; Thome, K.J.; Anderson, N.J.; Leigh, L.M.; Pinto, C.T.; Wenny, B.N. The Ground-Based Absolute Radiometric Calibration of the Landsat 9 Operational Land Imager. Remote Sens. 2024, 16, 1101. [Google Scholar] [CrossRef]
- Xiong, X.; Sun, J.; Xie, X.; Barnes, W.; Salomonson, V. On-Orbit Calibration and Performance of Aqua MODIS Reflective Solar Bands. IEEE Trans. Geosci. Remote Sens. 2010, 48, 535–546. [Google Scholar] [CrossRef]
- Jin, L.B.; Wang, H.; Zhao, Y.H.; Hu, B.; Shi, D.; Lian, M.L. Design of expandable diffuser board on GF-5 VIMI. Chin. Space Sci. Technol. 2020, 40, 81–87. [Google Scholar]
- Chen, Y.; Sun, K.; Li, W.; Hu, X.; Li, P.; Bai, T. Vicarious Calibration of FengYun-3D MERSI-II at Railroad Valley Playa Site: A Case for Sensors with Large View Angles. Remote Sens. 2021, 13, 1347. [Google Scholar] [CrossRef]
- Guo, Y.; Senthilnath, J.; Wu, W.; Zhang, X.; Zeng, Z.; Huang, H. Radiometric Calibration for Multispectral Camera of Different Imaging Conditions Mounted on a UAV Platform. Sustainability 2019, 11, 978. [Google Scholar] [CrossRef]
- Tang, H.F.; Tang, X.M.; Xie, J.F.; Chen, W.; Qian, Y.G. On-orbit radiometric calibration and validation of GF-7 satellite based on RadCalNet Baotou site. Natl. Remote Sens. Bull. 2023, 27, 1194–1204. [Google Scholar] [CrossRef]
- Stone, T.C. Acquisition of Moon Measurements by Earth Orbiting Sensors for Lunar Calibration. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1001706. [Google Scholar] [CrossRef]
- Xiong, X.; Sun, J.; Angal, A.; Wilson, T. Calibration Inter-Comparison of MODIS and VIIRS Reflective Solar Bands Using Lunar Observations. Remote Sens. 2022, 14, 4754. [Google Scholar] [CrossRef]
- Chen, R.; Guan, L.; Liu, M.; Qu, L. Cross-Calibration of HY-1D/COCTS Thermal Emissive Bands in the South China Sea. Remote Sens. 2024, 16, 292. [Google Scholar] [CrossRef]
- Dong, J.; Chen, Y.; Chen, X.; Xu, Q. Radiometric Cross-Calibration of Wide-Field-of-View Cameras Based on Gaofen-1/6 Satellite Synergistic Observations Using Landsat-8 Operational Land Imager Images: A Solution for Off-Nadir Wide-Field-of-View Associated Problems. Remote Sens. 2023, 15, 3851. [Google Scholar] [CrossRef]
- Gao, C.; Liu, Y.; Liu, J.; Ma, L.; Wu, Z.; Qiu, S.; Li, C.; Zhao, Y.; Han, Q.; Zhao, E.; et al. Determination of the Key Comparison Reference Value from Multiple Field Calibration of Sentinel-2B/MSI over the Baotou Site. Remote Sens. 2020, 12, 2404. [Google Scholar] [CrossRef]
- Tao, Z.; Han, J.; Xie, Y.; Li, H.; Yi, H.; Guan, X. A TOA Spectral Reflectance Model of Railroad Valley Playa Site to Compensate the Missing RadCalNet Data. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5629110. [Google Scholar] [CrossRef]
- Wang, S.; Wang, H.; Zhou, Y.; Liu, J.; Dai, P.; Du, X.; Wahab, M.A. Automatic laser profile recognition and fast tracking for structured light measurement using deep learning and template matching. Measurement 2021, 169, 108362. [Google Scholar] [CrossRef]
- Yakovleva, O.; Nikolaieva, K. Research of descriptor based image normalization and comparative analysis of SURF, SIFT, BRISK, ORB, KAZE, AKAZE descriptors. Adv. Inf. Syst. 2020, 4, 89–101. [Google Scholar] [CrossRef]
- Zhou, Q.; Tian, L.; Li, J.; Wu, H.; Zeng, Q. Radiometric cross-calibration of large-view-angle satellite sensors using global searching to reduce BRDF influence. IEEE Trans. Geosci. Remote Sens. 2020, 59, 5234–5245. [Google Scholar] [CrossRef]
- Antunes, M.A.H.; Gleriani, J.M.; Debiasi, P. Atmospheric effects on vegetation indices of TM and ETM+ images from a tropical region using the 6S model. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012. [Google Scholar]
- Belgiu, M.; Marshall, M.; Boschetti, M.; Pepe, M.; Stein, A.; Nelson, A. PRISMA and Sentinel-2 spectral response to the nutrient composition of grains. Remote Sens. Environ. 2023, 292, 113567. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, J.; Fan, W.; Qiu, W.; Luo, J. Partial Hadamard encoded synthetic transmit aperture for high frame rate imaging with minimal l 2-norm least squares method. Phys. Med. Biol. 2022, 67, 105002. [Google Scholar] [CrossRef]
- Hu, Y.; Li, X.-M.; Dou, C.; Jia, G.; Hu, Z.; Xu, A.; Ren, Y.; Yan, L.; Wang, N.; Cui, Z.; et al. Absolute radiometric calibration evaluation of the thermal infrared spectrometer onboard SDGSAT-1. Int. J. Digit. Earth 2023, 16, 4492–4511. [Google Scholar] [CrossRef]
- Tang, H.; Xie, J.; Chen, W.; Zhang, H.; Wang, H. Absolute Radiometric Calibration of ZY3-02 Satellite Multispectral Imager Based on Irradiance-Based Method. Remote Sens. 2023, 15, 448. [Google Scholar] [CrossRef]


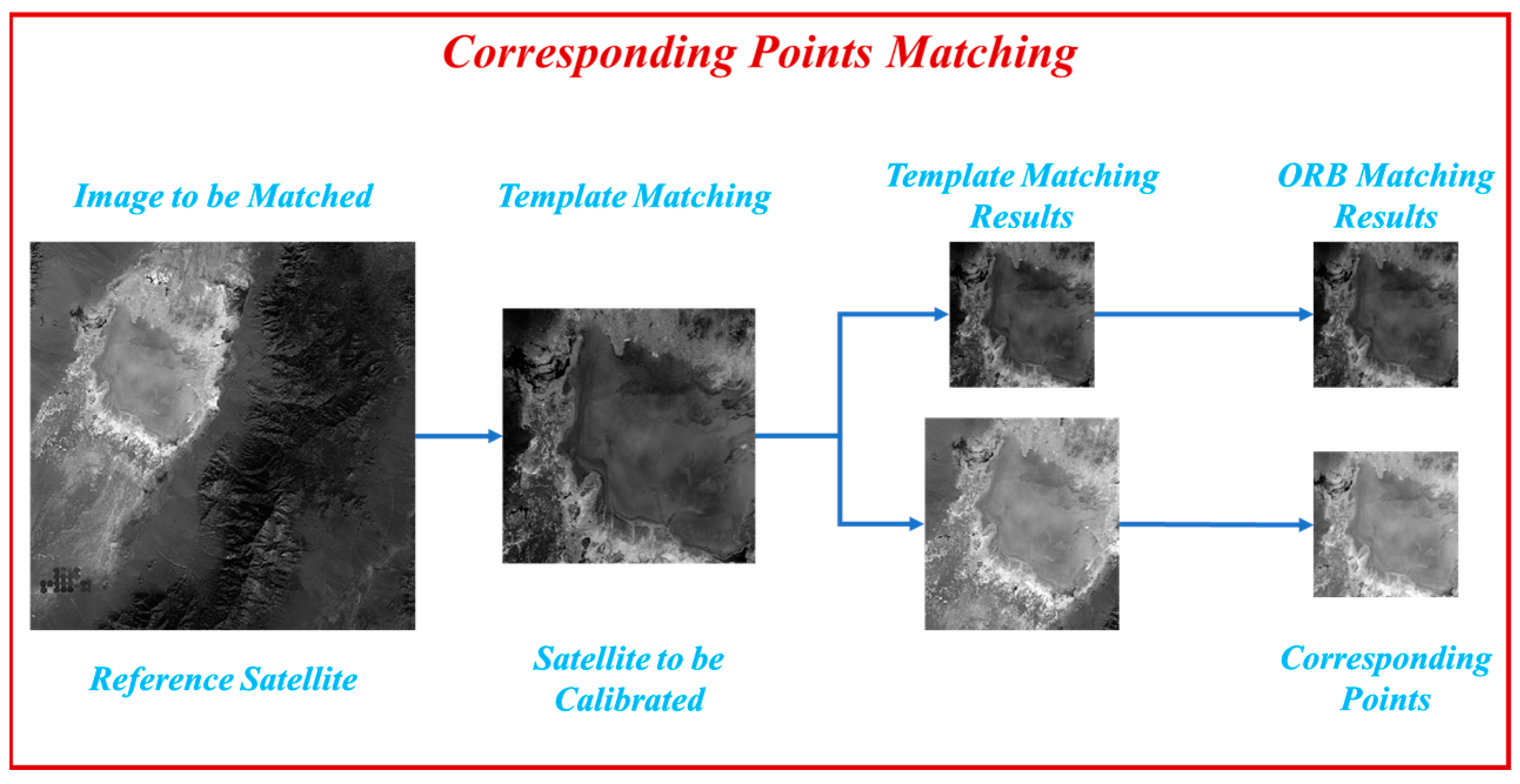
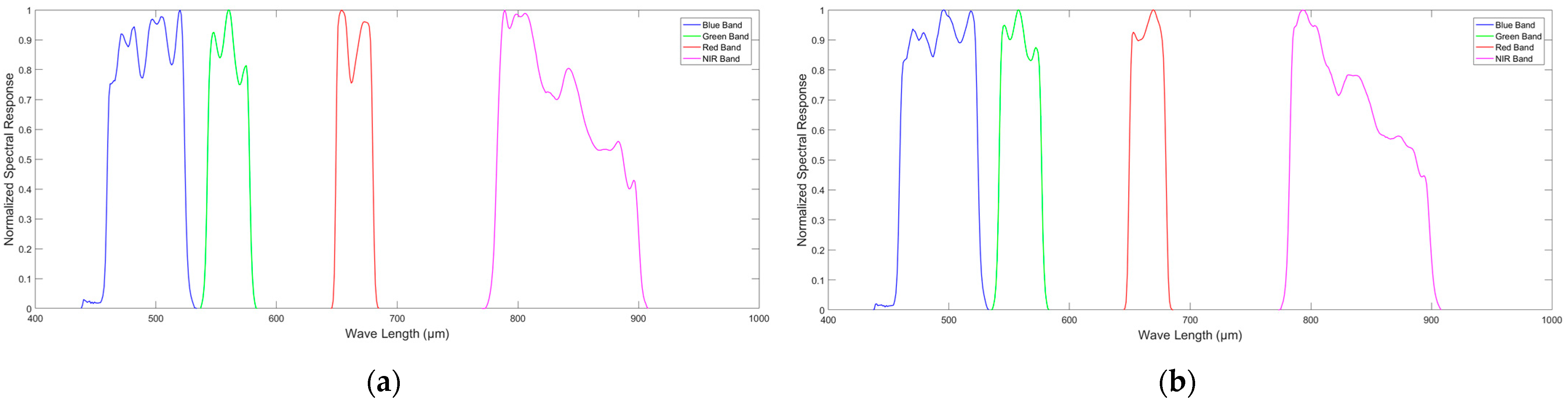






| Integration Level | Gain | Row Transfer Time (μs) | Total Number |
|---|---|---|---|
| 4 | 2 | 560.13 | 25 |
| 16 | 2 | 487.94 | 15 |
| 16 | 2 | 519.94 | 15 |
| 16 | 2 | 560.13 | 40 |
| 16 | 2 | 600.06 | 15 |
| 16 | 2 | 640.00 | 15 |
| 16 | 2 | 560.13 | 25 |
| 16 | 2 | 560.13 | 25 |
| 16 | 3 | 560.13 | 25 |
| 16 | 4 | 560.13 | 25 |
| 32 | 5 | 560.13 | 25 |
| 48 | 2 | 560.13 | 25 |
| 64 | 2 | 560.13 | 25 |
| Band | Resolution (m) | Width (km) | Center Wavelength (nm) | Band Width (nm) |
|---|---|---|---|---|
| Blue | 10 | 290 | 490 | 65 |
| Green | 560 | 35 | ||
| Red | 665 | 30 | ||
| NIR | 842 | 115 |
| Band | Resolution (m) | Width (km) | Spectral Band (nm) |
|---|---|---|---|
| Blue | 3 | More than 17 | 430–520 |
| Green | 520–640 | ||
| Red | 610–690 | ||
| NIR | 770–895 |
| Target Satellite | Imaging Time | Reference Satellite | Imaging Time | Integration Level | Gain | Row Transfer Time (μs) | Calibration Field | Sample Index |
|---|---|---|---|---|---|---|---|---|
| JL1GF03D11 | 2023-11-12 02:29:05 | Sentinel-2A | 2023-11-12 02:26:09 | 16-12-8-8 | 2-2-3-3 | 407.23 | Railroad Valley | Calibration |
| 2023-11-17 02:34:53 | Sentinel-2B | 2023-11-17 02:26:31 | 16-12-8-8 | 2-2-3-3 | 404.74 | Railroad Valley | Test 1 | |
| 2023-11-19 11:27:27 | Sentinel-2A | 2023-11-19 11:30:31 | 16-12-8-24 | 3-3-4-2 | 411.07 | Baotou Field | Test 2 | |
| 2023-11-24 11:32:31 | Sentinel-2B | 2023-11-24 11:30:40 | 16-12-8-24 | 3-3-4-2 | 397.82 | Baotou Field | Test 3 | |
| 2023-11-29 11:36:45 | Sentinel-2A | 2023-11-29 11:31:01 | 32-12-8-24 | 2-3-4-2 | 399.36 | Baotou Field | Test 4 |
| Band | Methods | (%) | RMSE |
|---|---|---|---|
| Blue | Laboratory radiometric calibration | 16.88 | 7.44 |
| Proposed method | 2.60 | 1.44 | |
| Green | Laboratory radiometric calibration | 10.28 | 4.42 |
| Proposed method | 4.33 | 2.15 | |
| Red | Laboratory radiometric calibration | 12.62 | 5.86 |
| Proposed method | 2.54 | 1.51 | |
| NIR | Laboratory radiometric calibration | 15.78 | 6.77 |
| Proposed method | 1.68 | 0.96 |
| Target Satellite | Imaging Time | Reference Satellite | Imaging Time | Integration Level | Gain | Row Transfer Time (μs) | Calibration Field |
|---|---|---|---|---|---|---|---|
| JL1GF03D01 | 2023-11-24 11:30:49 | Sentinel-2B | 2023-11-24 10:48:00 | 32-12-8-24 | 2-3-4-2 | 405.50 | Baotou |
| 2023-11-12 11:40:01 | Sentinel-2A | 2023-11-12 10:51:00 | 16-12-8-24 | 3-3-4-2 | 411.26 | Baotou | |
| JL1GF03D10 | 2023-12-07 11:41:29 | Sentinel-2B | 2023-12-07 11:35:00 | 16-12-8-8 | 3-2-3-3 | 388.42 | Baotou |
| 2023-12-02 11:41:11 | Sentinel-2A | 2023-12-02 11:32:00 | 32-12-8-24 | 2-3-4-2 | 389.57 | Baotou | |
| JL1GF03D11 | 2023-11-17 02:26:31 | Sentinel-2A | 2023-11-17 02:35:00 | 16-12-8-8 | 2-2-3-3 | 404.74 | Railroad Valley |
| 2023-11-24 11:30:49 | Sentinel-2B | 2023-11-24 11:32:00 | 16-12-8-24 | 3-3-4-2 | 397.82 | Baotou | |
| JL1GF03D13 | 2023-11-22 02:26:49 | Sentinel-2B | 2023-11-22 02:27:00 | 16-12-8-8 | 3-2-3-3 | 402.62 | Railroad Valley |
| 2023-11-27 02:27:11 | Sentinel-2A | 2023-11-27 02:32:00 | 16-12-8-8 | 3-2-3-3 | 393.41 | Railroad Valley | |
| JL1GF03D14 | 2023-11-09 11:29:41 | Sentinel-2A | 2023-11-09 11:30:00 | 16-12-8-8 | 3-3-3-3 | 405.89 | Baotou |
| 2023-11-14 11:30:09 | Sentinel-2B | 2023-11-14 11:37:00 | 16-12-8-8 | 3-3-4-3 | 409.54 | Baotou | |
| JL1GF03D16 | 2023-11-14 11:30:09 | Sentinel-2B | 2023-11-14 11:27:00 | 16-12-8-24 | 3-3-4-2 | 417.98 | Baotou |
| 2023-11-24 11:30:49 | Sentinel-2B | 2023-11-24 11:38:00 | 16-12-8-24 | 3-3-4-2 | 415.68 | Baotou | |
| JL1GF03D27 | 2023-11-17 11:40:29 | Sentinel-2B | 2023-11-17 11:32:00 | 16-12-8-24 | 3-3-4-2 | 403.78 | Baotou |
| 2023-12-04 11:31:19 | Sentinel-2B | 2023-12-04 11:36:00 | 16-12-8-24 | 3-3-4-2 | 405.50 | Baotou | |
| JL1GF03D30 | 2023-11-12 02:26:09 | Sentinel-2A | 2023-11-12 02:31:00 | 16-12-8-8 | 2-2-2-3 | 414.91 | Railroad Valley |
| 2023-09-13 11:35:41 | Sentinel-2A | 2023-09-13 11:28:00 | 16-12-8-8 | 2-2-3-3 | 399.55 | Baotou | |
| JL1GF03D34 | 2023-11-24 11:30:49 | Sentinel-2B | 2023-11-24 11:15:00 | 16-12-8-24 | 3-3-4-2 | 383.42 | Baotou |
| 2023-12-09 11:31:31 | Sentinel-2A | 2023-12-09 11:14:03 | 32-12-8-24 | 2-3-4-2 | 391.10 | Baotou | |
| JL1GF03D43 | 2023-11-29 11:31:41 | Sentinel-2A | 2023-11-29 13:09:00 | 16-12-8-8 | 2-2-3-3 | 406.27 | Baotou |
| 2023-11-15 02:36:29 | Sentinel-2B | 2023-11-15 03:10:00 | 16-12-8-24 | 3-3-4-2 | 405.89 | Railroad Valley |
| Satellite | Blue | Green | Red | NIR | Mean |
|---|---|---|---|---|---|
| JL1GF03D01 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 |
| JL1GF03D10 | 0.99 | 0.98 | 0.99 | 0.98 | 0.99 |
| JL1GF03D11 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 |
| JL1GF03D13 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 |
| JL1GF03D14 | 0.99 | 0.99 | 0.99 | 0.98 | 0.99 |
| JL1GF03D16 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 |
| JL1GF03D27 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 |
| JL1GF03D30 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 |
| JL1GF03D34 | 0.97 | 0.96 | 0.96 | 0.97 | 0.97 |
| JL1GF03D43 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 |
| Band | Methods | (%) | RMSE |
|---|---|---|---|
| Blue | Laboratory radiometric calibration | 9.61 | 8.12 |
| Proposed method | 4.86 | 1.72 | |
| Green | Laboratory radiometric calibration | 4.82 | 6.13 |
| Proposed method | 1.85 | 1.71 | |
| Red | Laboratory radiometric calibration | 8.71 | 7.32 |
| Proposed method | 1.98 | 1.64 | |
| NIR | Laboratory radiometric calibration | 12.53 | 6.46 |
| Proposed method | 1.15 | 1.60 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, L.; Jiang, Z.; Yu, S.; Liu, Y.; Wang, D.; Chen, M. A General On-Orbit Absolute Radiometric Calibration Method Compatible with Multiple Imaging Conditions. Remote Sens. 2024, 16, 3503. https://doi.org/10.3390/rs16183503
Fan L, Jiang Z, Yu S, Liu Y, Wang D, Chen M. A General On-Orbit Absolute Radiometric Calibration Method Compatible with Multiple Imaging Conditions. Remote Sensing. 2024; 16(18):3503. https://doi.org/10.3390/rs16183503
Chicago/Turabian StyleFan, Liming, Zhongjin Jiang, Shuhai Yu, Yunhe Liu, Dong Wang, and Maosheng Chen. 2024. "A General On-Orbit Absolute Radiometric Calibration Method Compatible with Multiple Imaging Conditions" Remote Sensing 16, no. 18: 3503. https://doi.org/10.3390/rs16183503
APA StyleFan, L., Jiang, Z., Yu, S., Liu, Y., Wang, D., & Chen, M. (2024). A General On-Orbit Absolute Radiometric Calibration Method Compatible with Multiple Imaging Conditions. Remote Sensing, 16(18), 3503. https://doi.org/10.3390/rs16183503






