Estimating Chlorophyll-a and Phycocyanin Concentrations in Inland Temperate Lakes across New York State Using Sentinel-2 Images: Application of Google Earth Engine for Efficient Satellite Image Processing
Abstract
1. Introduction
- Evaluate the suitability of linear regression to relate Chl-a and phycocyanin concentration to Sentinel-2 data;
- Evaluate different remote sensing-based indices to refine model fit;
- Consider the influence of temporal separation of in situ and remote sensing data on model accuracy;
- Assess the utility of model application for estimating Chl-a and phycocyanin concentration;
- Consider the influence of cloud mitigation approaches on model performance.
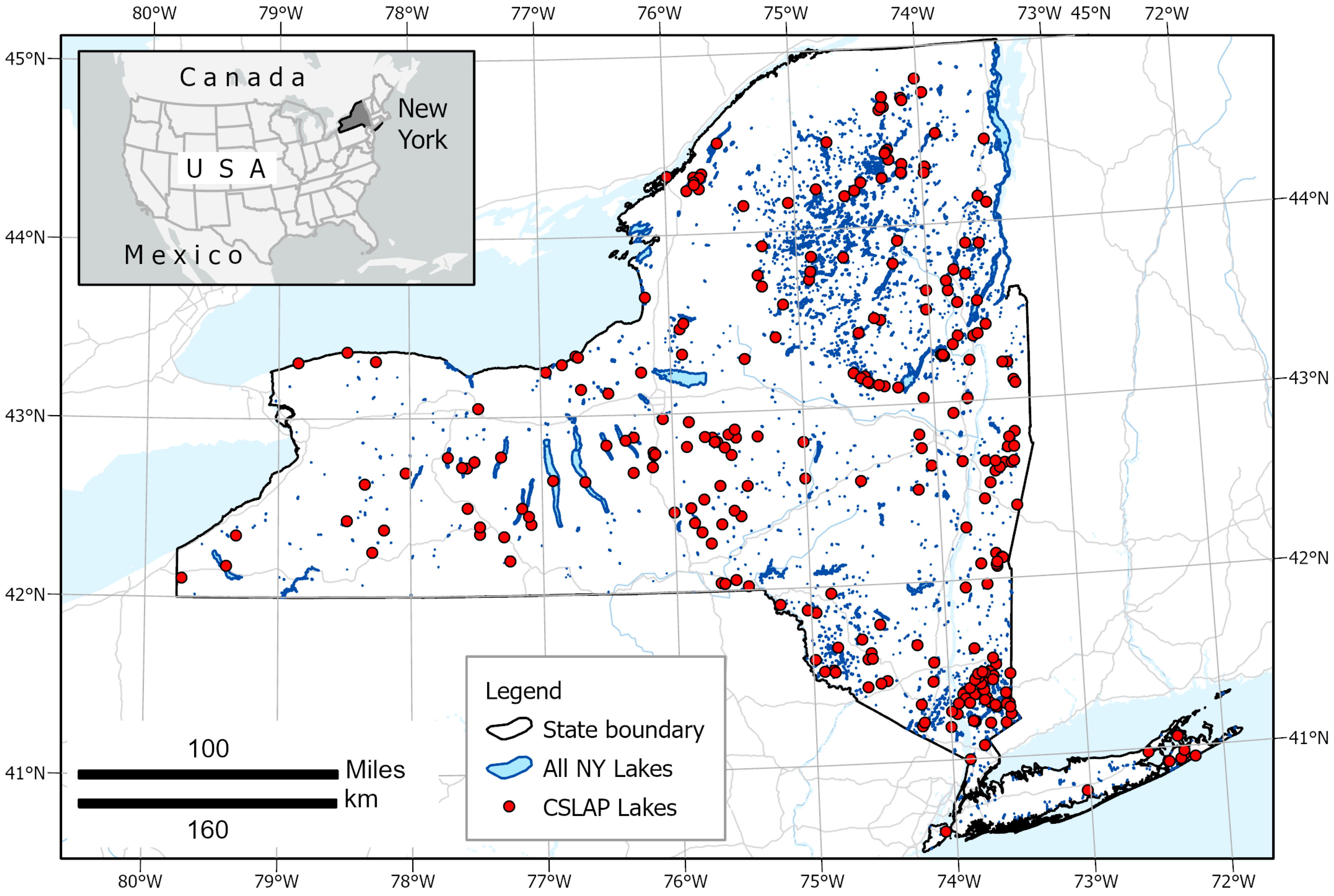
2. Study Site and Datasets
2.1. In Situ Water Data
2.2. Remote Sensing Data
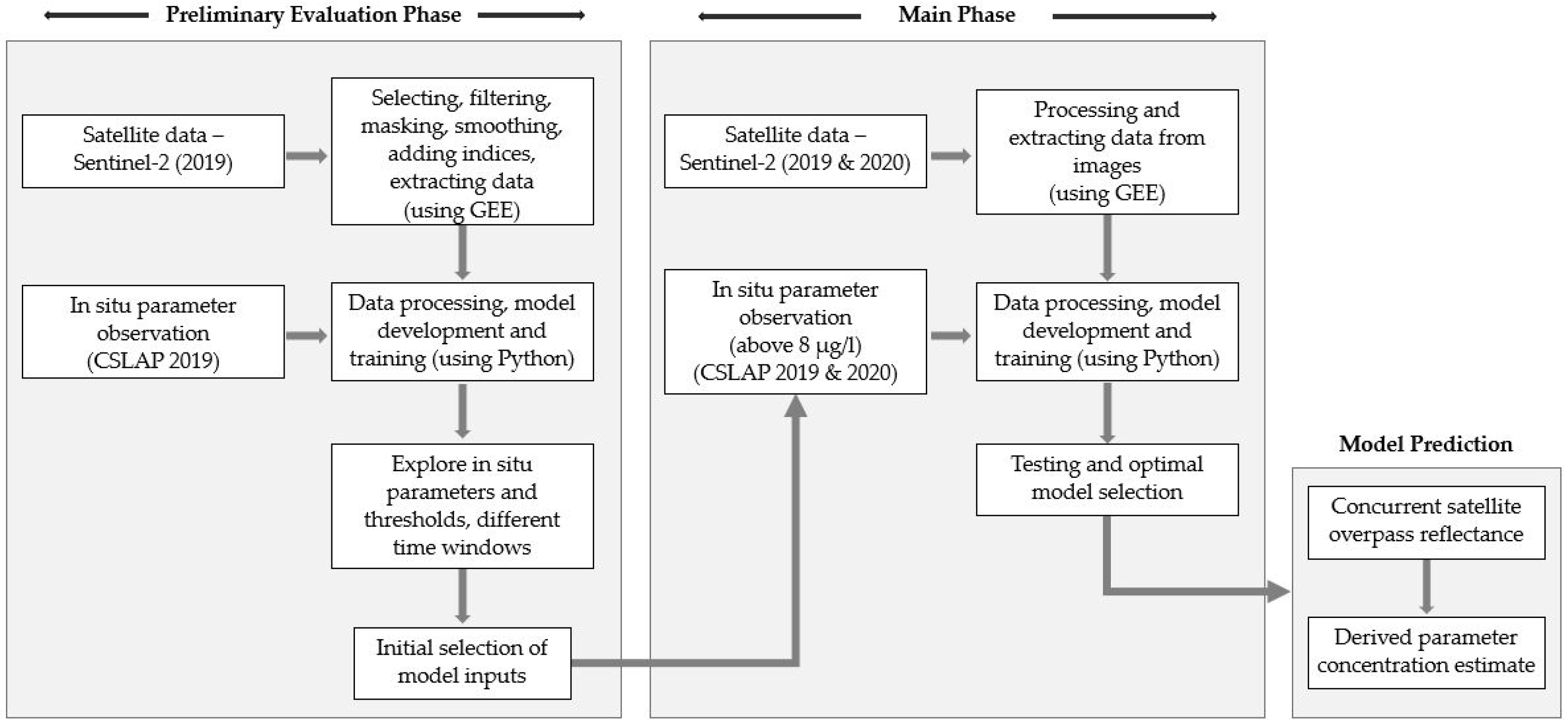
3. Materials and Methods
3.1. Sentinel-2 Data Extraction
3.2. Model Development
4. Results
4.1. Preliminary Phase
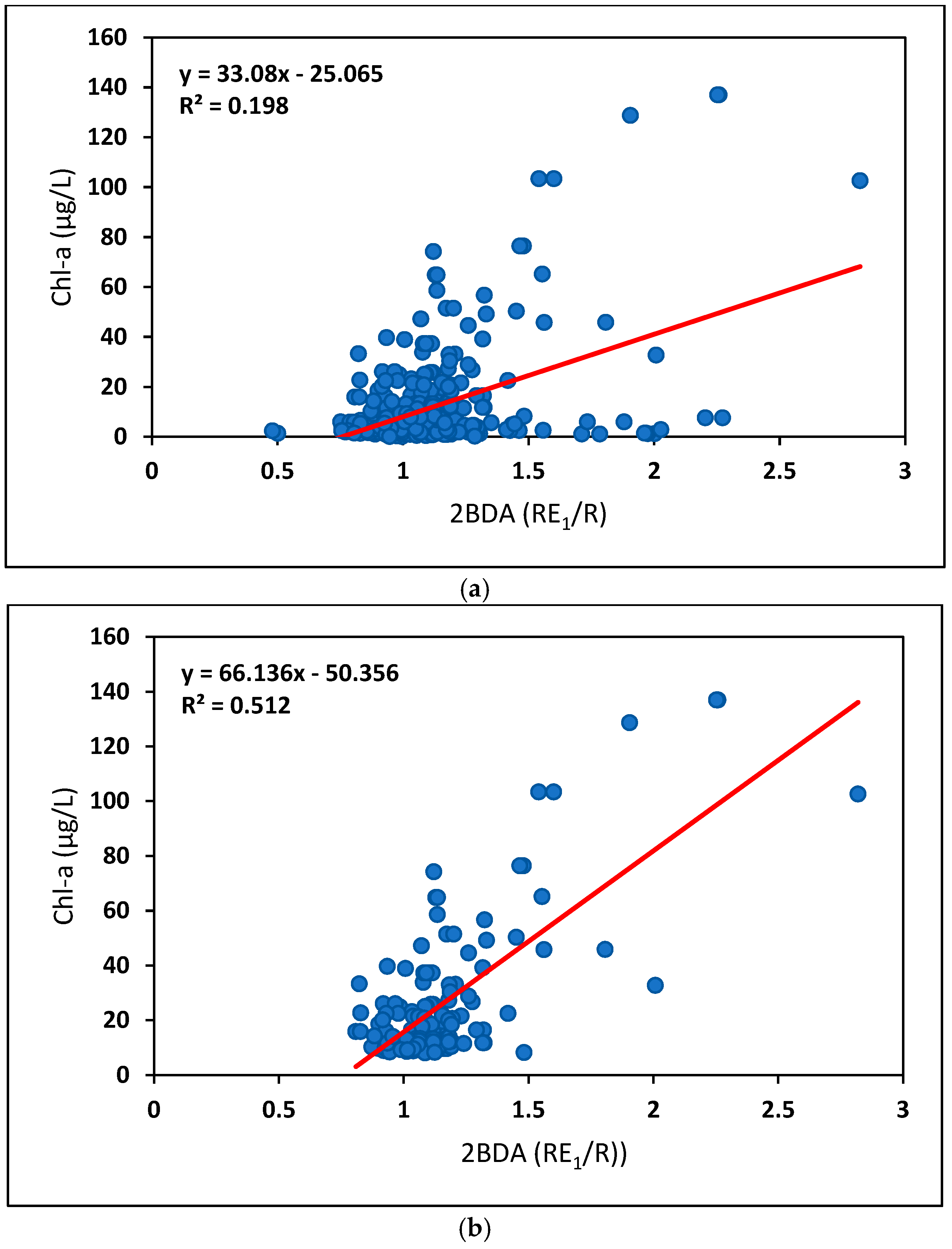
4.1.1. Comparison of In Situ Parameter Thresholds
4.1.2. Comparing Different Types of In Situ Measurements
4.1.3. Lake Characteristics
4.2. Main Phase
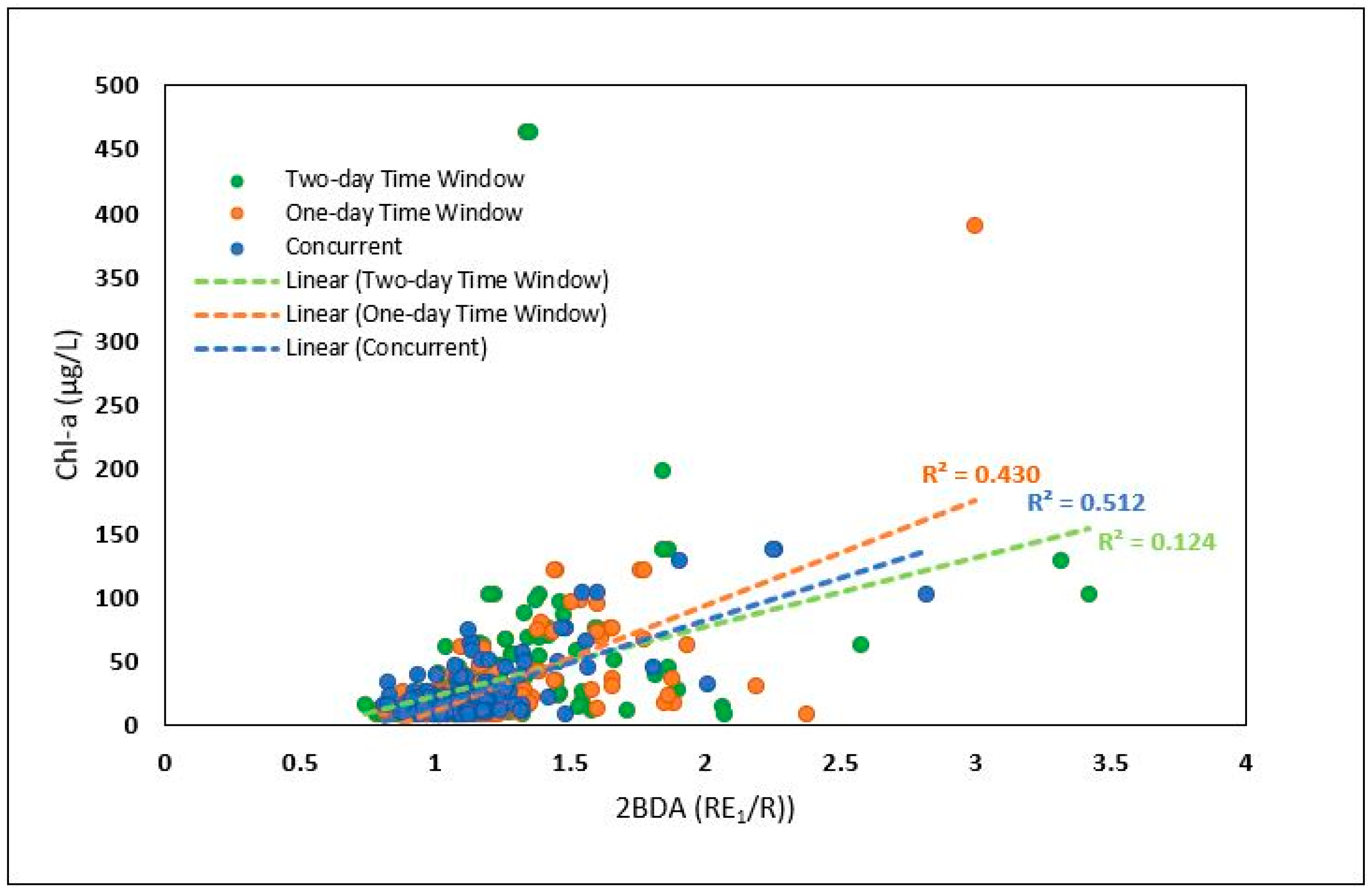
4.2.1. Comparison of Different Sentinel-2 Indices: Model Fit
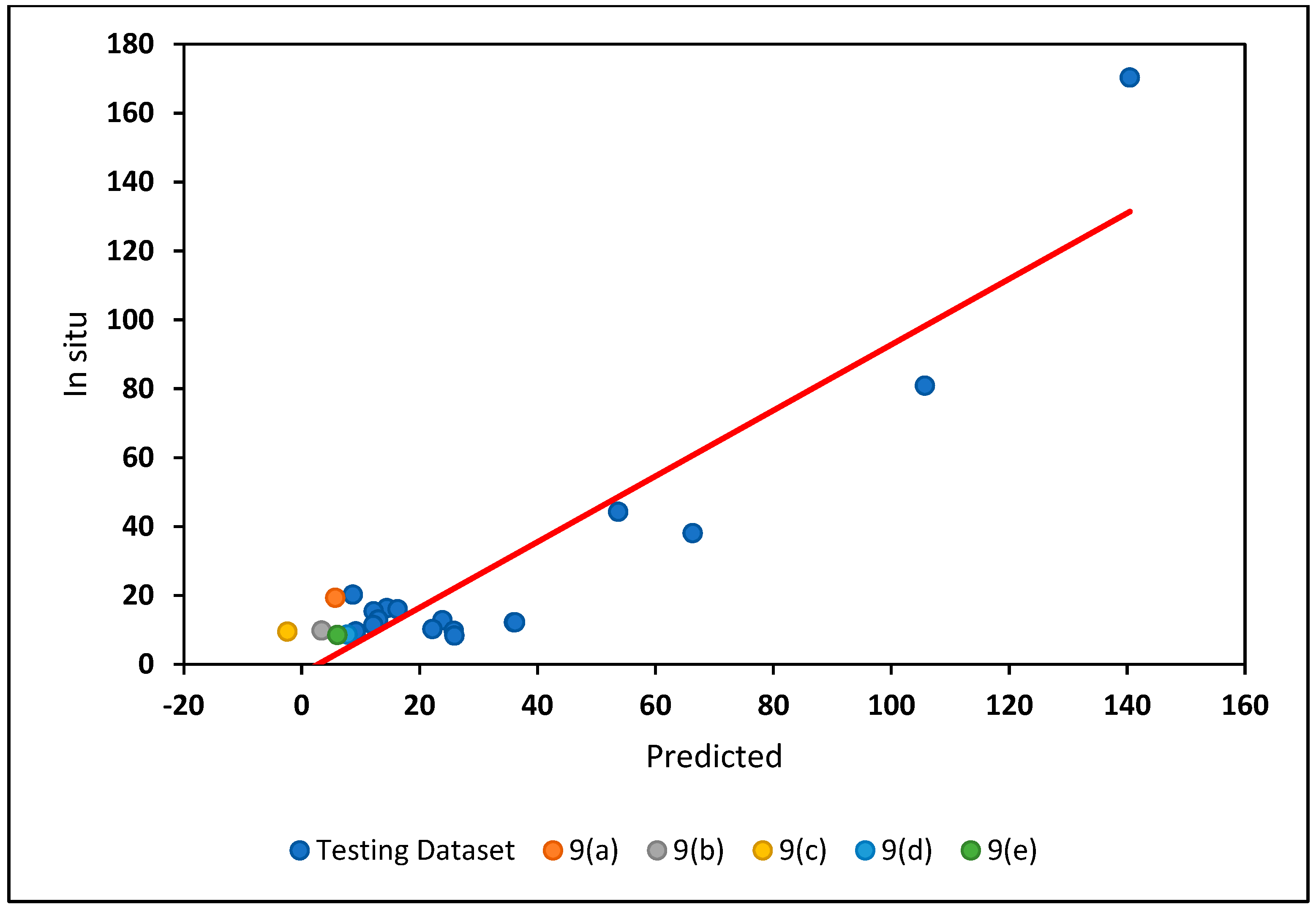
4.2.2. Assessment of Model Prediction Accuracy
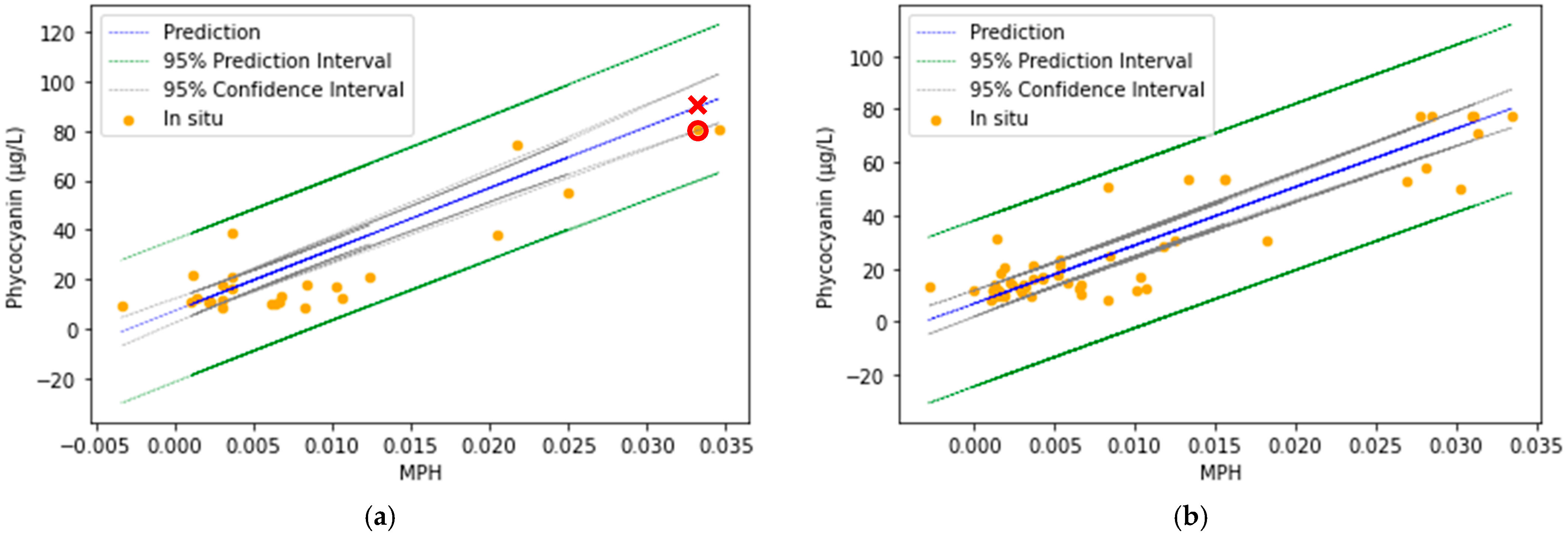
4.2.3. Confidence Interval for Test and Predicted Values of Phycocyanin
4.3. Alternate Cloud Mask Evaluation
4.3.1. Testing Cloud Score+ Thresholds
4.3.2. Applying Cloud Score+ to 2019 and 2020 Data
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ho, J.C.; Michalak, A.M.; Pahlevan, N. Widespread global increase in intense lake phytoplankton blooms since the 1980s. Nature 2019, 574, 667–670. [Google Scholar] [CrossRef]
- Otten, T.G.; Paerl, H.W. Health effects of toxic cyanobacteria in U.S. drinking and recreational waters: Our current understanding and proposed direction. Curr. Environ. Health Rep. 2015, 2, 75–84. [Google Scholar] [CrossRef] [PubMed]
- Michalak, A.M.; Anderson, E.J.; Beletsky, D.; Boland, S.; Bosch, N.S.; Bridgeman, T.B.; Chaffin, J.D.; Cho, K.; Confesor, R.; Daloğlu, I.; et al. Record-setting algal bloom in Lake Erie caused by agricultural and meteorological trends consistent with expected future conditions. Proc. Natl. Acad. Sci. USA 2013, 110, 6448–6452. [Google Scholar] [CrossRef] [PubMed]
- Gorney, R.M.; June, S.G.; Stainbrook, K.M.; Smith, A.J. Detections of cyanobacteria harmful algal blooms (cyanoHABs) in New York State, United States (2012–2020). Lake Reserv. Manag. 2023, 39, 21–36. [Google Scholar] [CrossRef]
- Moses, W.J.; Gitelson, A.A.; Berdnikov, S.; Povazhny, V. Estimation of chlorophyll-a concentration in case II waters using MODIS and MERIS data—Successes and challenges. Environ. Res. Lett. 2009, 4, 045005. [Google Scholar] [CrossRef]
- Zhang, Y.; Ma, R.; Duan, H.; Loiselle, S.; Xu, J. A spectral decomposition algorithm for estimating chlorophyll-a concentrations in Lake Taihu, China. Remote Sens. 2014, 6, 5090–5106. [Google Scholar] [CrossRef]
- Kutser, T.; Paavel, B.; Verpoorter, C.; Ligi, M.; Soomets, T.; Toming, K.; Casal, G. Remote sensing of black lakes and using 810 nm reflectance peak for retrieving water quality parameters of optically complex waters. Remote Sens. 2016, 8, 497. [Google Scholar] [CrossRef]
- Xu, M.; Liu, H.; Beck, R.; Lekki, J.; Yang, B.; Shu, S.; Liu, Y.; Benko, T.; Anderson, R.; Tokars, R.; et al. Regionally and locally adaptive models for retrieving chlorophyll-a concentration in inland waters from remotely sensed multispectral and hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2019, 57, 4758–4774. [Google Scholar] [CrossRef]
- Ansper, A.; Alikas, K. Retrieval of chlorophyll a from Sentinel-2 MSI data for the European Union Water framework directive reporting purposes. Remote Sens. 2019, 11, 64. [Google Scholar] [CrossRef]
- Yentsch, C.S. The influence of phytoplankton pigments on the colour of seawater. Deep Sea Res. 1960, 7, 1–9. [Google Scholar] [CrossRef]
- Clark, G.L.; Ewing, G.C.; Lorenzen, C.J. Spectra of backscattered light from the sea obtained from aircraft as a measure of chlorophyll concentration. Science 1970, 167, 1119–1121. [Google Scholar] [CrossRef] [PubMed]
- Hovis, W.A. The Nimbus-7 Coastal Zone Color Scanner (CZCS) Program. In Oceanography from Space; Gower, J.F.R., Ed.; Springer: Boston, MA, USA, 1981; Volume 13. [Google Scholar] [CrossRef]
- Clark, D.W. Phytoplankton pigment algorithms for the Nimbus-7 CZCS. In Oceanography from Space; Gower, J.F.R., Ed.; Plenum: New York, NY, USA, 1981; pp. 227–237In. [Google Scholar] [CrossRef]
- O’Reilly, J.E.; Maritorena, S.; Mitchell, G.; Siegel, D.A.; Carder, K.L.; Garver, S.A.; Kahru, M.; McClain, C. Ocean color chlorophyll algorithms for SeaWiFS. J. Geophys. Res. 1998, 103, 24937–24953. [Google Scholar] [CrossRef]
- Esaias, W.E.; Abbot, M.R.; Barton, I.J.; Brown, O.B.; Campbell, J.W.; Carder, K.L.; Clark, D.K.; Evans, R.H.; Hoge, F.E.; Gordon, H.R.; et al. An overview of MODIS capabilities for ocean science observations. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1250–1265. [Google Scholar] [CrossRef]
- Gons, H.J.; Rijkeboer, M.; Ruddick, K.G. A chlorophyll-retrieval algorithm for satellite imagery (Medium Resolution Imaging Spectrometer) of inland and coastal waters. J. Plankton Res. 2002, 24, 947–951. [Google Scholar] [CrossRef]
- New York State Department of Environmental Conservation. Priority Waterbody List—Lakes 2024, Shapefile. Available online: https://data.gis.ny.gov/datasets/nysdec::priority-waterbody-list-lakes/explore (accessed on 1 August 2024).
- European Space Agency (ESA). Sentinel-2, The Operational Copernicus Optical High Resolution Land Mission; European Space Agency: Paris, France, 2013; Available online: http://esamultimedia.esa.int/docs/S2-Data_Sheet.pdf (accessed on 30 September 2019).
- Batur, E.; Maktav, D. Assessment of surface water quality by using satellite images fusion based on PCA method in the Lake Gala, Turkey. IEEE Trans. Geosci. Remote Sens. 2019, 57, 2983–2989. [Google Scholar] [CrossRef]
- Bresciani, M.; Cazzaniga, I.; Austoni, M.; Sforzi, T.; Buzzi, F.; Morabito, G.; Giardino, C. Mapping phytoplankton blooms in deep subalpine lakes from Sentinel-2A and Landsat-8. Hydrobiologia 2018, 824, 197–214. [Google Scholar] [CrossRef]
- Soomets, T.; Uudeberg, K.; Jakovels, D.; Brauns, A.; Zagars, M.; Kutser, T. Validation and comparison of water quality products in Baltic Lakes using Sentinel-2 MSI and Sentinel-3 OLCI data. Sensors 2020, 20, 742. [Google Scholar] [CrossRef]
- Ha, N.T.T.; Thao, N.T.P.K.; Katsuaki, N.; Mai, T.N. Selecting the Best Band Ratio to Estimate Chlorophyll-a Concentration in a Tropical Freshwater Lake Using Sentinel-2A Images from a Case Study of Lake Ba Be (Northern Vietnam). ISPRS Int. J. Geo-Inf. 2017, 6, 2220–9964. [Google Scholar] [CrossRef]
- Beck, R.; Xu, M.; Zhan, S.; Johansen, R.; Liu, H.; Tong, S.; Yang, B.; Shu, S.; Wu, Q.; Wang, S.; et al. Comparison of satellite reflectance algorithms for estimating turbidity and cyanobacterial concentrations in productive freshwaters using hyperspectral aircraft imagery and dense coincident surface observations. J. Great Lakes Res. 2019, 45, 413–433. [Google Scholar] [CrossRef]
- Chen, J.; Zhu, W.; Tian, Y.Q.; Yu, Q.; Zheng, Y.; Huang, L. Remote estimation of colored dissolved organic matter and chlorophyll-a in Lake Huron using Sentinel-2 measurements. J. Appl. Remote Sens. 2017, 11, 036007. [Google Scholar] [CrossRef]
- Ogashawara, I.; Kiel, C.; Jechow, A.; Kohnert, K.; Ruhtz, T.; Grossart, H.-P.; Hölker, F.; Nejstgaard, J.C.; Berger, S.A.; Wollrab, S. The use of Sentinel-2 for chlorophyll-a spatial dynamics assessment: A comparative study on different lakes in Northern Germany. Remote Sens. 2021, 13, 1542. [Google Scholar] [CrossRef]
- Mandanici, E.; Bitelli, G. Preliminary comparison of Sentinel-2 and Landsat 8 imagery for a combined use. Remote Sens. 2016, 8, 1014. [Google Scholar] [CrossRef]
- Bresciani, M.; Pinardi, M.; Free, G.; Luciani, G.; Ghebrehiwot, S.; Laanen, M.; Peters, S.; Della Bella, V.; Padula, R.; Giardino, C. The use of multisource optical sensors to study phytoplankton spatio-temporal variation in a shallow turbid lake. Water 2020, 12, 284. [Google Scholar] [CrossRef]
- Wang, M.; Yao, Y.; Shen, Q.; Gao, H.; Li, J.; Zhang, F.; Wu, Q. Time-series analysis of surface-water quality in Xiong’an new area, 2016–2019. J. Indian Soc. Remote Sens. 2021, 49, 857–872. [Google Scholar] [CrossRef]
- Cazzaniga, I.; Bresciani, M.; Colombo, R.; Della Bella, V.; Padula, R.; Giardino, C. A comparison of Sentinel-3-OLCI and Sentinel-2-MSI-derived Chlorophyll-a maps for two large Italian lakes. Remote Sens. Lett. 2019, 10, 978–987. [Google Scholar] [CrossRef]
- Giardino, C.; Candiani, G.; Bresciani, M.; Lee, Z.; Gagliano, S.; Pepe, M. BOMBER: A tool for estimating water quality and bottom properties from remote sensing images. Comput. Geosci. 2012, 45, 313–318. [Google Scholar] [CrossRef]
- Niroumand-Jadidi, M.; Bovolo, F.; Bruzzone, L. Water quality retrieval from PRISMA hyperspectral images: First experience in a turbid lake and comparison with Sentinel-2. Remote Sens. 2020, 12, 3984. [Google Scholar] [CrossRef]
- Pereira-Sandoval, M.; Ruescas, A.; Urrego, P.; Ruiz-Verdú, A.; Delegido, J.; Tenjo, C.; Soria-Perpinyà, X.; Vicente, E.; Soria, J.; Moreno, J. Evaluation of atmospheric correction algorithms over Spanish inland waters for Sentinel-2 multi spectral imagery data. Remote Sens. 2019, 11, 1469. [Google Scholar] [CrossRef]
- International Ocean-Colour Coordinating Group (IOCCG). Remote Sensing of Ocean Colour in Coastal, and Other Optically Complex, Waters; Sathyendranath, S., Ed.; Reports of the International Ocean-Colour Coordinating Group, No. 3; IOCCG: Dartmouth, MA, Canada, 2000. [Google Scholar] [CrossRef]
- Matthews, M.W. A current review of empirical procedures of remote sensing in Inland and near-coastal transitional waters. Int. J. Remote Sens. 2011, 32, 6855–6899. [Google Scholar] [CrossRef]
- Morel, A.; Prieur, L. Analysis of variations in ocean color. Limnol. Oceanogr. 1977, 22, 709–722. [Google Scholar] [CrossRef]
- Fell, F.; Fischer, E.; Schaale, M.; Schroder, T. Retrieval of chlorophyll concentration from MERIS measurements in the spectral range of the sun-induced chlorophyll fluorescence. Proc. SPIE 2003, 4892, 116–123. [Google Scholar] [CrossRef]
- Matthews, M.W.; Bernard, S.; Winter, K. Remote sensing of cyanobacteria-dominant algal blooms and water quality parameters in Zeekoevlei, a small hypertrophic lake, using MERIS. Remote Sens. Environ. 2010, 114, 2070–2087. [Google Scholar] [CrossRef]
- Lins, R.C.; Martinez, J.M.; Marques, D.D.; Cirilo, J.A.; Fragoso, C.R. Assessment of chlorophyll-a remote sensing algorithms in a productive tropical estuarine-lagoon system. Remote Sens. 2017, 9, 516. [Google Scholar] [CrossRef]
- Gitelson, A.A. The peak near 700 nm on radiance spectra of algae and water: Relationships of its magnitude and position with chlorophyll. Int. J. Remote Sens. 1992, 13, 3367–3373. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Gritz, Y.; Merzlyak, M.N. Relationships between leaf chlorophyll content and spectral reflectance and algorithms for non-destructive chlorophyll assessment in higher plant leaves. J. Plant Physiol. 2003, 160, 271–282. [Google Scholar] [CrossRef]
- Le, C.; Li, Y.; Zha, Y.; Sun, D.; Huang, C.; Lu, H. A four-band semi-analytical model for estimating chlorophyll-a in highly turbid lakes: The case of Taihu Lake, China. Remote Sens. Environ. 2009, 113, 1175–1182. [Google Scholar] [CrossRef]
- Dekker, A.G. Detection of the Optical Water Quality Parameters for Eutrophic Waters by High Resolution Remote Sensing. Ph.D. Thesis, Free University, Amsterdam, The Netherlands, 1993. Available online: https://research.vu.nl/ws/portalfiles/portal/62846616/complete+dissertation.pdf (accessed on 23 August 2024).
- Schalles, J.F.; Yacobi, Y.Z. Remote detection and seasonal patterns of phycocyanin, carotenoid and chlorophyll pigments in eutrophic waters. Ergeb. Limnol. 2000, 55, 153–168. [Google Scholar]
- Simis, S.; Peters, S.; Gons, H. Remote sensing of the cyanobacterial pigment phycocyanin in turbid inland water. Limnol. Oceanogr. 2005, 50, 237–245. [Google Scholar] [CrossRef]
- Mishra, S.; Mishra, D.R.; Schluchter, W.M. A novel algorithm for predicting phycocyanin concentrations in cyanobacteria: A proximal hyperspectral remote sensing approach. Remote Sens. 2009, 1, 758–775. [Google Scholar] [CrossRef]
- Mishra, S.; Mishra, D.R. A novel remote sensing algorithm to quantify phycocyanin in cyanobacterial algal blooms. Environ. Res. Lett. 2014, 9, 114003. [Google Scholar] [CrossRef]
- Yan, Y.; Zhongjue, B.; Jingan, S. Phycocyanin concentration retrieval in inland waters: A comparative review of the remote sensing techniques and algorithms. J. Great Lakes Res. 2018, 44, 748–755. [Google Scholar] [CrossRef]
- Woźniak, M.; Bradtke, K.M.; Darecki, M.; Krężel, A. Empirical Model for Phycocyanin Concentration Estimation as an Indicator of Cyanobacterial Bloom in the Optically Complex Coastal Waters of the Baltic Sea. Remote Sens. 2016, 8, 212. [Google Scholar] [CrossRef]
- Sòria-Perpinyà, X.; Vicente, E.; Urrego, P.; Pereira-Sandoval, M.; Tenjo, C.; Ruíz-Verdú, A.; Delegido, J.; Soria, J.M.; Peña, R.; Moreno, J. Validation of Water Quality Monitoring Algorithms for Sentinel-2 and Sentinel-3 in Mediterranean Inland Waters with In Situ Reflectance Data. Water 2021, 13, 686. [Google Scholar] [CrossRef]
- Li, S.; Song, K.; Wang, S.; Liu, G.; Wen, Z.; Shang, Y.; Lyu, L.; Chen, F.; Xu, S.; Tao, H.; et al. Quantification of chlorophyll-a in typical lakes across China using Sentinel-2 MSI imagery with machine learning algorithm. Sci. Total Environ. 2021, 778, 146271. [Google Scholar] [CrossRef] [PubMed]
- Aptoula, E.; Ariman, S. Chlorophyll-a Retrieval from Sentinel-2 Images using convolutional neural network regression. IEEE Geosci. Remote Sens. Lett. 2021, 19, 6002605. [Google Scholar] [CrossRef]
- Yildiz, B.; Bilbao, J.I.; Sproul, A.B. A review and analysis of regression and machine learning models on commercial building electricity load forecasting. Renew. Sustain. Energy Rev. 2017, 73, 1104–1122. [Google Scholar] [CrossRef]
- Gong, C.; Yin, R.; Long, T.; Jiao, W.; He, G.; Wang, G. Spatial–Temporal Approach and Dataset for Enhancing Cloud Detection in Sentinel-2 Imagery: A Case Study in China. Remote Sens. 2024, 16, 973. [Google Scholar] [CrossRef]
- Main-Knorn, M.; Pflug, B.; Louis, J.; Debaecker, V.; Müller-Wilm, U.; Gascon, F. Sen2Cor for Sentinel-2. In Image and Signal Processing for Remote Sensing XXIII; SPIE: Bellingham, DC, USA, 2017; Volume 10427, pp. 37–48. [Google Scholar] [CrossRef]
- Coluzzi, R.; Imbrenda, V.; Lanfredi, M.; Simoniello, T. A first assessment of the Sentinel-2 Level 1-C cloud mask product to support informed surface analyses. Remote Sens. Environ. 2018, 217, 426–443. [Google Scholar] [CrossRef]
- Qiu, S.; Zhu, Z.; He, B. Fmask 4.0: Improved cloud and cloud shadow detection in Landsats 4–8 and Sentinel-2 imagery. Remote Sens. Environ. 2019, 231, 111205. [Google Scholar] [CrossRef]
- Zhang, H.; Huang, Q.; Zhai, H.; Zhang, L. Multi-temporal cloud detection based on robust PCA for optical remote sensing imagery. Comput. Electron. Agric. 2021, 188, 106342. [Google Scholar] [CrossRef]
- Pasquarella, V.J.; Brown, C.F.; Czerwinski, W.; Rucklidge, W.J. Comprehensive quality assessment of optical satellite imagery using weakly supervised video learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 2124–2134. [Google Scholar]
- Prestigiacomo, A.R.; June, S.G.; Gorney, R.M.; Smith, A.J.; Clinkhammer, A.C. An evaluation of a spectral fluorometer for monitoring chlorophyll a in New York State Lakes. Lake Reserv. Manag. 2022, 38, 318–333. [Google Scholar] [CrossRef]
- Carlson, R.E. A trophic state index for lakes. Limnol. Oceanogr. 1977, 22, 361–369. [Google Scholar] [CrossRef]
- NYSDEC Standard Operating Procedure: Collection of Lake Water Quality Samples; Albany: New York, USA, 2021; p. 39. Available online: https://extapps.dec.ny.gov/docs/water_pdf/soplakesampling721.pdf (accessed on 1 August 2024).
- Heskes, T. Practical confidence and prediction intervals. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 1996; Volume 9. [Google Scholar]
- Zimba, P.V.; Gitelson, A. Remote estimation of chlorophyll concentration in hyper-eutrophic aquatic systems: Model tuning and accuracy optimization. Aquaculture 2006, 256, 272–286. [Google Scholar] [CrossRef]
- Mishra, S.; Mishra, D.R. Normalized difference chlorophyll index: A novel model for remote estimation of chlorophyll—A concentration in turbid productive waters. Remote Sens. Environ. 2012, 117, 394–406. [Google Scholar] [CrossRef]
- Wynne, T.T.; Stumpf, R.P.; Tomlinson, M.C.; Warner, R.A.; Tester, P.A.; Dyble, J.; Fahnenstiel, G.L. Relating spectral shape to cyanobacterial Blooms in the Laurentian Great Lakes. Int. J. Remote Sens. 2008, 29, 3665–3672. [Google Scholar] [CrossRef]
- Gower, J.; King, S.; Borstad, G.; Brown, L. Detection of intense plankton blooms using the 709 nm band of the MERIS imaging spectrometer. Int. J. Remote Sens. 2005, 26, 2005–2012. [Google Scholar] [CrossRef]
- Matthews, M.W.; Bernard, S.; Robertson, L. An algorithm for detecting trophic status (chlorophyll-a), cyanobacterial-dominance, surface scums and floating vegetation in inland and coastal waters. Remote Sens. Environ 2012, 124, 637–652. [Google Scholar] [CrossRef]
- Alawadi, F. Detection of Surface Algal Blooms Using the Newly Developed Algorithm Surface Algal Bloom Index (SABI); SPIE: Bellingham, DC, USA, 2010; Volume 7825, pp. 782506-1–782506-14. [Google Scholar] [CrossRef]
- Kayastha, P.; Dzialowski, A.R.; Stoodley, S.H.; Wagner, K.L.; Mansaray, A.S. Effect of Time Window on Satellite and Ground-Based Data for Estimating Chlorophyll-a in Reservoirs. Remote Sens. 2022, 14, 846. [Google Scholar] [CrossRef]
- Zhao, D.; Huang, J.; Li, Z.; Yu, G.; Shen, H. Dynamic monitoring and analysis of chlorophyll-a concentrations in global lakes using Sentinel-2 images in Google Earth Engine. Sci. Total Environ. 2024, 912, 169152. [Google Scholar] [CrossRef]
- Maciel, F.P.; Haakonsson, S.; Ponce de León, L.; Bonilla, S.; Pedocchi, F. Satellite monitoring of chlorophyll-a threshold levels during an exceptional cyanobacterial bloom (2018–2019) in the Río de la Plata. Ribagua 2023, 10, 62–78. [Google Scholar] [CrossRef]
- Maciel, F.P.; Haakonsson, S.; Ponce de León, L.; Bonilla, S.; Pedocchi, F. Challenges for chlorophyll-a remote sensing in a highly variable turbidity estuary, an implementation with sentinel-2. Geocarto Int. 2023, 38. [Google Scholar] [CrossRef]
- Grendaitė, D.; Petkevičius, L. Identification of Algal Blooms in Lakes in the Baltic States Using Sentinel-2 Data and Artificial Neural Networks. IEEE Access 2024, 12, 27973–27988. [Google Scholar] [CrossRef]
- Cook, M.; Chapman, T.; Hart, S.; Paudel, A.; Balch, J. Mapping quaking aspen (Populus tremuloides Michx.) using seasonal Sentinel-1 and Sentinel-2 composite imagery across the Southern Rockies, USA. Remote Sens. 2024, 16, 1619. [Google Scholar] [CrossRef]
- Odermatt, D.; Gitelson, A.; Brando, V.E.; Schaepman, M. Review of constituent retrieval in optically deep and complex waters from satellite imagery. Remote Sens. Environ. 2012, 118, 116–126. [Google Scholar] [CrossRef]
- Topp, S.N.; Pavelsky, T.M.; Jensen, D.; Simard, M.; Ross, M.R.V. Research trends in the use of remote sensing for inland water quality science: Moving towards multidisciplinary applications. Water 2020, 12, 169. [Google Scholar] [CrossRef]
- Xu, M.; Liu, H.; Beck, R.; Lekki, J.; Yang, B.; Liu, Y.; Shu, S.; Wang, S.; Tokars, R.; Anderson, R.; et al. Implementation strategy and spatiotemporal extensibility of multipredictor ensemble model for water quality parameter retrieval with multispectral remote sensing data. IEEE Trans. Geosci. Remote Sens. 2021, 60, 4200616. [Google Scholar] [CrossRef]
- Chorus, I.; Testai, E. Assessing Exposure and short-term interventions: Recreational and occupational activities. In Toxic Cyanobacteria in Water: A Guide to Their Public Health Consequences, Monitoring and Management, 2nd ed.; Chorus, I., Welker, M., Eds.; CRC Press: Boca Raton, FL, USA; World Health Organization: Geneva, Switzerland, 2021. [Google Scholar] [CrossRef]


| Index | Label | Equation 1 | Citation |
|---|---|---|---|
| Two-band Ratio | 2BDA | [38] | |
| Three-band Ratio | 3BDA | [63] | |
| Normalized difference chlorophyll index | NDCI | [64] | |
| Cyanobacteria index | CI | [65] | |
| Maximum chlorophyll index | MCI | [66] | |
| Maximum peak height | MPH | [67] | |
| Surface algal bloom index | SABI | [68] |
| Chl-a | Phycocyanin Index | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Time Window | Metric | 2BDA | 2BDA | 3BDA | NDCI | CI | MCI | MPH | SABI |
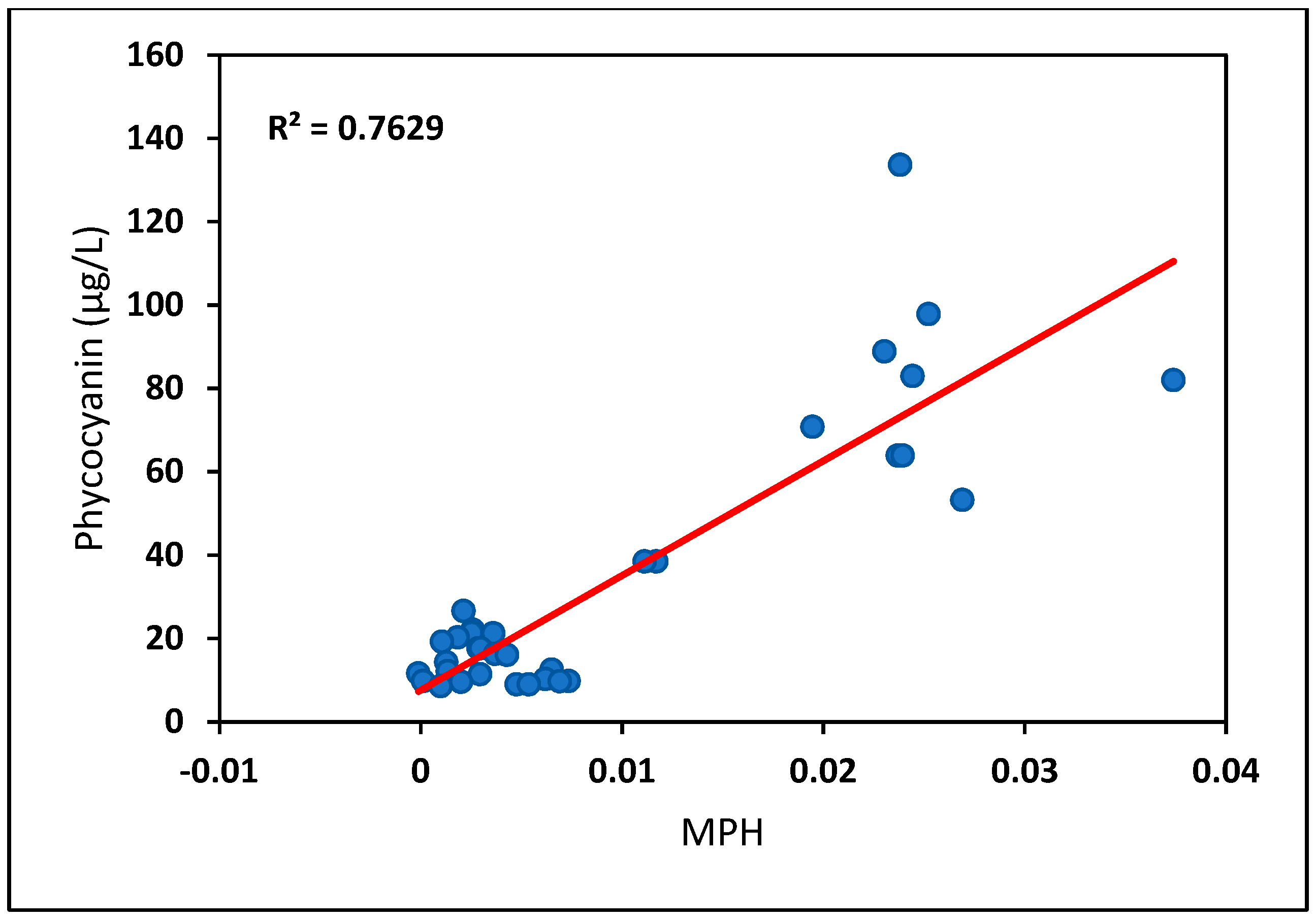
| Concurrent | R2 | 0.43 | 0.42 | 0.13 | 0.40 | 0.45 | 0.30 | 0.63 | 0.002 |
| RMSE | 21 | 32.4 | 39.8 | 32.9 | 31.6 | 36.2 | 27.0 | 42.6 | |
| MBE | 0.66 | −0.27 | −1.43 | 0.42 | −1.02 | −1.51 | 0.34 | −1.96 | |
| One-day time window | R2 | 0.29 | 0.31 | −0.01 | 0.35 | 0.48 | 0.43 | 0.71 | −0.04 |
| RMSE | 24.6 | 31.9 | 38.6 | 30.9 | 27.8 | 29 | 22 | 39.2 | |
| MBE | −3.05 | −4.91 | −6.09 | −5.71 | −6.12 | −4.59 | −4.45 | −7.85 | |
| Parameter | Time Window | Prediction Model (µg/L) |
|---|---|---|
| Chl-a | Concurrent | 43.78 × 2BDA − 25.860 |
| Chl-a | One-day | 33.75 × 2BDA − 15.078 |
| Phycocyanin | Concurrent | 2486.33 × MPH + 7.146 |
| Phycocyanin | One-day | 2191.88 × MPH + 6.891 |
| Chl-a Prediction | Phycocyanin Prediction | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Concurrent n = 81 | One-Day Time Window n = 179 | Concurrent n = 27 | One-Day Time Window n = 60 | |||||||||
| Field | Low | Moderate | High | Low | Moderate | High | Low | Moderate | High | Low | Moderate | High |
| Moderate | 0 | 35 | 15 | 1 | 77 | 26 | 1 | 14 | 5 | 2 | 29 | 4 |
| High | 0 | 11 | 20 | 0 | 22 | 53 | 0 | 1 | 6 | 1 | 0 | 24 |
| Cloud Score+ Threshold | ||||
|---|---|---|---|---|
| 30 | 40 | 50 | 60 | |
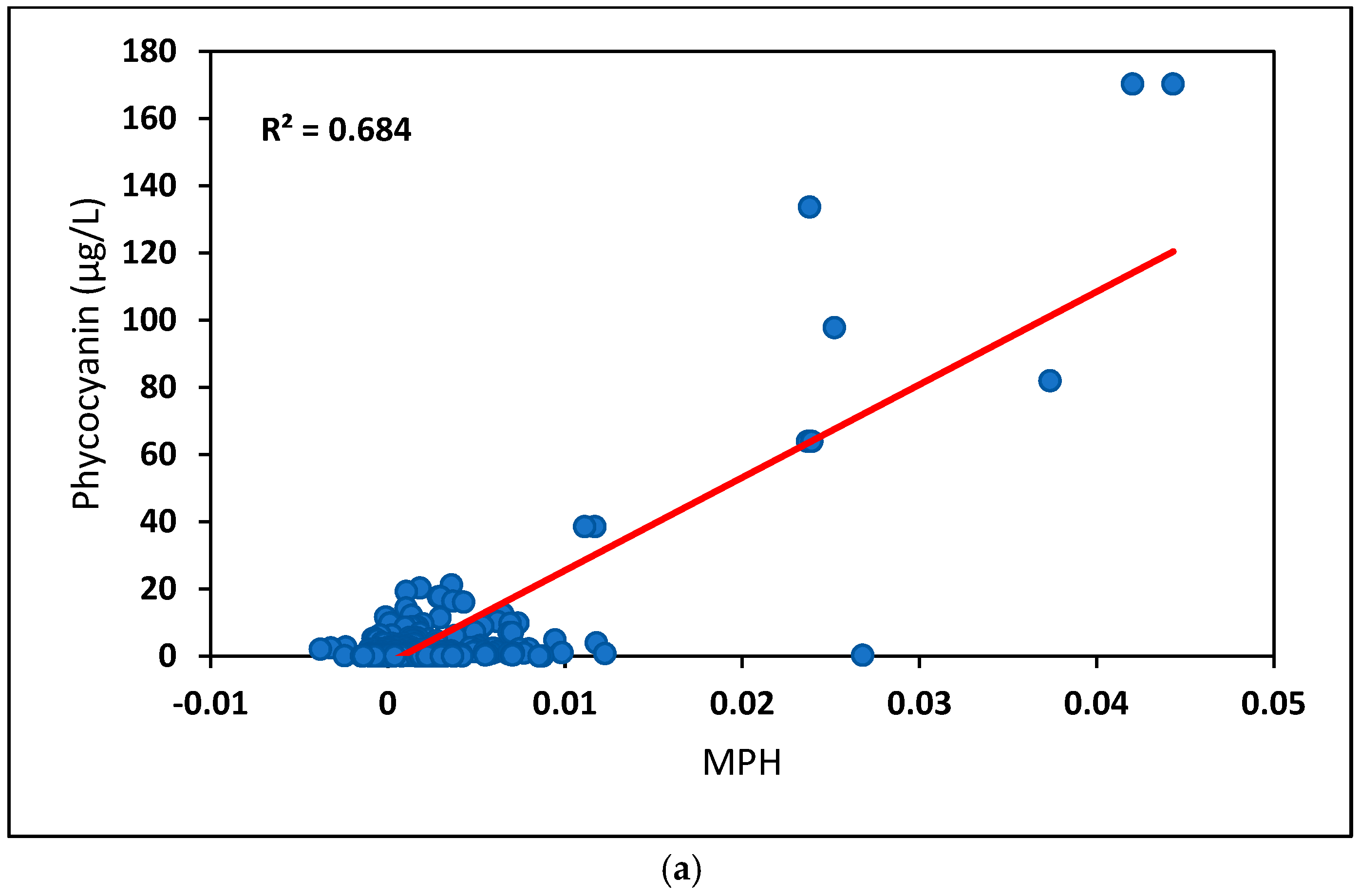
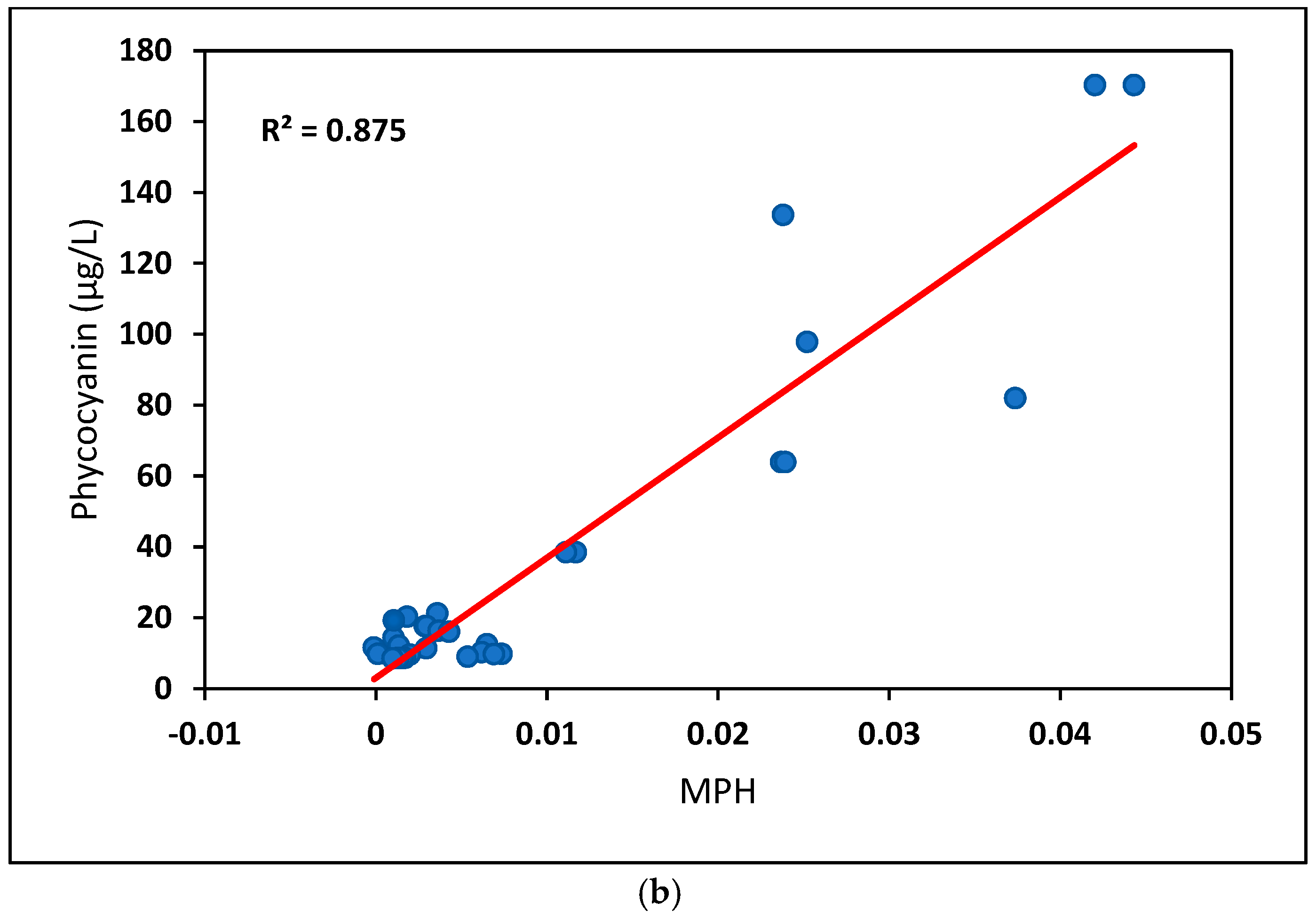
| All data | 0.62 (n = 359) | 0.67 (n = 321) | 0.68 (n = 263) | 0.62 (n = 196) |
| >8 μg/L | 0.81 (n = 42) | 0.86 (n = 40) | 0.87 (n = 32) | 0.80 (n = 27) |
| Chl-a-2BDA | Phycocyanin-MPH | |||||||
|---|---|---|---|---|---|---|---|---|
| Time Window | n | R2 | RMSE | MBE | n | R2 | RMSE | MBE |
| Concurrent | 65 | 0.466 | 22.5 | −1.96 | 22 | 0.839 | 14.9 | −3.87 |
| One-day | 144 | 0.231 | 24 | −1.2 | 48 | 0.623 | 18.3 | −1.91 |
| Parameter | Time Window | Prediction Model (µg/L) |
|---|---|---|
| Chl-a | Concurrent | 47.48 × 2BDA − 28.794 |
| Chl-a | One-day | 37.36 × 2BDA − 17.712 |
| Phycocyanin | Concurrent | 3101.5 × MPH + 2.992 |
| Phycocyanin | One-day | 3047.6 × MPH + 0.626 |
| Chl-a Prediction | Phycocyanin Prediction | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Concurrent n = 65 | One-Day Time Window n = 144 | Concurrent n = 22 | One-Day Time Window n = 48 | |||||||||
| Field | Low | Moderate | High | Low | Moderate | High | Low | Moderate | High | Low | Moderate | High |
| Moderate | 0 | 22 | 17 | 1 | 66 | 26 | 5 | 9 | 4 | 8 | 15 | 5 |
| High | 0 | 8 | 18 | 0 | 14 | 37 | 0 | 0 | 4 | 0 | 1 | 19 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akbarnejad Nesheli, S.; Quackenbush, L.J.; McCaffrey, L. Estimating Chlorophyll-a and Phycocyanin Concentrations in Inland Temperate Lakes across New York State Using Sentinel-2 Images: Application of Google Earth Engine for Efficient Satellite Image Processing. Remote Sens. 2024, 16, 3504. https://doi.org/10.3390/rs16183504
Akbarnejad Nesheli S, Quackenbush LJ, McCaffrey L. Estimating Chlorophyll-a and Phycocyanin Concentrations in Inland Temperate Lakes across New York State Using Sentinel-2 Images: Application of Google Earth Engine for Efficient Satellite Image Processing. Remote Sensing. 2024; 16(18):3504. https://doi.org/10.3390/rs16183504
Chicago/Turabian StyleAkbarnejad Nesheli, Sara, Lindi J. Quackenbush, and Lewis McCaffrey. 2024. "Estimating Chlorophyll-a and Phycocyanin Concentrations in Inland Temperate Lakes across New York State Using Sentinel-2 Images: Application of Google Earth Engine for Efficient Satellite Image Processing" Remote Sensing 16, no. 18: 3504. https://doi.org/10.3390/rs16183504
APA StyleAkbarnejad Nesheli, S., Quackenbush, L. J., & McCaffrey, L. (2024). Estimating Chlorophyll-a and Phycocyanin Concentrations in Inland Temperate Lakes across New York State Using Sentinel-2 Images: Application of Google Earth Engine for Efficient Satellite Image Processing. Remote Sensing, 16(18), 3504. https://doi.org/10.3390/rs16183504







