Abstract
Wheat (Triticum aestivum L.) production in the Northern Great Plains of North America has been challenged by wheat stem sawfly (WSS), Cephus cinctus Norton, for a century. Damaging WSS populations have increased, highlighting the need for reliable surveys. Remote sensing (RS) can be used to correlate reflectance measurements with nuanced phenomena like cryptic insect infestations within plants, yet little has been done with WSS. To evaluate interactions between WSS-infested wheat and spectral reflectance, we grew wheat plants in a controlled environment, experimentally infested them with WSS and recorded weekly hyperspectral measurements (350–2500 nm) of the canopies from prior to the introduction of WSS to full senescence. To assess the relationships between WSS infestation and wheat reflectance, we employed sparse multiway partial least squares regression (N-PLS), which models multidimensional covariance structures inherent in multitemporal hyperspectral datasets. Multitemporal hyperspectral measurements of wheat canopies modeled with sparse N-PLS accurately estimated the proportion of WSS-infested stems (R2 = 0.683, RMSE = 13.5%). The shortwave-infrared (1289–1380 nm) and near-infrared (942–979 nm) spectral regions were the most important in estimating infestation, likely due to internal feeding that decreases plant-water content. Measurements from all time points were important, suggesting aerial RS of WSS in the field should incorporate the visible through shortwave spectra collected from the beginning of WSS emergence at least weekly until the crop reaches senescence.
1. Introduction
The wheat stem sawfly (WSS) (Cephus cinctus Norton) is one of the most important insect pests of wheat (Triticum aestivum L.) production in the Northern Great Plains of North America [1,2]. For over a century, crop losses have occurred due to a lack of effective control strategies and the difficulty in monitoring infestation levels of this cryptic insect pest [3]. More than 95% of the WSS life cycle takes place within a host stem. Evidence of WSS infestation is often not apparent until the end of the growing season when stem lodging occurs; these losses can be very problematic in areas with large WSS infestations. Because of this cryptic feeding habit, the means of detection have largely been limited to careful observation during the period of adult emergence or manual dissection of stems to determine infestation status after the period of adult flight, at any point during the growing season. The effort required to comprehensively inventory WSS occurrence in fields is compounded by large expanses of dryland wheat across the Northern Great Plains of North America. The longstanding prominence of this pest and recent increases in damaging populations of WSS in Colorado, Nebraska, and Kansas [4,5] underscore the need for a rapid and efficient means of identifying and monitoring infestation levels. Linking the spectral reflectance of standing wheat crops to the degree of WSS infestation may present an objective tool for estimating the severity of WSS on the landscape and prescribing subsequent management or intervention.
WSS is an obligate internally feeding stem miner that requires its host to reach maturity to cause visually apparent damage; thus, its effects on host physiology while feeding are relatively subtle compared to many other forms of insect injury. WSS mainly feed on the parenchymous tissue in the innermost stem lining [6], which is initially a relatively benign form of damage when the larvae are neonates. When larvae exhaust the resources in a given internode, they burrow through stem nodes, which can result in damage to the vascular tissue of the host [7,8,9]. This damage to the xylem and phloem disrupts the transport of carbohydrates leading to visible dark bands beneath burrowed nodes [7] and eventually leads to 20 to 30% yield reductions [9,10]. Stem mining by WSS also reduces the photosynthetic capacity of the flag leaves of the host [9,11]. However, the presence of sub-nodal dark spots or decreased gas exchange parameters is often not detectable until at least the grain-filling stage [7,9,11]. Injury caused by WSS also increases photochemical efficiency in the head glumes of wheat [8]. These findings suggest that the physiological changes in wheat caused by the internal feeding of WSS may be expressed asymmetrically across plant tissues and are more likely to be detected at later growth stages.
Many studies have demonstrated the utility of remotely sensed data in quantifying the physiological status of wheat, such as nitrogen deficiency [12,13], Hessian fly infestation [14], wheat streak mosaic virus [15], Fusarium head blight [16,17], and senescence [18], among other applications. However, comparatively little work has been conducted to determine the efficacy of remote sensing (RS) for the detection of wheat stem mining pests such as WSS, although RS has been used to assess WSS habitat suitability [19]. Nansen et al. (2009) [20] conducted the only study to date on remote detection of WSS. They experimentally infested wheat with WSS and used a hyperspectral camera with a spectral range of 402–838 nm to take images of the wheat leaves three weeks after infestation. They found that differences in the reflectance of infested and uninfested leaves were detectable in the red-edge and near-infrared (NIR) portions of the electromagnetic spectrum. However, the reflectance of individual leaves is not directly comparable to the reflectance of the entire plant or the crop canopy, as radiation measured by the sensor is influenced by the incidence angle of light, head and leaf orientation, and light transmission through the canopy, which has been found to vary up to 15% when comparing leaves to canopies [21]. Furthermore, the camera used by Nansen et al. (2009) was not able to measure light in the shortwave-infrared (SWIR) portion of the electromagnetic spectrum, which is between 1300 and 2500 nm and has been found to be sensitive to changes in leaf-water content [22,23,24]. Therefore, we devised an experiment to collect multitemporal hyperspectral measurements of the visible—shortwave infrared (VSWIR, 350–2500 nm) from wheat canopies subjected to WSS infestation to more closely simulate the nature of data captured by aerial or satellite RS platforms.
Hyperspectral data offer identification of subtle reflectance differences due to their broad spectral range and fine spectral resolution, resulting in hundreds to thousands of contiguous bands [25]. The large number of very narrow bands leads to redundancy in the data, which is further compounded when hyperspectral measurements are repeated over multiple points in time. This redundancy and the high degree of complexity can lead to a decay in modeling performance, referred to as the Hughes phenomenon [26], which is often dealt with by employing dimensionality reductions, such as feature selection [27], feature extraction [28], and multivariate modeling like partial least squares (PLS) [29]. However, the aforementioned methods are not designed to account for repeated measures data. Hyperspectral reflectance profiles collected from the same sample over multiple points in time are repeated measures, which are more appropriately modeled with high-order arrays [30], otherwise known as tensors. Recent studies using repeated measures of multispectral and hyperspectral data have found satisfactory modeling performance using multiway partial least squares (N-PLS) [30,31]. N-PLS accounts for the repeated measures of these data by employing a trilinear method of decomposition [32,33] along the multidimensional tensor structure to account for the correlation among samples, wavelengths, and points in time. This method allows for a simplified model of the data using latent variables and beta coefficients that preserve the interpretation of the spectral and temporal dimensions.
The objective of our study is to evaluate the efficacy of repeated measures hyperspectral reflectance data for estimating the level of WSS infestation in a group of wheat plants exposed to female adults. We designed the experiment to emulate the manner in which RS of WSS across a wheat field would be carried out by assessing WSS infestation on a continuous scale within a group of adjacent wheat plants and by collecting reflectance measurements from above the canopy with a nadir orientation. We measured the canopy reflectance weekly starting just prior to introducing the WSS treatment and continuing until the wheat reached full senesce. This design captures the entirety of the growing season relevant to WSS interactions with wheat at an interval and duration that are similar to the temporal resolution of RS platforms like drones and satellites. The goal of this study is to identify spectral regions and time points that are important for RS of WSS. This knowledge may prove useful for estimating WSS infestations across larger areas based on RS platforms that measure reflectance in spectral regions found to be important in this study.
2. Materials and Methods
2.1. Plant Cultivation
The spring wheat cultivar Reeder was grown in 25.4 cm diameter pots with 10 seeds planted in the center. Reeder was chosen because it is a hollow-stem cultivar that is susceptible to WSS injury [34] and remains the second most planted cultivar among Montana spring wheat producers [35]. The plants were seeded in a 50:50 mix of Soil Mix (loam, washed concrete sand, and Canadian Sphagnum peat moss) and Sunshine Mix #1 (Canadian Sphagnum peat moss, perlite, vermiculite, starter nutrient charge, wetting agent, and dolomitic lime), which has a pH of 7.3. Plants were watered daily and fertilized twice weekly (Tuesdays and Thursdays) once they reached the three-leaf stage (Zadoks 13). For fertilizer, we used Jack’s Professional Nutrients (J.R. Peters, Allentown, PA, USA) of 20N:20P:20K applied at a rate of 100 ppm (200 ppm per week). The greenhouse maintained a temperature of 21 ± 3 °C and provided the plants with ambient sunlight in addition to a 15L:9D supplemental lighting period (GE Multivapor lamps model MVR1000/C/U, GE Lighting, General Electric Co., Cleveland, OH, USA). Fertilizer and watering were tapered off after reaching Zadoks 70 and ended at around Zadoks 80. In each pot, the seeds were placed together in the center to minimize the variation in canopy shape among samples.
This experiment consisted of five planting groups of 30 pots staggered in one-week intervals. Once a majority of the tillers in a planting group reached Zadoks 32, the 20 most uniform pots were selected and enclosed by mesh nets to begin the experimental treatment. For each planting group, 20 newly emerged female and five male adult WSS were introduced to each of the randomly assigned treatment pots (n = 15). The control pots (n = 5) were also fitted with mesh nets, but no WSS were introduced. After three days, the nets and WSS adults were removed. This unbalanced sample design favoring the treatment group was selected after attempting this same experiment during 2021 and 2022, which resulted in limited and variable infestation levels. These earlier trials also informed the arrangement of the seeds, where linear- or row-style orientations were observed to increase the between-sample spectral variability when compared to placing all seeds around the center. At the conclusion of the experiment, the stems were dissected individually to quantify the WSS-infested stems as a proportion of the total number of stems within each pot (Figure A1). Stems were categorized in one of the following four categories: uninfested, dead neonate, WSS burrowed through two or more nodes (feeding injury in three or more internodes), or WSS cut (Figure A2). WSS cut is the most damaging category as larva will burrow through all, or almost all nodes, encountering the xylem and phloem each time, before descending to the base of the stem where they ultimately severe the stem in the process of creating a hibernaculum in the lowest chamber. Because WSS mainly confers damage to the host by burrowing through internodes with stem cutting afterwards, we only considered stems in the categories of WSS cut or WSS burrowed through two or more nodes for our response variable, the proportion of adequately infested stems, p, defined in the following equation (Equation (1)).
2.2. Spectral Reflectance Sampling
Nadir reflectance measurements of the canopy of each pot in a replicate were collected weekly starting the day the WSS were introduced and continuing until the plants reached full senescence, evidenced by the dried wheat heads angling downwards. In total, each pot was sampled nine times, with the last sample taking place 56 days after the introduction of WSS (DAI). The last planting group matured at a much faster rate than the other groups resulting in only seven weeks of spectral sampling. This entire group was removed from the analysis because of its advanced rate of senescence. Two other sample pots died before the completion of the experiment and were also removed, leaving a final sample size of n = 78 pots (control = 19, treatment = 59). Reflectance samples were recorded with an ASD FieldSpec Pro spectrometer (Malvern Panalytical, Boulder, CO, USA) fitted to a sampling environment supplied with artificial lights (work lights with tungsten halogen bulbs 110–130 V, 300 W, color temperature = 2800 K, Qingdao, China), and opaque walls with minimal reflectance to eliminate outside light (Figure 1). Halogen lights were chosen as they emit light across the majority of the spectrum sampled by the ASD FieldSpec Pro (350–2500 nm) and have been found to be a suitable supplementary light source in laboratory settings [36]. The ASD FieldSpec Pro collects a reflectance reading centered at each wavelength between 350 and 2500 nm, yielding 2151 measurements across the spectrum. The trials in 2021 and 2022 demonstrated optimal spectral sampling was achieved by fixing the sensor sufficiently far above the top of a canopy to achieve a sampling area of 30 cm.

Figure 1.
(top left): Interior view of lights; (bottom left) view of the plant from where the sensor is situated; (right) outside view of the entire sampling environment. Sampling environment telescopes vertically to adjust sampling area of the ASD FieldSpec Pro to the canopy of each pot.
This specific distance was solved for using the equation defined by Danner et al. (2015) [37], which relates the ASD’s field of view, α, and the distance between sensor and target, d, to the observed sampling area, A (Equation (2)). At the beginning of each sampling event the mean height of the planting group’s canopy was measured, and the telescoping top of the sampling environment was adjusted accordingly. Next, we turned on the halogen lights and waited 10 min for them to warm up to allow for a stabilized emission spectrum as determined by preliminary empirical tests. A 30.5 × 30.5 cm Spectralon® white reference standard (Labsphere Inc., North Sutton, NH, USA) was placed in the sampling environment to calibrate the sensor before collecting the spectral samples. To collect the hyperspectral reflectance profiles, each pot was placed in the sampling environment, and the floor was secured around the base of the stems to remove the effect of soil on the spectral measurement. The mean reflectance of each wavelength was then recorded over a 10 s period.
2.3. Data Preprocessing
Spectral data were input into R [38] and converted from digital numbers to reflectances using the white reference and dark current measurements from each sampling event with the package asdreader (version 0.1.3) [39]. To account for measurement drift caused by internal heating over the course of sampling, the prospectr package (version 0.2.7) was used to apply a splice correction to each reflectance spectrum [40]. This process normalizes the reflectance measurements from the VNIR and SWIRII diodes of the ASD FieldSpec Pro to its central SWIRI diode [37,41]. The reflectance data were then grouped by their values of DAI, centered and scaled, and stored in a three-way array, as outlined by Bro (1996) [32] and Wold et al. (1987) [33].
Studies of hyperspectral data often discard regions of the spectrum because of noise or lack of emitted radiation, yet few describe an objective method to identify noisy spectra. We employed the inter-band redundancy analysis (IBRA) to identify and remove noisy regions of the spectrum [42]. The IBRA is a dimensionality reduction technique that calculates the variable inflation factor (VIF) between all pairs of bands to define the degree of collinearity between a band and its spectral neighbors [42]. A Python package of the algorithm and accompanying details a can be found at https://github.com/NISL-MSU/HSI-BandSelection (accessed on 3 March 2024). The result of this algorithm is the identification of salient bands based on how many bands left or right are needed to arrive at a band that holds sufficiently different information. This method works well in highlighting noisy spectral regions that are due to a lack of emitted radiation from a supplemental light source. Inconsistent and low emission in a given region creates unstable reflectance readings across adjacent narrow bands that are not filtered out by the algorithm but rather represented as salient information denoted by a lesser VIF value (Figure 2). To identify noisy spectra, we applied this algorithm to samples from the control group collected 14 days after the start of the experiment to ensure that canopies were filled in. Because the tungsten–halogen bulbs we used do not emit much radiation in the ultraviolet spectrum or in the longer shortwave infrared [43], we do not expect these regions to provide stable reflectance. Based on this analysis, we only considered bands greater than 520 nm but less than 1870 nm as suitable (Figure 2).
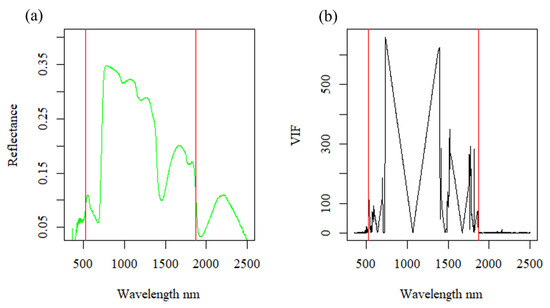
Figure 2.
Mean reflectance at 14 days after infestation: (a) red vertical lines indicate cut-off points of noisy spectra; (b) black lines are the VIF values calculated from the IBRA to the reflectance spectrum of all control samples from 14 days after infestation.
2.4. Sparse Multiway Partial Least Squares Regression Modeling
To account for the binomial nature of our response variable, y, and the proportion of adequately infested stems, p, we transformed the data with a logit link function. Because these data contained control samples with no infestation, a small displacement factor was added to every value to ensure the transformation of zeros would not result in a value of negative infinity (Equation (3)).
The data were then sorted in descending order based on these logit values, and every seventh value was placed into the validation group, while the remaining 85% were used to calibrate the model. The data were parsed out in this stratified manner because most samples had low infestation resulting in a non-normal distribution (Figure A3).
The package sNPLS (version 1.0.27) [44] was used in R (version 3.0.0) to fit the sparse N-PLS models. In this context, sparsity implies that insignificant spectral–temporal features are given a beta coefficient of 0, effectively dropping them from the model. Features retained by the model are fitted with a non-zero beta coefficient, where the magnitude is equivalent to the feature’s importance in explaining the variance in the proportion of adequately WSS-infested stems. A positive beta coefficient suggests increasing reflectance of the spectral–temporal feature is associated with an increase in the proportion of adequately WSS-infested stems. A negative beta coefficient indicates that decreased reflectance of the spectral–temporal feature is correlated with an increase in the proportion of infestation. Hervas et al. (2018) [45] implemented sparsity in the N-PLS algorithm using the least absolute shrinkage and selection operator (LASSO) [46]. Evaluation of root mean square error (RMSE) in the calibration set and the cross- validation set was used to select the optimal number of latent variables in the N-PLS model [31,47]. After selecting the final model, the logit values were back transformed to proportion of adequately infested stems per pot for interpretability. The methods used for data collection, preprocessing, and model selection are organized in Figure 3.
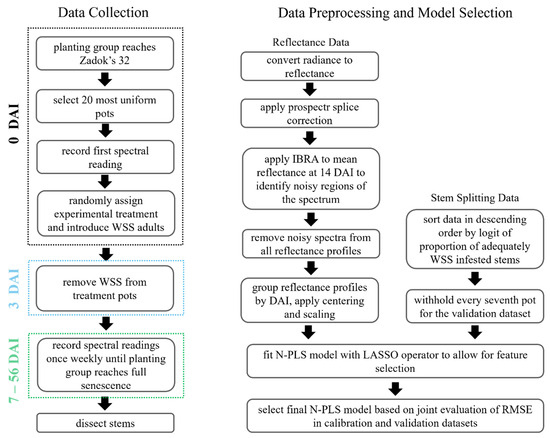
Figure 3.
Flowchart illustrating the experimental, data preprocessing, and analysis steps followed to link multitemporal hyperspectral reflectance to the proportion of adequately infested wheat stem sawfly (WSS) stems within a pot.
3. Results
The spectral reflectance of the wheat canopies over time is characterized by a waveform of absorption and reflectance features throughout the VSWIR that simplifies toward the end of the experiment (Figure 4). The pigments of young and vigorous plants utilize blue, green, but mostly red radiation for photosynthesis leading to low reflectance in the visible (VIS, 580–680 nm) [21]. In the early stages of the experiment the wheat canopies display elevated reflectance in the NIR (750–1250 nm), indicative of adequate nitrogen concentration [12] and healthy mesophyll tissue [21]. Low reflectance in the SWIR (>1300 nm) is owed to the water content of the wheat [13]. As the wheat and WSS larvae mature, the absorption features of VIS and SWIR dramatically increase in reflectance due to the plants undergoing senescence. During this process, the wheat plants redistribute nutrients to further develop the seed head [48], leading to a degradation of the photosystems [21] and a decrease in plant-water content [49]. Concurrent with plant senescence, the undulation across the NIR region appears to diminish.
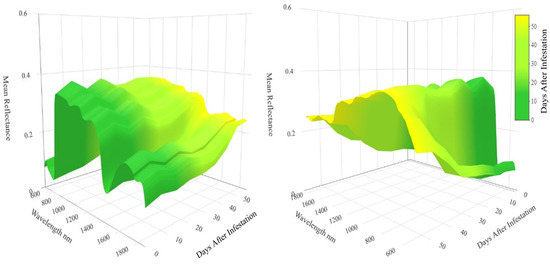
Figure 4.
Opposing viewpoints of the multitemporal reflectance of all sampled wheat canopies averaged at each point in time. Early time points are characterized by strong absorption features while these regions increase in reflectance as plant phenology and wheat stem sawfly infestation progresses.
The sparse N-PLS model that yielded the smallest RMSE for the validation dataset contained 13 latent variables (Figure 5). This model explained 58.3% of the variation in the calibration dataset and 68.3% of the variation in the validation dataset, as indicated by the coefficient of determination (R2) (Figure 6). The RMSE of the validation set implies the modeled estimate for a given pot, is on average 13.5 percentage points away from the actual value of proportion of adequately WSS-infested stems. Agreement between the relatively small values of the standard error (SE) and bias suggests no issues with under or overfitting.
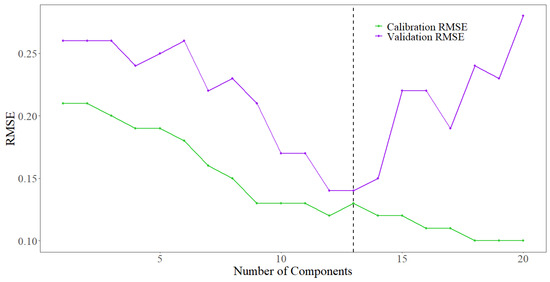
Figure 5.
RMSE of calibration and validation dataset based on number of latent variables. The vertical black dashed line indicates the sparse N-PLS model with 13 latent variables produced the optimal fit based on RMSE with the calibration and validation datasets.
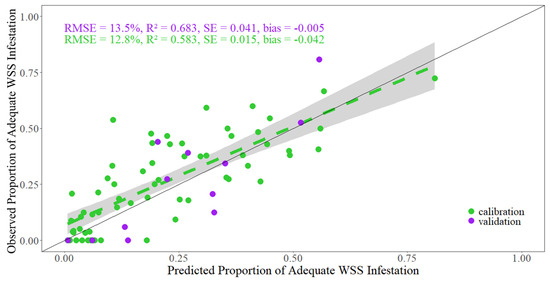
Figure 6.
Predicted vs. fitted values amongst the calibration and validation datasets. Spread of points along the 1:1 line suggests no issues with heteroscedasticity. The green dashed line represents the line of best fit, where the gray area is the 95% confidence interval.
After eliminating noisy spectra using the IBRA, 1351 wavelengths were found suitable for modeling, and with nine repeated measures of each spectrum, this represents 12,159 covariates. The final sparse N-PLS model selected 400 spectral–temporal features, amounting to only 3.3% of the input data (Figure 7). Of these features, there were 87 unique wavelengths with every time point retained. The wavelengths selected were not distributed randomly across the spectrum but rather grouped in spectrally adjacent clusters. The clusters in the VIS and near-infrared (NIR) regions at around 580 nm and 940 nm, respectively, were selected most consistently over time. Wavelengths selected from the SWIR region also exhibited spectral clustering but were more diffuse from the clustering pattern of the VIS and NIR regions and were selected less consistently over time. The values of the beta coefficients alternated from positive or negative over time but remained consistent within spectral clusters. The SWIR clusters centered on 1320 nm and 1400 nm are where the signs of the neighboring beta coefficients appear uncorrelated within a given time point.
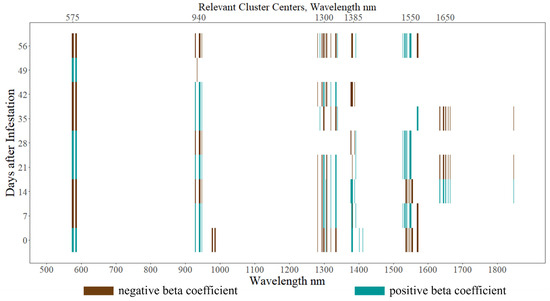
Figure 7.
Distribution of spectral–temporal features retained by the final sparse N-PLS model. Imposing sparsity via LASSO significantly reduced the number of spectral–temporal features from 12,159 to 400. The signs of the beta coefficients indicate the features’ relationship with estimating the proportion of adequate WSS infestation.
The radiation in the NIR and SWIR regions of the spectrum was most heavily weighted in the model (Figure 8 & Table 1), as indicated by the magnitudes of the beta coefficients. Notably, 18 of the 20 most important spectral–temporal features were wavelengths greater than 1250 nm from the SWIR region. Importance of features is relative to the magnitude of their beta coefficient as LASSO removed insignificant features [46] and the reflectance values are standardized across the spectral and temporal dimensions [31]. The feature with the greatest weight was 1339 nm from 56 DAI with a beta coefficient of 1.72, almost four times larger than second largest beta coefficient (−0.46 1308 nm given 21 DAI). Most of these heavily weighted features were spectral measurements collected in the first four weeks of the experiment.
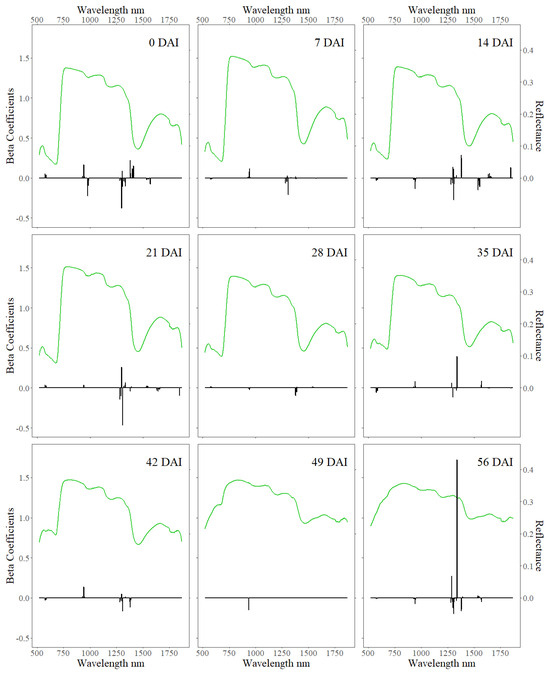
Figure 8.
Mean spectral reflectance and beta coefficients given days after infestation. The average spectral reflectance increased over time, especially in the VIS and SWIR absorption features, as phenology advanced and plants senesced. The signs and magnitudes of the beta coefficients represent their correlations and weights in estimating the proportion of adequately WSS-infested stems within a pot.

Table 1.
20 most important spectral–temporal features in sparse N-PLS model for estimating the proportion of adequately WSS-infested stems per pot as ranked by magnitude of beta coefficient.
4. Discussion
Our results indicate that multitemporal hyperspectral data fitted to a sparse N-PLS model can be used to estimate the level of adequate WSS infestation within wheat canopies, as suggested by the R2 of 0.68 with an RMSE of 13.5%. Imposing sparsity in the N-PLS algorithm reduced the number of spectral–temporal features by 96.7%, highlighting the redundancy inherent in multitemporal hyperspectral data [50]. The model that explained the greatest amount of variation in the validation dataset required 13 latent variables. Wavelengths retained by the final model belonged to discrete clusters throughout the VSWIR, yet the greatest weight was applied to wavelengths in the NIR and SWIR. All time points studied were found to be important in the model, illustrating the need for multitemporal measurements to detect the subtle spectral changes attributed to WSS infestation.
The spectral clusters that were found to be important were the VIS around green light (575 nm), NIR around 940 nm, and SWIR around 1300 nm. Spectral reflectance characteristics of vegetation in these regions is dictated by pigmentation and absorption for photosynthesis [51], integrity of mesophyll and cellular structure [22], and absorption related to water content [49], respectively.
The spectral–temporal feature with the beta coefficient of the greatest magnitude was 1309 nm at 56 DAI. The large positive slope of this coefficient indicates increasing reflectance of that spectral temporal feature is correlated with an increasing proportion of adequate WSS infestation. Previous studies have indicated that water-stressed plants illicit greater spectral reflectance at approximately 1300 nm compared to unstressed plants [24,49]. Macedo et al. (2007) [11] found the photosynthetic capacity of wheat infested by WSS was impacted to a similar degree as it was by water deficit. This suggests that wheat with a greater degree of adequate WSS infestation likely has less water content at 56 DAI, leading to greater reflectance at 1309 nm compared to wheat with a lesser or no degree of adequate WSS infestation. Morrill et al. (1992) [7] posited internodal travel by WSS may lead to damage of the xylem and phloem, in turn disrupting the transport of water and nutrients, which is corroborated by the increased reflectance at 1309 nm at 56 DAI. Overall, this spectral region contained the features given the greatest weight in the model highlighting the utility of the SWIR region in identifying WSS infestation in wheat.
The model beta coefficients within a spectral region exhibited an alternating pattern of positive and negative correlations between reflectance and proportion of adequately WSS-infested stems over time. This may suggest that the relationship between proportion of adequately WSS-infested stems and reflectance over time does not manifest in a linear relationship. This pattern is similar to the inconsistent effects of WSS infestation on vegetation indices over time that Nansen et al. (2009) [20] observed. In this same vein, Macedo et al. (2005 & 2007) [11,52] studied the effects of WSS infestation on the photochemical efficiency of wheat and found its impact on photosynthesis was dependent on environment (growth chamber, greenhouse, and field) and growth stage. In this study, wavelengths in the green region of light (500–600 nm) were important, which have a known link to photosynthesis [53]. The alternating correlations between reflectance of a given spectra over time and proportion of adequate WSS infestation is likely a function of the complex relationship drawn among the 13 latent variables required for this model. To understand the exact nature of WSS infestation and wheat reflectance as a consequence of the variation in physiology, studies with destructive vegetative tissue sampling are required. Nevertheless, the complexity present in the model adds to the growing body of evidence that WSS infestation impacts wheat physiology in a relatively subtle manner.
Radiation in the NIR (about 940 nm), especially during the beginning of the experiment, was important in estimating proportion of adequate WSS infestation. This region of light has a known utility for assessing plant condition, as seen in vegetation indices such as the normalized difference vegetation index [54], normalized difference nitrogen index [55], and the normalized difference water index [56]. It has also been observed that plant conditions, such as height and stem diameter, play important roles in female WSS host selection [57]. While we only selected the pots with the most uniform growing wheat and randomly assigned the treatment, it is possible that subtle differences in plant allometry or vigor impacted the success of WSS oviposition. This is consistent with the model weight applied to the early reflectance of the NIR and SWIR. This is likely true of other important spectral regions in the beginning of the experiment, whereas the reflectance at the end of the host life cycle is likely affected by WSS feeding impacts on host plant physiology. The prevalence of spectral features from early time points in this non-choice experiment indicate that RS of WSS infestation in wheat benefits from accounting for early plant condition. Furthermore, field conditions contrast this experiment in that WSS populations are not controlled and, therefore, may be drawn to locations of the field based on these same principles.
Nansen et al. (2009) [20] found evidence to suggest the spectral reflectance within the range of 402–838 nm of wheat leaves can be altered by WSS infestation up to 21 DAI, especially in the red-edge and NIR regions. Our results differ slightly in that the spectral region given the most importance was the SWIR, and all time points up to 56 DAI were important in estimating proportion of adequate WSS infestation. However, it is important to note that there are significant differences among these study designs: (1) we sampled canopy reflectance with a greater spectral range 520–1870 nm from before WSS introduction to full senescence of the host plant; (2) we employed a statistical method to incorporate the repeated measures of the data rather than treat measurements as independent; (3) we used LASSO to select important spectral temporal features as opposed to visual determination of wavelengths of interest; and (4) we considered the proportion of adequately WSS-infested stems in place of a binary outcome of infested or not. Both studies illustrate the need for multitemporal measurements and demonstrate the NIR region is important in discerning WSS infestation status in leaf and canopy reflectance of wheat. Our findings are consistent with previous studies of physiology of wheat infested by WSS in that impacts are often relatively nuanced [11,20,52].
Our results indicate that radiation across the VSWIR, but especially in the SWIR region, is important for assessing the degree of adequate WSS infestation from multitemporal hyperspectral measurements of wheat canopies. It also seems that accurate and precise estimates of this infestation are best achieved when spectral measurements are repeated across the life cycles of both WSS and its host. This suggests that RS of WSS infestation at the field scale is best suited to platforms that collect multiple bands throughout the VSWIR. The well-known satellite missions of Landsat and Sentinel-2 provide optical imagery throughout the VSWIR about every 10–16 days (depending on mission and latitude) at a spatial resolution of 10–60 m depending on the band. Many studies have demonstrated the utility of these satellites for estimating wheat yield [58], disease infection [59], and nutrient deficiency [60], among many other applications of wheat production. Given the large acreages dryland wheat is often planted to within the Northern Great Plains of North America, these two satellite missions may provide adequate spatial, spectral, and temporal requirements for estimating WSS infestation within wheat fields. However, more research should be conducted to understand the spatial distribution and variability of reflectance of WSS-infested host plants over a larger studied area.
5. Conclusions
To our knowledge, this is the first account of multitemporal hyperspectral non-imaging spectrometry of wheat canopies subjected to WSS infestation. This study is also novel in its use of the IBRA for eliminating noisy spectra and application of sparse N-PLS to multitemporal hyperspectral data. Estimating the proportion of adequately WSS-infested stems relies on measurements across the VSWIR with the greatest emphasis placed on the SWIR. It is also necessary that these measurements are recorded throughout the duration of larval feeding by WSS and concurrent developmental change in the plant host. These findings imply that field RS of WSS infestation will benefit from sensors that capture the aforementioned spectral range with a high temporal density over the course of the growing season.
Author Contributions
Conceptualization, L.S.E., S.L.P., R.K.D.P. and D.K.W.; methodology, L.S.E., S.L.P. and D.K.W.; software, L.S.E.; validation, S.L.P., R.K.D.P. and D.K.W.; formal analysis, L.S.E.; investigation, D.K.W.; resources, S.L.P. and D.K.W.; data curation, L.S.E.; writing—original draft preparation, L.S.E.; writing—review and editing, S.L.P., R.K.D.P. and D.K.W.; visualization, L.S.E.; supervision, D.K.W.; project administration, D.K.W.; funding acquisition, D.K.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Montana Wheat and Barley Committee, Great Falls, Montana, USA.
Data Availability Statement
Data and methods presented in the main analysis are available online: https://github.com/LochlinE/WSS-HyperSpec-Ermatinger_et_al2024, accessed on 20 September 2024.
Acknowledgments
We thank Megan Hofland for her guidance, Megan Hager and Jackson Strand for supporting plant cultivation, and the Montana State University Greenhouse for accommodating this work.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
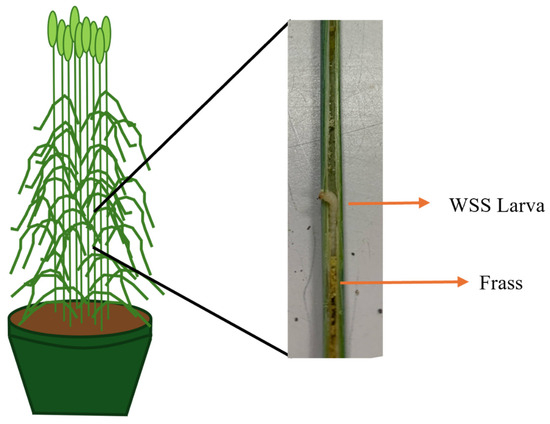
Figure A1.
Picture of wheat stem sawfly (WSS) larva feeding inside a wheat stem. The frass is excrement produced during and after feeding by WSS larvae. Photo by Jackson R. Strand.
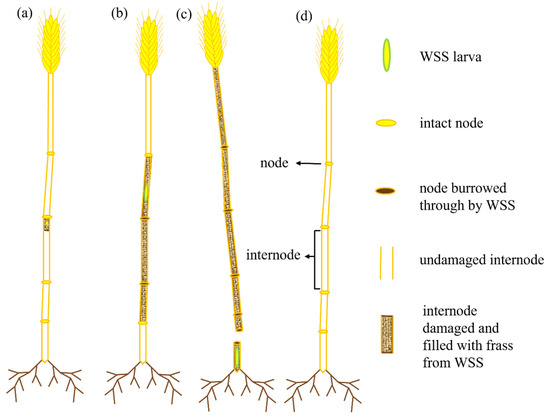
Figure A2.
Examples of possible wheat stem sawfly (WSS) infestation categories recorded at the conclusion of the experiment. A first instar larva that lived and died within a single internode is represented on the far left (a), denoted as dead neonate. A larva that burrowed through two or more nodes but ultimately died before cutting the stem is depicted in (b). The most significant possible form of WSS damage, WSS cut (c), occurs when a WSS larva burrows through all, or almost all nodes, and eventually severs the stem near the soil surface, where it creates a hibernaculum to prepare for diapause. An uninfested stem that did not experience WSS infestation will be devoid of frass and all nodes remain intact (d).
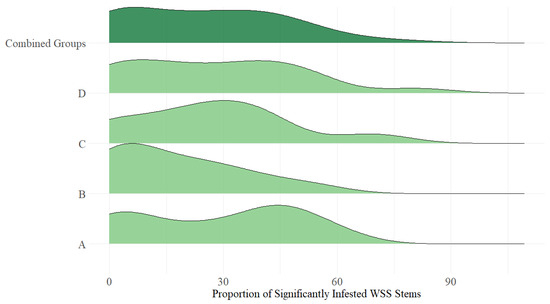
Figure A3.
Proportion of adequately wheat stem sawfly infested stems within a pot by planting replicate. Replicates were planted weekly with A being the first and D being the last. Infestation varied by planting replicate and did not display a normal distribution even when considering all replicates together.
References
- Beres, B.L.; Dosdall, L.M.; Weaver, D.K.; Cárcamo, H.A.; Spaner, D.M. Biology and Integrated Management of Wheat Stem Sawfly and the Need for Continuing Research. Can. Entomol. 2011, 143, 105–125. [Google Scholar] [CrossRef]
- Criddle, N. The Western-Stem Sawfly and its Control. Dom. Can. Dept. Ag. 1922, 6, 1–8. [Google Scholar]
- Knodel, J.; Shanower, T.; Beauzay, P. Integrated Pest Management of Wheat Stem Sawfly. 2010. Available online: https://library.ndsu.edu/ir/handle/10365/10435 (accessed on 18 February 2024).
- Cockrell, D.M.; Randolph, T.; Peirce, E.; Peairs, F.B. Survey of Wheat Stem Sawfly (Hymenoptera: Cephidae) Infesting Wheat in Eastern Colorado. J. Econ. Entomol. 2021, 114, 998–1004. [Google Scholar] [CrossRef] [PubMed]
- McCullough, C.T.; Hein, G.L.; Bradshaw, J.D. Phenology and Dispersal of the Wheat Stem Sawfly (Hymenoptera: Cephidae) into Winter Wheat Fields in Nebraska. J. Econ. Entomol. 2020, 113, 1831–1838. [Google Scholar] [CrossRef]
- Holmes, N.D. Food Relations of the Wheat Stem Sawfly, Cephus cinctus Nort. (Hymenoptera: Cephidae). Can. Entomol. 1954, 86, 159–167. [Google Scholar] [CrossRef]
- Morrill, W.L.; Gabor, J.W.; Kushnak, G.D. Wheat Stem Sawfly (Hymenoptera: Cephidae): Damage and Detection. J. Econ. Entomol. 1992, 85, 2413–2417. [Google Scholar] [CrossRef]
- Macedo, T.B.; Weaver, D.K.; Peterson, R.K.D. Characterization of the Impact of Wheat Stem Sawfly, Cephus cinctus Norton, on Pigment Composition and Photosystem II Photochemistry of Wheat Heads. Environ. Entomol. 2006, 35, 1115–1120. [Google Scholar] [CrossRef]
- Delaney, K.J.; Weaver, D.K.; Peterson, R.K.D. Photosynthesis and Yield Reductions from Wheat Stem Sawfly (Hymenoptera: Cephidae): Interactions with Wheat Solidness, Water Stress, and Phosphorus Deficiency. J. Econ. Entomol. 2010, 103, 516–524. [Google Scholar] [CrossRef]
- Seamans, H.L.; Manson, G.F.; Farstad, C.W. The Effect of the Wheat Stem Sawfly (Cephus cinctus Nort.) on the Heads and Grain of Infested Stems. Entomol. Soc. Ontario. 1945, 75, 10–15. [Google Scholar]
- Macedo, T.B.; Weaver, D.K.; Peterson, R.K.D. Photosynthesis in wheat at the grain filling stage is altered by larval wheat stem sawfly (Hymenoptera: Cephidae) injury and reduced water availability. J. Entomol. Sci. 2007, 42, 228–238. [Google Scholar] [CrossRef]
- Rodriguez, D.; Fitzgerald, G.J.; Belford, R.; Christensen, L.K. Detection of Nitrogen Deficiency in Wheat from Spectral Reflectance Indices and Basic Crop Eco-Physiological Concepts. Aust. J. Agric. Res. 2006, 57, 781–789. [Google Scholar] [CrossRef]
- Tilling, A.K.; O’Leary, G.J.; Ferwerda, J.G.; Jones, S.D.; Fitzgerald, G.J.; Rodriguez, D.; Belford, R. Remote Sensing of Nitrogen and Water Stress in Wheat. Field Crops Res. 2007, 104, 77–85. [Google Scholar] [CrossRef]
- Bhattarai, G.P.; Schmid, R.B.; McCornack, B.P. Remote Sensing Data to Detect Hessian Fly Infestation in Commercial Wheat Fields. Sci. Rep. 2019, 9, 6109. [Google Scholar] [CrossRef] [PubMed]
- Mirik, M.; Jones, D.C.; Price, J.A.; Workneh, F.; Ansley, R.J.; Rush, C.M. Satellite Remote Sensing of Wheat Infected by Wheat Streak Mosaic Virus. Plant Dis. 2011, 95, 4–12. [Google Scholar] [CrossRef] [PubMed]
- Bauriegel, E.; Giebel, A.; Geyer, M.; Schmidt, U.; Herppich, W.B. Early Detection of Fusarium Infection in Wheat Using Hyper-Spectral Imaging. Comput. Electron. Agric. 2011, 75, 304–312. [Google Scholar] [CrossRef]
- Ma, H.; Huang, W.; Dong, Y.; Liu, L.; Guo, A. Using UAV-Based Hyperspectral Imagery to Detect Winter Wheat Fusarium Head Blight. Remote Sens. 2021, 13, 3024. [Google Scholar] [CrossRef]
- Collins, W. Remote Sensing of Crop Type and Maturity. Photogramm. Eng. Remote Sens. 1978, 44, 43–55. [Google Scholar]
- Lestina, J.; Cook, M.; Kumar, S.; Morisette, J.; Ode, P.J.; Peairs, F. MODIS Imagery Improves Pest Risk Assessment: A Case Study of Wheat Stem Sawfly (Cephus cinctus, Hymenoptera: Cephidae) in Colorado, USA. Environ. Entomol. 2016, 45, 1343–1351. [Google Scholar] [CrossRef]
- Nansen, C.; Macedo, T.; Swanson, R.; Weaver, D.K. Use of Spatial Structure Analysis of Hyperspectral Data Cubes for Detection of Insect-Induced Stress in Wheat Plants. Int. J. Remote Sens. 2009, 30, 2447–2464. [Google Scholar] [CrossRef]
- Knipling, E.B. Physical and Physiological Basis for the Reflectance of Visible and Near-Infrared Radiation from Vegetation. Remote Sens. Environ. 1970, 1, 155–159. [Google Scholar] [CrossRef]
- Gates, D.M.; Keegan, H.J.; Schleter, J.C.; Weidner, V.R. Spectral Properties of Plants. Appl. Opt. 1965, 4, 11–20. [Google Scholar] [CrossRef]
- Tucker, C.J. Remote Sensing of Leaf Water Content in the Near Infrared. Remote Sens. Environ. 1980, 10, 23–32. [Google Scholar] [CrossRef]
- Seelig, H.D.; Hoehn, A.; Stodieck, L.S.; Klaus, D.M.; Adams Iii, W.W.; Emery, W.J. The Assessment of Leaf Water Content Using Leaf Reflectance Ratios in the Visible, Near-, and Short-Wave-Infrared. Int. J. Remote Sens. 2008, 29, 3701–3713. [Google Scholar] [CrossRef]
- Thomas, S.; Kuska, M.T.; Bohnenkamp, D.; Brugger, A.; Alisaac, E.; Wahabzada, M.; Mahlein, A.K. Benefits of Hyperspectral Imaging for Plant Disease Detection and Plant Protection: A Technical Perspective. J. Plant Dis. Prot. 2018, 125, 5–20. [Google Scholar] [CrossRef]
- Hughes, F.G. On the Mean Accuracy of Statistical Pattern Recognizers. IEEE 1986, 14, 55–63. [Google Scholar] [CrossRef]
- Georganos, S.; Grippa, T.; Vanhuysse, S.; Lennert, M.; Shimoni, M.; Kalogirou, S.; Wolff, E. Less is More: Optimizing Classification Performance Through Feature Selection in a Very-High-Resolution Remote Sensing Object-Based Urban Application. GISci. Remote Sens. 2018, 55, 221–242. [Google Scholar] [CrossRef]
- Romero, A.; Gatta, C.; Camps-Valls, G. Unsupervised Deep Feature Extraction for Remote Sensing Image Classification. IEEE Trans. Geosci. Remote Sens. 2015, 54, 1349–1362. [Google Scholar] [CrossRef]
- Schweiger, A.K.; Cavender-Bares, J.; Townsend, P.A.; Hobbie, S.E.; Madritch, M.D.; Wang, R.; Tilman, D.; Gamon, J.A. Plant Spectral Diversity Integrates Functional and Phylogenetic Components of Biodiversity and Predicts Ecosystem Function. Nat. Ecol. Evol. 2018, 2, 976–982. [Google Scholar] [CrossRef]
- Yu, H.; Guo, L.; Kharbach, M.; Han, W. Multi-Way Analysis Coupled with Near-Infrared Spectroscopy in Food Industry: Models and Applications. Foods 2021, 10, 802. [Google Scholar] [CrossRef]
- Lopez-Fornieles, E.; Brunel, G.; Rancon, F.; Gaci, B.; Metz, M.; Devaux, N.; Taylor, J.; Tisseyre, B.; Roger, J.M. Potential of Multiway PLS (N-PLS) Regression Method to Analyse Time-Series of Multispectral Images: A Case Study in Agriculture. Remote Sens. 2022, 14, 216. [Google Scholar] [CrossRef]
- Bro, R. Multiway Calibration. Multilinear PLS. J. Chemom. 1996, 10, 47–61. [Google Scholar] [CrossRef]
- Wold, S.; Geladi, P.; Esbensen, K.; Öhman, J. Multi-Way Principal Components-and PLS-Analysis. J. Chemom. 1987, 1, 41–56. [Google Scholar] [CrossRef]
- Varella, A.C.; Weaver, D.K.; Blake, N.K.; Hofland, M.L.; Heo, H.Y.; Cook, J.P.; Lamb, P.F.; Jordan, K.W.; Akhunov, E.; Chao, S.; et al. Analysis of Recombinant Inbred Line Populations Derived from Wheat Landraces to Identify New Genes for Wheat Stem Sawfly Resistance. Theor. Appl. Genet. 2019, 132, 2195–2207. [Google Scholar] [CrossRef]
- United States Department of Agriculture, N.A.S.S. Montana 2023 Wheat Varieties. 2023. Available online: https://agr.mt.gov/News/USDA-NASS-Wheat-and-Barley-Survey-Indicates-Top-2023-Varietals (accessed on 16 March 2024).
- Lee, H.; Cho, S.; Lim, J.; Lee, A.; Kim, G.; Song, D.J.; Chun, S.W.; Kim, M.J.; Mo, C. Performance Comparison of Tungsten-Halogen Light and Phosphor-Converted NIR LED in Soluble Solid Content Estimation of Apple. Sensors 2023, 23, 1961. [Google Scholar] [CrossRef]
- Danner, M.; Locherer, M.; Hank, T.; Richter, K. Spectral Sampling with the ASD FieldSpec 4—Theory, Management, Problems, Interpretation. In EnMAP Field Guides Technical Report, GFZ Data Services; EnMAP: Potsdam, Germany, 2015. [Google Scholar] [CrossRef]
- R Core Team. R Language Definition; R Foundation for Statistical Computing: Vienna, Austria, 2023. [Google Scholar]
- Roudier, P.; Lalibert’, E. Asdreader. 2017. Available online: https://cran.r-project.org/web/packages/asdreader/index.html (accessed on 23 January 2024).
- Stevens, A.; Ramirez-Lopez, L. Prospectr. 2024. Available online: https://cran.r-project.org/web/packages/prospectr/index.html (accessed on 23 January 2024).
- Hatchell, D.C. ASD Technical Guide 3rd Ed. Section 0–1 Section 0 Technical Guide. 1999. Available online: https://www.yumpu.com/en/document/view/11346134/analytical-spectral-devices-inc-asd-technical-guide (accessed on 23 January 2024).
- Morales, G.; Sheppard, J.W.; Logan, R.D.; Shaw, J.A. Hyperspectral Dimensionality Reduction Based on Inter-Band Redundancy Analysis and Greedy Spectral Selection. Remote Sens. 2021, 13, 3649. [Google Scholar] [CrossRef]
- Thoms, L.J.; Girwidz, R. Training and Assessment of Experimental Competencies from a Distance: Optical Spectrometry via the Internet. Il Nuovo C. C 2015, 38, 59–63. [Google Scholar] [CrossRef]
- Hervas, D. sNPLS. 2022. Available online: https://cran.r-project.org/web/packages/sNPLS/index.html (accessed on 1 May 2024).
- Hervás, D.; Prats-Montalbán, J.M.; Lahoz, A.; Ferrer, A. Sparse N-way partial least squares with R package sNPLS. Chemom. Intell. Lab. Syst. 2018, 179, 54–63. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression Shrinkage and Selection via the Lasso. J. R. Stat. Soc. Ser. B 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Goodarzi, M.; Freitas, M.P. On the use of PLS and N-PLS in MIA-QSAR: Azole Antifungals. Intell. Lab. Syst. 2009, 96, 59–62. [Google Scholar] [CrossRef]
- Bidinger, F.; Musgrave, R.B.; Fischer, R.A. Contribution of Stored Pre-Anthesis Assimilate to Grain Yield in Wheat and Barley. Nature 1977, 270, 431–433. [Google Scholar] [CrossRef]
- Hunt, E.R., Jr.; Rock, B.N. Detection of Changes in Leaf Water Content Using Near-and Middle-Infrared Reflectances. Remote Sens. Environ. 1989, 30, 43–54. [Google Scholar] [CrossRef]
- Zhang, W.; Li, X.; Zhao, L. Discovering the Representative Subset with Low Redundancy for Hyperspectral Feature Selection. Remote Sens. 2019, 11, 1341. [Google Scholar] [CrossRef]
- Woolley, J.T. Reflectance and Transmittance of Light by Leaves. Plant Physiol. 1971, 47, 656–662. [Google Scholar] [CrossRef]
- Macedo, T.B.; Peterson, R.K.; Weaver, D.K.; Morrill, W.L. Wheat Stem Sawfly, Cephus cinctus Norton, Impact on Wheat Primary Metabolism: An Ecophysiological Approach. Environ. Entomol. 2005, 34, 719–726. [Google Scholar] [CrossRef]
- Liu, J.; Van Iersel, M.W. Photosynthetic Physiology of Blue, Green, and Red Light: Light Intensity Effects and Underlying Mechanisms. Front. Plant Sci. 2021, 12, 619987. [Google Scholar] [CrossRef]
- Tucker, C.J. Red and Photographic Infrared Linear Combinations for Monitoring Vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef]
- Serrano, L.; Penuelas, J.; Ustin, S.L. Remote Sensing of Nitrogen and Lignin in Mediterranean Vegetation from AVIRIS Data: Decomposing Biochemical from Structural Signals. Remote Sens. Environ. 2002, 81, 355–364. [Google Scholar] [CrossRef]
- Gao, B.C. NDWI—A Normalized Difference Water Index for Remote Sensing of Vegetation Liquid Water from Space. Remote Sens Environ. 1996, 58, 257–266. [Google Scholar] [CrossRef]
- Buteler, M.; Weaver, D.K. Host Selection by the Wheat Stem Sawfly in Winter Wheat and the Role of Semiochemicals Mediating Oviposition Preference. Èntomol. Exp. Appl. 2012, 143, 138–147. [Google Scholar] [CrossRef]
- Xiao, G.; Zhang, X.; Niu, Q.; Li, X.; Li, X.; Zhong, L.; Huang, J. Winter Wheat Yield Estimation at the Field Scale using Sentinel-2 Data and Deep Learning. Comput. Electron. Agric. 2024, 216, 108555. [Google Scholar] [CrossRef]
- Ma, H.; Jing, Y.; Huang, W.; Shi, Y.; Dong, Y.; Zhang, J.; Liu, L. Integrating Early Growth Information to Monitor Winter Wheat Powdery Mildew Using Multi-Temporal Landsat-8 Imagery. Sensors 2018, 18, 3290. [Google Scholar] [CrossRef] [PubMed]
- Crema, A.; Boschetti, M.; Nutini, F.; Cillis, D.; Casa, R. Influence of Soil Properties on Maize and Wheat Nitrogen Status Assessment from Sentinel-2 Data. Remote Sens. 2020, 12, 2175. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).