Abstract
Climate change is a major issue in wastewater management at local and regional levels, as it affects the frequency of flooding and therefore the need to update infrastructure and design regulations. To this end, rainfall data are the main input to hydraulic models used for the design of drainage systems and, in advanced contexts, for their real-time monitoring. Field observations are of great interest and water authorities are increasing the number of existing rain gauges, but at present they are scarce and require maintenance, so their number needs to be considered with their O&M costs. Remote sensors, including both the existing satellite rain products (SRPs) and radar imagery (RI), can complete the spatial distribution of rainfall and optimise the cost of observations. While most SRPs are based on re-analysis and have a lag in availability, RI can be obtained in near real time and is becoming increasingly popular in weather forecasting applications. Unfortunately, actual rainfall forecasts from RI observations are not accurate enough for real-time monitoring of drainage systems. In this paper, the Colour Pattern Regression (CPR) algorithm is used to recalibrate the 6 h rainfall values from RI provided by the Agencia Estatal de Meteorología (AEMET) with the observed rain gauge data, using as a case study the metropolitan area of Palma (Spain).
1. Introduction
The specific and local outcomes of climate change are uncertain and lead to impacts on the hydrological cycle by altering the frequency, intensity, spatial extent, or duration of weather and climate extremes, such as heavy precipitation events or droughts [1]. However, in the context of global warming and climate change, it is generally accepted that both temperature and precipitation patterns will change on a planetary scale [2] and, in this sense, the latest report of the Intergovernmental Panel on Climate Change (IPCC) [3] states that the frequency and intensity of heavy precipitation events have increased since the 1950s over most land areas for which observational data are sufficient for trend analysis, and that anthropogenic climate change is likely to be the main driver. An increase in the intensity of rainfall in urban contexts, together with an increase in urbanisation activities, leads to the need to increase the capacity of urban drainage systems.
Rainfall is characterised by a high spatio-temporal variability, which in turn complicates its quantitative description [4]. On one hand, rain gauges can be considered as a very precise measurement estimation of the actual rainfall, but cannot reproduce its spatial distribution [5]; and, on the other hand, meteorological radar presents a good spatial distribution of the rainfall, but a poorer quantitative estimation.
The combination of meteorological radar and distributed hydrological models results in a fundamental tool for flood risk management [4], but also the application of rainfall prediction techniques, or nowcasting, based on weather radar is ideal for this purpose due to its good spatial coverage (around a km2) and temporal resolution (less than 15 min) [6,7,8]. The benefit of using radar-based nowcasts as inputs to hydrological models has also been shown in urban catchments and flood forecasting [8,9,10]. Regardless, urban catchments are usually smaller than rural watersheds, the runoff transformation of the catchments is higher, and their reactive capacity is lower because natural retention is much less, so the immediacy and accuracy of rainfall information is of paramount interest.
However, the use of meteorological radar for operational applications in urban hydrology has been rare so far, either because of the more complex error characterisation of radar data compared to direct observations in rain gauges, or because of the actual expansion and development of the technical infrastructure—i.e., radar networks are not available everywhere. In addition, it is also a feature of radar measurements that the uncertainty of the measurement increases with higher rain intensities, which is of primary interest in urban hydrology, especially in high-intensity contexts [7]. Both measurement devices—i.e., meteorological radar and rain gauges—are complementary and thus the simultaneous use of both can provide the best spatial estimate of rainfall as required for urban hydrological applications.
This paper applies the Colour Pattern Regression (CPR) algorithm [11] to re-calibrate the 6 h rainfall images coming from the meteorological radar provided by [12]. In order to verify the suitability of the methodology, a case study was selected in Palma de Mallorca (Spain), where rainfall patterns and the capacity of the sewerage system affect the number of discharges into the Mediterranean Sea, which in turn affects water quality and the possibility of beach closures, ultimately affecting the tourism sector [13]. Only in the period 2015–2021 is there an average of 45 days per year when more than one discharge body is flowing—see Figure 1. In this context, the present study aims not only to quantify the spatio-temporal distribution of rainfall, coupling the spatial distribution of the meteorological radar with the observed rainfall of the rain gauges, while questioning the quantification of the radar, but also to improve the capabilities of a prospective digital twin of the sewerage system, facilitating the future infrastructure planning and maintenance of the EMAYA system.
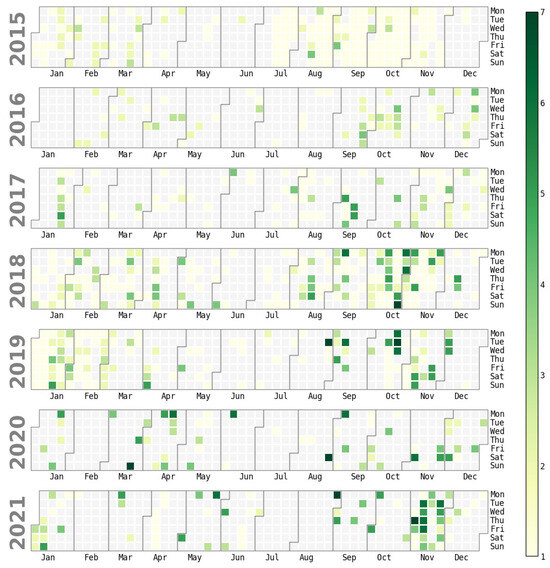
Figure 1.
Daily discharge calendar for the period 2015–2021. Green colour intensity indicates the number of discharges affected. Source: EMAYA.
2. Materials and Methods
2.1. Case Study
The city of Palma is located in the south of the island of Mallorca and is the capital of the Balearic Islands region of Spain, with an area of around 210 km2 and elevations ranging from 0 m, on the coast, to around 400 m in the municipality, but with heights of over 1000 m in the Tramuntana mountains, around 20 km north of the city centre (Figure 2).
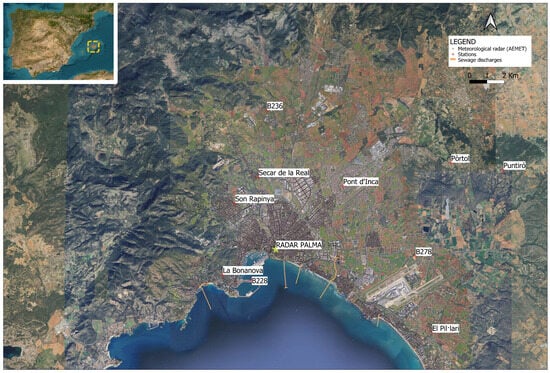
Figure 2.
Location map: location of the city of Palma in the island of Mallorca (Spain); hydro-meteorological and radar stations of the present study and sewage overflow discharges (in orange) into the Mediterranean Sea.
Since 1943, the Empresa Municipal de Agua y Alcantarillado, S.A. (EMAYA) has been responsible for both water and waste management in the city of Palma, which has a population of 420,000 [14]. The tributary basins of the city have a Mediterranean climate, with a high seasonality of rainfall, experiencing bigger registers in autumn, which include records of more than 100 mm/day [15]. The rainwater is collected in either the storm or mixed sewer system, which ends up in the Palma II wastewater treatment plant, and both the treatment discharges and the overflows from the collection system end up in the Mediterranean Sea. Likewise, tourist activities are also affected by these discharges, as they affect the quality of bathing water and cause beach closures, so minimising the occurrence of such events is a priority for the EMAYA. In this sense, the recent update of the national regulation by means of Royal Decree 665/2023 [16] and the proposal for the adaptation of the Urban Wastewater Treatment Directive [17] establish criteria for the design of infrastructures that limit the discharge of wastewater into the sea.
Annual rainfall in this area ranges from 201.3 to 702.2 mm/year, with an annual average of 449 mm over the period 1980–2010 [18]. The rainy season from September to November accounts for 52.2% of the annual rainfall, while the dry season in summer (from June to August) accounts for 10% [19].
2.2. Conceptual Model
The aim of this study is to calibrate the meteorological radar with observed precipitation at rain gauging stations in the context of the Palma city drainage system. The 6 h cumulative rainfall product from the meteorological radar of [12] was used to verify the agreement of the Marshall–Palmer relationship between the observed reflectivity and the calculated rainfall and the observed rainfall in the existing rain gauges. The methodology used in this study is shown in Figure 3. It includes the following steps: (1) data homogenisation and quality control using the RainFA software [13]; (2) identification of 73 daily events with more than 10 mm accumulated rainfall in a single gauging station used for both spatial interpolation (3) and meteorological radar data acquisition (5); (3) spatial interpolation of the rainfall data at the gauging stations using the Inverse Distance Weighting (IDW) method; (4) as a result of the spatial interpolation (3), raster maps of observed precipitation were obtained and used for GIS calculations in QGIS, using the CPR algorithm plugin (7); (5) 6 h accumulated rainfall product from the meteorological radar [12] data acquisition and geo-referencing using the European Space Agency (ESA) SeNtinel Applications Platform (SNAP) software; (6) transforming the geo-referenced meteorological radar maps into a 3-band RGB image using the colour legend provided by [12]; (7) applying the Colour Pattern Regression (CPR) algorithm [11] to obtain simulated raster maps of precipitation, minimising the differences between the spatially distributed IDW observed precipitation from (4) and the colour ramp from the radar images computed in (6)—converting the 1-band product provided by [12] to 3-band RGB images; (7) this procedure is generalised to recalibrate satellite precipitation meteorological radar products for Palma de Mallorca (Spain) in the period 2015–2021.
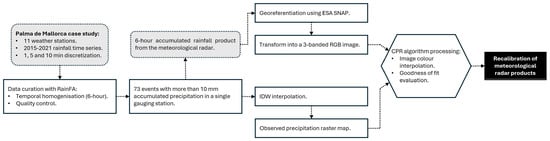
Figure 3.
Flowchart for the methodology adopted in the present study.
2.3. Rainfall Stations Data
Precipitation data were collected from 11 different rain gauges operated by AEMET—i.e., B228, B236, and B278—and the non-profit regional meteorological association Balears Meteo [20]—i.e., El Pil·lari, La Bonanova, Pòrtol, Son Rapinya, Pont d’Inca, Puntiró, Secar de la Real, and Son Ferriol. The data sets were collected from 2015 to 2021 and are recorded at different frequencies—i.e., 1, 5, and 10 min. A data quality control software called RainFA [21] was used to detect outliers and temporal homogenisation. First, the various time series were adjusted to a 10 min time step, summing 2 or 10 registers where appropriate, and then four different data quality controls were applied: (1) user-defined thresholds, using the standard procedure of converting to Nan the negative numbers and the records greater than 40 mm in 10 min; (2) box and whisker and bivariate Highest Density Region (HDR) boxplots, using the summary statistics of the distribution to obtain the quartiles and the potential outliers, comparing stations in pairs with the HDR boxplots and looking for the correspondence of common values densities; (3) double-mass curves, comparing the cumulative rainfall of a single station with the average records of all stations and looking for trend anomalies; and (4) trend analysis, looking for non-stationary series with the Mann–Kendall test. As a result, the Son Ferriol station data set was removed from the study as it had less than two years of data and its registers did not agree with the rest of the stations in the bivariate HDR boxplots and double-mass curve analysis. In addition, 4 discrete values were discarded from the rest of the time series.
Following this data regularisation, daily precipitation events were discretised and those with cumulative registers greater than 10 mm were selected for calibration of the radar imagery. Storm dates were used to request meteorological radar data from AEMET and, where available, to accumulate precipitation into four daily 6 h values in accordance with the radar products described in Section 2.4.
The 6 h accumulated rainfall was represented as a point-vector shapefile in QGIS and spatially distributed using the Inverse Distance Weighting (IDW) method to produce raster maps of the observed rainfall, which were compared with the different radar images using the CPR algorithm QGIS plugin.
2.4. Meteorological Radar
The meteorological data come from the 6 h accumulated precipitation product provided by the Spanish Meteorological Service (AEMET, [12]). The instrument is equipped with Doppler capability and operates in the 5.6 GHz band [22]. It currently provides raster images for a circle of 240 km radius (long-range mode) reprojected to EPSG:4326 (World Geodetic System 1984, WGS84) centred on the Illes Balears radar (39.57ºN, 2.65ºE). Each image has 494 × 536 pixels and a spatial resolution of 1 × 1 km2 in the long-range mode.
The 6 h accumulated precipitation product in mm is the sum of the hourly precipitation products of the period, calculated using the Marshall–Palmer precipitation relation [23], shown in Equation (1).
where Z is the reflectivity factor, R is the rain rate (in mm/h), and a and b are constant variables that depend on the type of precipitation. According to [4,5,7,12], for rainfall precipitation they take the following values: a = 200 and b = 1.6.
However, the same source [12] states that there is no clear relationship between reflectivity and rain water content, nor between reflectivity and rain rate, as the latter is also affected by the velocity at which rain falls. They conclude by suggesting the use of reflectivity raster maps—as detected by radar—instead of rain rates.
Ref. [24] studied the variation of these coefficients with the raindrop size distribution associated with different types of rainfall—e.g., ‘orographic’, ‘thunderstorm’, ‘stratiform’, or ‘showers’. They concluded that (1) for a given rainfall rate, ‘orographic’ rainfall presents smaller raindrop sizes and larger concentrations than ‘thunderstorms’, as would be expected for these types of rainfall, and this explains the smaller prefactors—i.e., a coefficients—and larger exponents—i.e., b coefficients—of the exponential Z-R relationships of the ‘orographic’ rainfall when compared to ‘thunderstorms’; (2) it has been difficult to obtain clear conclusions for the other types of rainfall; and (3) the coefficients adopted in [12] are used in many parts of the world because they are close to the mean power law of different authors [24,25,26] for rain rates between 1 and 50 mm/h.
The 6 h radar data acquired was manually geo-referenced using the tool Ground Control Points (GCP) Manager of the ESA SNAP [27] software and then transformed into a 3-banded RGB raster image by means of a colour classification algorithm using the rasterio [28] Python library.
2.5. CPR Algorithm
The CPR algorithm is an add-on module to the open-source QGIS software implemented as a raster interpolation method to determine the relationship between 3-band colour raster products and raster maps [11]. It was developed to fill the gap of establishing correlations between raster maps and aerial colour patterns, using a linear regression between the observed (O) values of the raster maps and the RGB bands of the aerial images—referred to as simulated, S, values.
After (1) normalizing the pixel sizes and (2) clipping with a mask, both layers can be treated as matrices of size m × n and the objective function can be written as follows—Equation (2):
where the observed values (O) are represented in Equation (3) and the simulated values (S) are represented as a matrix polynomial equation—i.e., Equation (4)—using three parameters—i.e., R, G, and B—which are minimised in the calculation process.
The QGIS CPR algorithm plugin also implements three goodness-of-fit metrics, (1) the Normalised Nash–Sutcliffe Efficiency Coefficient (NNSE), (2) Kling–Gupta Efficiency (KGE), and (3) the Percent Bias Index (PBIAS), which ultimately establish four categories of performance metrics: Very good, Good, Satisfactory, and Unsatisfactory. In the present case, the pixel size of both products—i.e., the IDW-interpolated rainfall raster map and the 3-band coloured radar image—is the same, so there is no spatially distributed metric, but a single performance number of each date–time evaluation.
Refs. [29,30], among others, defined values of the goodness-of-fit metrics for hydrological modelling of streamflow and suspended sediment for different time steps, but there is no reference of the corresponding values for rainfall data from radar observations at the 6 h time step. However, the QGIS CPR algorithm allows the user to adjust the thresholds to suit the needs of the problem.
2.6. Evaluation Procedure
In line with the goodness-of-fit evaluation measurements of the CPR algorithm, three quantitative performance metrics were used to measure, in this case, the accuracy of the meteorological radar predictions with respect to the observed raster maps. The statistics used are (see Table 1): (1) root mean square error (RMSE); (2) the Nash–Sutcliffe efficiency coefficient (NSE); and (3) percent bias (PBIAS). The RMSE explains the deviation between two sets of values, which in this case correspond to the difference between the inferred value from the colour pattern of the CPR process—i.e., observed data—and the corresponding value that was assigned in the colour legend of the meteorological radar product—i.e., simulated data. NSE indicates how well the correlation of observed and simulated data fits the 1:1 line when plotted together, while PBIAS indicates the degree of over- or under-estimation of the observed value as a percentage.

Table 1.
Evaluation performance metrics.
Where and are, respectively, observed and simulated data, i is the data index and n is the total number of measurements, and is the average value of observed data.
3. Results
As mentioned in Section 2.3, rainfall data were curated and homogenised to a 10 min time step using the RainFA software [21]. Daily rainfall values were then detected and those with a cumulative rainfall greater than 10 mm and their preceding and following days were used to obtain the meteorological radar products from [12]. Up to four daily meteorological radar images—i.e., 6 h radar images at 00:00, 06:00, 12:00, and 18:00—were obtained from 73 different dates, resulting in the following findings: (1) there are 54 days with a gauged rainfall greater than 10 mm and available radar inputs; (2) there are 19 images (out of 161) with observed rainfall—i.e., records greater than 0.0 mm and up to 17.8 mm—where the available meteorological radar image was not able to detect rainfall in the area of interest; and (3) during these days, a total of 21 (out of 42) meteorological radar images represent rainfall while there are no records of observed rainfall at the gauging stations. This means that in the case study and in the situation of moderate to extreme rainfall [31], the radar products are able to detect 88.2% of the 6 h time slots with rainfall, but the radar also detects rainfall in the 50.0% of cases where there is no register at the gauging stations.
The rainfall records were then accumulated in accordance with the meteorological radar images and spatially distributed using the IDW interpolation method. The monthly distribution of the selected storm events is shown in Figure 4 and is in line with the values referred to in [19] and presented in Section 2.1, indicating that the most frequent period of moderate to extreme rainfall in the 2015–2021 period is September to November, accounting for 49.3% of the total events, while the period from June to August accounts for only 9.6%. Although the percentages are very similar, the reference values—i.e., annual rainfall vs. number of moderate to extreme rainfall events—are completely different, suggesting a direct relationship between monthly rainfall and the distribution of storms throughout the year, which should be studied in detail.
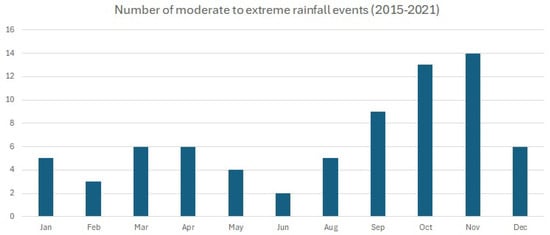
Figure 4.
Monthly distribution of moderate to extreme rainfall storm events in Palma de Mallorca (Spain) for the period 2015–2021.
As mentioned in the Section 2.4, the radar images were manually georeferenced using the GCP Manager tool of the ESA SNAP software [27] and then transformed into a three-band RGB raster image using two different colour label dictionaries for dates before and after 1 January 2016. The following Table 2 shows the three-band RGB value dictionary for both periods.

Table 2.
Colour coding of cumulative rainfall values from meteorological radar for storm events before and after 1 January 2016.
The corresponding date–time pairs of (1) the three-band RGB meteorological radar image and (2) the 6 h cumulative rainfall IDW interpolated raster maps were used to apply the CPR algorithm to assess the validity of the meteorological radar cumulative rainfall values while improving the spatial distribution of the on-site weather stations. The results of the application of the CPR algorithm are presented in Figure 5 and Table A1, including the following: (a–b) date–time of the rainfall event; (c–e) R-G-B calculated parameters; (f–h) goodness-of-fit statistics—i.e., NNSE, KGE, and PBIAS—of the performance of the algorithm; and (i) maximum observed 6 h cumulative rainfall value.
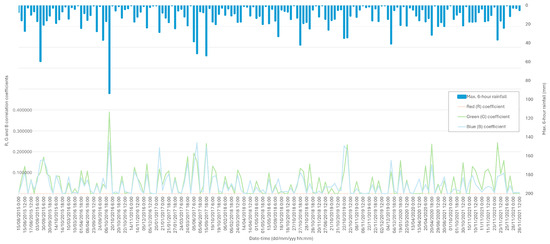
Figure 5.
CPR algorithm results including, for each date and time evaluated, the calculated R, G, and B correlation coefficients and the maximum 6 h cumulative rainfall value observed at any of the existing gauging stations.
The model parameters of the CPR algorithm take on coherent values with the colour ranges shown in Table 2, generally showing larger values with increasing rainfall and including Green shades for higher amounts of rainfall. In this sense, there is a correspondence between the maximum values of rainfall accumulated in rain gauges within 6 h slots and the colour thresholds identified in the meteorological radar legend mentioned above. Figure 6 shows the distribution values of rainfall associated with only Blue tones and including Green tones: (a) shows the dispersion of the results for both coefficients, showing a direct proportionality between their values and the maximum amount of rainfall registered, and, as expected, greater Green coefficient values than the Blue ones for higher rainfall and (b) highlights the Q1 and Q3 quartiles—which account for 50% of the values—in the graph, resulting in a remarkable similarity with the Blue and Green rainfall thresholds of the meteorological radar legend. However, despite the promising general results, a more detailed study is carried out in Section 4 for the different thresholds.
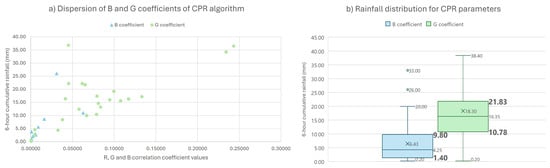
Figure 6.
Maximum 6 h observed rainfall for meteorological radar images that include only Blue and also Green values. (a) Shows the dispersion of both CPR algorithm parameters, and (b) presents the box and whisker results.
Regarding the CPR algorithm performance statistics, using the KGE values proposed in [11] as a reference—i.e., values between 0 and 1 indicate Very good performance, between −0.5 and 0 are considered Good, and values greater than −2 are considered Satisfactory—137 out of 142 radar images that were able to detect precipitation have at least a Satisfactory performance that explains the spatial distribution of precipitation according to its colour pattern, 106 have a Good performance, while only 28 have a Very Good performance. In terms of NNSE, the thresholds proposed in [11] cannot be considered as a reference, in line with the final conclusion and future work of the referenced publication. Consistent with the KGE statistic performance ranking, the variation in NNSE values suggests the use of the following thresholds: (1) NNSE > 0.40 for Very good performance, (2) 0.40 > NNSE > 0.30 for Good performance, and (3) 0.30 > NNSE > 0.20 for Satisfactory performance, resulting in NNSE < 0.20 as Unsatisfactory models, see Figure 7a. Finally, PBIAS is positive in all cases, indicating that the IDW spatially distributed gauged values are overestimating the simulated values from the colour patterns of the meteorological radar. In addition, using the same KGE classification, PBIAS results are also in agreement with performance ratings established in [11], concentrating both Very good and Good performance within the range of [11.5; 35.2]% and obtaining an average of 51.4% for Satisfactory models, as presented in Figure 7b.
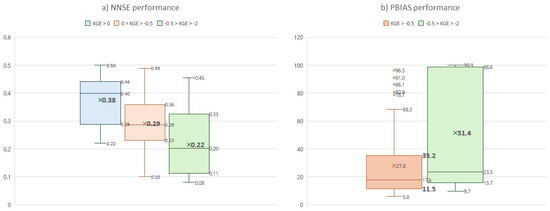
Figure 7.
Performance rating result analysis for (a) NNSE and (b) PBIAS statistics.
4. Discussion
As seen in the previous Section 3, the results of the CPR algorithm in terms of the KGE statistic are at least Satisfactory in practically all cases, and Good in most of them—i.e., 96.5% and 74.6%, respectively. This means that the colour patterns of the meteorological radar products are a good indicator of the rainfall observed in the rain gauges. However, this does not mean that there is a unique relationship between radar observations (which ultimately quantify reflectivity [7,12]), referred to as Z in Equation (1), and rain rate, referred to as R. In this sense, Einfalt et al. [7], among others, highlight the difficulties in the transformation between Z and R and the considerable deviations in their results [7,32,33]. In particular, by applying different equations [23,34,35], can be seen that the most important differences exist for higher rainfall intensities [7], but in the present case, data on these ranges are missing and so it is only possible to assess the results for rainfall intensities below 32 mm.
In order to assess the ability of the meteorological radar to match the observations of rain gauges, the following procedure was applied for every date–time: (1) create a mask of the different colour categories of the meteorological radar; (2) apply the masks to the IDW-interpolated rainfall raster map and calculate its basic statistics—i.e., minimum, maximum, and average; (3) construct an observed array with the increasing colour categories’ minimum and maximum values; (4) compare the observed array with the simulated array, generated from the meteorological radar legend as [0.5, 1; 1, 2; 2, 4; 4, 8; 8, 16; 16, 32; 32, 64; 64, 128; 128, 256]; and (5) evaluate their goodness of fit using the performance metrics described in Section 2.6. First, an evaluation was performed using the RMSE, discarding the date–time registers that exceeded the maximum observed rainfall at the rain gauges, and found that 114 out of 142 (i.e., 80.3%) did not exceed this condition. Table A2 shows the corresponding performance statistics for the selected dates.
Using the recommended values in [29] for the NSE statistic, only 28 of the models have a performance rating of Very good and a total of 44 have a performance rating of at least Good, corresponding to 19.7% and 31.0%, respectively. In addition, most of the models (i.e., 39 out of 44) have a positive PBIAS, meaning that the observed values in the rain gauge exceed the simulated values in the meteorological radar legend. Even for at least Satisfactory models, 63 out of 142 (only 44.4%), PBIAS is positive in 55 cases—i.e., 87.3%. Such results invite reconsideration of the Marshall–Palmer relation (Equation (1)) coefficients for the transformation of radar reflectivity into rain rate (Z-R), as it is clearly underestimating the rainfall results.
The minimum and maximum values were then presented in ranges and their evolution studied for the Satisfactory, Good, and Very good performance models, in order to identify appropriate thresholds that take into account the rainfall variability in the context of Palma de Mallorca. Only the ranges with a minimum number of registers greater than five were considered, and so corresponded to [0.5, 1]; [1, 2]; [2, 4]; [4, 8]; [8, 16]; [16, 32]. Figure 8 shows the distribution boxplots of the corresponding combinations.
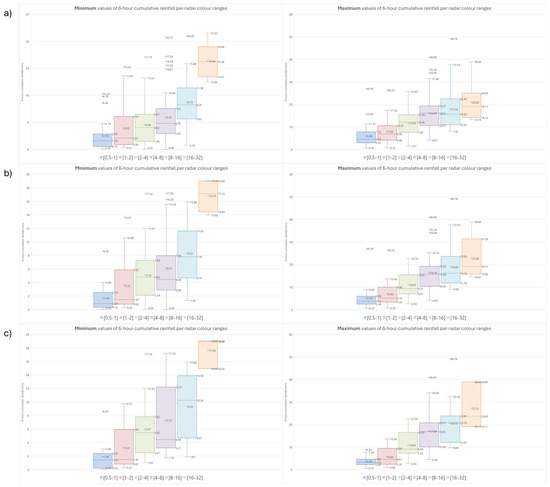
Figure 8.
Minimum and maximum values of the 6 h observed rainfall for meteorological radar image colour ranges. Corresponding to (a) Satisfactory, (b) Good, and (c) Very good performance models.
As a result of the analysis, the following thresholds were defined: [0.5, 2.5]; [2.5, 4.5]; [4.5, 6.5]; [6.5, 12]; [12, 16]; [16, 28]. Comparing them with the original ones used by AEMET [12], it is noticeable that below 16 mm of accumulated rainfall, the simulated values used in the meteorological radar legend underestimate the observed rainfall in the rain gauges. This result is consistent with the PBIAS statistics result mentioned above.
Next, the evaluation procedure to assess the ability of the meteorological radar to match the observations of rain gauges, was adapted to assess its capacity of being matched by the CPR-interpolated raster map. In this case, the procedure was repeated from step (2) and the masks were applied to the CPR-interpolated raster map instead of being applied to the IDW-interpolated rainfall raster map, and, as the map was constructed from the colour patterns, a single value corresponded to every colour instead of a series of them. The observed array was compared with the same simulated array (4) and the performance metrics were calculated (5).
The results were then evaluated for the at least Satisfactory models in NSE of the previous evaluation procedure—i.e., the IDW-interpolated rainfall raster map—and showed that 42 out of 63 of the cases (66.7%) could also be considered as Satisfactory, 30 out of 44 (68.2%) could also be considered as Good, and 17 out of 28 (60.7%) could also be considered as Very good. Using the same distribution evaluation as for the IDW-interpolated raster map—i.e., see Figure 8—the defined thresholds were also appropriate, thus validating both the new proposed ranges and the use of the CPR algorithm to recalibrate the meteorological radar estimates.
Finally, the Marshall–Palmer precipitation relationship (Equation (1)) was recalculated for the new rainfall thresholds, first changing the units of the reflectivity factor from Z (in mm6/m3) to Z (in dBZ) using the following relationship, [4,12], and then minimising the distance between the calculated values of Z (dBZ) and the reference thresholds of the equivalent 6 h meteorological radar product in [12]—i.e., [12, 18]; [18, 24]; [24, 30]; [30, 36]; [36, 42]; [42, 48]. The coefficient a was fixed at 200 after warming up the results and comparing them with the bibliographical references [7,32,33,34,35], and the b calculation resulted in 1.335. Figure 9 shows the resulting Z-R curve compared with three other existing curves: (a) the Marshall–Palmer relationship, ; (b) the tropical climate relationship, ; and (c) the convective storm relationship, .
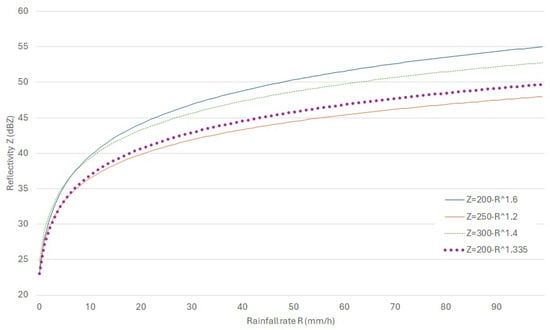
Figure 9.
Comparison of the resulting curve with several Z-R relationships adopted from [7,32].
For the period 2015–2021 and the analysis of moderate to extreme events—i.e., rainfall rates up to 28 mm/h—the Z-R relationship is very similar to that for tropical climates and significantly different from the standard Marshall–Palmer coefficients.
5. Conclusions
The EMAYA is developing a digital twin of the urban drainage system of the city of Palma in Mallorca (Spain), whose main input data for being operational is rainfall, both for nowcasting and forecasting solutions. On-site observations with rain gauges are of utmost interest due to their estimation precision, but their network needs to be increased in density to improve their spatial resolution, thus increasing the O&M costs. A trade-off between cost and precision is needed and remote sensors, such as satellite observation products, represent an alternative to optimise the cost of the rain gauge network, but their measurements should be calibrated to improve their precision. The present manuscript uses the CPR algorithm to recalibrate the meteorological radar information and validates its results by calculating the new thresholds from the IDW-interpolated rainfall raster map. The meteorological radar has demonstrated its ability to detect rainfall, with up to 88.2% of the 6 h time slots containing rainfall. Results from the application of the CPR algorithm suggest that the colour patterns of the meteorological radar products are a good indicator of the rainfall observed at the rain gauges. New thresholds for the meteorological radar colour patterns were calculated from the IDW-interpolated raster map. When the new ranges were applied to the CPR-calculated raster map, the same values were obtained, validating the use of the CPR algorithm to recalibrate the meteorological radar estimates.
Finally, in terms of methodology, the CPR algorithm should be adapted to the QGIS plugin if it is to be used for this particular purpose, with the following performance rating values for NNSE: Very good > 0.40 > Good > 0.30 > Satisfactory > 0.20 > Unsatisfactory, in accordance with the reference paper [11].
Author Contributions
P.B.-G.: conceptualisation; methodology; software; validation; formal analysis; investigation; resources; data curation; writing—original draft; writing—review and editing; project administration. P.E.-P.: methodology; investigation; resources; data curation; writing—original draft; visualisation; supervision. J.L.J.-G.: software; resources; data curation. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Acknowledgments
The authors are grateful to the EMAYA for the provision of precipitation data from both BalearsMeteo and AEMET. In addition, we would like to thank Vicente M. Candela Canales for supporting the R&D investments and programmes within the Vielca companies.
Conflicts of Interest
Author Pablo Blanco-Gómez was employed by the company Vielca Ingenieros S.A., author Pau Estrany-Planas was employed by the company Empresa Municipal de Agua y Alcantarillado (EMAYA) and author José Luis Jiménez-García was employed by the company Vielca Medio Ambiente S.L. All authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Appendix A

Table A1.
CPR algorithm results including, for each date and time evaluated, the calculated R, G, and B correlation coefficients; the goodness-of-fit performance metrics NNSE, KGE, and PBIAS; and the maximum 6 h cumulative rainfall value observed at any of the existing gauging stations.
Table A1.
CPR algorithm results including, for each date and time evaluated, the calculated R, G, and B correlation coefficients; the goodness-of-fit performance metrics NNSE, KGE, and PBIAS; and the maximum 6 h cumulative rainfall value observed at any of the existing gauging stations.
| Date (dd.mm.yyyy) | Time | R | G | B | NNSE | KGE | PBIAS | Max. 6 h Rainfall (mm) |
|---|---|---|---|---|---|---|---|---|
| 15.08.2015 | 00:00 | 0.00000 | 0.00000 | 0.00000 | 7.2 | |||
| 06:00 | 0.00000 | 0.07215 | 0.04543 | 0.2356 | −0.0955 | 17.34 | 16.0 | |
| 12:00 | 0.00000 | 0.13040 | 0.10193 | 0.2358 | −0.4239 | 17.37 | 27.3 | |
| 18:00 | 0.00000 | 0.00000 | 0.00000 | 2.4 | ||||
| 17.08.2015 | 00:00 | 0.00000 | 0.00000 | 0.00000 | 0.0 | |||
| 12:00 | 0.00000 | 0.06695 | 0.06369 | 0.1681 | −0.4435 | 11.01 | 10.0 | |
| 18:00 | 0.00000 | 0.00000 | 0.02048 | 0.1376 | −0.4658 | 21.99 | 6.4 | |
| 03.09.2015 | 00:00 | 0.00000 | 0.00000 | 0.00000 | 0.0 | |||
| 06:00 | 0.00000 | 0.07827 | 0.05904 | 0.0821 | −1.0190 | 24.18 | 16.8 | |
| 18:00 | 0.00000 | 0.00000 | 0.00000 | 0.0 | ||||
| 04.09.2015 | 00:00 | 0.00000 | 0.00000 | 0.00000 | 0.0 | |||
| 06:00 | 0.00000 | 0.00000 | 0.00000 | 0.0 | ||||
| 12:00 | 0.00000 | 0.10180 | 0.15863 | 0.3607 | −0.2188 | 20.91 | 59.4 | |
| 30.09.2015 | 06:00 | 0.00000 | 0.17489 | 0.16232 | 0.0182 | −4.9178 | 10.55 | 20.8 |
| 12:00 | 0.00000 | 0.09469 | 0.12309 | 0.0220 | −4.3269 | 14.91 | 16.0 | |
| 18:00 | 0.00000 | 0.08330 | 0.03743 | 0.2351 | 0.0246 | 22.89 | 11.0 | |
| 14.10.2015 | 00:00 | 0.00000 | 0.00000 | 0.00000 | 2.6 | |||
| 06:00 | 0.00000 | 0.08402 | 0.08700 | 0.2648 | −0.2994 | 8.52 | 18.9 | |
| 12:00 | 0.00000 | 0.08306 | 0.04668 | 0.2149 | −0.1749 | 12.48 | 15.0 | |
| 18:00 | 0.00000 | 0.00000 | 0.00000 | 6.6 | ||||
| 10.03.2016 | 00:00 | 0.00000 | 0.00000 | 0.00336 | 0.2374 | −0.5855 | 99.45 | 1.4 |
| 06:00 | 0.00125 | 0.05175 | 0.08024 | 0.2333 | −0.0440 | 15.05 | 14.2 | |
| 12:00 | 0.00000 | 0.00000 | 0.00239 | 0.3860 | −0.1869 | 25.44 | 2.0 | |
| 18:00 | 0.00000 | 0.02299 | 0.00595 | 0.3177 | −0.3048 | 17.78 | 3.8 | |
| 01.04.2016 | 00:00 | 0.00000 | 0.00000 | 0.00000 | 0.0 | |||
| 06:00 | 0.00000 | 0.00000 | 0.00047 | 0.4022 | 0.2410 | 46.83 | 0.2 | |
| 18:00 | 0.00000 | 0.10986 | 0.07559 | 0.2154 | −0.2947 | 14.35 | 24.2 | |
| 08.04.2016 | 00:00 | 0.00000 | 0.00000 | 0.00000 | 0.0 | |||
| 06:00 | 0.00000 | 0.00000 | 0.00000 | 0.0 | ||||
| 12:00 | 0.00000 | 0.03800 | 0.03575 | 0.2859 | −0.0751 | 9.96 | 8.4 | |
| 18:00 | 0.00000 | 0.10770 | 0.06489 | 0.2355 | −0.1122 | 10.85 | 15.6 | |
| 20.09.2016 | 00:00 | 0.00000 | 0.00000 | 0.00000 | 0.0 | |||
| 06:00 | 0.00000 | 0.00000 | 0.00000 | 0.0 | ||||
| 18:00 | 0.00000 | 0.00000 | 0.01405 | 0.4421 | −0.0589 | 9.04 | 10.4 | |
| 23.09.2016 | 00:00 | 0.00000 | 0.00000 | 0.00000 | 0.0 | |||
| 06:00 | 0.00000 | 0.00000 | 0.00000 | 0.0 | ||||
| 12:00 | 0.00000 | 0.00022 | 0.00057 | 0.4691 | −0.0067 | 61.73 | 0.4 | |
| 18:00 | 0.00000 | 0.04947 | 0.04101 | 0.3805 | −0.1296 | 27.37 | 27.6 | |
| 24.09.2016 | 06:00 | 0.00000 | 0.00000 | 0.00179 | 0.2736 | −0.3238 | 91.18 | 0.8 |
| 12:00 | 0.00000 | 0.00000 | 0.00000 | 0.0 | ||||
| 18:00 | 0.00000 | 0.04508 | 0.07379 | 0.0828 | −0.7453 | 93.85 | 36.8 | |
| 06.10.2016 | 00:00 | 0.00000 | 0.00000 | 0.00000 | 0.0 | |||
| 06:00 | 0.00000 | 0.00000 | 0.00000 | 0.0 | ||||
| 18:00 | 0.00000 | 0.02568 | 0.02218 | 0.4651 | 0.1650 | 28.74 | 16.8 | |
| 20.10.2016 | 00:00 | 0.00000 | 0.39039 | 0.24741 | 0.4444 | 0.1087 | 8.11 | 93.4 |
| 06:00 | 0.00000 | 0.00000 | 0.00000 | 0.4 | ||||
| 12:00 | 0.00000 | 0.00000 | 0.00893 | 0.2981 | −0.0525 | 30.25 | 5.6 | |
| 18:00 | 0.00000 | 0.00000 | 0.00000 | 1.0 | ||||
| 22.10.2016 | 00:00 | 0.00000 | 0.00000 | 0.00000 | 0.0 | |||
| 06:00 | 0.00000 | 0.08369 | 0.06124 | 0.1820 | −0.3293 | 11.51 | 13.2 | |
| 12:00 | 0.00000 | 0.00000 | 0.00955 | 0.1035 | −0.3691 | 58.08 | 4.2 | |
| 18:00 | 0.00000 | 0.00553 | 0.00608 | 0.4221 | 0.0685 | 65.81 | 3.2 | |
| 14.11.2016 | 00:00 | 0.00000 | 0.00000 | 0.00019 | 0.2941 | −0.6089 | 96.53 | 0.2 |
| 06:00 | 0.00000 | 0.12595 | 0.10495 | 0.1063 | −0.8459 | 10.07 | 17.4 | |
| 12:00 | 0.00000 | 0.07472 | 0.07435 | 0.0793 | −1.2213 | 13.68 | 12.2 | |
| 18:00 | 0.00000 | 0.04710 | 0.01978 | 0.1239 | −0.5720 | 20.78 | 6.8 | |
| 05.12.2016 | 00:00 | 0.00000 | 0.00000 | 0.00000 | 0.8 | |||
| 06:00 | 0.00000 | 0.14227 | 0.09337 | 0.2800 | −0.0774 | 10.91 | 23.6 | |
| 12:00 | 0.00000 | 0.00000 | 0.00407 | 0.1001 | −0.1867 | 80.88 | 1.8 | |
| 18:00 | 0.00000 | 0.00000 | 0.00000 | 0.4 | ||||
| 20.01.2017 | 00:00 | 0.00000 | 0.00028 | 0.00039 | 0.3807 | −0.1015 | 24.46 | 0.2 |
| 12:00 | 0.00000 | 0.11805 | 0.21976 | 0.0113 | −6.6076 | 19.89 | 28.4 | |
| 21.01.2017 | 00:00 | 0.00000 | 0.04255 | 0.01485 | 0.4328 | 0.0494 | 10.25 | 7.8 |
| 06:00 | 0.00000 | 0.09288 | 0.06763 | 0.3744 | 0.3401 | 5.82 | 13.2 | |
| 18:00 | 0.00000 | 0.10836 | 0.09454 | 0.2368 | −0.0259 | 11.34 | 18.0 | |
| 27.01.2017 | 00:00 | 0.00000 | 0.00011 | 0.00025 | 0.4884 | −0.1857 | 14.78 | 0.2 |
| 06:00 | 0.00000 | 0.00000 | 0.00000 | 0.0 | ||||
| 12:00 | 0.00000 | 0.00000 | 0.00000 | 0.0 | ||||
| 18:00 | 0.00000 | 0.07822 | 0.06495 | 0.3207 | 0.0997 | 21.44 | 24.5 | |
| 24.03.2017 | 00:00 | 0.00000 | 0.00929 | 0.00474 | 0.4543 | −0.5686 | 22.93 | 5.7 |
| 06:00 | 0.00000 | 0.00000 | 0.00316 | 0.2479 | −0.4220 | 68.34 | 3.8 | |
| 12:00 | 0.00000 | 0.06980 | 0.05400 | 0.2533 | −0.3400 | 9.68 | 12.0 | |
| 18:00 | 0.00000 | 0.17729 | 0.14679 | 0.0423 | −2.6738 | 6.47 | 21.4 | |
| 05.06.2017 | 00:00 | 0.00000 | 0.00000 | 0.00000 | 0.2 | |||
| 06:00 | 0.00000 | 0.19373 | 0.13172 | 0.3190 | −0.2191 | 11.40 | 38.4 | |
| 12:00 | 0.00000 | 0.15269 | 0.24340 | 0.1852 | −0.2550 | 17.51 | 51.0 | |
| 18:00 | 0.00000 | 0.00000 | 0.00970 | 0.2031 | −0.6666 | 99.71 | 6.4 | |
| 15.09.2017 | 00:00 | 0.00000 | 0.00000 | 0.00000 | 0.0 | |||
| 06:00 | 0.00000 | 0.00000 | 0.00000 | 0.0 | ||||
| 12:00 | 0.00000 | 0.03276 | 0.00816 | 0.4757 | 0.2122 | 36.01 | 7.4 | |
| 18:00 | 0.00000 | 0.23895 | 0.22310 | 0.1300 | −0.5430 | 18.21 | 53.4 | |
| 19.10.2017 | 00:00 | 0.00000 | 0.00000 | 0.00000 | 3.0 | |||
| 06:00 | 0.00000 | 0.13118 | 0.08103 | 0.0879 | −1.1058 | 11.55 | 17.4 | |
| 12:00 | 0.00000 | 0.10523 | 0.08516 | 0.3308 | −0.3131 | 9.57 | 20.1 | |
| 18:00 | 0.00000 | 0.00000 | 0.01224 | 0.1166 | −0.6815 | 99.79 | 9.2 | |
| 06.02.2018 | 00:00 | 0.00000 | 0.00000 | 0.00592 | 0.3361 | −0.1933 | 24.24 | 2.6 |
| 06:00 | 0.00000 | 0.08240 | 0.05643 | 0.2170 | −0.2045 | 10.25 | 10.2 | |
| 12:00 | 0.00000 | 0.02353 | 0.01287 | 0.1926 | −0.3882 | 16.71 | 3.4 | |
| 18:00 | 0.00000 | 0.03915 | 0.04833 | 0.2194 | −0.2970 | 16.43 | 10.9 | |
| 24.03.2018 | 00:00 | 0.00000 | 0.00000 | 0.00000 | 0.0 | |||
| 06:00 | 0.00000 | 0.00000 | 0.01617 | 0.3350 | −0.5376 | 15.75 | 8.6 | |
| 12:00 | 0.00000 | 0.11271 | 0.08759 | 0.1488 | −0.4621 | 10.96 | 17.8 | |
| 18:00 | 0.00000 | 0.07926 | 0.01915 | 0.4287 | 0.2006 | 25.10 | 17.4 | |
| 14.04.2018 | 00:00 | 0.00000 | 0.00000 | 0.00049 | 0.4229 | −0.5057 | 86.38 | 0.8 |
| 06:00 | 0.00000 | 0.00000 | 0.00319 | 0.1126 | −0.5187 | 51.59 | 1.6 | |
| 12:00 | 0.00000 | 0.00000 | 0.06276 | 0.1274 | −0.7198 | 12.38 | 11.0 | |
| 18:00 | 0.00000 | 0.00000 | 0.00233 | 0.2930 | 0.1242 | 67.58 | 1.2 | |
| 01.05.2018 | 00:00 | 0.00000 | 0.00000 | 0.00000 | 0.0 | |||
| 06:00 | 0.00000 | 0.05953 | 0.03050 | 0.3111 | −0.1460 | 20.20 | 13.6 | |
| 12:00 | 0.00000 | 0.01665 | 0.00620 | 0.4207 | −0.2361 | 39.47 | 11.3 | |
| 18:00 | 0.00000 | 0.00000 | 0.01888 | 0.3354 | −0.2971 | 46.07 | 20.0 | |
| 13.05.2018 | 00:00 | 0.00000 | 0.00000 | 0.00000 | 0.8 | |||
| 06:00 | 0.00000 | 0.09960 | 0.06807 | 0.2157 | −0.1736 | 10.65 | 19.2 | |
| 12:00 | 0.00000 | 0.00000 | 0.00087 | 0.3859 | −0.7393 | 99.81 | 3.8 | |
| 18:00 | 0.00000 | 0.00000 | 0.00000 | 0.0 | ||||
| 10.09.2018 | 00:00 | 0.00000 | 0.00000 | 0.00000 | 0.0 | |||
| 06:00 | 0.00000 | 0.04152 | 0.02772 | 0.4184 | 0.0128 | 17.39 | 16.4 | |
| 12:00 | 0.00000 | 0.00000 | 0.07143 | 0.1713 | −0.2488 | 87.10 | 33.0 | |
| 18:00 | 0.00000 | 0.00000 | 0.00000 | 0.0 | ||||
| 18.10.2018 | 00:00 | 0.00000 | 0.01173 | 0.00556 | 0.4698 | −0.1350 | 12.38 | 4.6 |
| 06:00 | 0.00000 | 0.00000 | 0.01046 | 0.3471 | −0.0280 | 58.97 | 6.0 | |
| 12:00 | 0.00000 | 0.00000 | 0.00856 | 0.3937 | 0.0805 | 22.62 | 6.8 | |
| 18:00 | 0.00000 | 0.04283 | 0.02574 | 0.3943 | −0.3513 | 16.30 | 14.7 | |
| 27.10.2018 | 00:00 | 0.00000 | 0.00000 | 0.00000 | 0.0 | |||
| 06:00 | 0.00000 | 0.00000 | 0.00000 | 0.2 | ||||
| 12:00 | 0.00000 | 0.03770 | 0.04636 | 0.3741 | −0.1232 | 17.01 | 13.2 | |
| 18:00 | 0.00000 | 0.12069 | 0.10040 | 0.4276 | 0.0497 | 8.52 | 42.0 | |
| 28.10.2018 | 00:00 | 0.00000 | 0.10680 | 0.07288 | 0.2799 | −0.0575 | 10.16 | 19.0 |
| 06:00 | 0.00000 | 0.00000 | 0.00000 | 17.8 | ||||
| 12:00 | 0.00000 | 0.14157 | 0.04913 | 0.3249 | −0.2707 | 26.34 | 24.8 | |
| 18:00 | 0.00000 | 0.00465 | 0.00962 | 0.4130 | 0.3374 | 50.92 | 4.6 | |
| 20.11.2018 | 00:00 | 0.00000 | 0.00000 | 0.00000 | 0.0 | |||
| 06:00 | 0.00000 | 0.00000 | 0.00064 | 0.2869 | −0.4719 | 96.26 | 0.4 | |
| 12:00 | 0.00000 | 0.07763 | 0.01208 | 0.4994 | 0.3678 | 16.11 | 12.0 | |
| 18:00 | 0.00000 | 0.00000 | 0.00057 | 0.2448 | −0.1070 | 78.67 | 0.2 | |
| 27.08.2019 | 00:00 | 0.00000 | 0.00000 | 0.00000 | 0.0 | |||
| 06:00 | 0.00000 | 0.00000 | 0.00000 | 0.0 | ||||
| 12:00 | 0.00000 | 0.05519 | 0.03457 | 0.3435 | −0.2175 | 12.21 | 14.5 | |
| 18:00 | 0.00000 | 0.00000 | 0.03086 | 0.3576 | −0.0165 | 25.81 | 26.0 | |
| 21.10.2019 | 00:00 | 0.00000 | 0.02466 | 0.03156 | 0.4677 | −0.1902 | 11.82 | 15.8 |
| 06:00 | 0.00000 | 0.00000 | 0.04910 | 0.2771 | 0.0332 | 9.74 | 14.4 | |
| 12:00 | 0.00000 | 0.00000 | 0.01786 | 0.2474 | −0.2132 | 10.99 | 5.1 | |
| 18:00 | 0.00000 | 0.03262 | 0.01347 | 0.2389 | −0.0012 | 15.15 | 4.4 | |
| 22.10.2019 | 00:00 | 0.00000 | 0.10469 | 0.22899 | 0.1012 | −0.7995 | 20.79 | 34.8 |
| 06:00 | 0.00000 | 0.23423 | 0.20588 | 0.2094 | −0.2307 | 7.15 | 34.2 | |
| 12:00 | 0.00000 | 0.00000 | 0.00185 | 0.3723 | −0.7435 | 99.94 | 11.2 | |
| 18:00 | 0.00000 | 0.00000 | 0.00077 | 0.3272 | 0.0168 | 43.17 | 0.6 | |
| 08.11.2019 | 00:00 | 0.00000 | 0.05782 | 0.02405 | 0.2880 | −0.2068 | 24.35 | 12.4 |
| 06:00 | 0.00000 | 0.00000 | 0.00516 | 0.3753 | −0.2356 | 17.00 | 4.6 | |
| 12:00 | 0.00000 | 0.00000 | 0.00029 | 0.3174 | −0.6104 | 98.56 | 0.2 | |
| 18:00 | 0.00000 | 0.00000 | 0.00045 | 0.4147 | −0.7258 | 99.45 | 2.0 | |
| 22.11.2019 | 00:00 | 0.00000 | 0.00000 | 0.00000 | 0.0 | |||
| 06:00 | 0.00000 | 0.00000 | 0.00339 | 0.2201 | 0.0332 | 45.39 | 1.4 | |
| 12:00 | 0.00000 | 0.07973 | 0.04286 | 0.2222 | −0.1929 | 25.22 | 16.2 | |
| 18:00 | 0.00000 | 0.00000 | 0.00273 | 0.4851 | 0.1760 | 20.68 | 3.4 | |
| 02.12.2019 | 00:00 | 0.00000 | 0.00000 | 0.00000 | 0.0 | |||
| 06:00 | 0.00000 | 0.06222 | 0.03772 | 0.3141 | −0.3692 | 24.47 | 16.8 | |
| 12:00 | 0.00000 | 0.00000 | 0.00107 | 0.2720 | 0.1651 | 68.15 | 0.4 | |
| 18:00 | 0.00000 | 0.00000 | 0.00000 | 0.2 | ||||
| 04.12.2019 | 00:00 | 0.00000 | 0.00000 | 0.00000 | 14.6 | |||
| 12:00 | 0.00000 | 0.10460 | 0.15849 | 0.2332 | −0.1179 | 17.44 | 40.8 | |
| 18:00 | 0.00000 | 0.00000 | 0.01396 | 0.2982 | −0.1009 | 12.56 | 5.2 | |
| 19.01.2020 | 00:00 | 0.00000 | 0.00000 | 0.00000 | 0.0 | |||
| 06:00 | 0.00000 | 0.00000 | 0.00310 | 0.1425 | −0.3678 | 44.53 | 1.6 | |
| 18:00 | 0.00000 | 0.15813 | 0.11034 | 0.3567 | 0.2541 | 5.89 | 21.0 | |
| 22.03.2020 | 00:00 | 0.00000 | 0.00093 | 0.00036 | 0.3250 | −0.9038 | 88.16 | 1.0 |
| 06:00 | 0.00000 | 0.00000 | 0.00000 | 0.0 | ||||
| 12:00 | 0.00000 | 0.06516 | 0.05396 | 0.3103 | −0.4007 | 23.37 | 21.7 | |
| 18:00 | 0.00000 | 0.00439 | 0.00470 | 0.3867 | −0.3081 | 79.32 | 2.4 | |
| 13.04.2020 | 00:00 | 0.00000 | 0.00000 | 0.00000 | 4.6 | |||
| 06:00 | 0.00000 | 0.00000 | 0.03392 | 0.2056 | −0.5397 | 13.42 | 11.1 | |
| 12:00 | 0.00000 | 0.00000 | 0.07010 | 0.2372 | −0.0397 | 6.40 | 16.0 | |
| 18:00 | 0.00000 | 0.00000 | 0.00000 | 0.0 | ||||
| 20.04.2020 | 00:00 | 0.00000 | 0.00000 | 0.00867 | 0.4431 | 0.1717 | 6.80 | 4.3 |
| 06:00 | 0.00000 | 0.13323 | 0.04410 | 0.2566 | 0.0114 | 30.80 | 17.2 | |
| 12:00 | 0.00000 | 0.00000 | 0.01009 | 0.3816 | −0.3378 | 31.09 | 13.7 | |
| 18:00 | 0.00000 | 0.23645 | 0.13889 | 0.3362 | −0.1299 | 11.68 | 31.4 | |
| 29.08.2020 | 0:00 | 0.00000 | 0.00000 | 0.00000 | 0.0 | |||
| 06:00 | 0.00000 | 0.00000 | 0.00000 | 0.4 | ||||
| 12:00 | 0.00000 | 0.04537 | 0.03412 | 0.3928 | −0.2837 | 21.97 | 22.2 | |
| 18:00 | 0.00000 | 0.00000 | 0.04043 | 0.0846 | −0.5687 | 99.05 | 18.0 | |
| 30.08.2021 | 0:00 | 0.00000 | 0.00000 | 0.00000 | 0.0 | |||
| 06:00 | 0.00000 | 0.00000 | 0.00000 | 0.0 | ||||
| 12:00 | 0.00000 | 0.06166 | 0.07989 | 0.2982 | −0.4465 | 14.54 | 22.2 | |
| 18:00 | 0.00000 | 0.00000 | 0.00000 | 3.8 | ||||
| 01.10.2021 | 0:00 | 0.00000 | 0.00000 | 0.00000 | 0.2 | |||
| 06:00 | 0.00000 | 0.00000 | 0.00000 | 0.0 | ||||
| 12:00 | 0.00000 | 0.08098 | 0.02229 | 0.3358 | −0.6754 | 23.51 | 14.6 | |
| 18:00 | 0.00000 | 0.00000 | 0.01700 | 0.1630 | −0.3035 | 86.12 | 10.0 | |
| 30.10.2021 | 0:00 | 0.00000 | 0.00000 | 0.00000 | 0.0 | |||
| 06:00 | 0.00000 | 0.00000 | 0.01168 | 0.4004 | −0.4089 | 14.25 | 7.3 | |
| 12:00 | 0.00000 | 0.14804 | 0.07711 | 0.2142 | −0.1048 | 9.75 | 21.4 | |
| 18:00 | 0.00000 | 0.00000 | 0.00092 | 0.2177 | −0.6203 | 95.64 | 1.0 | |
| 10.11.2021 | 0:00 | 0.00000 | 0.00000 | 0.05640 | 0.0326 | −2.8578 | 26.87 | 17.4 |
| 06:00 | 0.00000 | 0.12993 | 0.08696 | 0.1337 | −0.5915 | 9.68 | 17.6 | |
| 12:00 | 0.00000 | 0.10863 | 0.04335 | 0.2869 | −0.3597 | 15.72 | 17.2 | |
| 18:00 | 0.00000 | 0.05921 | 0.02528 | 0.1956 | −0.5300 | 15.94 | 7.4 | |
| 11.11.2021 | 0:00 | 0.00000 | 0.01903 | 0.00740 | 0.3762 | −0.1392 | 14.80 | 3.6 |
| 06:00 | 0.00000 | 0.10492 | 0.02616 | 0.3295 | −0.4307 | 18.84 | 17.0 | |
| 12:00 | 0.00000 | 0.11718 | 0.03424 | 0.2605 | −0.6268 | 22.02 | 16.3 | |
| 18:00 | 0.00000 | 0.07882 | 0.02975 | 0.2020 | −0.6140 | 20.55 | 10.4 | |
| 23.11.2021 | 0:00 | 0.00000 | 0.00665 | 0.00285 | 0.2659 | −0.1517 | 34.97 | 1.5 |
| 06:00 | 0.00000 | 0.24326 | 0.08213 | 0.3929 | 0.0298 | 18.78 | 36.5 | |
| 12:00 | 0.00000 | 0.09404 | 0.08781 | 0.1373 | −0.5594 | 10.69 | 16.4 | |
| 18:00 | 0.00000 | 0.15801 | 0.09698 | 0.2743 | 0.0039 | 9.00 | 24.0 | |
| 25.11.2021 | 0:00 | 0.00000 | 0.00000 | 0.00000 | 0.0 | |||
| 06:00 | 0.00000 | 0.00000 | 0.00023 | 0.4554 | −0.4072 | 91.03 | 0.2 | |
| 12:00 | 0.00000 | 0.08443 | 0.03864 | 0.2621 | −0.3625 | 15.06 | 11.5 | |
| 18:00 | 0.00000 | 0.00000 | 0.00000 | 0.0 | ||||
| 28.11.2021 | 0:00 | 0.00000 | 0.00000 | 0.00364 | 0.2483 | −0.0208 | 43.75 | 2.6 |
| 06:00 | 0.00000 | 0.00000 | 0.00540 | 0.2860 | 0.0646 | 60.55 | 3.0 | |
| 12:00 | 0.00000 | 0.00000 | 0.00558 | 0.4726 | 0.2432 | 44.82 | 5.2 | |
| 18:00 | 0.00000 | 0.00000 | 0.00000 | 0.0 |
Appendix B

Table A2.
Goodness-of-fit RMSE, NSE, and PBIAS performance statistics of the observed—i.e., IDW-interpolated rainfall raster map—and simulated—i.e., radar legend—thresholds taking into account the different colour patterns of the meteorological radar legend.
Table A2.
Goodness-of-fit RMSE, NSE, and PBIAS performance statistics of the observed—i.e., IDW-interpolated rainfall raster map—and simulated—i.e., radar legend—thresholds taking into account the different colour patterns of the meteorological radar legend.
| Date (dd.mm.yyyy) | Time | Max. 6 h Rainfall (mm) | RMSE | NSE | PBIAS |
|---|---|---|---|---|---|
| 15.08.2015 | 06:00 | 16.0 | 9.23 | −0.5913 | 5.34 |
| 12:00 | 27.3 | 9.45 | 0.7722 | 31.60 | |
| 17.08.2015 | 12:00 | 10.0 | 9.99 | −0.7789 | −81.19 |
| 18:00 | 6.4 | 2.85 | 0.6621 | 29.64 | |
| 03.09.2015 | 06:00 | 16.8 | 9.58 | −0.0695 | 36.11 |
| 04.09.2015 | 12:00 | 59.4 | 41.40 | −2.2250 | −22.79 |
| 30.09.2015 | 06:00 | 20.8 | 9.24 | 0.8715 | 23.05 |
| 12:00 | 16.0 | 9.27 | 0.6088 | 14.63 | |
| 18:00 | 11.0 | 4.74 | 0.5797 | 37.66 | |
| 14.10.2015 | 06:00 | 18.9 | 5.15 | 0.8460 | 17.87 |
| 12:00 | 15.0 | 5.86 | 0.4344 | 39.38 | |
| 10.03.2016 | 00:00 | 1.4 | 0.27 | 0.9875 | 10.74 |
| 01.04.2016 | 00:00 | 24.2 | 8.96 | 0.6436 | 53.91 |
| 08.04.2016 | 12:00 | 8.4 | 5.47 | 0.1734 | −86.58 |
| 18:00 | 15.6 | 6.93 | 0.4540 | 52.20 | |
| 20.09.2016 | 18:00 | 10.4 | 4.34 | 0.3055 | 19.50 |
| 23.09.2016 | 18:00 | 27.6 | 16.98 | −0.9877 | −5.11 |
| 24.09.2016 | 06:00 | 0.8 | 0.75 | 0.4110 | −123.65 |
| 18:00 | 36.8 | 19.09 | −6.0217 | −15.04 | |
| 20.10.2016 | 00:00 | 93.4 | 42.35 | 0.3597 | 86.39 |
| 12:00 | 5.6 | 2.50 | 0.6456 | 15.59 | |
| 22.10.2016 | 06:00 | 13.2 | 5.00 | 0.7227 | 29.52 |
| 12:00 | 4.2 | 1.38 | 0.8849 | 36.53 | |
| 14.11.2016 | 06:00 | 17.4 | 10.54 | −0.0971 | 42.08 |
| 12:00 | 12.2 | 8.64 | 0.2936 | −24.03 | |
| 18:00 | 6.8 | 4.16 | −0.0462 | −10.10 | |
| 05.12.2016 | 06:00 | 23.6 | 8.99 | 0.7362 | 22.95 |
| 12:00 | 1.8 | 1.44 | −0.1816 | −93.84 | |
| 20.01.2017 | 12:00 | 28.4 | 17.52 | 0.5718 | 5.63 |
| 21.01.2017 | 00:00 | 7.8 | 3.79 | 0.0680 | −38.67 |
| 06:00 | 13.2 | 2.78 | 0.9410 | 9.52 | |
| 18:00 | 18.0 | 7.56 | 0.7016 | 5.54 | |
| 27.01.2017 | 18:00 | 24.5 | 14.35 | −1.5837 | −15.46 |
| 24.03.2017 | 06:00 | 3.8 | 0.82 | 0.8335 | −11.65 |
| 12:00 | 12.0 | 3.77 | 0.8652 | 0.76 | |
| 18:00 | 21.4 | 11.17 | 0.7997 | 60.22 | |
| 05.06.2017 | 06:00 | 38.4 | 15.99 | 0.7309 | 64.99 |
| 12:00 | 51.0 | 19.95 | 0.7926 | 52.22 | |
| 18:00 | 6.4 | 1.69 | 0.9390 | 69.07 | |
| 15.09.2017 | 12:00 | 7.4 | 4.65 | −1.6078 | −80.89 |
| 18:00 | 53.4 | 26.20 | 0.3097 | 71.38 | |
| 19.10.2017 | 06:00 | 17.4 | 9.33 | 0.4002 | 63.78 |
| 12:00 | 20.1 | 6.63 | 0.8291 | 34.45 | |
| 18:00 | 9.2 | 2.32 | 0.9279 | 75.49 | |
| 06.02.2018 | 06:00 | 10.2 | 3.72 | 0.8709 | 1.13 |
| 18:00 | 10.9 | 9.97 | −1.6244 | −46.31 | |
| 24.03.2018 | 06:00 | 8.6 | 2.21 | 0.7689 | 20.83 |
| 12:00 | 17.8 | 8.86 | 0.6369 | 11.37 | |
| 18:00 | 17.4 | 6.79 | 0.1904 | −7.45 | |
| 14.04.2018 | 06:00 | 1.6 | 1.54 | −0.6957 | −120.78 |
| 12:00 | 11.0 | 5.74 | 0.7878 | 59.80 | |
| 18:00 | 1.2 | 0.71 | 0.6839 | −73.59 | |
| 01.05.2018 | 06:00 | 13.6 | 7.94 | −0.5120 | −4.61 |
| 12:00 | 11.3 | 10.04 | −5.6762 | −145.24 | |
| 18:00 | 20.0 | 7.22 | 0.4642 | 60.94 | |
| 13.05.2018 | 06:00 | 19.2 | 7.64 | 0.6772 | 48.25 |
| 12:00 | 3.8 | 0.58 | 0.0968 | −244.89 | |
| 10.09.2018 | 06:00 | 16.4 | 8.14 | −0.1452 | −6.57 |
| 12:00 | 33.0 | 18.90 | 0.6923 | 93.54 | |
| 18.10.2018 | 06:00 | 6.0 | 2.73 | 0.4035 | −6.27 |
| 12:00 | 6.8 | 3.01 | 0.7267 | 51.87 | |
| 18:00 | 14.7 | 5.60 | 0.3686 | 23.13 | |
| 27.10.2018 | 12:00 | 13.2 | 10.21 | −0.6154 | −107.91 |
| 18:00 | 42.0 | 16.67 | 0.1749 | 70.63 | |
| 28.10.2018 | 00:00 | 19.0 | 7.85 | 0.7816 | 36.96 |
| 12:00 | 24.8 | 7.29 | 0.5871 | 30.00 | |
| 20.11.2018 | 12:00 | 12.0 | 3.17 | 0.6958 | −2.35 |
| 27.08.2019 | 12:00 | 14.5 | 4.71 | 0.5455 | −10.51 |
| 18:00 | 26.0 | 11.16 | 0.4794 | 80.78 | |
| 21.10.2019 | 00:00 | 15.8 | 12.23 | −0.8259 | −85.84 |
| 06:00 | 14.4 | 6.62 | 0.5615 | 66.65 | |
| 12:00 | 5.1 | 2.01 | 0.7679 | 20.71 | |
| 22.10.2019 | 00:00 | 34.8 | 19.79 | 0.4640 | 2.46 |
| 06:00 | 34.2 | 16.79 | 0.8677 | 62.81 | |
| 12:00 | 11.2 | 1.23 | −0.3087 | −295.49 | |
| 08.11.2019 | 00:00 | 12.4 | 5.57 | 0.4514 | 29.06 |
| 06:00 | 4.6 | 2.05 | 0.3953 | −48.81 | |
| 18:00 | 2.0 | 0.68 | −3.5196 | −569.22 | |
| 22.11.2019 | 12:00 | 16.2 | 9.18 | −0.2618 | 17.01 |
| 18:00 | 3.4 | 1.22 | 0.8331 | 21.61 | |
| 02.12.2019 | 06:00 | 16.8 | 5.73 | 0.5225 | 29.25 |
| 04.12.2019 | 12:00 | 40.8 | 18.91 | 0.2574 | 2.67 |
| 18:00 | 5.2 | 2.79 | −0.0720 | −41.81 | |
| 19.01.2020 | 06:00 | 1.6 | 1.11 | 0.5882 | −49.47 |
| 18:00 | 21.0 | 5.90 | 0.9492 | 33.90 | |
| 22.03.2020 | 12:00 | 21.7 | 10.24 | 0.2119 | 32.67 |
| 13.04.2020 | 06:00 | 11.1 | 2.60 | 0.8930 | 35.14 |
| 12:00 | 16.0 | 9.36 | 0.8015 | 79.60 | |
| 20.04.2020 | 00:00 | 4.3 | 1.76 | 0.7482 | 17.41 |
| 06:00 | 17.2 | 9.04 | 0.4237 | 60.34 | |
| 12:00 | 13.7 | 3.78 | 0.4156 | 15.91 | |
| 18:00 | 31.4 | 14.65 | 0.5662 | 67.41 | |
| 29.08.2020 | 12:00 | 22.2 | 7.96 | 0.2838 | 32.47 |
| 18:00 | 18.0 | 6.88 | 0.8178 | 78.23 | |
| 30.08.2021 | 12:00 | 22.2 | 7.62 | 0.7229 | 21.23 |
| 01.10.2021 | 12:00 | 14.6 | 4.43 | 0.5907 | 25.26 |
| 18:00 | 10.0 | 5.10 | 0.7766 | 79.70 | |
| 30.10.2021 | 06:00 | 7.3 | 2.19 | 0.5441 | −23.15 |
| 12:00 | 21.4 | 8.08 | 0.5341 | 61.97 | |
| 18:00 | 1.0 | 0.44 | 0.7635 | −143.45 | |
| 10.11.2021 | 00:00 | 17.4 | 11.39 | 0.6121 | 86.23 |
| 06:00 | 17.6 | 7.03 | 0.7300 | 51.50 | |
| 12:00 | 17.2 | 6.15 | 0.5433 | 47.45 | |
| 18:00 | 7.4 | 4.09 | 0.2967 | 7.21 | |
| 11.11.2021 | 06:00 | 17.0 | 6.05 | 0.5533 | 44.87 |
| 12:00 | 16.3 | 4.92 | 0.6556 | 42.23 | |
| 18:00 | 10.4 | 4.25 | 0.5489 | 26.02 | |
| 23.11.2021 | 06:00 | 36.5 | 12.25 | 0.3974 | 54.68 |
| 12:00 | 16.4 | 8.72 | 0.4762 | −10.23 | |
| 18:00 | 24.0 | 10.90 | 0.7974 | 57.30 | |
| 25.11.2021 | 12:00 | 11.5 | 3.12 | 0.7256 | 13.63 |
| 28.11.2021 | 00:00 | 2.6 | 1.61 | 0.1114 | −72.87 |
| 06:00 | 3.0 | 0.87 | 0.8947 | 1.95 | |
| 12:00 | 5.2 | 1.89 | 0.6879 | −10.62 |
References
- IPCC. Managing the Risks of Extreme Events and Disasters to Advance Climate Change Adaptation. A Special Report of Working Groups I and II of the Intergovernmental Panel on Climate Change; Field, C.B., Barros, V., Stocker, T.F., Qin, D., Dokken, D.J., Ebi, K.L., Mastrandrea, M.D., Mach, K.J., Plattner, G.-K., Allen, S.K., et al., Eds.; University Press: Cambridge, UK; New York, NY, USA, 2012; p. 582. [Google Scholar]
- Verma, S.; Bhattarai, R.; Bosch, N.S.; Cooke, R.C.; Kalita, P.K.; Markus, M. Climate Change Impacts on Flow, Sediment and Nutrient Export in a Great Lakes Watershed Using SWAT. CLEAN-Soil Air Water 2015, 43, 1464–1474. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2023: Synthesis Report (Full Volume) Contribution of Working Groups I, II and III to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Core Writing Team, Lee, H., Romero, J., Eds.; IPCC: Geneva, Switzerland, 2023; p. 184. [Google Scholar] [CrossRef]
- Ortiz, E.; Todini, E. Combinación Bayesiana de datos pluviométricos e imágenes del Radar Meteorológico mediante Block Kriging y Filtro de Kalman. Aplicación en España. In Proceedings of the XXXI Jornadas Científicas de la AME y el 11º Encuentro Hispano-Luso de Meteorología, Sevilla, Spain, 1–3 March 2010; p. 6. [Google Scholar]
- Erena, M.; López, J.; García, P.; Caro, M.; Belda, F.; Palenzuela, J.; Toledano, F.; Torralba, P.; González-Barbera, G.; García-Pintado, J. Estimación de precipitación combinada radar-pluviómetros y publicación mediante servicios OGC. In Proceedings of the XV Congreso Nacional de Tecnologías de la Información Geográfica, AGE-CSIC, Madrid, Spain, 19–21 September 2012; pp. 451–458. [Google Scholar]
- Pulkkinen, S.; Chandrasekar, V.; Harri, A.M. Nowcasting of Precipitation in the High-Resolution Dallas–Fort Worth (DFW) Urban Radar Remote Sensing Network. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2018, 11, 2773–2787. [Google Scholar] [CrossRef]
- Einfalt, T.; Arnbjerg-Nielsen, K.; Golz, C.; Jensen, N.E.; Quirmbach, M.; Vaes, G.; Vieux, B. Towards a roadmap for use of radar rainfall data in urban drainage. J. Hydrol. 2004, 299, 186–202. [Google Scholar] [CrossRef]
- Thorndahl, S.; Einfalt, T.; Willems, P.; Nielsen, J.E.; ten Veldhuis, M.C.; Arnbjerg-Nielsen, K.; Rasmussen, M.R.; Molnar, P. Weather radar rainfall data in urban hydrology. Hydrol. Earth Syst. Sci. 2017, 21, 1359–1380. [Google Scholar] [CrossRef]
- Liguori, S.; Rico-Ramirez, M.; Schellart, A.; Saul, A. Using probabilistic radar rainfall nowcasts and NWP forecasts for flow prediction in urban catchments. Atmos. Res. 2012, 103, 80–95. [Google Scholar] [CrossRef]
- Heuvelink, D.; Berenguer, M.; Brauer, C.C.; Uijlenhoet, R. Hydrological application of radar rainfall nowcasting in the Netherlands. Environ. Int. 2020, 136, 105431. [Google Scholar] [CrossRef] [PubMed]
- Blanco-Gómez, P.; Amurrio-Garcia, C.; Jiménez-García, J.L.; Cecilia, J.M. CPR Algorithm—A new interpolation methodology and QGIS plugin for Colour Pattern Regression between aerial images and raster maps. SoftwareX 2023, 22, 101356. [Google Scholar] [CrossRef]
- Agencia Estatal de Meteorología. Interpretación: Radar. 2024. Available online: https://www.aemet.es/es/eltiempo/observacion/radar/ayuda (accessed on 6 September 2024).
- Estrany-Planas, P.; Blanco-Gómez, P.; Vilarrasa, V. Aplicación del análisis regional de frecuencias a las series diarias de precipitación usando la metodología de los L-moments en la ciudad de Palma para la caracterización de la lluvia de diseño. In Proceedings of the VII Jornadas de Ingeniería del Agua—La resiliencia de las Infraestructuras Hidráulicas ante el Cambio Climático, Cartagena, Spain, 18–19 October 2023; pp. 359–372. [Google Scholar] [CrossRef]
- Empresa Municipal de Agua y Alcantarillado, S.A. (EMAYA). La Història i les Històries d’EMAYA; Secció de Comunicació EMAYA: Palma de Mallorca, Spain, 2008; p. 51. Available online: https://www.emaya.es/media/2924/la-histo-ria-i-les-histo-ries-demaya-web.pdf (accessed on 6 September 2024).
- Grimalt, M.; Rosello, J. Inundaciones en la Ciudad de Palma de Mallorca: Distribución de los Episodios y Tipos de Tiempo Asociados. In El Clima: Aire, Agua, Tierra y Fuego; Montavez, J.P., Ed.; Asociación Española de Climatología: Cartagena, Spain, 2018; pp. 245–258. [Google Scholar]
- Ministerio de la Presidencia, Relaciones con las Cortes y Memoria Democrática. Real Decreto 665/2023, de 18 de Julio, por el que se Modifica el Reglamento del Dominio Público Hidráulico, Aprobado por Real Decreto 849/1986, de 11 de Abril; el Reglamento de la Administración Pública del Agua, Aprobado por Real Decreto 927/1988, de 29 de Julio; y el Real Decreto 9/2005, de 14 de Enero, por el que se Establece la Relación de Actividades Potencialmente Contaminantes del Suelo y los Criterios y estáNdares para la Declaración de Suelos Contaminados. 2023. Available online: https://www.boe.es/diario_boe/txt.php?id=BOE-A-2023-18806 (accessed on 6 September 2024).
- Council of European Communities. Council Directive 91/271/EEC of 21 May 1991 Concerning Urban Waste-Water Treatment. 1991. Available online: http://data.europa.eu/eli/dir/1991/271/oj (accessed on 6 September 2024).
- Torrens Calleja, J.M.; Rosselló Geli, J.; Grimalt Gelabert, M. Recopilación de Información Vinculada a Temporales de Viento, Precipitaciones Torrenciales e Inundaciones en la Ciudad de Palma de Mallorca Entre los Años 2000 y 2015; RUA: Alicante, Spain, 2016. [Google Scholar]
- YACU. Estudio de Caracterización del Régimen Extremo de Precipitaciones en la Isla de Mallorca. Informe Final; Direcció General de Recursos Hídrics: Conselleria de Medi Ambient, Govern Balear: Illas, Spain, 2002; p. 621. [Google Scholar]
- BALEARSMETEO. Balears Meteo, Network of Amateur Weather Stations in the Balearic Islands. 2024. Available online: http://balearsmeteo.com/ (accessed on 6 September 2024).
- Blanco-Gómez, P.; Ortiz-Vallespi, J.; Estray-Plana, P.; Orihuela-Martínez, J. Rainfall Frequency Analysis (RainFA) Package. 2023. Available online: https://github.com/vielca/RainFA (accessed on 6 September 2024).
- Cánovas-García, F.; García-Galiano, S.; Alonso-Sarría, F. Assessment of Satellite and Radar Quantitative Precipitation Estimates for Real Time Monitoring of Meteorological Extremes Over the Southeast of the Iberian Peninsula. Remote Sens. 2018, 10, 1023. [Google Scholar] [CrossRef]
- Marshall, J.S.; Palmer, W.M.K. The distribution of raindrops with size. J. Atmos. Sci. 1948, 5, 165–166. [Google Scholar] [CrossRef]
- Uijlenhoet, R. Raindrop size distributions and radar reflectivity-rain rate relationships for radar hydrology. Hydrol. Earth Syst. Sci. 2001, 5, 615–627. [Google Scholar] [CrossRef]
- Battan, L. Radar Observation of the Atmosphere; The University of Chicago Press: Chicago, IL, USA, 1973; p. 324. [Google Scholar]
- List, R. A Linear Radar Reflectivity–Rainrate Relationship for Steady Tropical Rain. J. Atmos. Sci. 1988, 45, 3564–3572. [Google Scholar] [CrossRef]
- SNAP. ESA Sentinel Application Platform v9.0.0. 2022. Available online: http://step.esa.int (accessed on 6 September 2024).
- Gillies, S. Rasterio: Geospatial Raster I/O for Python Programmers. 2013. Available online: https://github.com/rasterio/rasterio (accessed on 6 September 2024).
- Moriasi, N.D.; Arnold, J.G.; Van Liew, W.M.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Brighenti, T.M.; Bonumá, N.B.; Grison, F.; de Almeida Mota, A.; Kobiyama, M.; Chaffe, P.L.B. Two calibration methods for modeling streamflow and suspended sediment with the swat model. Ecol. Eng. 2019, 127, 103–113. [Google Scholar] [CrossRef]
- Zambrano-Bigiarini, M.; Nauditt, A.; Birkel, C.; Verbist, K.; Ribbe, L. Temporal and spatial evaluation of satellite-based rainfall estimates across the complex topographical and climatic gradients of Chile. Hydrol. Earth Syst. Sci. 2017, 21, 1295–1320. [Google Scholar] [CrossRef]
- Vieux, B.E.; Bedient, P.B. Estimation of Rainfall for Flood Prediction from WSR-88D Reflectivity: A Case Study, 17–18 October 1994. Weather Forecast. 1998, 13, 407–415. [Google Scholar] [CrossRef]
- Aziding, K.; Badron, K.; Basri, A.B.; Ismail, A.F.; Ahmad, Y.A. Enhanced Technique for Prediction of Z-R Relationship in Tropical Region. J. Physics Conf. Ser. 2023, 2559, 012009. [Google Scholar] [CrossRef]
- Orellana-Alvear, J.; Célleri, R.; Rollenbeck, R.; Bendix, J. Analysis of Rain Types and Their Z–R Relationships at Different Locations in the High Andes of Southern Ecuador. J. Appl. Meteorol. Climatol. 2017, 56, 3065–3080. [Google Scholar] [CrossRef]
- Yeo, J.; Lee, Y.; Ong, J. Radar measured rain attenuation with proposed Z–R relationship at a tropical location. AEU-Int. J. Electron. Commun. 2015, 69, 458–461. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
