Mission Planning and Trajectory Optimization in UAV Swarm for Track Deception against Radar Network

Abstract

In this article, a mission planning and trajectory optimization scheme in unmanned aerial vehicle (UAV) swarm for track deception against radar networks is proposed. The core of this scheme is to formulate the track deception problem as a model with the objective of simultaneously maximizing the number of phantom tracks while minimizing the total flight distance of the UAV swarm, subject to the constraints of UAV kinematic performance, phantom track rotation angles, and a homology test. It is shown that the formulated track deception problem is a mixed-integer programming, multivariable, and non-linear optimization model. By incorporating mission planning based on platform reuse and a particle swarm optimization (PSO) algorithm, a three-stage solution methodology is proposed to tackle the above problem. Through joint optimization for mission planning and flight trajectories of the UAV swarm, a low-speed UAV swarm is capable of generating a number of high-speed phantom tracks. Numerical results demonstrate that the proposed scheme enables a low-speed UAV swarm to generate as many high-speed phantom tracks as possible, effectively achieving track deception against radar network.

1. Introduction

1.1. Literature Review and Motivation

In recent years, radar network systems have garnered significant attention for their robust capabilities in anti-reconnaissance, anti-suppression jamming, and anti-deception jamming in the realm of electronic countermeasures [1,2]. A sophisticated method of active jamming involving the use of phantom tracks created by unmanned aerial vehicle (UAV) swarms to deceive radar networks has gained considerable interest from researchers and practitioners. These UAVs utilize digital radio frequency memory (DRFM) to manipulate and delay intercepted radar signals, thereby causing the radar to identify the phantom targets. However, due to the homology test rules employed by radar networks, the fusion center can only recognize a phantom target as valid after multiple radars simultaneously identify it. Therefore, it is essential to execute mission planning and trajectory optimization for the UAV swarm to effectively collaborate in deceiving the radars within the radar network system [3].

As one of the critical problems for track deception by the UAV swarm, the UAV swarm trajectory planning has been developed. For instance, López et al. [4] propose a 4D trajectory planning algorithm based on the fast marching square (FM2) method for UAV swarms, leveraging the light propagation phenomenon to integrate UAV movement with speed. Cao et al. [5] focus on trajectory planning for multiple tethered UAVs, proposing a tether-aware representation of homotopy to avoid collision and entanglement. Moreover, Du et al. [6] investigate a chance-constrained optimization method for probabilistic geo-fence scenarios. Taking into account the complex missions and environments faced by UAV swarms, Bai et al. [7] present a multi-UAV cooperative trajectory planning model based on multi-objective optimization, using the NSGA-III algorithm to find a Pareto optimal solution. Tang et al. [8] categorize scenarios into three types, each with a distinct mission redistribution strategy, to address dynamic emergent adjustment situations. They employ fuzzy C-means clustering and the ant colony optimization (ACO) algorithm to solve the task reallocation problem. In [9], the authors enhance the artificial electric field algorithm (AEFA) through parameter adaptation, reverse learning, and Cauchy mutation. They then apply this improved algorithm to 3D robot path planning and conduct simulation experiments to assess the effects of the enhanced mechanisms, the number of control points, and the number of robots. In [10], the authors put forward a trajectory homotopy optimization framework for multi-UAVs using Gaussian probability field (GPF) grid maps, which consider the dynamic mission planning with obstacles and perception constraints.

In addressing the issue of high computational complexity associated with an increasing number of discrete waypoints, Guo et al. [11] propose a flexible path discretization scheme to reduce the selected waypoints and decompose the 3D UAV path into three 1D paths to compress the path representation. The work in [12] integrates the spatial skeleton extraction method and the greedy algorithm with the rapidly exploring random tree (RRT) to enhance UAV path planning efficiency. In [13], the authors introduce a novel recursive smooth trajectory (RST) approach, which aims at constructing a smooth polynomial trajectory satisfying various dynamics constraints.

In practical scenarios, track deception by the UAV swarm must adhere to the line of sight (LOS) criterion, i.e., the radar, UAV, and phantom target remain aligned at the same time. To deal with this problem, Maithripala et al. [14] compute the UAV’s feasible flight sector based on UAV kinematic performance constraints and then calculate the phantom target’s flight sector using proportional navigation laws. Later on, they [15] incorporate the differential geometric method into phantom track generation with feasibility analysis. Additionally, Purvis et al. [16] present generalized boundaries for UAV initial conditions and feasible regions based on linear and circular phantom trajectories, integrating these into a discrete collaborative control problem solved with coordination functions. Dhananjay et al. [17] utilize the LOS guidance for trajectory planning, using the distance between the same phantom targets generated by the different UAVs as the performance metrics. Shima et al. [18] utilize a distributed control architecture under communication constraints to manage UAV swarms for track deception. In [19], the authors analyze track deception under infinite duration and minimum control cost conditions. To address the problem of track deception in 3D space, Maithripala et al. [20] propose a 3D phantom track generation scheme based on parameterized differential space curves in ${ℝ}^3$. Lee and Bang [21] extend the LOS guidance methodology in [17] to 3D space using predictive controllers. Furthermore, by projecting the radars and UAVs onto the vertical plane, the work in [22] extends 2D trajectories to 3D trajectories. The study in [23] positions the boundary navigation UAV by applying a navigation decoy signal to induce UAV swarm.

Generally, the problem of track deception against radar networks amounts to optimizing the trajectories of UAVs or phantom targets. The work in [24] analyzes the positional coupling between UAVs and phantom targets, defining a joint cost function that includes the flight costs of the UAV swarm and phantom targets. Purvis et al. [25,26] consider UAV kinematic performance constraints, incorporating a smooth penalty function into the cost function and employing optimal control methods to compute the trajectories of UAVs. In [27], the authors aim to minimize UAV flight distance, establishing an intelligent UAV swarm track deception mathematical model for radar networks and solving it with a PSO algorithm. Xu and Basset [28] employ a biomimetic intelligence algorithm for the longest sustainable constant-speed trajectory planning, simplifying multidimensional optimization into 1D problems. Compared to the studies in [14,15,16,17,18,19,20,21,22], the research mentioned above, which employ optimization methods to solve the track deception problem, utilize penalty terms to handle constraints, thereby ensuring the feasibility of the generated UAV and phantom target trajectories. These approaches allow for the adaptation to various mission requirements under different environmental conditions by setting appropriate optimization objectives. However, when faced with more stringent constraints, such methods require extensive computational searches of the solution space to find feasible solutions. In contrast, the studies in [14,15,16,17,18,19,20,21,22] derive solutions that satisfy the constraints, theoretically ensuring the feasibility of the generated UAV and phantom target trajectories.

Aiming at the track deception with the UAV swarm controlling errors or radar position errors, Liu and Li [29] analyze the effects of radar site detection errors and pre-set location errors of UAV on track deception, proposing a bias compensation mechanism. In [30], the authors derive boundary conditions for the effective deceptive interference of radar networks using DRFM under constant spatial resolution, analyzing the impact of relay delay errors on deceptive interference effectiveness for typical radar systems. In [31], the authors propose UAV time-difference-of-arrival (TDOA) passive localization, establishing a linear time-varying model and using extended Kalman filter (EKF) to reduce localization errors, which considers the radar with insufficient prior position information and site errors. To address scenarios where prior knowledge of radar positions is unavailable, Wang et al. [32] employ a UAV swarm equipped with TDOA and frequency-difference-of-arrival (FDOA) techniques to locate radars and generate phantom targets.

Nevertheless, most of the previous literature focuses on feasible trajectories of phan-tom targets and UAV swarms, while neglecting the problem of efficient track deception. That is to say, considering maximizing the number of phantom targets and the generation of high-speed phantom targets simultaneously is crucial for the application of this technique. As aforementioned, the studies in [24,25,26,27,28] only optimize the trajectories of UAVs to obtain feasible trajectories satisfying all constraints, whereas these approaches do not concentrate on efficient track deception. To be specific, due to the homology test, it is necessary to generate identical phantom targets by the UAVs for different radars, requiring a considerable number of UAVs to produce a small number of phantom targets. In addition, it is challenging to utilize the low-speed UAV swarm to generate high-speed phantom targets, which are more credible and menacing to the radar network. Hence, it is essential to determine the optimal mission planning and trajectories for the UAVs. This gap motivates this article.

1.2. Major Contributions

The major contributions and results of this article are summarized as follows:

• The problem of phantom track generation by UAV swarm against radar network is formulated as a mathematical optimization model under the constraints of the UAV kinematic performance, phantom track rotation angles, and homology test. Previous studies on track deception primarily aimed to obtain feasible flight trajectories, with little focus on efficient track deception. Thus, we propose a mission planning and trajectory optimization scheme to produce numerous high-speed phantom tracks using a UAV swarm. To be more specific, our goal is to maximize the number of phantom targets while minimizing the total flight distance of the UAV swarm. This is achieved by jointly conducting mission planning and optimizing the trajectories of UAV swarm and phantom track rotation angles within the constraints of UAV kinematic performance, phantom track rotation angles, and homology test.
• In order to tackle this mixed-integer programming, multivariable, non-linear, dual-objective optimization problem, we design a three-stage solution methodology, which incorporates the mission planning based on platform reuse and PSO algorithm. Generally speaking, since the UAVs and phantom targets must adhere to the LOS criterion, it is challenging and rather difficult to determine the feasible and optimal solution. By exploiting the problem partition, we transform the origin problem into two subproblems, solving them by the mission planning based on platform reuse and PSO algorithm, respectively, to find the suboptimal solutions.
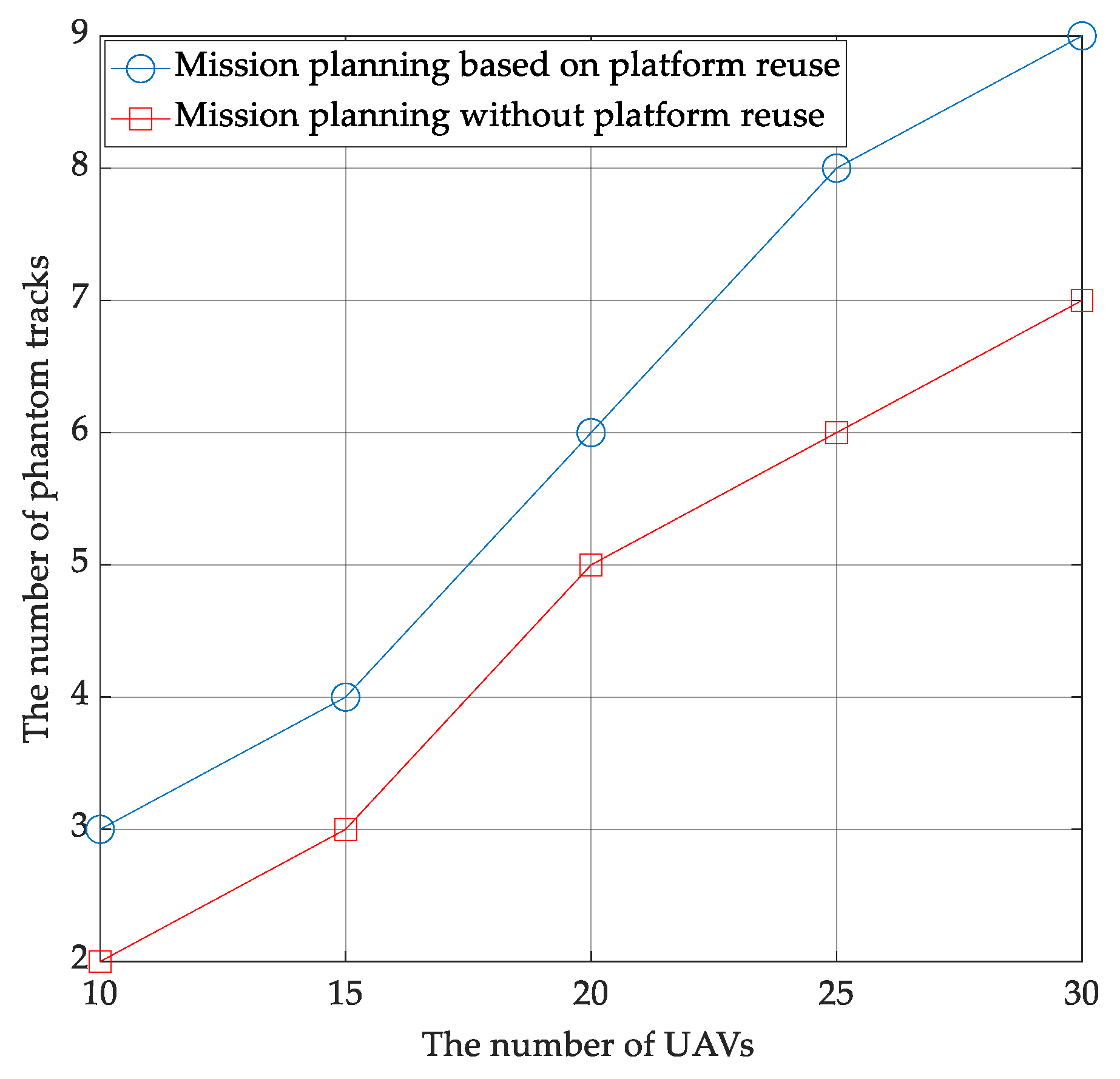
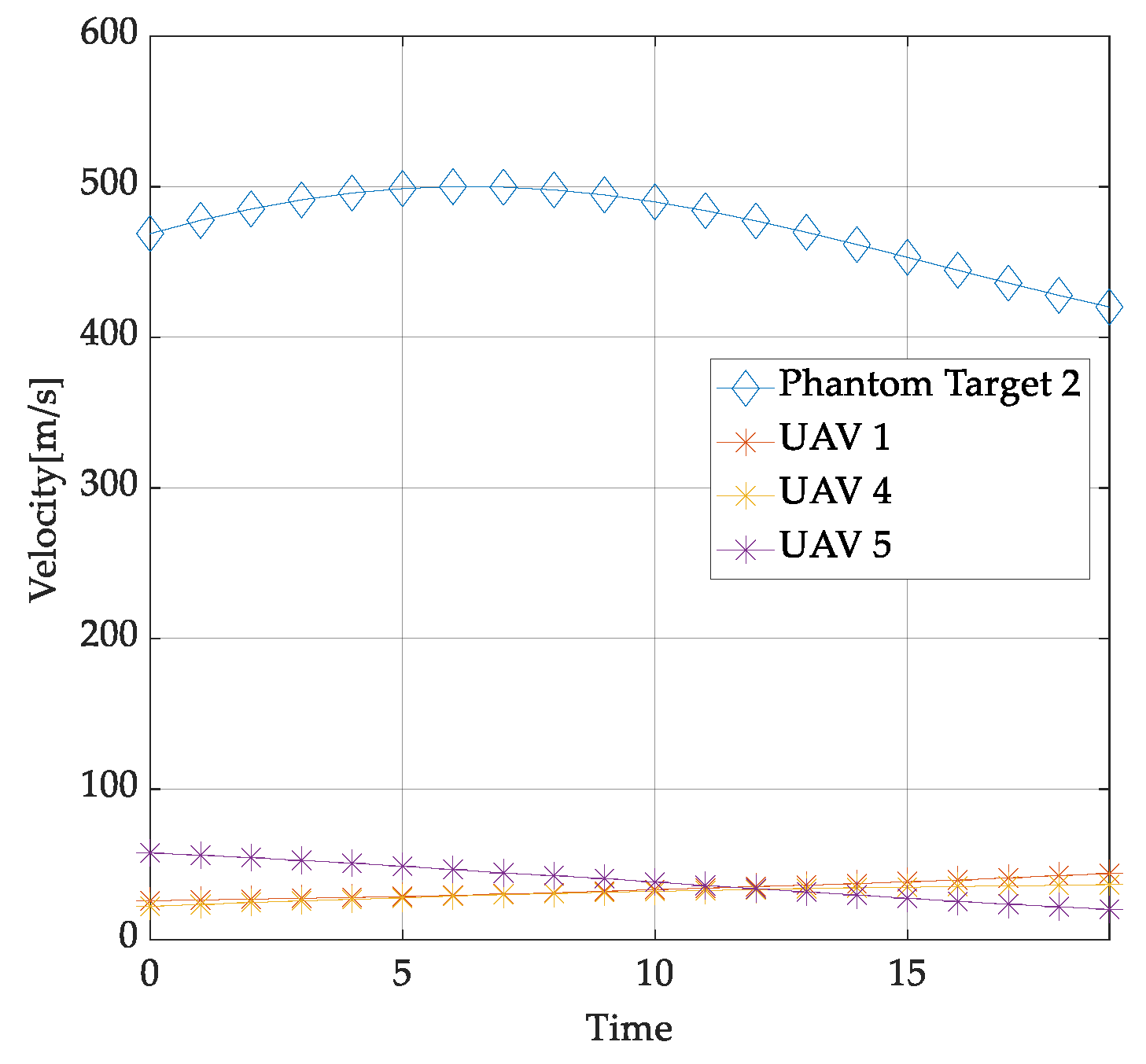
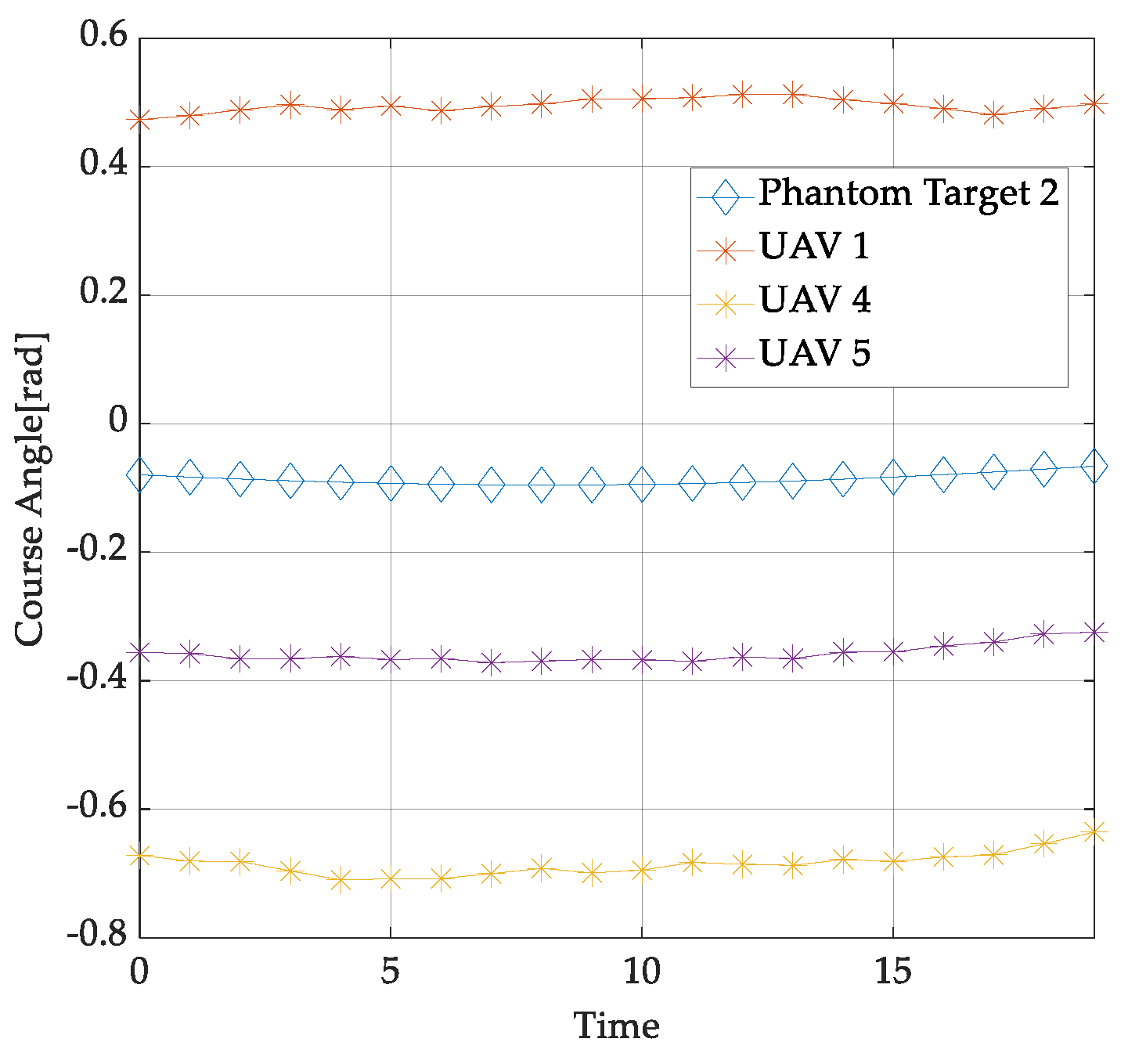
• Numerical simulation is provided to validate the superiority of the proposed mission planning and trajectory optimzation scheme in terms of the number of phantom targets and velocity performance. The results demonstrate that the proposed scheme can generate more high-speed phantom targets. Additionally, the UAVs maintain low speeds consistently with smooth motion curves, indicating feasible trajectories without excessive maneuvering.

1.3. Organization of the Article

The rest of this article is organized as follows: Section 2 outlines the fundamental principles of track deception, including essential prerequisites. Section 3.1 introduces the track deception model using a single UAV. By considering the number of generated phantom targets and UAV velocity performance simultaneously in Section 3.2 to evaluate the deception performance, the formulation of the track deception scheme is presented in Section 3.3. Section 4 outlines the corresponding solution method. The simulation results and performance analyses are provided in Section 5. Finally, Section 6 concludes this article.

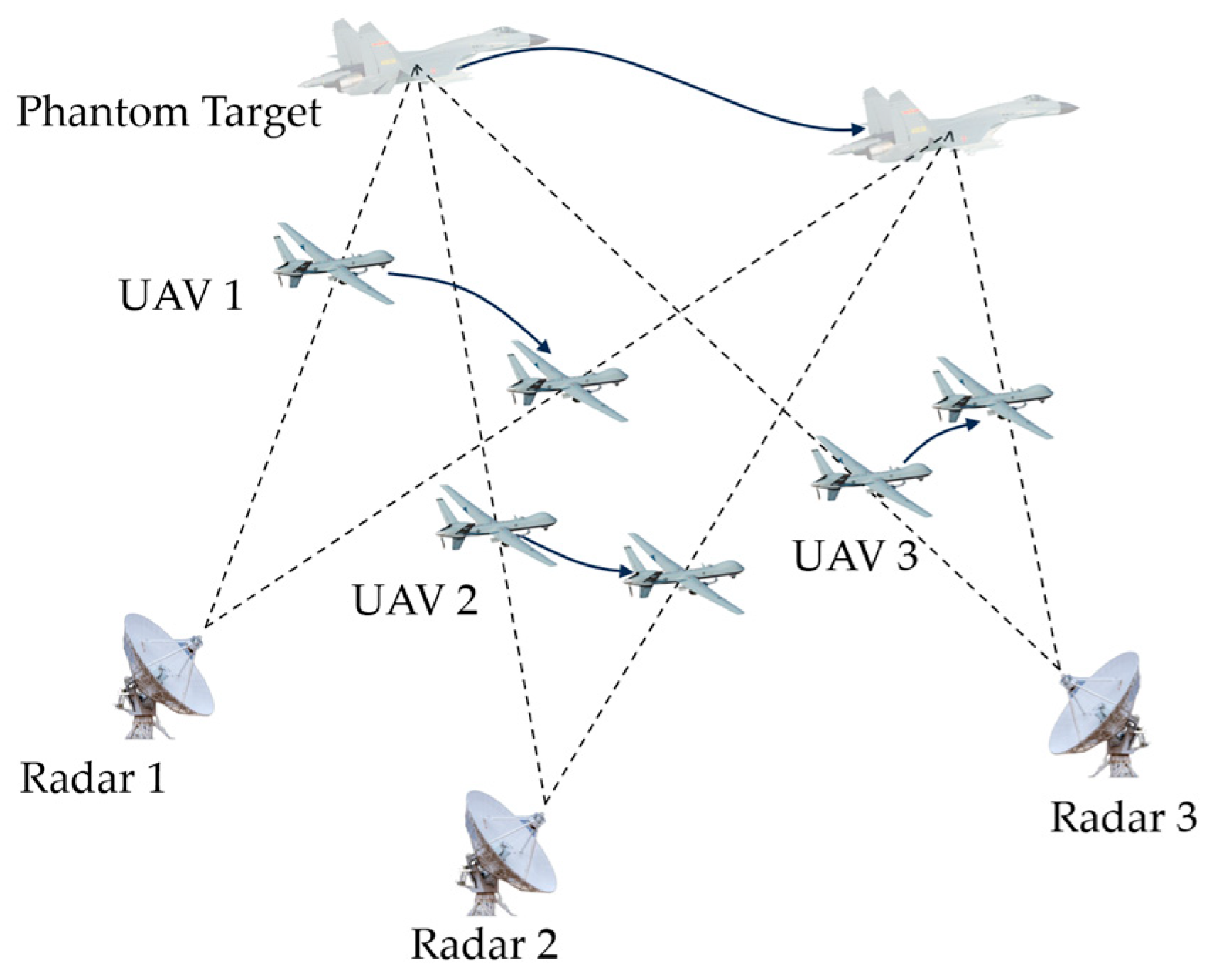
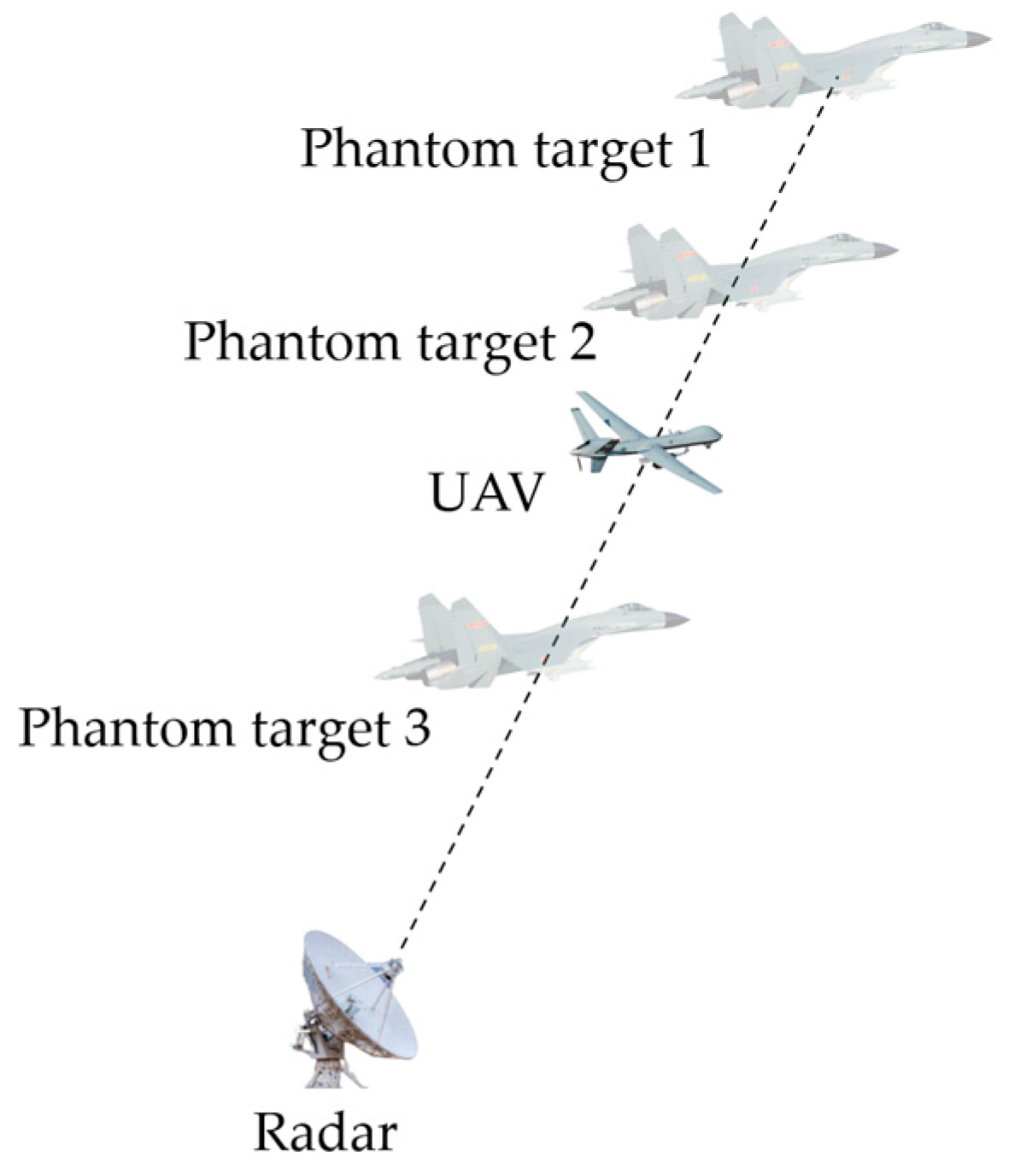
2. Fundamental Principle of Track Deception

The fundamental principle of track deception is to exploit the ranging principle of common pulse system radar. The UAVs, equipped with DRFM, retransmit intercepted radar signals after a delay, causing the radar to perceive these signals as phantom targets. Multiple continuous phantom waypoints can thereby form a phantom track.

The radar network system often employs the homology test rules to verify identified targets. When radars transmit the position information of a target to the fusion center, the fusion center considers it a valid track point if multiple radars report the same spatial positions simultaneously. Figure 1 illustrates how multiple continuous valid track points can form a reasonable track, with dashed lines representing the lines of sight of radars and wavy arrows indicating the flight trajectories of UAV or phantom target. To deceive the radar network system, the UAV swarm must create spatially overlapping phantom targets for multiple radars at continuous intervals, passing the homology test and generating a phantom track.

To successfully conduct phantom track deception, some assumptions are made to simplify the considered problem as follows:

Assumption 1: In the radar network system, the position information and transmitting signal parameters of each radar are known, and all radars operate as single-input single-output systems;

Assumption 2: The UAV can only deceive the same radar to generate one or more phantom targets at the same time;

Assumption 3: The flight velocity, flight height, pitch angle, and course angle of the UAV are all controlled within a reasonable range. The UAV can fly to the specified position at the specified times according to the preset flight path to retransmit the specified parameter signals.

3. System Model

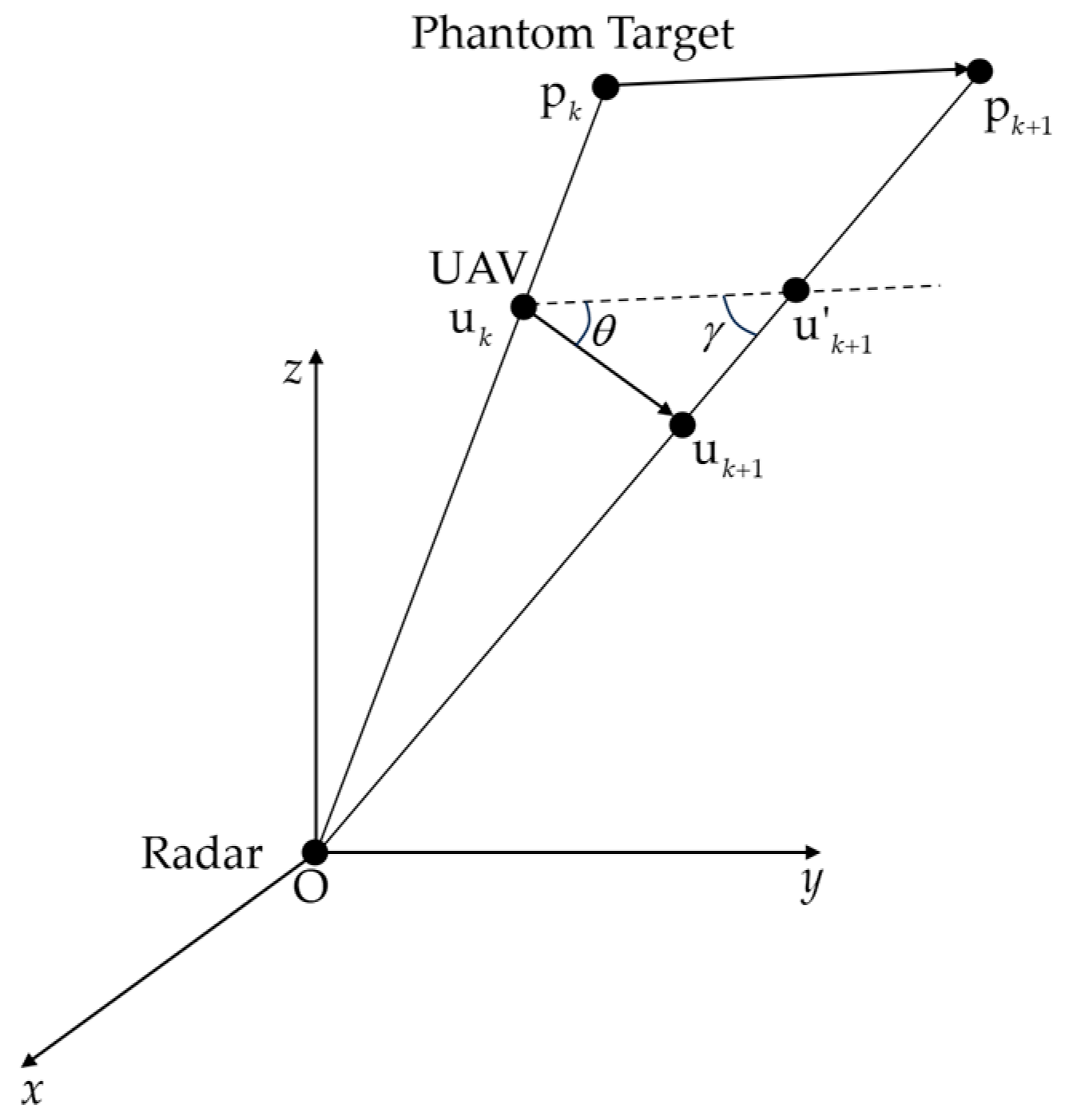
3.1. Track Deception Model by Single UAV

If the phantom track is known, the motion parameters of the UAV at any given time can be determined, as the radar, UAV, and phantom target consistently adhere to the LOS criterion.

First, consider the initial position of the UAV. Since the radar, UAV, and phantom target consistently adhere to the LOS criterion, the initial position of the UAV can be determined if the initial flight height $z_{\mathrm{u},0}$ is specified:

$$\{\begin{array}{l}{x}_{\mathrm{u},0}={\displaystyle \frac{z_{\mathrm{u},0}}{z_{\mathrm{p},0}}}{x}_{\mathrm{p},0}\\ y_{\mathrm{u},0}={\displaystyle \frac{z_{\mathrm{u},0}}{z_{\mathrm{p},0}}}{y}_{\mathrm{p},0}\\ z_{\mathrm{u},0}=z_{\mathrm{u},0}\end{array}$$

(1)

Consider the position of the UAV at time $\left(k+1\right)$ given that the position of the UAV at time $k$ is known. As shown in Figure 2, assuming that the velocity direction of the UAV aligns with that of the phantom target, the position of the UAV ${{\mathrm{u}}^{\prime }}_{k+1}$ at time $\left(k+1\right)$ can be expressed as follows:

$$\{\begin{array}{l}{x}_{{\mathrm{u}}^{\prime },k+1}={\displaystyle \frac{z_{\mathrm{u},k}}{z_{\mathrm{p},k}}}{x}_{\mathrm{p},k+1}\\ y_{{\mathrm{u}}^{\prime },k+1}={\displaystyle \frac{z_{\mathrm{u},k}}{z_{\mathrm{p},k}}}{y}_{\mathrm{p},k+1}\\ z_{{\mathrm{u}}^{\prime },k+1}={\displaystyle \frac{z_{\mathrm{u},k}}{z_{\mathrm{p},k}}}{z}_{\mathrm{p},k+1}\end{array}$$

(2)

In practice, the velocity direction of the UAV may not necessarily align with that of the phantom target. Let $\theta$ represent the angle between the two velocity directions. If $\theta >0$, ${\mathrm{u}}_{k+1}$ is positioned above ${{\mathrm{u}}^{\prime }}_{k+1}$; otherwise, ${\mathrm{u}}_{k+1}$ is located below ${{\mathrm{u}}^{\prime }}_{k+1}$. The distance between ${\mathrm{u}}_{k+1}$ and ${{\mathrm{u}}^{\prime }}_{k+1}$ can be computed as follows:

$$\left|\overrightarrow{{\mathrm{u}}_{k+1}{{\mathrm{u}}^{\prime }}_{k+1}}\right|={\displaystyle \frac{\sin \left|\theta \right|}{\sin \left(\pi -\left|\theta \right|-\phi \right)}}\left|\overrightarrow{{\mathrm{u}}_k{{\mathrm{u}}^{\prime }}_{k+1}}\right|$$

(3)

where $\phi$ can be written as follows:

$$\phi =\{\begin{array}{l}\arccos \left({\displaystyle \frac{\overrightarrow{{\mathrm{Op}}_{k+1}}·\overrightarrow{{\mathrm{p}}_k{\mathrm{p}}_{k+1}}}{\left|\overrightarrow{{\mathrm{Op}}_{k+1}}\right|\left|\overrightarrow{{\mathrm{p}}_k{\mathrm{p}}_{k+1}}\right|}}\right)\begin{array}{cc}& \left(\theta <0\right)\end{array}\\ \pi -\arccos \left({\displaystyle \frac{\overrightarrow{{\mathrm{Op}}_{k+1}}·\overrightarrow{{\mathrm{p}}_k{\mathrm{p}}_{k+1}}}{\left|\overrightarrow{{\mathrm{Op}}_{k+1}}\right|\left|\overrightarrow{{\mathrm{p}}_k{\mathrm{p}}_{k+1}}\right|}}\right)\begin{array}{cc}& \left(\theta >0\right)\end{array}\end{array}$$

(4)

Since the coordinates of ${{\mathrm{u}}^{\prime }}_{k+1}$ have been described in Formula (2), the actual position coordinates of the UAV at time $\left(k+1\right)$ are

$${\mathrm{u}}_{k+1}=\{\begin{array}{l}{{\mathrm{u}}^{\prime }}_{k+1}-\left|\overrightarrow{{\mathrm{u}}_{k+1}{{\mathrm{u}}^{\prime }}_{k+1}}\right|\overrightarrow{n}\begin{array}{cc}& \left(\theta <0\right)\end{array}\\ {{\mathrm{u}}^{\prime }}_{k+1}+\left|\overrightarrow{{\mathrm{u}}_{k+1}{{\mathrm{u}}^{\prime }}_{k+1}}\right|\overrightarrow{n}\begin{array}{cc}& \left(\theta >0\right)\end{array}\end{array}$$

(5)

where $\overrightarrow{n}$ denotes the unit vector of $\overrightarrow{{\mathrm{Op}}_{k+1}}$.

To sum up, if the phantom track is known, the trajectory planning of a single UAV can be completed by controlling $\theta$, which is the angle between the speed direction of the UAV and that of the phantom target at each time.

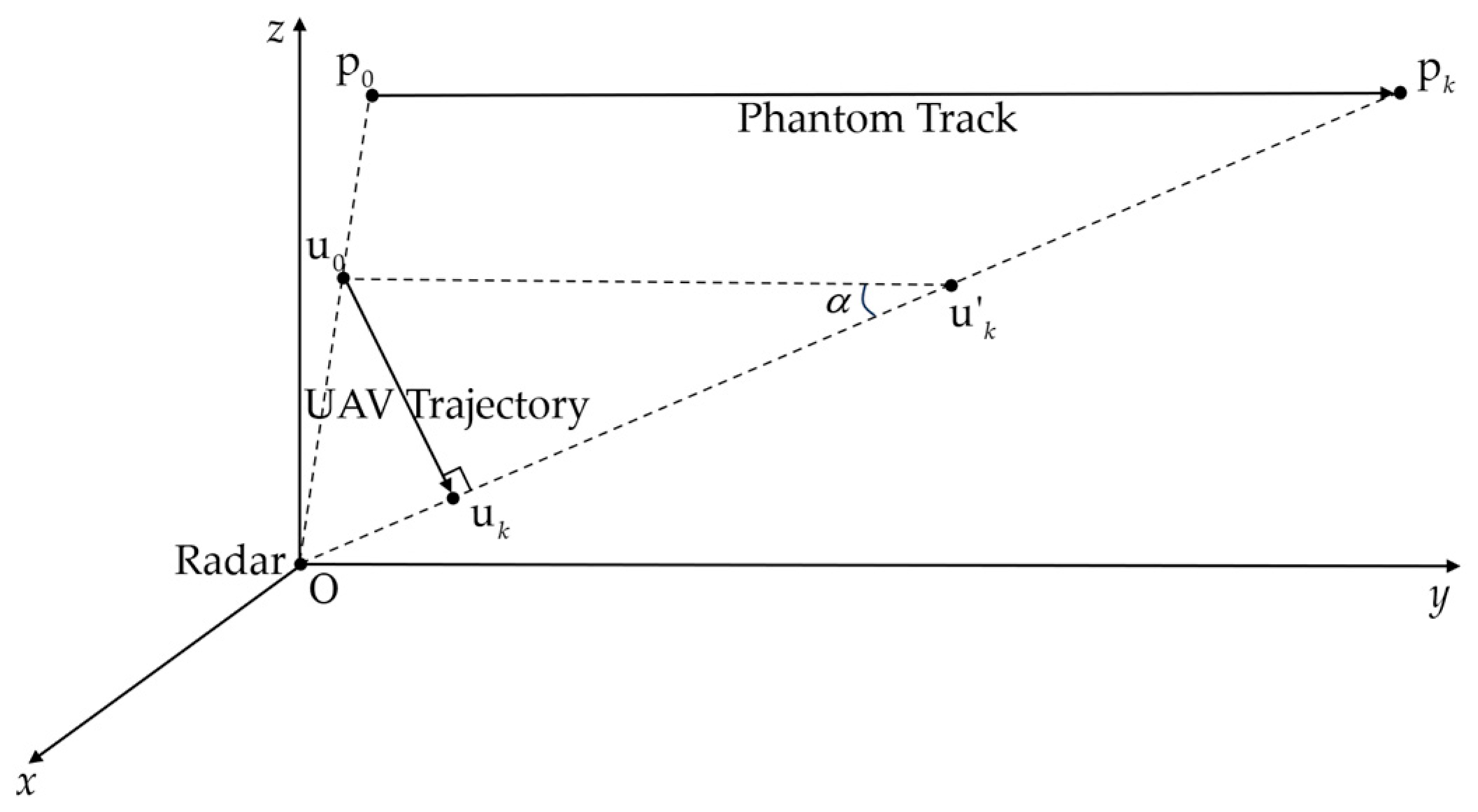
3.2. Performance Metric for Track Deception

To generate more phantom tracks with a limited number of UAVs, we define the phantom track number cost function $J_1$ as follows:

$$J_1\triangleq -{\displaystyle \frac{1}{S}}{\displaystyle \sum _{n=1}^S{G}_n}$$

(6)

where $G_n$ represents the number of phantom tracks generated by the n-th UAV and $S$ represents the total number of UAVs in a UAV swarm.

Due to the constant time interval between two waypoints of a UAV and a phantom target at consecutive time steps, we can reduce the UAVs’ velocity by selecting appropriate waypoints to minimize the total flight distance, given that high-speed phantom tracks have been established. To enable low-speed UAV swarm to generate high-speed phantom targets, we define the cost function $J_2$ as follows:

$$J_2\triangleq {\displaystyle \frac{\overline{z_{\mathrm{p}}}}{h_{\mathrm{u},\min }\overline{D_{\mathrm{p}}}S}}{\displaystyle \sum _{n=1}^S{\displaystyle \sum _{k=1}^K{d}_{{\mathrm{u}}_n,k}}}$$

(7)

where $S$ denotes the number of UAVs; $K$ denotes the number of deception moments; $\overline{z_{\mathrm{p}}}$ and $\overline{D_{\mathrm{p}}}$ denote the average flight height and average flight distance of the phantom target, respectively; $h_{\mathrm{u},\min }$ denotes the lower limit of UAV flying height; and $d_{{\mathrm{u}}_n,k}$ denotes the flight distance of the $n$-th UAV in the $k$-th time interval.

Therefore, considering maximizing the number of phantom tracks and minimizing the total flight distance of UAV swarms, the optimization objective is defined as follows:

$$J\triangleq {\omega }_1\left(-{\displaystyle \frac{1}{S}}{\displaystyle \sum _{n=1}^S{G}_n}\right)+{\omega }_2{\displaystyle \frac{\overline{z_{\mathrm{p}}}}{h_{\mathrm{u},\min }\overline{D_{\mathrm{p}}}S}}{\displaystyle \sum _{n=1}^S{\displaystyle \sum _{k=1}^K{d}_{{\mathrm{u}}_n,k}}}$$

(8)

where ${\omega }_1$ and ${\omega }_2$ represent the weighting coefficients of the cost function $J_1$ and $J_2$, respectively.

In this paper, we consider the influence of three types of parameters on the optimization objective:

The influence of the mission planning for UAV swarm on cost function $J_1$: As illustrated in Figure 3, since each UAV can generate multiple phantom targets for the same radar, a greater number of phantom tracks can be generated by rationally conducting mission planning, which can be described by ${\mu }_{n,m,r}$:

$${\mu }_{n,m,r}=\{\begin{array}{ll}1& \mathrm{If} \mathrm{the} n\text{-}\mathrm{th} \mathrm{UAV} \mathrm{deceives} \mathrm{the} r\text{-}\mathrm{th} \mathrm{radar} \\ & \mathrm{into} \mathrm{generating} \mathrm{the} m\text{-}\mathrm{th} \mathrm{phantom} \mathrm{target}\\ 0& \mathrm{otherwise}\end{array}$$

(9)

The influence of UAV trajectory on the cost function $J_1$ and $J_2$: Each UAV in the UAV swarm has multiple potential trajectories to choose from. Optimal trajectories must be determined to maximize the number of phantom tracks and minimize the total flight distance, while effectively conducting mission planning for the UAV swarm.

The influence of the orientation relationship between the phantom track and the radar network on the cost function $J_2$: As shown in Figure 4, for the straight-line phantom track, when the UAV trajectory is perpendicular to the straight line connecting the radar and the last position of the phantom target, the shortest UAV trajectory is obtained. Since ${\mathrm{u}}_0{{\mathrm{u}}^{\prime }}_k\parallel {\mathrm{p}}_0{\mathrm{p}}_k$ and ${\mathrm{u}}_0{\mathrm{u}}_k\perp {\mathrm{Op}}_k$, the flying distance of the UAV is computed as follows:

$$d={\displaystyle \frac{h_{\mathrm{u}}}{h_{\mathrm{p}}}}\left|\overrightarrow{{\mathrm{p}}_0{\mathrm{p}}_k}\right|\sin \alpha$$

(10)

When the initial height of the UAV is constant, the shortest flight distance depends solely on $\alpha$, which is determined by the relative positional relationship between the radar and the phantom track. Therefore, the orientation relationship between the phantom track and radar networks is one of the significant factors influencing the flight distance of UAVs.

In this paper, this orientation relation is quantified by the rotation angles $\gamma$ on the $xy$-plane, which modifies the phantom track as follows:

$$\left[\begin{array}{l}{x^{\prime }}_{\mathrm{p}}^k\\ {y^{\prime }}_{\mathrm{p}}^k\\ {z^{\prime }}_{\mathrm{p}}^k\end{array}\right]=\left[\begin{array}{ccc}\cos \gamma & \sin \gamma & 0\\ -\sin \gamma & \cos \gamma & 0\\ 0& 0& 1\end{array}\right]\left(\left[\begin{array}{l}{x}_{\mathrm{p}}^k\\ y_{\mathrm{p}}^k\\ z_{\mathrm{p}}^k\end{array}\right]-\left[\begin{array}{l}{x}_{\mathrm{p}}^{mid}\\ y_{\mathrm{p}}^{mid}\\ z_{\mathrm{p}}^{mid}\end{array}\right]\right)+\left[\begin{array}{l}{x}_{\mathrm{p}}^{mid}\\ y_{\mathrm{p}}^{mid}\\ z_{\mathrm{p}}^{mid}\end{array}\right]$$

(11)

where $(x_{\mathrm{p},mid},y_{\mathrm{p},mid},z_{\mathrm{p},mid})$ represents the coordinates of the phantom track at the intermediate time.

3.3. Problem Formulaion

To conduct track deception by the UAV swarm, some physical limitations and constraints must be taken into consideration. First, we consider the UAV kinematic performance constraints, such that

$$\{\begin{array}{l}{v}_{\mathrm{u},\min }\le v_{{\mathrm{u}}_n,k}\le v_{\mathrm{u},\max }\\ \Delta {\alpha }_{\mathrm{u},\min }\le \Delta {\alpha }_{{\mathrm{u}}_n,k}\le \Delta {\alpha }_{\mathrm{u},\max }\\ {\beta }_{\mathrm{u},\min }\le {\beta }_{{\mathrm{u}}_n,k}\le {\beta }_{\mathrm{u},\max }\\ h_{\mathrm{u},\min }\le h_{{\mathrm{u}}_n,k}\le h_{\mathrm{u},\max }\\ d_{{\mathrm{u}}_{n1},{\mathrm{u}}_{n2}}\ge d_{\mathrm{safe}}\end{array}$$

(12)

where $v_{{\mathrm{u}}_n,k}$ represents UAV velocity; $v_{\mathrm{u},\min }$ and $v_{\mathrm{u},\max }$ represent the minimum and maximum values of UAV velocity, respectively; $\Delta {\alpha }_{{\mathrm{u}}_n,k}$ represents the yew angle of UAV; $\Delta {\alpha }_{\mathrm{u},\min }$ and represent the minimum and maximum values of the yew angle, respectively; ${\beta }_{{\mathrm{u}}_n,k}$ represents the pitch angle of UAV; ${\beta }_{\mathrm{u},\min }$ and ${\beta }_{\mathrm{u},\max }$ represent the minimum and maximum values of the pitch angle, respectively; $h_{{\mathrm{u}}_n,k}$ represents the flight height of UAV; $h_{\mathrm{u},\min }$ and $h_{\mathrm{u},\max }$ represent the minimum and maximum values of flight height, respectively; $d_{{\mathrm{u}}_{n1},{\mathrm{u}}_{n2}}$ represents the distance between UAVs; and $d_{\mathrm{safe}}$ represents the safe distance between UAVs.

Then, since the phantom track reflects the mission intent, the phantom track must maintain a certain direction, namely:

$${\gamma }_{\min }\le \gamma \le {\gamma }_{\max }$$

(13)

where $\gamma$ represents the phantom track rotation angles and ${\gamma }_{\min }$ and ${\gamma }_{\max }$ represent the minimum and maximum values of the phantom track rotation angles, respectively.

Moreover, to pass the homology test, the following formula must be satisfied for any phantom track:

$${\displaystyle \sum _{r=1}^R{H}_{m,r}\ge N_{\mathrm{R}}}$$

(14)

where $R$ represents the number of radars in the radar network; $N_{\mathrm{R}}$ represents how many radars in the radar network must identify the identical phantom target; and $H_{m,r}$ is a Boolean variable defined as follows:

$$H_{m,r}=\{\begin{array}{ll}1& \mathrm{if} \mathrm{a} \mathrm{UAV} \mathrm{is} \mathrm{positioned} \mathrm{on} \mathrm{the} \mathrm{line} \mathrm{segment} \\ & \mathrm{between} \mathrm{the} m\text{-}\mathrm{th} \mathrm{phantom} \mathrm{target} \mathrm{and} \mathrm{the} r\text{-}\mathrm{th} \mathrm{radar}\\ 0& \mathrm{otherwise}\end{array}$$

(15)

In general, the primary goal of the proposed mission planning and trajectory optimization scheme is to maximize the number of phantom trajectories and minimize the total flight distance of the UAV swarm, subject to the constraints of UAV kinematic performance, phantom track rotation angles, and homology test. By jointly conducting mission planning and optimizing the trajectories of UAV swarm and phantom track rotation angles, the optimization problem can be formulated in the following:

$$\begin{array}{c}\underset{\mathit{\mu },\mathit{\theta },{\mathit{z}}_0,\mathit{\gamma }}{\min }{\omega }_1\left(-{\displaystyle \frac{1}{S}}{\displaystyle \sum _{n=1}^S{G}_n}\right)+{\omega }_2{\displaystyle \frac{\overline{z_{\mathrm{p}}}}{h_{\mathrm{u},\min }\overline{D_{\mathrm{p}}}S}}{\displaystyle \sum _{n=1}^S{\displaystyle \sum _{k=1}^K{d}_{{\mathrm{u}}_n,k}}}\\ \mathrm{s}.\mathrm{t}.:\{\begin{array}{l}(12)–(14)\\ {\mu }_{n,m,r}\in \left\{0,1\right\}\\ H_{m,r}\in \left\{0,1\right\}\end{array}\end{array}$$

(16)

4. Solution Technique

The formulated optimization model in Equation (16) is a mixed-integer programming, multivariable, and non-linear optimization problem, which is difficult to solve directly. Due to the LOS criterion, the UAVs must be positioned along the line connecting the phantom targets and the radar. Although directly solving problem (16) may yield an optimal solution, finding a feasible solution that simultaneously ensures efficient path planning and maximizes the number of phantom targets satisfying the LOS criterion is challenging and time-consuming. Therefore, in this paper, we leverage a three-stage solution methodology by incorporating the mission planning based on platform reuse and PSO to tackle this problem. The specific solving stages are as follows:

Stage (1) Problem Partition: Since the radar, UAVs, and phantom targets must strictly adhere to the LOS criterion, obtaining a feasible solution is challenging if simultaneously considering the mission planning and trajectory optimization. Therefore, Equation (16) is partitioned as

$$\begin{array}{l}\begin{array}{cc}& \end{array}\underset{\mathit{\mu }}{\max }{\displaystyle \sum _{n=1}^S{G}_n}\\ \mathrm{s}.\mathrm{t}.:\{\begin{array}{l}{\displaystyle \sum _{r=1}^R{H}_{m,r}\ge N_{\mathrm{R}}}\\ {\mu }_{n,m,r}\in \{0,1\}\\ H_{m,r}\in \{0,1\}\end{array}\end{array}$$

(17)

and

$$\begin{array}{l}\begin{array}{cc}& \end{array}\underset{\mathit{\theta },{\mathit{z}}_0,\mathit{\gamma }}{\min }{\displaystyle \sum _{n=1}^S{\displaystyle \sum _{k=1}^K{d}_{{\mathrm{u}}_n,k}}}\\ \mathrm{s}.\mathrm{t}.:\{\begin{array}{l}{v}_{\mathrm{u},\min }\le v_{{\mathrm{u}}_n,k}\le v_{\mathrm{u},\min }\\ \Delta {\alpha }_{\mathrm{u},\min }\le \Delta {\alpha }_{{\mathrm{u}}_n,k}\le \Delta {\alpha }_{\mathrm{u},\max }\\ {\beta }_{\mathrm{u},\min }\le {\beta }_{{\mathrm{u}}_n,k}\le {\beta }_{\mathrm{u},\max }\\ h_{\mathrm{u},\min }\le h_{{\mathrm{u}}_n,k}\le h_{\mathrm{u},\max }\\ d_{{\mathrm{u}}_{n1},{\mathrm{u}}_{n2}}\ge d_{\mathrm{safe}}\\ {\gamma }_{\min }\le \gamma \le {\gamma }_{\max }\end{array}\end{array}$$

(18)

Stage (2) The Mission Planning for UAV Swarm: As shown in Figure 3, multiple phantom tracks generated by the same UAV also adhere to the LOS criterion. Hence, a phantom track generation method based on the proportional factor is first proposed.

In the space cartesian coordinate system with radar as the origin, as shown in Figure 2, the proportional factor ${\rho }_{m_2,m_1,k}$ of the $m_2$-th phantom target associating with the $m_1$-th phantom target at time $k$ is defined as

$${\rho }_{m_2,m_1,k}={\displaystyle \frac{r_{{\mathrm{p}}_{m_2},k}}{r_{{\mathrm{p}}_{m_1},k}}}={\rho }_{m_2,m_1}+{\rho }_{m_2,m_1,k}^{\mathrm{flu}}$$

(19)

where $r_{{\mathrm{p}}_{m_1},k}$ and $r_{{\mathrm{p}}_{m_2},k}$ denote the $m_1$-th phantom target and $m_2$-th phantom target range from radar, respectively; ${\rho }_{m_2,m_1}$ denotes the constant proportional factor, which gives the basic range of motion for the $m_2$-th phantom target; and ${\rho }_{m_2,m_1,k}^{\mathrm{flu}}$ denotes the fluctuation proportional factor at time $k$, which makes the trajectory of the $m_2$-th phantom target different from that of the $m_1$-th phantom target.

Therefore, the coordinates of the $m_2$-th phantom target at time $k$ are

$$\{\begin{array}{l}{x}_{{\mathrm{p}}_{m_2},k}={\rho }_{m_2,m_1,k}{x}_{{\mathrm{p}}_{m_1},k}\\ y_{{\mathrm{p}}_{m_2},k}={\rho }_{m_2,m_1,k}{y}_{{\mathrm{p}}_{m_1},k}\\ z_{{\mathrm{p}}_{m_2},k}={\rho }_{m_2,m_1,k}{z}_{{\mathrm{p}}_{m_1},k}\end{array}$$

(20)

Building on this basis and considering the hardware constraints, it is assumed that each UAV can generate at most two phantom targets. Equation (17) is then solved by conducting the mission planning based on platform reuse.

Suppose that the phantom target needs to pass the homology test of $N_{\mathrm{R}}$ radars. As shown in

Table 1. Table of mission planning for UAV swarm.

Phantom Track	UAV
1	UAV 1	UAV 2	…	$\mathrm{UAV} N_{\mathrm{R}}$
2	UAV 1	$\mathrm{UAV}\left(N_{\mathrm{R}}+1\right)$	…	$\mathrm{UAV}\left(2N_{\mathrm{R}}-1\right)$
3	UAV 2	$\mathrm{UAV}\left(2N_{\mathrm{R}}\right)$	…	$\mathrm{UAV}\left(3N_{\mathrm{R}}-2\right)$
…	…	…	…	…
$M$	$\mathrm{UAV}\left(M-1\right)$	$\mathrm{UAV}\left(\left(M-1\right)N_{\mathrm{R}}+3-M\right)$	…	$\mathrm{UAV}\left(N_{\mathrm{R}}+\left(M-1\right)\left(N_{\mathrm{R}}-1\right)\right)$

, for the first phantom track, the 1st to $N_{\mathrm{R}}$-th UAVs generate the first phantom track and pass the homology test. For the $m$-th phantom track $(m>1)$, the $\left(m-1\right)$-th UAV is used as the first UAV in this group, and $\left(N_{\mathrm{R}}-1\right)$ additional UAVs are introduced to ensure that the generated $m$-th phantom track passes the homology test. Subsequently, the task assignment for the remaining UAVs is carried out sequentially.

This mission planning ensures that at least one UAV in each UAV group generates two phantom targets, and the number of UAVs required to generate $L$ phantom tracks is as follows:

$$S=N_{\mathrm{R}}+\left(L-1\right)\left(N_{\mathrm{R}}-1\right)$$

(21)

where $S$ denotes the number of UAVs.

This is fewer than the $\left(N_{\mathrm{R}}L\right)$ UAVs required under the mission planning where UAVs are not reused.

Given $S$ UAVs $(S\ge N_R)$, the maximum number of phantom tracks by applying the above mission planning can be computed as follows:

$$L_{\max }=1+\lfloor {\displaystyle \frac{S-N_{\mathrm{R}}}{N_{\mathrm{R}}-1}}\rfloor$$

(22)

where $L_{\max }$ represents the maximum number of generated phantom tracks and $\lfloor ·\rfloor$ represents the round-down operator.

If ${\displaystyle \frac{S-N_{\mathrm{R}}}{N_{\mathrm{R}}-1}}$ is not an integer, some UAVs in the swarm will not be utilized. Therefore, consider dividing the UAV swarm into $n$ clusters, and for each cluster, assign the UAV-generated phantom targets according to the mission planning given in Table 1, ensuring that each UAV is utilized efficiently.

Specifically, if the number of phantom tracks generated by the $i$-th UAV cluster is $L_i$, then the number of UAVs required by the above mission planning is

$$S_i=N_{\mathrm{R}}+\left(L_i-1\right)\left(N_{\mathrm{R}}-1\right)$$

(23)

where $S_i$ denotes the number of UAVs in the $i$-th UAV cluster.

Since the number of UAVs in the UAV swarm is $S$, then

$${\displaystyle \sum _{i=1}^n{S}_i=S}$$

(24)

By substituting Formula (23) into Equation (24), we obtain the following result:

$$n=S-L\left(N_{\mathrm{R}}-1\right)$$

(25)

where $L$ represents the number of phantom targets generated by UAV swarm.

Therefore, to maximize the number of phantom tracks generated by the UAV swarm, $n$ must be minimum and satisfy $n\ge 1$. So $L_{\max }$ can be computed as follows:

$$L_{\max }=\lfloor {\displaystyle \frac{S-1}{N_{\mathrm{R}}-1}}\rfloor$$

(26)

where $\lfloor ·\rfloor$ represents the round-down operator. By substituting $L_{\max }$ into Formula (25), we can obtain $n_{\min }$.

After obtaining $L_{\max }$ and $n_{\min }$ from Formula (26), the number of phantom tracks $L_i$ generated by each UAV cluster can be allocated, and it needs to satisfy Equation (27):

$$\{\begin{array}{l}{\displaystyle \sum _{i=1}^{n_{\min }}{L}_i=L_{\max }}\\ L_i\ge 1\end{array}$$

(27)

After obtaining $L_i$, the number of UAVs and the mission planning of the $i$-th UAV cluster can be obtained from Formula (23) and Table 1.

For a given phantom target, the UAV being first utilized should select a radar that has not yet been deceived by other UAVs in the group. Furthermore, a UAV that has generated a phantom target should continue to deceive the radar that was deceived when the UAV was first utilized.

Stage (3) The Trajectory Optimization for UAV Swarm with Given Mission Planning: After conducting mission planning, the trajectories of UAVs can be identified by solving the optimization model (18). This optimization model is a multivariable, non-linear optimization problem. Given the PSO algorithm’s fast convergence and strong global optimization capabilities in high-dimensional problems, we employ this algorithm to solve Equation (18).

The idea behind the PSO algorithm originates from the study of bird flocking behavior, where birds find the optimal destination by sharing information collectively as a group. Assuming that the group consists of $m$ particles, the position vector and velocity vector of the $j$-th particle in the search space in the $t$-th generation are, respectively,

$${\mathit{X}}_j^{\left(t\right)}=\left({\mathit{x}}_{j_1}^{\left(t\right)},{\mathit{x}}_{j_2}^{\left(t\right)},\cdots ,{\mathit{x}}_{j_S}^{\left(t\right)},{\mathit{x}}_{j_{S+1}}^{\left(t\right)}\right)$$

(28)

$${\mathit{V}}_j^{\left(t\right)}=\left({\mathit{v}}_{j_1}^{\left(t\right)},{\mathit{v}}_{j_2}^{\left(t\right)},\cdots ,{\mathit{v}}_{j_S}^{\left(t\right)},{\mathit{v}}_{j_{S+1}}^{\left(t\right)}\right)$$

(29)

where every vector in $\left({\mathit{x}}_{j_1}^{\left(t\right)},{\mathit{x}}_{j_2}^{\left(t\right)},\cdots ,{\mathit{x}}_{j_S}^{\left(t\right)}\right)$ represents the vector composed of the initial UAV flight height and the velocity angles at every time; ${\mathit{x}}_{j_{S+1}}^{\left(t\right)}$ represents the rotation angles vector of the phantom track; and $\left({\mathit{v}}_{j_1}^{\left(t\right)},{\mathit{v}}_{j_2}^{\left(t\right)},\cdots ,{\mathit{v}}_{j_S}^{\left(t\right)},{\mathit{v}}_{j_{S+1}}^{\left(t\right)}\right)$ represents the particle velocity of the above parameters.

Each iteration cycle of PSO generates a new position state according to its position vector, velocity vector, individual history information, population information, and disturbance. In the algorithm, the $j$-th particle in the $\left(t+1\right)$-th generation on the $d$-th dimension is calculated as follows:

$$v_{j,d}^{\left(t+1\right)}=\omega \cdot v_{j,d}^{\left(t\right)}+c_1\cdot r_1\cdot \left(p_{j,d}^{\left(t\right)}-x_{j,d}^{\left(t\right)}\right)+c_2\cdot r_2\cdot \left(p_{l,d}^{\left(t\right)}-x_{j,d}^{\left(t\right)}\right)$$

(30)

$$x_{j,d}^{\left(t+1\right)}=x_{j,d}^{\left(t\right)}+v_{j,d}^{\left(t+1\right)}$$

(31)

where $\omega$ denotes inertia weight; $c_1$ and $c_2$ denotes learning factor; $r_1$ and $r_2$ are randoms on $\left(0,1\right)$; $v_{j,d}^{\left(t\right)}$ and $v_{j,d}^{\left(t+1\right)}$ denote the velocity of $j$-th particle in the $t$-th and (t + 1)-th generation on the $d$-th dimension, respectively; $x_{j,d}^{\left(t\right)}$ and $x_{j,d}^{\left(t+1\right)}$ denote the position of $j$-th particle in the $t$-th and $\left(t+1\right)$-th generation on the $d$-th dimension, respectively; and $p_{j,d}^{\left(t\right)}$ and $p_{l,d}^{\left(t\right)}$ denote the best position of the $j$-th particle and the swarm in the $t$-th generation on the $d$-th dimension, respectively. The detailed steps of the PSO algorithm for trajectory optimization are outlined in Algorithm 1, which provides a framework for obtaining the optimal flight trajectories and phantom track rotation angles while adhering to the constraints imposed by UAV kinematic performance and phantom track rotation angle.

Algorithm 1: The Detailed Steps of the PSO Algorithm for Trajectory Optimization in UAV Swarm

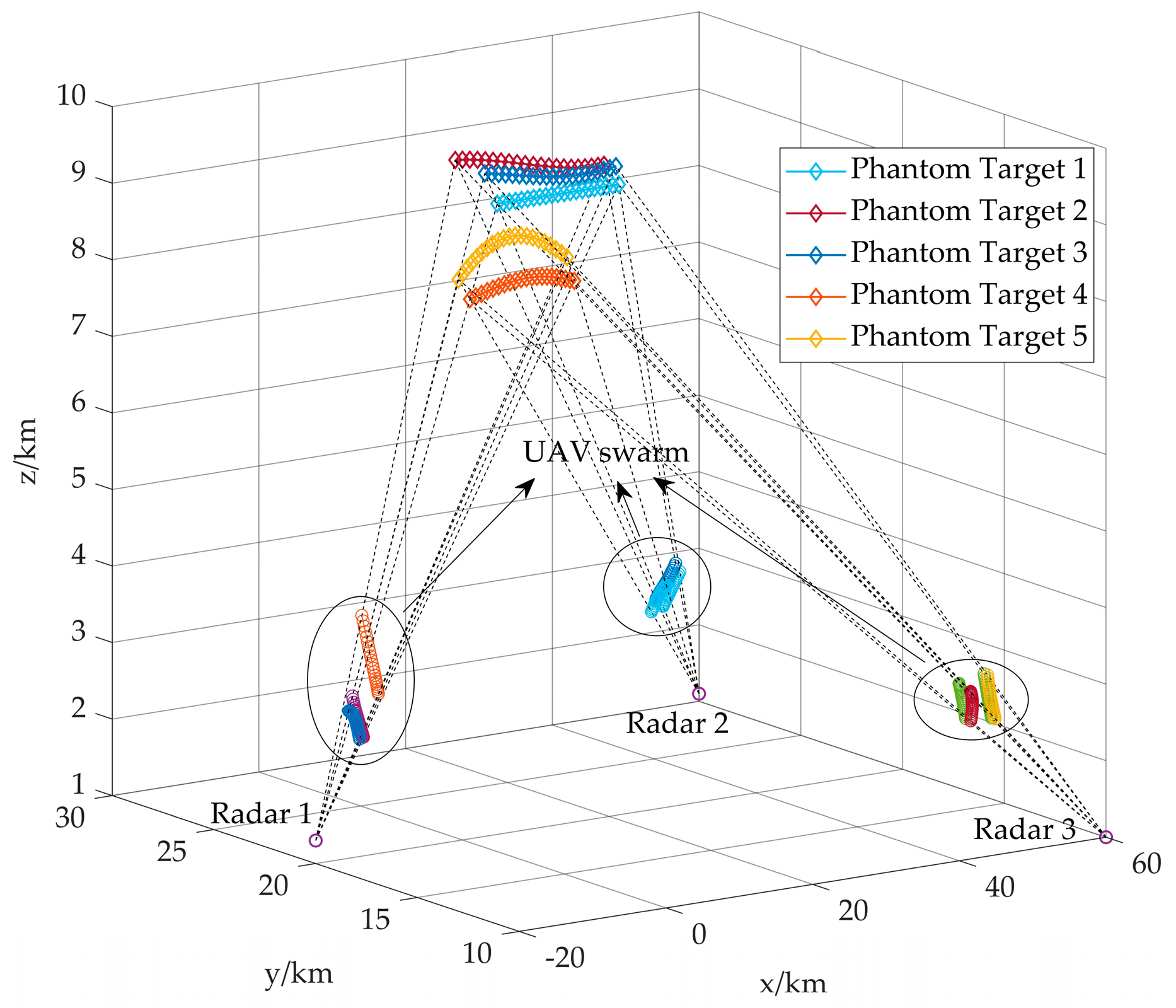
5. Numerical Simulation

5.1. Experiment 1

Experiment 1 considers UAV swarms consisting of 10, 15, 20, 25, and 30 UAVs, respectively, to deceive a radar network system composed of 4 pulse radars.

Figure 5 presents a comparative analysis of the number of phantom tracks generated using different numbers of UAVs for track deception under two distinct mission planning schemes.

Table 2. Mission planning for Cluster 1 in Experiment 1.

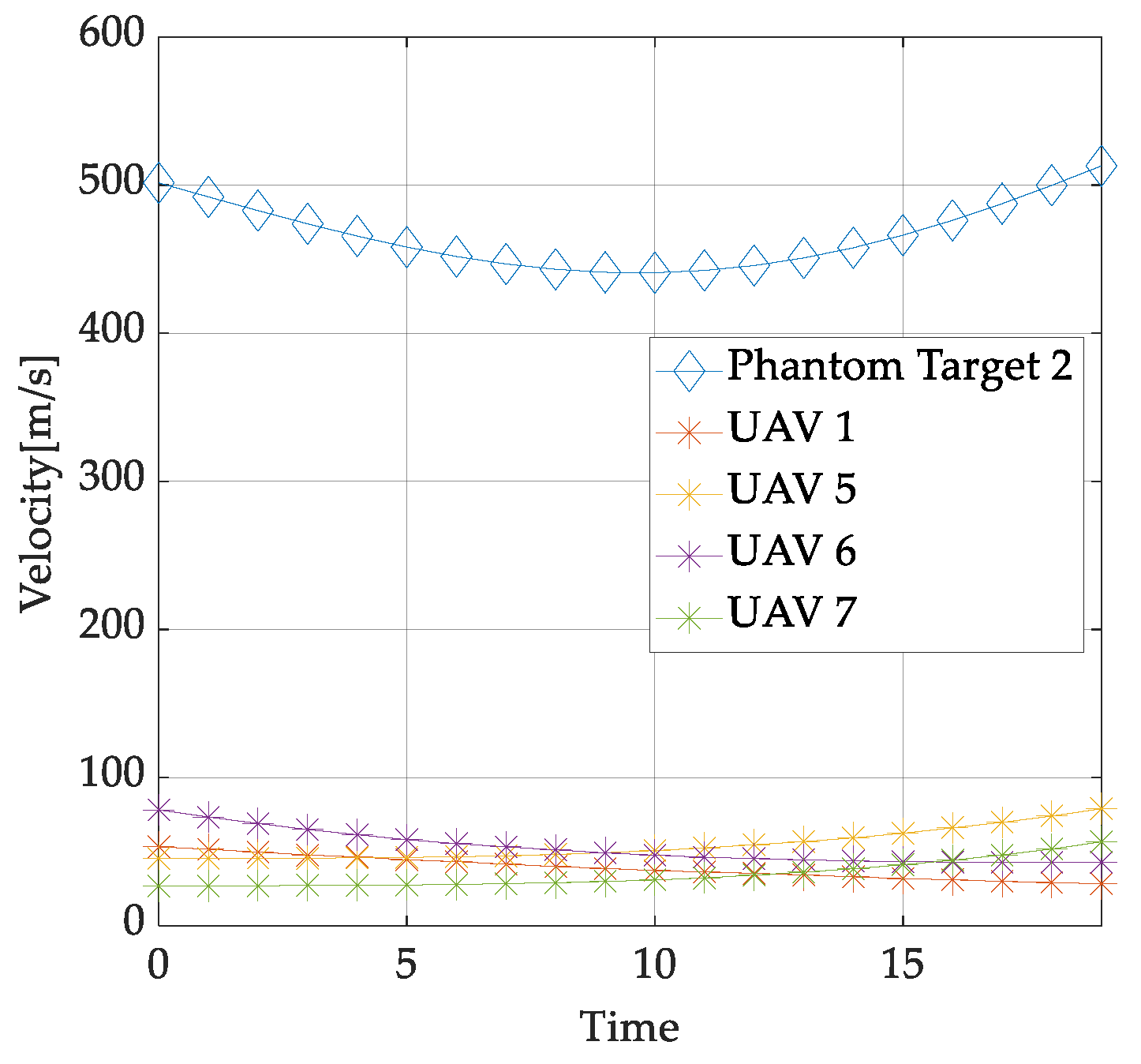
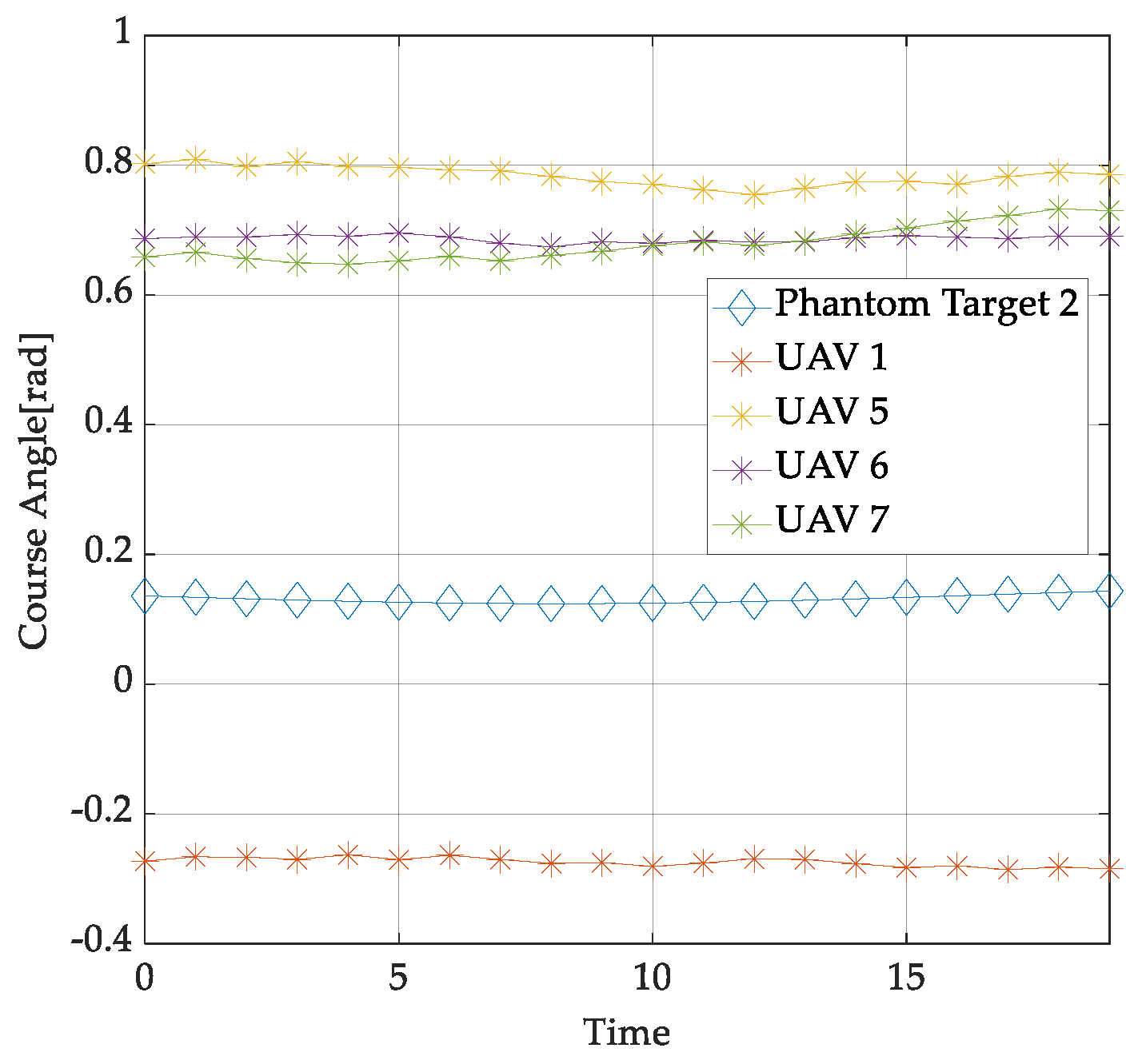
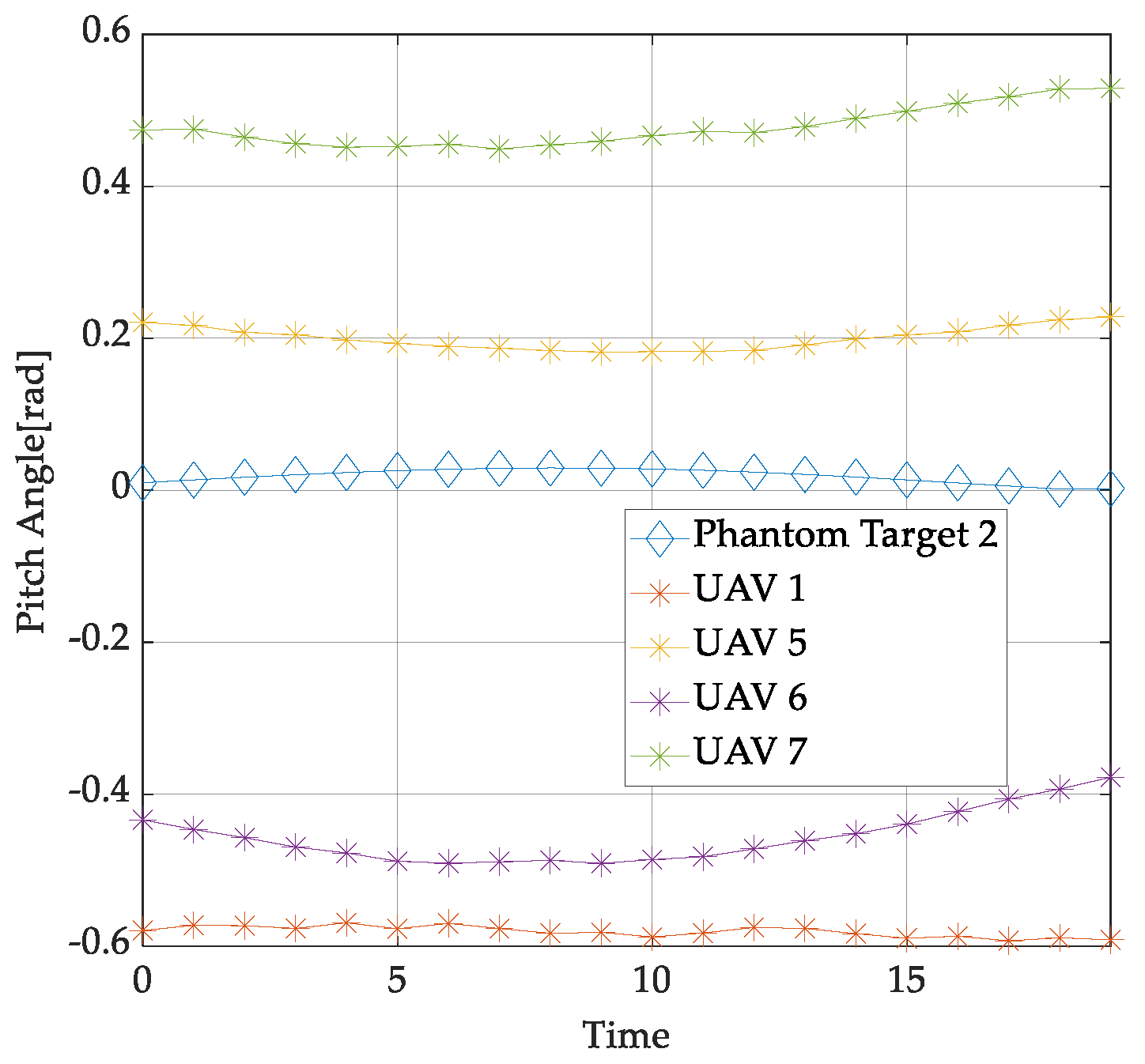
Phantom Track	UAV
1	UAV 1	UAV 2	UAV 3	UAV 4
2	UAV 1	UAV 5	UAV 6	UAV 7
3	UAV 2	UAV 8	UAV 9	UAV 10
4	UAV 3	UAV 11	UAV 12	UAV 13

,

Table 3. Mission planning for Cluster 2 in Experiment 1.

Phantom Track	UAV
5	UAV 14	UAV 15	UAV 16	UAV 17
6	UAV 14	UAV 18	UAV 19	UAV 20
7	UAV 15	UAV 21	UAV 22	UAV 23

and

Table 4. Mission planning for Cluster 3 in Experiment 1.

Phantom Track	UAV
8	UAV 24	UAV 25	UAV 26	UAV 27
9	UAV 24	UAV 28	UAV 29	UAV 30

, focusing on the scenario with 30 UAVs, detail the mission planning employed by each cluster within the UAV swarm.

It is evident that, for the same number of UAVs, the mission planning based on platform reuse can generate a greater number of phantom tracks. By dividing the UAV swarm into three clusters, this scheme ensures the optimal utilization of each UAV, thereby producing more phantom tracks. In contrast, without this scheme, UAVs remain underutilized in all configurations except the swarm composed of 20 UAVs, resulting in lower overall UAV utilization.

5.2. Experiment 2

In this experiment, we consider a radar network system composed of three pulse radars, where the coordinates of each radar are $\left(60,10,1\right)$ km, $\left(60,30,1.1\right)$ km, and $\left(-20,20,1.3\right)$ km. The safe distance between UAVs is 50m. The simulation parameters are provided in

Table 5. Simulation parameters.

Symbol	Value	Symbol	Value
$v_{\mathrm{u},\min }$	20 m/s	$v_{\mathrm{u},\max }$	100 m/s
$h_{\mathrm{u},\min }$	2.5 km	$h_{\mathrm{u},\max }$	5.5 km
$\Delta {\alpha }_{\mathrm{u},\min }$	0 rad	$\Delta {\alpha }_{\mathrm{u},\max }$	0.5 rad
${\beta }_{\mathrm{u},\max }$	−1 rad	${\beta }_{\mathrm{u},\max }$	1 rad
${\gamma }_{\min }$	$-\pi /4$ rad	${\gamma }_{\max }$	$\pi /4$ rad

.

The motion equation of the first phantom track is as follows:

$$\{\begin{array}{l}{x}_{{\mathrm{p}}_1,k}=0.8\cdot k+10\left(k=0,1,\cdots 21\right)\\ y_{{\mathrm{p}}_1,k}=0.4\cdot k+10\\ z_{{\mathrm{p}}_1,k}=9\end{array}$$

(32)

The remaining phantom track proportional factors are as follows:

$$\{\begin{array}{l}{\rho }_{2,1,k}=1.05+0.02\sin \left({\displaystyle \frac{\pi }{20}}k+0.6\pi \right)\\ {\rho }_{3,1,k}=1.05+0.02\sin \left({\displaystyle \frac{\pi }{20}}k+0.8\pi \right)\\ {\rho }_{4,1,k}=0.85+0.02\sin \left({\displaystyle \frac{\pi }{20}}k\right)\\ {\rho }_{5,4,k}=1.05+0.05\sin \left({\displaystyle \frac{\pi }{20}}k\right)\end{array}$$

(33)

Figure 6 illustrates the UAV swarm track deception against the radar network in Scenario 2. The results indicate that 11 UAVs are required for effective track deception. The UAV swarm generates five phantom targets with distinct trajectories, ensuring that UAVs are positioned along the LOS between the three radars and any phantom target at all times. By retransmitting intercepted signals with specified parameters, the UAV swarm can generate multiple phantom tracks, thereby deceiving the radar network.

The results also reveal that due to the constant proportional factor being greater than 1, the flight distance of the second phantom track is longer than that of the first. Conversely, the flight distance of the fourth phantom track, with a proportional factor less than 1, is shorter than that of the first phantom track. Therefore, to ensure that the speed of the generated phantom tracks is realistic, the constant proportional factor should not deviate significantly from 1. Additionally, a reasonably set proportional factor can enable phantom targets to simulate formation flights in the same area, thereby enhancing the authenticity of the phantom tracks.

Given that the motion state of each UAV in the swarm is similar, any individual UAV can represent the motion state of the entire swarm. Figure 7, Figure 8 and Figure 9 illustrate the flight velocity, course angle, and pitch angle of the phantom target and three UAVs, specifically phantom track 2 and the 1st, 4th, and 5th UAVs. The results demonstrate that all UAVs in this group adhere to the kinematic performance constraints and successfully generate a high-speed phantom target at approximately 400 m/s while maintaining a low speed of about 50 m/s.

5.3. Experiment 3

Experiment 3 considers the task of generating multiple supersonic phantom targets to deceive the radar network. The experiment involves a UAV swarm consisting of 20 UAVs confronting a radar network equipped with four pulse radars, in which the coordinates of each radar are $\left(-32,15,0.3\right)$ km, $\left(62,12,0.8\right)$ km, $\left(-22,33,0.5\right)$ km, and $\left(54,25,1\right)$ km. The simulation parameters are the same as in Experiment 2.

Calculations indicate that the UAV swarm can generate six phantom tracks when divided into two clusters. Each UAV cluster generates three phantom tracks. The motion equations for the first phantom tracks generated by the two clusters are set as follows:

$$\{\begin{array}{l}{x}_{{\mathrm{p}}_1,k}=0.3\cdot k+10\\ y_{{\mathrm{p}}_1,k}=0.4\cdot k+20\\ z_{{\mathrm{p}}_1,k}=9\end{array}$$

(34)

$$\{\begin{array}{l}{x}_{{\mathrm{p}}_4,k}=0.4\cdot k\\ y_{{\mathrm{p}}_4,k}=30\\ z_{{\mathrm{p}}_4,k}=10\end{array}$$

(35)

The remaining phantom track proportional factors are as follows:

$$\{\begin{array}{l}{\rho }_{2,1,k}={\rho }_{5,4,k}=1.03+0.02\sin \left({\displaystyle \frac{\pi }{20}}k+0.6\pi \right)\\ {\rho }_{3,1,k}={\rho }_{6,4,k}=0.95+0.03\sin \left({\displaystyle \frac{\pi }{20}}k+0.2\pi \right)\end{array}$$

(36)

Figure 10 illustrates the UAV swarm track deception for the radar network in Scenario 3. Figure 11, Figure 12 and Figure 13 display the flight velocity, course angle, and pitch angle of the phantom target and three UAVs, using phantom track 2 and the 1st, 5th, 6th, and 7th UAVs as examples.

The results demonstrate that all UAVs are effectively utilized, leading to the generation of more phantom tracks. Figure 10 demonstrates how the UAV swarm successfully generates multiple phantom tracks above the radar network. Figure 11 shows an example where phantom target 2, a supersonic phantom target with a flight velocity of about 450 m/s, is generated by low-speed UAVs 1, 5, 6, and 7. Each phantom track produced by the UAV clusters adheres to the LOS criterion, ensuring that the relative orientation of phantom tracks and radars is consistent with that of the first phantom track. Consequently, dividing the UAV swarm into clusters allows for the generation of phantom targets flying in formation across different directions. Additionally, each UAV satisfies its kinematic performance constraints, with smooth motion parameter curves, indicating that no excessive maneuvering is required. This results in highly feasible trajectories. Furthermore, although the UAVs tasked with deceiving the same radars operate within the same regions, adequate separation between them is maintained to prevent any risk of collision. The UAV trajectories are approximately aligned with the vertical lines that are perpendicular to the LOS between the radars and the phantom targets at different time steps, as shown in Figure 10. This is consistent with the shortest trajectory analysis presented in Figure 4.

6. Conclusions

In this paper, we propose a mission planning and trajectory optimization scheme in UAV swarm for track deception against radar network. By jointly conducting mission planning and optimizing the trajectories of the UAV swarm and the phantom track rotation angles, our approach enables a low-speed UAV swarm to generate an increased number of high-speed phantom tracks. To address this mixed-integer programming, multivariable, and non-linear optimization problem, we adopt a three-stage solution methodology incorporating the mission planning based on platform reuse and PSO algorithm. The numerical results demonstrate that the proposed scheme can generate various trajectories for UAVs and phantom targets while considering constraints such as UAV kinematic performance, phantom track rotation angles, and the homology test, thus effectively achieving track deception against radar network. Future research may focus on the deception effect of phantom tracks with prior errors and explore optimal UAV swarm control methods in scenarios with insufficient prior information, which may lead to errors.