Modified Hybrid Integration Algorithm for Moving Weak Target in Dual-Function Radar and Communication System
Abstract
1. Introduction
2. Signal Model
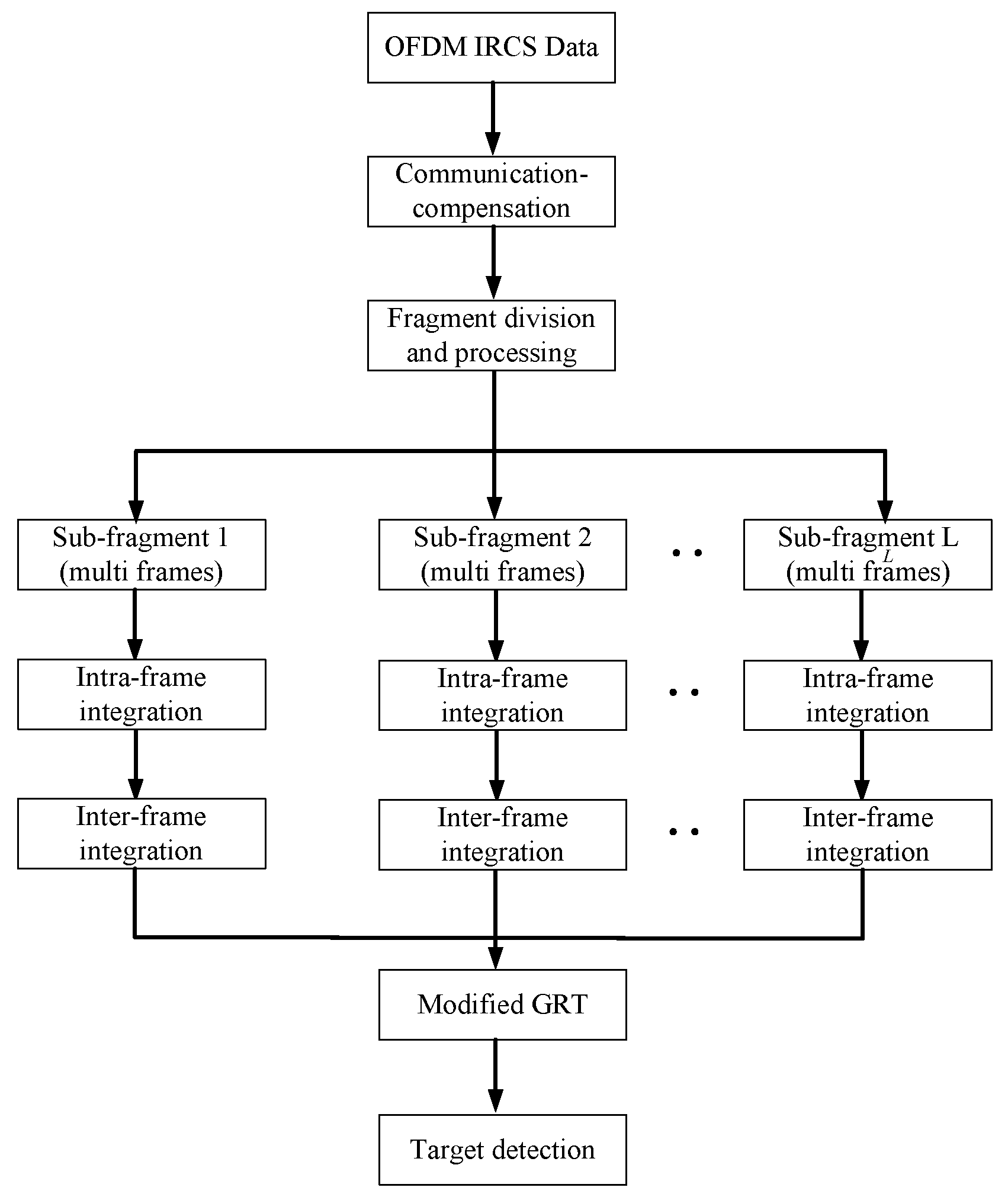
3. Modified Hybrid Integration Processing
3.1. Communication Compensation of Receiver Signal
3.2. DFRC OFDM Radar Signal in Modulation Symbol Frequency
3.3. Modified Hybrid Integration of OFDM IRCS Frequency Signal
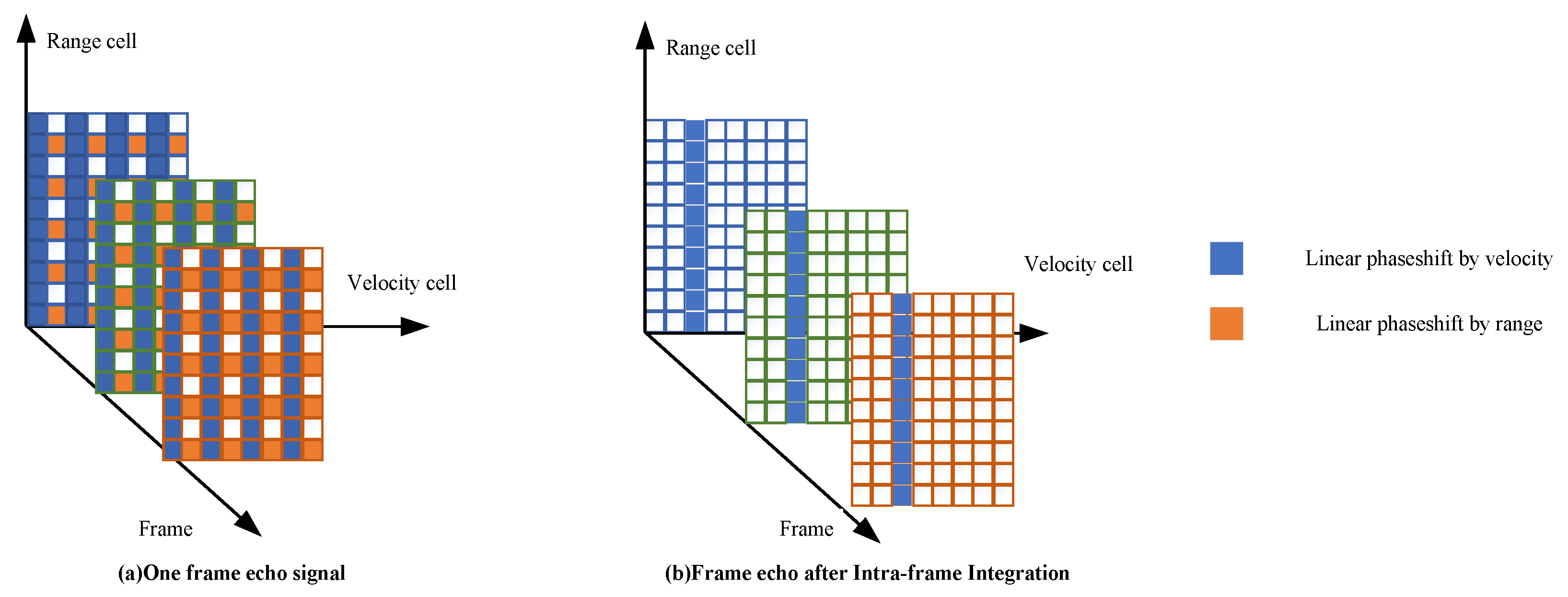
3.3.1. Intra-Frame Integration
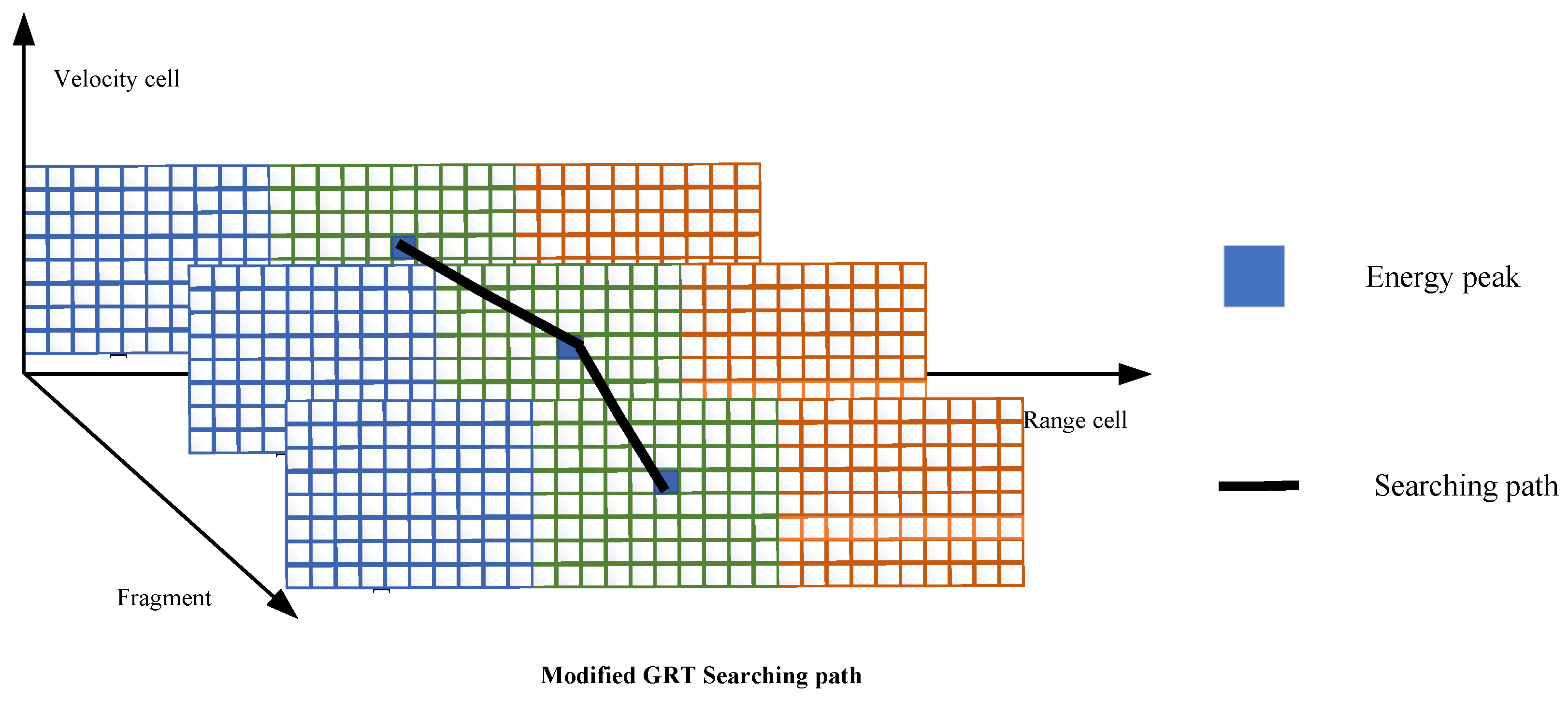
3.3.2. Multi-Inter-Frame Integration
4. Performance Analysis of Different Methods
4.1. SNR Gains of Different Methods for Highly Maneuvering Targets
4.2. Computational Complexities of Different Methods
5. Numerical Results
5.1. Radar Detection Performance Analysis
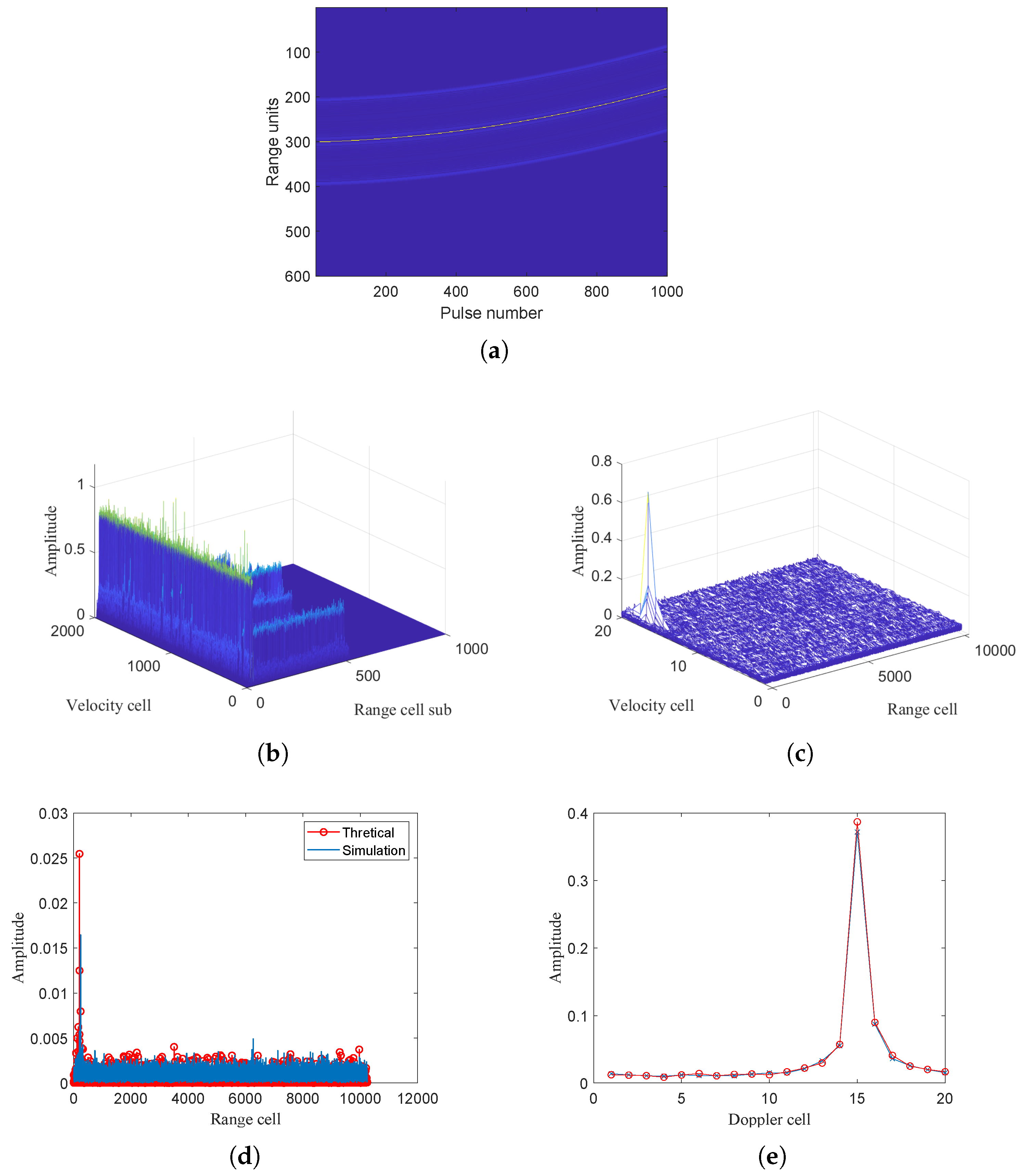
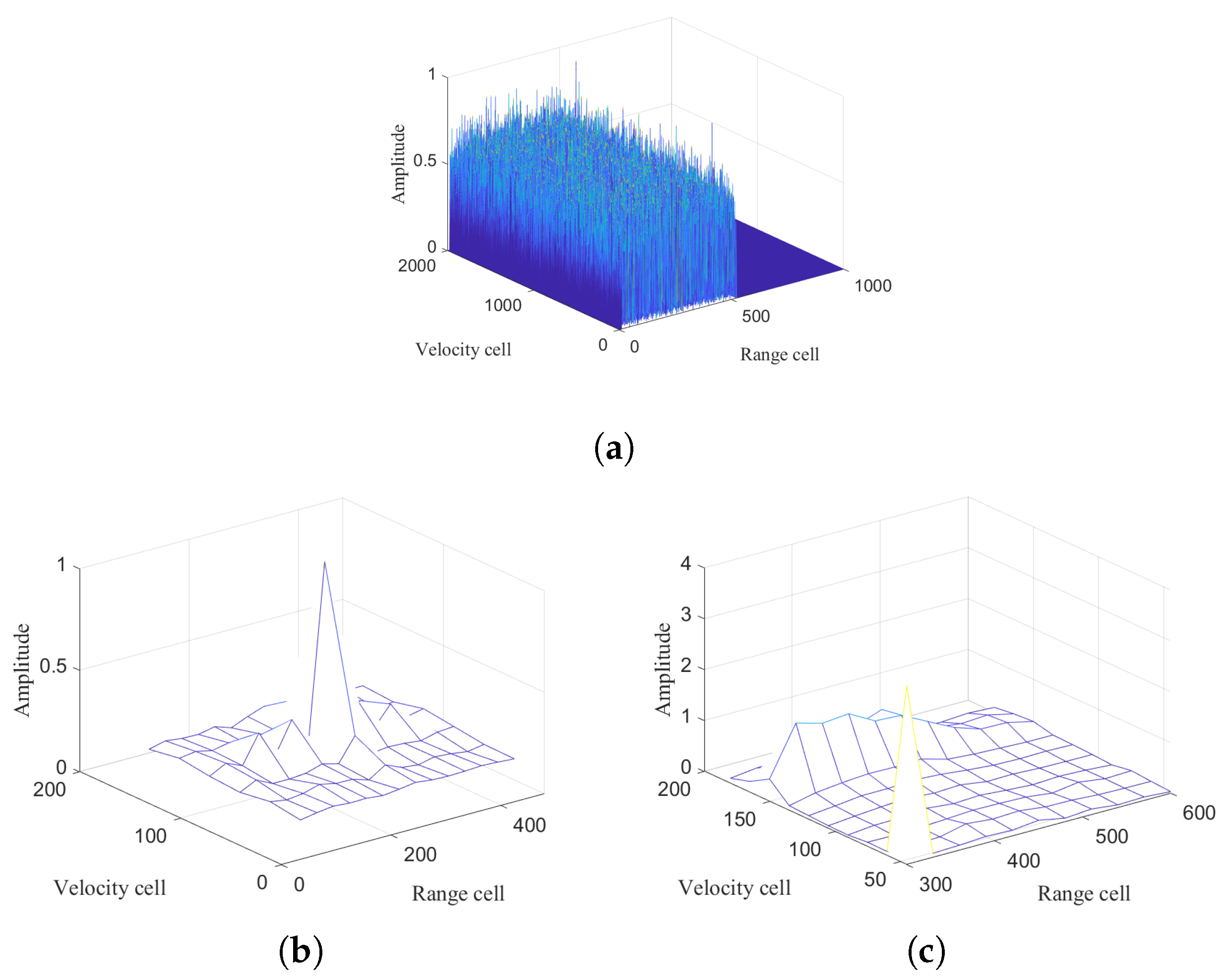
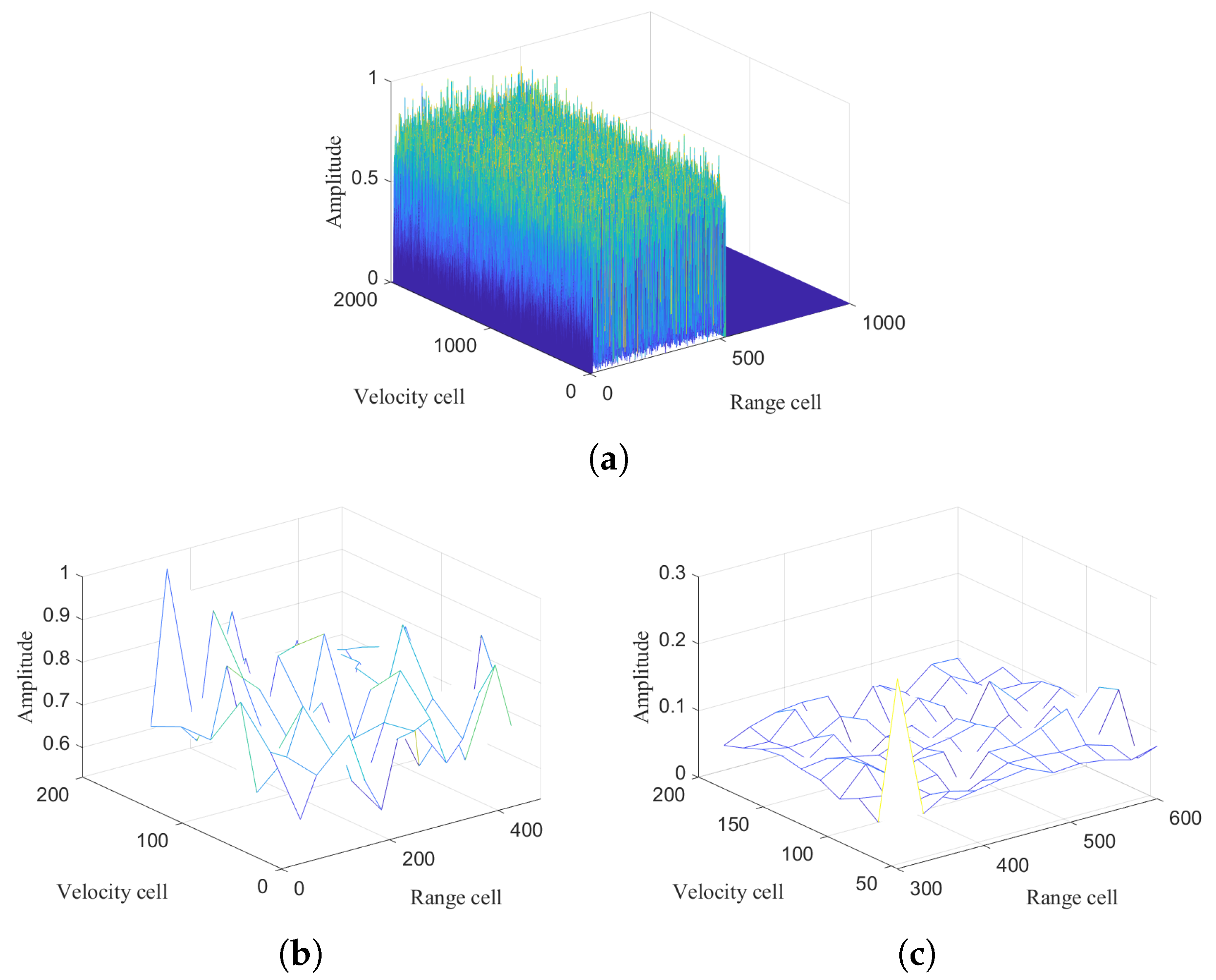
5.1.1. Integrated Output Response
5.1.2. Different Methods’ Output Responses
5.1.3. Integration for Weak Targets
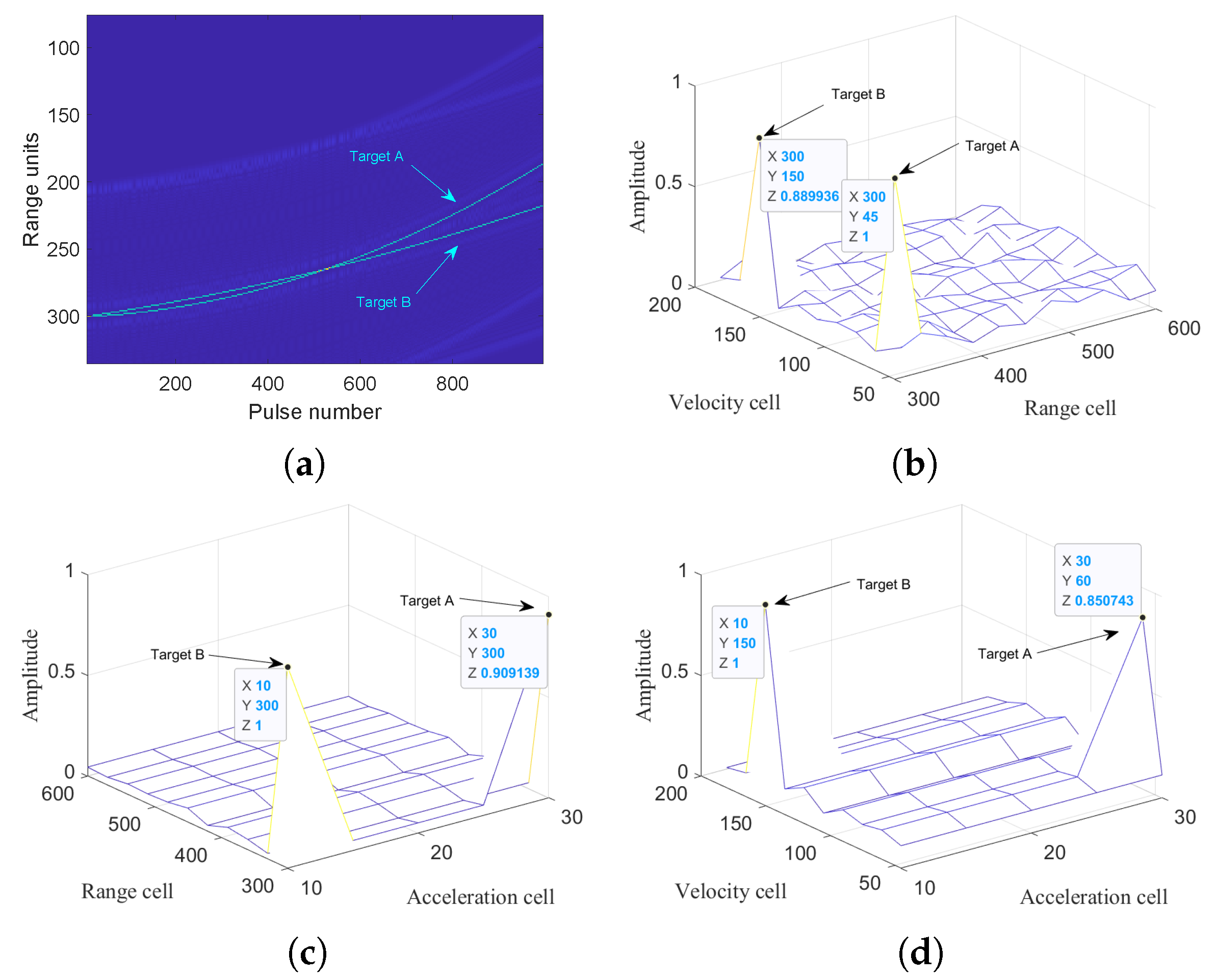
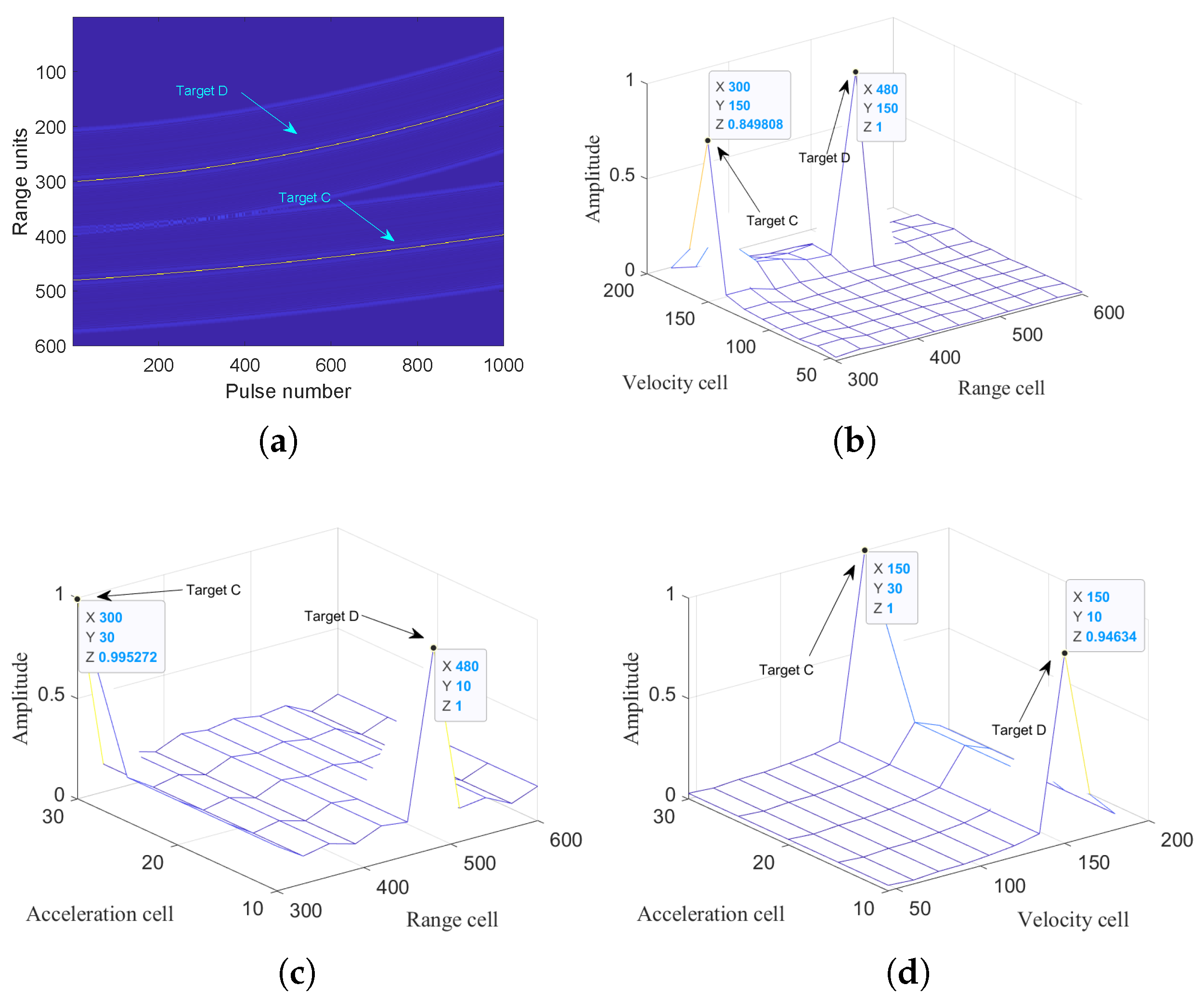
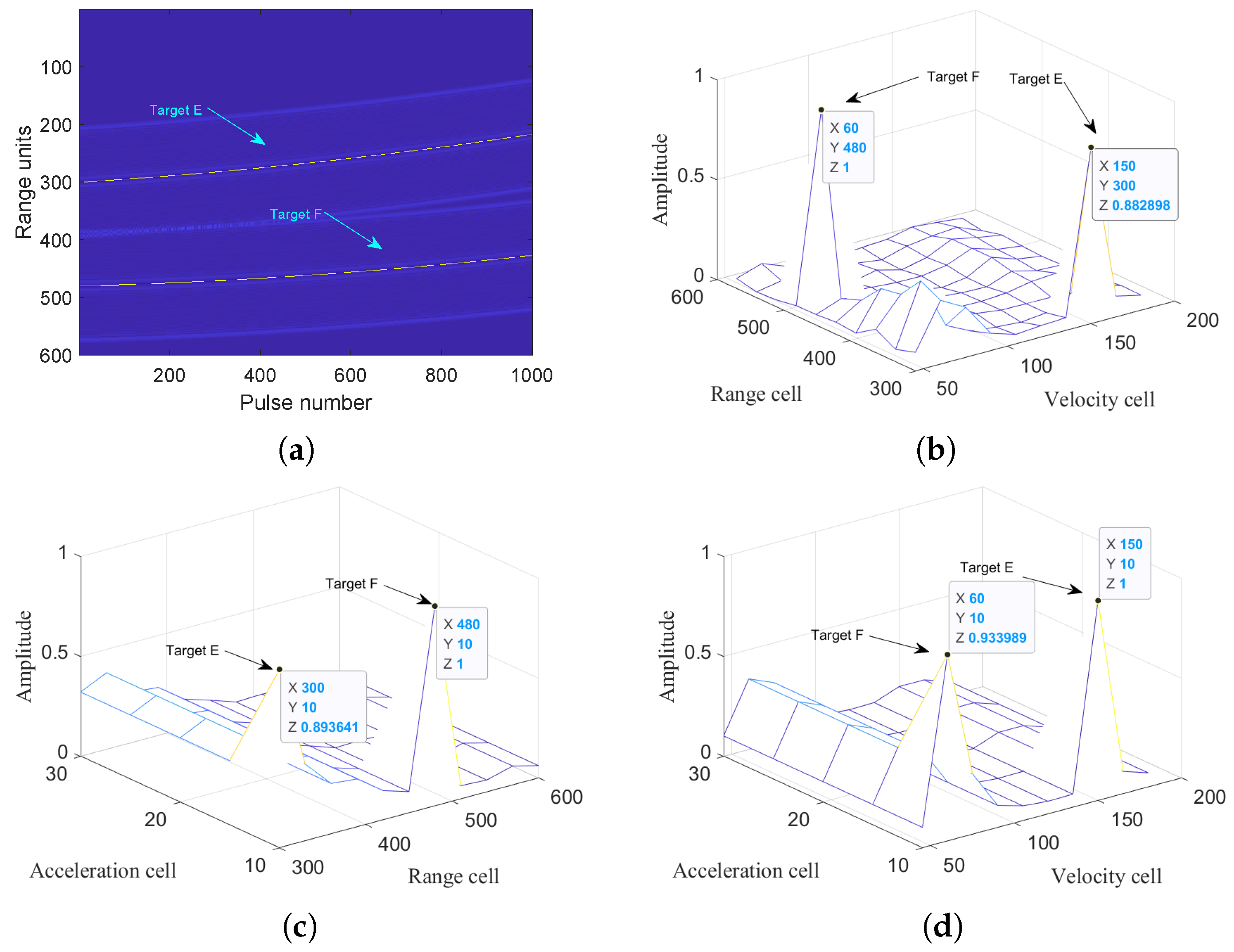
5.1.4. Integration for Multi-Targets
Scenario 1
Scenario 2
Scenario 3
5.1.5. Communication Bit Error Ratio
5.1.6. Detection Performance
5.1.7. Computation Complexity
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Trees, H. Detection, Estimation, and Modulation Theory, Part I: Detection, Estimation, and Linear Modulation Theory; Wiley: Hoboken, NJ, USA, 1968. [Google Scholar]
- Stiglitz, M. Radar Handbook, 2nd ed.; McGraw-Hill Professional: New York, NY, USA, 1990. [Google Scholar]
- Skolnik, M.I. Introduction to Radar Systems/m.i. Skolnik; Mcgraw Hill Electrical Engineering: New York, NY, USA, 2002. [Google Scholar]
- HINEDI. Digital Communications—1e; HINEDI: Fall River, MA, USA, 2000. [Google Scholar]
- Tavik, G.C.; Olin, I.D. The advanced multifunction rf concept. IEEE Trans. Microw. Theory Tech. 2005, 53, 1009–1020. [Google Scholar] [CrossRef]
- Han, L.; Wu, K. Multifunctional transceiver for future intelligent transportation systems. IEEE Trans. Microw. Theory Tech. 2011, 59, 1879–1892. [Google Scholar] [CrossRef]
- Moghaddasi, J.; Wu, K. Multifunctional transceiver for future radar sensing and radio communicating data-fusion platform. IEEE Access 2016, 4, 818–838. [Google Scholar] [CrossRef]
- Sturm, C.; Wiesbeck, W. Waveform design and signal processing aspects for fusion of wireless communications and radar sensing. Proc. IEEE 2011, 99, 1236–1259. [Google Scholar] [CrossRef]
- Sit, Y.L.; Nuss, B.; Zwick, T. On mutual interference cancellation in a mimo ofdm multiuser radar-communication network. IEEE Trans. Veh. Technol. 2018, 67, 3339–3348. [Google Scholar] [CrossRef]
- Liu, Y.; Liao, G.; Yang, Z.; Xu, J. Design of integrated radar and communication system based on mimo-ofdm waveform. J. Syst. Eng. Electron. 2017, 28, 669–680. [Google Scholar]
- Liu, Y.; Liao, G.; Xu, J.; Yang, Z.; Zhang, Y. Adaptive ofdm integrated radar and communications waveform design based on information theory. IEEE Commun. Lett. 2017, 21, 2174–2177. [Google Scholar] [CrossRef]
- Liu, Y. Transmit power adaptation for orthogonal frequency division multiplexing integrated radar and communication systems. J. Appl. Remote Sens. 2017, 11, 1. [Google Scholar] [CrossRef]
- Liao, G.; Liu, Y.; Yang, Z. Robust ofdm integrated radar and communications waveform design based on information theory. Signal Process. 2018, 162, 317–329. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, Z.; Liao, G.; Xu, J. Multiobjective optimal waveform design for ofdm integrated radar and communication systems. Signal Process. Off. Publ. Eur. Signal Process. (EURASIP) 2017, 141, 331–342. [Google Scholar] [CrossRef]
- Liu, J.; Xu, Z. Joint range and angle estimation for an integrated system combining mimo radar with ofdm communication. Multidimens. Signal Process. 2019, 30, 2. [Google Scholar] [CrossRef]
- Liu, Y. Range and angle estimation for mimo-ofdm integrated radar and communication systems. In Proceedings of the 2016 CIE International Conference on Radar (RADAR), Guangzhou, China, 10–13 October 2016. [Google Scholar]
- Chiriyath, A.R.; Ragi, S.; Mittelmann, H.D.; Bliss, D.W. Novel radar waveform optimization for a cooperative radar-communications system. IEEE Trans. Aerosp. Electron. Syst. 2019, 55, 1160–1173. [Google Scholar] [CrossRef]
- Hassanien, A.; Amin, M.G.; Zhang, Y.D.; Ahmad, F. Signaling strategies for dual-function radar communications: An overview. IEEE Aerosp. Electron. Syst. Mag. 2016, 31, 36–45. [Google Scholar] [CrossRef]
- Takase, H.; Shinriki, M. Dual-function radar-communications: Information embedding using sidelobe control and waveform diversity. IEEE Trans. Signal Process. 2016, 64, 2168–2181. [Google Scholar]
- Takase, H.; Shinriki, M. A dual-use radar and communication system with complete complementary codes. In Proceedings of the 2014 15th International Radar Symposium (IRS), Gdansk, Poland, 16–18 June 2014. [Google Scholar]
- Romero, R.A.; Shepherd, K.D. Friendly spectrally shaped radar waveform with legacy communication systems for shared access and spectrum management. IEEE Access 2015, 3, 1541–1554. [Google Scholar] [CrossRef]
- Guan, Y.; Dai, Y.; Zhang, W.; Lin, D.; He, D. Dtmb application in shanghai sfn transmission network. IEEE Trans. Broadcast. 2013, 59, 183–187. [Google Scholar] [CrossRef]
- Zheng, Z.W. Effects of power amplifier distortion and channel estimation errors on the performance of dvb-h system with multiple-antenna receiver. IEEE Trans. Consum. Electron. 2009, 55, 1810–1818. [Google Scholar] [CrossRef]
- Welch, G.; Bishop, G.; Union, E.B.; Committee, L.S.I. Tr 101 190—v1.3.2—Digital Video Broadcasting (dvb); Implementation Guidelines for dvb Terrestrial Services; Transmission Aspects; ETSI: Valbonne, France, 2003. [Google Scholar]
- Huang, J.; Presti, L.; Garello, R. Digital video broadcast-terrestrial (dvb-t) single frequency networks positioning in dynamic scenarios. Sensors 2013, 13, 10191–10218. [Google Scholar] [CrossRef]
- IEEE. Wireless lan medium access control (mac) and physical layer (phy) specifications; high-speed physical layer in the 5ghz band. In IEEE 802.11a-Part 11; IEEE: Piscataway Township, NJ, USA, 1999. [Google Scholar]
- Afaqui, M.S.; Garcia-Villegas, E.; Lopez-Aguilera, E. Ieee 802.11ax: Challenges and requirements for future high efficiency wifi. In IEEE Wireless Communications; IEEE: Piscataway Township, NJ, USA, 2016; pp. 130–137. [Google Scholar]
- Zhang, T.; Xia, X.G.; Kong, L. Irci free range reconstruction for sar imaging with arbitrary length ofdm pulse. IEEE Trans. Signal Process. 2014, 62, 4748–4759. [Google Scholar] [CrossRef]
- Sen, S. Ofdm radar space-time adaptive processing by exploiting spatio-temporal sparsity. IEEE Trans. Signal Process. 2013, 61, 118–130. [Google Scholar] [CrossRef]
- Sen, S.; Nehorai, A. Sparsity-based multi-target tracking using ofdm radar. IEEE Trans. Signal Process. 2011, 59, 1902–1906. [Google Scholar] [CrossRef]
- Yl, A.; Rsb, B.; Gl, A.; Sz, A. Passive mimo radar detection exploiting known format of the communication signal observed in colored noise with unknown covariance matrix. Signal Process. 2020, 174, 107611. [Google Scholar]
- Liu, Y.; Liao, G.; Xu, J.; Yang, Z.; Yin, Y. Improving detection performance of passive mimo radar by exploiting the preamble information of communications signal. IEEE Syst. J. 2020, 15, 4391–4402. [Google Scholar] [CrossRef]
- Liu, Y.J.; Liao, G.S.; Yang, Z.W. Ambiguity function analysis of integrated radar and communication waveform based on ofdm. Syst. Eng. Electron. 2016, 38, 2008–2018. [Google Scholar]
- Li, X.; Cui, G.; Wei, Y.; Kong, L. Fast coherent integration for maneuvering target with high-order range migration via trt-skt-lvd. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 2803–2814. [Google Scholar] [CrossRef]
- Li, X.; Sun, Z.; Yeo, T.S. Computational efficient refocusing and estimation method for radar moving target with unknown time information. IEEE Trans. Comput. Imaging 2020, 6, 544–557. [Google Scholar] [CrossRef]
- Li, X.; Cui, G.; Yi, W.; Kong, L.J. Coherent integration for maneuvering target detection based on radon-lv’s distribution. IEEE Signal Process. Lett. 2015, 22, 1467–1471. [Google Scholar] [CrossRef]
- Tian, J.; Xia, X.; Cui, W.; Yang, G.; Wu, S. A coherent integration method via radon-nufrft for random pri radar. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 2101–2109. [Google Scholar] [CrossRef]
- Wang, J.; Wei, Y.; Kirubarajan, T.; Kong, L. An efficient recursive multiframe track-before-detect algorithm. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 190–204. [Google Scholar] [CrossRef]
- Carlson, B.D.; Evans, E.D.; Wilson, S.L. Search radar detection and track with the hough transform, part i: System concept. IEEE Trans. Aerosp. Electron. Syst. 1994, 30, 102–108. [Google Scholar] [CrossRef]
- Carlson, B.D.; Wilson, E.S.L.; Lincoln, M. Search radar detection and track with the hough transform part ii: Detection statistics vans, member, ieeb. IEEE Trans. Aerosp. Electron. Syst. 2002, 30, 109–115. [Google Scholar] [CrossRef]
- Perry, R.P.; Dipietro, R.C.; Fante, R.L. Sar imaging of moving targets. IEEE Trans. Aerosp. Electron. Syst. 1999, 35, 188–200. [Google Scholar] [CrossRef]
- Perry, R.P.; Dipietro, R.C.; Fante, R.L. Coherent integration with range migration using keystone formatting. In Proceedings of the 2007 IEEE Radar Conference, Waltham, MA, USA, 17–20 April 2007. [Google Scholar]
- Xu, J.; Yu, J.; Peng, Y.; Xia, X. Radon-fourier transform for radar target detection, i: Generalized doppler filter bank. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 1186–1202. [Google Scholar] [CrossRef]
- Xu, J.; Yu, J.; Peng, Y.N.; Xia, X.G. Radon-fourier transform for radar target detection (ii): Blind speed sidelobe suppression. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 2473–2489. [Google Scholar] [CrossRef]
- Ji, Y.; Jia, X.; Peng, Y.N.; Xia, X.G. Radon-fourier transform for radar target detection (iii): Optimality and fast implementations. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 991–1004. [Google Scholar]
- Xu, J.; Yu, J.; Peng, Y.N.; Xia, X.G.; Long, T. Space-time radon-fourier transform and applications in radar target detection. Radar Sonar Navig. Iet 2012, 6, 846–857. [Google Scholar] [CrossRef]
- Xu, J.; Xia, X.G.; Peng, S.B.; Yu, J.; Peng, Y.N.; Qian, L.C. Radar maneuvering target motion estimation based on generalized radon-fourier transform. IEEE Trans. Signal Process. 2012, 60, 6190–6201. [Google Scholar]
- IEEE. IEEE 802.16m Technology Introduction, White Paper; IEEE: Piscataway Township, NJ, USA, 2011. [Google Scholar]
- Jiang, D. Ieee 802.11p: Towards an international standard for wireless access in vehicular environments. In Proceedings of the VTC Spring 2008—IEEE Vehicular Technology Conference, Marina Bay, Singapore, 11–14 May 2008. [Google Scholar]
- IEEE. Wireless lan medium access control (mac) and physical layer (phy) specifications: Amendment 5: Enhancements for higher throughput. In The Editors of IEEE802.11; IEEE: Piscataway Township, NJ, USA, 1997. [Google Scholar]
- Kumari, P.; Choi, J.; González-Prelcic, N.; Heath, R.W. Ieee 802.11ad-based radar: An approach to joint vehicular communication-radar system. IEEE Trans. Veh. Technol. 2017, 67, 3012–3027. [Google Scholar] [CrossRef]
- Kay, S. Fundamentals of Statistical Signal Processing, Volume II: Detection Theory; Pearson Education: New York, NY, USA, 1993. [Google Scholar]




| Method | All Complexity (Flops) |
|---|---|
| MHI | 1.9 × Flops |
| HI | 6 × Flops |
| MTD | 1.2 × Flops |
| Parameter | Value |
|---|---|
| Carrier frequency | 3 GHz |
| Number of subcarriers | 512 |
| Elementary OFDM symbol duration | 0.1 ms |
| Subcarrier spacing | 10 kHz |
| Cyclic prefix length | 0.025 ms |
| Total OFDM symbol duration | 0.125 ms |
| Total signal bandwidth | 5.12 MHz |
| Radar range resolution | 30 m |
| Unambiguous range | 15 km |
| Unambiguous velocity | [−800 m/s, 800 m/s] |
| Velocity resolution | 1.55 m/s |
| Radar PRI | 100 |
| Subfragment length | 40 pulses |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ji, W.; Liu, T.; Song, Y.; Yin, H.; Tian, B.; Zhu, N. Modified Hybrid Integration Algorithm for Moving Weak Target in Dual-Function Radar and Communication System. Remote Sens. 2024, 16, 3601. https://doi.org/10.3390/rs16193601
Ji W, Liu T, Song Y, Yin H, Tian B, Zhu N. Modified Hybrid Integration Algorithm for Moving Weak Target in Dual-Function Radar and Communication System. Remote Sensing. 2024; 16(19):3601. https://doi.org/10.3390/rs16193601
Chicago/Turabian StyleJi, Wenshuai, Tao Liu, Yuxiao Song, Haoran Yin, Biao Tian, and Nannan Zhu. 2024. "Modified Hybrid Integration Algorithm for Moving Weak Target in Dual-Function Radar and Communication System" Remote Sensing 16, no. 19: 3601. https://doi.org/10.3390/rs16193601
APA StyleJi, W., Liu, T., Song, Y., Yin, H., Tian, B., & Zhu, N. (2024). Modified Hybrid Integration Algorithm for Moving Weak Target in Dual-Function Radar and Communication System. Remote Sensing, 16(19), 3601. https://doi.org/10.3390/rs16193601








