Abstract
In this study, we describe a deep learning (DL)-based workflow for the three-dimensional (3D) geophysical inversion of magnetotelluric (MT) data. We derived a mathematical connection between a 3D resistivity model and the surface-observed electric/magnetic field response by using a fully connected neural network framework (U-Net). Limited by computer hardware functionality, the resistivity models were generated by using a random walk technique to enlarge the generalization coverage of the neural network model, and 15,000 paired datasets were utilized to train and validate it. Grid search was used to select the optimal configuration parameters. With the optimal model framework from the parameter tuning phase, the metrics showed stable convergence during model training/validation. In the test period, the trained model was applied to predict the resistivity distribution by using both the simulated synthetic and the real MT data from the Mount Meager area, British Columbia. The reliability of the model prediction was verified with noised input data from the synthetic model. The calculated results can be used to reconstruct the position and shape trends of bodies with anomalous resistivity, which verifies the stability and performance of the DL-based 3D inversion algorithm and showcases its potential practical applications.
1. Introduction
Geophysical survey methods, such as reflection seismic, electromagnetic (EM) and potential fields, have been widely used in exploration for natural resources and fundamental research on deep geological structures [1,2,3]. Inversion is a popular technique in geophysical data analysis that produces models of the subsurface physical properties and is a reversed process based on a physical law system [4]. The essential step during the inversion process involves the iterative optimization of a created objective function. The advantages of traditional iterative inversion methods include obtaining better details of the subsurface physical structure and their suitability for large survey areas. However, iterative inversion techniques face some challenges, such as the need for an acceptable reference model, the non-uniqueness of the calculated model, and the large time consumption of the calculations.
Although regularization stabilizers and weight matrices have been employed to improve the accuracy of inverse solutions, further techniques are needed to improve prediction. An alternative inversion technique and computer hardware improvements have permitted the emergence of a data-driven deep neural network framework to predict subsurface physical models from several different geophysical methods [5,6]. Das et al. [7] proposed a convolutional neural network-based inversion framework for obtaining elastic models from full-waveform seismograms. This application of the DL algorithm demonstrates that it has great potential in predicting reservoir properties directly. Puzyrev [8] and Moghadas [9] presented 1D inversion results of electromagnetic induction (CSEM and TEM survey) data with convolutional neural network frameworks. Guo et al. [10] employed a supervised descent method (SDM) for 2D MT data inversion to reduce uncertainty and involved the design of a general training set from prior knowledge of the survey field to balance the computation time and accuracy of the machine learning inversion procedure. For potential field inversion with deep learning, previous researchers have presented gravity and magnetic inversion with a deep learning approach [11,12]. All these studies have demonstrated the potential applicability of DL-based inversion for different geophysical methods.
Because of the output uncertainty and large computational requirements, the use of traditional 3D inversion processes is always a challenging task. To overcome the drawbacks of the high computational needs and unstable output of traditional iterative inversion methods, employing DL architectures to retrieve unknown 3D geo-electric structures can be considered. Based on the previous study of one-dimensional (1D) magnetotelluric (MT) inversion [13], here, the neural network model is extended to solve a 3D inversion problem. In this work, we propose MT 3D inversion based on the 3D U-Net network. U-Net is a fully convolutional neural network which was originally used for image segmentation and object detection [14,15,16] and has been used in different DL practical applications [13,16]. The 3D U-Net framework can also be used in inversion workflows by building a mathematical connection between a 3D resistivity model and the observed MT response with optimized weight parameters. The common challenge in 3D inversion is the large amount of forward modelling, which requires powerful computational hardware. DL inversion needs a large amount of modelling computation for generating training/validation datasets. Furthermore, the datasets need to show a wider coverage for neural network models. To balance these factors, one main difference in this study is that we developed random walk for data generation to enlarge the coverage of model generalization with smaller datasets, which reduces the computation time of model training. Compared with traditional iterative inversion methods, the main advantages of this inversion method are the instant prediction after the neural network is created and the relative reliability of the output to different noise levels.
In this paper, we start by summarizing the MT method, as well as its inversion, and then describe the deep learning (DL)-based 3D inversion workflow for MT data analysis. We present evidence of data generation with a random walk generator, model training/validation and parameter tuning, followed by practical testing with synthetic models and real MT data from the Mount Meager volcanic area in British Columbia, Canada. This area is of interest due to its potential for geothermal energy. Related Python codes were developed to realize the algorithm workflow, and independent MT datasets were created to validate the trained neural network model.
2. Methods
2.1. Magnetotelluric Method
The MT method is a passive electromagnetic (EM) technique that uses natural EM signals to image the subsurface resistivity distribution. The EM signal is assumed to be generated outside the Earth (solar wind and lightning), and it includes a time-varying magnetic field and its induced orthogonal secondary electric field (Figure 1). As small fraction of EM signal travels into the Earth and induces electrical currents, the measured EM field at the Earth’s surface contains electrical resistivity information of the subsurface. Magnetotelluric has been used extensively in mineral and geothermal exploration by analyzing the retrieved subsurface resistivity distribution (e.g., [1,2]). During an MT survey, the electric field and magnetic fields are collected in the time domain, and they are then converted into the frequency domain. The electromagnetic induction phenomenon can be described by Maxwell equations [1,4,17], as follows:
where is the magnetic flux density, , is the magnetic permeability, is the electric current density, is the electrical conductivity, is the permittivity and is the total electric charge density.
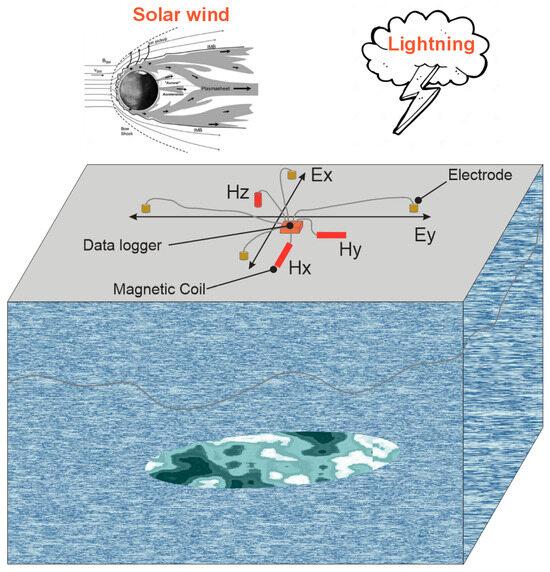
Figure 1.
Diagram illustrating the principles of an MT survey (Ex and Ey: electric fields; Hx, Hy and Hz are magnetic fields).
For a 3D structure in the subsurface, the electric and magnetic fields can be obtained by solving a discrete Maxwell equation (Equation (1)) with boundary conditions. The recorded time-series signal of the electric and magnetic fields at the Earth’s surface can be converted into the frequency domain, with their ratio being expressed as an impedance tensor, and tipper . The tensors can be written in Cartesian coordinates as
Impedance is associated with amplitude and phase, and is related to the apparent resistivity and phase of each frequency. The vertical transfer function can be used to define the induction vectors to understand the lateral conductivity variation [18].
An understanding of the traditional inverse problem and computational procedure will assist in designing the workflow of the deep learning inversion. In general, the MT data inversion process aims to predict the resistivity of the Earth’s interior from observed data [13,19,20,21]. The data values (impedance or apparent resistivity) depend on the subsurface resistivity distribution. Mathematically, the traditional inversion technique conducts iterative operations to minimize the parametric function, which includes both a misfit functional and a stabilizing functional. The objective function can be defined as follows (Equation (4)):
where is a parametric objective function and is a model-stabilizing functional; is a regularization parameter; is the unknown model parameter (resistivity in this case); and represents the observed response data. The objective function can be given by
Based on the least squares criterion, the model-stabilizing functional can be simplified as follows:
where is and are the data weighting matrix and model weight matrix, respectively; is an operator of the theoretical data from the model parameters; is the reference model; and is total number of model parameters.
There are different inversion optimization methods that minimize the objective functional (Equation (4)), such as least squares, Gauss–Newton and nonlinear conjugate gradient. These techniques and software have been developed and applied on MT inversion in the past decades [4,21,22], e.g., the Occam and ModEM open-source packages. Here, we use the ModEM (version 1.2.0) package to conduct 3D forward modelling for calculating the impedance of the MT response.
2.2. Deep Learning-Based 3D Inversion Workflow
The fundamental workflow of DL-based 3D inversion is similar to a 1D CNN [13]. The main differences are the neural network structure, the feature types of the input dataset and the number of training/validation datasets required. This DL-based inversion algorithm builds a relationship between the observed data and a physical model, which can be expressed as [12]. is a neural network, and represents the parameters in the network. The physical property is predicted with a trained neural network model by minimizing the objective function , which is similar to Equation (4) of the traditional inversion, written as the optimization of the neural network parameters .
2.2.1. Neural Network Architecture
Based on the previous U-Net architecture [15,23], a 3D network structure was re-designed for conducting the inversion procedure, which connects the observed response data (input) and the physical property model (output). This U-Net architecture (Figure 2) shows feature extraction and output shape reconstruction, which include an encoding path to extract feature information and a decoding path to restore the extracted information. The output data are reconstructed through a combination of convolutions and up-sampling.
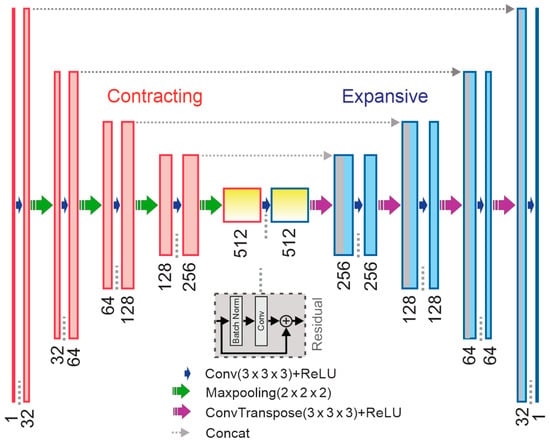
Figure 2.
A schematic of the 3D U-Net architecture, consisting of an encoder analysis path and a decoder synthesis path.
Similar to the standard 2D U-Net, the 3D network contains data analysis and a synthesis path, each with four layers defined by setting different kernel sizes. In the 3D U-Net, the number of filters denoted at the bottom of the box increases from 32 to 128. The increased number of filters allows the neural network to propagate contextual information to complex layers for a better understanding of the features. Each layer contains two 3 × 3 × 3 filters in convolutional operators, followed by a rectified linear unit (ReLU) activation function, . Compared with the sigmoid function, ReLU shows its advantage of overcoming the vanishing gradient problem. A residual block is added into each layer to make the network deeper. A 2 × 2 × 2 max pooling with strides of two in each dimension is added between layers, which is followed by 0.3 dropout (Figure 2). The stride is a parameter to control the filter movement; the max-pooling layer is a method to down-sample features by calculating the maximum value for each patch of a feature, and the dropout layer is a regularization method that randomly sets some hidden layer neurons to zero during each epoch. In the last output layer, expansive features are concatenated into one interpretation as a fully connected layer, and a 1 × 1 × 1 convolutional operator is added to reset the dimensionality of the output channels to the output size. More details of this network framework can be found in Long [14], Ronneberger et al. [15], Chen et al. [16], Çiçek et al. [23], Hochreiter [24] and Zhou et al. [25].
2.2.2. Dataset Preparation
The generation of the dataset is an essential step in supervised learning that decides if the coverage of a trained network model is generalized. In DL-based inversion, the geophysical data are collected as normal on the Earth’s surface and are then used as input for neural network training. The subsurface resistivity of a study area is used as the mask of the neural network output. Unlike the 1D deep learning inversion, the training datasets for the 3D model cannot be generated randomly in the entire solution space because of the heavy computational cost. To save computation time, and to enhance the representativeness of the dataset’s general distribution characteristics, a random walk method was used for data generation [12]. This sets a maximum of four cells randomly and then extends the resistivity values to the surrounding cubic area (Figure 3). The resistivity value of cells in the random paths are assigned in the range (1–1000 ) in common logarithmic space, and the surrounding values are interpolated. Different anomaly combinations are included to improve dataset diversity.
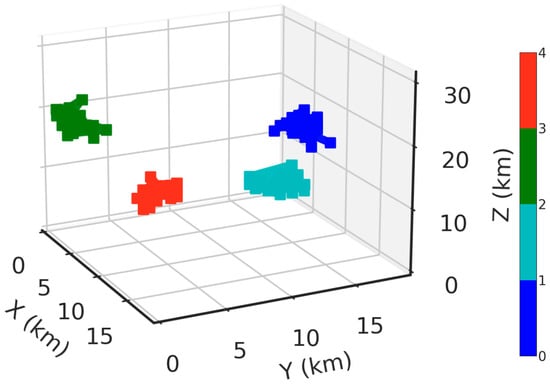
Figure 3.
A sample of the resistivity model from the random walk generator (the color represents resistivity values in common logarithmic space).
Based on the distribution of the MT stations, synthetic resistivity models are generated, and the impedance responses are simulated. For this synthetic model study, the physical model is gridded with 17 × 17 × 25 cells, the thickness of the layers is fixed throughout the model and starts from 20 m at the top and increases with an index to 3500 m in the bottom layer. The number of stations is 49 (Figure 4), with 32 frequency points ranging from 0.001 to 100 Hz for data generation. A total of 15,000 pairs of model samples and responses are generated for this synthetic case study.
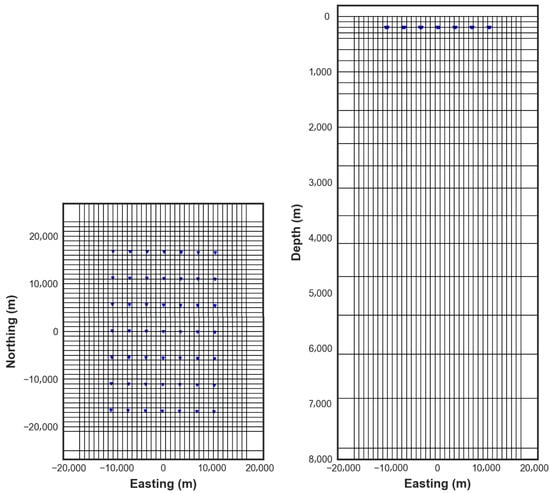
Figure 4.
Plane (left) and vertical (right) views of the synthetic model mesh grid with MT stations indicated (blue dots).
The ModEM forward package is used to simulate the surface response of each physical model and to build the datasets for model training. The data format for the DL algorithm is the same as the input and output of the MTpy package [26]. The pairs of input (real and imaginary impedance) and output (resistivity model) are created for optimizing the neural network parameters. To prevent an unbalanced range of input features affecting model stability, the data are standardized before being input into model training. The common logarithmic resistivity is set as the target parameter, and the input is scaled to with mean and standard deviation of the feature values during the model training/validation process.
2.2.3. Loss Function
Similar to traditional inversion, the neural network training process needs to define a loss function as a metric to evaluate the model’s predictive performance. A loss function is used to compare the model’s predicted values and the true values so that the weights can be updated to reduce the metrics during evaluation. For the inversion regression problem, the popular loss functions are mean absolute error (MAE), mean squared error (MSE), root mean squared error (RMSE), and their combinations (Equation (8)).
where is the predicted value, is the input model and is the total number of output data.
In order to select an optimal loss function, the proposed neural network and generated training datasets are used to discover the influence of different loss functions for a 3D inversion workflow. Figure 5 shows the convergence curves of different loss functions (MAE, MSE and RMSE). In general, both the training and validation curves of the loss functions converge stably. The convergence of RMSE and MAE decreases rapidly in the early training stage. Comparing the curves of MAE and RMSE, RMSE is relatively stable in the later period of epochs. The magnitude of oscillations of RMSE is smaller than that of MAE. The MSE curve shows much smoother convergence, but the difference between training and validation loss is relatively large at the beginning, since it effectively penalizes larger errors more severely. The minimum metric values of validation are 0.05883, 0.01418 and 0.09238 during 150 epochs.
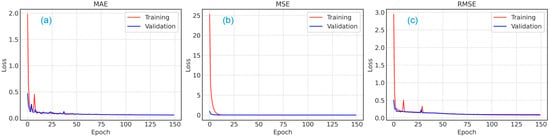
Figure 5.
The convergence curves of model training and validation with different loss functions ((a) MAE, (b) MSE and (c) RMSE).
Based on the comparison in Figure 5, RMSE is chosen as the loss function metric for network training. The adaptive moment estimation optimizer (Adam) is used to stabilize the training process and converge the objective function [27]; it is an optimization algorithm commonly used in deep learning. During parameter testing, the initial learning rate is 0.0001 and is decreased linearly to a smaller value with a ratio of 0.8 if there is no improvement in the metric over 5 consecutive epochs.
2.2.4. Hyperparameters Tuning
During network model training, parameter selection affects the convergence of the loss function. Inappropriate parameters lead an objective function to land on the local minima, giving rise to low prediction performance. Finding optimal hyperparameters is a significant step in stabilizing model training and obtaining an accurate prediction [12]. Popular search approaches are grid search and random search, where the two major tuning parameters are learning rate and batch size. In this test, the grid search method is employed to search for all possible configurations and identify the set of the best parameters. Because of the limited computational capacity, the two-dimensional case is tested, and the parameter range is chosen based on previous model training experience.
The range of values (0.000001, 0.01) was considered for the learning rate, and training processing was conducted to check for convergence within 10 epochs as the learning rate increased. Based on Figure 6, the optimal range of the learning rate was assumed to be (4 × 10−5, 4 × 10−4). The learning rates selected were 0.00001, 0.00005, 0.0001 and 0.0005, and the batch sizes were set to 8, 16, 24 and 32. Each position of the grid was then searched to optimize these hyperparameter values based on the convergence loss function. A computer with a 16-core CPU, 128 G of memory and one Nvidia Quadro-RTX 5000 GPU was used for conducting the grid search calculation. Figure 7 displays the minimum value distribution of the metrics. The region in yellow represents the best area for choosing a learning rate and a batch size for model training. Based on the scores, the final optimal hyperparameters chosen were 0.00005 and 32 (purple ellipse area). During model training and validation, the weights with the best validation metrics were saved for prediction. The maximum epoch was set to 150, with an early-stopping parameter of 30.
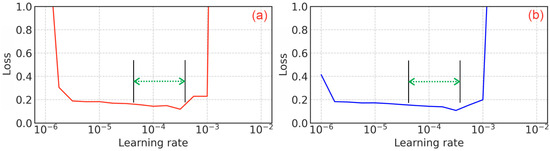
Figure 6.
Learning rate search showing the metric curves of minimized loss function vs. learning rates ((a) training and (b) validation; the green double arrows display the optimal range of the learning rate).
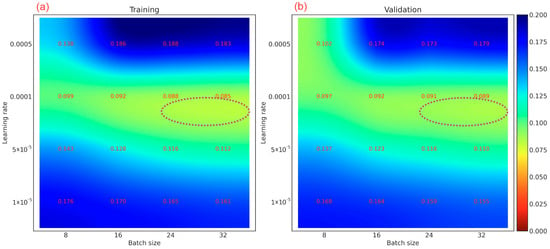
Figure 7.
The grid search layout results showing the distribution contour and minimized metric values, where (a) model training and (b) model validation.
2.2.5. Inversion Process
The process of DL-based 3D inversion is illustrated in Figure 8. It includes the components of deep learning network and convolutional neural network architecture of MT 3D inversion, which includes three main stages: dataset preparation, model training and validation, and prediction. The process is as follows: (1) The random resistivity models are generated by 3D random seeds and by forward modelling the surface response with ModEM, with data engineering to exaggerate the datasets and data standardizing normalization pre-processing to ensure uniformity of the input feature values, and the data are split into training and validation groups in a 80/20 ratio. (2) A neural network model is created, and the initial network parameters and training parameters are set, for example, filter number, kernel size, a batch size of 32, a learning rate of 0.00005, a kernel size of 3 × 3 × 3, etc. (3) The weight of the neural network is calculated based on the loss function by using the Adam algorithm, and the network optimizes the end-to-end mapping relationship by batch iteration. (4) The parameters are reset, and a grid search for better predicted results is performed, selecting the optimal parameters with a minimum verification metric and saving the final weight values. (5) The results are predicted with synthetic test datasets and comparison with the true models, and the resistivity distribution model is reconstructed for interpretation. Model training/validation took about 35 h of computation time with one Nvidia Quadro-RTX 5000 GPU. Compared with the ModEM iterative inversion, the training period took a similar amount of time, but the model prediction step was instantaneous. More GPUs can speed up the model training process. Python and related libraries (e.g., Scikit-learn, Tensorflow and Keras), were used to conduct this 3D DL inversion procedure [28,29]. MTpy and ModEM open-source packages were selected to create resistivity models and generate forward response datasets [26,30].
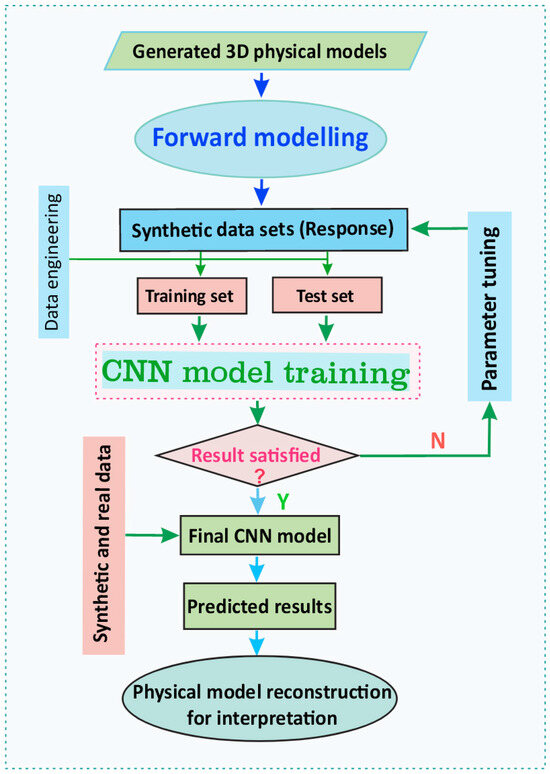
Figure 8.
The schematic workflow of DL-based 3D inversion, including dataset preparation, parameter tuning and model training/validation/testing.
3. Results
3.1. Synthetic Model
In order to test the reliability and quantitative functionality of the proposed inversion framework, three different styles of synthetic models were created to verify the trained model. Three-dimensional MT modelling processing (ModEM) was used to compute the impedance and the tipper. The same grid parameters were used for synthetic and forward modelling, which included 49 stations (as in Figure 4). A cut-off was used to disregard the background resistivity value to make the comparison more intuitive. The first model was a dipping dike as a single anomaly body (Figure 9a), where the resistivity of the surrounding background was 400.0 and the resistivity of the anomaly was 30.0 . For forward modelling, the same station geometric distribution and frequency range were used. Figure 9b illustrates the predicted result with a resistivity cut-off of 30.0 . The predicted anomalous center reconstructed the true model, and the depth of the anomalies showed a similar range as the true model.
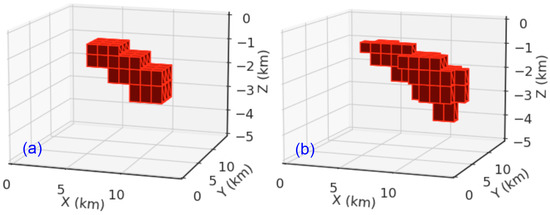
Figure 9.
Three-dimensional view of single slipped dike synthetic model ((a) true model; (b) predicted model).
For verifying the capability of the trained model to identify conductors and resistors, the second model was a T-shaped anomaly with different anomalous resistivity. The resistivity of the conductor and resistor of the T-shaped anomaly were 30.0 and 795.0 , respectively, with a background resistivity of 400.0 (Figure 10a,b). For comparison, the cut-offs of 30.0 and 795.0 were used to display the anomalies clearly. We can see that the predicted results (Figure 10c,d) generally reconstruct the shape of anomalies. Although the model shape and anomalous resistivity affected the predicted results, which led to some false structures at the bottom and side boundaries, the trained inversion model could produce a reasonable resistivity distribution image of the subsurface.
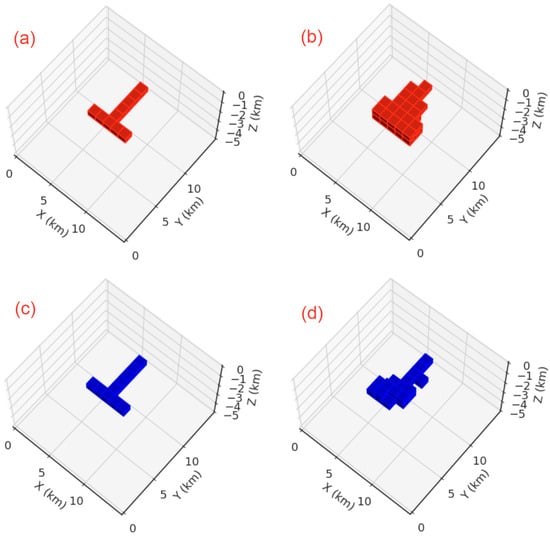
Figure 10.
The model sensitivity testing with synthetic models including an anomaly with the same shape and different resistivity ((a,b) conductor anomaly model and prediction; (c,d) resistor anomaly model and prediction).
The third model comprised two anomalous bodies. Two different resistivity distribution styles were created (Figure 11) for checking the potential interactive effect between two bodies. The first one (a, b) displayed double conductor anomalies (30.0 ) and inversion result with the DL model; the second one (c, d) was the model with one conductor (30.0 ) and one resistor (795.0 ). A cut-off (less than 30.0 and greater than 795.0 ) was used to disregard the background value of the model and display the resistivity anomalies for easier comparison. From the predicted results on the right side of the figure, one can see that both anomalies can be created in a general overview and that the depth of the two bodies corresponds to the true model. Although the resistivity values in some areas are lower than the true model, the cut-off anomalous values of the prediction can display the trend and central position and the edges of the anomalies. In general, the output can retrieve real values with an acceptable level of accuracy. For a qualitative comparison, the calculated RMSE values were 0.046 and 0.0595, which verifies that the predicted model by the neural network is reliable and can reconstruct true structures accurately for different anomaly types.
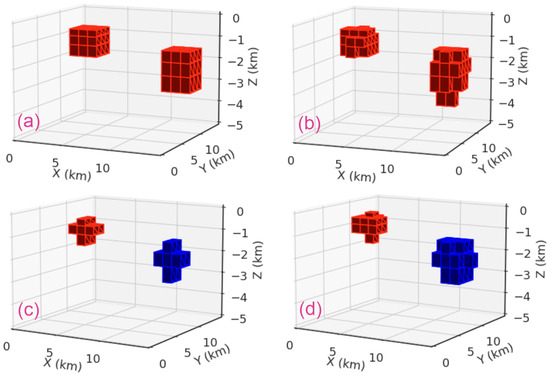
Figure 11.
Synthetic models of two anomalies at different depths and the DL 3D inversion results ((a,c) true models; (b,d) predicted results).
During synthetic model testing (Figure 11), forward modelling was conducted to calculate the impedance from the true and predicted models. Figure 12 shows the response (real and imaginary parts) contours of real data and forwarded by the predicted model with all MT stations at frequencies of 3.5 Hz (a, c) and 0.0044 Hz (b, d). One can see that the impedance distribution values are slightly biased by lower values than the real data; however, it still effectively displays the trend of impedance variation. This indicates that the proposed DL method can yield inversion results with acceptable accuracy.
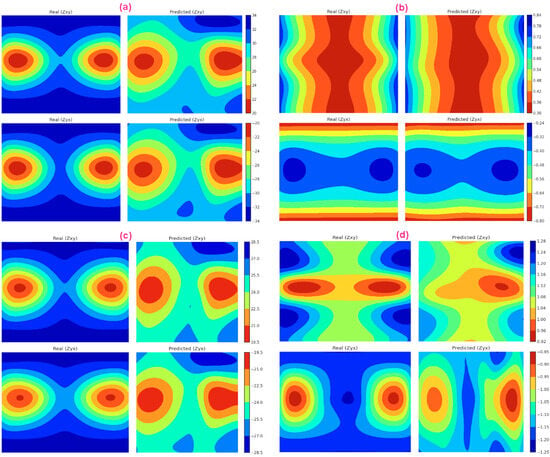
Figure 12.
The comparison of simulated impedance at two different frequencies from the true model and the predicted results of the two-body synthetic model ((a,b) real part; (c,d) imaginary part; (a,c) 3.5 Hz; (b,d) 0.0044 Hz).
3.2. Noise Test
For real world geophysical data, the noise level is a significant factor in deciding if the inverted physical parameters and interpretation of subsurface features are meaningful. In this study, we used noise-free datasets to train and validate the CNN model. To check the stability and performance of the network model prediction in the presence of noise, input datasets with different noise levels were tested. One model with two anomalies at the same depth was used (Figure 13), and different levels (0%, 5% and 10%) of random white noise with a normal Gaussian distribution were added to the impedance tensor before applying it to the input layer.
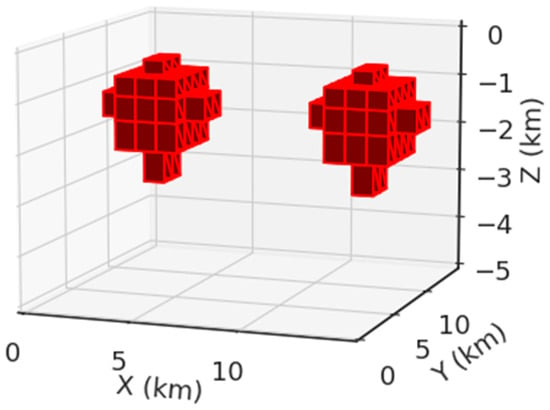
Figure 13.
The synthetic model containing two anomalous conductors at the same depth.
Figure 14 displays the horizontal slice of DL inversion resistivities with the noised data. Notably, one can see that the predicted results all show the trend of the true model resistivity variations, which verifies that the effect of noise is minimal. Table 1 lists the noise effect on the final predicted output. The RMSE and correlation coefficient varied with different noise levels. Overall, the predicted results are acceptable. The network model could still predict the anomaly locations with 10% added noise. The RMSE was 0.04384, slightly higher than results with 0% noise, which demonstrates the limited effect of noise to the trained model prediction. Although the higher RMSE had lower R2 with the increase in the noise level (Table 1), the trained network model could still produce stable results.
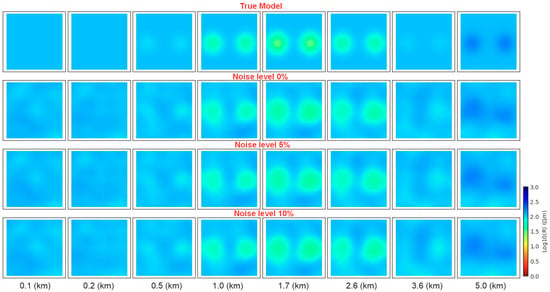
Figure 14.
The horizontal slice of model and predicted results with different noise levels (0%, 5% and 10%).

Table 1.
RMSE and R2 of predicted model with different noise levels.
3.3. Real-Data Application
A field-data application of this 3D DL-based inversion algorithm was implemented to validate its reliability. MT data were acquired from the Mount Meager volcanic area, British Columbia, Canada, in 2019 and 2020; this area is part of a geothermal energy assessment project aimed at improving our understanding of the magmatic and hydrothermal conduit system beneath Mount Meager (see Figure 15) [2,3]. The purpose of the MT survey was to comprehend the basic geological structure of the surroundings and to locate the conductive zones that are related to either the magma chamber or upwelling conductive thermal fluids. The MT field data were acquired with a Phoenix MTU-5A system to record variations in the geomagnetic field and its induced electric field. The broadband magnetotelluric (BBMT) time-series data were processed into the frequency domain by using a robust estimation of the geomagnetic transfer functions [3,18].
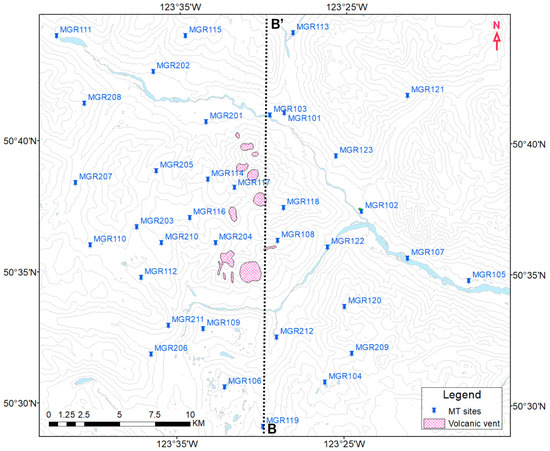
Figure 15.
MT site distribution with cross section B-B’ location in Mount Meager study area, British Columbia, Canada.
The calculated impedance components and tipper data from 35 stations with a frequency range of 100–0.001 Hz were used in model testing. These stations are marked with blue pins in Figure 15. The 3D resistivity model in this area was 19 × 19 × 25 with a 2.0 km cell size horizontally. The vertical cell size of the top grid was 20 m, and the size increased layer by layer to a total depth of about 30 km. The same hyperparameters were used for model training and validation, and the model training process took about 40 h. Based on the 3D inversion results with the trained DL model, the resistivity model was sliced into profiles which crossed the main structure of the study area. Figure 16 shows horizontal slices at different depths, which reveal a resistivity anomaly (purple dashed-line square) in the depth range 5.0 to 8.0 km and display the trend of the conductor interpreted as a potential magma body. In general, the prediction of DL inversion is consistent with the ModEM inversion result in a previous study [3].
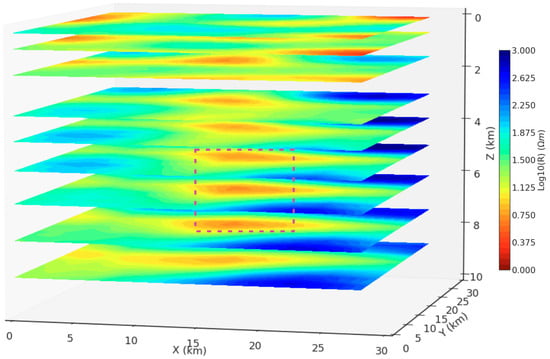
Figure 16.
Horizontal sliced iso-resistivity maps at different depths between 0.5 and 10 km (the purple dashed line indicates the main resistivity anomaly).
For a further comparison with iterative inversion, the plots in Figure 17a,c,e display both the horizontal profiles (depths of 6.0 and 7.0 km) and a vertical profile (along B-B’ in Figure 15) of the predicted 3D resistivity model. This inversion determines the high conductive zone below 5.0 km, which shows satisfactory results and is in good agreement with the 3D iterative inversion method (Figure 17b,d,f). The identified shallow conductive features with both inversion methods (Figure 17e,f) are interpreted as a hydrothermal system, where the deep conductive zone is interpreted as a magma body [31]. Despite a larger cell size being used to decrease computation time in the DL model and forward modelling, without topography, the predicted results still reflect the position and trend of the conductive body. Due to the effect of data noise and topography, one can see a shift in the anomaly center and an artifact in the near-surface area by making a comparison with the results of the traditional iterative inversion. Overall, the DL inversion results show the location of the conductivity anomalies, and the retrieved resistivity distribution represents an actual case for geological interpretation, which displays similar interpretated structures at Mount Meager [2]. Because this study is focused on methodological development and experience and some real MT data in the Meager Creek area are not available, further detailed geological interpretation and analysis cannot be provided here.
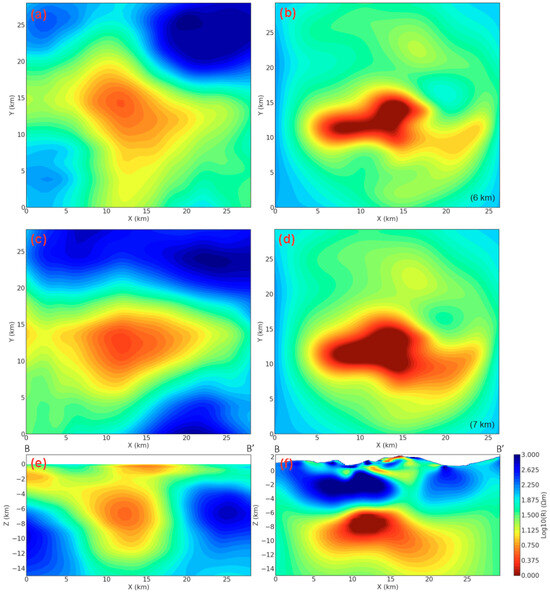
Figure 17.
Slices of the inversion results with DL-based inversion and ModEM iterative inversion. (a–d) Horizontal slices at depths of 6.0 and 7.0 km; (e,f) vertical slices along profile B-B’ in Figure 15; (a,c,e) 3D DL-based inversion; (b,d,f) ModEM iterative inversion.
4. Discussion
The computation time of the MT 3D CNN inversion workflow is mainly attributed to generating the synthetic datasets and training/validating the model weight parameters. Compared with traditional inversion methods, this algorithm needs data pairs for model training, which is costly in terms of time. However, the prediction period is short once a neural network model is created. In general, data generation with random walk improves the generalized coverage of the trained model, so using relatively fewer datasets can still produce a stable model, which reduces the computation time for a 3D inversion problem. Only one GPU is available for data preparation and model training in this study. Multiple GPUs will speed up dataset generation and model training, which will make forward modelling with a fine-mesh grid possible.
The metric contour map from the grid search with two parameters displays a minimum area for choosing the optimized parameters. The applications of synthetic models and real field data demonstrated the accountability of calculating the resistivity distribution, displaying the advantage of this method. Noise testing further verified the reliability of the proposed method (Figure 14). As a data-driven mathematical method, the overall test results of this study demonstrate that the CNN architecture can be used to simulate physical laws and simplify the MT inversion procedure.
Despite the advantages of deep learning in geophysical MT inversion, some limitations and challenges need to be noted.
Firstly, there is the biased coverage of the generated training datasets. Even when a random walk generator was used for creating training datasets, the number of resistivity models and their simulated response was limited by the computational capacity. This limits the minimum cell size and the total number of mesh grids, which leads to potential inaccuracies in model training and prediction. In this study, we could only test a mesh grid of 19 × 19 × 25. Generating more diversified training datasets by combining a prior-information-based generator will improve the model prediction, but this method will reduce the generalization of the trained neural network.
The second limitation is the complexity of the neural network model. Although U-Net has been popularly used in image segmentation, model complexity is still not enough in physical law simulation. The available datasets and computational power, e.g., #GPUs, need be considered when designing a complex neural network model. Additional investigation by testing a deeper complex neural network framework is necessary.
The third limitation is stability with topographic real noised data. For real data, adding topography to forward modelling is operationally possible. The computational capacity limits the mesh gridding of the topography. With the current hardware capacity, adding the topography effect to the simulation might lead to simulated response bias and model prediction inaccuracies. Obtaining a better resistivity range based on different sources, e.g., core analysis and well logs, will make the predicted result more comparable with iterative inversion.
These limitations mean that DL-based inversion lacks the capability to recover the same level of detail as ModEM inversion. Further research on optimizing this proposed inversion algorithm will enhance the reliability and performance of the convolutional neural network application in MT data inversion. Increasing model generalization and enhancing the noise tolerance capability of the model are crucial to ensuring the inversion model’s applicability.
5. Conclusions
Geophysical inversion is a significant and challenging step in deriving an interpretable physical model. The main purpose of this study is to improve and verify the performance of DL-based 3D inversion for MT data. The optimal parameters of a neural network framework were investigated to establish connections between MT impedance data and subsurface resistivity properties. The 3D U-Net framework displays its advantage in simulating physical laws. By using the random walk technique for data generation, we can create relative fewer datasets for model training and validation, which decreases computational cost and maintains the stability of the network model. By comparing the effect of model training parameters, the best optimal neural network parameters can be selected via parameter tuning for optimizing the weight parameters. This experience demonstrated that parameter tuning is an essential step to obtain a set of optimized parameters for model training. Lastly, the practical application of the 3D inversion method for MT synthetic and real data verified its reliability and potential. In future research, the topographic effect needs be considered with a smaller-cell-size model, and parameter tuning will be performed with a higher-dimensional search of multiple network parameters. This will produce integrated hyperparameters to improve the prediction accuracy of the trained network model.
Author Contributions
X.L.: methodology, software and original draft preparation; J.A.C.: resources, data curation, validation, and review and editing; V.T.: data curation, validation, and review and editing; S.E.G.: resources, review and editing, and project administration. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by Garibaldi Geothermal Energy Project (funded by NRCan and Geoscience BC) under Geoscience for New Energy Supply (GNES/GeoEnergy) and the Critical Mineral Geoscience Data (CMGD) program of Natural Resources Canada. This research received no external funding.
Data Availability Statement
The authors have not been granted permission to share the original MT data from the Mount Meager study area.
Acknowledgments
The authors are grateful to Martyn Unsworth and Cedar Hanneson from University of Alberta for providing the MT field data and ModEM output file and to Research Scientist Rebecca Swinscoe at Geological Survey of Canada for reviewing and discussions. The authors are grateful to the journal editors and reviewers for their rigorous reviews, with helpful suggestions and comments. The outcome represents a contribution of the GeoEnergy program. The NRCan Contribution number is 20230357.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Craven, J.A.; Farquharson, C.G.; Mackie, R.L.; Siripunvaraporn, W.; Tuncer, V.; Unsworth, M.J. A comparison of two- and three-dimensional modelling of audio-magnetotelluric data collected at the world’s richest uranium mine, Saskatchewan, Canada. In Proceedings of the 18th International Workshop on Electromagnetic Induction in the Earth, El Vendrell, Spain, 17–23 September 2006. [Google Scholar]
- Grasby, S.E.; Ansari, S.M.; Bryant, R.; Calahorrano-DiPatre, A.; Chen, Z.; Craven, J.A.; Dettmer, J.; Gilbert, H.; Hanneson, C.; Harris, M.; et al. Garibaldi Geothermal Energy Project Mount Meager 2019—Field Report. Geoscience BC Report 2020-09; Natural Resources Canada/CMSS/Information Management: Ottawa, ON, Canada, 2020; p. 153. [Google Scholar]
- Hanneson, C.; Unsworth, M.J. Magnetotelluric imaging of the magmatic and geothermal systems beneath Mount Meager, southwestern Canada. Can. J. Earth Sci. 2023. e-First. [Google Scholar] [CrossRef]
- Zhdanov, M.S. Geophysical Inverse Theory and Regularization Problems; Elsevier Science B.V.: Amsterdam, The Netherlands, 2002; pp. 214–229. [Google Scholar]
- Kim, Y.; Nakata, N. Geophysical inversion versus machine learning in inverse problems. Lead. Edge 2018, 37, 894–901. [Google Scholar] [CrossRef]
- Russell, B. Machine learning and geophysical inversion; a numerical study. Lead. Edge 2019, 38, 512–519. [Google Scholar] [CrossRef]
- Das, V.; Pollack, A.; Wollner, U.; Mukerji, T. Convolutional neural network for seismic impedance inversion. Geophysics 2019, 84, R869–R880. [Google Scholar] [CrossRef]
- Puzyrev, V. Deep learning electromagnetic inversion with convolutional neural networks. Geophys. J. Int. 2019, 218, 817–832. [Google Scholar] [CrossRef]
- Moghadas, D. One-dimensional deep learning inversion of electromagnetic induction data using convolutional neural network. Geophys. J. Int. 2020, 222, 247–259. [Google Scholar] [CrossRef]
- Guo, R.; Li, M.; Yang, F.; Xu, S.; Abubakar, A. Application of supervised descent method for 2D magnetotelluric data inversion. Geophysics 2020, 85, WA53–WA65. [Google Scholar] [CrossRef]
- Hu, Z.; Liu, S.; Hu, X.; Fu, L.; Qu, J.; Wang, H.; Chen, Q. Inversion of magnetic data using deep neural networks. Phys. Earth Planet. Inter. 2021, 311, 106653. [Google Scholar] [CrossRef]
- Wang, Y.F.; Zhang, Y.J.; Fu, L.H.; Li, H.W. Three-dimensional gravity inversion based on 3D U-Net. Appl. Geophys. 2021, 18, 451–460. [Google Scholar]
- Liu, X.; Craven, J.A.; Tschirhart, V. Retrieval of Subsurface Resistivity from Magnetotelluric Data Using a Deep-Learning-Based Inversion Technique. Minerals 2023, 13, 461. [Google Scholar] [CrossRef]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. arXiv 2014, arXiv:1411.4038 https://arxiv.org/abs/1411.4038. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Medical image Computing and Computer-Assisted Intervention–MICCAI 2015: 18th International Conference, Munich, Germany, 5–9 October 2015; Springer: Berlin/Heidelberg, Germany, 2015; Volume 9351, pp. 234–241. [Google Scholar]
- Chen, Z.; Liu, X.; Yang, J.; Little, E.; Zhou, Y. Deep learning-based method for SEM image segmentation in mineral characterization, an example from Duvernay Shale samples in Western Canada Sedimentary Basin. Comput. Geosci. 2020, 138, 104450. [Google Scholar] [CrossRef]
- Ward, S.H.; Hohmann, G.W. Electromagnetic Theory for Geophysical Applications. Electromagn. Methods Appl. Geophys. 1987, 1, 201. [Google Scholar]
- Egbert, G.D.; Booker, J.R. Robust estimation of geomagnetic transfer functions. Geophys. J. R. Astron. Soc. 1986, 87, 173–194. [Google Scholar] [CrossRef]
- Mackie, R.L.; Madden, T.R. Three-dimensional magnetotelluric inversion using conjugate gradients. Geophys. J. Int. 1993, 115, 215–219. [Google Scholar] [CrossRef]
- Farquharson, C.G.; Craven, J.A. Three-dimensional inversion of magnetotelluric data for mineral exploration: An example from the McArthur River uranium deposit, Saskatchewan, Canada. J. Appl. Geophys. 2009, 68, 450–458. [Google Scholar] [CrossRef]
- Egbert, G.D.; Kelbert, A. Computational recipes for electromagnetic inverse problems. Geophys. J. Int. 2012, 189, 251–267. [Google Scholar] [CrossRef]
- Constable, S.C.; Parker, R.L.; Constable, C.G. Occam’s inversion: A practical algorithm for generating smooth models from electromagnetic sounding data. Geophysics 1987, 52, 289–300. [Google Scholar] [CrossRef]
- Çiçek, Ö.; Abdulkadir, A.; Lienkamp, S.S.; Brox, T.; Ronneberger, O. 3D U-Net: Learning Dense Volumetric Segmentation from Sparse Annotation. arXiv 2016. [Google Scholar] [CrossRef]
- Hochreiter, S. The Vanishing Gradient Problem during Learning Recurrent Neural Nets and Problem Solutions. Int. J. Uncertain. Fuzziness Knowl.-Based Syst. 1998, 6, 107–116. [Google Scholar] [CrossRef]
- Zhou, Z.; Rahman Siddiquee, M.M.; Tajbakhsh, N.; Liang, J. Unet++: A nested u-net architecture for medical image segmentation. In Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support: 4th International Workshop, DLMIA 2018, and 8th International Workshop, ML-CDS 2018, Held in Conjunction with MICCAI 2018, Granada, Spain, 20 September 2018; Springer: Berlin/Heidelberg, Germany, 2018; Volume 11045, pp. 3–11. [Google Scholar] [CrossRef]
- Krieger, L.; Peacock, J.R. MTpy: A Python toolbox for magnetotellurics. Comput. Geosci. 2014, 72, 167–175. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Keras (Webpage). 2015. Available online: https://keras.io (accessed on 1 July 2022).
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A. Tensorflow: A system for large-scale machine learning. In Proceedings of the 12th USENIX Symposium on Operating Systems Design and Implementation (OSDI 16), Savannah, GA, USA, 2–4 November 2016; Volume 16, pp. 265–283. [Google Scholar]
- Kelbert, A.; Meqbel, N.; Egbert, G.D.; Tandon, K. ModEM: A modular system for inversion of electromagnetic geophysical data. Comput. Geosci. 2014, 66, 40–53. [Google Scholar] [CrossRef]
- Jones, A.G.; Dumas, I. Electromagnetic images of a volcanic zone. Phys. Earth Planet. Inter. 1993, 81, 289–314. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).