Relationship between Vegetation and Soil Moisture Anomalies Based on Remote Sensing Data: A Semiarid Rangeland Case
Abstract
1. Introduction
2. Material and Methods
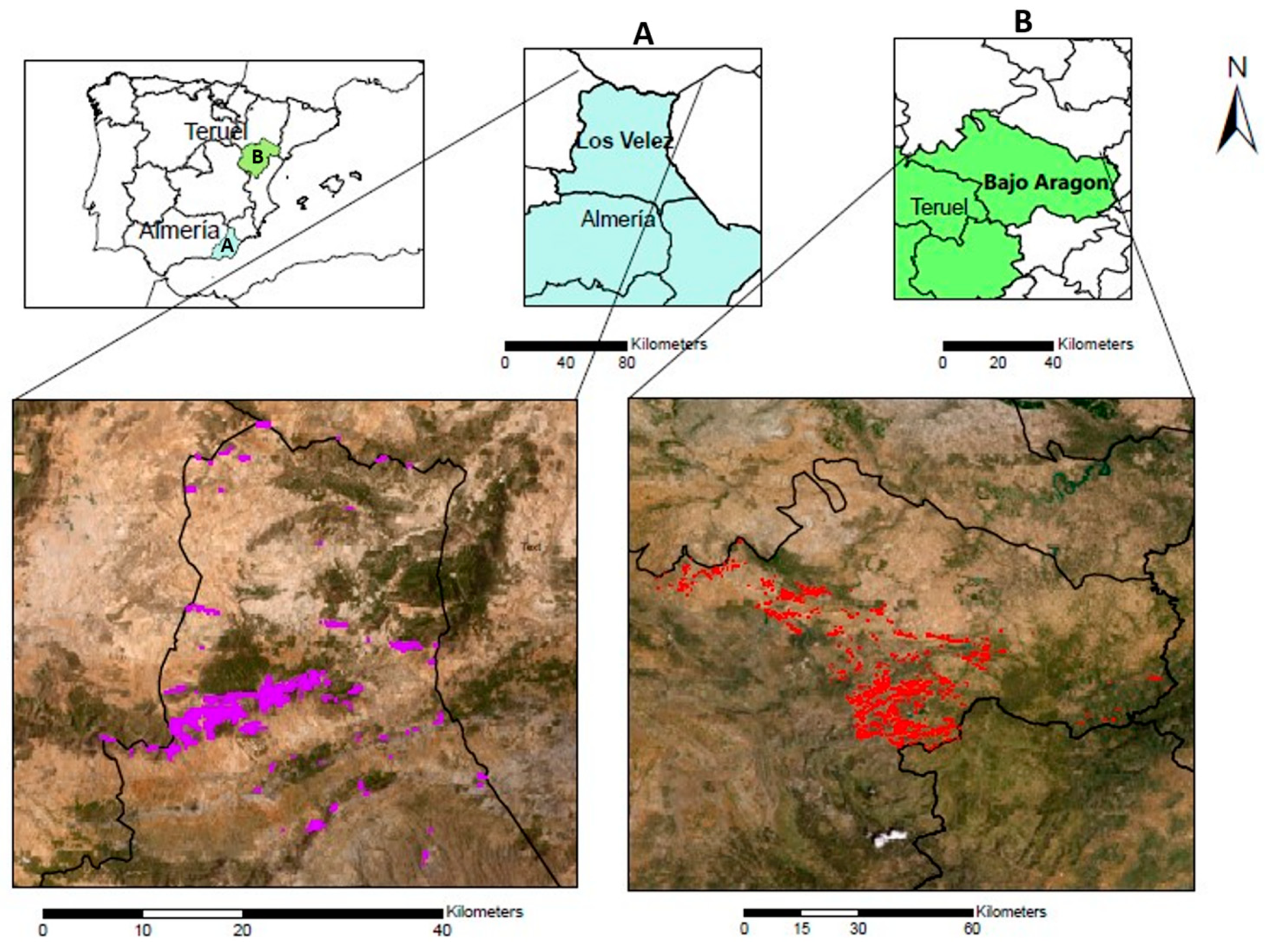
2.1. Area of Study
2.2. Data Collection
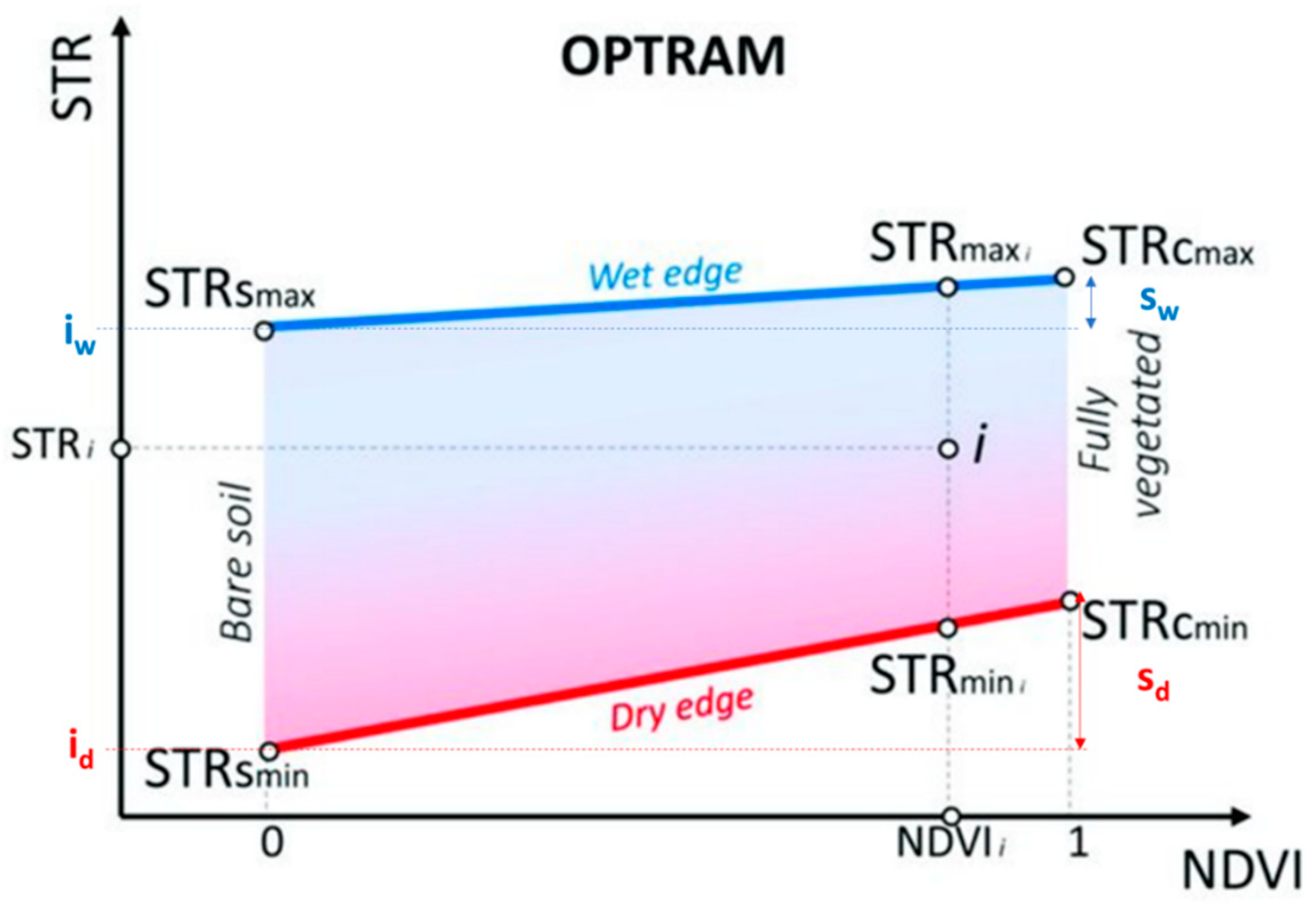
2.3. Estimation of Vegetation and Soil Moisture Content Indices
2.4. Estimation of Probabilities of WCI and VCI Anomalies
3. Results
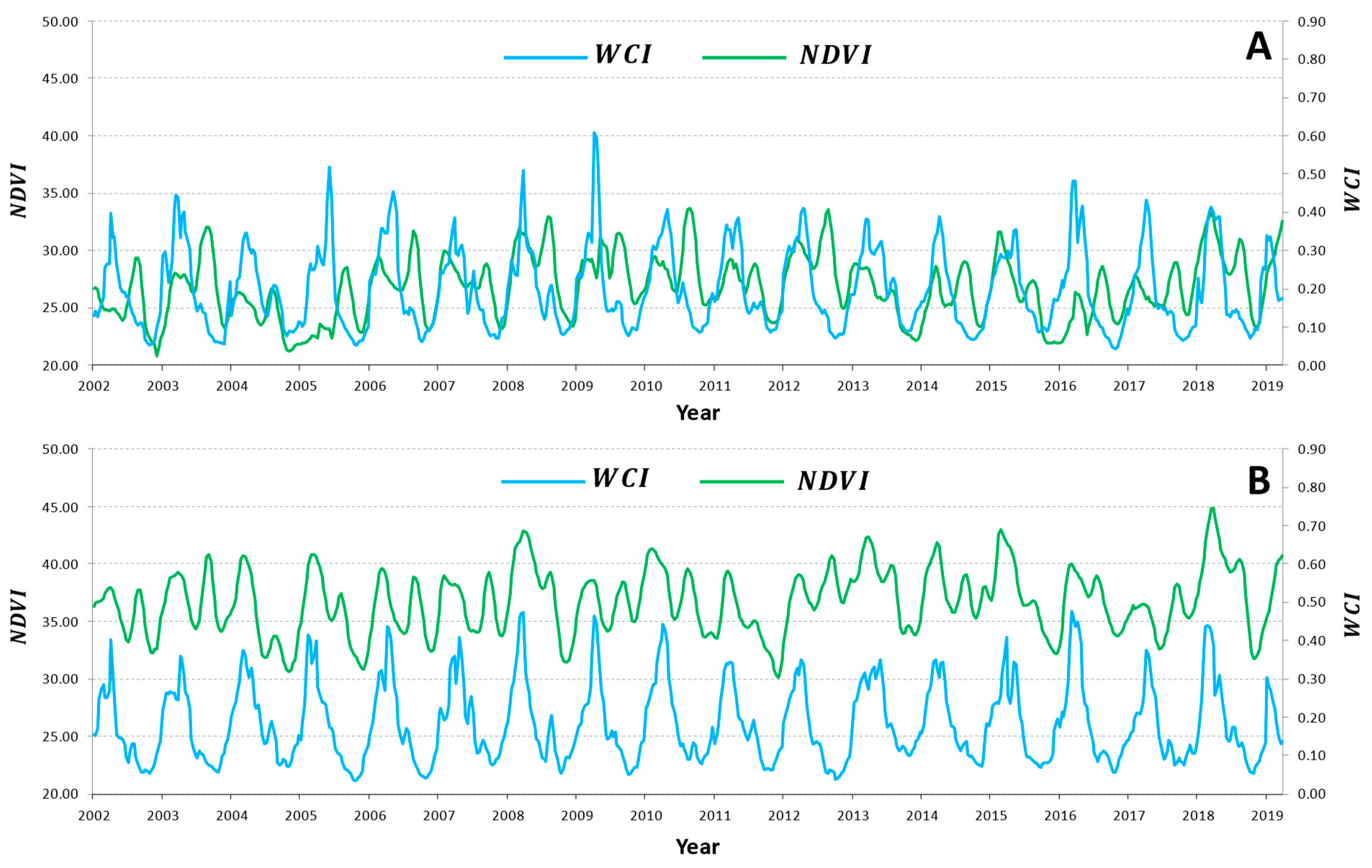
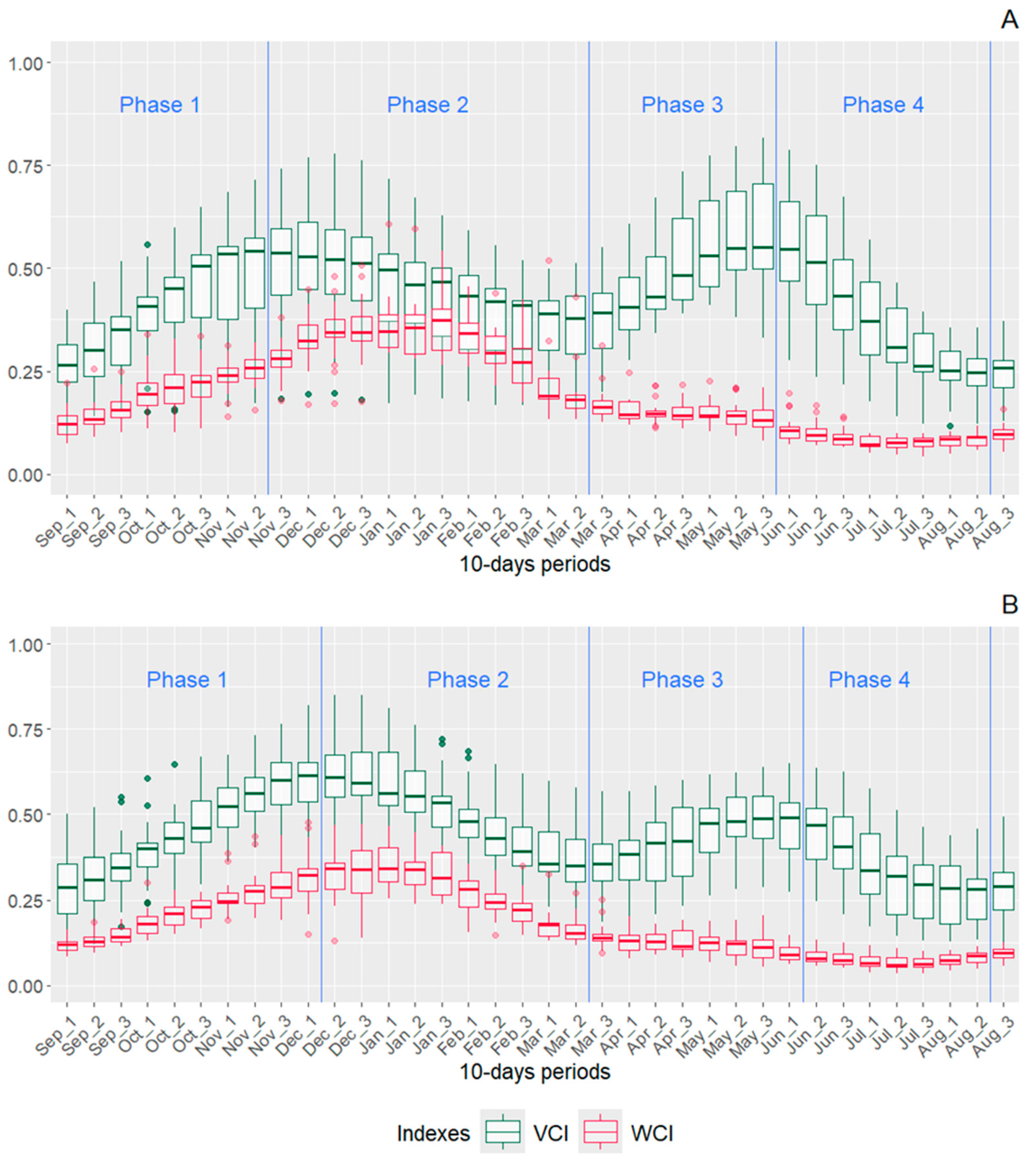
3.1. Soil Moisture and Vegetation Indices
3.2. Water and Vegetation Condition Indices
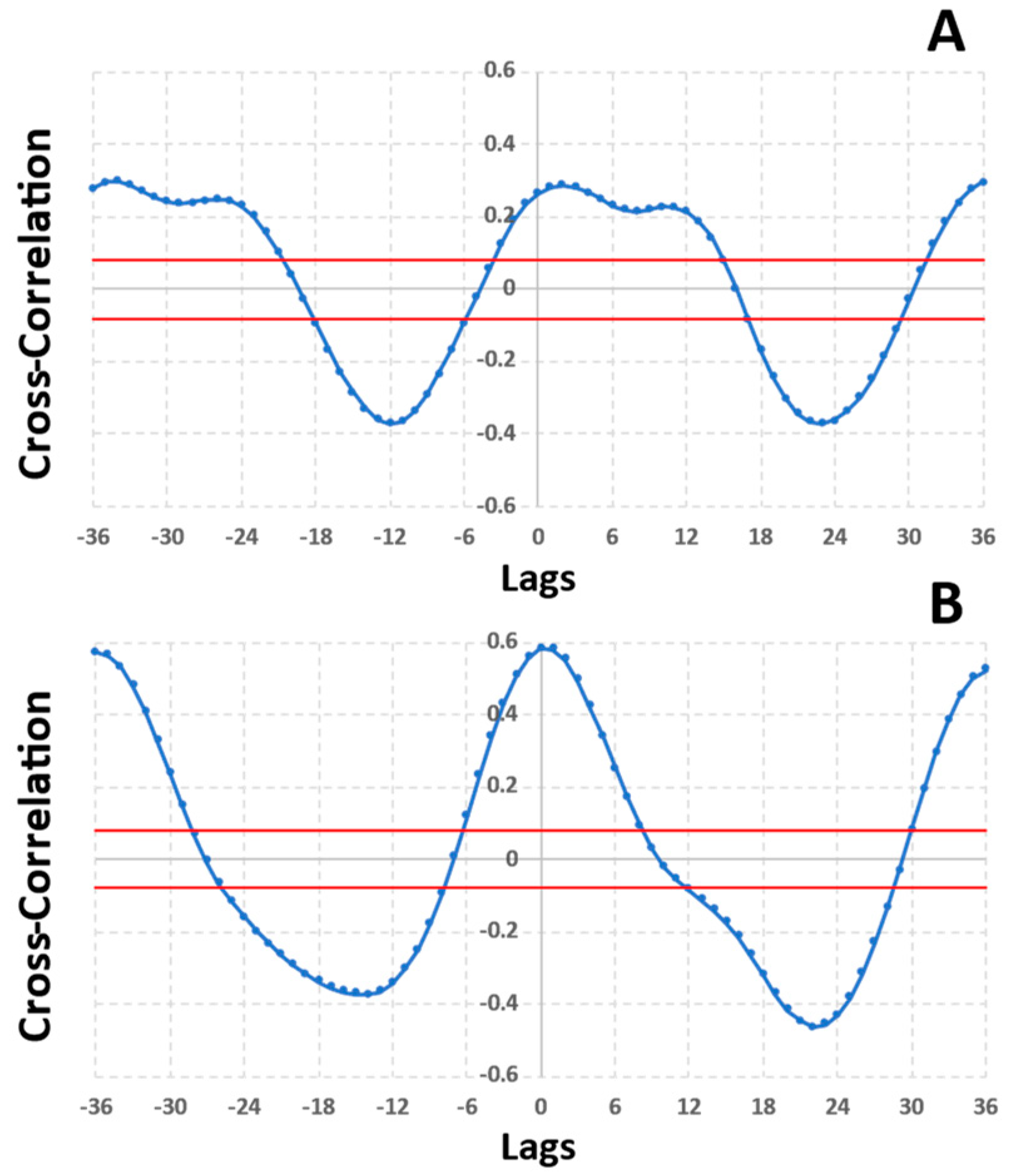
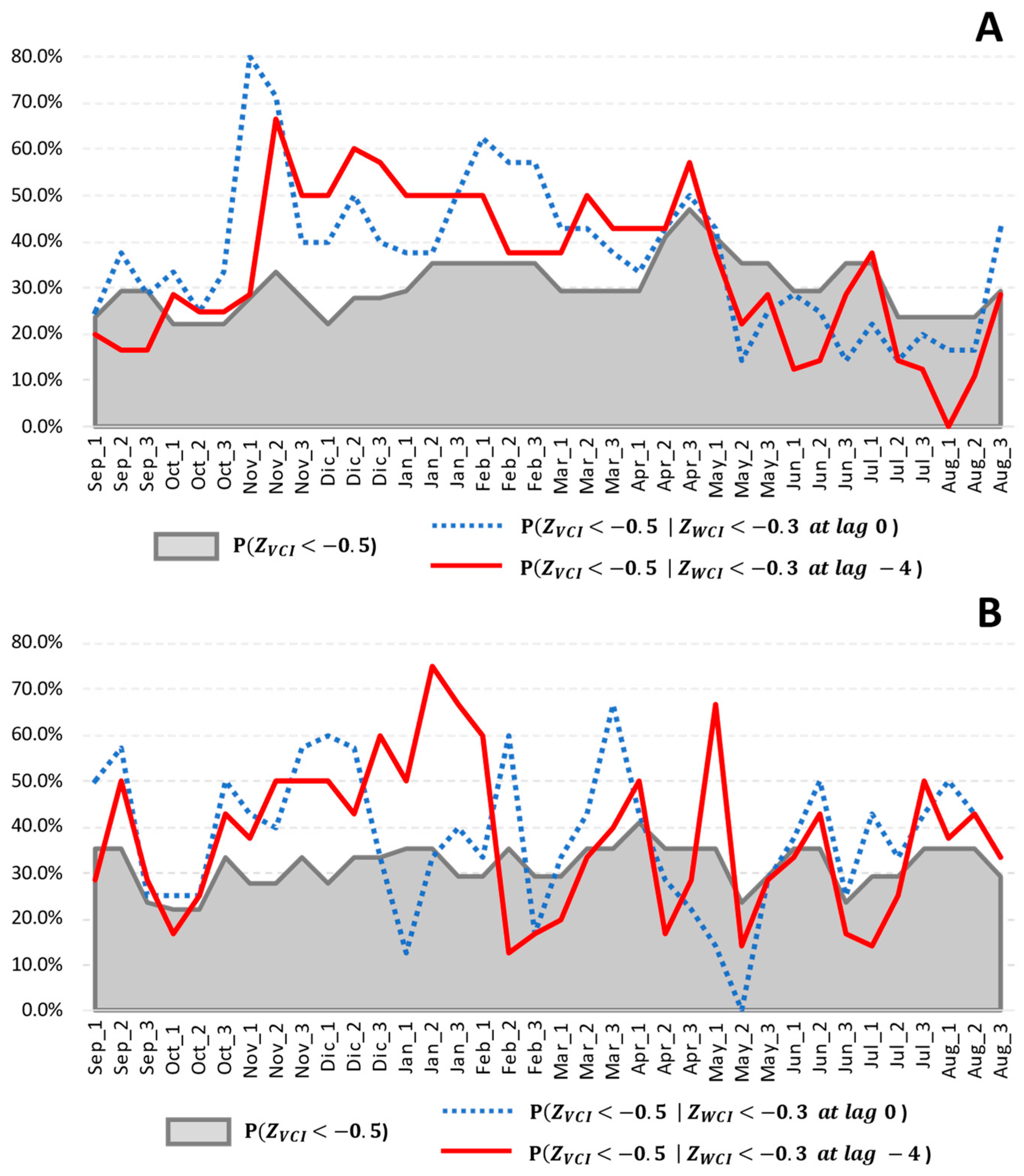
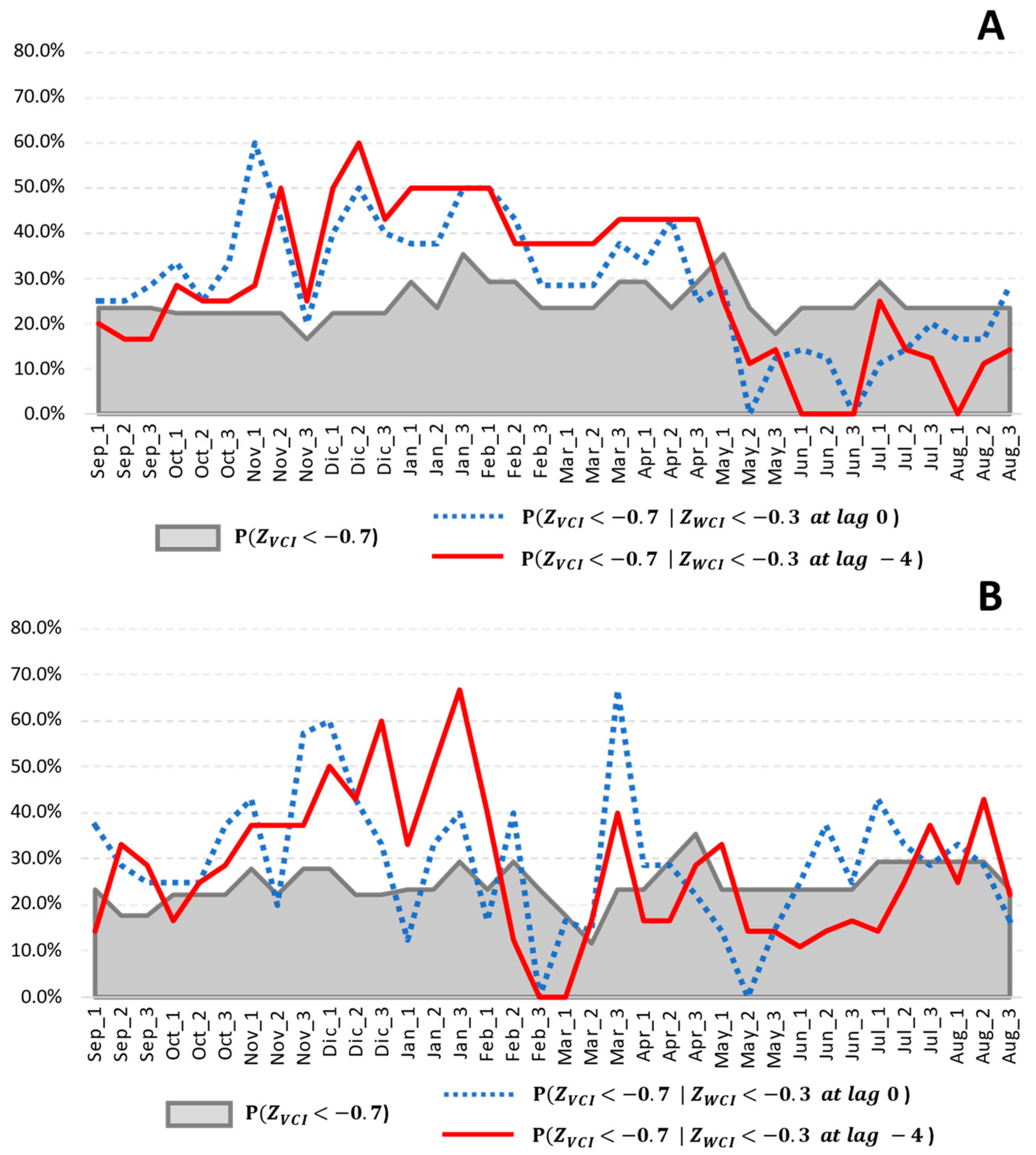
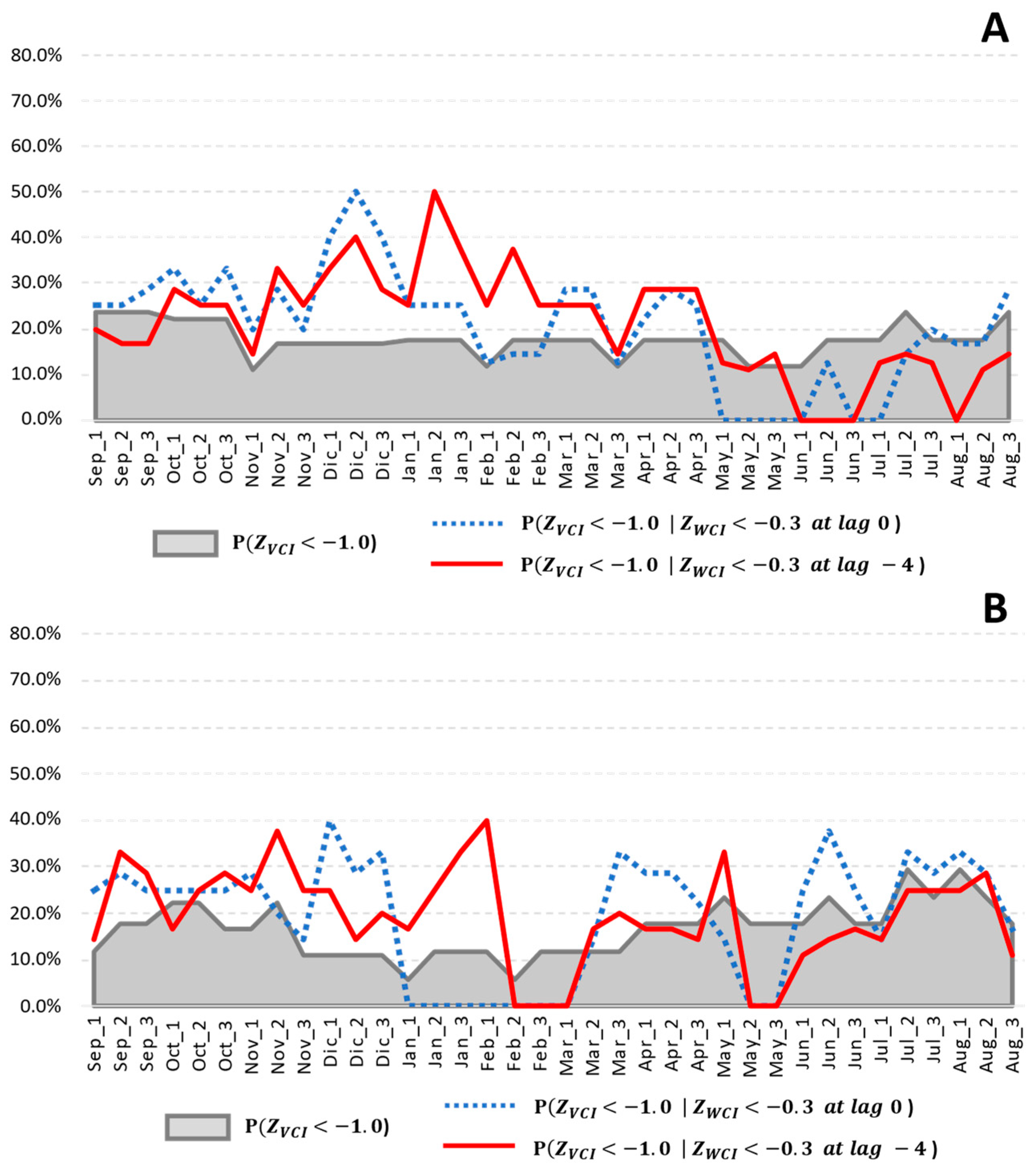
3.3. Relationship of VCI and WCI Anomalies
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Adegoke, J.O.; Carleton, A.M. Relations between Soil Moisture and Satellite Vegetation Indices in the U.S. Corn Belt. J. Hydrometeorol. 2002, 3, 395–405. [Google Scholar] [CrossRef]
- Felegari, S.; Sharifi, A.; Moravej, K.; Golchin, A.; Tariq, A. Investigation of the relationship between ndvi index, soil moisture, and precipitation data using satellite images. In Sustainable Agriculture Systems and Technologies; Wiley Online Library: Hoboken, NJ, USA, 2022; pp. 314–325. [Google Scholar] [CrossRef]
- Sharma, M.; Bangotra, P.; Gautam, A.S.; Gautam, S. Sensitivity of normalised difference vegetation index (NDVI) to land surface temperature, soil moisture and precipitation over district Gautam Buddh Nagar, UP, India. Stoch. Environ. Res. Risk Assess. 2022, 36, 1779–1789. [Google Scholar] [CrossRef] [PubMed]
- Hirschi, M.; Mueller, B.; Dorigo, W.; Seneviratne, S.I. Using remotely sensed soil moisture for land-atmosphere coupling diagnostics: The role of surface vs. root-zone soil moisture variability. Remote Sens. Environ. 2014, 154, 246–252. [Google Scholar] [CrossRef]
- Albergel, C.; Udiger, C.R.; Pellarin, T.; Calvet, J.-C.; Fritz, N.; Froissard, F.; Suquia, D.; Petitpa, A.; Piguet, B.; Martin, E. Hydrology and Earth System Sciences From near-surface to root-zone soil moisture using an exponential filter: An assessment of the method based on in-situ observations and model simulations. Hydrol. Earth Syst. Sci. 2008, 12, 1323–1337. [Google Scholar] [CrossRef]
- Babaeian, E.; Sadeghi, M.; Jones, S.B.; Montzka, C.; Vereecken, H.; Tuller, M. Ground, proximal, and satellite remote sensing of soil moisture. Rev. Geophys. 2019, 57, 530–616. [Google Scholar] [CrossRef]
- Liu, W.T.; Kogan, F.N. Monitoring regional drought using the vegetation condition index. Int. J. Remote Sens. 1996, 17, 2761–2782. [Google Scholar] [CrossRef]
- Wang, X.; Xie, H.; Guan, H.; Zhou, X. Different responses of MODIS-derived NDVI to root-zone soil moisture in semi-arid and humid regions. J. Hydrol. 2007, 340, 12–24. [Google Scholar] [CrossRef]
- Guan, Y.; Lu, H.; Yin, C.; Xue, Y.; Jiang, Y.; Kang, Y.; He, L.; Heiskanen, J. Vegetation response to climate zone dynamics and its impacts on surface soil water content and albedo in China. Sci. Total. Environ. 2020, 747, 141537. [Google Scholar] [CrossRef]
- Schnur, M.T.; Xie, H.; Wang, X. Estimating root zone soil moisture at distant sites using MODIS NDVI and EVI in a semi-arid region of southwestern USA. Ecol. Inform. 2010, 5, 400–409. [Google Scholar] [CrossRef]
- Allaby, M. Droughts; Infobase Publishing: New York, NY, USA, 2014. [Google Scholar]
- American Meteorological Society: Meteorological drought—Policy statement. Bull. Am. Meteorol. Soc. 1997, 78, 847–849.
- American Meteorological Society: AMS statement on meteorological drought. Bull. Am. Meteorol. Soc. 2004, 85, 771–773.
- Wilhite, D.A.; Buchanan-Smith, M. Drought as hazard: Understanding the natural and social context. Drought Water Cris. Sci. Technol. Manag. Issues 2005, 3, 29. [Google Scholar]
- Kim, D.-W.; Byun, H.-R.; Choi, K.-S. Evaluation, modification, and application of the Effective Drought Index to 200-Year drought climatology of Seoul, Korea. J. Hydrol. 2009, 378, 1–12. [Google Scholar] [CrossRef]
- Mahmoudi, P.; Rigi, A.; Kamak, M.M. Evaluating the sensitivity of precipitation-based drought indices to different lengths of record. J. Hydrol. 2019, 579, 124181. [Google Scholar] [CrossRef]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; Volume 17, pp. 179–183. [Google Scholar]
- Byun, H.-R.; Wilhite, D.A. Objective quantification of drought severity and duration. J. Clim. 1999, 12, 2747–2756. [Google Scholar] [CrossRef]
- Willeke, G.; Hosking, J.R.M.; Wallis, J.R.; Guttman, N.B. The national drought atlas. Inst. Water Resour. Rep. 1994, 94. [Google Scholar]
- AghaKouchak, A.; Farahmand, A.; Melton, F.S.; Teixeira, J.; Anderson, M.C.; Wardlow, B.D.; Hain, C.R. Remote sensing of drought: Progress, challenges and opportunities. Rev. Geophys. 2015, 53, 452–480. [Google Scholar] [CrossRef]
- Wang, L.; Qu, J.J. Satellite remote sensing applications for surface soil moisture monitoring: A review. Front. Earth Sci. China 2009, 3, 237–247. [Google Scholar] [CrossRef]
- Hao, Z.; AghaKouchak, A. Multivariate standardised drought index: A parametric multi-index model. Ad. Water Resour. 2013, 57, 12–18. [Google Scholar] [CrossRef]
- Sheffield, J.; Goteti, G.; Wen, F.; Wood, E.F. A simulated soil moisture based drought analysis for the United States. J. Geophys. Res. Atmos. 2004, 109. [Google Scholar] [CrossRef]
- Babaeian, E.; Sadeghi, M.; Franz, T.E.; Jones, S.; Tuller, M. Mapping soil moisture with the OPtical TRApezoid Model (OPTRAM) based on long-term MODIS observations. Remote. Sens. Environ. 2018, 211, 425–440. [Google Scholar] [CrossRef]
- Sadeghi, M.; Babaeian, E.; Tuller, M.; Jones, S.B. The optical trapezoid model: A novel approach to remote sensing of soil moisture applied to Sentinel-2 and Landsat-8 observations. Remote. Sens. Environ. 2017, 198, 52–68. [Google Scholar] [CrossRef]
- Chen, M.; Zhang, Y.; Yao, Y.; Lu, J.; Pu, X.; Hu, T.; Wang, P. Evaluation of the OPTRAM Model to Retrieve Soil Moisture in the Sanjiang Plain of Northeast China. Earth Space Sci. 2020, 7, e2020EA001108. [Google Scholar] [CrossRef]
- Ambrosone, M.; Matese, A.; Di Gennaro, S.F.; Gioli, B.; Tudoroiu, M.; Genesio, L.; Miglietta, F.; Baronti, S.; Maienza, A.; Ungaro, F.; et al. Retrieving soil moisture in rainfed and irrigated fields using Sentinel-2 observations and a modified OPTRAM approach. Int. J. Appl. Earth Obs. Geoinf. 2020, 89, 102113. [Google Scholar] [CrossRef]
- Ma, C.; Johansen, K.; McCabe, M.F. Combining Sentinel-2 data with an optical-trapezoid approach to infer within-field soil moisture variability and monitor agricultural production stages. Agric. Water Manag. 2022, 274, 107942. [Google Scholar] [CrossRef]
- Skees, J.R.; Gober, S.; Varangis, P.; Lester, R.; Kalavakonda, V. Developing Rainfall-Based Index Insurance in Morocco; World Bank Publications: Washington, DC, USA, 2001; Volume 2577. [Google Scholar]
- Wilhite, D. Drought Monitoring and Early Warning: Concepts, Progress and Future Challenges; World Meteorological Organization, WMO: Geneva, Switzerland, 2006. [Google Scholar]
- Sepulcre-Canto, G.; Horion, S.; Singleton, A.; Carrao, H.; Vogt, J. Development of a Combined Drought Indicator to detect agricultural drought in Europe. Nat. Hazards Earth Syst. Sci. 2012, 12, 3519–3531. [Google Scholar] [CrossRef]
- Jiménez-Donaire, M.d.P.; Tarquis, A.; Giráldez, J.V. Evaluation of a combined drought indicator and its potential for agricultural drought prediction in southern Spain. Nat. Hazards Earth Syst. Sci. 2020, 20, 21–33. [Google Scholar] [CrossRef]
- Shofiyati, R.; Takeuchi, W.; Pasaribu, S.M.; Irawan, Y.R. Space-based drought analysis to support agricultural insurance facing climate change. IOP Conf. Ser. Earth Environ. Sci. 2021, 648, 012130. [Google Scholar] [CrossRef]
- Canedo Rosso, C.; Hochrainer-Stigler, S.; Pflug, G.; Condori, B.; Berndtsson, R. Early warning and drought risk assessment for the Bolivian Altiplano agriculture using high resolution satellite imagery data. Nat. Hazards Earth Syst. Sci. Discuss. 2018, 2018, 1–23. [Google Scholar] [CrossRef]
- Desai, B.; Maskrey, A.; Peduzzi, P.; de Bono, A.; Herold, C.; United Nations Office for Disaster Risk Reduction (UNISDR). Making Development Sustainable: The Future of Disaster Risk Management, Global Assessment Report on Disaster Risk Reduction; United Nations Office for Disaster Risk Reduction (UNISDR): Geneva, Switzerland, 2015. [Google Scholar]
- Azhdari, Z.; Bazrafshan, O.; Shekari, M.; Zamani, H. Three-dimensional risk analysis of hydro-meteorological drought using multivariate nonlinear index. Theor. Appl. Clim. 2020, 142, 1311–1327. [Google Scholar] [CrossRef]
- Hao, Y.; Hao, Z.; Fu, Y.; Feng, S.; Zhang, X.; Wu, X.; Hao, F. Probabilistic assessments of the impacts of compound dry and hot events on global vegetation during growing seasons. Environ. Res. Lett. 2021, 16, 074055. [Google Scholar] [CrossRef]
- Ribeiro, A.F.S.; Russo, A.; Gouveia, C.M.; Páscoa, P.; Pires, C.A.L. Probabilistic modelling of the dependence between rainfed crops and drought hazard. Nat. Hazards Earth Syst. Sci. 2019, 19, 2795–2809. [Google Scholar] [CrossRef]
- Sanz, E.; Martín-Sotoca, J.J.; Saa-Requejo, A.; Moratiel, R.; Almeida-Ñauñay, A.; Faraslis, I.; Tarquis, A.M. Temporal Coincidence of Soil Water and Vegetation Anomalies in Arid Rangelands. In Proceedings of the Estudios en la Zona No Saturada del Suelo VOL, Sevilla, Spanish, 7–9 November 2023; XVI. ZNS’23. pp. 109–114, ISBN 978-84-09-55828-5. [Google Scholar]
- Aguilar Ruiz, J. Mapa de Suelos Escala 1:100 000. Provincia de Almería; Proyecto Lucdeme; Ministerio de Agricultura, Alimentación y Medio Ambiente (MAGRAMA): Madrid, Spain, 2004. [Google Scholar]
- Grupo de Agroenergética de la E.T.S.I. Agrónomos (UPM). Caracterización de las Comarcas Agrarias de España; Tomo 6. Provincia de Almería; Ministerio de Agricultura, Alimentación y Medio Ambiente (MAGRAMA): Madrid, Spain, 2014. [Google Scholar]
- Cueto, M.; Blanca, G. Flora del Parque Natural de Sierra María-Los Vélez; Sociedad Almeriense de Historia Natural: Almería, Spain, 1997. [Google Scholar]
- Del Palacio Fernández-Montes, E.; Martín Fernández, L.; Hernández Álvarez, J.; Rojo Serrano, L. Inventario Nacional de Suelos. Teruel; Ministerio de Agricultura y Pesca, Alimentación y Medio Ambiente: Madrid, Spain, 2015; ISBN 978-84-491-1507-3. [Google Scholar]
- Ibarra, P.; Nieto, V.; Echeverría, M.T.; Lozano, M.V.; Albero, M.J.; Julián, A.; Peña, J.L. La diversidad paisajística de Aragón. Utilidad de la cartografía de Paisaje a escala regional para el conocimiento, planificación y gestión del territorio. In Proceedings of the Actas del XXIII Congreso de Geógrafos Españoles AGE, Palma, Spanish, 23–25 October 2013; Espacios insulares y de frontera. Una visión geográfica. pp. 597–607. [Google Scholar]
- San Miguel, A. Pastos Naturales Españoles. Caracterización, Aprovechamiento y Posibilidades de Mejora; Coedición Fundación Conde del Valle de Salazar- Mundi-Prensa: Madrid, Spain, 2001; 320p, ISBN 8471149915. [Google Scholar]
- Ibarra Benlloch, P. La diversidad edáfica del territorio aragonés. In Geografía física de Aragón; Peña, J.L., Longares, L.A., Sánchez, M., Eds.; Universidad de Zaragoza: Zaragoza, Spain, 2004; pp. 41–53. ISBN 84-96214-29-X. [Google Scholar]
- Grupo de Agroenergética de la E.T.S.I. Agrónomos (UPM). Caracterización de las Comarcas Agrarias de España; Tomo 45. Provincia de Teruel; Ministerio de Agricultura, Alimentación y Medio Ambiente (MAGRAMA): Madrid, Spain, 2014. [Google Scholar]
- Fondo Español de Garantía Agraria (FEGA). Visor SIGPAC. Ministerio de Agricultura, Pesca y Alimentación. Gobierno de España. Available online: https://www.fega.gob.es/es/pepac-2023-2027/sistemas-gestion-y-control/sigpac (accessed on 20 June 2024).
- Team, A. Application for Extracting and Exploring Analysis Ready Samples (AppEEARS); NASA EOSDIS Land Processes Distributed Active Archive Center (LP DAAC): Sioux Falls, SD, USA; USGS/Earth Resources Observation and Science (EROS) Center: Sioux Falls, SD, USA, 2020; Available online: https://Lpdaacsvc.Cr.Usgs.Gov/Appeears/ (accessed on 2 June 2020).
- Sistema de Información Agroclimática para el Regadío (SIAR). Ministerio de Agricultura, Pesca y Alimentación. Gobierno de España. Available online: https://servicio.mapa.gob.es/websiar/Inicio.aspx (accessed on 20 June 2024).
- Kogan, F. Application of vegetation index and brightness temperature for drought detection. Adv. Space Res. 1995, 15, 91–100. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A multiscalar drought index sensitive to global warming: The standardised precipitation evapotranspiration index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Almeida-Ñauñay, A.F.; Villeta, M.; Quemada, M.; Tarquis, A.M. Assessment of Drought Indexes on Different Time Scales: A Case in Semiarid Mediterranean Grasslands. Remote. Sens. 2022, 14, 565. [Google Scholar] [CrossRef]
- Pei, Z.; Fang, S.; Wang, L.; Yang, W. Comparative analysis of drought indicated by the SPI and SPEI at various timescales in inner Mongolia, China. Water 2020, 12, 1925. [Google Scholar] [CrossRef]
- He, J.; Yang, X.; Li, Z.; Zhang, X.; Tang, Q. Spatiotemporal variations of meteorological droughts in China during 1961–2014: An investigation based on multi-threshold identification. Int. J. Disaster Risk Sci. 2016, 7, 63–76. [Google Scholar] [CrossRef]
- Ma, Q.; Li, Y.; Liu, F.; Feng, H.; Biswas, A.; Zhang, Q. SPEI and multi-threshold run theory based drought analysis using multi-source products in China. J. Hydrol. 2022, 616, 128737. [Google Scholar] [CrossRef]
- Sanz, E.; Saa-Requejo, A.; Díaz-Ambrona, C.H.; Ruiz-Ramos, M.; Rodríguez, A.; Iglesias, E.; Esteve, P.; Soriano, B.; Tarquis, A.M. Normalized Difference Vegetation Index Temporal Responses to Temperature and Precipitation in Arid Rangelands. Remote. Sens. 2021, 13, 840. [Google Scholar] [CrossRef]
- Wang, J.; Rich, P.M.; Price, K.P. Temporal responses of NDVI to precipitation and temperature in the central Great Plains, USA. Int. J. Remote Sens. 2003, 24, 2345–2364. [Google Scholar] [CrossRef]
- Cui, L.; Shi, J. Temporal and spatial response of vegetation NDVI to temperature and precipitation in eastern China. J. Geogr. Sci. 2010, 20, 163–176. [Google Scholar] [CrossRef]
- Rembold, F.; Meroni, M.; Urbano, F.; Csak, G.; Kerdiles, H.; Perez-Hoyos, A.; Lemoine, G.; Leo, O.; Negre, T. ASAP: A new global early warning system to detect anomaly hot spots of agricultural production for food security analysis. Agric. Syst. 2019, 168, 247–257. [Google Scholar] [CrossRef] [PubMed]
- Haigh, T.R.; Otkin, J.A.; Mucia, A.; Hayes, M.; Burbach, M.E. Drought Early Warning and the Timing of Range Managers’ Drought Response. Adv. Meteorol. 2019, 2019, 9461513. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martín-Sotoca, J.J.; Sanz, E.; Saa-Requejo, A.; Moratiel, R.; Almeida-Ñauñay, A.F.; Tarquis, A.M. Relationship between Vegetation and Soil Moisture Anomalies Based on Remote Sensing Data: A Semiarid Rangeland Case. Remote Sens. 2024, 16, 3369. https://doi.org/10.3390/rs16183369
Martín-Sotoca JJ, Sanz E, Saa-Requejo A, Moratiel R, Almeida-Ñauñay AF, Tarquis AM. Relationship between Vegetation and Soil Moisture Anomalies Based on Remote Sensing Data: A Semiarid Rangeland Case. Remote Sensing. 2024; 16(18):3369. https://doi.org/10.3390/rs16183369
Chicago/Turabian StyleMartín-Sotoca, Juan José, Ernesto Sanz, Antonio Saa-Requejo, Rubén Moratiel, Andrés F. Almeida-Ñauñay, and Ana M. Tarquis. 2024. "Relationship between Vegetation and Soil Moisture Anomalies Based on Remote Sensing Data: A Semiarid Rangeland Case" Remote Sensing 16, no. 18: 3369. https://doi.org/10.3390/rs16183369
APA StyleMartín-Sotoca, J. J., Sanz, E., Saa-Requejo, A., Moratiel, R., Almeida-Ñauñay, A. F., & Tarquis, A. M. (2024). Relationship between Vegetation and Soil Moisture Anomalies Based on Remote Sensing Data: A Semiarid Rangeland Case. Remote Sensing, 16(18), 3369. https://doi.org/10.3390/rs16183369







