A Target Detection Algorithm Based on Fusing Radar with a Camera in the Presence of a Fluctuating Signal Intensity
Abstract
1. Introduction
2. Information Fusion Model
3. Realization of Fusion
3.1. Radar Data Processing
3.1.1. Signal Model of the FMCW Radar
3.1.2. The Improved DBSCAN Algorithm
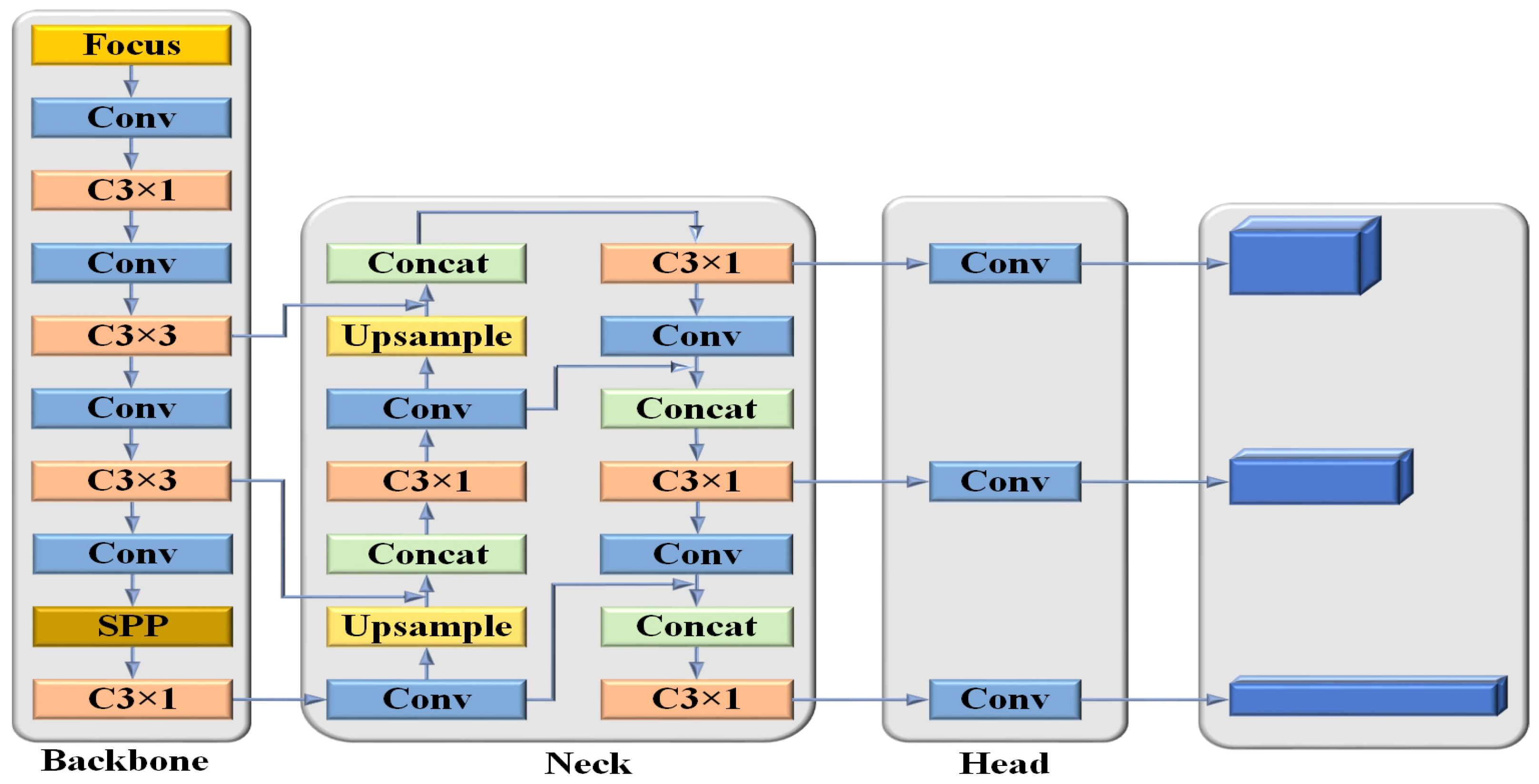
3.2. Video Data Processing
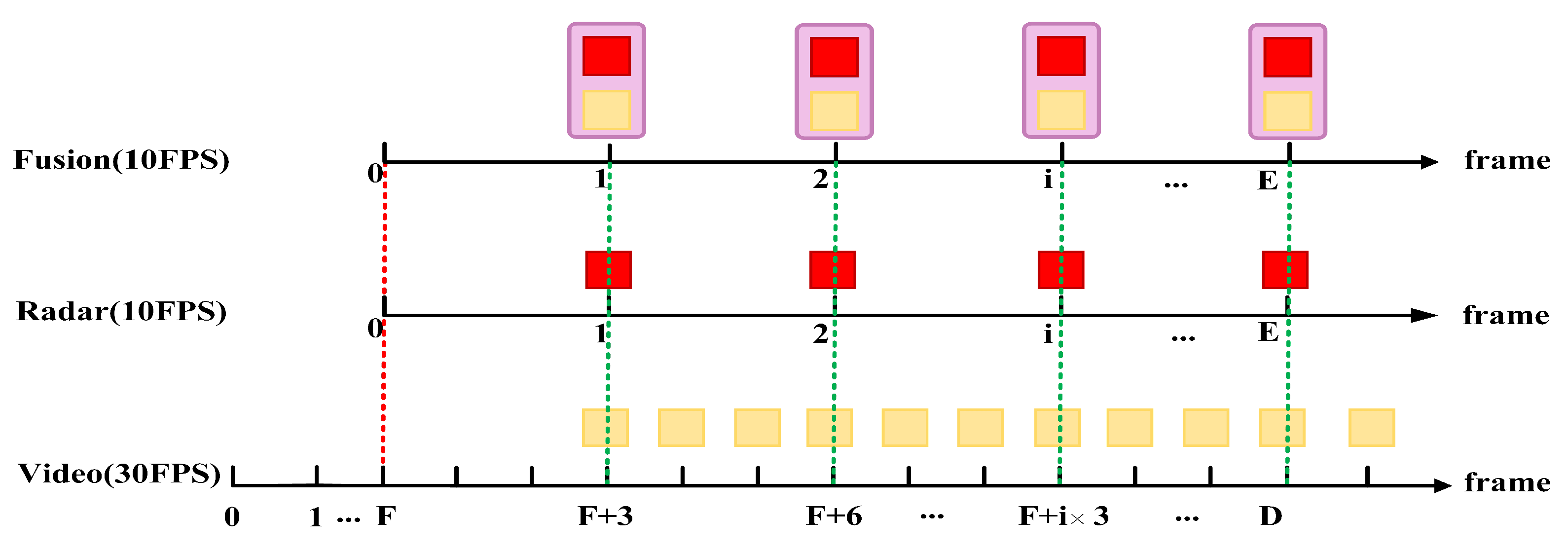
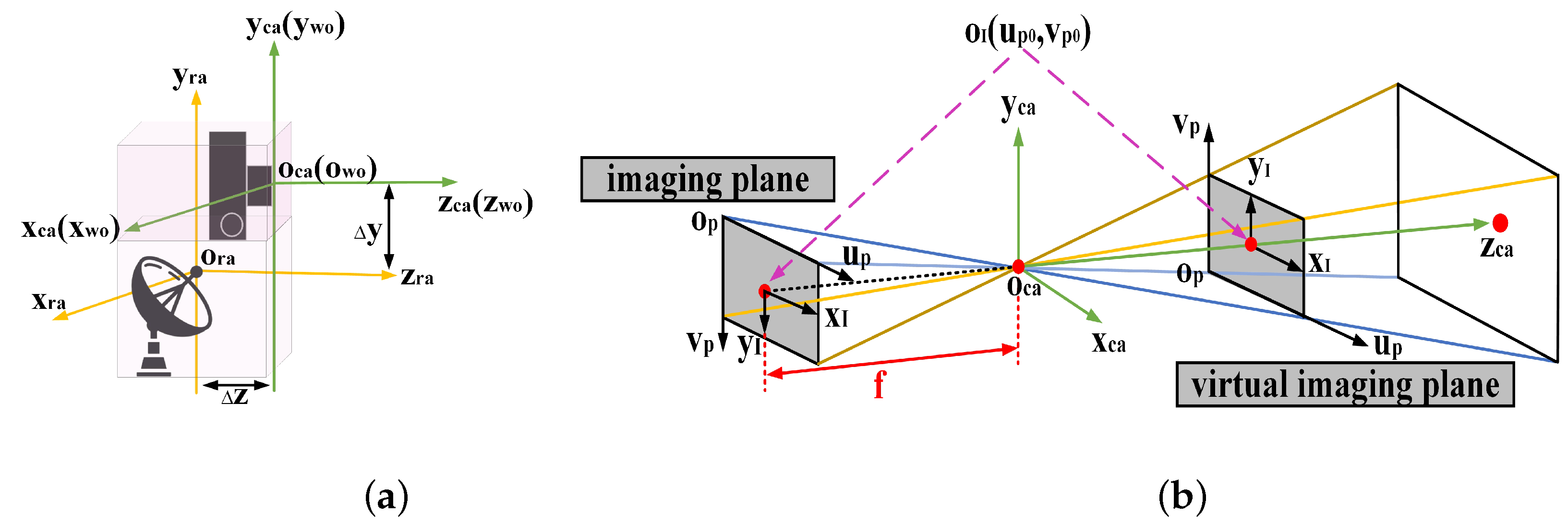
3.3. Spatio-Temporal Calibration
3.3.1. Temporal Alignment
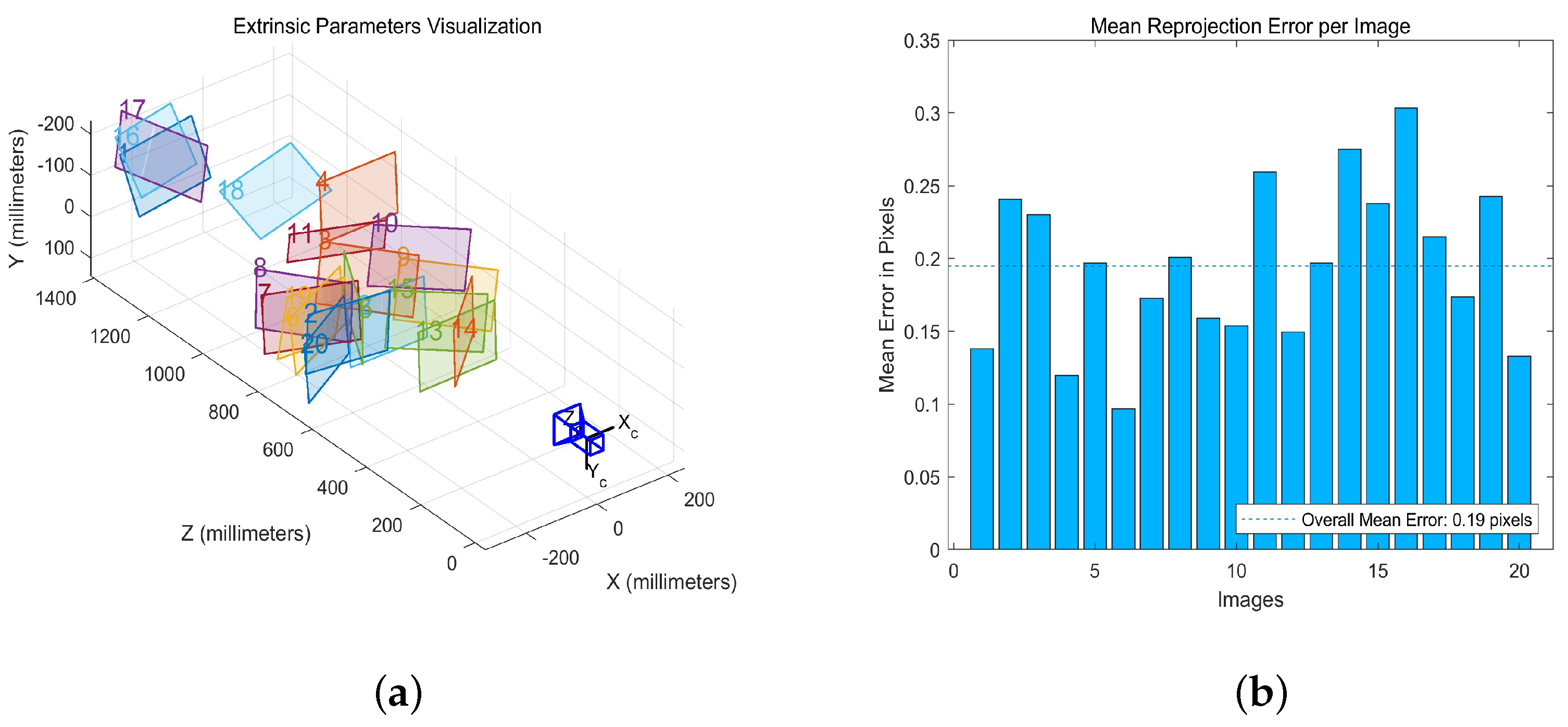
3.3.2. Spatial Calibration
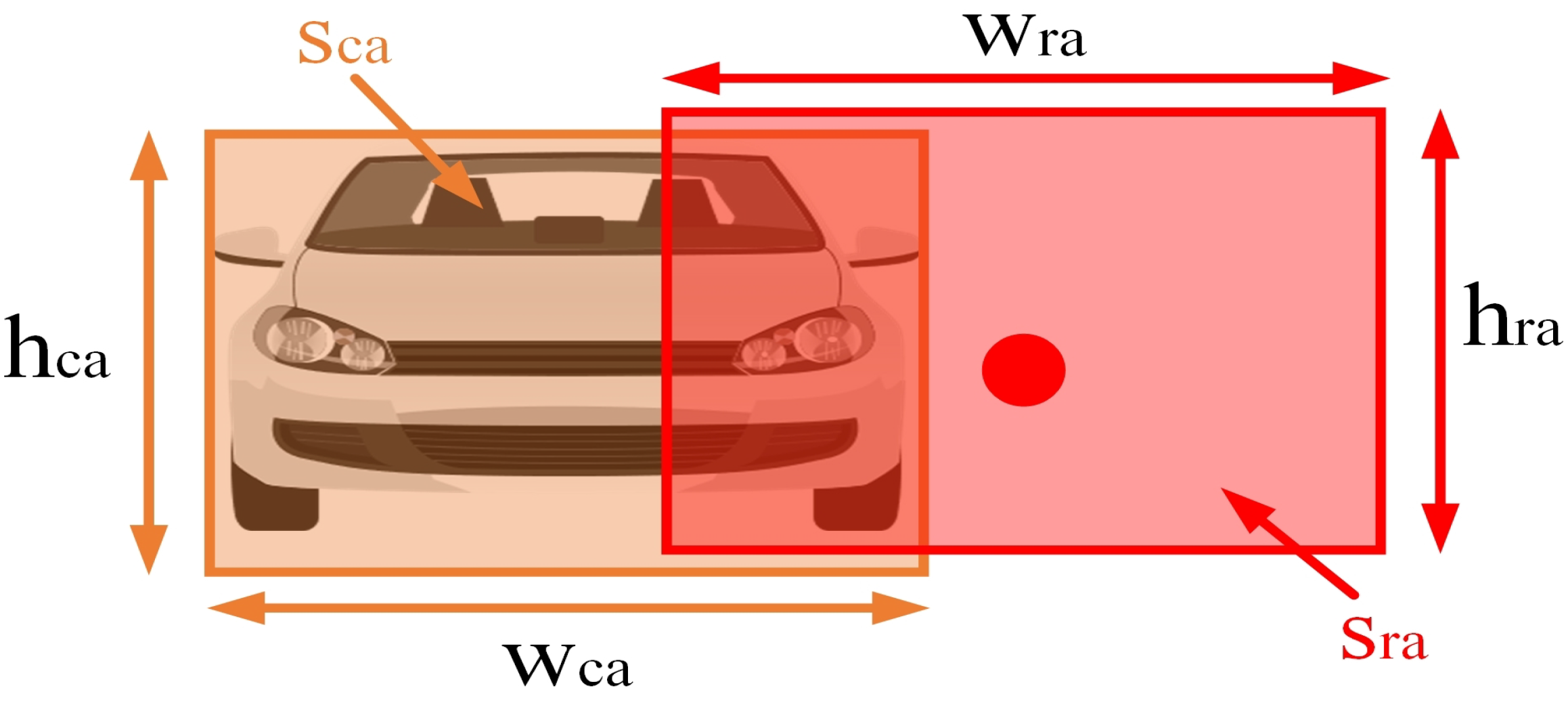
3.4. Information Fusion Strategy
3.5. Evaluation Indicators
4. Results and Discussion
4.1. Validation of YOLOv5s Algorithm
4.2. Validation of SAO-DBSCAN Algorithm
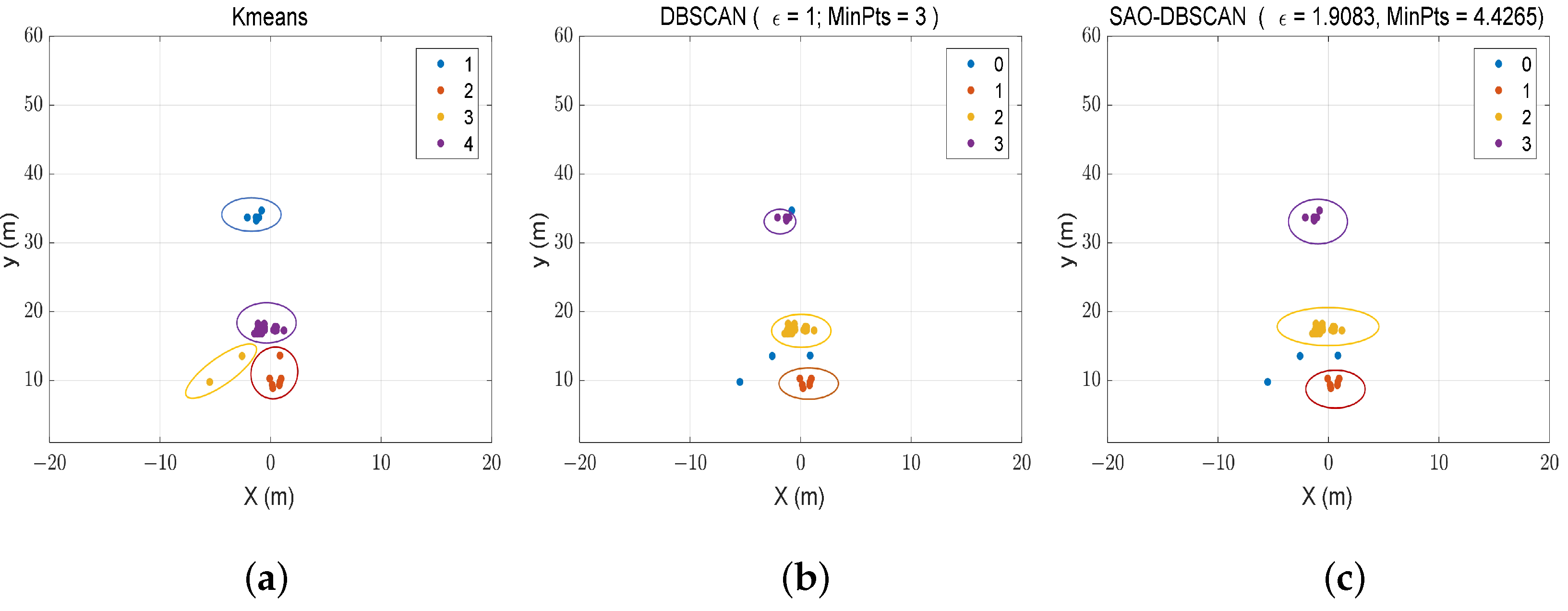
4.2.1. Comparison with Kmeans Algorithm
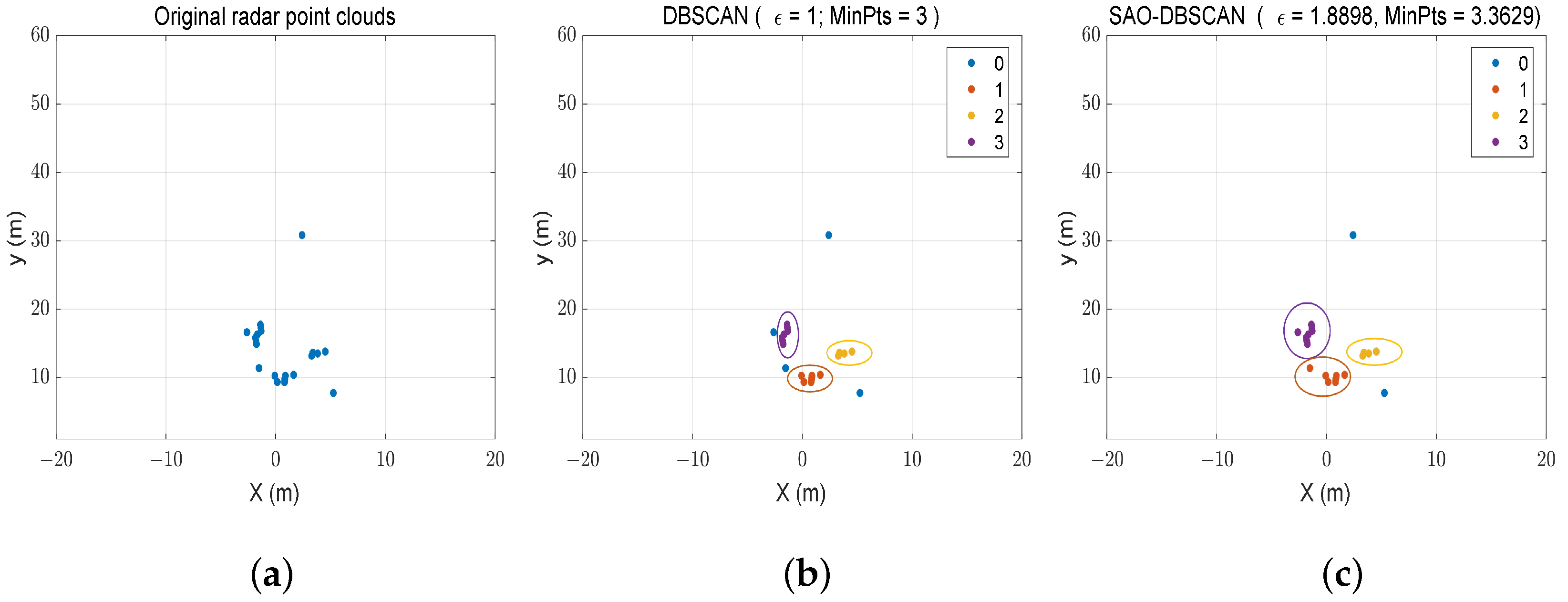
4.2.2. Comparison with DBSCAN Algorithm
4.3. Validation of Information Fusion
4.3.1. Visualization of Information Fusion
4.3.2. Performance Analysis of Algorithms
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ansariyar, A.; Taherpour, A.; Masoumi, P.; Jeihani, M. Accident Response Analysis of Six Different Types of Distracted Driving. Komunikácie 2023, 25, 78–95. [Google Scholar] [CrossRef]
- Bachute, M.R.; Subhedar, J.M. Autonomous driving architectures: Insights of machine learning and deep learning algorithms. Mach. Learn. Appl. 2021, 6, 100164. [Google Scholar] [CrossRef]
- Fernandes, D.; Silva, A.; Névoa, R.; Simões, C.; Gonzalez, D.; Guevara, M.; Novais, P.; Monteiro, J.; Melo-Pinto, P. Point-cloud based 3D object detection and classification methods for self-driving applications: A survey and taxonomy. Inf. Fusion 2021, 68, 161–191. [Google Scholar] [CrossRef]
- Hafeez, F.; Sheikh, U.U.; Alkhaldi, N.; Al Garni, H.Z.; Arfeen, Z.A.; Khalid, S.A. Insights and strategies for an autonomous vehicle with a sensor fusion innovation: A fictional outlook. IEEE Access 2020, 8, 135162–135175. [Google Scholar] [CrossRef]
- Ravindran, R.; Santora, M.J.; Jamali, M.M. Camera, LiDAR, and radar sensor fusion based on Bayesian neural network (CLR-BNN). IEEE Sens. J. 2022, 22, 6964–6974. [Google Scholar] [CrossRef]
- Yeong, D.J.; Velasco-Hernandez, G.; Barry, J.; Walsh, J. Sensor and sensor fusion technology in autonomous vehicles: A review. Sensors 2021, 21, 2140. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Ibanez-Guzman, J. Lidar for autonomous driving: The principles, challenges, and trends for automotive lidar and perception systems. IEEE Signal Process. Mag. 2020, 37, 50–61. [Google Scholar] [CrossRef]
- Şentaş, A.; Tashiev, İ.; Küçükayvaz, F.; Kul, S.; Eken, S.; Sayar, A.; Becerikli, Y. Performance evaluation of support vector machine and convolutional neural network algorithms in real-time vehicle type and color classification. Evolut. Intell. 2020, 13, 83–91. [Google Scholar] [CrossRef]
- Duan, J.; Ye, H.; Zhao, H.; Li, Z. Deep Cascade AdaBoost with Unsupervised Clustering in Autonomous Vehicles. Electronics 2022, 12, 44. [Google Scholar] [CrossRef]
- Chen, L.; Lin, S.; Lu, X.; Cao, D.; Wu, H.; Guo, C.; Liu, C.; Wang, F.Y. Deep neural network based vehicle and pedestrian detection for autonomous driving: A survey. IEEE Trans. Intell. Transp. Syst. 2021, 22, 3234–3246. [Google Scholar] [CrossRef]
- Huang, F.; Chen, S.; Wang, Q.; Chen, Y.; Zhang, D. Using deep learning in an embedded system for real-time target detection based on images from an unmanned aerial vehicle: Vehicle detection as a case study. Int. J. Digit. Earth 2023, 16, 910–936. [Google Scholar] [CrossRef]
- Michaelis, C.; Mitzkus, B.; Geirhos, R.; Rusak, E.; Bringmann, O.; Ecker, A.S.; Bethge, M.; Brendel, W. Benchmarking robustness in object detection: Autonomous driving when winter is coming. arXiv 2019, arXiv:1907.07484. [Google Scholar]
- Yi, C.; Zhang, K.; Peng, N. A multi-sensor fusion and object tracking algorithm for self-driving vehicles. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2019, 233, 2293–2300. [Google Scholar] [CrossRef]
- Shi, J.; Wen, F.; Liu, T. Nested MIMO radar: Coarrays, tensor modeling, and angle estimation. IEEE Trans. Aerosp. Electron. Syst. 2020, 57, 573–585. [Google Scholar] [CrossRef]
- Shi, J.; Yang, Z.; Liu, Y. On parameter identifiability of diversity-smoothing-based MIMO radar. IEEE Trans. Aerosp. Electron. Syst. 2021, 58, 1660–1675. [Google Scholar] [CrossRef]
- Shi, J.; Wen, F.; Liu, Y.; Liu, Z.; Hu, P. Enhanced and generalized coprime array for direction of arrival estimation. IEEE Trans. Aerosp. Electron. Syst. 2022, 59, 1327–1339. [Google Scholar] [CrossRef]
- Wei, Z.; Zhang, F.; Chang, S.; Liu, Y.; Wu, H.; Feng, Z. Mmwave radar and vision fusion for object detection in autonomous driving: A review. Sensors 2022, 22, 2542. [Google Scholar] [CrossRef]
- Hyun, E.; Jin, Y. Doppler-spectrum feature-based human—Vehicle classification scheme using machine learning for an FMCW radar sensor. Sensors 2020, 20, 2001. [Google Scholar] [CrossRef]
- Lu, Y.; Zhong, W.; Li, Y. Calibration of multi-sensor fusion for autonomous vehicle system. Int. J. Veh. Des. 2023, 91, 248–262. [Google Scholar] [CrossRef]
- Tang, X.; Zhang, Z.; Qin, Y. On-road object detection and tracking based on radar and vision fusion: A review. IEEE Intell. Transp. Syst. Mag. 2021, 14, 103–128. [Google Scholar] [CrossRef]
- Chen, B.; Pei, X.; Chen, Z. Research on target detection based on distributed track fusion for intelligent vehicles. Sensors 2019, 20, 56. [Google Scholar] [CrossRef]
- Lv, P.; Wang, B.; Cheng, F.; Xue, J. Multi-objective association detection of farmland obstacles based on information fusion of millimeter wave radar and camera. Sensors 2022, 23, 230. [Google Scholar] [CrossRef] [PubMed]
- Jha, H.; Lodhi, V.; Chakravarty, D. Object detection and identification using vision and radar data fusion system for ground-based navigation. In Proceedings of the 2019 6th IEEE International Conference on Signal Processing and Integrated Networks (SPIN), Noida, India, 7–8 March 2019; pp. 590–593. [Google Scholar]
- Zewge, N.S.; Kim, Y.; Kim, J.; Kim, J.H. Millimeter-wave radar and RGB-D camera sensor fusion for real-time people detection and tracking. In Proceedings of the 2019 7th IEEE International Conference on Robot Intelligence Technology and Applications (RiTA), Daejeon, Republic of Korea, 1–3 November 2019; pp. 93–98. [Google Scholar]
- Jibrin, F.A.; Deng, Z.; Zhang, Y. An object detection and classification method using radar and camera data fusion. In Proceedings of the 2019 IEEE International Conference on Signal, Information and Data Processing (ICSIDP), Chongqing, China, 11–13 December 2019; pp. 1–6. [Google Scholar]
- Wang, L.; Zhang, Z.; Di, X.; Tian, J. A roadside camera-radar sensing fusion system for intelligent transportation. In Proceedings of the 2020 17th IEEE European Radar Conference (EuRAD), Utrecht, The Netherlands, 13–15 January 2021; pp. 282–285. [Google Scholar]
- Wu, Y.; Li, D.; Zhao, Y.; Yu, W.; Li, W. Radar-vision fusion for vehicle detection and tracking. In Proceedings of the 2023 IEEE International Applied Computational Electromagnetics Society Symposium (ACES), Monterey, CA, USA, 26–30 March 2023; pp. 1–2. [Google Scholar]
- Cheng, D.; Xu, R.; Zhang, B.; Jin, R. Fast density estimation for density-based clustering methods. Neurocomputing 2023, 532, 170–182. [Google Scholar] [CrossRef]
- Deng, L.; Liu, S. Snow ablation optimizer: A novel metaheuristic technique for numerical optimization and engineering design. Expert Syst. Appl. 2023, 225, 120069. [Google Scholar] [CrossRef]
- Peng, D.; Ding, W.; Zhen, T. A novel low light object detection method based on the YOLOv5 fusion feature enhancement. Sci. Rep. 2024, 14, 4486. [Google Scholar] [CrossRef]
- YenIaydin, Y.; Schmidt, K.W. A lane detection algorithm based on reliable lane markings. In Proceedings of the 2018 26th IEEE Signal Processing and Communications Applications Conference (SIU), Izmir, Turkey, 2–5 May 2018; pp. 1–4. [Google Scholar]
- Yang, Y.; Wang, X.; Wu, X.; Lan, X.; Su, T.; Guo, Y. A Robust Target Detection Algorithm Based on the Fusion of Frequency-Modulated Continuous Wave Radar and a Monocular Camera. Remote Sens. 2024, 16, 2225. [Google Scholar] [CrossRef]
- Wu, J.X.; Xu, N.; Wang, B.; Ren, J.Y.; Ma, S.L. Research on Target Detection Algorithm for 77 GHz Automotive Radar. In Proceedings of the 2022 IEEE 16th International Conference on Solid-State & Integrated Circuit Technology (ICSICT), Nangjing, China, 25–28 October 2022; pp. 1–3. [Google Scholar]
- Zhao, R.; Yuan, X.; Yang, Z.; Zhang, L. Image-based crop row detection utilizing the Hough transform and DBSCAN clustering analysis. IET Image Process. 2024, 18, 1161–1177. [Google Scholar] [CrossRef]
- McCrory, M.; Thomas, S.A. Cluster Metric Sensitivity to Irrelevant Features. arXiv 2024, arXiv:2402.12008. [Google Scholar]
- Saleem, S.; Animasaun, I.; Yook, S.J.; Al-Mdallal, Q.M.; Shah, N.A.; Faisal, M. Insight into the motion of water conveying three kinds of nanoparticles shapes on a horizontal surface: Significance of thermo-migration and Brownian motion. Surfaces Interfaces 2022, 30, 101854. [Google Scholar] [CrossRef]
- Liu, Y.; Jiang, B.; He, H.; Chen, Z.; Xu, Z. Helmet wearing detection algorithm based on improved YOLOv5. Sci. Rep. 2024, 14, 8768. [Google Scholar] [CrossRef]
- Yang, J.; Huang, W. Pedestrian and vehicle detection method in infrared scene based on improved YOLOv5s model. Autom. Mach. Learn. 2024, 5, 90–96. [Google Scholar]
- Liu, C.; Zhang, G.; Qiu, H. Research on target tracking method based on multi-sensor fusion. J. Chongqing Univ. Technol. 2021, 35, 1–7. [Google Scholar]
- Du, Y.; Qin, B.; Zhao, C.; Zhu, Y.; Cao, J.; Ji, Y. A novel spatio-temporal synchronization method of roadside asynchronous MMW radar-camera for sensor fusion. IEEE Trans. Intell. Transp. Syst. 2021, 23, 22278–22289. [Google Scholar] [CrossRef]
- Lu, P.; Liu, Q.; Guo, J. Camera calibration implementation based on Zhang Zhengyou plane method. In Proceedings of the 2015 Chinese Intelligent Systems Conference, Yangzhou, China, 17–18 October 2015; Springer: Berlin/Heidelberg, Germany, 2016; Volume 1, pp. 29–40. [Google Scholar]
- Qin, P.; Hou, X.; Zhang, S.; Zhang, S.; Huang, J. Simulation research on the protection performance of fall protection net at the end of truck escape ramp. Sci. Prog. 2021, 104, 00368504211039615. [Google Scholar] [CrossRef] [PubMed]
- Zhao, X.; Liu, K.; Gao, K.; Li, W. Hyperspectral time-series target detection based on spectral perception and spatial-temporal tensor decomposition. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5520812. [Google Scholar] [CrossRef]
- Wang, C.Y.; Yeh, I.H.; Liao, H.Y.M. Yolov9: Learning what you want to learn using programmable gradient information. arXiv 2024, arXiv:2402.13616. [Google Scholar]












| Internal Parameters | Horizontal Axis/Pixel | Vertical Axis/Pixel |
|---|---|---|
| Equivalent focal length | ||
| Principal point |
| Value of IOU | Information on the Bounding Box | Sensor Detection Results | Output |
|---|---|---|---|
| Both radar and camera recognize the same object. | Output the valid information recognized by radar and camera. | ||
| Radar misses the target. | Output the valid information detected by camera. | ||
| camera misses the target. | Output the valid information detected by radar. | ||
| There is no target. | There is no information to output. |
| Name | Version | Function |
|---|---|---|
| Radar | Texas Instruments (TI) AWR2243 | - - |
| Camera | Hewlett-Packard (HP) 1080p | - - |
| GPU | NVIDIA GeForce RTX 3060 | - - |
| CPU | i5-11400 | - - |
| Operating system | Windows11 | - - |
| Python | 3.8 | - - |
| Pytorch | 11.3 | - - |
| CUDA | 12.3 | - - |
| Pycharm | 2023 | Running YOLOs for detecting targets in images |
| MATLAB | R2022b | Running radar and fusion algorithms |
| Detection Scene | Algorithm | Sensors Combination Solutions | Recall | Precision | Balance-Score |
|---|---|---|---|---|---|
| Scene 1 | DBSCAN | radar | 95.24% | 90.70% | 0.93 |
| SAO-DBSCAN | radar | 99.26% | 90.93% | 0.95 | |
| Fusion [29] | Camera-radar | 99.31% | 97.96% | 0.98 | |
| Fusion (ours) | Camera-radar | 99.08% | 97.96% | 0.99 | |
| Scene 2 | DBSCAN | radar | 94.87% | 66.82% | 0.78 |
| SAO-DBSCAN | radar | 93.53% | 95.44% | 0.94 | |
| Fusion [29] | Camera-radar | 99.11% | 68.10% | 0.81 | |
| Fusion (ours) | Camera-radar | 99.11% | 95.59% | 0.97 |
| Algorithm | Time Overhead/s | Space Overhead/MB |
|---|---|---|
| Fusion [29] | 0.94 | 1291 |
| Fusion (ours) | 0.90 | 1301 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Wang, X.; Wu, X.; Lan, X.; Su, T.; Guo, Y. A Target Detection Algorithm Based on Fusing Radar with a Camera in the Presence of a Fluctuating Signal Intensity. Remote Sens. 2024, 16, 3356. https://doi.org/10.3390/rs16183356
Yang Y, Wang X, Wu X, Lan X, Su T, Guo Y. A Target Detection Algorithm Based on Fusing Radar with a Camera in the Presence of a Fluctuating Signal Intensity. Remote Sensing. 2024; 16(18):3356. https://doi.org/10.3390/rs16183356
Chicago/Turabian StyleYang, Yanqiu, Xianpeng Wang, Xiaoqin Wu, Xiang Lan, Ting Su, and Yuehao Guo. 2024. "A Target Detection Algorithm Based on Fusing Radar with a Camera in the Presence of a Fluctuating Signal Intensity" Remote Sensing 16, no. 18: 3356. https://doi.org/10.3390/rs16183356
APA StyleYang, Y., Wang, X., Wu, X., Lan, X., Su, T., & Guo, Y. (2024). A Target Detection Algorithm Based on Fusing Radar with a Camera in the Presence of a Fluctuating Signal Intensity. Remote Sensing, 16(18), 3356. https://doi.org/10.3390/rs16183356







