A Dual-Stream Deep Learning-Based Acoustic Denoising Model to Enhance Underwater Information Perception
Abstract
1. Introduction
- We propose a dual-branch UWASD model based on deep neural networks, which predicts amplitude and phase masks separately. The amplitude and phase blocks exchange information through cross connections, improving the capability of feature representation. Therefore, compared to existing methods (such as SEGAN [25] and DPT_FSNet [26]), our model more effectively recovers the phase information of underwater acoustic signals.
- In the amplitude block, a frequency characteristics transformation module that extracts convolutional features between channels was designed, obtaining global correlations of the amplitude spectrum. This enhances the reconstruction of the amplitude feature map, thus boosting the ability of the model to learn features from the underwater acoustic target signal.
- Our proposed model effectively denoises signal from unknown ship types, better restoring line spectra in low-frequency components, making the target signals in the low-frequency line spectra more prominent. This enhancement is beneficial for improving the accuracy of subsequent blind target detection and classification algorithms.
- Extensive experiments were conducted to verify the validity of the proposed model. When compared with classic traditional algorithms and deep learning algorithms, our model demonstrated superior performance in underwater signal denoising.
2. Problem Analysis and DS_FCTNet Model
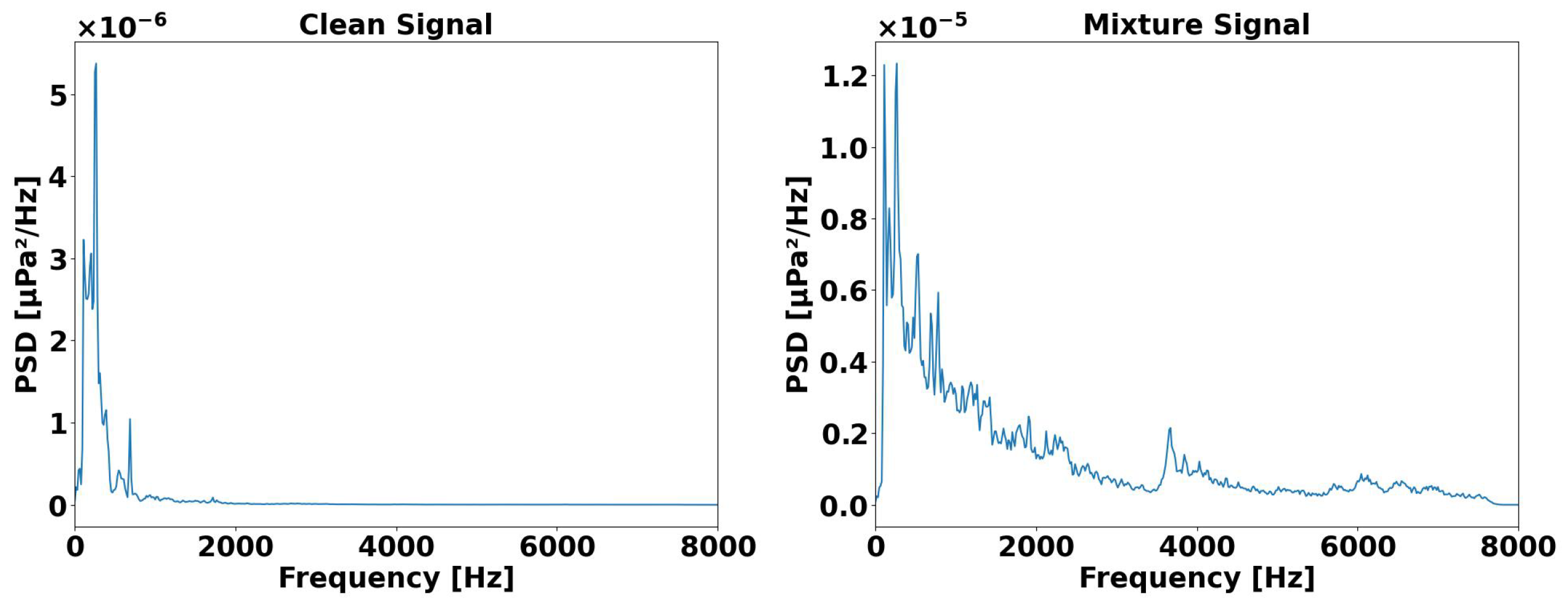
2.1. Problem Analysis
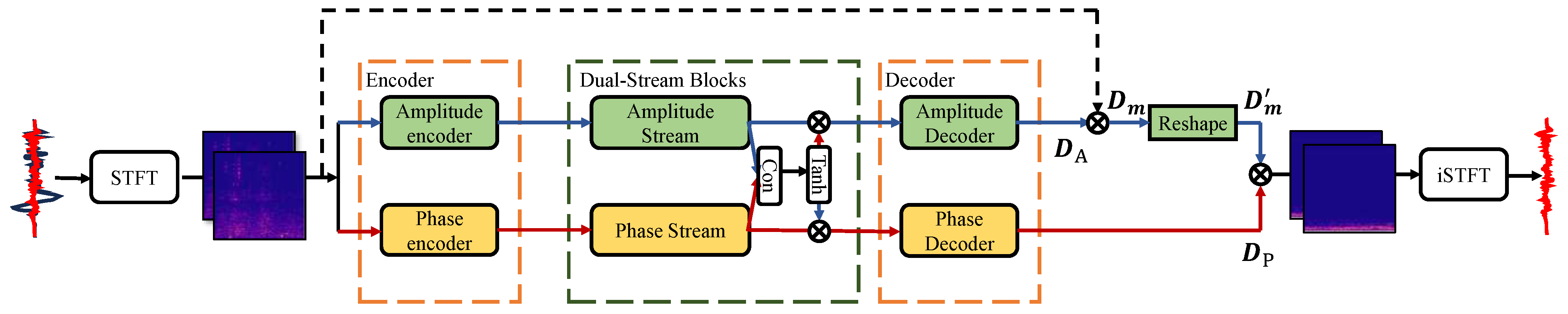
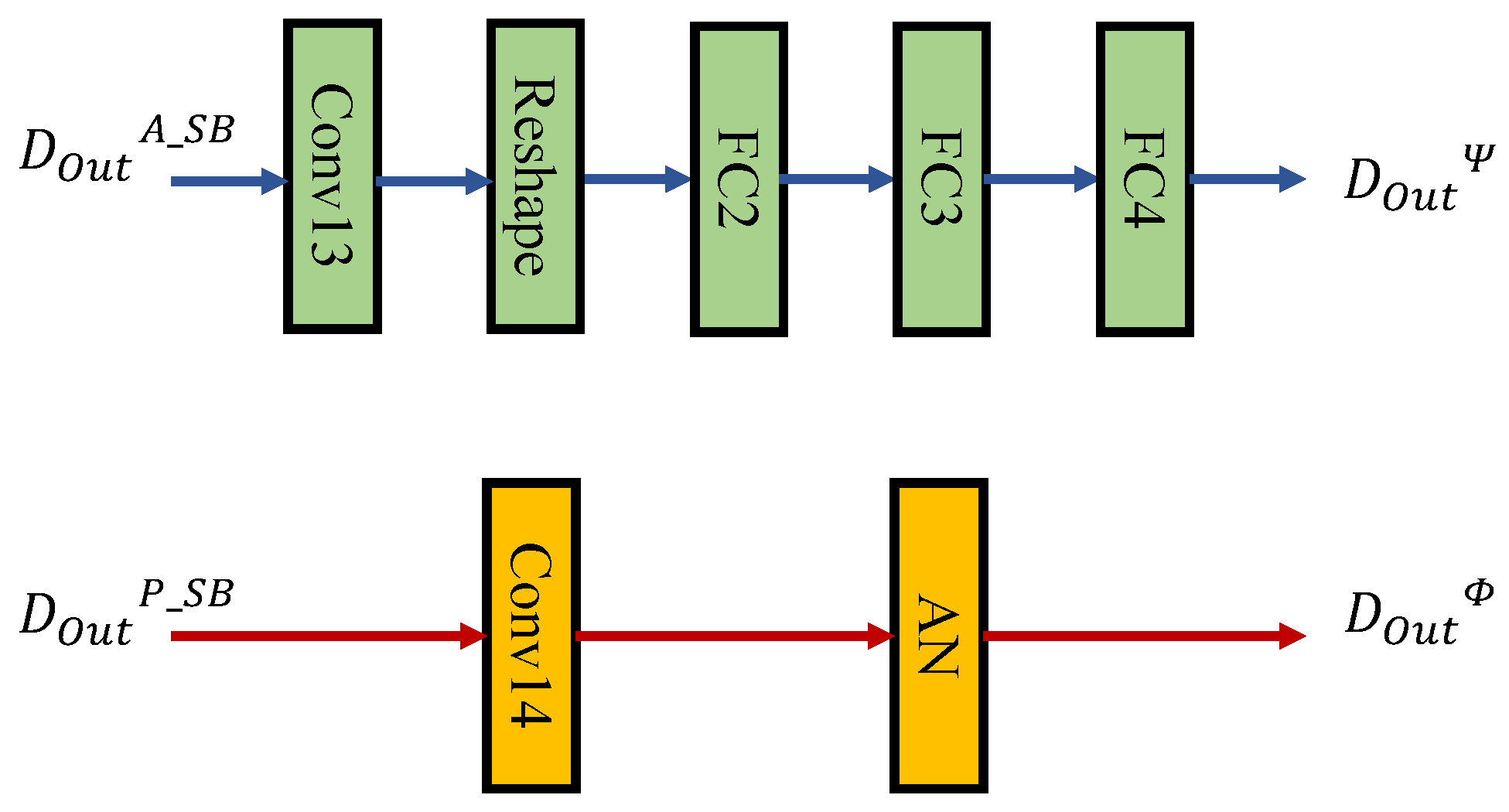
2.2. DS_FCTNet Model
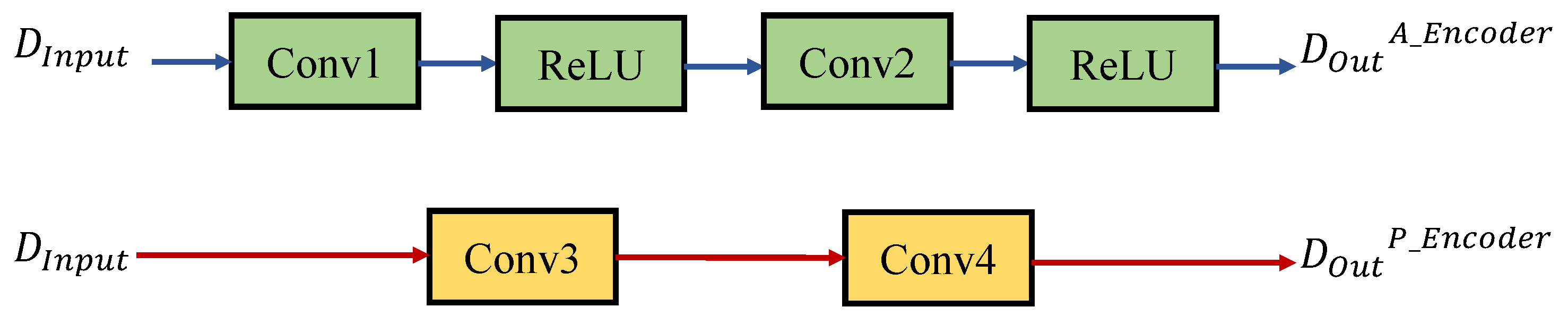
2.2.1. Encoder
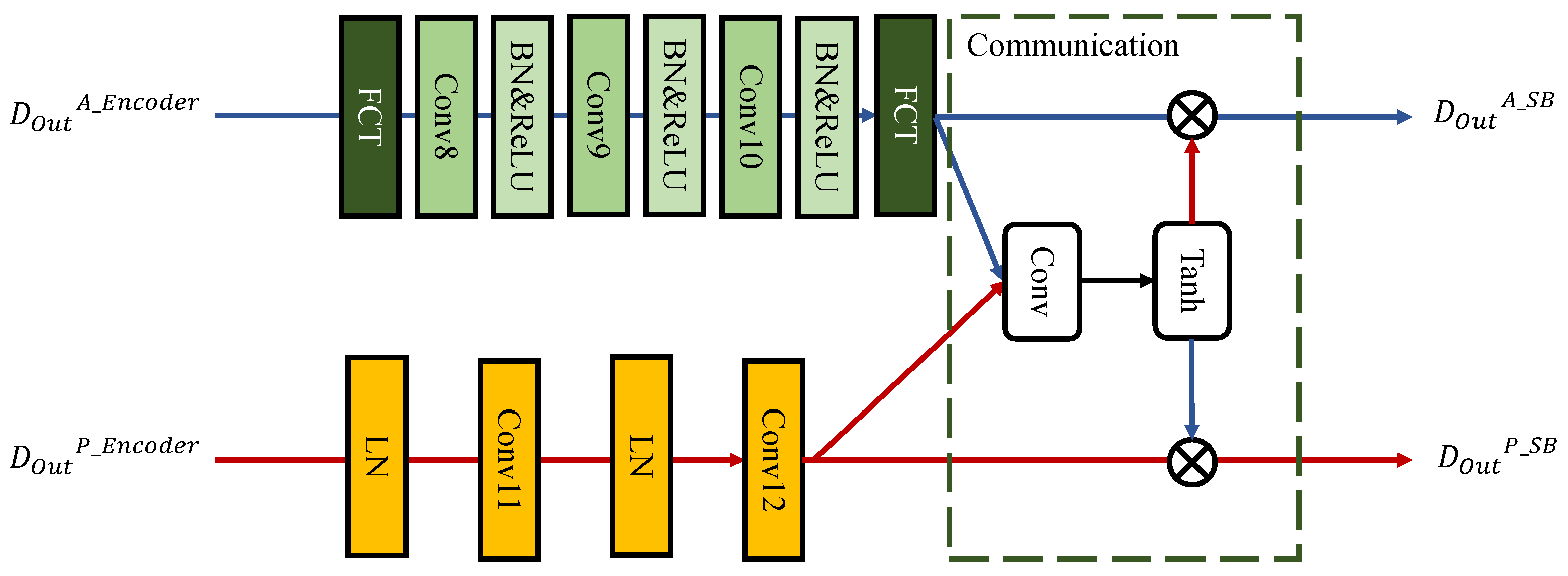
2.2.2. Dual-Stream Blocks (DSBs)
2.2.3. Decoder
2.2.4. Loss Function
3. Experimental Setup
3.1. Dataset
3.2. Experimental Parameters
3.3. Evaluation Metrics
4. Experimental Comparison and Analysis
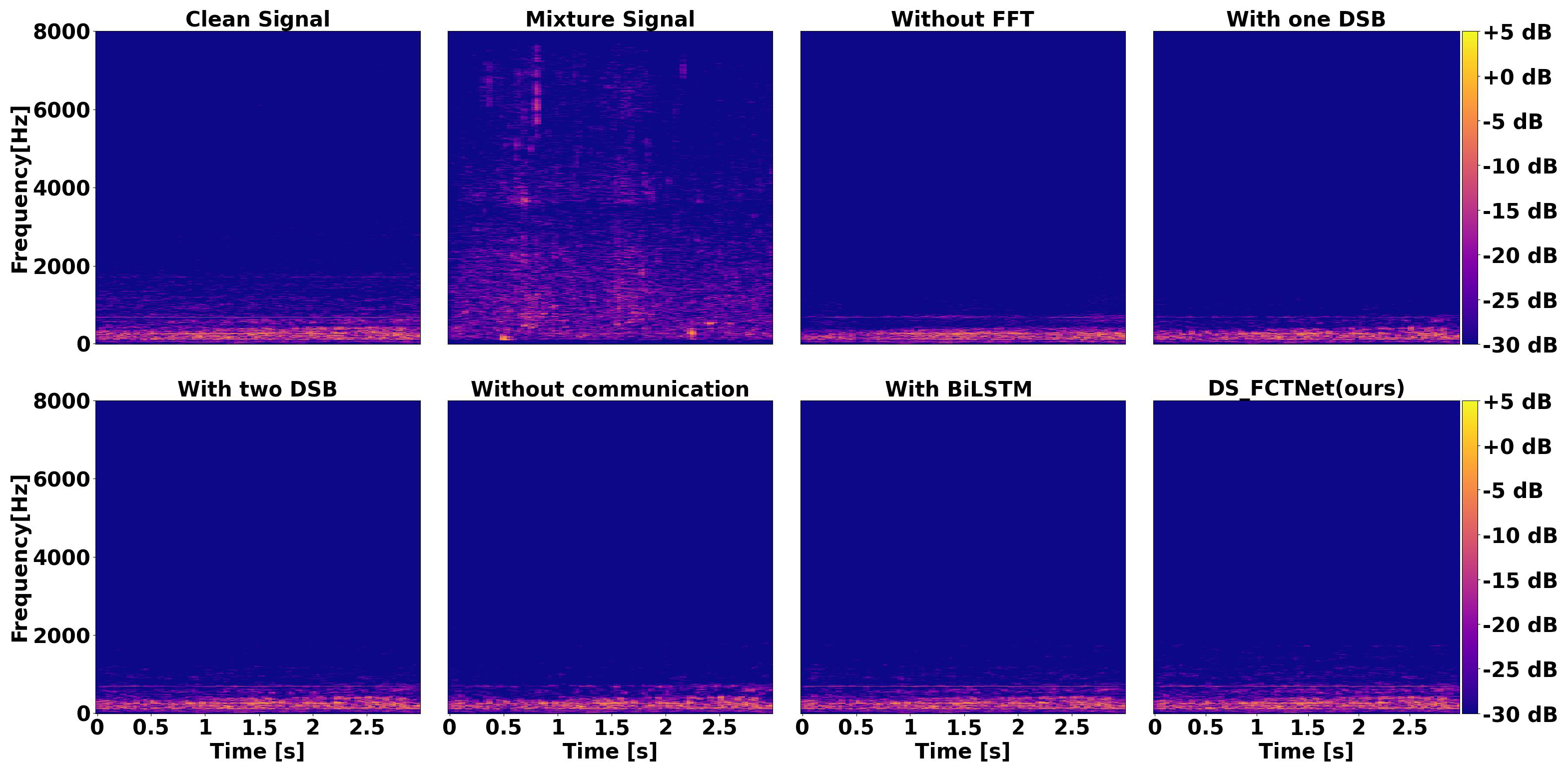
4.1. Comparison of Ablation Experiments
4.1.1. With or Without Communication
4.1.2. With or Without FCT
4.1.3. Compare the Number of DSBs
4.1.4. With or Without BiLSTM
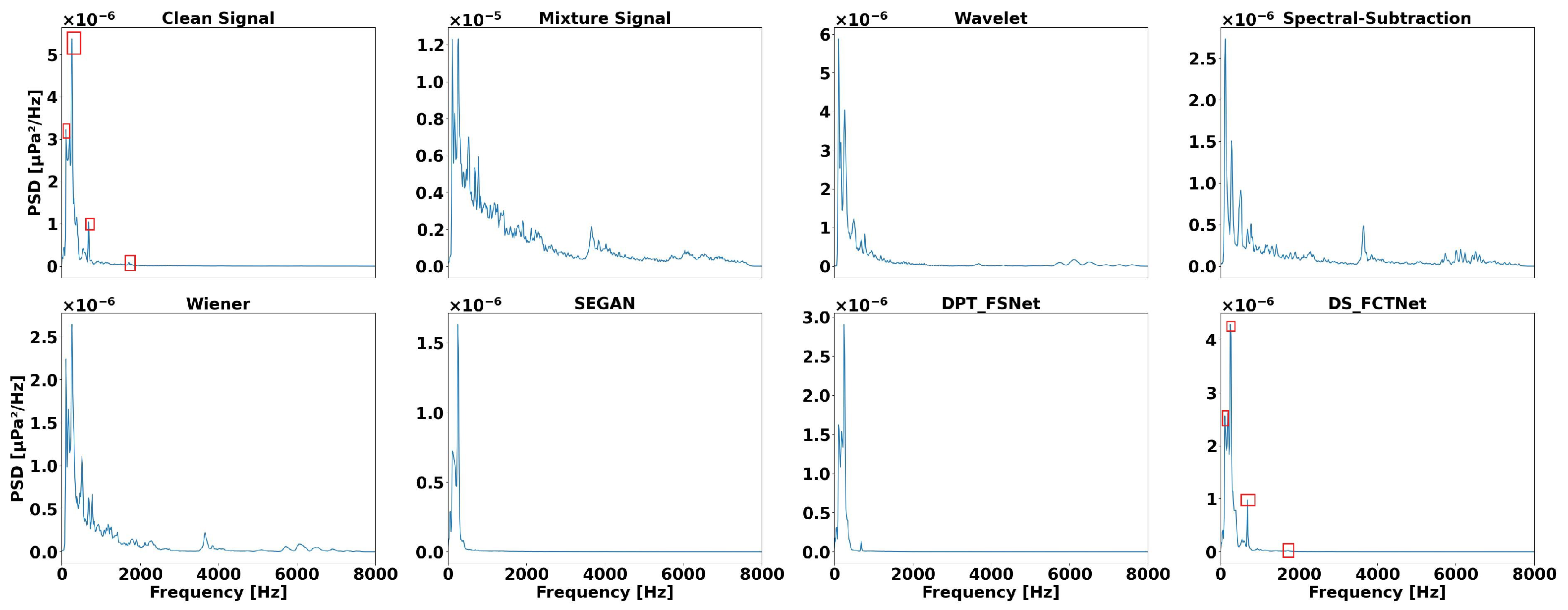
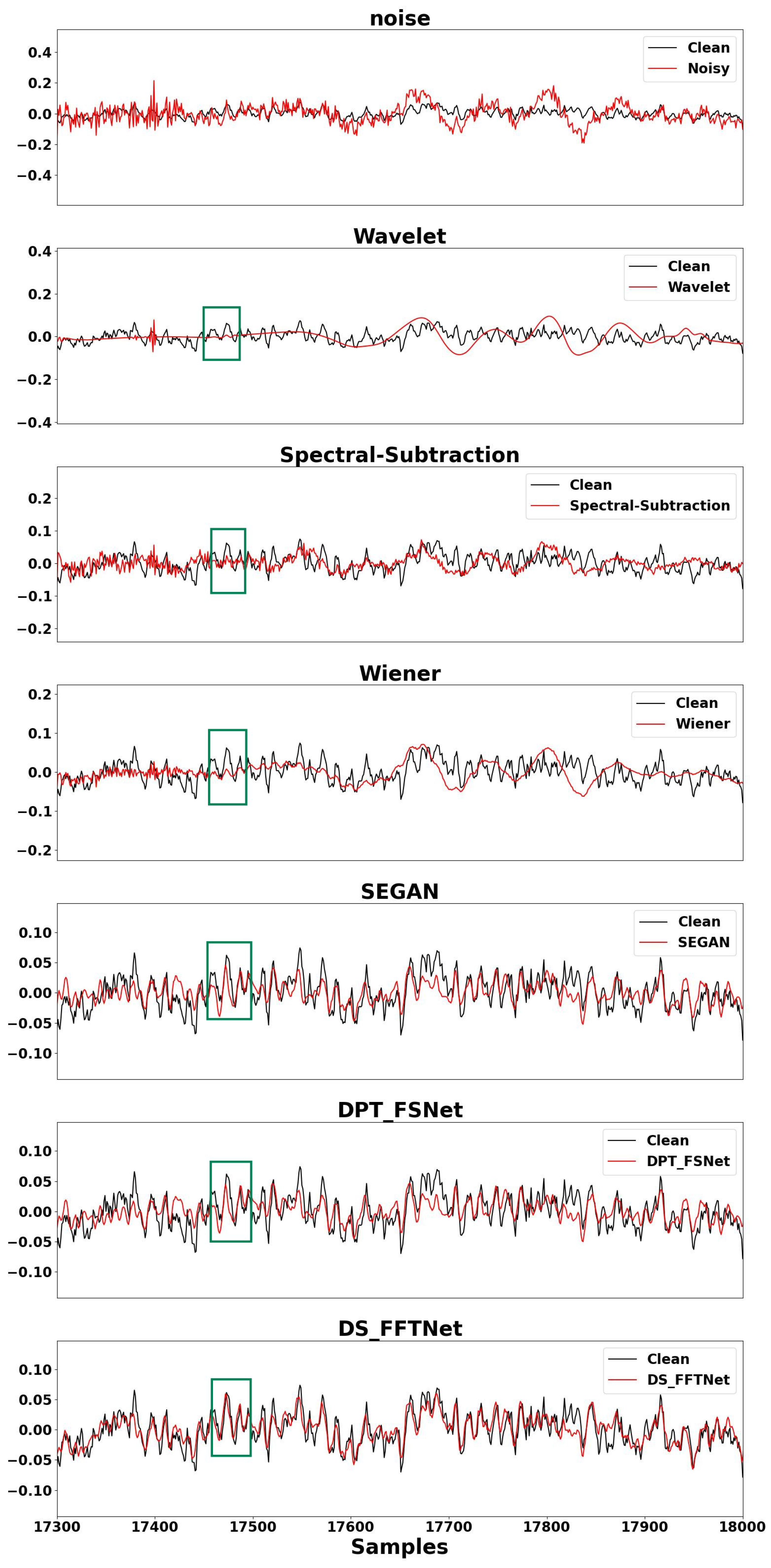
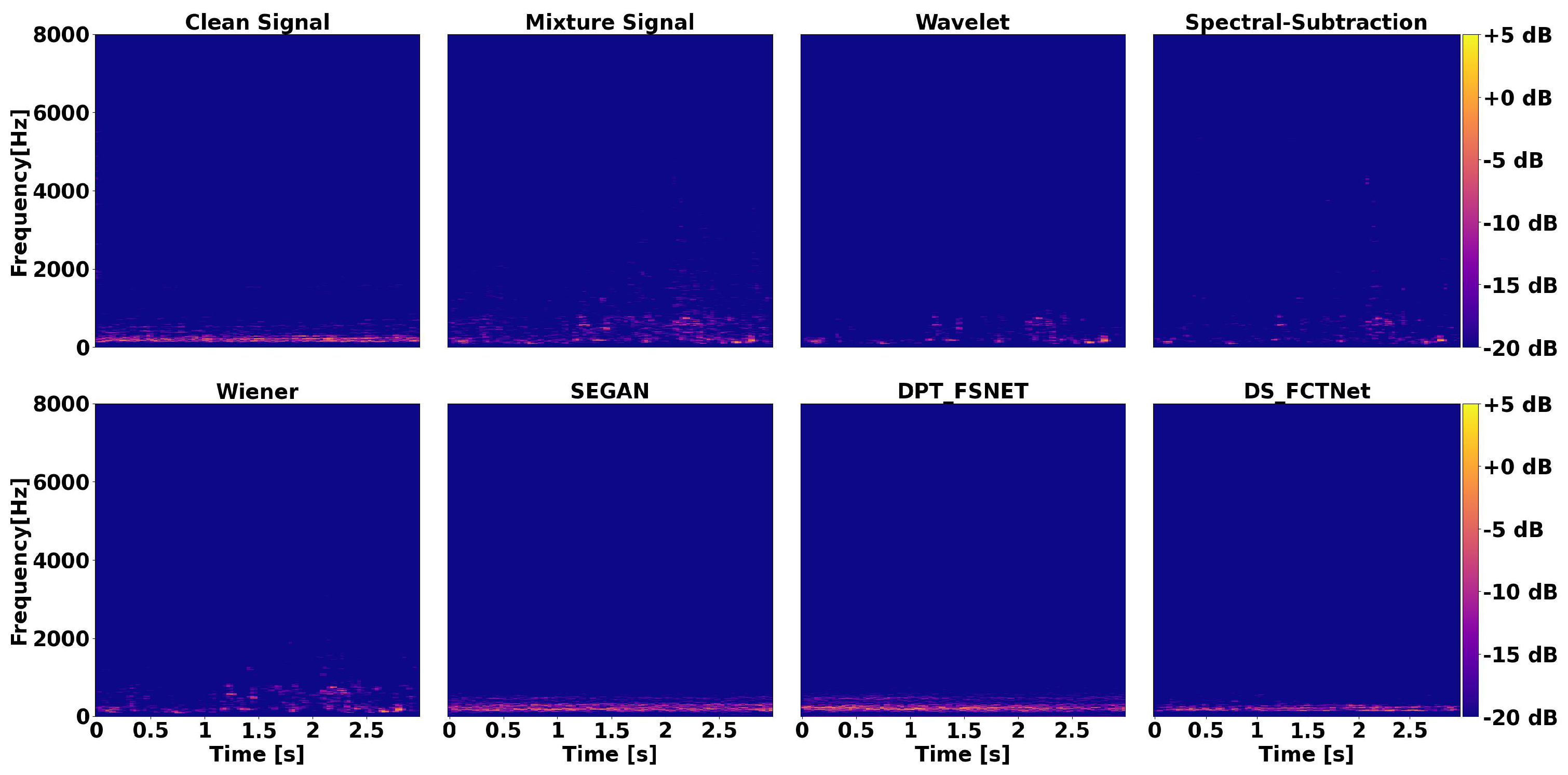
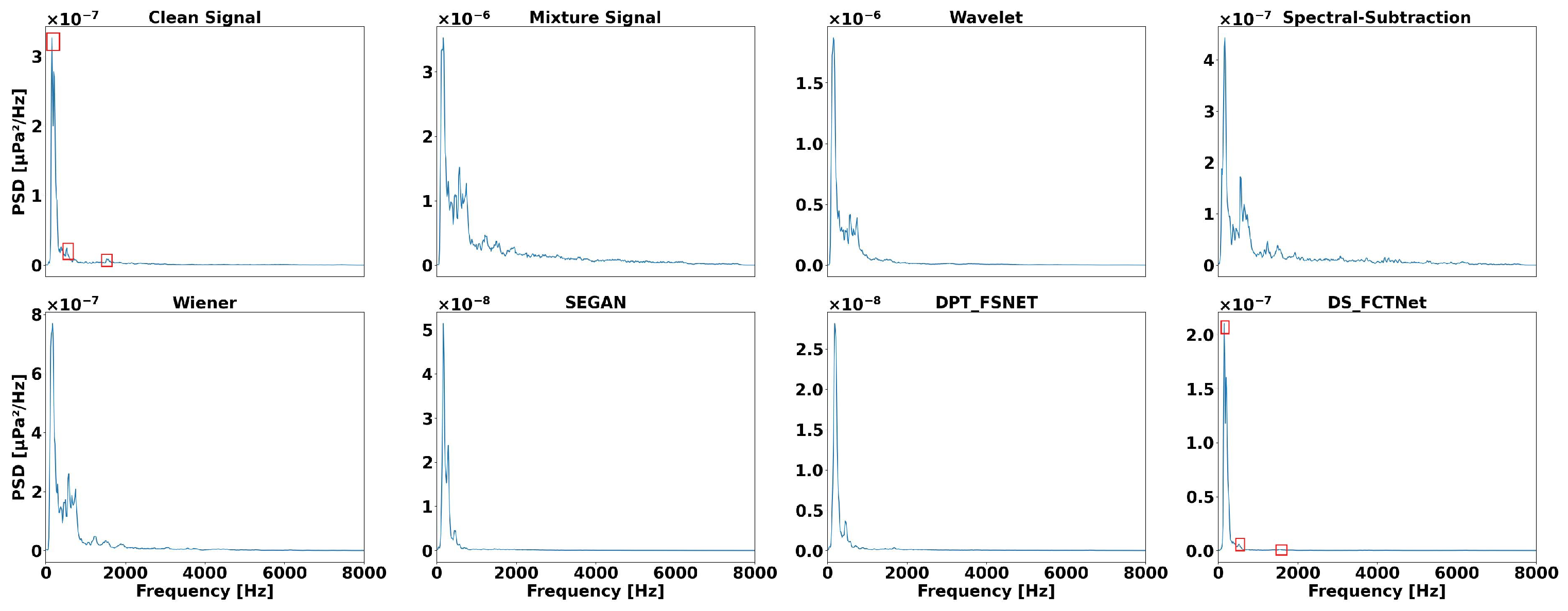
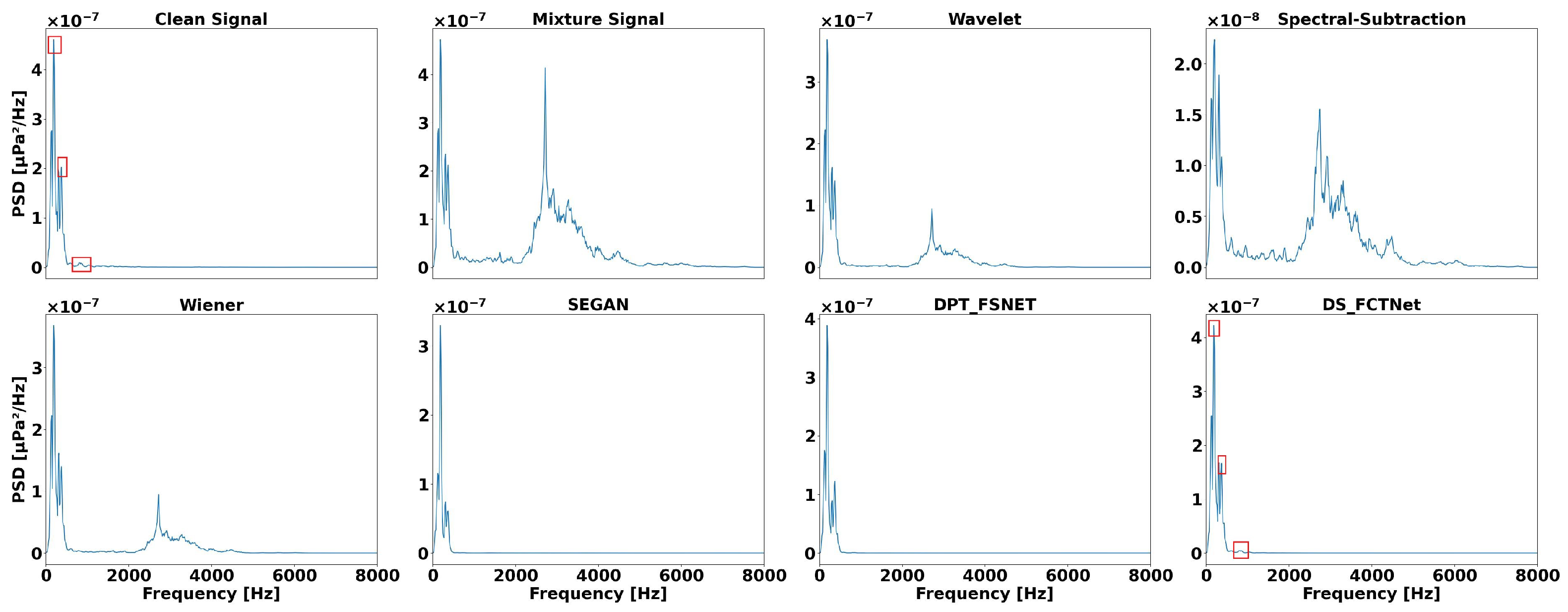
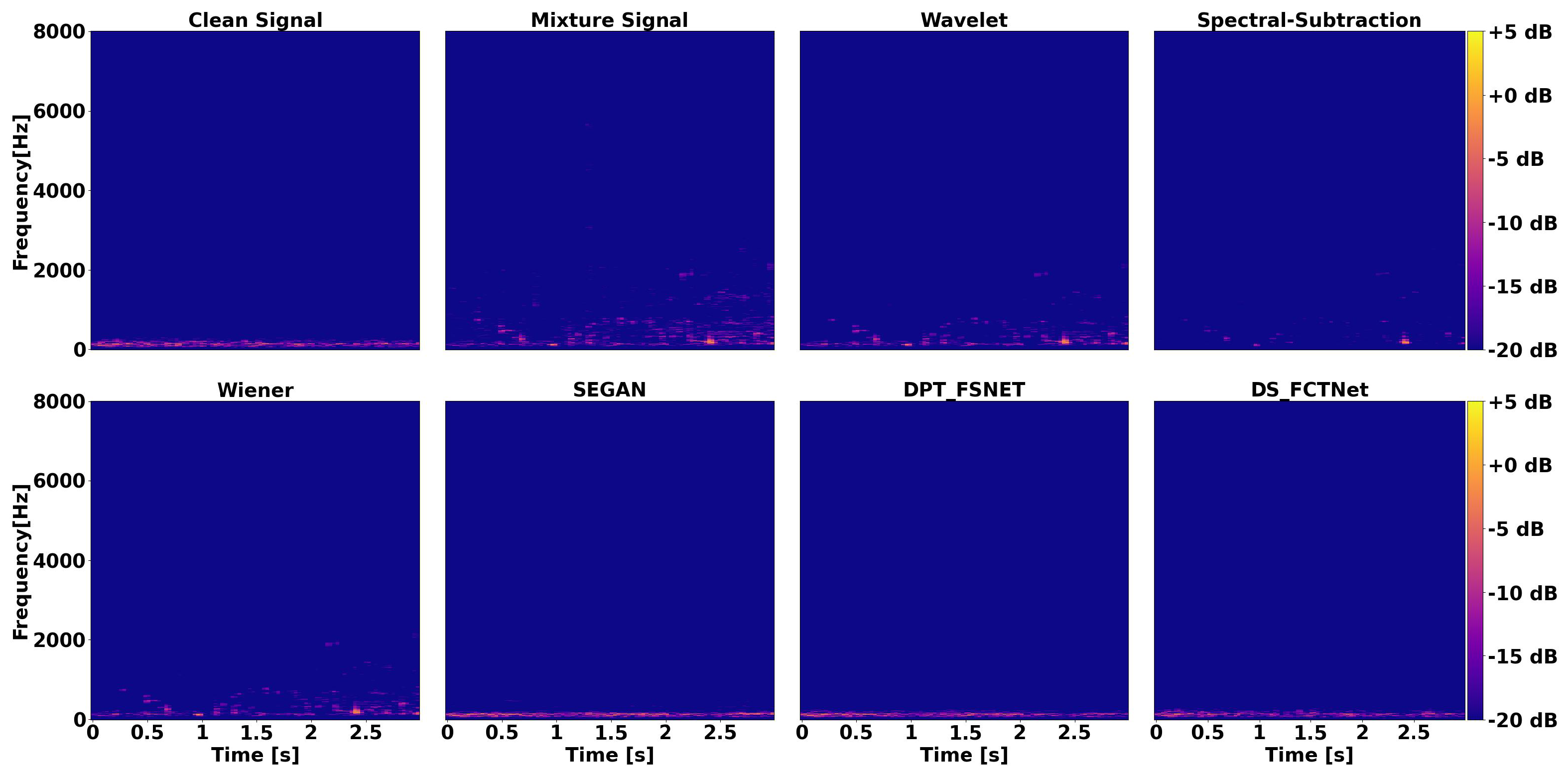
4.2. Method Comparison
4.3. Denoising Untrained Ships
4.4. Denoising Unknown Ship Types
4.5. Robustness Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fernandes, J.d.C.V.; de Moura Junior, N.N.; de Seixas, J.M. Deep learning models for passive sonar signal classification of military data. Remote Sens. 2022, 14, 2648. [Google Scholar] [CrossRef]
- Hummel, H.I.; van der Mei, R.; Bhulai, S. A survey on machine learning in ship radiated noise. Ocean. Eng. 2024, 298, 117252. [Google Scholar] [CrossRef]
- Koh, S.; Chia, C.S.; Tan, B.A. Underwater signal denoising using deep learning approach. In Proceedings of the Global Oceans 2020: Singapore–US Gulf Coast, Singapore, 5–30 October 2020; pp. 1–6. [Google Scholar]
- Zhu, S.; Zhang, G.; Wu, D.; Jia, L.; Zhang, Y.; Geng, Y.; Liu, Y.; Ren, W.; Zhang, W. High Signal-to-Noise Ratio MEMS Noise Listener for Ship Noise Detection. Remote Sens. 2023, 15, 777. [Google Scholar] [CrossRef]
- Du, L.; Wang, Z.; Lv, Z.; Han, D.; Wang, L.; Yu, F.; Lan, Q. A Method for Underwater Acoustic Target Recognition Based on the Delay-Doppler Joint Feature. Remote Sens. 2024, 16, 2005. [Google Scholar] [CrossRef]
- Zhu, X.; Dong, H.; Salvo Rossi, P.; Landrø, M. Feature Selection Based on Principal Component Regression for Underwater Source Localization by Deep Learning. Remote Sens. 2021, 13, 1486. [Google Scholar] [CrossRef]
- Wang, M.; Qiu, B.; Zhu, Z.; Ma, L.; Zhou, C. Passive tracking of underwater acoustic targets based on multi-beam LOFAR and deep learning. PLoS ONE 2022, 17, e0273898. [Google Scholar] [CrossRef]
- Boll, S. Suppression of acoustic noise in speech using spectral subtraction. IEEE Trans. Acoust. Speech Signal Process. 1979, 27, 113–120. [Google Scholar] [CrossRef]
- Chen, J.; Benesty, J.; Huang, Y.; Doclo, S. New insights into the noise reduction Wiener filter. IEEE Trans. Audio Speech Lang. Process. 2006, 14, 1218–1234. [Google Scholar] [CrossRef]
- Weiss, L.G.; Dixon, T.L. Wavelet-based denoising of underwater acoustic signals. J. Acoust. Soc. Am. 1997, 101, 377–383. [Google Scholar] [CrossRef]
- Alter, O.; Brown, P.O.; Botstein, D. Singular value decomposition for genome-wide expression data processing and modeling. Proc. Natl. Acad. Sci. USA 2000, 97, 10101–10106. [Google Scholar] [CrossRef]
- Li, Y.; Wang, L. A novel noise reduction technique for underwater acoustic signals based on complete ensemble empirical mode decomposition with adaptive noise, minimum mean square variance criterion and least mean square adaptive filter. Def. Technol. 2020, 16, 543–554. [Google Scholar] [CrossRef]
- Liu, Y.; Niu, H.; Li, Z. A multi-task learning convolutional neural network for source localization in deep ocean. J. Acoust. Soc. Am. 2020, 148, 873–883. [Google Scholar] [CrossRef] [PubMed]
- Hu, R.; Monebhurrun, V.; Himeno, R.; Yokota, H.; Costen, F. An uncertainty analysis on finite difference time-domain computations with artificial neural networks: Improving accuracy while maintaining low computational costs. IEEE Antennas Propag. Mag. 2022, 65, 60–70. [Google Scholar] [CrossRef]
- Le, X.; Chen, H.; Chen, K.; Lu, J. DPCRN: Dual-path convolution recurrent network for single channel speech enhancement. arXiv 2021, arXiv:2107.05429. [Google Scholar]
- Song, R.; Feng, X.; Wang, J.; Sun, H.; Zhou, M.; Esmaiel, H. Underwater Acoustic Nonlinear Blind Ship Noise Separation Using Recurrent Attention Neural Networks. Remote Sens. 2024, 16, 653. [Google Scholar] [CrossRef]
- Luo, Y.; Chen, Z.; Yoshioka, T. Dual-path rnn: Efficient long sequence modeling for time-domain single-channel speech separation. In Proceedings of the ICASSP 2020–2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Virtual, 4–9 May 2020; pp. 46–50. [Google Scholar]
- Zhou, A.; Zhang, W.; Li, X.; Xu, G.; Zhang, B.; Ma, Y.; Song, J. A Novel Noise-Aware Deep Learning Model for Underwater Acoustic Denoising. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–13. [Google Scholar] [CrossRef]
- Zhou, A.; Zhang, W.; Xu, G.; Li, X.; Deng, K.; Song, J. dBSA-Net: Dual Branch Self-Attention Network for Underwater Acoustic Signal Denoising. IEEE/ACM Trans. Audio Speech Lang. Process. 2023, 31, 1851–1865. [Google Scholar] [CrossRef]
- Zhou, A.; Zhang, W.; Li, X.; Xu, G.; Zhang, B.; Song, J. Noise-Aware Subband Attention Network for Underwater Acoustic Signal Denoising. In Proceedings of the 2022 IEEE Smartworld, Ubiquitous Intelligence & Computing, Scalable Computing & Communications, Digital Twin, Privacy Computing, Metaverse, Autonomous & Trusted Vehicles (Smartworld/UIC/ScalCom/DigitalTwin/PriComp/Meta), Haikou, China, 15–18 December 2022; pp. 610–617. [Google Scholar]
- Zhou, W.; Li, J. Self-Noise Suppression for AUV without Clean Data: A Noise2Noise Approach. In Proceedings of the 2023 IEEE Underwater Technology (UT), Tokyo, Japan, 6–9 March 2023; pp. 1–5. [Google Scholar]
- Wang, X.; Zhao, Y.; Teng, X.; Sun, W. A stacked convolutional sparse denoising autoencoder model for underwater heterogeneous information data. Appl. Acoust. 2020, 167, 107391. [Google Scholar] [CrossRef]
- Russo, P.; Di Ciaccio, F.; Troisi, S. DANAE: A denoising autoencoder for underwater attitude estimation. arXiv 2020, arXiv:2011.06853. [Google Scholar]
- Testolin, A.; Diamant, R. Underwater acoustic detection and localization with a convolutional denoising autoencoder. In Proceedings of the 2019 IEEE 8th International Workshop on Computational Advances in Multi-Sensor Adaptive Processing (CAMSAP), Piscataway, NJ, USA, 15–18 December 2019; pp. 281–285. [Google Scholar]
- Pascual, S.; Bonafonte, A.; Serra, J. SEGAN: Speech enhancement generative adversarial network. arXiv 2017, arXiv:1703.09452. [Google Scholar]
- Dang, F.; Chen, H.; Zhang, P. DPT-FSNet: Dual-path transformer based full-band and sub-band fusion network for speech enhancement. In Proceedings of the ICASSP 2022–2022 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Virtual, 7–13 May 2022; pp. 6857–6861. [Google Scholar]
- Santos-Domínguez, D.; Torres-Guijarro, S.; Cardenal-López, A.; Pena-Gimenez, A. Shipsear: An underwater vessel noise database. Appl. Acoust. 2016, 113, 64–69. [Google Scholar] [CrossRef]





| Parameter | Value |
|---|---|
| Window length of STFT | 512 samples |
| Frame shift of STFT | 256 samples |
| Channel of Amplitude | 96 |
| 8 | |
| Channel of Phase | 48 |
| epoch | 150 |
| batch | 8 |
| Learning rate(warm-up) | 0.0005 |
| Optimizer | Adam |
| Model | Description |
|---|---|
| Without FCT | DS_FCTNet applied with three DSBs and BiLSTM, without FCT. |
| With one DSB | DS_FCTNet applied with FCT, one DSB, BiLSTM and communication. |
| With two DSBs | DS_FCTNet applied with FCT, two DSBs and BiLSTM. |
| Without communication | DS_FCTNet applied with FCT, one DSB, BiLSTM and without communication |
| With BiLSTM | DS_FCTNet applied with FCT, three DSBs and BiLSTM. |
| DS_FCTNet (ours) | DS_FCTNet applied with FCT, three DSBs, and without BiLSTM. |
| Methods | −5 dB | −10 dB | −15 dB | |||
|---|---|---|---|---|---|---|
| SDR | SSNR | SDR | SSNR | SDR | SSNR | |
| Noise | −4.99 | −3.75 | −9.77 | −8.17 | −14.71 | −12.91 |
| Without FCT | 3.2 | 3.27 | 1.9 | 2.03 | 1.14 | 1.12 |
| With one DSB | 3.97 | 4.07 | 3.01 | 3.26 | 2.51 | 2.5 |
| With two DSB | 4.69 | 4.80 | 4.08 | 4.12 | 3.88 | 3.91 |
| Without communication | 3.86 | 3.94 | 2.75 | 2.95 | 2.09 | 2.08 |
| With BiLSTM | 4.96 | 5.08 | 4.44 | 4.82 | 4.36 | 4.41 |
| DS_ FCTNet (ours) | 5.28 | 5.40 | 4.79 | 5.19 | 4.73 | 4.78 |
| Methods | −5 dB | −10 dB | −15 dB | |||
|---|---|---|---|---|---|---|
| SDR | SSNR | SDR | SSNR | SDR | SSNR | |
| noise | −4.99 | −3.75 | −9.77 | −8.17 | −14.71 | −12.91 |
| Wavelet | −1.1 | 0.17 | −5.17 | −2.36 | −7.57 | −4.55 |
| Spectral−Subtraction | −0.88 | −0.68 | −3.21 | −2.42 | −6.1 | −5.13 |
| Wiener | 0.82 | 1.33 | −3.11 | −0.96 | −6.27 | −4.74 |
| SEGAN | 2.69 | 2.74 | 1.50 | 1.54 | 0.8 | 0.77 |
| DPT_FSNET | 3.18 | 3.18 | 1.83 | 1.93 | 1.04 | 1.01 |
| DS_FCTNet | 5.28 | 5.40 | 4.79 | 5.19 | 4.73 | 4.78 |
| Methods | −5 dB | −10 dB | −15 dB | |||
|---|---|---|---|---|---|---|
| SDRi | SSNRi | SDRi | SSNRi | SDRi | SSNRi | |
| Wavelet | 5.25 | 5.36 | 8.41 | 8.85 | 10.34 | 10.16 |
| Spectral-Subtraction | 4.58 | 4.53 | 18.06 | 8.20 | 9.73 | 8.42 |
| Wiener | 6.43 | 6.50 | 12.48 | 7.63 | 7.16 | 5.79 |
| SEGAN | 7.48 | 7.46 | 11.76 | 12.09 | 16.94 | 15.94 |
| DPT_FSNET | 7.52 | 7.51 | 11.39 | 11.70 | 17.23 | 16.68 |
| DS_FCTNet | 8.42 | 8.57 | 13.04 | 13.35 | 18.85 | 19.39 |
| Methods | −5 dB | −10 dB | −15 dB | |||
|---|---|---|---|---|---|---|
| SDR | SSNR | SDR | SSNR | SDR | SSNR | |
| noise | −5 | −4.64 | −10 | −9.56 | −15 | −13.63 |
| Wavelet | 0.11 | 1.06 | −4.51 | −2.59 | −8.71 | −6.12 |
| Spectral−Subtraction | −0.68 | −0.75 | −2.92 | −2.83 | −6.28 | −5.59 |
| Wiener | 0.87 | 1.22 | −2.14 | −1.4 | −6.48 | −5.15 |
| SEGAN | 2.25 | 2.48 | 1.15 | 1.4 | 0.62 | 0.47 |
| DPT_FSNET | 3.16 | 3.29 | 3.07 | 3.28 | 2.55 | 2.64 |
| DS_FCTNet | 5.98 | 6.39 | 6.36 | 6.71 | 5.51 | 5.38 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, W.; Liu, Y.; Chen, D. A Dual-Stream Deep Learning-Based Acoustic Denoising Model to Enhance Underwater Information Perception. Remote Sens. 2024, 16, 3325. https://doi.org/10.3390/rs16173325
Gao W, Liu Y, Chen D. A Dual-Stream Deep Learning-Based Acoustic Denoising Model to Enhance Underwater Information Perception. Remote Sensing. 2024; 16(17):3325. https://doi.org/10.3390/rs16173325
Chicago/Turabian StyleGao, Wei, Yining Liu, and Desheng Chen. 2024. "A Dual-Stream Deep Learning-Based Acoustic Denoising Model to Enhance Underwater Information Perception" Remote Sensing 16, no. 17: 3325. https://doi.org/10.3390/rs16173325
APA StyleGao, W., Liu, Y., & Chen, D. (2024). A Dual-Stream Deep Learning-Based Acoustic Denoising Model to Enhance Underwater Information Perception. Remote Sensing, 16(17), 3325. https://doi.org/10.3390/rs16173325








