Integration of a Mobile Laser Scanning System with a Forest Harvester for Accurate Localization and Tree Stem Measurements
Abstract
1. Introduction
2. Materials and Methods
2.1. Harvester System
2.2. Test Site
2.3. Data Acquisition with the Harvester System
2.4. Reference Data
2.4.1. Reference for Harvester Positioning
2.4.2. Reference for Tree Attributes
3. Algorithms for Real-Time Localization and Offline Tree Attribute Estimation
3.1. Algorithms for Real-Time Localization and Mapping from MLS Data
3.1.1. Scan Pre-Processing
3.1.2. Smoothing and Mapping Framework
3.1.3. Analysis of Positioning Estimation
3.2. Algorithms for Tree Stem Measurements from the SLAM-Corrected Point Cloud
3.2.1. Digital Terrain Model
3.2.2. Detection of Tree Stems
3.2.3. Calibration and Correction of Stem Diameter Bias
3.2.4. Estimation of Stem Curve and DBH
3.2.5. Statistical Analysis of Stem Detection and Stem Attribute Estimation
4. Results
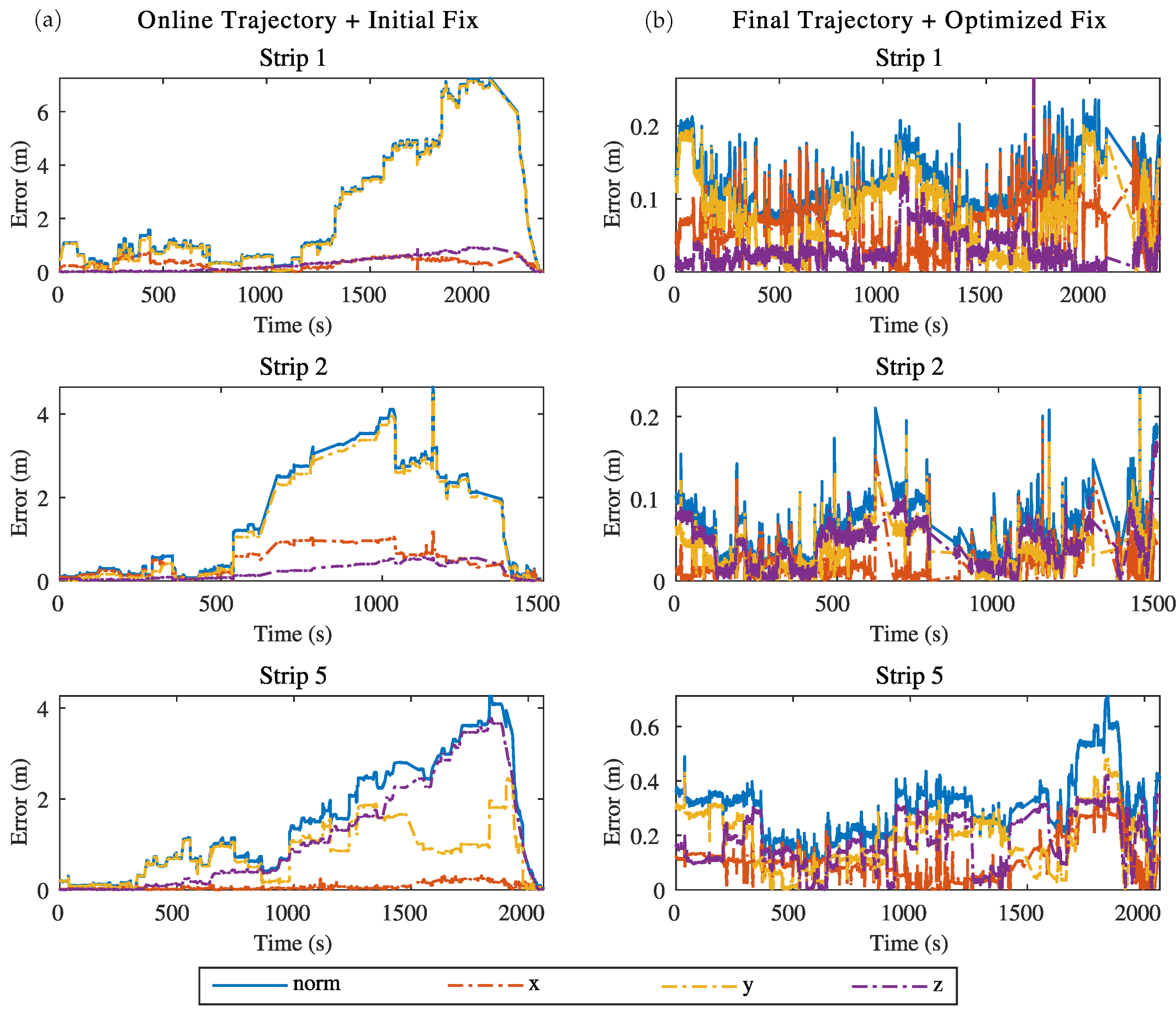
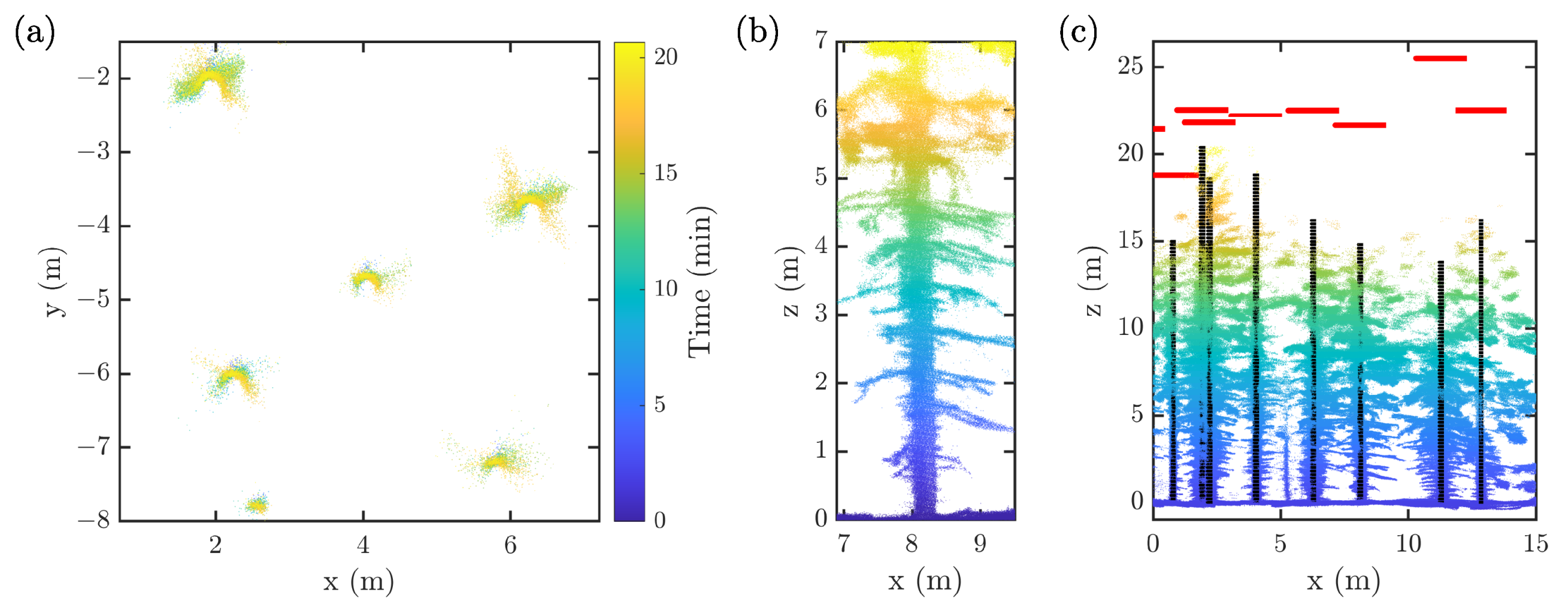
4.1. Results for Harvester Localization Using SLAM
4.2. Results for Stem Detection and Stem Attribute Estimation
5. Discussion
5.1. Discussion on Harvester Localization Using SLAM
5.2. Discussion on Stem Detection and Stem Attribute Estimation
5.3. Current Limitations and Potential Future Applications
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| GNSS | Global Navigation Satellite Systema |
| DBH | Diameter at Breast Height |
| SLAM | Simultaneous Localization and Mapping |
| ALS | Airborne Laser Scanning |
| IMU | Inertial Measurement Unit |
| NDT | Normal Distributions Transform |
| MLS | Mobile Laser Scanning |
| DOF | Degrees of Freedom |
| EKF | Extended Kalman Filter |
| SE(3) | Special Euclidean Group |
Appendix A. Strip-Wise Results for Stem Detection and Stem Attribute Estimation
| Completeness (%) | ||||||
|---|---|---|---|---|---|---|
| DBH ∈[0, 20) cm | DBH ∈[20, 28) cm | DBH ∈[28, 36) cm | DBH ∈ cm | Overall |
Correctness
(%) | |
| accurate attributes | ||||||
| Test strip 1 | 8.1 (9/111) | 48.1 (38/79) | 65.4 (34/52) | 60.0 (6/10) | 34.5 (87/252) | 95.6 (87/91) |
| Test strip 2 | 12.8 (5/39) | 50.0 (31/62) | 51.5 (34/66) | 68.2 (15/22) | 45.0 (85/189) | 97.7 (85/87) |
| Test strip 5 | 11.8 (2/17) | 42.4 (42/99) | 54.5 (50/91) | 56.3 (9/16) | 46.2 (103/223) | 97.2 (103/106) |
| All strips | 9.6 (16/167) | 46.3 (111/240) | 56.5 (118/209) | 62.5 (30/48) | 41.4 (275/664) | 96.8 (275/284) |
| tree map | ||||||
| Test strip 1 | 53.2 (59/111) | 92.4 (73/79) | 94.2 (49/52) | 80.0 (8/10) | 75.0 (189/252) | 74.1 (189/255) |
| Test strip 2 | 33.3 (13/39) | 87.1 (54/62) | 83.3 (55/66) | 100.0 (22/22) | 76.2 (144/189) | 76.6 (144/188) |
| Test strip 5 | 58.8 (10/17) | 85.7 (84/98) | 92.3 (84/91) | 81.3 (13/16) | 86.0 (191/222) | 83.4 (191/229) |
| All strips | 49.1 (82/167) | 88.3 (211/239) | 90.0 (188/209) | 89.6 (43/48) | 79.0 (524/663) | 78.0 (524/672) |
| DBH | ||||||
| Bias (cm) | Bias (%) | RMSE (cm) | RMSE (%) | MAE (cm) | MAE (%) | |
| Parameter mode accurate attributes | ||||||
| Test strip 1 | −0.3 | −1.2 | 1.9 | 6.9 | 1.3 | 4.6 |
| Test strip 2 | 0.6 | 1.9 | 1.9 | 6.3 | 0.9 | 3.1 |
| Test strip 5 | 0.0 | 0.0 | 2.4 | 8.2 | 1.0 | 3.5 |
| All strips | 0.1 | 0.2 | 2.1 | 7.3 | 1.0 | 3.4 |
| Parameter mode tree map | ||||||
| Test strip 1 | −0.4 | −1.5 | 3.9 | 16.2 | 1.5 | 6.3 |
| Test strip 2 | −0.2 | −0.7 | 2.5 | 8.6 | 1.3 | 4.6 |
| Test strip 5 | −0.4 | −1.3 | 3.0 | 10.5 | 1.6 | 5.7 |
| All strips | −0.3 | −1.2 | 3.2 | 12.0 | 1.5 | 5.5 |
| Stem Curve | ||||||
| Bias (cm) | Bias (%) | RMSE (cm) | RMSE (%) | MAE (cm) | MAE (%) | |
| Parameter mode accurate attributes | ||||||
| Test strip 1 | −0.2 | −0.6 | 2.3 | 8.5 | 1.4 | 5.3 |
| Test strip 2 | 0.4 | 1.4 | 2.3 | 7.9 | 1.2 | 4.0 |
| Test strip 5 | 0.2 | 0.6 | 2.4 | 8.5 | 1.0 | 3.5 |
| All strips | 0.1 | 0.5 | 2.3 | 8.3 | 1.2 | 4.3 |
| Parameter mode tree map | ||||||
| Test strip 1 | 0.2 | 0.8 | 4.4 | 18.9 | 2.0 | 8.4 |
| Test strip 2 | −0.2 | −0.8 | 3.0 | 10.5 | 1.7 | 5.9 |
| Test strip 5 | −0.2 | −0.8 | 3.2 | 11.6 | 1.8 | 6.6 |
| All strips | −0.1 | −0.3 | 3.6 | 13.9 | 1.8 | 6.9 |
References
- Visser, R.; Obi, O.F. Automation and robotics in forest harvesting operations: Identifying near-term opportunities. Croat. J. For. Eng. 2021, 42, 13–24. [Google Scholar] [CrossRef]
- Ponsse. Ponsse to Demonstrate New Solutions at FinnMETKO 2022; Ponsse: Vieremä, Finland, 2022; Available online: https://www.ponsse.com/company/news/-/asset_publisher/P4s3zYhpxHUQ/content/ponsse-to-demonstrate-new-solutions-at-finnmetko-2022#/ (accessed on 2 August 2024).
- Ryding, J.; Williams, E.; Smith, M.J.; Eichhorn, M.P. Assessing handheld mobile laser scanners for forest surveys. Remote Sens. 2015, 7, 1095–1111. [Google Scholar] [CrossRef]
- Kukko, A.; Kaijaluoto, R.; Kaartinen, H.; Lehtola, V.V.; Jaakkola, A.; Hyyppä, J. Graph SLAM correction for single scanner MLS forest data under boreal forest canopy. ISPRS J. Photogramm. Remote Sens. 2017, 132, 199–209. [Google Scholar] [CrossRef]
- Pierzchała, M.; Giguère, P.; Astrup, R. Mapping forests using an unmanned ground vehicle with 3D LiDAR and graph-SLAM. Comput. Electron. Agric. 2018, 145, 217–225. [Google Scholar] [CrossRef]
- Cabo, C.; Del Pozo, S.; Rodríguez-Gonzálvez, P.; Ordóñez, C.; González-Aguilera, D. Comparing terrestrial laser scanning (TLS) and wearable laser scanning (WLS) for individual tree modeling at plot level. Remote Sens. 2018, 10, 540. [Google Scholar] [CrossRef]
- Nevalainen, P.; Li, Q.; Melkas, T.; Riekki, K.; Westerlund, T.; Heikkonen, J. Navigation and mapping in forest environment using sparse point clouds. Remote Sens. 2020, 12, 4088. [Google Scholar] [CrossRef]
- Hyyppä, E.; Kukko, A.; Kaijaluoto, R.; White, J.C.; Wulder, M.A.; Pyörälä, J.; Liang, X.; Yu, X.; Wang, Y.; Kaartinen, H.; et al. Accurate derivation of stem curve and volume using backpack mobile laser scanning. ISPRS J. Photogramm. Remote Sens. 2020, 161, 246–262. [Google Scholar] [CrossRef]
- Hyyppä, E.; Hyyppä, J.; Hakala, T.; Kukko, A.; Wulder, M.A.; White, J.C.; Pyörälä, J.; Yu, X.; Wang, Y.; Virtanen, J.P.; et al. Under-canopy UAV laser scanning for accurate forest field measurements. ISPRS J. Photogramm. Remote Sens. 2020, 164, 41–60. [Google Scholar] [CrossRef]
- Bienert, A.; Georgi, L.; Kunz, M.; von Oheimb, G.; Maas, H.G. Automatic extraction and measurement of individual trees from mobile laser scanning point clouds of forests. Ann. Bot. 2021, 128, 787–804. [Google Scholar] [CrossRef]
- Liang, X.; Kukko, A.; Balenović, I.; Saarinen, N.; Junttila, S.; Kankare, V.; Holopainen, M.; Mokroš, M.; Surovỳ, P.; Kaartinen, H.; et al. Close-range remote sensing of forests: The state of the art, challenges, and opportunities for systems and data acquisitions. IEEE Geosci. Remote Sens. Mag. 2022, 10, 32–71. [Google Scholar] [CrossRef]
- Kaartinen, H.; Hyyppä, J.; Vastaranta, M.; Kukko, A.; Jaakkola, A.; Yu, X.; Pyörälä, J.; Liang, X.; Liu, J.; Wang, Y.; et al. Accuracy of Kinematic Positioning Using Global Satellite Navigation Systems under Forest Canopies. Forests 2015, 6, 3218–3236. [Google Scholar] [CrossRef]
- Durrant-Whyte, H.; Bailey, T. Simultaneous localization and mapping: Part I. IEEE Robot. Autom. Mag. 2006, 13, 99–110. [Google Scholar] [CrossRef]
- Pohjala, J.; Vahtila, M.; Ovaskainen, H.; Kankare, V.; Hyyppä, J.; Kärhä, K. Effect of Prior Tree Marking on Cutting Productivity and Harvesting Quality. Croat. J. For. Eng. J. Theory Appl. For. Eng. 2024, 45, 25–42. [Google Scholar] [CrossRef]
- Hauglin, M.; Hansen, E.; Sørngård, E.; Næsset, E.; Gobakken, T. Utilizing accurately positioned harvester data: Modelling forest volume with airborne laser scanning. Can. J. For. Res. 2018, 48, 913–922. [Google Scholar] [CrossRef]
- Saukkola, A.; Melkas, T.; Riekki, K.; Sirparanta, S.; Peuhkurinen, J.; Holopainen, M.; Hyyppä, J.; Vastaranta, M. Predicting forest inventory attributes using airborne laser scanning, aerial imagery, and harvester data. Remote Sens. 2019, 11, 797. [Google Scholar] [CrossRef]
- Rossmann, J.; Schluse, M.; Schlette, C.; Buecken, A.; Krahwinkler, P.; Emde, M. Realization of a highly accurate mobile robot system for multi purpose precision forestry applications. In Proceedings of the 2009 International Conference on Advanced Robotics, Munich, Germany, 22–26 June 2009; pp. 1–6. [Google Scholar]
- Sihvo, S.; Virjonen, P.; Nevalainen, P.; Heikkonen, J. Tree Detection around Forest Harvester Based on Onboard LiDAR Measurements. In Proceedings of the 2018 Baltic Geodetic Congress, BGC-Geomatics 2018, Olsztyn, Poland, 21–23 June 2018; pp. 364–367. [Google Scholar]
- Salmivaara, A.; Miettinen, M.; Finér, L.; Launiainen, S.; Korpunen, H.; Tuominen, S.; Heikkonen, J.; Nevalainen, P.; Sirén, M.; Ala-Ilomäki, J.; et al. Wheel rut measurements by forest machine-mounted LiDAR sensors–accuracy and potential for operational applications? Int. J. For. Eng. 2018, 29, 41–52. [Google Scholar] [CrossRef]
- Jutila, J.; Kannas, K.; Visala, A. Tree measurement in forest by 2D laser scanning. In Proceedings of the 2007 IEEE International Symposium on Computational Intelligence in Robotics and Automation (CIRA), Jacksonville, FL, USA, 20–23 June 2007; pp. 491–496. [Google Scholar]
- Miettinen, M.; Öhman, M.; Visala, A.; Forsman, P. Simultaneous localization and mapping for forest harvesters. In Proceedings of the IEEE International Conference on Robotics and Automation, Rome, Italy, 10–14 April 2007; pp. 517–522. [Google Scholar]
- Hyyti, H.; Visala, A. Feature Based Modeling and Mapping of Tree Trunks and Natural Terrain Using 3D Laser Scanner Measurement System. IFAC Proc. Vol. 2013, 46, 248–255. [Google Scholar] [CrossRef]
- Tremblay, J.F.; Béland, M.; Pomerleau, F.; Gagnon, R.; Giguère, P. Automatic 3D Mapping for Tree Diameter Measurements in Inventory Operations. arXiv 2019, arXiv:1904.05281. [Google Scholar]
- Xu, X.; Zhang, L.; Yang, J.; Cao, C.; Wang, W.; Ran, Y.; Tan, Z.; Luo, M. A Review of Multi-Sensor Fusion SLAM Systems Based on 3D LIDAR. Remote Sens. 2022, 14, 2835. [Google Scholar] [CrossRef]
- Zhang, J.; Singh, S. Low-drift and real-time lidar odometry and mapping. Auton. Robot. 2017, 41, 401–416. [Google Scholar] [CrossRef]
- Shan, T.; Englot, B.; Meyers, D.; Wang, W.; Ratti, C.; Rus, D. LIO-SAM: Tightly-coupled Lidar Inertial Odometry via Smoothing and Mapping. arXiv 2020, arXiv:2007.00258. [Google Scholar]
- Qu, C.; Shivakumar, S.S.; Liu, W.; Taylor, C.J. LLOL: Low-Latency Odometry for Spinning Lidars. arXiv 2021, arXiv:2110.01725. [Google Scholar]
- Xu, W.; Cai, Y.; He, D.; Lin, J.; Zhang, F. FAST-LIO2: Fast Direct LiDAR-inertial Odometry. arXiv 2021, arXiv:2107.06829. [Google Scholar]
- Rossmann, J.; Krahwinkler, P.; Schlette, C. Navigation of Mobile Robots in Natural Environments: Using Sensor Fusion in Forestry. J. Syst. Cybern. Inform. 2010, 8, 67–71. [Google Scholar]
- Chen, Y.; Tang, J.; Khoramshahi, E.; Hakala, T.; Kaartinen, H.; Jaakkola, A.; Hyyppa, J.; Zhu, Z.; Chen, R. Scan matching technology for forest navigation with map information. In Proceedings of the IEEE/ION Position, Location and Navigation Symposium, PLANS 2016, Savannah, GA, USA, 11–14 April 2016; pp. 198–203. [Google Scholar]
- Li, Q.; Nevalainen, P.; Queralta, J.P.; Heikkonen, J.; Westerlund, T. Localization in Unstructured Environments: Towards Autonomous Robots in Forests with Delaunay Triangulation. Remote Sens. 2020, 12, 1870. [Google Scholar] [CrossRef]
- de Lima, L.C.; Ramezani, M.; Borges, P.; Brunig, M. Air-Ground Collaborative Localisation in Forests Using Lidar Canopy Maps. IEEE Robot. Autom. Lett. 2023, 8, 1818–1825. [Google Scholar] [CrossRef]
- Bauwens, S.; Bartholomeus, H.; Calders, K.; Lejeune, P. Forest inventory with terrestrial LiDAR: A comparison of static and hand-held mobile laser scanning. Forests 2016, 7, 127. [Google Scholar] [CrossRef]
- Balenović, I.; Liang, X.; Jurjević, L.; Hyyppä, J.; Seletković, A.; Kukko, A. Hand-Held Personal Laser Scanning–Current Status and Perspectives for Forest Inventory Application. Croat. J. For. Eng. J. Theory Appl. For. Eng. 2021, 42, 165–183. [Google Scholar]
- Vandendaele, B.; Martin-Ducup, O.; Fournier, R.A.; Pelletier, G.; Lejeune, P. Mobile laser scanning for estimating tree structural attributes in a temperate hardwood Forest. Remote Sens. 2022, 14, 4522. [Google Scholar] [CrossRef]
- Liang, X.; Hyyppä, J.; Kukko, A.; Kaartinen, H.; Jaakkola, A.; Yu, X. The use of a mobile laser scanning system for mapping large forest plots. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1504–1508. [Google Scholar] [CrossRef]
- Hyyppä, E.; Kukko, A.; Kaartinen, H.; Yu, X.; Muhojoki, J.; Hakala, T.; Hyyppä, J. Direct and automatic measurements of stem curve and volume using a high-resolution airborne laser scanning system. Sci. Remote Sens. 2022, 5, 100050. [Google Scholar] [CrossRef]
- Hyyppä, E.; Yu, X.; Kaartinen, H.; Hakala, T.; Kukko, A.; Vastaranta, M.; Hyyppä, J. Comparison of backpack, handheld, under-canopy UAV, and above-canopy UAV laser scanning for field reference data collection in boreal forests. Remote Sens. 2020, 12, 3327. [Google Scholar] [CrossRef]
- Ouster. OS0: Ultra-Wide View High-Resolution Imaging Lidar; Revision: 12/07/2020, Hardware Version: Rev C; Ouster, Inc.: San Francisco, CA, USA, 2020; Available online: https://data.ouster.io/downloads/datasheets/datasheet-rev05-v2p1-os0.pdf (accessed on 1 August 2024).
- Leica. Leica Nova TS60; Retrieved 12.2.2024; Leica: Heerbrugg, Switzerland, 2020; Available online: https://leica-geosystems.com/products/total-stations/robotic-total-stations/leica-nova-ts60 (accessed on 1 August 2024).
- Chen, S.; Liu, H.; Feng, Z.; Shen, C.; Chen, P. Applicability of personal laser scanning in forestry inventory. PLoS ONE 2019, 14, e0211392. [Google Scholar] [CrossRef]
- Hunčaga, M.; Chudá, J.; Tomaštík, J.; Slámová, M.; Koreň, M.; Chudỳ, F. The Comparison of Stem Curve Accuracy Determined from Point Clouds Acquired by Different Terrestrial Remote Sensing Methods. Remote Sens. 2020, 12, 2739. [Google Scholar] [CrossRef]
- Gollob, C.; Ritter, T.; Nothdurft, A. Forest inventory with long range and high-speed personal laser scanning (PLS) and simultaneous localization and mapping (SLAM) technology. Remote Sens. 2020, 12, 1509. [Google Scholar] [CrossRef]
- Faitli, T.; Hakala, T.; Kaartinen, H.; Hyyppä, J.; Kukko, A. Real-Time Lidar-Inertial Positioning and Mapping for Forestry Automation. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2023, XLVIII-1/W1-2023, 145–150. [Google Scholar]
- Forster, C.; Carlone, L.; Dellaert, F.; Scaramuzza, D. On-Manifold Preintegration for Real-Time Visual-Inertial Odometry. IEEE Trans. Robot. 2017, 33, 1–21. [Google Scholar] [CrossRef]
- Solà, J.; Deray, J.; Atchuthan, D. A micro Lie theory for state estimation in robotics. arXiv 2018, arXiv:1812.01537. [Google Scholar]
- Dellaert, F.; Kaess, M. Factor Graphs for Robot Perception. Found. Trends Robot. 2017, 6, 1–139. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of the KDD, Portland, OR, USA, 2–4 August 1996; Volume 96, pp. 226–231. [Google Scholar]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Muhojoki, J.; Tavi, D.; Hyyppä, E.; Lehtomäki, M.; Faitli, T.; Kaartinen, H.; Kukko, A.; Hakala, T.; Hyyppä, J. Benchmarking Under-and Above-Canopy Laser Scanning Solutions for Deriving Stem Curve and Volume in Easy and Difficult Boreal Forest Conditions. Remote Sens. 2024, 16, 1721. [Google Scholar] [CrossRef]
- Forsman, M.; Börlin, N.; Olofsson, K.; Reese, H.; Holmgren, J. Bias of cylinder diameter estimation from ground-based laser scanners with different beam widths: A simulation study. ISPRS J. Photogramm. Remote Sens. 2018, 135, 84–92. [Google Scholar] [CrossRef]
- Ringdahl, O.; Hohnloser, P.; Hellström, T.; Holmgren, J.; Lindroos, O. Enhanced Algorithms for Estimating Tree Trunk Diameter Using 2D Laser Scanner. Remote Sens. 2013, 5, 4839–4856. [Google Scholar] [CrossRef]
- Kuželka, K.; Surovỳ, P. Noise Analysis for Unbiased Tree Diameter Estimation from Personal Laser Scanning Data. Remote Sens. 2024, 16, 1261. [Google Scholar] [CrossRef]
- Hyyppä, E.; Muhojoki, J.; Yu, X.; Kukko, A.; Kaartinen, H.; Hyyppä, J. Efficient coarse registration method using translation-and rotation-invariant local descriptors towards fully automated forest inventory. ISPRS Open J. Photogramm. Remote Sens. 2021, 2, 100007. [Google Scholar] [CrossRef]
- Wielgosz, M.; Puliti, S.; Wilkes, P.; Astrup, R. Point2Tree (P2T)–framework for parameter tuning of semantic and instance segmentation used with mobile laser scanning data in coniferous forest. arXiv 2023, arXiv:2305.02651. [Google Scholar]
- Xiang, B.; Wielgosz, M.; Kontogianni, T.; Peters, T.; Puliti, S.; Astrup, R.; Schindler, K. Automated forest inventory: Analysis of high-density airborne LiDAR point clouds with 3D deep learning. arXiv 2023, arXiv:2312.15084. [Google Scholar] [CrossRef]
- National Land Survey of Finland. Laser Scanning Data 5 p; National Land Survey of Finland: Helsinki, Finland, 2023. Available online: https://www.maanmittauslaitos.fi/en/maps-and-spatial-data/datasets-and-interfaces/product-descriptions/laser-scanning-data-5-p (accessed on 1 August 2024).
- Maltamo, M.; Kinnunen, H.; Kangas, A.; Korhonen, L. Predicting stand age in managed forests using National Forest Inventory field data and airborne laser scanning. For. Ecosyst. 2020, 7, 44. [Google Scholar] [CrossRef]
- Yu, X.; Hyyppä, J.; Kukko, A.; Maltamo, M.; Kaartinen, H. Change detection techniques for canopy height growth measurements using airborne laser scanner data. Photogramm. Eng. Remote Sens. 2006, 72, 1339–1348. [Google Scholar] [CrossRef]
- Polewski, P.; Yao, W.; Cao, L.; Gao, S. Marker-free coregistration of UAV and backpack LiDAR point clouds in forested areas. ISPRS J. Photogramm. Remote Sens. 2019, 147, 307–318. [Google Scholar] [CrossRef]
- Ghorbani, F.; Chen, Y.C.; Hollaus, M.; Pfeifer, N. A Robust and Automatic Algorithm for TLS - ALS Point Cloud Registration in Forest Environments based on Tree Locations. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 4015–4035. [Google Scholar]
















| Property | Value for Ouster OS0-128 Rev C |
|---|---|
| Range | 45 m for >90% detection probability |
| 50 m for >50% detection probability | |
| Range accuracy | ±3 cm for lambertian targets |
| ±10 cm for retroreflectors | |
| Field of view (vertical) | 90% (−45° to +45°) |
| Field of view (horizontal) | 360° |
| Vertical resolution | 128 |
| Horizontal resolution | 1024 |
| Rotation rate | 10 Hz |
| Pulse repetition rate | 1.31 MHz |
| Laser wavelength | 865 nm |
| Beam diameter exiting sensor | 5 mm |
| Beam divergence | 6.1 mrad (0.35°) |
|
Test Strip | Length of Strip (m) | Number of Trees | Stem Density (1/ha) | Mean DBH (cm) | Mean Tree Height (m) | Mean Stem Volume () |
|---|---|---|---|---|---|---|
| 1 | 93 | 252 | 630 | 22.3 (±7.6) | 18.3 (±4.2) | 0.47 (±0.36) |
| 2 | 76 | 190 | 540 | 27.0 (±7.9) | 21.4 (±3.9) | 0.75 (±0.45) |
| 5 | 139 | 216 | 490 | 27.9 (±5.7) | 22.7 (±2.4) | 0.79 (±0.34) |
| Positioning RMSE (m) | ||||||||
|---|---|---|---|---|---|---|---|---|
| Final Trajectory | Online Trajectory | |||||||
| x | y | z | norm | x | y | z | norm | |
| Initial Fix | ||||||||
| Test strip 1 | 0.135 | 0.405 | 0.358 | 0.557 | 0.360 | 3.023 | 0.400 | 3.070 |
| Test strip 2 | 0.019 | 0.150 | 0.194 | 0.246 | 0.546 | 1.820 | 0.276 | 1.920 |
| Test strip 5 | 0.203 | 0.871 | 1.547 | 1.787 | 0.100 | 0.974 | 1.592 | 1.869 |
| All strips | 0.150 | 0.588 | 0.961 | 1.136 | 0.353 | 2.206 | 0.998 | 2.447 |
| Optimized Fix | ||||||||
| Test strip 1 | 0.074 | 0.094 | 0.038 | 0.126 | 0.354 | 2.661 | 0.078 | 2.686 |
| Test strip 2 | 0.025 | 0.043 | 0.051 | 0.071 | 0.534 | 1.688 | 0.073 | 1.772 |
| Test strip 5 | 0.131 | 0.214 | 0.200 | 0.321 | 0.116 | 1.751 | 0.304 | 1.781 |
| All strips | 0.093 | 0.143 | 0.125 | 0.212 | 0.348 | 2.162 | 0.193 | 2.199 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Faitli, T.; Hyyppä, E.; Hyyti, H.; Hakala, T.; Kaartinen, H.; Kukko, A.; Muhojoki, J.; Hyyppä, J. Integration of a Mobile Laser Scanning System with a Forest Harvester for Accurate Localization and Tree Stem Measurements. Remote Sens. 2024, 16, 3292. https://doi.org/10.3390/rs16173292
Faitli T, Hyyppä E, Hyyti H, Hakala T, Kaartinen H, Kukko A, Muhojoki J, Hyyppä J. Integration of a Mobile Laser Scanning System with a Forest Harvester for Accurate Localization and Tree Stem Measurements. Remote Sensing. 2024; 16(17):3292. https://doi.org/10.3390/rs16173292
Chicago/Turabian StyleFaitli, Tamás, Eric Hyyppä, Heikki Hyyti, Teemu Hakala, Harri Kaartinen, Antero Kukko, Jesse Muhojoki, and Juha Hyyppä. 2024. "Integration of a Mobile Laser Scanning System with a Forest Harvester for Accurate Localization and Tree Stem Measurements" Remote Sensing 16, no. 17: 3292. https://doi.org/10.3390/rs16173292
APA StyleFaitli, T., Hyyppä, E., Hyyti, H., Hakala, T., Kaartinen, H., Kukko, A., Muhojoki, J., & Hyyppä, J. (2024). Integration of a Mobile Laser Scanning System with a Forest Harvester for Accurate Localization and Tree Stem Measurements. Remote Sensing, 16(17), 3292. https://doi.org/10.3390/rs16173292










