Abstract
The isle of Gavdos, and its wider area, is one of the few places worldwide where the calibration and validation of altimetric satellites has been carried out during the last, more than, two decades using dedicated techniques at sea and on land. The sea-surface calibration employed for the determination of the bias in the satellite altimeter’s sea-surface height relies on the use of a gravimetric geoid in collocation with data from tide gauges, permanent global navigation satellite system (GNSS) receivers, as well as meteorological and oceanographic sensors. Hence, a high-accuracy and high-resolution gravimetric geoid model in the vicinity of Gavdos and its surrounding area is of vital importance. The existence of such a geoid model resides in the availability of reliable, in terms of accuracy, and dense, in terms of spatial resolution, gravity data. The isle of Gavdos presents varying topographic characteristics with heights larger than 400 m within small spatial distances of ~7 km. The small size of the island and the significant bathymetric variations in its surrounding marine regions make the determination of the gravity field and the geoid a challenging task. Given the above, the objective of the present work was two-fold. First, to collect new land gravity data over the isle of Gavdos in order to complete the existing database and cover parts of the island where voids existed. Relative gravity campaigns have been designed to cover as homogenously as possible the entire island of Gavdos and especially areas where the topographic gradient is large. The second focus was on the determination of a high-resolution, , and high-accuracy gravimetric geoid for the wider Gavdos area, which will support activities on the determination of the absolute altimetric bias. The relative gravity campaigns have been designed and carried out employing a CG5 relative gravity meter along with geodetic grade GNSS receivers to determine the geodetic position of the acquired observations. Geoid determination has been based on the newly acquired and historical gravity data, GNSS/Leveling observations, and topography and bathymetry databases for the region. The modeling was based on the well-known remove–compute–restore (RCR) method, employing least-squares collocation (LSC) and fast Fourier transform (FFT) methods for the evaluation of the Stokes’ integral. Modeling of the long wavelength contribution has been based on EIGEN6c4 and XGM2019e global geopotential models (GGMs), while for the contribution of the topography, the residual terrain model correction has been employed using both the classical, space domain, and spectral approaches. From the results achieved, the final geoid model accuracy reached the ±1–3 cm level, while in terms of the absolute differences to the GNSS/Leveling data per baseline length, 28.4% of the differences were below the level and 55.2% below the . The latter improved drastically to 52.8% and 81.1%, respectively, after deterministic fit to GNSS/Leveling data, while in terms of the relative differences, the final geoid reaches relative uncertainties of 11.58 ppm (±1.2 cm) for baselines as short as 0–10 km, which improves to 10.63 ppm (±1.1 cm) after the fit.
1. Introduction
The geoid is the only surface to be used as a reference in geodesy to measure heights from, whether these are orthometric, normal, or dynamic ones, since it is a zero-level equipotential surface and provides a direct metric of physical heights [1]. Hence, the geoid itself plays a crucial role not only to geodesy as, e.g., a vertical reference system [2], but to an ever-widening area of the rest of geosciences, i.e., to all scientific fields that focus on studying our dynamic Earth system. This synergy is especially prominent with oceanography, as geodetic and oceanographic applications rely on each other when the focus is over marine areas. For example, in order to determine the marine geoid, the mean dynamic ocean topography (MDOT) is needed, as is the separation of the geoid from the mean sea surface (MSS), while for the determination of geostrophic currents from satellite altimetry data, which are in essence (geometric) heights above the reference ellipsoid, the geoid needs to be known [3]. An activity where local geoid modeling is of fundamental importance, within the previous synergistic context, is the calibration/validation (Cal/Val) of altimeters on-board satellites. The latter is needed both when the exploitation of synchronous multi-satellite mission data is concerned and when historical data need to be combined with recent and future ones. Refs. [3,4] provide an overview of both the need for high-accuracy and high-resolution geoid modeling in support of altimeter Cal/Val activities and to the various options of altimetric Cal/Val itself.
The isle of Gavdos poses a significant outpost in the satellite altimetry Cal/Val, as it is the only such site that resides directly below a crossover point of the orbits of the reference altimetry missions [4]. In that respect it has been used during the last 25 years for Cal/Val operations, not only for the Jason missions, but as today an ESA Permanent Facility for Altimetry Calibration (PFAC) in Crete for SARAL/Altika, HY2 (HY-2A, HY-2B, HY-2C), Cryosat-2, and the Copernicus Sentinel satellites (Sentinel-3A, Sentinel-3B, Sentinel-6 MF) [5]. To determine the absolute altimetric bias, one can reside on the waveform retracking using active microwave transponders and make relative comparisons against external data coming from tide gauge (TG), leveling, global navigation satellite system (GNSS), and meteorological and oceanographic sensors [4]. In the latter case, a reference surface is needed, which will connect the altimetry-derived sea surface heights (SSHs), which refer to a conventional reference ellipsoid, with and to the local/regional network of sensors that realize the local/regional height reference system and datum. As stated already, the only appropriated zero-level equipotential surface to serve as a reference for physical heights is the geoid, which is customarily realized through acquisition of local and satellite data and proper modeling.
In the frame of the present investigation, the main scope is to derive the most accurate, based on the available gravity data, local geoid modeling for the ESA PFAC in Crete [5], in order to serve as the reference for the past (during mission reprocessing), ongoing, and future satellite altimetry Cal/Val activities. Similar efforts have been carried out in the past by [3], but in the meantime, the realization and the improvements in both satellite gravimetry and the acquisition of new local gravity data offer the opportunity for an improved geoid estimation. With that in mind, an effort has been carried out during 2018 and 2023 to acquire high-quality relative gravity data, mainly over the isle of Gavdos and around the main ESA PFAC Crete sites over mainland Crete. The plan initially was to carry out the two campaigns within a smaller timespan and realize the geoid determination much earlier, but given the limitations due to the pandemic and travel restrictions, this was not possible. This work is therefore composed of two main parts. The first one provides details on the design of the gravity campaigns, measuring strategies, and results to densify the available land gravity data over Gavdos and around the Crete Cal/Val sites. Then, the second and major part refers to the determination of a high-accuracy and resolution geoid model for the wider Gavdos and Crete area and its validation with external data. Section 2 outlines the relative gravity campaign and design, along with the geoid determination methodology employed. Section 3 provides the results from the local gravity data acquisition and the formulation of the land gravity database to be used for geoid modeling. Section 4 of the paper is devoted to the analytical geoid determination, using both spectral and stochastic methods, and to the validation of the achieved results, in both an absolute and relative sense.
2. Gravity Campaigns over Gavdos and Crete and Gravity Database
For the determination of a high-accuracy and resolution gravimetric geoid model, it is imperative that the area under study be covered by dense and high-quality land and marine gravity data. Given the Cal/Val activities carried out during the last 25 years over Gavdos and the wider western part of Crete [4,5], several research initiatives have been carried out in order to determine a gravimetric geoid model in support of the altimetric absolute bias determination. Early geoid and gravity field modeling activities have been initiated in 2001 by [6] relying on historic land and marine gravity data, the EGM1996 [7] Global Geopotential Model (GGM) as reference and employing spectral, fast Fourier transform (FFT)-based [8], stochastic, least squares collocation (LSC) [9,10] methods, and the remove–compute–restore (RCR) approach [11]. Ref. [12] has updated this first solution by incorporating airborne gravity data from a dedicated campaign and satellite altimetry data from the ERS1 and GEOSAT missions within a multiple-input multiple-output system theory [13] spectral approach. Refs. [4,14] has employed the same database and methods as in [12], but this time geoid determination has been carried out directly at the sub-satellite points of the Jason 1 and Jason 2 tracks in order to avoid interpolation errors from FFT-based methods that produce the geoid on a grid. The next major advancement in geoid modeling over the Crete and Gavdos Cal/Val sites has been carried out by [3], where the available historic land and marine gravity data have been re-evaluated with an LSC-based blunder-detection and removal procedure [15] and GGMs from the Global Ocean Circulation Mission (GOCE), namely GOCO02s [16], and EGM2008 [17] have been used as references. Since then, the developed gravimetric and combined geoid models have been customarily used for the regular Cal/Val activities, employing in all cases a point-wise LSC estimation directly at the altimetric tracks under investigation [18,19,20,21]. Hence, no major breakthrough has been developed, mainly because it was apparent that despite improvements in GGMs, digital topography models (DTMs), and digital bathymetry models (DBMs) for the evaluation of topographic effects on gravity during the RCR method [15], the main factor that could possibly contribute to an improved geoid would be the acquisition of new high-quality gravity data, especially over Gavdos.
With the above in mind, a gravity campaign was designed using a CG5 relative gravity meter (S/N 070540268, MicroGLaCost, Lafayette, CO, USA), which belongs to the Laboratory of Gravity Field Research and Applications (GravLab) of the Aristotle University of Thessaloniki. In-situ measurements were to be carried out at all Cal/Val main sites, i.e., Candanos (CDN1), Chrysoskalitisa (CRS1), Rodakino (RDK1), Sougia (SUG1), and over Gavdos to Karave (KVR—GVD8 and GVD0) and the Pass 109 (ascending) and Pass 018 (descending) crossover point (GVD1). The objective was to derive absolute gravity at local benchmarks (BMs), which are connected to the tide gauge (TG) and GNSS antenna zero reference points (ref. [19] should be consulted for an extensive outlook of the location of the aforementioned BMs). Moreover, two extensive relative surveys have been designed and carried out over Gavdos to densify the available gravity database towards a more precise geoid determination, which will also lead to a more reliable and robust determination of the absolute bias of altimetric satellites. This planning included also a re-evaluation of the existing land gravity data used for geoid modeling in the area [15], so as to cover parts of the island where voids in the available database exist. This was especially important in Tripiti, the peninsula at the southernmost tip of Gavdos, and the beaches of Pyrgos and Ai-Giannis in the north, where no data existed at all. Therefore, relative gravity campaigns have been designed to cover, as homogenously as possible, the entire island of Gavdos, especially areas where the topographic gradient is large. In view of the subsequent geoid determination, a collection and homogenization of the historical gravity data and the construction of a common gravity database were carried out. This follows with the collection and database generation of the topography/bathymetry model, to be used to evaluate the topographic effects on gravity and the geoid, and the GGMs that will provide the long-to-medium characteristics of the gravity field spectrum.
2.1. Relative Gravity Survey Planning and Ties to the Gravimetric Network
In the design of the relative gravity surveys, the first goal was the determination of the absolute potential values, in terms of gravity, at the main Cal/Val sites established during the last 25 years in the islands of Crete and Gavdos. The second goal was to carry out a more focused survey over the island of Gavdos towards the determination of a high-resolution and accuracy geoid. To guarantee homogeneity between the various data sources, the reference system used for the gravity data is of vital importance within the RCR procedure. The Potsdam Gravity Datum of 1909, having a mean bias of ~14 mGal, is the one usually used in historic campaigns, while the International Gravity Standardization Net (IGSN71) [22] forms the basis for the determination of location-dependent gravity variations [23] in modern campaigns. Within geoid modeling and during the validation and quality check of the available gravity data, an investigation was carried out as to the gravity reference system (GrRS) that the available data refer to (Potsdam, GRS67, GRS80), and after the appropriate transformations, all gravity data were finally referred to GRS80 [24]. The entire geoid processing was carried out in IGSN71/GRS80, and the tide-free (TF) system was used [25,26], with the GRS80 defining parameters needed for the normal gravity and normal potential determination.
As in all relative gravity campaigns aiming at the determination of absolute gravity observations, a local tie is needed so that the derived gravity differences relative to the known point will lead to an absolute gravity determination. If we assume that the absolute gravity value at a gravimetric BM is known, being denoted by P, then given relative gravity observations between points P and Q, one can determine the absolute gravity at the new point location Q as:
Therefore, in the frame of the campaign planned in Crete and Gavdos, a fundamental point was to identify and use a gravity BM, which would thereafter be used as a reference. Two such choices existed in mainland Crete, i.e., to either rely the survey on the first- and second-order gravimetric network of the Hellenic Military Geographic Service (HMGS), realized through the network of the HMGS BMs, or to a network of absolute gravity BMs measured by the University of Hamburg—UoH (personal communication). The two networks should primarily realize the gravity field over Crete without any distortions between them in either the scale or the reference system. The HMGS network consisted of three gravity BMs from HMGS, namely point Chania Airport, being a first-order point, and two BMs in Hora Sfakion and Palaiochora, Crete, being second-order densification points. Naturally, the selection of the BM to be used as reference was the one at the Chania airport, being a first-order point, hence of higher accuracy, which unfortunately was destroyed. As far as the UoH database was concerned, there were three points that coincided with the ones from HMGS. Table 1 reports the absolute gravity values at the stations of Chania airport, Hora Sfakion, and Palaiochora, both from HMGS and UoH. It should be noted that gravity by HMGS refers to GRS80 and the Potsdam system, so that a mean correction between Potsdam and IGSN71 equal to −13.6 mGal has been used to transfer them to the most recent gravity reference system. As it can be seen from Table 1, the gravity values at Chania Airport from both databases agree at the 13 μGal level, which is evidence that both values refer to the same point. On the other hand, the points in Palaiochora and Chora Sfakion show differences at the 180 mGal to 210 mGal level, which were an indication that not only different points have been measured but that one of them contains blunders. The last column in Table 1 reports the gravity difference for the BMs in Hora Sfakion and Palaiochora, for each database, with respect to the gravity BM of Chania airport. Given that (a) the gravity gradient for the entire Greek territory ranges at the 280 mGal level, (b) all BMs are within a small distance (1–3 km) from the coastline and at low altitudes, and (c) the gravity gradient over the entire island of Crete is at the ~120 mGal only (e.g., as derived by EGM208), a first conclusion was that the values reported in the HMGS database for Hora Sfakion and Palaiochora contain significant blunders. The latter has also been confirmed when the actual gravity observations have been carried out in September to October 2018, during the first relative campaign.

Table 1.
Gravity values and their difference in Potsdam and IGSN gravity reference systems for the BMs at Chania Airport, Palaiochora and Hora Sfakion, Crete, from the UoH and HMGS databases. Unit: [mGal].
Another interesting point identified during the campaign planning was that BM Palaiochora in the UoH database does not refer to the HMGS BM, but to an HMGS geodetic BM close to the port of the town. This has been confirmed by both the geodetic coordinates of the point and the actual gravity observations carried out, which showed that the absolute gravity value provided by the UoH group is both reliable and rigorous w.r.t. the one at Chania airport; hence, it was the one used as a reference for the relative surveys.
The campaign has been carried out using GravLab’s CG5 relative gravity meter, with the campaign planning being based on a forth-and-back schema, starting always from a known gravity BM where the gravity was known, occupying stations, and then returning for campaign closure to the same initial BM. This allows for the compensation of residual drift during the day and its distribution in that day’s occupied stations. For the determination of the daily residual drift, assuming that during the specific campaign a number of n stations have been occupied, the residual drift was determined based on the, corrected for tides, air pressure, and temperature, observations at the initial point BM1 as:
where denotes the residual drift, and are the gravity observations in mGal at BM1 at the end of the campaign (time ) and the beginning of the campaign. Note that the drift after Equation (2) is determined in , so that after its determination, the observed gravity difference between station and the initial point , i.e.,:
where and are the observed gravity values at points BM1, being the base station, and BMi, being the densification point, can be corrected for the residual drift as
Then, the final corrected gravity for point i can be determined as:
where denotes the determined gravity at point and is the known gravity at the base BM1. Using simple error propagation, formal errors can be determined at each occupied gravity station as:
where denotes the accuracy of gravity at point , is the known accuracy of the base gravity station and the propagated error of the individual gravity observations with the CG-5 at the base and densification BMs. Assuming uncorrelated errors, Equation (6) can be further analyzed as:
where and are the individual standard deviations determined during the individual measurements at the gravity BMs. Given that the first class of measurements, i.e., the ties to the absolute stations, need to be of superior quality, since the relative densification ones will be based on those, the star method according to the measurement scheme (1-2-1) or the profile method (ABCDEDCBA) or a combination of both have been used, and the standard deviation of the measurements did not exceed 10 μGal. Moreover, the gravimeter was left alone for 10 min at each point in order to stabilize the measuring system and allow the instrument to reach the ambient temperature, and at each reference station, 6 measurements have been performed to collect at least a minimum of 5 valid measurement cycles within the 10 μGal level. During the relative densification points over Gavdos, the collected number of readings was reduced to 4 so that at least a minimum of 3 valid measurement cycles within the 10 μGal level, have been collected. Finally, the geodetic coordinates of the BMs were determined with semi-kinematic N-RTK GNSS observations using a virtual reference station as a base.
As final product, given the estimation of the final gravity at each station, gravity anomalies , free-air gravity anomalies , simple and complete Bouguer anomalies can be estimated. Gravity anomaly at each station was estimated as:
where denotes normal gravity at the level surface of the reference ellipsoid (GRS80) evaluated with Somigliana’s formula [27]. Finally, free-air gravity anomalies have been determined using a mean normal gradient of as:
where is the orthometric height of the station. Regarding the determination of orthometric heights and the vertical reference system used, this is tied to the Hellenic Vertical Datum as realized by the available GNSS/Leveling BMs over Crete and Gavdos (presented in Section 2.3). These datasets, described analytically in the sequel, will be used for the evaluation of the derived geoid models over Crete and Gavdos and form a set of available collocated GNSS/leveling observations on BMs over the entire Hellenic area. Greece does not have a unified vertical network with all orthometric heights referring to the same zero level, located in the TG station at the Piraeus harbor [28,29,30].
2.2. The New Local Gravity Database over Gavdos
In order to evaluate the results achieved during the gravity campaign, a comparison of the gravity values determined at the same gravity BMs during different occupation times and days was performed. The campaigns have been carried out in October 2018 and August 2023, the latter being solely a densification campaign over Gavdos. During the campaigns, some of the fundamental gravity BMs have been occupied over several instances; hence, observations for the same BM at different occupations are available. The main BMs investigated refer to the gravity BM of HMGS in Hora Sfakion (SFK1), TUCg, which is the main gravity BM occupied by UoH at the premises of the Technical University of Crete (TUC), SLR0, which is the main Cal/Val site at TUC, PAL1, which is the HMGS gravity BM at Palaiochora, PAL2 and PAL3, which are the UoH gravity BM in Palaiochora, coinciding with a geodetic BM by HMGS. In the latter, PAL2 refers to the gravity at the top of the BM and PAL3 at the bottom. SFK1 was occupied three times, two sequential ones on 29 September 2018 and another one on 2 October 2018. The differences between the measured gravity differences w.r.t. SLR0 were 24.5 μGal for the first two occupations during 29 September 2018, while the third one on 2 October was just 9.3 μGal apart from the former. The larger deviation of the first measurement on the 29th of September is attributed to the fact that it was the first measurement of the day after SLR0 with rainy and windy conditions, which contributed to a worst measurement, surely within the accuracy limit of the instrument. TUCg, being the UoH gravity BM at the premises of TUC in Chania, shows a relative gravity difference w.r.t. SLR0 of −3.6 μGal and 0.7 μGal, measured during two different occupation days on 2 October and 3 October 2018. PAL1, being the HMGS gravity BM in Palaiochora, has been occupied four times, i.e., two consecutive ones on 30 September and another two on 2 October and 3 October 2018. The first two agree to the 6.2 μGal level and deviate by 5 μGal to 11 μGal from the two independent ones. The latter, measured during two different days, are only within 1.4 μGal apart. PAL2 is the main UoH gravity BM in Palaiochora and coincides with the top of the HMGS geodetic BM (pillar) in the town. PAL3 is its counterpart at the base of the BM. The BMs have been occupied twice, on 1 October and 3 October 2018, and show differences of 7.9 μGal (PAL2) and 4.9 μGal (PAL3), which are within the noise level of the instrument (1σ).
With the finalization of the data processing, the final gravity values at the base and densification BMs have been determined along with the final propagated errors. During the 2018 campaign, a total number of 85 gravity benchmarks have been measured, while in the August 2023 campaign, the isle of Gavdos was densified with 20 more measurements, resulting in a total number of 105 observations over the study area (see Figure 1). In Figure 1, the entire gravity database to be used for geoid modeling is presented. Green refers to the October 2018 (line Gavdos and Crete 2018 land gravity in Table 2) campaign, and blue refers to the August 2023 (line Gavdos and Crete 2023 land gravity in Table 2) campaigns. Complementary to these, as will be discussed in Section 2.3, black denotes the reprocessed BGI shipborne gravity data (line BGI in Table 2), magenta denotes the reprocessed Morelli shipborne gravity data (line Morelli debiased in Table 2), red denotes Gravlab’s land gravity database (line Greek geoid 2010 land gravity in Table 2), gray denotes Gravlab’s marine gravity database (line Greek geoid 2010 marine gravity in Table 2), brown denotes the old SHOM marine gravity data (line SHOM marine gravity in Table 2), cyan the new SHOM marine gravity data (line SHOM new marine gravity in Table 2), yellow the SIO29.1 altimetry-derived gravity (line SIO29.1 in Table 2), and light-yellow the DTU2021 altimetry-derived gravity (line DTU2021 in Table 2).
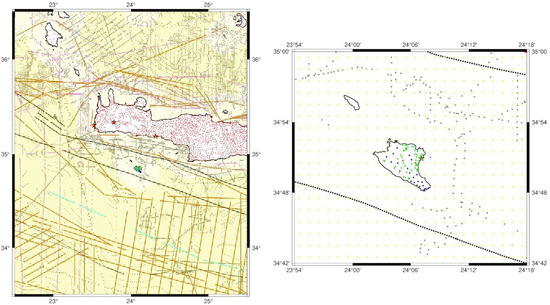
Figure 1.
The gravity database to be used for the geoid determination over Crete and Gavdos.

Table 2.
Statistics of the original gravity anomalies per database and for the entire area. Unit: [mGal].
2.3. The Gravity Database for Geoid Modeling
Complementary to the previously described local gravity data over Gavdos, an extensive database of land and marine gravity data has been generated based on archived observations in the form of free-air gravity anomalies. In all cases, the data have been unified according to the standards for the various reference systems outlined in detail in Section 2.1. We have thus selected from the available databases in the area observations within and , which is a wider area than the area denoted in the frame of the Cal/Val activities. This was necessary in order to avoid edge effects in the targeted region. The final database over the study area consists of both land and marine gravity data from various sources, which refer to the wider region.
The first database comes from the original shipborne gravity data by Morelli [31], available from the French Hydrographic and Oceanographic Office (Service Hydrographique et Océanographique de la Marine—SHOM) and the Bureau Gravimétrique Internationale (BGI) for the wider Mediterranean basin. They comprise of 2768 free-air gravity anomalies and have been processed by SHOM and BGI [32], in the frame of the GEOMED2 project [33], in an effort to compile existing biases and tilts in the Morelli database (black dots in Figure 1). An additional database comprises 2486 free-air gravity anomalies, available from the repositories of BGI, that refer to original shipborne gravity collected during various campaigns. These data sets have been processed as well by SHOM and BGI in the frame of the GEOMED2 project [33] in an effort to compile existing biases in the BGI database for the wider Mediterranean basin (magenta dots in Figure 1).
Moreover, land data from the Greek Geoid database developed by [3,15,34,35,36] within GravLab has been used, consisting of 1460 land gravity anomalies, after blunder detection and removal with LSC (red dots in Figure 1). The original data have been collected during international campaigns and international projects [37,38]. From the same Greek Geoid database (gray dots in Figure 1), a set of 17,050 marine free-air gravity anomalies is available, again after blunder detection and removal with LSC. The data have been collected during international campaigns and international projects [39,40], marine free-air gravity anomalies from GEODAS [39], marine gravity data from the digitization of Morelli’s maps [40] as well as a few absolute gravity stations over mainland Crete. It should be noted that this database consists of validated data; hence, several points from, e.g., the Morelli contour maps have been rejected.
The marine database has been augmented by archived shipborne campaigns by SHOM, consisting of 29,280 marine free-air gravity anomalies (brown dots in Figure 1), processed and cleaned by [32,41] of existing biases within the campaigns themselves with a crossover adjustment and validation against EIGEN6c4 [42]. From the same database and the GEOMED2 project [33], an additional 1223 marine gravity anomalies (cyan dots in Figure 1) are available, from campaigns that have not been included in the historical BGI and SHOM archives.
Finally, given that the area under study is not well covered over the marine areas with the existing shipborne gravity data, the DTU2021 [43] and SIO29.1 [44] global gravity models, derived from altimetry observations, have been used as fill-in. Given that the DTU2021 model incorporates SAR and SARin data from the Cryosat2 mission as well as geodetic mission data from SARAL/Altika, it was selected to use its information in coastal areas, up to 20 km from the coastline. In these areas, low-resolution mode (LRM) radar altimetry suffers the most; hence, improved information is expected from the aforementioned mission. The rest of the marine regions have been filled with SIO altimetry-derived marine gravity, resulting in a total number of 7205 observations from DTU2021 (light-yellow dots in Figure 1) and 22,543 from SIO29.1 (yellow dots in Figure 1). The complete database consists of 84,119 free-air gravity anomalies covering the land and marine areas of the study region as well as the isle of Gavdos (see Figure 1), with the variation in the gravity field being depicted in Figure 2 and the analytical statistics of the various databases being reported in Table 2.
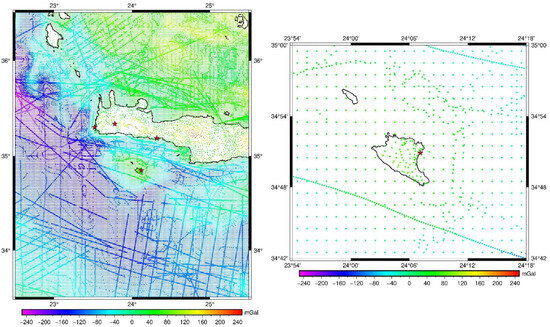
Figure 2.
The compiled land and marine gravity data for the gravimetric geoid determination over Gavdos.
2.4. GNSS/Leveling Data for Geoid Validaiton
As already mentioned, a set of GNSS/Leveling BMs were available, consisting of 121 points, two of which are located in Gavdos. The geometric heights of these BMs were determined in the frame of the organization of the Hellenic Cadastre by Ktimatologio S.A., performing a nationwide GNSS campaign to collect high-quality GNSS observations on geodetic BMs, with a mean accuracy of 2–5 cm [28]. The leveling heights correspond to orthometric heights coming from the HMGS, with their formal accuracy being at the 1–2 cm level, but, in reality, their accuracy is largely unknown [5,28,30]. Their statistics are presented in Table 3, while Figure 3 depicts their distribution. It should be noted that the geoid heights reported in Table 3 for the GNSS/Leveling data () refer to geometric ones, formed as . Of main importance for the geoid validation purposes are the two BMs located directly over Gavdos, since they are fundamental HMGS geodetic BMs and well surveyed with gravity based on the dedicated Gavdos campaigns.

Table 3.
Statistics of the available GNSS/Leveling data over Crete and Gavdos used for the gravimetric geoid validation. Unit: [m].
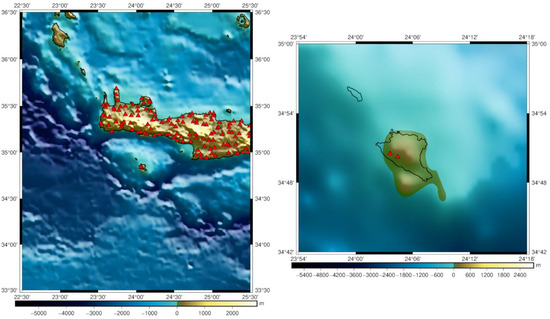
Figure 3.
Distribution of the available GNSS/Leveling data (red triangles) for the gravimetric geoid validation over Crete and Gavdos.
3. Geoid Modelling Methodology and Geoid Development
3.1. Gravity Reductions within Remove–Compute–Restore
The determination of the gravimetric geoid solution for the wider area of the calibration sites will be based on the newly acquired and historical gravity data, marine gravity data from dedicated shipborne campaigns, GNSS/Leveling observations, satellite altimetry data from DTU and SIO, and the databases on the topography and bathymetry of the region. Geoid modeling was based on the well-known RCR method [9], which, given the availability of gravity-field-related data, is based on the removal of long and short wavelengths from the input data sources. During the remove step, the low frequencies of the gravity field spectrum are represented by a GGM, which is given in the form of a spherical harmonic expansion of the potential to some degree and order. The GGM contribution has been evaluated from the EIGEN6c4 [42] and the XGM2019e [45], which are the latest combined GGMs based also on GOCE data and provide the overall best results over the Greek territory [29,30,46,47]. EIGEN6c4 uses the space-wise approach, which is a multi-step collocation procedure, to encompass GOCE data as well as terrestrial measurements for the shorter wavelengths. XGM2019e includes as data sources the satellite model GOCO06s in the longer wavelength area combined with terrestrial measurements for the shorter wavelengths. Reduced gravity anomalies have been computed as:
where
represents the contribution of the GGM. In Equation (11) a is the semi-major axis of the reference ellipsoid, M denotes Earth’s mass, G is the gravitation constant, (cosθ) are the generalized Legendre functions, the fully normalized spherical harmonic coefficients of the disturbing potential, denote degree and order of the expansion, is the co-latitude, denotes the geocentric latitude, and denotes the geocentric longitude. As evaluated in [33,48], the models can be used either to their full harmonic degree of expansion or limited to some cut-off degree. From the experiments performed in [33,48] EIGEN6c4 was found to provide optimal results when limited to an and then coupled with higher-order residual terrain model (RTM) effects, while XGM2019e is optimal when used to its full d/o of expansion . With that in mind, the reduced values based on Equation (10) were evaluated for EIGEN6c4 to d/o 1000 and 2190 and XGM2019e to its full d/o of expansion, so that reduced gravity anomalies were determined as:
within the RCR, the higher frequencies to be removed refer to the effects of the topography/bathymetry of the area under study, represented by a high-resolution digital topography and bathymetry model. The aim of the remove step is to generate a so-called residual gravity anomaly field () which will be smooth enough so that prediction can be carried out. Given that the residual gravity anomaly field has the characteristics of a stationary random signal, in essence its errors are random in nature and not systematic, so that its mean is zero or close to zero, and the prediction can be carried out with some optimal estimator [49].
Among the available topographic reduction methods, e.g., Bouguer, terrain correction, isostatic, etc., the one that will be used is the so-called residual terrain model (RTM) reduction, since it provides smooth gravity anomaly residuals. Additionally, another advantage of the RTM reduction is that the quantity to be restored in the restore step to the geoid heights, is considerably small compared to the indirect effect on the geoid from other methods (e.g., Helmert), and no assumption about isostatic compensation is needed. The RTM reduction for gravity anomalies has been evaluated following two approaches. The first one is based on the classical scheme described by [50,51], where the contribution of the topography represented by a high-resolution DTM is evaluated relative to a smooth but varying elevation surface [10,52]. For the classical RTM, the SRTM-based 3 arcsec DTM generated for the entire Greek territory by [10] is used, while the reference DTM is based on that one, using block averages to generate a smooth model based on the reduced field to be evaluated, i.e., the maximum d/o of the GGM used as reference (either d/o 1000 or 2190 in the present study). The evaluation of this step is performed within the GravSoft gravity field processing package [53]. The second technique applies the solution to the spectral filter problem of residual terrain correction (RTC) [54] using a combination of a spherical harmonic expansion of the Earth’s potential [55] and ultra-high-resolution RTC effects from a pre-computed global model [53]. In the classical RTM approach, the RTM effects on gravity are computed as [10]:
where Href represents the height of the reference surface used, H the height of the topographic masses of the computation point according to the fine resolution DTBM, E denotes the integration area, is the height of the running point, ρ is the mean density of Earth’s upper lithosphere, and the distance between the computation point (x,y,H) and the running point . In the spectral approach for the evaluation of RTM effects on gravity, the contribution is evaluated as:
where are the RTM effects from the spherical harmonic expansion of the topographic potential from the dv_ell2190 model [53] to d/o 2190 and are the ultra-high-resolution RTM effects from the ERTM2160 model [54]. Note that in the case of EIGEN6c4 and XGM2019e that the GGMs are evaluated to d/o 2190 only the second term in Equation (16) is needed, hence the spectral RTM in that case will be evaluated as:
This different evaluation is of course not a problem in the classical RTM approach, since the reference topography surface is constructed so as to correspond to the maximum degree of evaluation of the GGM (either d/o 1000 or 2190). In that sense, we have detailed two evaluations of the RTM effects with the classic approach, i.e., one corresponding to d/o from 1001 onwards, hence the reference DTM resolution is set to 11′, and another corresponding to d/o 2191 and above, hence the reference DTM resolution is set to 5′. In that case, it will be:
In Equations (15)–(19), the superscript and denote the classical and spectral RTM approaches. Given the RTM reduction and the available reduced gravity anomalies outlined in Equations (12) and (13), the residual gravity anomaly field can be computed by removing the contribution of the topography. So that from the three previously mentioned reduced fields, residual ones will be estimated as:
which will be the ones used for the estimation of the geoid.
3.2. Geoid Determination Methodology
Based on such determined residuals, the various geoid models using EIGEN6c4 to d/o 1000 and 2190 and XGM2019e as references, along with the classic and spectral RTM approaches, are to be evaluated. Among the various approaches for geoid determination, two methods, i.e., LSC and FFT, have been used. This is done for the sake of redundancy and cross-validation between the two methods. The computation step refers to the estimation of residual geoid heights (Nres) from the available Δgres, so that the determination of the final geoid can be carried out during the restore step. The latter refers to the restoration of the signals removed, i.e., to the contribution of the GGM to geoid heights and that of the topography. The final geoid model, either with LSC and FFT, was determined both on a regular 1 arcmin × 1 arcmin grid over a wider area around Gavdos ( and ), which is to serve as a reference model, as well as on the main Cal/Val stations CDN0, CRS1, GVD0, GVD0, RDK1, and SUG0. The prediction with LSC was carried out as [10]:
where is the vector of observed Δgres, is the covariance matrix of the observation, is the cross-covariance matrix computed from the observed Δgres with the predicted Nres LSC, and describes the observed residual gravity anomalies noise. To estimate the needed covariance and cross-covariance matrices, an analytical model of the covariance function that will describe the statistical characteristics of the gravity field in the area was determined. The model of [55] was used as an analytical model, which was fitted to the empirical covariance functions of the residual gravity anomaly fields. The so-derived statistical characteristics of the gravity anomalies are then used to fully populate the necessary auto- and cross-covariance matrices needed for geoid estimation so that residual geoid heights from LSC (Nres LSC) can be determined using Equation (26). Finally, the contribution of the topography to geoid heights through the RTM reduction (NRTM), either classical or spectral, and that of the EIGEN6c4 and XGM2019e GGMs (NGGM) was used to determine the final geoid as:
When FFT is to be used for the determination of the residual geoid heights, then either 1D/2D FFT [8,56] with the Wong–Gore modification for the Stokes kernel [56], after applying 100% zero padding in all directions, will be employed. In that case, the residual geoid heights are estimated from the available residual gravity anomalies as:
where denotes normal gravity, is the radius of the Earth, and the grid spacing in the latitudinal and longitudinal directions, is the band-limited Stokes kernel to the maximum degree of the GGM expansion, and and denote the number of parallels and meridians (rows and columns of the available gravity residual grid) with spacing and :
where is the classical Stokes kernel, L is the degree of expansion below which terms are to be removed, and in the Legendre polynomial, with ψ being the spherical distance between points i and j. Finally, Equation (28) becomes:
with being the direct and being the inverse FFT. The FFT geoid is determined as:
3.3. Reduction in Gravity Anomalies for the Long and Short Wavelengths
Following Equations (12)–(14), the reduced free-air gravity anomalies to EIGEN6c4 d/o 1000, EIGEN6c4 d/o 2190, and XGM2019e d/o 2190 have been computed with the statistics being reported in Table 4. As it can be seen, all models managed to reduce the std of the gravity anomalies from 78.404 mGal to 12.541 mGal for EIGEN6c4 to d/o 1000, 4.945 mGal for EIGEN6c4 to d/o 2190, and 5.399 mGal for XGM2019e to d/o 2190. Figure 4 presents the original and reduced EIGEN6c4 field when the latter is evaluated to d/o 2190. As it is expected, given the limited expansion of EIGEN6c4 to d/o, the statistical properties of the reduced field are not as smooth as when reducing to a higher d/o. The long and medium wavelength contributions of the GGMs manage to resolve most of the characteristics of the gravity field in the area, with a few rougher short-wavelength features being present over the mountainous areas of Crete (see Figure 4). For the original and reduced fields, the empirical covariance functions have been estimated as well, where a significant reduction was found. The variance drops substantially from 8399.78 mGal2 for the original gravity anomalies to only 103.08 mGal2 for EIGEN6c4 to d/o 1000, 12.89 mGal2 for EIGEN6c4 to d/o 2190, and 16.58 mGal2 for XGM2019e to d/o 2190. Among the two GGM evaluations to d/o 2190, EIGEN6c4 provides slightly smoother reduced values compared to XGM2019e, with the std being smaller by 0.45 mGal, the mean by 0.12 mGal, and the range by 9.2 mGal, showing that in this first assessment, EIGEN6c4 might be the preferable solution to be used as a reference field (see Table 4). The same holds for the variance computed in the empirical covariance functions, with EIGEN6c4 having a smaller variance by ~3.7 mGal2 while its correlation length is 3.79 km and that of XGM2019e 4.54 km.

Table 4.
Statistics of the original gravity anomalies, EIGEN6c4 and XGM2019 contributions, and reduced gravity anomalies. Units: [mGal].
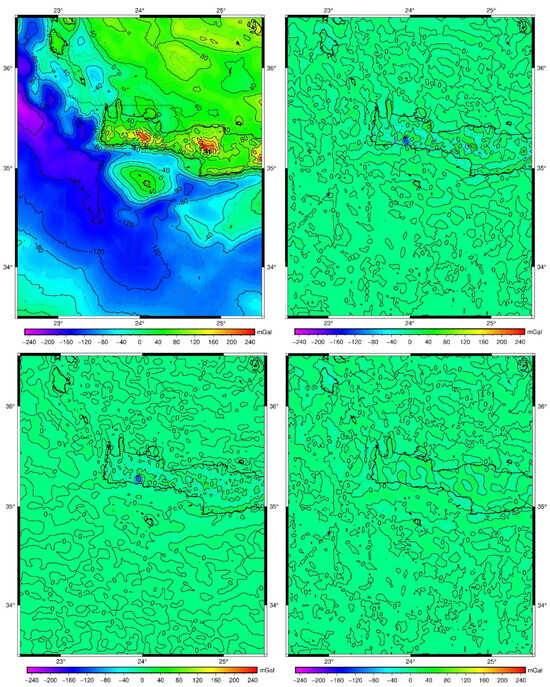
Figure 4.
Original (top left), reduced to EIGEN6c4 d/o 2190 (top right), classical RTM contribution (bottom left) and residual field to EIGEN6c4 d/o 2190 and classical RTM (bottom right).
For the computation of the residuals outlined in Equations (20)–(26), the already reduced fields have been treated for the contribution of the topography, so that in essence the RTM effects corresponding to degrees 1001–90,000 are removed from the reduced signal relative to EIGEN6c4 to d/o 1000 and the RTM effects corresponding to degrees 2191–90,000 are removed from the reduced signals relative to EIGEN6c4 and XGM2019e to d/o 2190. As already mentioned, both the classical and spectral approaches for the estimation of the RTM effects have been evaluated, with their statistics being reported in Table 5 and the effects being depicted in Figure 4, along with the residuals, for EIGEN6c4 to d/o 2190 and the classical RTM approach. For the sake of convenience, the first column in Table 5 reports the GGM that has been used as reference in each of the residual fields. From the spatial representation of the RTM effects, it became evident that both the classical and spectral RTM approaches ( and )) represent larger wavelengths when evaluated from d/o 1001, which can be seen from the larger std of the RTM effects in Table 5. The ultra-high degree topographic effects are represented by for the classical and have a much smaller signal power and depict the same features. The statistics of all six sets of residual gravity anomalies are summarized in Table 5, where it is apparent that they all have, within the sub-mGal level, a comparable performance in terms of the mean value. For EIGEN6c4 to d/o 2190, the reduced field has a mean of −0.479 mGal and a std of 4.945 mGal (see Table 4), which for the classical RTM are reduced to −0.215 mGal and 4.519 mGal, while the spectral RTM improves the mean by 0.03 mGal and provides a larger std by 0.07 mGal. The aforementioned statistics dictate that the statistical characteristics of the EIGEN6c4 residuals are practically the same, with none of the two approaches being superior. For XGM2019e, the results are comparable with a slightly worse std compared to EIGEN6c4 by ~0.5 mGal std. The mean of the reduced field is lower by 0.27 and 0.29 mGal and the std by 0.33 and 0.26 mGal for the classic and spectral RTM residual fields. Between the classic and spectral RTM residuals, the ones with the classic approach provide a smaller std, while the spectral one provides a smaller mean value. The residual fields are practically the same and have mean values that are very close and below the mGal level, which implies that the residual fields are unbiased. In terms of the std of the residual fields, these are quite close to the error of the input gravity data, which for the historical ones has been estimated to the 4.7 mGal level [34,35].

Table 5.
Statistics of the various RTM effects and residual gravity anomalies. Units: [mGal].
In the case of the reduced gravity to EIGEN6c4 to d/o 1000 (see Table 4), the mean and the std are significantly reduced with both RTM approaches (see Table 5). In the classical RTM approach, the mean reduces to −0.47 mGal while the spectral approach reaches a std of −0.257, which is close to the one when EIGEN6c4 to d/o 2190 is used. Given that the reduced gravity to EIGEN6c4 to d/o 1000 has a much larger std, the classical RTM reduces the std only to 9.663 mGal, which is much higher compared to all other residual fields. The spectral RTM manages to reduce it further by 3.6 mGal, being at the 6.089 mGal level, which is again higher than those of the residuals when the higher-order GGMs are used. This shows that the EIGEN6c4 residual fields, when the GGM is evaluated to d/o 1000, are slightly not as smooth as the rest and may lead to inferior geoid estimates.
Moreover, the empirical covariance functions of all six residual fields have been determined and depicted in Figure 5. From Figure 5, it becomes clear that the residuals to EIGEN6c4 to d/o 1000 have a much larger variance even after the removal of the topographic effects: 63.12 mGal2 when the classical (denoted as RF after [50]) RTM is used and 29.13 mGal2 when the spectral (denoted as HK after [54]) one is employed. The fact that the classical RTM does not manage to reduce the data as the spectral one does is attributed to the limitations of the DTM/DBM and the method itself given a high d/o expansion of the GGM. Figure 5 also depicts (right plot) a zoomed version of the empirical covariance function of the residuals to EIGEN6c4 and XGM2019e to d/o 2190 up to a spherical distance of 0.5o to better present their behavior. The aforementioned conclusions are based on the statistics of the residual fields and are confirmed by the covariance functions as well, with the EIGEN6c4 residuals providing the smaller variances, 11.97 mGal2 and 11.88 mGal2 for the spectral and classical RTM, compared to XGM2019e, 15.78 mGal2 and 16.57 mGal2 for the spectral and classical RTM, respectively. The correlation lengths of the empirical covariance functions are 4.53 km (EIGEN6c4 to d/o 2190 and classical RTM), 3.78 km (EIGEN6c4 to d/o 2190 and spectral RTM), 5.35 km (XGM2019e to d/o 2190 and classical RTM), 4.71 km (XGM2019e to d/o 2190 and spectral RTM), 5.36 km (EIGEN6c4 to d/o 1000 and classical RTM), and 8.06 km (EIGEN6c4 to d/o 1000 and spectral RTM). Among the models with the smaller variance, the residuals to EIGEN6c4 with the classic RTF approach have the smaller std, and the ones with the spectral RTM have the smaller mean. Hence, these two datasets will be the ones used as references for the geoid modeling investigations.
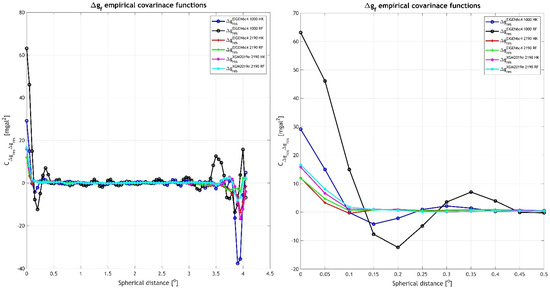
Figure 5.
Empirical covariance functions of the residual gravity anomaly fields after reduction to EIGEN6c4 (d/o 1000 and 2190), XGM2019e (d/o 2190) and the removal of RTM effects with the classic (RF) and spectral (HK) approach.
3.4. Geoid Model Development and Validation
The first set of tests for the geoid determination has been performed by carrying out a 2D-FFT evaluation of the Stokes kernel with a Wong–Gore modification. For all FFT methods, the available residual gravity fields need to be gridded; hence, a common 1′ × 1′ grid has been compiled, on which the six residual fields have been gridded. Gridding has been carried out in each case with kriging, given its similarities to LSC, employing the individual variances and correlation lengths of the empirical covariance functions previously described. It should be noted that for the newly acquired gravity data, the formal observation errors have been used, while for the historical data, a mean error of 4.7 mGal was adopted, as previously described. The followed procedure conveniently propagates prediction errors so that the error field of the gridded data can be estimated as well. As expected, given the smaller std and variance, the smaller prediction errors were found for EIGEN6c4 to d/o 2190, with classic and spectral RTM performing equally well.
As already mentioned, the geoid models determined have been evaluated against the set of 121 GNSS/Leveling BMs; hence, first an evaluation of the optimal cut-off degrees of the Wong–Gore kernel was investigated. This was carried out by evaluating various harmonic degrees for the tapering, and then evaluating the differences to the GNSS/Leveling data. From the results acquired, the optimal ones were reached for tapering between degrees 100 and 120, providing a mean of 6.7 cm and a std of 16.6 cm. From these results, and especially the mean, it is also evident that the solutions are almost unbiased, as the differences between the GNSS/Leveling data are within the few cm level, whereas the previous version of the geoid model had a bias of 1.059 m with respect to the same leveling data [3]. The latter was due to inconsistencies in the metadata information for the GNSS and Leveling data and the apparent non-homogeneity of their vertical reference system. In any case, the above is a good proof that all the data pre-processing for datum homogenization, in terms of the horizontal, vertical, and gravity reference systems, has been carried out with proper care. The remaining, small, bias is attributed to the bias of the Hellenic vertical datum relative to the conventional used as a reference. The differences are formed in all cases as hence, the negative difference implies that the Greek vertical datum is above the IAG conventional global geoid. The same evaluation was performed for all other residual fields, after evaluation with a 2D-FFT and the Wong–Gore modification in the band 100–120, with their statistics being presented in Table 6. As it can be seen, the EIGEN6c4 d/o 2190 solution with the evaluation of the RTM effects with the classic approach provides the overall smallest std at the 16.3 cm level, while the mean is at the 7.4 cm. The EIGEN6c4 d/o 2190 solution with the spectral RTM effects provides a slightly inferior solution in terms of the std, but this is statistically insignificant. The XGM2019e solutions are slightly inferior by 3–6 mm compared to the EIGEN6c4 to d/o 2190, while those when using EIGEN6c4 to d/o 1000 and then RTM effects look to have a significant bias at the ~15 cm level.

Table 6.
Statistics of the geoid height differences between the various 2D-FFT Wong–Gore gravimetric geoid models and the GNSS/Leveling data. Units: [m].
Useful insights on the solutions can be gained by the determined geoid heights from all 2D-FFT solutions at the Cal/Val stations over mainland Crete and Gavdos (see Table 7). A first conclusion is that when EIGEN6c4 is used to d/o 1000 and then coupled with RTM effects for the higher frequencies, it provides individual station estimates that differ significantly from the others. This can be seen for the CDN station, for which the EGIEN6c4 to d/1000 and classical RTM effects geoid differs by 5–8 cm from the rest. For the EIGEN6c4 solutions using the GGM to d/o 2190, the estimated geoid heights agree at the 0.5–3 cm level, which is a great proof on the consistency of the solutions and the homogeneity of the 2D-FFT method.

Table 7.
Geoid heights at the Cal/Val stations from the various 2D-FFT Wong–Gore gravimetric geoid models. Units: [m].
A final validation of the 2D-FFT solutions was performed at the two HMGS triangulation BMs that are located over Gavdos. As mentioned in the prequel, among the available GNSS/Leveling data used for the validation of the geoid models, two of them are located over the isle of Gavdos. They belong to the HMGS map-chart 245 (called “ΝHΣOΣ ΓAΥΔOΣ”—“Gavdos island”), and their point ids are 245004 and 245005. Point 245004 is a first-order triangulation BM, while 245005 is a fourth-order one. Based on the online archives of HGMS (https://www.gys.gr/hmgs-geoindex.html, accessed on 30 September 2023) the first-order point is declared decommissioned and/or destroyed; hence, its observations (ellipsoidal and orthometric height) might be problematic. Table 8 presents the estimated geoid heights at the two triangulation BMs after interpolation from the 2D-FFT predicted grid with LSC. It can be seen that the overall best agreement is found once again for the EIGEN6c4 geoid models when the GGM is used to its full expansion. Between the spectral and the classical RTM effects, the latter seem to provide better statistics at the few mm level.

Table 8.
Geoid height differences at the two HMGS triangulation BMs over Gavdos from the various 2D-FFT Wong–Gore, 1D-FFT, and LSC gravimetric geoid models. Units: [cm].
The next set of tests referred to the use of the 1D-FFT approach with no modification to the Stokes kernel, given the small size of the area under study, and an infinite integration radius; hence, all data are used for the computation. The same residual gravity fields as in the 2D-FFT case have been employed. For all FFT methods, the same six 1 arcmin residual fields have been used, as described in the previous step. Table 9 presents the statistics of the differences between the various 1D-FFT gravimetric geoid models and the available GNSS/Leveling data, where it can be seen that the solutions are improved by 1–2 cm compared to the 2D-FFT ones, with EIGEN6c4 (d/o 2190 and classical RTM effects) providing the overall smallest std at the 15.1 cm level with a mean of −1.6 cm. Table 10 summarizes the geoid height estimates at the Cal/Val sites, which compared to the 2D-FFT estimates show variations at the 4–6 cm level, especially for the solutions with the classical RTM effects. To quantify these large differences, the mean sea surface (MSS) values at the CRS1, GVD8, RDK1, and SUG0 stations have been provided by GeoMatLab and used in collocation with a dynamic ocean topography (DOT) model for the area based on GOCE data from [3]. In essence, these experiments combined geoid heights from the gravimetric geoid and DOT data to match the MSS recorded independently from the TG stations, since their combination should yield . It should be noted that these DOT values referred to the old GRS80 and not used in this study, so the DOT values need to be corrected for a bias of 26 cm. As it can be seen in Table 11, the agreement of the estimated with 1D-FFT gravimetric geoid using EIGEN6c4 to d/o 2190 and the classical RTM effects with respect to the measured MSS values at the Cal/Val sites is at the 1–4 cm level, showing the overall great performance of the derived geoid model. Finally, the derived 1D-FFT models are compared in terms of the differences at the two GNSS/Leveling BMs over Gavdos, with the statistics being summarized in Table 8. As it can be seen, the two solutions, when the classical RTM effects are used, are superior to the rest and provide agreement to the GNSS/Leveling of the order of 1 cm. For the sake of completeness, Figure 6 depicts the geoid model that provides the overall best results, being the one relying on EIGEN6c4 with the classical RTM effects, along with the differences to the GNSS/Leveling data and its propagated errors. Given that FFT does not allow the propagation of errors, the image displays the propagated errors of the interpolated residual gravity anomalies after the interpolation with kriging.

Table 9.
Statistics of the geoid height differences between the various 1D-FFT gravimetric geoid models and the GNSS/Leveling data. Units: [m].

Table 10.
Geoid heights at the Cal/Val stations from the various 1D-FFT gravimetric geoid models. Units: [m].

Table 11.
Geoid heights at the Cal/Val stations from the EIGEN6c4 (d/o 2190 and classical RTM effects) 1D-FFT gravimetric geoid model, DOT for the stations based on GOCE data, and MSS from the tide-gauge records. Units: [m].
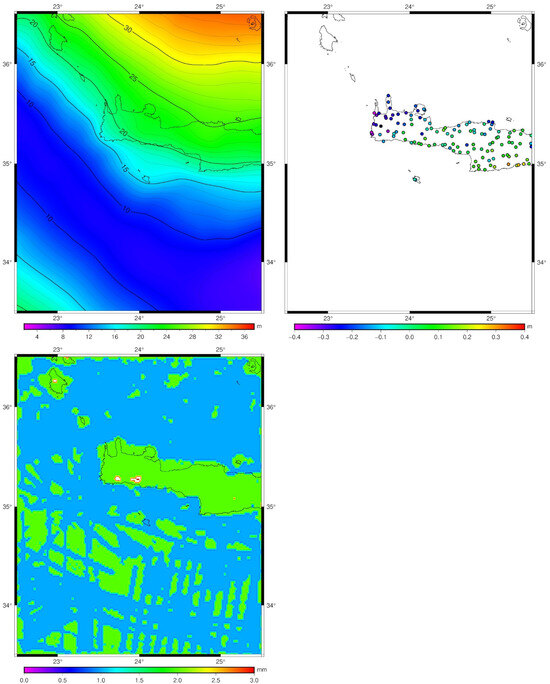
Figure 6.
The final 1D-FFT gravimetric geoid model (EIGEN6c4 to d/o 2190 and classical RTM effects), its differences to the GNSS/Leveling data and the propagated geoid errors.
Following the FFT-based geoid development, the LSC-based solutions have been carried out. As the first step in the LSC geoid modeling, the analytical covariance function model was fitted to the empirical model. This has been done for the residuals to EIGEN6c4 (d/o 2190) using the classical RTM approach, resulting in an analytical model with a variance of 11.89 mGal2 and a correlation length of 4.46 km. The fit of the analytical model resulted in a depth to Bjerhammar’s sphere of −2.40804 km and a scale factor of 0.3466. LSC-based geoid determination has been carried out only with the gravity residuals of the best of the FFT-based models, i.e., EIGEN6c4 with classical RTM effects, as it was the one that provided the overall best fit to the GNSS/Leveling BMs. Two scenarios have been examined, one where an area-wide computation has been carried out for the entire area under study, employing all 84,119 irregular gravity observations. In that scenario, the geoid model for the entire area is determined along with a prediction at the six Cal/Val stations (CDN0, CRS1, GVO0, GVD8, RDK1, and SUG0). In the second scenario, the LSC prediction is carried out for each individual station separately using irregular gravity data within a 1° area in its vicinity. Given the correlation length of 4.46 km of the analytical covariance function, selecting data at 0.5° (~55 km) around the station is deemed as more than enough, given that at these distances the covariance is practically zero, hence data farther than that do not contribute to the solution.
Around each station, residual gravity data referenced to EIGEN6c4 to d/o 2190 and classic RTF effects have been collected, with the collected residual gravity anomalies being 9135 for CDN0, 9516 for CRS1, 8130 for GVD0 and GVD8, 7043 for RDK1, and 7838 for SUG0. Table 12 tabulates the predicted, with both area-wide LSC and local LSC, geoid heights at the Cal/Val stations along with their prediction error, while also the misclosure to the MSS values at the CRS1, GVD8, RDK1, and SUG0 stations, using the previously mentioned DOT, is also reported. As it can be seen, the predictions for all stations and both 1D-FFT (see Table 10) and LSC are very close to each other and within the 1–2 cm level, which practically confirms the consistency of the two methods followed and the results achieved. Given the accuracy of the gravity data used, which for the historical campaigns is estimated at the 4–5 mGal level, the achieved agreement within the 1–2 cm level is considered more than satisfactory and within the foreseen levels to be used in altimetry Cal/Val.

Table 12.
Statistics of the final 1D-FFT and LSC-based geoid heights, the associated prediction errors, differences with the GNSS/Leveling data and differences over the entire area with the 1D-FFT gravimetric geoid. Units: [m].
During the second LSC geoid determination scenario, LSC is used to carry out geoid determination for the entire area under study, employing all 84,119 irregular gravity observations. Once again, the gravity residuals to EIGEN6c4 to d/o2190 using the classical RTM effects have been employed, as has the analytical covariance function discussed above. Figure 7 depicts the final LSC-based geoid for the entire area under study, along with the associated prediction errors and differences to the GNSS/Leveling data, with the statistics being tabulated in Table 12. It should be noted that the statics of the geoid errors are at the few mm level, which can be regarded as quite optimistic, but they reflect the availability of very dense and high-quality gravity data for the geoid estimation. From the statistics of the differences to the available GNSS/Leveling data of the LSC geoid (see Table 12), a std at the 15.4 cm level is found, which is comparable to that of the 1D-FFT solution. In fact, from the same table it can be seen that the std of the differences between the two geoid models, i.e., the 1D-FFT and the LSC ones, is at the 1.2 cm level, while for most of the area the difference is a constant bias by 4.2 cm, which can be seen as well with the largest bias of the LSC solution to the GNSS/Leveling data. Of course, this bias is still small and can be handled during the fit to the GNSS/leveling data in the parametric fit of the models.
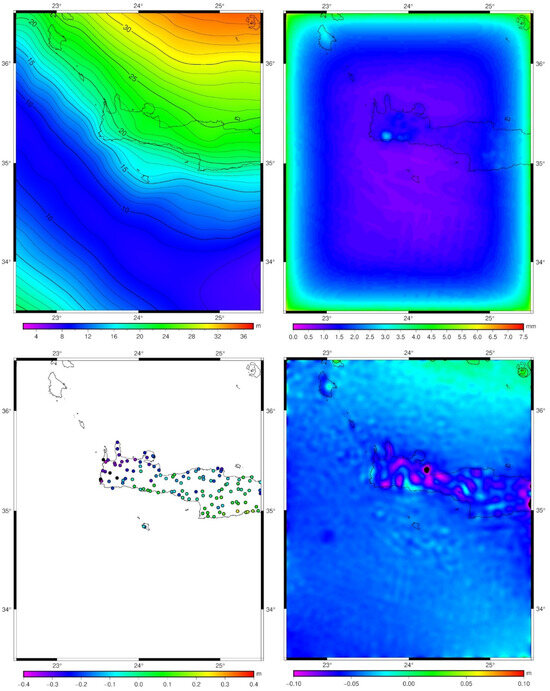
Figure 7.
The final LSC (area wide) gravimetric geoid model (top left), associated error (top right), its differences to the GNSS/Leveling data (bottom left) and differences to the 1D-FFT geoid (bottom right).
From Figure 7, it can be seen that the main differences are located over the western mountainous part of mainland Crete, which is attributed to the few gravity data available over that region, which influence mainly the LSC-based geoid, given also the small correlation length. As in the cases for the 1D-FFT geoid model and the local LSC one, an analytical prediction employing all available gravity data has been performed for the Cal/Val stations during the area-wide LSC solution. The statistics of the predictions are tabulated in Table 13 along with their prediction errors, while also the misclosure to the MSS values at the CRS1, GVD8, RDK1, and SUG0 stations, using the previously mentioned DOT, is also reported. From that table, it can be seen that the LSC-based geoid solution provides the overall best results with the Cal/Val stations, giving the smallest residuals when combined with the DOT and MSS data and the smaller prediction errors. A final note for the LSC-based geoid refers to the comparison with the two HMGS BMs over Gavdos, namely BMs 245004 and 245005, where the LSC geoid gives a geoid height difference of −6.1 cm and +1.7 cm, respectively (see Table 8), which is comparable to the 1D-FFT solution.

Table 13.
Geoid heights and their errors at the Cal/Val stations from the local LSC around each station, and area-wide LSC, and differences to the MSS from the tide-gauge records. Units: [m].
3.5. Geoid Model Validation and Fit to the Greek Vertical Reference Frame
To quantify the improvement in the new gravimetric geoid models, the differences to the available GNSS/Leveling data have been used. The validation of the geoid model was performed through the comparisons with available GNSS/Leveling observations on land previously described by estimating absolute and relative differences between all formed baselines with the GNSS/Leveling data ), as an additional validation to the evaluation of the statistics of the differences and especially the mean and standard deviation presented in Section 3.4 [29,30]. Additionally, the formed vectors of observations and differences between the gravimetric and GNSS/Leveling geoid heights are used in a deterministic least-squares adjustment using various parametric models, e.g., first-, second-, or third-order polynomial ones, bias and tilt models, and similarity transformation ones [28,29]. It should be stressed that the result after the adjustment of the hybrid geoid model is not a gravimetric geoid model anymore, but it can be adjusted to fit the Greek leveling network; hence, it can probably form a surface from which geoid heights fitted to the GNSS/Leveling data will be derived. Moreover, as also pointed out by [29,30,57], over-parameterization of the least-squares fit, by, e.g., selecting a third-order polynomial model results in model parameters with no physical meaning, as in most cases a simple bias and tilt model is enough to describe the differences in the vertical reference systems between leveling, GNSS, and a gravimetric geoid. Nevertheless, such over-parametrization can be beneficial [58,59] as it removes any systematic differences and provides stochastic residual differences that can be modeled by LSC to provide a hybrid, deterministic, and stochastic fit of the gravimetric geoid to the GNSS/Leveling data in support of surveying and engineering applications.
The geoid models validated were the 1D-FFT geoid using EIGEN6c4 (d/o 2190 and classical RTM effects) and the corresponding LSC-based geoid. In the evaluation process, many parametric models have been assessed and evaluated, both absolute and relative differences of the geoid models under investigation. In the sequel, we discuss only the statistics after the fit to a third-order polynomial model, since it offered the overall best minimization of the residual differences after the fit. From the residuals to the GNSS/Leveling data (see Figure 6 and Figure 7 as well as Table 9 and Table 12), it is evident that the GNSS/Leveling data in the northern part of Crete, i.e., not in the vicinity of the Cal/Val sites, show some strong negative residuals. Therefore, first a 2σ test has been carried out in order to remove any blunders. It should be noted that a less strict 3σ was not carried out, as all residuals are within the 3σ limit. After the 2σ to the 1D-FFT geoid, 5 BMs that reside only in the north-west part of Crete are removed. The residuals after the fit have an improved std at the 14.0 cm level, which improves the results of the 1D-FFT gravimetric geoid, hence showing that part of the large differences is due to the low-quality of the GNSS/Leveling data. From the fit to the parametric models, the simple NS-tilt and EW-tilt ones drop the std of the fitted residuals to 10.1 cm and 11.2 cm, respectively, the 4-parameter and 5-parameter ones to 9.2 cm, the second-order polynomial to 8.6 cm, and the third-order polynomial to 7.6 cm. Given that the accuracy of the GNSS/Leveling data is largely unknown, but assumed at the 3–4 cm level, the fitted geoid reaches the 1–3 cm level accuracy, which is the foreseen accuracy level. This also confirms the very good fit of the selected 1D-FFT gravimetric geoid with the two GNSS/Leveling BMs over the isle of Gavdos, where cm-level accuracy has been found. From the adjusted residual geoid height differences, the determined corrector surface has been computed as well, which can be used to fit the gravimetric geoid model to the GNSS/Leveling data for the entire area under study. It is interesting to notice that the third-order polynomial corrector surface provides a small correction of the order of ±10 cm for the wider Gavdos and Crete area, showing the conformity of the solution to the GNSS/Leveling data.
Of interest are the absolute and relative differences of the adjusted residuals as well, since they show the performance of the gravimetric geoid model relative to the GNSS/Leveling data baseline length and can provide a quantitative measure of its accuracy. The original gravimetric geoid with the 1D-FFT approach has a relative accuracy of 11.6 ppm (1.2 cm/km) for baselines between 0 and 10 km, which reduces to 10.80 ppm (1.1 cm/km) for the fitted geoid (see Figure 8). These results show that even for such short baselines, the gravimetric geoid and its fitted version are well within the 1 cm/km accuracy level in terms of the differences with the GNSS/Leveling data. Of course, for larger baselines, the relative error drops quickly below the 1 cm/km error and reaches the 1 mm/km for baselines larger than 80 km. In terms of the absolute differences to the GNSS/Leveling data, for the 1D-FFT gravimetric geoid, 26.8% of the differences are below the 1 cm level and 52.0% below the 2 cm one. For the hybrid 1D-FFT geoid, these statistics improve drastically to 53.2% below the 1 cm level and 81.2% below the 2 cm one.
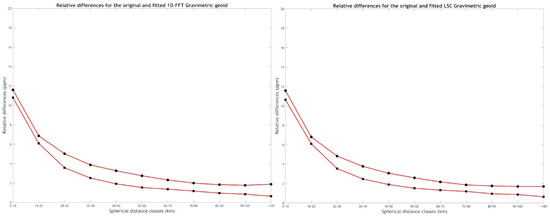
Figure 8.
Relative differences in the original 1D-FFT gravimetric (circles) and fitted with the third-order polynomial (squares) geoid (left) and the original LSC gravimetric (circles) and fitted with the third-order polynomial (squares) geoid (right).
The same evaluation process has been carried out for the LSC-based geoid model, assessing for all the aforementioned parametric models both the absolute and relative differences against the GNSS/Leveling data. Once again, the same set of GNSS/Leveling data in the northern part of Crete, i.e., not in the vicinity of the Cal/Val sites, have been removed after a 2σ test, removing again only 5 BMs. The residuals after the fit have an improved std at the 12.9 cm level, which is significantly better than that of the 1D-FFT geoid, and it shows once again that the main part of the rather large differences is due to the low-quality of the GNSS/Leveling data. From the fit to the parametric models, it was found that the simple NS-tilt and EW-tilt ones drop the std of the fitted residuals to 9.4 cm and 10.9 cm, respectively, which is about 1 cm better than that of the 1D-FFT geoid. The 4-parameter and 5-parameter ones drop the std to 8.8 cm (~0.5 cm better than the 1D-FFT), while the second-order polynomial to 8.3 cm and the third-order polynomial to 7.5 cm. It should be noted that the improved LSC geoid relative to the 1D-FFT one is the smallest for the fit after the third-order polynomial, but this is due to the over-parametrization of that model, which manages to model most of the residual differences. Once again, given that the accuracy of the GNSS/Leveling data is largely unknown but assumed at the 3–4 cm level, the fitted LSC geoid reaches the 1–3 cm level accuracy, which is the foreseen accuracy level by the project. This also confirms the very good fit of the LSC gravimetric geoid with the two GNSS/Leveling BMs over the isle of Gavdos, where cm-level accuracy has been found. For the LSC-geoid, the third-order polynomial corrector surface provided again a small correction of the order of ±5–10 cm for the wider Gavdos and Crete area, showing the conformity of the solution to the GNSS/Leveling data. The absolute and relative differences have been determined as well, both for the original model and after the fit with the third-order polynomial deterministic model. Before fit, the LSC-based geoid reaches relative accuracies of 11.58 ppm for baselines as short as 0–10 km, which improves to 10.63 ppm after the fit (see Figure 8). These results are slightly superior to the ones achieved with the 1D-FFT geoid, but being at the 0.2 ppm (2 mm/km) level, they are considered negligible. For larger baselines, the relative error drops quickly below the 1 cm/km error and is below the 1 mm/km level for baselines larger than 80 km. In Figure 8, where the relative differences for the two fitted geoid models, 1D-FFT and LSC, with the third-order polynomial model are depicted, it can be seen that indeed, for all baseline lengths, the LSC-based geoid manages to provide equal or better performance than the 1D-FFT solution, despite the fact that it is insignificant. Finally, for the LSC gravimetric geoid, 28.4% of the differences are below the level and 55.2% below the 2 one, which is about 2–3% better than the 1D-FFT model. For the hybrid LSC geoid, these statistics improve drastically to 52.8% below the level and 81.1% below the 2 one.
4. Conclusions
The aim of this investigation has been the determination of an analytical gravimetric geoid model for the area of Crete and Gavdos with a 1 arcmin resolution in support of the continuous altimetry Cal/Val activities in the region. Various geoid models have been determined, investigating different GGMs to model the long wavelength part of the spectrum and two approaches to treat the terrain through RTM effects towards the modeling of the short wavelength part of the spectrum using the RCR technique. Two main approaches with various variants have been used to estimate geoid heights, namely a spectral FFT-based and a stochastic LSC-based one. Within each of them, different variants have been tested, like 2D-FFT, 1D-FFT, local LSC and global LSC. These various methodologies and approaches have been evaluated in order to validate both their coherency and final achievable internal and external accuracy.
From the results achieved and the various gravimetric geoid models estimated, two of them have been considered as the optimal ones to be used within the Cal/Val activities. Both geoid solutions stem from the gravity residuals using EIGEN6c4 to d/o 2190 as a reference model and the classical RTM approach, in which in one case the 1D-FFT approach is used, while in the other the estimation is carried out with the area-wide LSC. The latter provides approximately the same results as the local LSC around each Cal/Val station, as the 1–2 cm difference between the two is not considered statistically significant, given the quality of the historical gravity data and that of the GNSS/Leveling observations, against which the geoid models are validated.
For the Cal/Val activities, it is recommended to use the LSC-based gravimetric geoid, as when geoid height values are needed at points where altimetric sea surface heights are available, then a direct estimation can be carried out without the need to interpolate from the estimated geoid grid (as happens in the 1D-FFT case). Moreover, prediction errors can be estimated; hence, the estimated geoid heights can be accompanied by their respective errors to be used in the Cal/Val error propagation.
The final geoid model, given the accuracy of the GNSS/Leveling observations used for its validation, reaches the desired 1–3 cm level accuracy. In terms of the absolute differences to the GNSS/Leveling data per baseline length, the LSC-based geoid provides 28.4% of the differences below the level and 55.2% below the 2 one, while after fit these statistics improve drastically to 52.8% below the level and 81.1% below the 2 one. In terms of the relative differences, the LSC-based geoid reaches relative accuracies of 11.58 ppm (1.2 cm) for baselines as short as 0–10 km, which improves to 10.63 ppm (1.1 cm) after the fit. For larger baselines, the relative error drops to 6 mm/km error for baselines between 10 and 20 km and is below the 1 mm/km level for baselines larger than 80 km. It can thus provide the basis for improved representations of the local gravity field and geoid variations in the vicinity of the Cal/Val stations and over the study area in general.
Author Contributions
Conceptual design of the experiment and analysis, I.N.T., G.S.V. and S.M.; Gravity campaign data acquisition G.S.V., I.N.T., D.P. and X.F.; gravity reductions and geoid estimation by FFT and LSC I.N.T. and G.S.V.; geoid validation G.S.V. and I.N.T.; writing—original draft preparation, I.N.T. and G.S.V.; writing—review and editing, S.M., D.P., X.F. and C.D.; visualization, G.S.V.; supervision, I.N.T.; project administration, S.M., C.D. and I.N.T.; funding acquisition, S.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the European Space Agency (ESA) in the frame of the FRM4S6 Project (4000129892/20/NL/FF/ab) project.
Data Availability Statement
The GNSS/Leveling data have been provided by the Hellenic Cadastre S.A. in the frame of a memorandum of understanding with the Department of Geodesy and Surveying, AUTH. Global Geopotential Models have been downloaded from the ICDEM service (http://icgem.gfz-potsdam.de/, accessed on 30 September 2023). The topography and bathymetry model used for the evaluation of the topographic effects have ben compiled by the authors in [15]. Historical gravity data over the area are available by BGI and SHOM (https://bgi.obs-mip.fr/, accessed on 30 September 2023) through the GEOMED2 project. The data collected during the gravity surveys over Crete and Gavdos are available on request from the authors.
Acknowledgments
The work and efforts of M.-F. Lequentrec-Lalancette and C. Salaűn at the French Hydrographic and oceanographic Office (Service Hydrographique et Océanographique de la Marine—SHOM); S. Bonvalot and F. Reinquin at Bureau Gravimétrique Internationale (BGI) and S. Bruinsma at Centre National d’Etudes Spatiales (CNES), in homogenizing, adjusting and cleaning historical gravity data, also within GEOMED2, is greatly appreciated.
Conflicts of Interest
Author Dimitrios Piretzidis was employed by the company Space Geomatica P.C. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Sjöberg, L.E.; Abrehdary, M. Geoid or Quasi-Geoid? A Short Comparison. In X Hotine-Marussi Symposium on Mathematical Geodesy HMS 2022; Freymueller, J.T., Sánchez, L., Eds.; International Association of Geodesy Symposia; Springer: Berlin/Heidelberg, Germany, 2023; Volume 155. [Google Scholar] [CrossRef]
- Sánchez, L.; Barzaghi, R.; Vergos, G. Operational Infrastructure to Ensure the Long-Term Sustainability of the International Height Reference System and Frame (IHRS/IHRF); International Association of Geodesy Symposia; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2024. [Google Scholar] [CrossRef]
- Tziavos, I.N.; Vergos, G.S.; Mertikas, S.P.; Daskalakis, A.; Grigoriadis, V.N.; Tripolitsiotis, A. The contribution of local gravimetric geoid models to the calibration of satellite altimetry data and an outlook of the latest GOCE GGM performance in GAVDOS. Adv. Space Res. 2013, 51, 1502–1522. [Google Scholar] [CrossRef]
- Mertikas, S.P.; Ioannides, R.T.; Tziavos, I.N.; Vergos, G.S.; Hausleitner, W.; Frantzis, X.; Tripolitsiotis, A.; Partsinevelos, P.; Andrikopoulos, D. Statistical Models and Latest Results in the Determination of the Absolute Bias for the Radar Altimeters of Jason Satellites using the Gavdos Facility. Mar. Geod. 2010, 33, 114–149. [Google Scholar] [CrossRef]
- Mertikas, S.P.; Donlon, C.; Kokolakis, C.; Piretzidis, D.; Cullen, R.; Féménias, P.; Fornari, M.; Frantzis, X.; Tripolitsiotis, A.; Bouffard, J.; et al. The ESA Permanent Facility for Altimetry Calibration in Crete: Advanced Services and the Latest Cal/Val Results. Remote Sens. 2024, 16, 223. [Google Scholar] [CrossRef]
- Andritsanos, V.D.; Vergos, G.S.; Tziavos, I.N.; Pavlis, E.C.; Mertikas, S.P. A high resolution geoid for the establishment of the GAVDOS multi-satellite calibration site. In Gravity Geoid and Geodynamics 2000, Proceedings of the GGG2000 IAG International Symposium, Banff, AB, Canada, 31 July–4 August 2000; Sideris, M.G.S., Ed.; International Association of Geodesy Symposia; Springer: Berlin/Heidelberg, Germany, 2001; Volume 123, pp. 347–354. [Google Scholar] [CrossRef]
- Lemoine, F.G.; Kenyon, S.C.; Factor, J.K.; Trimmer, R.G.; Pavlis, N.K.; Chinn, D.S.; Cox, C.M.; Klosko, S.M.; Luthcke, S.B.; Torrence, M.H.; et al. The Development of the joint NASA GSFC and NIMA Geopotential Model EGM96; Technical Paper NASA/TP-1998-206861; National Aeronautics and Space Administration: Greenbelt, MD, USA, 1998; 575p.
- Sideris, M.G. Geoid Determination by FFT Techniques. In Geoid Determination: Theory and Methods; Lecture Notes in Earth System Sciences; Springer: Berlin/Heidelberg, Germany, 2013; Volume 110, pp. 453–516. [Google Scholar] [CrossRef]
- Sansò, F.; Sideris, M.G. The Local Modelling of the Gravity Field by Collocation. In Geoid Determination: Theory and Methods; Lecture Notes in Earth System Sciences; Springer: Berlin/Heidelberg, Germany, 2013; Volume 110, pp. 203–258. [Google Scholar] [CrossRef]
- Tscherning, C.C. Geoid Determination by 3D Least-Squares Collocation. In Geoid Determination: Theory and Methods; Lecture Notes in Earth System Sciences; Springer: Berlin/Heidelberg, Germany, 2013; Volume 110, pp. 311–336. [Google Scholar] [CrossRef]
- Sansò, F. Observables of physical geodesy and their analytical representation. In Geoid Determination: Theory and Methods; Sansò, F., Sideris, M.G., Eds.; Lecture Notes in Earth System Sciences; Springer: Berlin/Heidelberg, Germany, 2013; Volume 110. [Google Scholar] [CrossRef]
- Mertikas, S.P.; Pavlis, E.C.; Tziavos, I.N.; Koutroulis, E.; Palamartchoul, K.; Papadopoulos, T.; Vergos, G.S. Permanent facility for calibration/validation of satellite altimetry: GAVDOS. In Remote Sensing of the Ocean and Sea Ice 2004; SPIE: Bellingham, WA, USA, 2004; Volume 5569, pp. 14–25. [Google Scholar] [CrossRef]
- Andritsanos, V.D.; Tziavos, I.N. Estimation of Gravity Field Parameters by a Multiple Input/Output System. Phys. Chem. Earth Part A Solid Earth Geod. 2000, 25, 39–46. [Google Scholar] [CrossRef]
- Mertikas, S.; Daskalakis, A.; Hausleitner, W.; Tziavos, I.N.; Vergos, G.S.; Zervakis, V.; Partsinevelos, P.; Frantzis, X.; Andrikopoulos, D.; Tripolitsiotis, A. Calibration of satellite radar altimeters at Gavdos Cal/Val facility using three different methodologies. In Proceedings of the ESA Living Planet Symposium, Bergen, Norway, 28 June–2 July 2010. ESA Special Publication SP-686. [Google Scholar]
- Tziavos, I.N.; Vergos, G.S.; Grigoriadis, V.N. Investigation of topographic reductions and aliasing effects to gravity and the geoid over Greece based on various digital terrain models. Surv. Geophys. 2010, 31, 23–67. [Google Scholar] [CrossRef]
- Pail, R.; Goiginger, H.; Schuh, W.D.; Höck, E.; Brockmann, J.M.; Fecher, T.; Gruber, T.; Mayer-Gürr, T.; Kusche, J.; Jäggi, A.; et al. Combined satellite gravity field model GOCO01S derived from GOCE and GRACE. Geophys. Res. Lett. 2010, 37, L20314. [Google Scholar] [CrossRef]
- Pavlis, N.K.; Holmes, S.A.; Kenyon, S.C.; Factor, J.K. The Development and Evaluation of the Earth Gravitational Model 2008 (EGM2008). J. Geophys. Res. Solid Earth 2012, 117, 8916. [Google Scholar] [CrossRef]
- Mertikas, S.P.; Zhou, X.; Qiao, F.; Daskalakis, A.; Lin, M.; Peng, H.; Tziavos, I.N.; Vergos, G.; Tripolitsiotis, A.; Frantzis, X. First preliminary results for the absolute calibration of the Chinese HY-2 altimetric mission using the CRS1 calibration facilities in West Crete, Greece. Adv. Space Res. 2015, 57, 78–95. [Google Scholar] [CrossRef]
- Mertikas, S.P.; Donlon, C.; Féménias, P.; Mavrocordatos, C.; Galanakis, D.; Tripolitsiotis, A.; Frantzis, X.; Tziavos, I.N.; Vergos, G.; Guinle, T. Fifteen Years of Cal/Val Service to Reference Altimetry Missions: Calibration of Satellite Altimetry at the Permanent Facilities in Gavdos and Crete, Greece. Remote Sens. 2018, 10, 1557. [Google Scholar] [CrossRef]
- Mertikas, S.; Donlon, C.; Féménias, P.; Mavrocordatos, C.; Galanakis, D.; Tripolitsiotis, A.; Frantzis, X.; Kokolakis, C.; Tziavos, I.N.; Vergos, G.; et al. Absolute Calibration of the European Sentinel-3A Surface Topography Mission over the Permanent Facility for Altimetry Calibration in west Crete, Greece. Remote Sens. 2018, 10, 1808. [Google Scholar] [CrossRef]
- Mertikas, S.P.; Donlon, C.; Femenias, P.; Mavrocordatos, C.; Galanakis, D.; Guinle, T.; Boy, F.; Tripolitsiotis, A.; Frantzis, X.; Tziavos, I.N.; et al. Absolute Calibration of Sentinel-3A and Jason-3 Altimeters with Sea-Surface and Transponder Techniques in West Crete, Greece. In Fiducial Reference Measurements for Altimetry, Proceedings of the International Review Workshop on Satellite Altimetry Cal/Val Activities and Applications, Chania, Greece, 23–26 April 2018; Mertikas, S., Pail, R., Eds.; International Association of Geodesy Symposia; Springer: Cham, Switzerland, 2019; Volume 150. [Google Scholar] [CrossRef]
- Morelli, C.; Gantar, C.; Honkasalo, T.; McConnell, R.K.; Tanner, I.G.; Szabo, B.; Uotila, U.; Whalen, C.T. The International Gravity Standardisation Net 1971 (IGSN71); IAG: Paris, France, 1974. [Google Scholar]
- Wilmes, H.; Vitushkin, L.; Pálinkáš, V.; Falk, R.; Wziontek, H.; Bonvalot, S. Towards the Definition and Realization of a Global Absolute Gravity Reference System. In International Symposium on Earth and Environmental Sciences for Future Generations, Proceedings of the IAG General Assembly, Prague, Czech Republic, 22 June–2July 2015; Freymueller, J.T., Sánchez, L., Eds.; International Association of Geodesy Symposia; Springer: Cham, Switzerland, 2016; Volume 147, pp. 25–29. [Google Scholar] [CrossRef]
- Moritz, H. Geodetic Reference System 1980. J. Geod. 2000, 74, 128–133. [Google Scholar] [CrossRef]
- Ekman, M. Impacts of geodynamic phenomena on systems for height and gravity. Bull. Geod. 1989, 63, 281–296. [Google Scholar] [CrossRef]
- Ekman, M. The permanent problem of the permanent tide. What to do with it in geodetic reference systems? Bull. Inf. Marées Terr. 1996, 125, 9508–9513. [Google Scholar]
- Heiskanen, W.A.; Moritz, H. Physical Geodesy; WH Freeman: San Francisco, CA, USA, 1967. [Google Scholar]
- Kotsakis, C.; Katsambalos, K.; Ampatzidis, D. Estimation of the zero-height geopotential level in a local vertical datum from inversion of co-located GPS, leveling and geoid heights: A case study in the Hellenic islands. J. Geod. 2012, 86, 423–439. [Google Scholar] [CrossRef]
- Vergos, G.S.; Grigoriadis, V.N.; Tziavos, I.N.; Kotsakis, C. Evaluation of GOCE/GRACE Global Geopotential Models over Greece with Collocated GPS/Levelling Observations and Local Gravity Data. In Gravity, Geoid and Height Systems, Proceedings of the IAG Symposium GGHS2012, Venice, Italy, 9-12 October 2012; Marti, U., Ed.; International Association of Geodesy Symposia; Springer: Cham, Switzerland, 2014; Volume 141, pp. 85–92. [Google Scholar] [CrossRef]
- Vergos, G.S.; Erol, B.; Natsiopoulos, D.A.; Grigoriadis, V.N.; Işık, M.S.; Tziavos, I.N. Preliminary Results of GOCE-Based Height System Unification between Greece and Turkey over Marine and Land Areas. Acta. Geod. Geophys. 2018, 53, 61–79. [Google Scholar] [CrossRef]
- Allan, T.D.; Morelli, C. A Geophysical Study of the Mediterranean Sea; Technical Reports; NATO Subcommittee on Oceanographic Research: Paris, France, 1971; Volume 55, p. 141. [Google Scholar]
- Lequentrec-Lalancette, M.F.; Salaűn, C.; Bonvalot, S.; Rouxel, D.; Bruinsma, S. Exploitation of Marine Gravity Measurements of the Mediterranean in the Validation of Global Gravity Field Models. In International Symposium on Earth and Environmental Sciences for Future Generations, Proceedings of the IAG General Assembly, Prague, Czech Republic, 22 June–2 July 2015; Freymueller, J.T., Sánchez, L., Eds.; International Association of Geodesy Symposia; Springer: Cham, Switzerland, 2016; Volume 147. [Google Scholar] [CrossRef]
- Barzaghi, R.; Carrion, D.; Vergos, G.S.; Tziavos, I.N.; Grigoriadis, V.N.; Natsiopoulos, D.A.; Bruinsma, S.; Reinquin, F.; Seoane, L.; Bonvalot, S.; et al. GEOMED2: High-Resolution Geoid of the Mediterranean. In International Symposium on Advancing Geodesy in a Changing World, Proceedings of the IAG Scientific Assembly, Kobe, Japan, 30 July–4 August 2017; International Association of Geodesy Symposia; Springer: Cham, Switzerland, 2018; Volume 149. [Google Scholar] [CrossRef]
- Vergos, G.S.; Tziavos, I.N.; Andritsanos, V.N. On the Determination of Marine Geoid Models by Least-Squares Collocation and Spectral Methods Using Heterogeneous Data. In A Window on the Future of Geodesy, Proceedings of the International Association of Geodesy IAG General Assembly, Sapporo, Japan, 30 June–11 July 2003; Sansò, F., Ed.; International Association of Geodesy Symposia; Springer: Berlin/Heidelberg, Germany, 2005; Volume 128. [Google Scholar] [CrossRef]
- Vergos, G.S.; Tziavos, I.N.; Andritsanos, V.N. Gravity Data Base Generation and Geoid Model Estimation Using Heterogeneous Data. In Gravity, Geoid and Space Missions, Proceedings of the GGSM 2004 IAG International Symposium, Porto, Portugal, 30 August–3 September 2004; Jekeli, C., Bastos, L., Fernandes, J., Eds.; International Association of Geodesy Symposia; Springer: Berlin/Heidelberg, Germany, 2005; Volume 129. [Google Scholar] [CrossRef]
- Grigoriadis, V. Geodetic and Geophysical Approximation of the Earth’s Gravity Field and Applications in the Hellenic Area. Ph.D. Thesis, Aristotle University of Thessaloniki, Thessaloniki, Greece, 2009. [Google Scholar]
- Casten, U.; Makris, J. Erkundung der Krustenstruktur von Kreta Durch Detaillierete Schwere-und Magnetfeldmessung-gen; Project Report; Ca 83/8-1 bis 3 Ma 719/54-1 bis 3; DFG: Bonn, Germany, 2001. [Google Scholar]
- Lagios, E.; Chailas, S.; Hipkin, R.G. Newly compiled gravity and topographic data banks of Greece. Geophys. J. Int. 1996, 126, 287–290. [Google Scholar] [CrossRef]
- National Geophysical Data Center. GEODAS Marine Trackline Geophysics—Gravity, Bathymetry, Seismic, Geo-Physical Data; National Geophysical Data Center: Boulder, CO, USA, 2001. [Google Scholar]
- Behrend, D.; Denker, H.; Schmidt, K. Digital gravity data sets for the Mediterranean Sea derived from available maps. BGI Bull. D’ Inf. 1996, 78, 31–39. [Google Scholar]
- Lequentrec-Lalancette, M.F.; Rouxel, D. Comparison of a Marine Gravimetric Geoid and Global Satellite Model in the Atlantic Ocean. In ESA Living Planet Symposium; Lacoste-Francis, H., Ed.; ESA: Paris, France, 2010; Volume 686, p. 499. ISBN 978-92-9221-250-6. [Google Scholar]
- Förste, C.; Bruinsma, S.; Abrikosov, O.; Jean-Michel, L.; Marty, J.C.; Flechtner, F.; Balmino, G.; Barthelmes, F.; Biancale, R. EIGEN-6C4 the Latest Combined Global Gravity Field Model Including GOCE Data up to Degree and Order 2190 of GFZ Potsdam and GRGS Toulouse; GFZ Data Services; ICGEM: Potsdam, Germany, 2014. [Google Scholar] [CrossRef]
- Andersen, O.B.; Knudsen, P. The DTU17 Global Marine Gravity Field: First Validation Results. In Fiducial Reference Measurements for Altimetry, Proceedings of the International Review Workshop on Satellite Altimetry Cal/Val Activities and Applications, Chania, Greece, 23–26 April 2018; Mertikas, S., Pail, R., Eds.; International Association of Geodesy Symposia; Springer: Cham, Switzerland, 2019; Volume 150. [Google Scholar] [CrossRef]
- Sandwell, D.T.; Müller, R.D.; Smith, W.H.F.; Garcia, E.; Francis, R. New global marine gravity model from CryoSat-2 and Jason-1 reveals buried tectonic structure. Science 2014, 346, 65–67. [Google Scholar] [CrossRef]
- Zingerle, P.; Pail, R.; Gruber, T.; Oikonomidou, X. The combined global gravity field model XGM2019e. J. Geod. 2000, 94, 66. [Google Scholar] [CrossRef]
- Grigoriadis, V.N.; Andritsanos, V.D.; Natsiopoulos, D.A.; Vergos, G.S.; Tziavos, I.N. Geoid Studies in Two Test Areas in Greece Using Different Geopotential Models towards the Estimation of a Reference Geopotential Value. Remote Sens. 2023, 15, 4282. [Google Scholar] [CrossRef]
- Natsiopoulos, D.A.; Mamagiannou, E.G.; Pitenis, E.A.; Vergos, G.S.; Tziavos, I.N. GOCE Downward Continuation to the Earth’s Surface and Improvements to Local Geoid Modeling by FFT and LSC. Remote Sens. 2023, 15, 991. [Google Scholar] [CrossRef]
- Grigoriadis, V.N.; Vergos, G.S.; Barzaghi, R.; Carrion, D.; Koç, Ö. Collocation and FFT-based geoid estimation within the Colorado 1 cm geoid experiment. J. Geod. 2021, 95, 52. [Google Scholar] [CrossRef]
- Moritz, H. Advanced Physical Geodesy, 2nd ed.; Wichmann: Karlsruhe, Gremany, 1980. [Google Scholar]
- Forsberg, R. A Study of Terrain Corrections, Density Anomalies and Geophysical Inversion Methods in Gravity Field Modelling; Rep. No. 355; Ohio State University: Columbus, OH, USA, 1984. [Google Scholar]
- Tziavos, I.N.; Sideris, M.G. Topographic Reductions in Gravity and Geoid Modeling. In Geoid Determination: Theory and Methods; Sansò, F., Sideris, M., Eds.; Lecture Notes in Earth System Sciences; Springer: Berlin/Heidelberg, Germany, 2013; Volume 110. [Google Scholar] [CrossRef]
- Forsberg, R.; Tscherning, C.C. An Overview Manual for the GRAVSOFT Geodetic Gravity Field Modelling Programs, 2nd ed.; DTU Space: Kongens Lyngby, Denmark, 2008. [Google Scholar]
- Rexer, M.; Hirt, C.; Bucha, B.; Holmes, S. Solution to the spectral filter problem of residual terrain modelling (RTM). J. Geod. 2018, 92, 675–690. [Google Scholar] [CrossRef]
- Hirt, C.; Kuhn, M.; Claessens, S.; Pail, R.; Seitz, K.; Gruber, T. Study of the earth′s short-scale gravity field using the ERTM2160 gravity model. Comput. Geosci. 2014, 73, 71–80. [Google Scholar] [CrossRef]
- Tscherning, C.C.; Rapp, R.H. Closed Covariance Expressions for Gravity Anomalies, Geoid Undulations, and Deflections of the Vertical Implied by Anomaly Degree Variance Models; Rep. No 208; Department of Geodetic Science and Surveying, The Ohio State University: Columbus, OH, USA, 1974; pp. 1–89. [Google Scholar]
- Haagmans, R.; de Min, E.; von Gelderen, M. Fast Evaluation of Convolution Integrals on the Sphere Using 1D FFT, and a Comparison with Existing Methods for Stokes’ Integral. Man. Geod. 1993, 18, 227–241. [Google Scholar]
- Wong, L.; Gore, R. Accuracy of Geoid Heights from Modified Stokes Kernels. Geophys. J. Int. 1969, 18, 81–91. [Google Scholar] [CrossRef]
- Vergos, G.S.; Grebenitcharsky, R.S.; Al-Qahtani, A.; Al-Shahrani, S.; Natsiopoulos, D.A.; Al-Jubreen, S.; Tziavos, I.N.; Golubinka, J. Development of the National Gravimetric Geoid Model for the Kingdom of Saudi Arabia. In Gravity, Positioning and Reference Frames; REFAG 2022; Freymueller, J.T., Sánchez, L., Eds.; International Association of Geodesy Symposia; Springer: Cham, Switzerland, 2023; Volume 156. [Google Scholar] [CrossRef]
- Grebenitcharsky, R.S.; Vergos, G.S.; Al-Shahrani, S.; Al-Qahtani, A.; Iuri, G.; Othman, A.; Aljebreen, S. Hybrid Geoid Modeling for the Kingdom of Saudi Arabia. In Gravity, Positioning and Reference Frames; REFAG 2022; Freymueller, J.T., Sánchez, L., Eds.; International Association of Geodesy Symposia; Springer: Cham, Switzerland, 2023; Volume 156. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).