Aboveground Biomass Mapping in SemiArid Forests by Integrating Airborne LiDAR with Sentinel-1 and Sentinel-2 Time-Series Data
Abstract
1. Introduction
2. Materials
2.1. Study Area
2.2. Field Data
2.3. Remote-Sensing Data Acquisition and Preprocessing
2.3.1. UAV-LiDAR Data
2.3.2. Sentinel Data
3. Methods
3.1. Predictor Variables
3.1.1. LiDAR Metrics
3.1.2. Sentinel-1 Metrics
3.1.3. Sentinel-2 Metrics
3.2. Modelling Methods
3.3. Modeling Framework and Accuracy Evaluation
4. Results
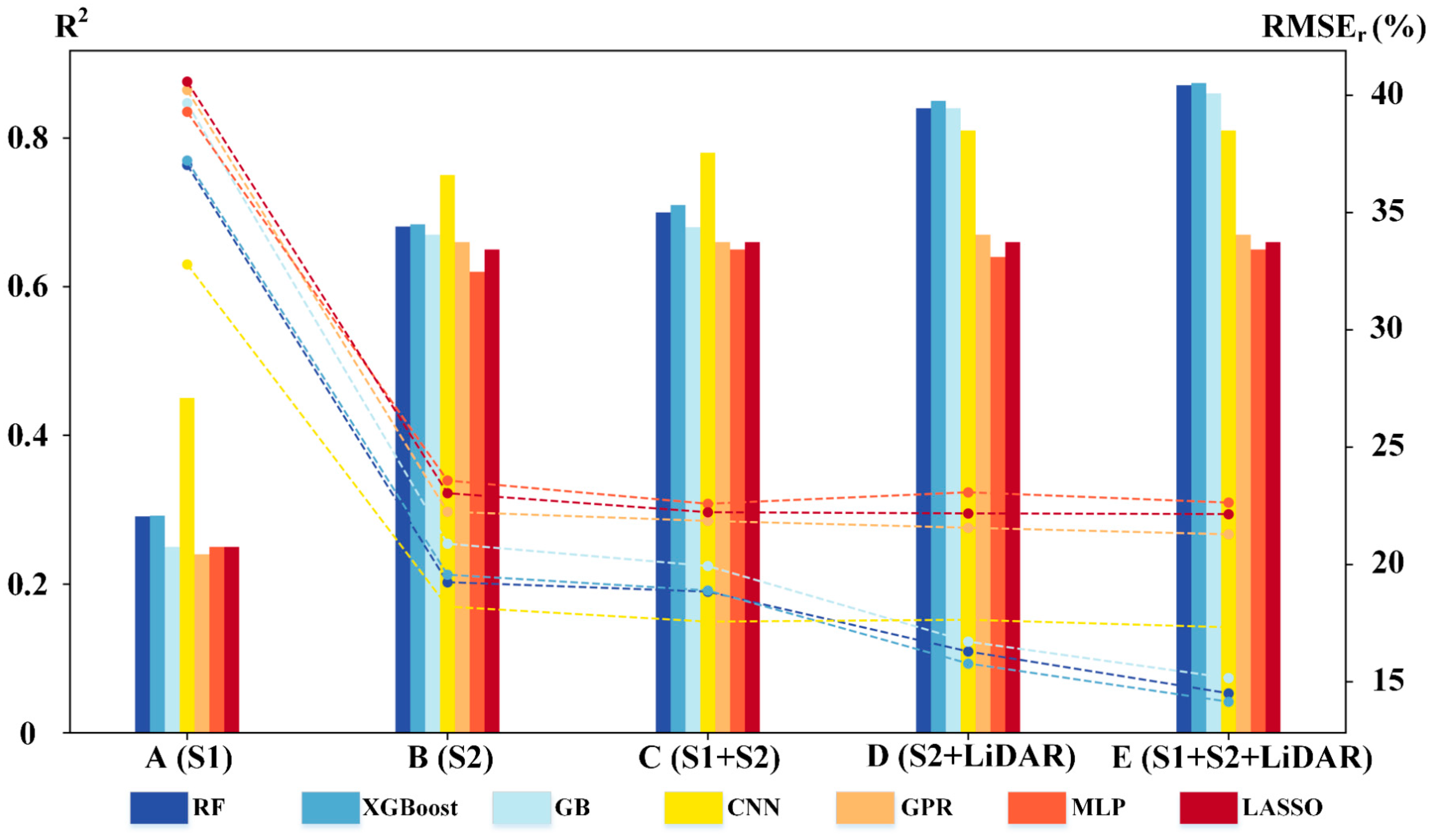
4.1. Effectiveness of Prediction Models and Data Sources for AGB Estimation
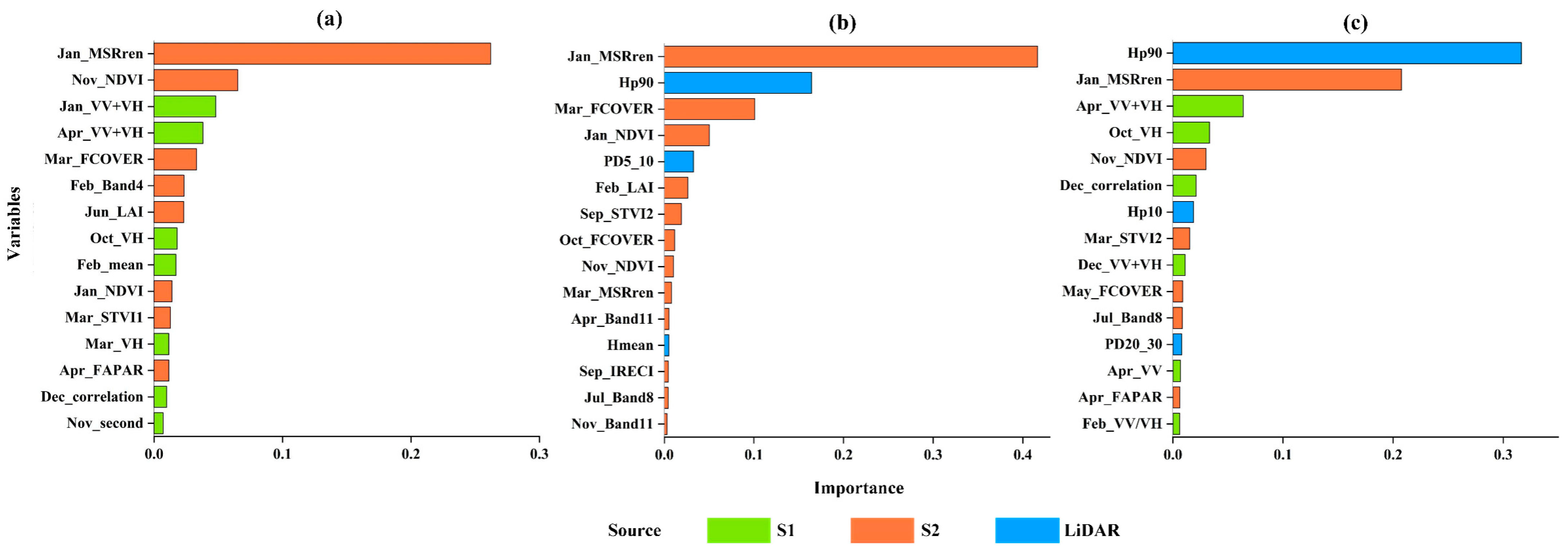
4.2. Optimal Variables and Image Acquisition Time to Model AGB
4.3. Spatial Distribution of AGB
5. Discussion
5.1. Difference Data Sources for Modeling AGB
5.2. Performance of Prediction Models
5.3. Contribution of Predictor in Estimating AGB
5.4. Impact of Seasonality on Data Selection
6. Conclusions
- (1)
- Multi-temporal S2 (S2annual) demonstrated superior accuracy compared to S1 (S1annual), and the complementary use of the two types of data (S1S1annual) obtained better prediction performance. The addition of single-temporal LiDAR variables with rich vertical structure information further enhanced the AGB estimation accuracy (S2Li vs S2annual and S1S2Li vs S1S2ananul). Moreover, single-temporal LiDAR variables are more informative than yearly monthly time-series S1, despite the temporal nature of S1 (S1S2annual vs S2Li and S2Li vs S1S2Li);
- (2)
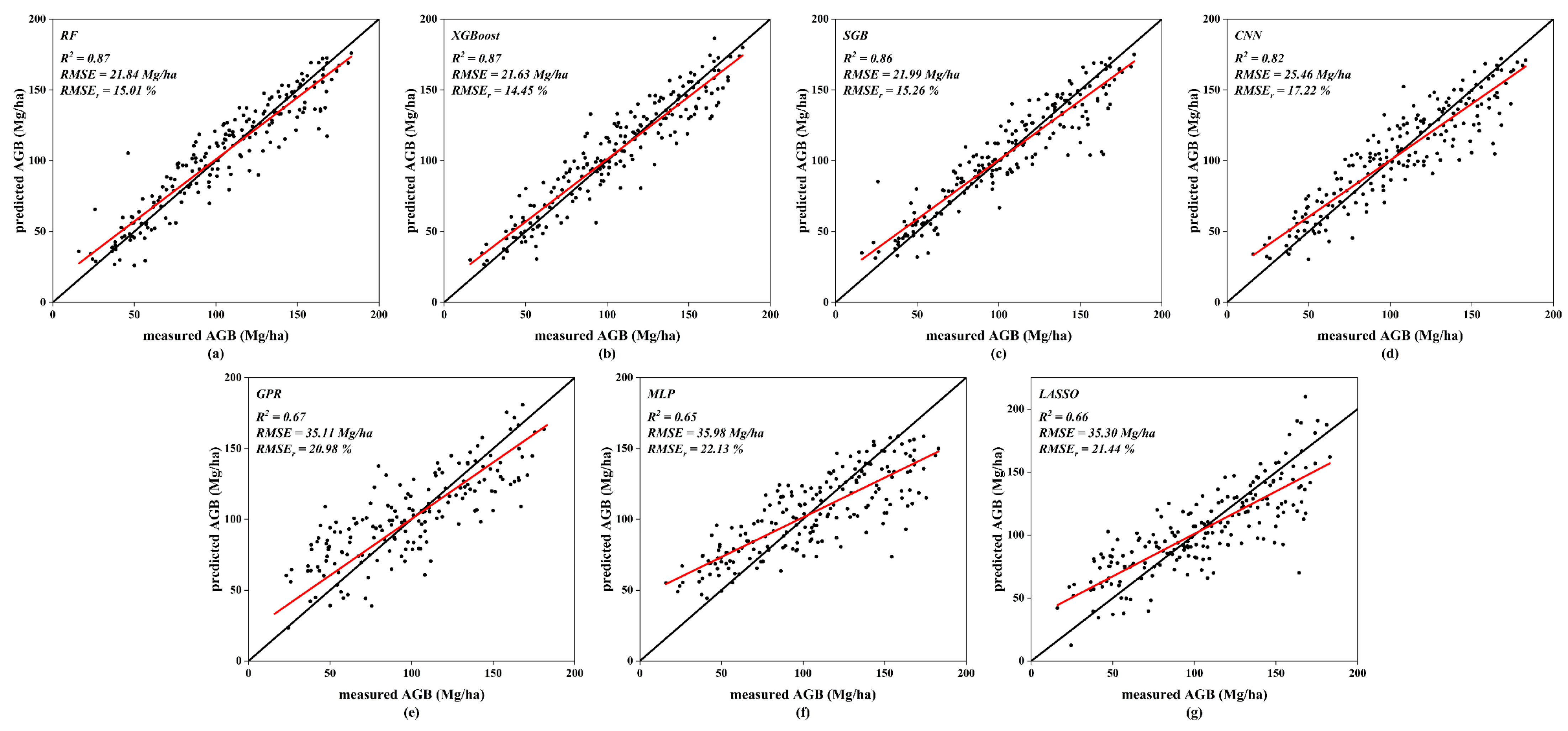
- Compared with other tested machine-learning algorithms, XGBoost produced the best performance with the optimal combination of data sources (S1, S2, and LiDAR) (R2 = 0.87, RMSE = 21.63 Mg/ha, and RMSEr = 14.45%). The superior performance of the tree-based models demonstrated their robustness, stability, and flexibility;
- (3)
- The variables sum (VV + VH) in S1 and the texture information based on VH (e.g., correlation and mean) were determined as sensitive to AGB mapping. The most-contributing S2 predictors were considered to be MSRren, NDVI, and FCOVER. Among the LiDAR metrics, the height-related Hp90 was the most important factor. These variables have been proven to be applicable for AGB mapping in semiarid forests;
- (4)
- Semiarid forests are characterized by distinct dry seasons and climatic variations. The variables obtained during the dry season were more conducive to estimating AGB than those obtained during the rainy season, regardless of whether optical or SAR data were used. This finding made it less necessary for S2 to acquire cloud-free images in the challenging rainy season in dry forests.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhao, H.; Li, Z.; Zhou, G.; Qiu, Z.; Wu, Z. Site-Specific Allometric Models for Prediction of Above- and Belowground Biomass of Subtropical Forests in Guangzhou, Southern China. Forests 2019, 10, 862. [Google Scholar] [CrossRef]
- Herold, M.; Román-Cuesta, R.M.; Mollicone, D.; Hirata, Y.; Van Laake, P.; Asner, G.P.; Souza, C.; Skutsch, M.; Avitabile, V.; MacDicken, K. Options for monitoring and estimating historical carbon emissions from forest degradation in the context of REDD+. Carbon Balance Manag. 2011, 6, 13. [Google Scholar] [CrossRef]
- Lu, D.; Chen, Q.; Wang, G.; Liu, L.; Li, G.; Moran, E. A survey of remote sensing-based aboveground biomass estimation methods in forest ecosystems. Int. J. Digit. Earth 2016, 9, 63–105. [Google Scholar] [CrossRef]
- Schröder, J.M.; Ávila Rodríguez, L.P.; Günter, S. Research trends: Tropical dry forests: The neglected research agenda? For. Policy Econ. 2021, 122, 102333. [Google Scholar] [CrossRef]
- Mora, F.; Jaramillo, V.J.; Bhaskar, R.; Gavito, M.; Siddique, I.; Byrnes, J.E.K.; Balvanera, P. Carbon Accumulation in Neotropical Dry Secondary Forests: The Roles of Forest Age and Tree Dominance and Diversity. Ecosystems 2018, 21, 536–550. [Google Scholar] [CrossRef]
- Akindele, S.O.; LeMay, V.M. Development of tree volume equations for common timber species in the tropical rain forest area of Nigeria. For. Ecol. Manag. 2006, 226, 41–48. [Google Scholar] [CrossRef]
- Baldi, G.; Verón, S.R.; Jobbágy, E.G. The imprint of humans on landscape patterns and vegetation functioning in the dry subtropics. Glob. Chang. Biol. 2013, 19, 441–458. [Google Scholar] [CrossRef]
- Diodato, L.; Fuster, A. Composition of insect assemblage canopy of subtropical dry forests of Semiarid Chaco, Argentina. Caldasia 2016, 38, 197–210. [Google Scholar] [CrossRef]
- Gasparri, N.I.; Parmuchi, M.G.; Bono, J.; Karszenbaum, H.; Montenegro, C.L. Assessing multi-temporal Landsat 7 ETM+ images for estimating above-ground biomass in subtropical dry forests of Argentina. J. Arid Environ. 2010, 74, 1262–1270. [Google Scholar] [CrossRef]
- Santos, C.A.G.; do Nascimento, T.V.M.; da Silva, R.M. Analysis of forest cover changes and trends in the Brazilian semiarid region between 2000 and 2018. Environ. Earth Sci. 2020, 79, 418. [Google Scholar] [CrossRef]
- Tiessen, H.; Feller, C.; Sampaio, E.V.S.B.; Garin, P. Carbon sequestration and turnover in semiarid savannas and dry forest. Clim. Chang. 1998, 40, 105–117. [Google Scholar] [CrossRef]
- He, Z.B.; Yang, J.J.; Du, J.; Zhao, W.Z.; Liu, H.; Chang, X.X. Spatial variability of canopy interception in a spruce forest of the semiarid mountain regions of China. Agric. For. Meteorol. 2014, 188, 58–63. [Google Scholar] [CrossRef]
- Cunliffe, A.M.; Brazier, R.E.; Anderson, K. Ultra-fine grain landscape-scale quantification of dryland vegetation structure with drone-acquired structure-from-motion photogrammetry. Remote Sens. Environ. 2016, 183, 129–143. [Google Scholar] [CrossRef]
- Mensah, S.; Lokossou, C.J.M.; Assogbadjo, A.E.; Kakaï, R.G. Seasonal variation of environment and conspecific density-dependence effects on early seedling growth of a tropical tree in semi-arid savannahs. Glob. Ecol. Conserv. 2023, 43, e02455. [Google Scholar] [CrossRef]
- Rejou-Mechain, M.; Tymen, B.; Blanc, L.; Fauset, S.; Feldpausch, T.R.; Monteagudo, A.; Phillips, O.L.; Richard, H.; Chave, J. Using repeated small-footprint LiDAR acquisitions to infer spatial and temporal variations of a high-biomass Neotropical forest. Remote Sens. Environ. 2015, 169, 93–101. [Google Scholar] [CrossRef]
- Du, L.M.; Pang, Y.; Wang, Q.; Huang, C.Q.; Bai, Y.; Chen, D.S.; Lu, W.; Kong, D. A LiDAR biomass index-based approach for tree- and plot-level biomass mapping over forest farms using 3D point clouds. Remote Sens. Environ. 2023, 290, 113543. [Google Scholar] [CrossRef]
- Naik, P.; Dalponte, M.; Bruzzone, L. Prediction of Forest Aboveground Biomass Using Multitemporal Multispectral Remote Sensing Data. Remote Sens. 2021, 13, 1282. [Google Scholar] [CrossRef]
- Dube, T.; Mutanga, O. Evaluating the utility of the medium-spatial resolution Landsat 8 multispectral sensor in quantifying aboveground biomass in uMgeni catchment, South Africa. ISPRS J. Photogramm. Remote Sens. 2015, 101, 36–46. [Google Scholar] [CrossRef]
- Baig, S.; Qazi, W.A.; Akhtar, A.M.; Waqar, M.M.; Ammar, A.; Gilani, H.; Mehmood, S.A. Above Ground Biomass Estimation of Dalbergia sissoo Forest Plantation from Dual-Polarized ALOS-2 PALSAR Data. Can. J. Remote Sens. 2017, 43, 297–308. [Google Scholar] [CrossRef]
- Hayashi, M.; Motohka, T.; Sawada, Y. Aboveground Biomass Mapping Using ALOS-2/PALSAR-2 Time-Series Images for Borneo’s Forest. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 5167–5177. [Google Scholar] [CrossRef]
- Dlamini, M.; Chirima, G.; Sibanda, M.; Adam, E.; Dube, T. Characterizing Leaf Nutrients ofWetland Plants and Agricultural Crops with Nonparametric Approach Using Sentinel-2 Imagery Data. Remote Sens. 2021, 13, 4249. [Google Scholar] [CrossRef]
- Ahmed, O.S.; Shemrock, A.; Chabot, D.; Dillon, C.; Williams, G.; Wasson, R.; Franklin, S.E. Hierarchical land cover and vegetation classification using multispectral data acquired from an unmanned aerial vehicle. Int. J. Remote Sens. 2017, 38, 2037–2052. [Google Scholar] [CrossRef]
- Matikainen, L.; Karila, K.; Hyyppa, J.; Litkey, P.; Puttonen, E.; Ahokas, E. Object-based analysis of multispectral airborne laser scanner data for land cover classification and map updating. ISPRS J. Photogramm. Remote Sens. 2017, 128, 298–313. [Google Scholar] [CrossRef]
- Yu, R.Y.; Li, S.S.; Zhang, B.; Zhang, H.Q. A Deep Transfer Learning Method for Estimating Fractional Vegetation Cover of Sentinel-2 Multispectral Images. IEEE Geosci. Remote Sens. Lett. 2022, 19, 6005605. [Google Scholar] [CrossRef]
- Zhang, X.; Friedl, M.A.; Schaaf, C.B. Global vegetation phenology from Moderate Resolution Imaging Spectroradiometer (MODIS): Evaluation of global patterns and comparison with in situ measurements. J. Geophys. Res. 2006, 111, 367–375. [Google Scholar] [CrossRef]
- Lin, J.; Chen, D.; Wu, W.; Liao, X. Estimating aboveground biomass of urban forest trees with dual-source UAV acquired point clouds. Urban For. Urban Green. 2022, 69, 127521. [Google Scholar] [CrossRef]
- Ryan, C.M.; Hill, T.; Woollen, E.; Ghee, C.; Mitchard, E.; Cassells, G.; Grace, J.; Woodhouse, I.H.; Williams, M. Quantifying small-scale deforestation and forest degradation in African woodlands using radar imagery. Glob. Chang. Biol. 2012, 18, 243–257. [Google Scholar] [CrossRef]
- Berger, M.; Moreno, J.; Johannessen, J.A.; Levelt, P.F.; Hanssen, R.F. ESA’s sentinel missions in support of Earth system science. Remote Sens. Environ. 2012, 120, 84–90. [Google Scholar] [CrossRef]
- Shoko, C.; Mutanga, O. Examining the strength of the newly-launched Sentinel 2 MSI sensor in detecting and discriminating subtle differences between C3 and C4 grass species. ISPRS J. Photogramm. Remote Sens. 2017, 129, 32–40. [Google Scholar] [CrossRef]
- Drusch, M.; Del Bello, U.; Carlier, S.; Colin, O.; Fernandez, V.; Gascon, F.; Hoersch, B.; Isola, C.; Laberinti, P.; Martimort, P.; et al. Sentinel-2: ESA’s Optical High-Resolution Mission for GMES Operational Services. Remote Sens. Environ. 2012, 120, 25–36. [Google Scholar] [CrossRef]
- Wang, D.; Wan, B.; Qiu, P.; Su, Y.; Guo, Q.; Wang, R.; Sun, F.; Wu, X. Evaluating the Performance of Sentinel-2, Landsat 8 and Pléiades-1 in Mapping Mangrove Extent and Species. Remote Sens. 2018, 10, 1468. [Google Scholar] [CrossRef]
- Wulder, M.A.; White, J.C.; Nelson, R.F.; Næsset, E.; Ørka, H.O.; Coops, N.C.; Hilker, T.; Bater, C.W.; Gobakken, T. Lidar sampling for large-area forest characterization: A review. Remote Sens. Environ. 2012, 121, 196–209. [Google Scholar] [CrossRef]
- Disney, M. Terrestrial LiDAR: A three-dimensional revolution in how we look at trees. New Phytol. 2019, 222, 1736–1741. [Google Scholar] [CrossRef] [PubMed]
- Milenkovic, M.; Schnell, S.; Holmgren, J.; Ressl, C.; Lindberg, E.; Hollaus, M.; Pfeifer, N.; Olsson, H. Influence of footprint size and geolocation error on the precision of forest biomass estimates from space-borne waveform LiDAR. Remote Sens. Environ. 2017, 200, 74–88. [Google Scholar] [CrossRef]
- Liu, Y.; Gong, W.; Xing, Y.; Hu, X.; Gong, J. Estimation of the forest stand mean height and aboveground biomass in Northeast China using SAR Sentinel-1B, multispectral Sentinel-2A, and DEM imagery. ISPRS J. Photogramm. Remote Sens. 2019, 151, 277–289. [Google Scholar] [CrossRef]
- Wang, D.; Wan, B.; Liu, J.; Su, Y.; Guo, Q.; Qiu, P.; Wu, X. Estimating aboveground biomass of the mangrove forests on northeast Hainan Island in China using an upscaling method from field plots, UAV-LiDAR data and Sentinel-2 imagery. Int. J. Appl. Earth Obs. Geoinf. 2020, 85, 101986. [Google Scholar] [CrossRef]
- Feng, Y.Y.; Lu, D.S.; Chen, Q.; Keller, M.; Moran, E.; Dos-Santos, M.N.; Bolfe, E.L.; Batistella, M. Examining effective use of data sources and modeling algorithms for improving biomass estimation in a moist tropical forest of the Brazilian Amazon. Int. J. Digit. Earth 2017, 10, 996–1016. [Google Scholar] [CrossRef]
- Tian, X.; Su, Z.B.; Chen, E.X.; Li, Z.Y.; van der Tol, C.; Guo, J.P.; He, Q.S. Estimation of forest above-ground biomass using multi-parameter remote sensing data over a cold and arid area. Int. J. Appl. Earth Obs. Geoinf. 2012, 14, 160–168. [Google Scholar] [CrossRef]
- Chen, L.; Ren, C.; Zhang, B.; Wang, Z.; Xi, Y.J.F. Estimation of Forest Above-Ground Biomass by Geographically Weighted Regression and Machine Learning with Sentinel Imagery. Forests 2018, 9, 582. [Google Scholar] [CrossRef]
- Chen, L.; Wang, Y.; Ren, C.; Zhang, B.; Wang, Z. Optimal Combination of Predictors and Algorithms for Forest Above-Ground Biomass Mapping from Sentinel and SRTM Data. Remote Sens. 2019, 11, 414. [Google Scholar] [CrossRef]
- Forkuor, G.; Benewinde Zoungrana, J.-B.; Dimobe, K.; Ouattara, B.; Vadrevu, K.P.; Tondoh, J.E. Above-ground biomass mapping in West African dryland forest using Sentinel-1 and 2 datasets—A case study. Remote Sens. Environ. 2020, 236, 111496. [Google Scholar] [CrossRef]
- Dimobe, K.; Kuyah, S.; Dabré, Z.; Ouédraogo, A.; Thiombiano, A. Diversity-carbon stock relationship across vegetation types in W National park in Burkina Faso. For. Ecol. Manag. 2019, 438, 243–254. [Google Scholar] [CrossRef]
- Fang, J.Y.; Liu, G.H.; Xu, S.L. Biomass and net production of forest vegetation in China. Acta Ecol. Sin. 1996, 16, 497–508. [Google Scholar]
- Zhang, L.; Zhang, X.; Shao, Z.; Jiang, W.; Gao, H. Integrating Sentinel-1 and 2 with LiDAR data to estimate aboveground biomass of subtropical forests in northeast Guangdong, China. Int. J. Digit. Earth 2023, 16, 158–182. [Google Scholar] [CrossRef]
- Shao, Z.F.; Zhang, L.J.; Wang, L. Stacked Sparse Autoencoder Modeling Using the Synergy of Airborne LiDAR and Satellite Optical and SAR Data to Map Forest Above-Ground Biomass. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 5569–5582. [Google Scholar] [CrossRef]
- Zhao, X.; Guo, Q.; Su, Y.; Xue, B. Improved progressive TIN densification filtering algorithm for airborne LiDAR data in forested areas. ISPRS J. Photogramm. Remote Sens. 2016, 117, 79–91. [Google Scholar] [CrossRef]
- Hyyppä, J.; Yu, X.; Hyyppä, H.; Vastaranta, M.; Holopainen, M.; Kukko, A.; Kaartinen, H.; Jaakkola, A.; Vaaja, M.; Koskinen, J.; et al. Advances in Forest Inventory Using Airborne Laser Scanning. Remote Sens. 2012, 4, 1190–1207. [Google Scholar] [CrossRef]
- Agency, E.S. Sentinel-1 User Handbook; European Space Agency: Paris, France, 2013.
- Lukin, V.; Rubel, O.; Kozhemiakin, R.; Abramov, S.; Shelestov, A.; Lavreniuk, M.; Meretsky, M.; Vozel, B.; Chehdi, K.J.R.A.; Sensing, A.i.R. Despeckling of multitemporal sentinel SAR images and its impact on agricultural area classification. Remote Sens. 2018, 11, 13. [Google Scholar] [CrossRef]
- Small, D.; Schubert, A. Guide to ASAR Geocoding; ESA-ESRIN Technical Note RSL-ASAR-GC-AD; ESA: Paris, France, 2008; Volume 1, p. 36.
- Sentinel-2_Team. Sentinel-2 User Handbook; European Space Agency: Paris, France, 2015.
- Louis, F.; Couroussé, T.; Gautron, S. Immunohistochemical Methods for the Study of the Expression of Low-Affinity Monoamine Transporters in the Brain. In Neurotransmitter Transporters: Investigative Methods; Bönisch, H., Sitte, H.H., Eds.; Springer: New York, NY, USA, 2016; pp. 91–108. [Google Scholar] [CrossRef]
- Zhang, Z.; Cao, L.; She, G. Estimating Forest Structural Parameters Using Canopy Metrics Derived from Airborne LiDAR Data in Subtropical Forests. Remote Sens. 2017, 9, 940. [Google Scholar] [CrossRef]
- de Almeida, C.T.; Galvao, L.S.; Ometto, J.P.H.B.; Jacon, A.D.; de Souza Pereira, F.R.; Sato, L.Y.; Lopes, A.P.; de Alencastro Graça, P.M.L.; de Jesus Silva, C.V.; Ferreira-Ferreira, J.; et al. Combining LiDAR and hyperspectral data for aboveground biomass modeling in the Brazilian Amazon using different regression algorithms. Remote Sens. Environ. 2019, 232, 111323. [Google Scholar] [CrossRef]
- Thomas, V.; Treitz, P.; McCaughey, J.H.; Morrison, I. Mapping stand-level forest biophysical variables for a mixedwood boreal forest using lidar: An examination of scanning density. Can. J. For. Res. 2006, 36, 34–47. [Google Scholar] [CrossRef]
- Kelsey, K.C.; Neff, J.C. Estimates of Aboveground Biomass from Texture Analysis of Landsat Imagery. Remote Sens. 2014, 6, 6407–6422. [Google Scholar] [CrossRef]
- Dube, T.; Mutanga, O. Investigating the robustness of the new Landsat-8 Operational Land Imager derived texture metrics in estimating plantation forest aboveground biomass in resource constrained areas. ISPRS J. Photogramm. Remote Sens. 2015, 108, 12–32. [Google Scholar] [CrossRef]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I. Textural Features for Image Classification. IEEE Trans. Syst. Man Cybern. 1973, 6, 610–621. [Google Scholar] [CrossRef]
- Ronoud, G.; Fatehi, P.; Darvishsefat, A.A.; Tomppo, E.; Praks, J.; Schaepman, M.E. Multi-Sensor Aboveground Biomass Estimation in the Broadleaved Hyrcanian Forest of Iran. Can. J. Remote Sens. 2021, 47, 818–834. [Google Scholar] [CrossRef]
- Dahms, T.; Seissiger, S.; Borg, E.; Vajen, H.; Fichtelmann, B.; Conrad, C. Important Variables of a RapidEye Time Series for Modelling Biophysical Parameters of Winter Wheat. Photogramm. Fernerkund. Geoinf. 2016, 2016, 285–299. [Google Scholar] [CrossRef]
- Castillo, J.A.A.; Apan, A.A.; Maraseni, T.N.; Salmo, S.G. Estimation and mapping of above-ground biomass of mangrove forests and their replacement land uses in the Philippines using Sentinel imagery. ISPRS J. Photogramm. Remote Sens. 2017, 134, 70–85. [Google Scholar] [CrossRef]
- Friedman, J.H. Stochastic gradient boosting. Comput. Stat. Data Anal. 2002, 38, 367–378. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Belgiu, M.; Drăguţ, L. Random forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Chen, T.; He, T.; Benesty, M. xgboost: Extreme Gradient Boosting. arXiv 2016, arXiv:1603.02754. [Google Scholar]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Verrelst, J.; Rivera, J.P.; Veroustraete, F.; Munoz-Mari, J.; Clevers, J.; Camps-Valls, G.; Moreno, J. Experimental Sentinel-2 LAI estimation using parametric, non-parametric and physical retrieval methods—A comparison. ISPRS J. Photogramm. Remote Sens. 2015, 108, 260–272. [Google Scholar] [CrossRef]
- Sinha, S.K.; Padalia, H.; Dasgupta, A.; Verrelst, J.; Rivera, J.P. Estimation of leaf area index using PROSAIL based LUT inversion, MLRA-GPR and empirical models: Case study of tropical deciduous forest plantation, North India. Int. J. Appl. Earth Obs. Geoinf. 2020, 86, 102027. [Google Scholar] [CrossRef]
- Verrelst, J.; Munoz, J.; Alonso, L.; Delegido, J.; Rivera, J.P.; Camps-Valls, G.; Moreno, J. Machine learning regression algorithms for biophysical parameter retrieval: Opportunities for Sentinel-2 and -3. Remote Sens. Environ. 2012, 118, 127–139. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression Shrinlcage and Selection via the Lasso. J. R. Stat. Soc. Ser. B Stat. Methodol. 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef]
- Pham, T.D.; Yoshino, K.; Bui, D.T. Biomass estimation of Sonneratia caseolaris (l.) Engler at a coastal area of Hai Phong city (Vietnam) using ALOS-2 PALSAR imagery and GIS-based multi-layer perceptron neural networks. GISci. Remote Sens. 2017, 54, 329–353. [Google Scholar] [CrossRef]
- Vafaei, S.; Soosani, J.; Adeli, K.; Fadaei, H.; Naghavi, H.; Pham, T.D.; Tien Bui, D. Improving Accuracy Estimation of Forest Aboveground Biomass Based on Incorporation of ALOS-2 PALSAR-2 and Sentinel-2A Imagery and Machine Learning: A Case Study of the Hyrcanian Forest Area (Iran). Remote Sens. 2018, 10, 172. [Google Scholar] [CrossRef]
- Zhao, P.; Lu, D.; Wang, G.; Liu, L.; Li, D.; Zhu, J.; Yu, S. Forest aboveground biomass estimation in Zhejiang Province using the integration of Landsat TM and ALOS PALSAR data. Int. J. Appl. Earth Obs. Geoinf. 2016, 53, 1–15. [Google Scholar] [CrossRef]
- Ploton, P.; Barbier, N.; Couteron, P.; Antin, C.M.; Ayyappan, N.; Balachandran, N.; Barathan, N.; Bastin, J.F.; Chuyong, G.; Dauby, G.; et al. Toward a general tropical forest biomass prediction model from very high resolution optical satellite images. Remote Sens. Environ. 2017, 200, 140–153. [Google Scholar] [CrossRef]
- Liang, Y.Y.; Kou, W.L.; Lai, H.Y.; Wang, J.; Wang, Q.H.; Xu, W.H.; Wang, H.; Lu, N. Improved estimation of aboveground biomass in rubber plantations by fusing spectral and textural information from UAV-based RGB imagery. Ecol. Indic. 2022, 142, 109286. [Google Scholar] [CrossRef]
- Tamga, D.K.; Latifi, H.; Ullmann, T.; Baumhauer, R.; Bayala, J.; Thiel, M. Estimation of Aboveground Biomass in Agroforestry Systems over Three Climatic Regions in West Africa Using Sentinel-1, Sentinel-2, ALOS, and GEDI Data. Sensors 2023, 23, 349. [Google Scholar] [CrossRef]
- Almeida, D.R.A.d.; Broadbent, E.N.; Ferreira, M.P.; Meli, P.; Zambrano, A.M.A.; Gorgens, E.B.; Resende, A.F.; de Almeida, C.T.; do Amaral, C.H.; Corte, A.P.D.; et al. Monitoring restored tropical forest diversity and structure through UAV-borne hyperspectral and lidar fusion. Remote Sens. Environ. 2021, 264, 112582. [Google Scholar] [CrossRef]
- Longo, M.; Keller, M.; dos-Santos, M.N.; Leitold, V.; Pinagé, E.R.; Baccini, A.; Saatchi, S.; Nogueira, E.M.; Batistella, M.; Morton, D.C. Aboveground biomass variability across intact and degraded forests in the Brazilian Amazon. Glob. Biogeochem. Cycles 2016, 30, 1639–1660. [Google Scholar] [CrossRef]
- Gao, L.H.; Chai, G.Q.; Zhang, X.L. Above-Ground Biomass Estimation of Plantation with Different Tree Species Using Airborne LiDAR and Hyperspectral Data. Remote Sens. 2022, 14, 2568. [Google Scholar] [CrossRef]
- Latifi, H.; Fassnacht, F.; Koch, B. Forest structure modeling with combined airborne hyperspectral and LiDAR data. Remote Sens. Environ. 2012, 121, 10–25. [Google Scholar] [CrossRef]
- Krofcheck, D.J.; Litvak, M.E.; Lippitt, C.D.; Neuenschwander, A. Woody Biomass Estimation in a Southwestern US Juniper Savanna Using LiDAR-Derived Clumped Tree Segmentation and Existing Allometries. Remote Sens. 2016, 8, 453. [Google Scholar] [CrossRef]
- Wang, Y.T.; Jia, X.; Chai, G.Q.; Lei, L.T.; Zhang, X.L. Improved estimation of aboveground biomass of regional coniferous forests integrating UAV-LiDAR strip data, Sentinel-1 and Sentinel-2 imageries. Plant Methods 2023, 19, 65. [Google Scholar] [CrossRef]
- Li, C.H.; Zhou, L.Z.; Xu, W.B. Estimating Aboveground Biomass Using Sentinel-2 MSI Data and Ensemble Algorithms for Grassland in the Shengjin Lake Wetland, China. Remote Sens. 2021, 13, 1595. [Google Scholar] [CrossRef]
- Uniyal, S.; Purohit, S.; Chaurasia, K.; Amminedu, E.; Rao, S.S. Quantification of carbon sequestration by urban forest using Landsat 8 OLI and machine learning algorithms in Jodhpur, India. Urban For. Urban Green. 2022, 67, 127445. [Google Scholar] [CrossRef]
- Laurin, G.V.; Balling, J.; Corona, P.; Mattioli, W.; Papale, D.; Puletti, N.; Rizzo, M.; Truckenbrodt, J.; Urban, M. Above-ground biomass prediction by Sentinel-1 multitemporal data in central Italy with integration of ALOS2 and Sentinel-2 data. J. Appl. Remote Sens. 2018, 12, 016008. [Google Scholar] [CrossRef]
- Mundava, C.; Helmholz, P.; Schut, A.G.; Corner, R.; McAtee, B.; Lamb, D. Evaluation of vegetation indices for rangeland biomass estimation in the Kimberley area of Western Australia. American journal of pathology. Am. J. Pathol. 2014, 2, 47–53. [Google Scholar] [CrossRef]

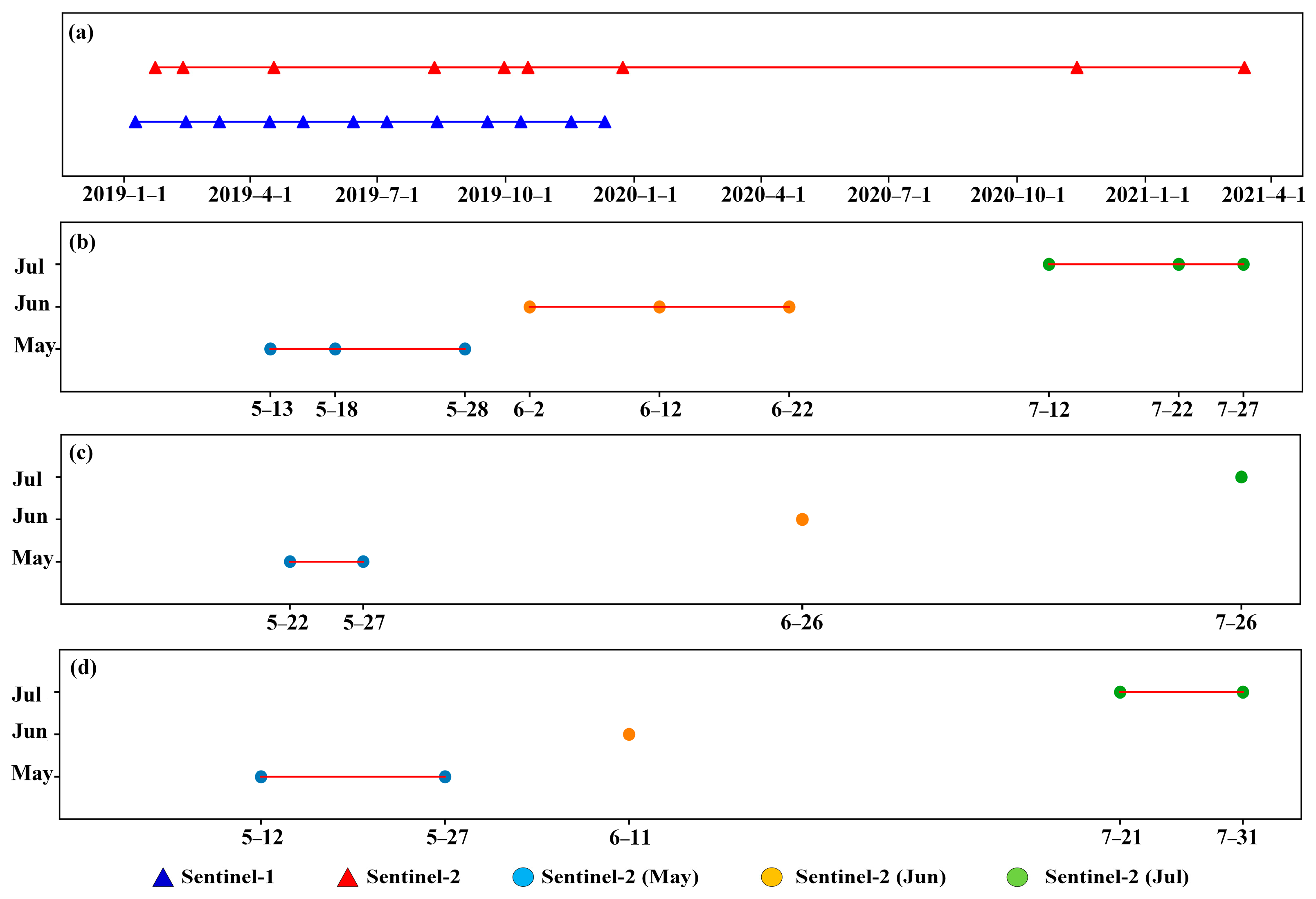
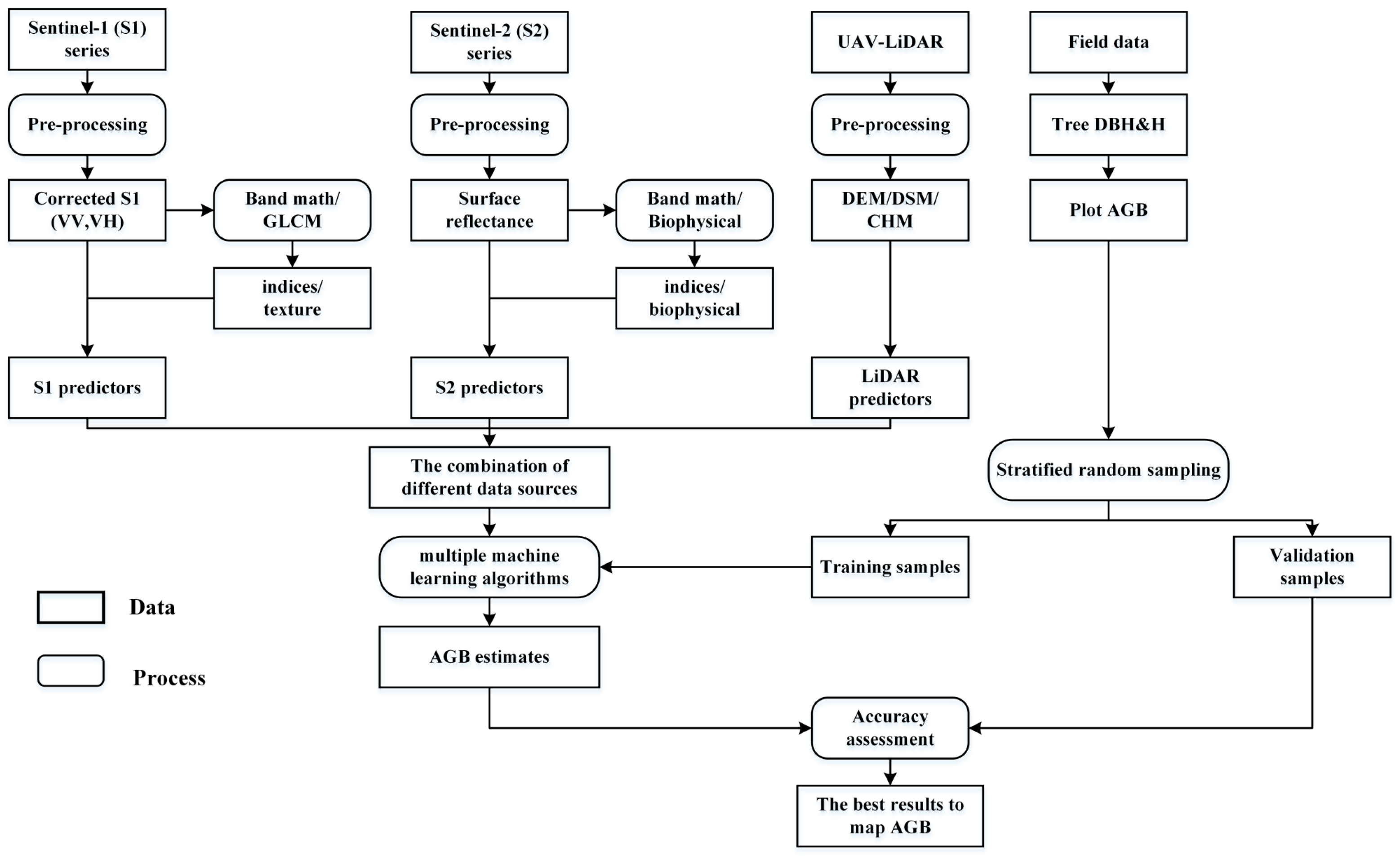


| Sensor | Feature | Abbreviation | Definition/Formula |
|---|---|---|---|
| UAV-LiDAR | Height | HpX | Xth (10, 20, 30, 40, 50, 60, 70, 80, or 90th) percentile of height distribution |
| Hmean | Mean height | ||
| Hmax | Maximum height | ||
| Hvar | Variance of height | ||
| Hske | Skewness of height distribution | ||
| Hkur | Kurtosis of height distribution | ||
| Hcv | Coefficient of height variation | ||
| Canopy cover | PDa_b | The proportion within a height interval a_b (2_5, 5_10, 10_15, 15_30) to the total number of all first returns | |
| COV | Canopy cover | ||
| CRR | Canopy relief ratio | ||
| S1 | Polarization | VV | Vertical transmit–vertical channel |
| VH | Vertical transmit–horizontal channel | ||
| Indices | VH − VV | Difference | |
| VH + VV | Sum | ||
| VV/VH | Quotient | ||
| Textural Features | Correlation | ||
| Second moment | |||
| Variance | |||
| Entropy | |||
| Contrast | |||
| Dissimilarity | |||
| Homogeneity | |||
| Mean | |||
| S2 | Spectral Bands | Band 2 | 490 nm, Blue, |
| Band 3 | 560 nm, Green, | ||
| Band 4 | 665 nm, Red, | ||
| Band 5 | 705 nm, Red edge, | ||
| Band 6 | 749 nm, Red edge, | ||
| Band 7 | 783 nm, Red edge, | ||
| Band 8 | 842 nm, Near Infrared (NIR), | ||
| Band 8A | 865 nm, Near Infrared (NIR), | ||
| Band 11 | 1610 nm, SWIR-1, | ||
| Band 12 | 2190 nm, SWIR-2, | ||
| Conventional near infrared indices | RVI | B8/B4 | |
| DVI | B8 − B4 | ||
| EVI | [2.5∗(B8 − B4)]/[B8 + 6∗B4 − 7.5∗B2 + 1] | ||
| NDVI | (B8 − B4)/(B8 + B4) | ||
| Red edge indices | MSRren | [(B8a/B5) − 1]/[(B8a/B5) − 1]1/2 | |
| MSRren | [(B5 − B4) − 0.2 × (B5 − B3)] × (B5/B4) | ||
| MTCI | (B6 − B5)/(B5 − B4) | ||
| IRECI | (B7 − B4)/(B5/B6) | ||
| TNDVI | [(B8 − B4)/(B8 + B4) + 0.5]1/2 | ||
| Shortwave infrared indices | STVI1 | (B11∗B4)/B8 | |
| STVI2 | B8/(B4∗B12) | ||
| STVI3 | B8/(B4∗B11) | ||
| Biophysical Variables | FAPAR | Fraction of Absorbed Photosynthetically Active Radiation | |
| FCOVER | Fraction of Vegetation Cover | ||
| LAI | Leaf Area Index |
| Type | Abbr. | Model | Parameters |
|---|---|---|---|
| tree-based | SGB | Stochastic Gradient Boosting | min_samples_split, learning_rate, max_depth, n_estimators |
| RF | Random Forest | n_estimators, max_depth, max_features | |
| XGBoost | eXtreme Gradient Boosting | n_estimators, max_depth, colsample_bytree, subsample | |
| kernel-based | GPR | Gaussian Process Regression | length_scale, alpha |
| linear | LASSO | Least Absolute Shrinkage and Selection Operator | max_iter, alpha |
| neural network-based | CNN | Convolutional Neural Network | learning_rate, num_epochs, batch_size |
| MLP | Multilayer Perceptron | hidden_layer_sizes, max_iter, activation function |
| Experiment | Number of Predictors | Description/Objective |
|---|---|---|
| A: Annual time series of SAR (S1annual) | 156 | Annual time-series raw polarization bands and their derivatives including difference, sum, quotient bands, and texture features |
| B: Annual time series of optical (S2annual) | 300 | Annual time-series spectral bands and their derivatives, including biophysical parameters and three types of vegetation indices |
| C: Annual time-series of SAR and optical (S1S2annual) | 456 | All obtained annual time-series SAR and optical predictors |
| D: Optical and LiDAR (S2Li) | 321 | Annual time-series optical and single-temporal LiDAR metrics |
| E: Optical, SAR, and LiDAR (S1S2Li) | 477 | All obtained annual time-series SAR, optical predictors, and single-temporal LiDAR metrics |
| Range (Mg/ha) | 16.32–50 | 50–100 | 100–150 | 150–186.50 |
| Number of plots | 112 | 256 | 300 | 136 |
| Modeling | Number of training plots (75%) | 603 | ||
| Number of validation plots (25%) | 201 | |||
| Experiment | Model | R2 | RMSE (Mg/ha) | RMSRr (%) |
|---|---|---|---|---|
| A (S1annual) | RF | 0.29 | 54.47 | 37.53 |
| XGBoost | 0.29 | 54.46 | 37.52 | |
| SGB | 0.25 | 56.32 | 39.76 | |
| CNN | 0.45 | 47.36 | 32.69 | |
| GPR | 0.24 | 56.51 | 39.92 | |
| MLP | 0.25 | 56.27 | 38.79 | |
| LASSO | 0.25 | 56.45 | 39.88 | |
| B (S2annual) | RF | 0.68 | 34.57 | 19.74 |
| XGBoost | 0.68 | 34.64 | 19.86 | |
| SGB | 0.67 | 35.16 | 20.98 | |
| CNN | 0.75 | 30.08 | 18.10 | |
| GPR | 0.66 | 35.87 | 21.94 | |
| MLP | 0.62 | 38.83 | 23.07 | |
| LASSO | 0.65 | 36.28 | 22.33 | |
| C (S1S2annual) | RF | 0.70 | 33.86 | 19.34 |
| XGBoost | 0.71 | 33.35 | 19.19 | |
| SGB | 0.68 | 34.95 | 20.03 | |
| CNN | 0.78 | 28.68 | 17.46 | |
| GPR | 0.66 | 35.42 | 21.55 | |
| MLP | 0.65 | 35.92 | 22.08 | |
| LASSO | 0.66 | 35.41 | 21.52 | |
| D (S2Li) | RF | 0.84 | 23.16 | 16.79 |
| XGBoost | 0.85 | 22.74 | 16.08 | |
| SGB | 0.84 | 23.92 | 16.81 | |
| CNN | 0.81 | 26.02 | 17.54 | |
| GPR | 0.67 | 35.18 | 21.26 | |
| MLP | 0.64 | 36.63 | 22.57 | |
| LASSO | 0.66 | 35.33 | 21.47 | |
| E (S1S2Li) | RF | 0.87 | 21.84 | 15.01 |
| XGBoost | 0.87 | 21.63 | 14.45 | |
| SGB | 0.86 | 21.99 | 15.26 | |
| CNN | 0.82 | 25.46 | 17.22 | |
| GPR | 0.67 | 35.11 | 20.98 | |
| MLP | 0.65 | 35.98 | 22.13 | |
| LASSO | 0.66 | 35.30 | 21.44 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Yin, X.; Wang, Y.; Chen, J. Aboveground Biomass Mapping in SemiArid Forests by Integrating Airborne LiDAR with Sentinel-1 and Sentinel-2 Time-Series Data. Remote Sens. 2024, 16, 3241. https://doi.org/10.3390/rs16173241
Zhang L, Yin X, Wang Y, Chen J. Aboveground Biomass Mapping in SemiArid Forests by Integrating Airborne LiDAR with Sentinel-1 and Sentinel-2 Time-Series Data. Remote Sensing. 2024; 16(17):3241. https://doi.org/10.3390/rs16173241
Chicago/Turabian StyleZhang, Linjing, Xinran Yin, Yaru Wang, and Jing Chen. 2024. "Aboveground Biomass Mapping in SemiArid Forests by Integrating Airborne LiDAR with Sentinel-1 and Sentinel-2 Time-Series Data" Remote Sensing 16, no. 17: 3241. https://doi.org/10.3390/rs16173241
APA StyleZhang, L., Yin, X., Wang, Y., & Chen, J. (2024). Aboveground Biomass Mapping in SemiArid Forests by Integrating Airborne LiDAR with Sentinel-1 and Sentinel-2 Time-Series Data. Remote Sensing, 16(17), 3241. https://doi.org/10.3390/rs16173241





