Improved Winter Wheat Yield Estimation by Combining Remote Sensing Data, Machine Learning, and Phenological Metrics
Abstract
1. Introduction
2. Materials and Methods
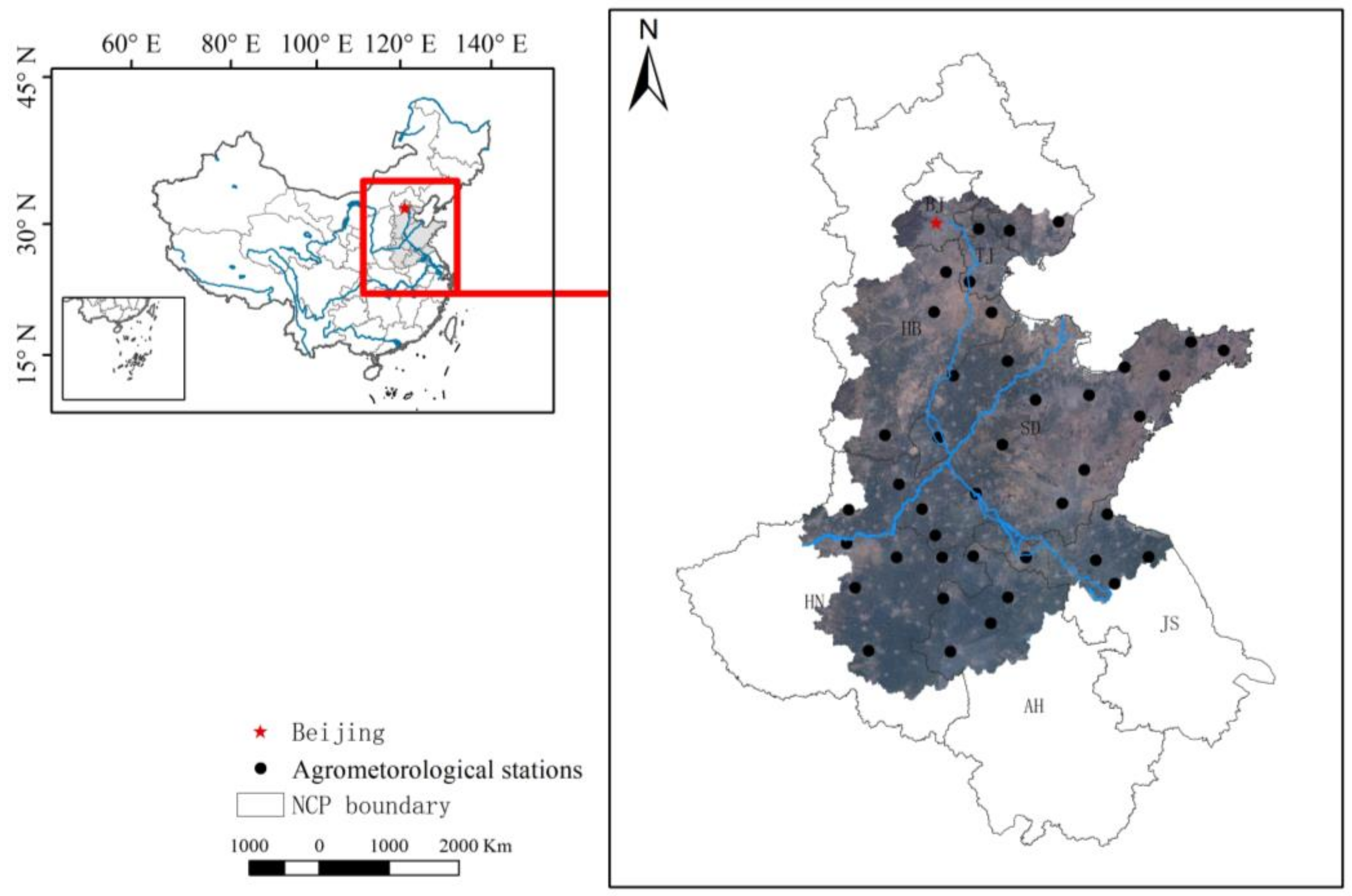
2.1. Study Area
2.2. Data and Processing
2.2.1. Remote Sensing Data
2.2.2. Meteorological Data
2.2.3. Other Data
2.3. Methodology
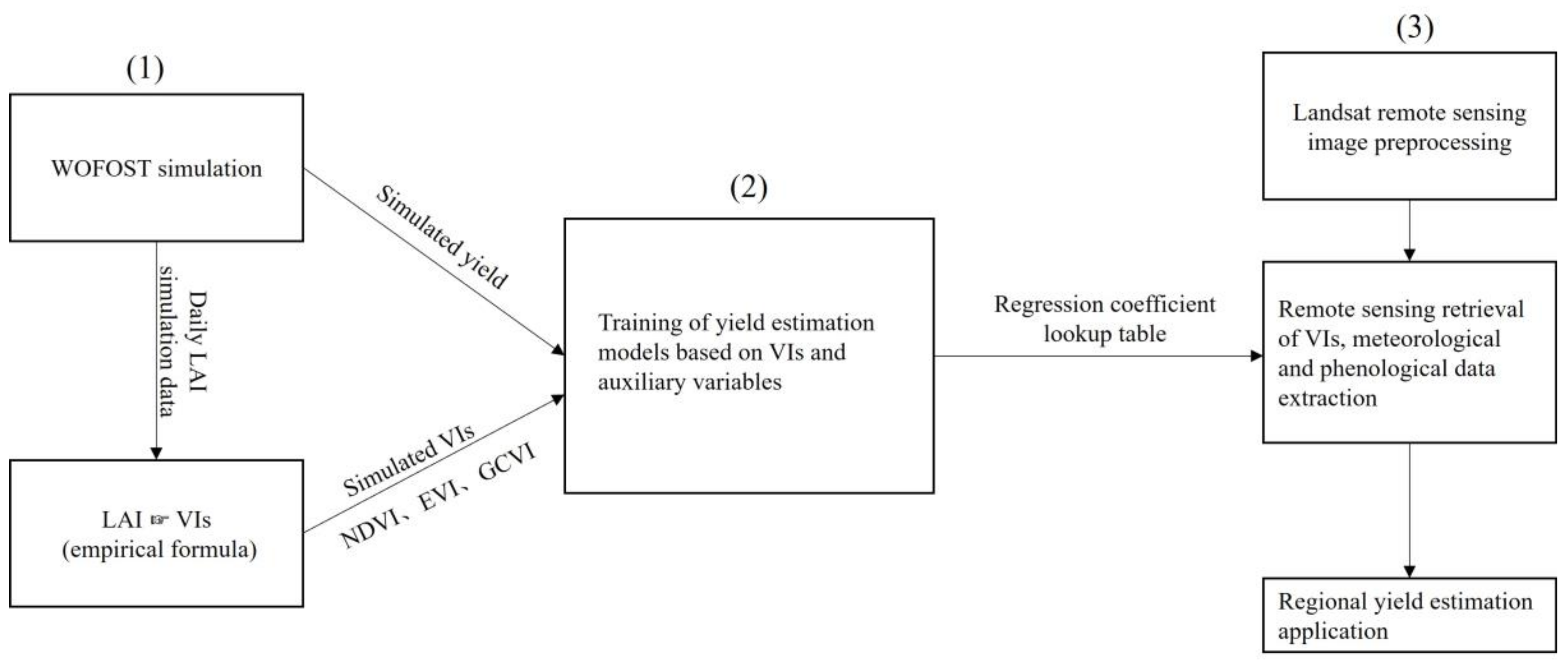
2.3.1. Application of the SCYM Method Framework
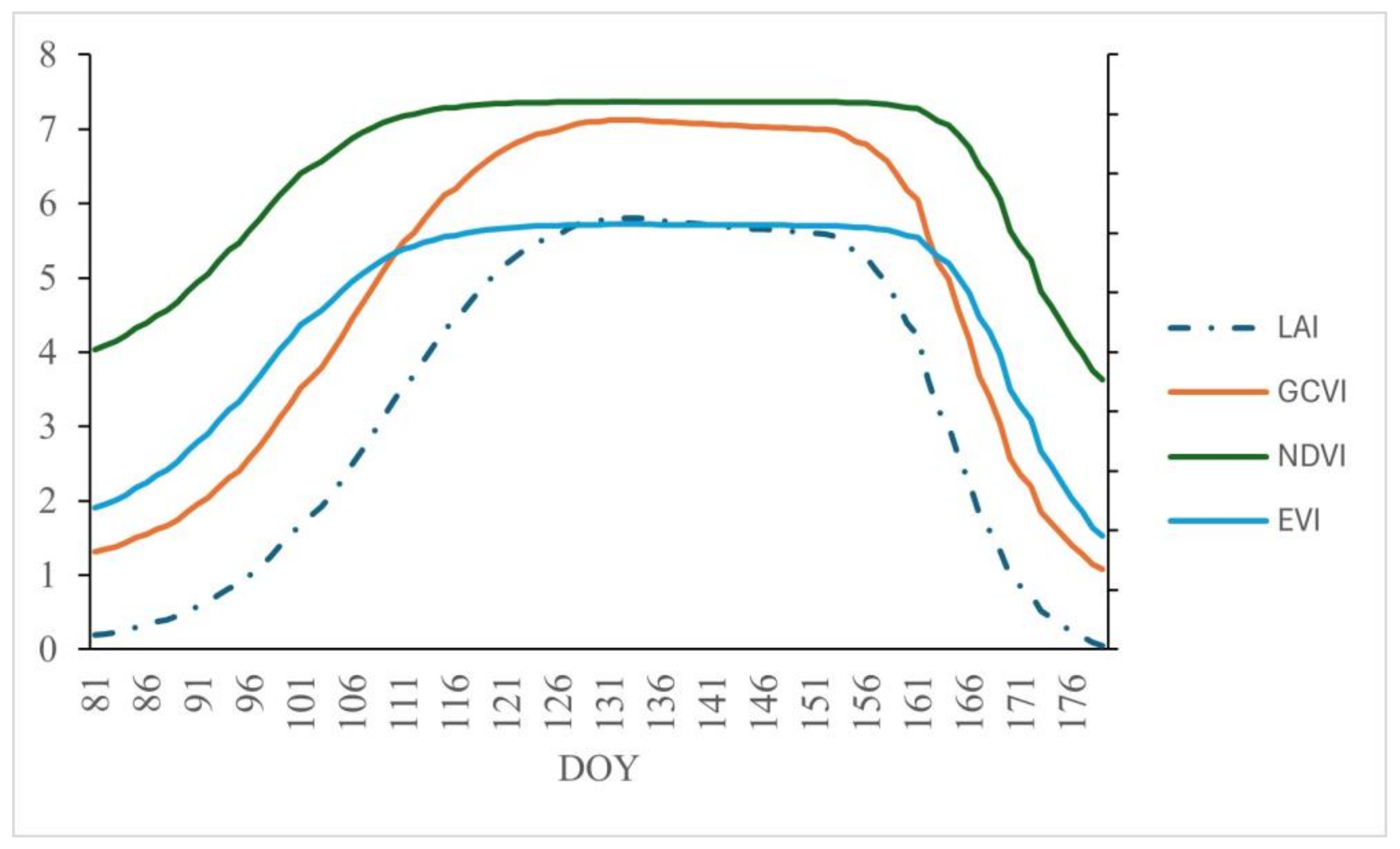
2.3.2. Crop Growth Data Simulation
2.3.3. Model Training and Evaluation
2.3.4. Experimental Design
- (1)
- VI Only: This experiment focuses on modeling yield estimation using only vegetation indices (GCVI, NDVI, EVI). It is intended to evaluate the effectiveness of different VIs in predicting winter wheat yield at the field scale;
- (2)
- Weather Only: In this experiment, the model is trained using only meteorological variables. The goal is to assess how meteorological factors alone contribute to yield estimation accuracy;
- (3)
- VI + Weather: This experiment combines vegetation indices with meteorological variables in the model. It explores the potential improvement in yield estimation accuracy when both VIs and weather data are used together;
- (4)
- VI + Phe: Here, the model uses both vegetation indices and phenological variables. The experiment aims to determine the added value of phenological information in improving yield estimation accuracy;
- (5)
- VI + Weather + Phe: This comprehensive experiment incorporates vegetation indices, meteorological variables, and phenological variables into the model. It evaluates the optimal combination of these inputs for enhancing yield prediction accuracy.
3. Results
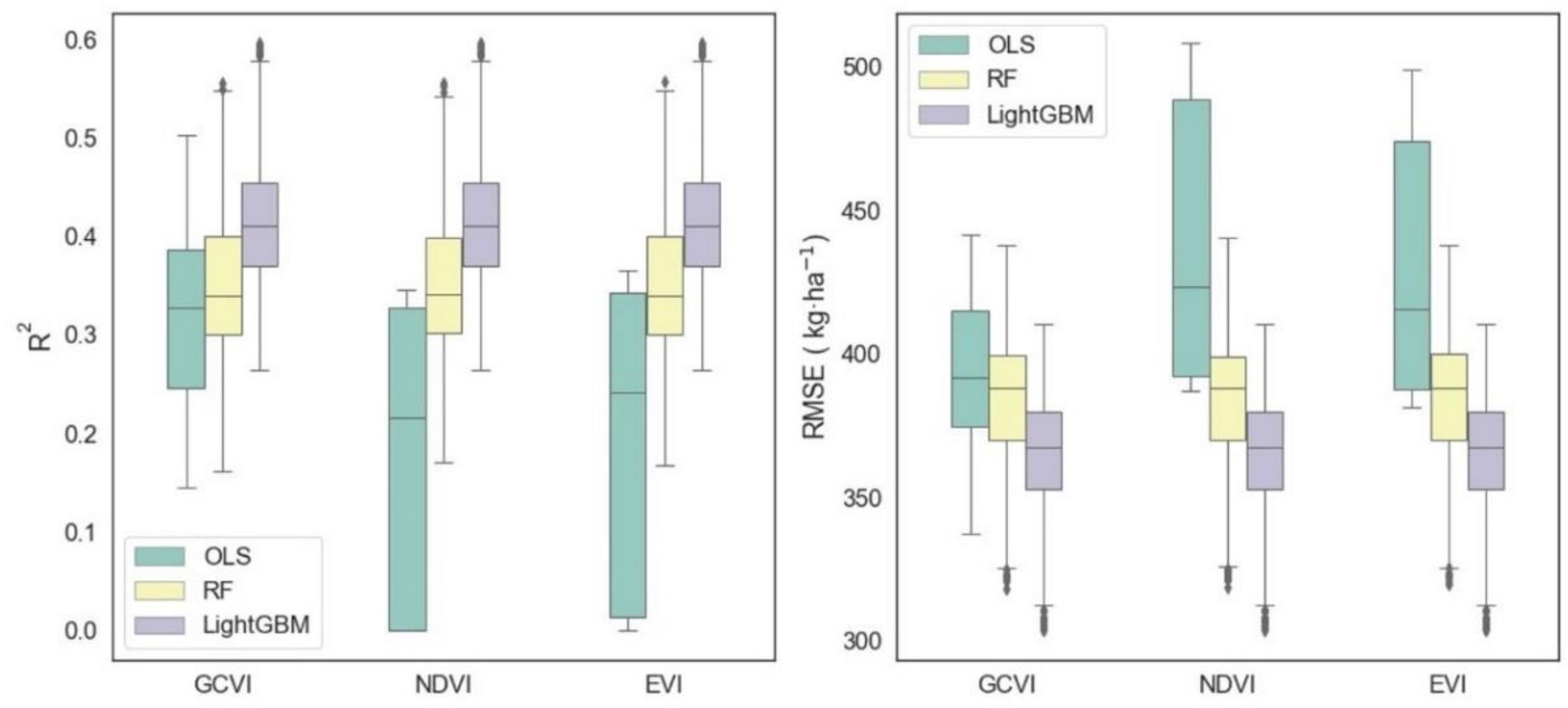
3.1. Accuracy of the Prediction Models with Only Vegetation Index
3.2. Contribution and Importance of Weather Variables and Phenological Metrics
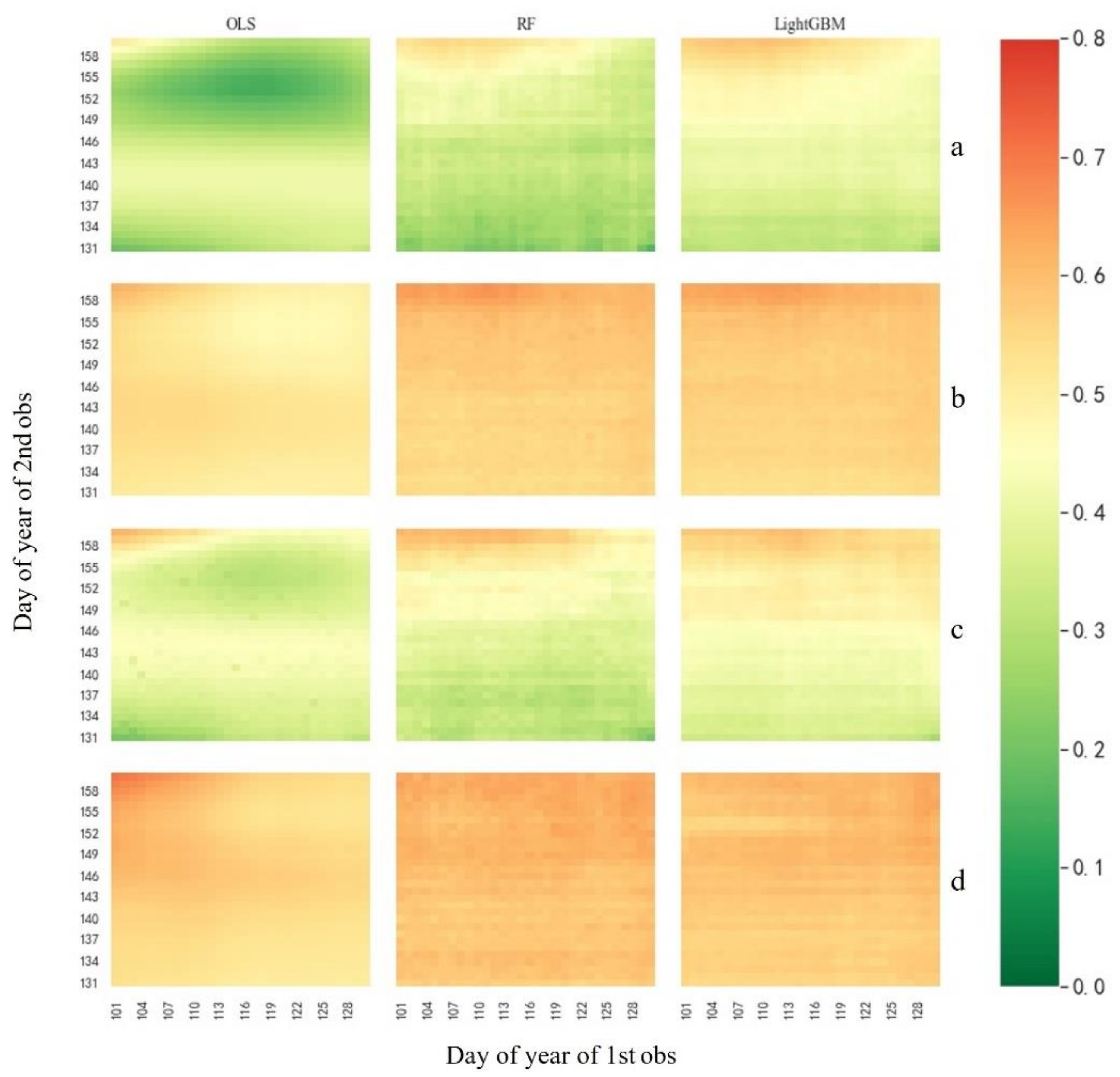
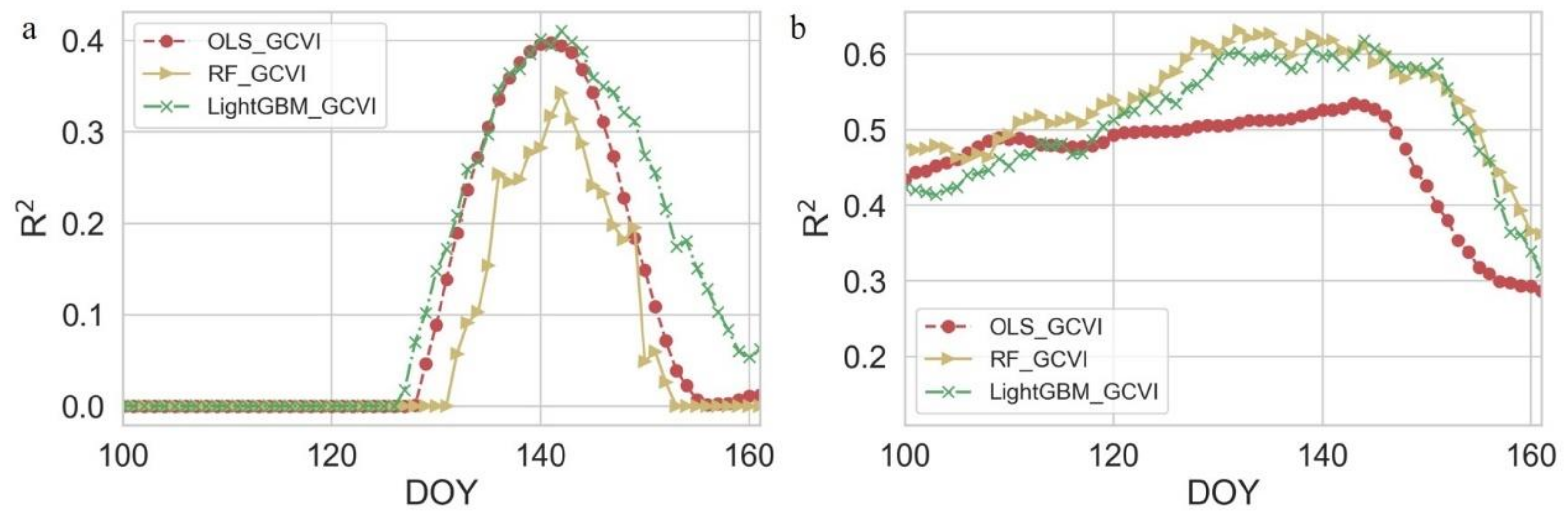
3.3. Impact of Vegetation Index Observation Dates on Yield Estimation Models
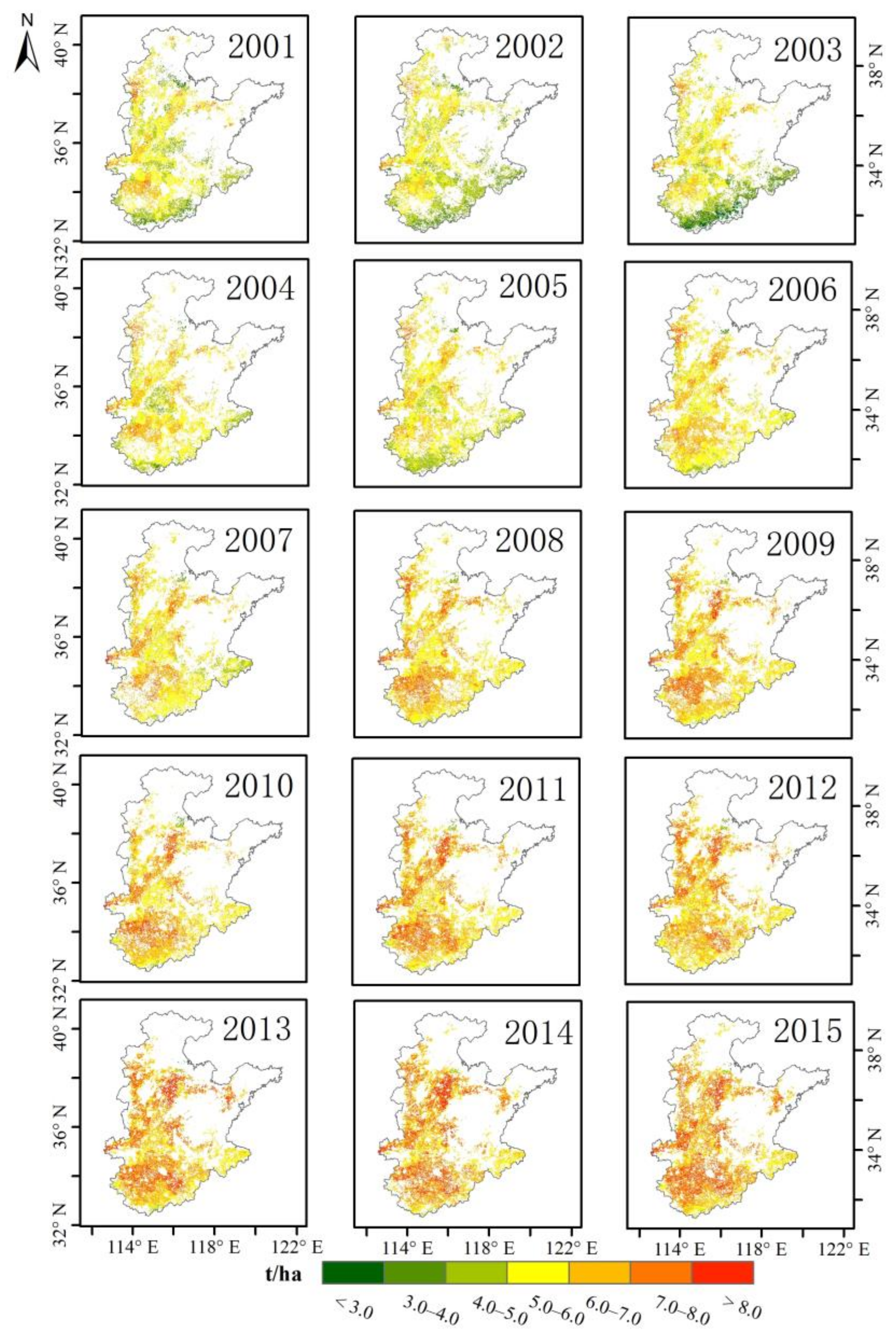
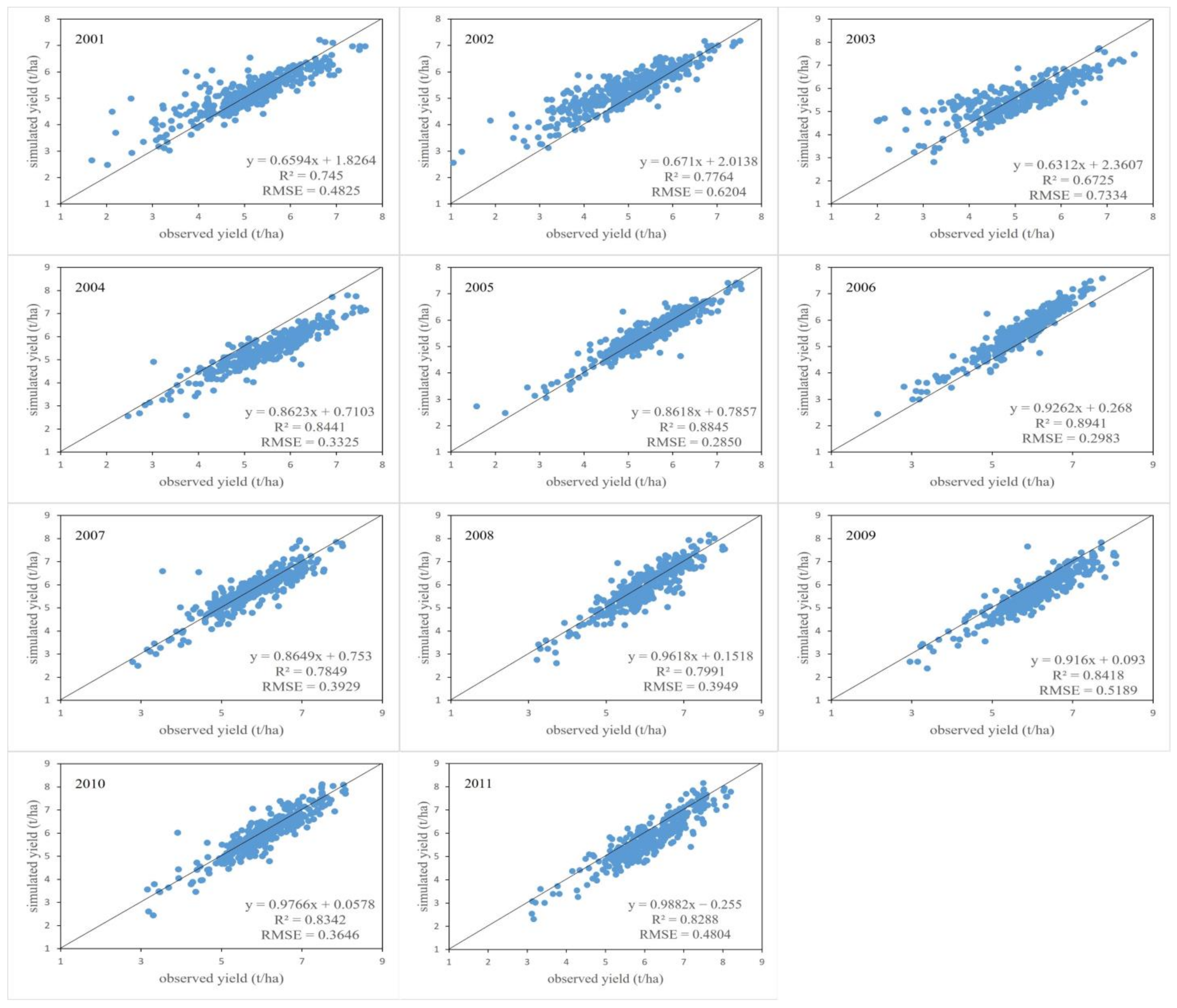
3.4. Winter Wheat Yield Spatial Mapping and Accuracy Evaluation
4. Discussion
4.1. Comparison of the Performance of Vegetation Indices in Yield Estimation
4.2. Comparing the Performances of OLS and ML Methods in Predicting Crop Yield
4.3. Effects of Image Observation Date on Yield Estimation
4.4. Uncertainties and Outlook
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shiferaw, B.; Smale, M.; Braun, H.-J.; Duveiller, E.; Reynolds, M.; Muricho, G. Crops that feed the world 10. Past successes and future challenges to the role played by wheat in global food security. Food Secur. 2013, 5, 291–317. [Google Scholar] [CrossRef]
- Sun, H.; Wang, Y.; Wang, L. Impact of climate change on wheat production in China. Eur. J. Agron. 2024, 153, 127066. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, Z.; Luo, Y.; Cao, J.; Tao, F. Combining optical, fluorescence, thermal satellite, and environmental data to predict county-level maize yield in China using machine learning approaches. Remote Sens. 2019, 12, 21. [Google Scholar] [CrossRef]
- Van Klompenburg, T.; Kassahun, A.; Catal, C. Crop yield prediction using machine learning: A systematic literature review. Comput. Electron. Agric. 2020, 177, 105709. [Google Scholar] [CrossRef]
- Basso, B.; Liu, L. Seasonal crop yield forecast: Methods, applications, and accuracies. Adv. Agron. 2019, 154, 201–255. [Google Scholar]
- Prasad, A.K.; Chai, L.; Singh, R.P.; Kafatos, M. Crop yield estimation model for Iowa using remote sensing and surface parameters. Int. J. Appl. Earth Obs. Geoinf. 2006, 8, 26–33. [Google Scholar] [CrossRef]
- Lobell, D.B.; Asseng, S. Comparing estimates of climate change impacts from process-based and statistical crop models. Environ. Res. Lett. 2017, 12, 015001. [Google Scholar] [CrossRef]
- Sakamoto, T. Incorporating environmental variables into a MODIS-based crop yield estimation method for United States corn and soybeans through the use of a random forest regression algorithm. ISPRS J. Photogramm. Remote Sens. 2020, 160, 208–228. [Google Scholar] [CrossRef]
- Huang, H.; Huang, J.; Li, X.; Zhuo, W.; Wu, Y.; Niu, Q.; Su, W.; Yuan, W. A dataset of winter wheat aboveground biomass in China during 2007–2015 based on data assimilation. Sci. Data 2022, 9, 200. [Google Scholar] [CrossRef]
- Shahhosseini, M.; Hu, G.; Huber, I.; Archontoulis, S.V. Coupling machine learning and crop modeling improves crop yield prediction in the US Corn Belt. Sci. Rep. 2021, 11, 1606. [Google Scholar] [CrossRef]
- Manivasagam, V.; Rozenstein, O. Practices for upscaling crop simulation models from field scale to large regions. Comput. Electron. Agric. 2020, 175, 105554. [Google Scholar] [CrossRef]
- Peng, B.; Guan, K.; Tang, J.; Ainsworth, E.A.; Asseng, S.; Bernacchi, C.J.; Cooper, M.; Delucia, E.H.; Elliott, J.W.; Ewert, F. Towards a multiscale crop modelling framework for climate change adaptation assessment. Nat. Plants 2020, 6, 338–348. [Google Scholar] [CrossRef]
- Báez-González, A.D.; Chen, P.y.; Tiscareño-López, M.; Srinivasan, R. Using satellite and field data with crop growth modeling to monitor and estimate corn yield in Mexico. Crop Sci. 2002, 42, 1943–1949. [Google Scholar] [CrossRef]
- Shanahan, J.F.; Schepers, J.S.; Francis, D.D.; Varvel, G.E.; Wilhelm, W.W.; Tringe, J.M.; Schlemmer, M.R.; Major, D.J. Use of remote-sensing imagery to estimate corn grain yield. Agron. J. 2001, 93, 583–589. [Google Scholar] [CrossRef]
- Dias, H.B.; Sentelhas, P.C. Evaluation of three sugarcane simulation models and their ensemble for yield estimation in commercially managed fields. Field Crops Res. 2017, 213, 174–185. [Google Scholar] [CrossRef]
- Kephe, P.N.; Ayisi, K.K.; Petja, B.M. Challenges and opportunities in crop simulation modelling under seasonal and projected climate change scenarios for crop production in South Africa. Agric. Food Secur. 2021, 10, 1–24. [Google Scholar] [CrossRef]
- Appiah, M.; Bracho-Mujica, G.; Svane, S.; Styczen, M.; Kersebaum, K.C.; Rötter, R.P. The impact of high quality field data on crop model calibration. In Proceedings of the EGU General Assembly Conference 2022, Vienna, Austria, 23–27 May 2022. [Google Scholar] [CrossRef]
- Schauberger, B.; Jägermeyr, J.; Gornott, C. A systematic review of local to regional yield forecasting approaches and frequently used data resources. Eur. J. Agron. 2020, 120, 126153. [Google Scholar] [CrossRef]
- Lobell, D.B.; Burke, M.B. On the use of statistical models to predict crop yield responses to climate change. Agric. For. Meteorol. 2010, 150, 1443–1452. [Google Scholar] [CrossRef]
- Li, Y.; Guan, K.; Yu, A.; Peng, B.; Zhao, L.; Li, B.; Peng, J. Toward building a transparent statistical model for improving crop yield prediction: Modeling rainfed corn in the US. Field Crops Res. 2019, 234, 55–65. [Google Scholar] [CrossRef]
- Clevers, J. A simplified approach for yield prediction of sugar beet based on optical remote sensing data. Remote Sens. Environ. 1997, 61, 221–228. [Google Scholar] [CrossRef]
- Sehgal, V.; Sastri, C.; Kalra, N.; Dadhwal, V. Farm-level yield mapping for precision crop management by linking remote sensing inputs and a crop simulation model. J. Indian Soc. Remote Sens. 2005, 33, 131–136. [Google Scholar] [CrossRef]
- Sibley, A.M.; Grassini, P.; Thomas, N.E.; Cassman, K.G.; Lobell, D.B. Testing remote sensing approaches for assessing yield variability among maize fields. Agron. J. 2014, 106, 24–32. [Google Scholar] [CrossRef]
- Lobell, D.B.; Thau, D.; Seifert, C.; Engle, E.; Little, B. A scalable satellite-based crop yield mapper. Remote Sens. Environ. 2015, 164, 324–333. [Google Scholar] [CrossRef]
- Jin, Z.; Azzari, G.; Lobell, D.B. Improving the accuracy of satellite-based high-resolution yield estimation: A test of multiple scalable approaches. Agric. For. Meteorol. 2017, 247, 207–220. [Google Scholar] [CrossRef]
- Azzari, G.; Jain, M.; Lobell, D.B. Towards fine resolution global maps of crop yields: Testing multiple methods and satellites in three countries. Remote Sens. Environ. 2017, 202, 129–141. [Google Scholar] [CrossRef]
- Deines, J.M.; Patel, R.; Liang, S.-Z.; Dado, W.; Lobell, D.B. A million kernels of truth: Insights into scalable satellite maize yield mapping and yield gap analysis from an extensive ground dataset in the US Corn Belt. Remote Sens. Environ. 2021, 253, 112174. [Google Scholar] [CrossRef]
- Waldner, F.; Horan, H.; Chen, Y.; Hochman, Z. High temporal resolution of leaf area data improves empirical estimation of grain yield. Sci. Rep. 2019, 9, 15714. [Google Scholar] [CrossRef]
- Zhao, Y.; Xiao, D.; Bai, H. The simultaneous prediction of yield and maturity date for wheat–maize by combining satellite images with crop model. J. Sci. Food Agric. 2024. online. [Google Scholar] [CrossRef] [PubMed]
- Jain, M.; Singh, B.; Srivastava, A.; Malik, R.K.; McDonald, A.; Lobell, D.B. Using satellite data to identify the causes of and potential solutions for yield gaps in India’s Wheat Belt. Environ. Res. Lett. 2017, 12, 094011. [Google Scholar] [CrossRef]
- Seifert, C.A.; Azzari, G.; Lobell, D.B. Satellite detection of cover crops and their effects on crop yield in the Midwestern United States. Environ. Res. Lett. 2018, 13, 064033. [Google Scholar] [CrossRef]
- Zeng, Y.; Hao, D.; Huete, A.; Dechant, B.; Berry, J.; Chen, J.M.; Joiner, J.; Frankenberg, C.; Bond-Lamberty, B.; Ryu, Y. Optical vegetation indices for monitoring terrestrial ecosystems globally. Nat. Rev. Earth Environ. 2022, 3, 477–493. [Google Scholar] [CrossRef]
- Wang, Q.; Adiku, S.; Tenhunen, J.; Granier, A. On the relationship of NDVI with leaf area index in a deciduous forest site. Remote Sens. Environ. 2005, 94, 244–255. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, Z.; Luo, Y.; Cao, J.; Xie, R.; Li, S. Integrating satellite-derived climatic and vegetation indices to predict smallholder maize yield using deep learning. Agric. For. Meteorol. 2021, 311, 108666. [Google Scholar] [CrossRef]
- Shuai, G.; Basso, B. Subfield maize yield prediction improves when in-season crop water deficit is included in remote sensing imagery-based models. Remote Sens. Environ. 2022, 272, 112938. [Google Scholar] [CrossRef]
- Zhu, X.; Guo, R.; Liu, T.; Xu, K. Crop yield prediction based on agrometeorological indexes and remote sensing data. Remote Sens. 2021, 13, 2016. [Google Scholar] [CrossRef]
- Han, D.; Wang, P.; Tansey, K.; Zhang, S.; Tian, H.; Zhang, Y.; Li, H. Improving wheat yield estimates by integrating a remotely sensed drought monitoring index into the simple algorithm for yield estimate model. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 10383–10394. [Google Scholar] [CrossRef]
- Sakamoto, T.; Gitelson, A.A.; Arkebauer, T.J. MODIS-based corn grain yield estimation model incorporating crop phenology information. Remote Sens. Environ. 2013, 131, 215–231. [Google Scholar] [CrossRef]
- Li, S.; Sun, Z.; Zhang, X.; Zhu, W.; Li, Y. An improved threshold method to detect the phenology of winter wheat. In Proceedings of the 2018 7th International Conference on Agro-Geoinformatics (Agro-Geoinformatics), Hangzhou, China, 6–9 August 2018; pp. 1–5. [Google Scholar]
- Cheng, E.; Zhang, B.; Peng, D.; Zhong, L.; Yu, L.; Liu, Y.; Xiao, C.; Li, C.; Li, X.; Chen, Y. Wheat yield estimation using remote sensing data based on machine learning approaches. Front. Plant Sci. 2022, 13, 1090970. [Google Scholar] [CrossRef] [PubMed]
- Ashapure, A.; Jung, J.; Chang, A.; Oh, S.; Yeom, J.; Maeda, M.; Maeda, A.; Dube, N.; Landivar, J.; Hague, S. Developing a machine learning based cotton yield estimation framework using multi-temporal UAS data. ISPRS J. Photogramm. Remote Sens. 2020, 169, 180–194. [Google Scholar] [CrossRef]
- Guo, H.; Li, M.; Wang, L.; Wang, Y.; Zang, X.; Zhao, X.; Wang, H.; Zhu, J. Evaluation of groundwater suitability for irrigation and drinking purposes in an agricultural region of the North China Plain. Water 2021, 13, 3426. [Google Scholar] [CrossRef]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Balaghi, R.; Tychon, B.; Eerens, H.; Jlibene, M. Empirical regression models using NDVI, rainfall and temperature data for the early prediction of wheat grain yields in Morocco. Int. J. Appl. Earth Obs. Geoinf. 2008, 10, 438–452. [Google Scholar] [CrossRef]
- Son, N.; Chen, C.; Chen, C.; Minh, V.; Trung, N. A comparative analysis of multitemporal MODIS EVI and NDVI data for large-scale rice yield estimation. Agric. For. Meteorol. 2014, 197, 52–64. [Google Scholar] [CrossRef]
- Abatzoglou, J.T.; Dobrowski, S.Z.; Parks, S.A.; Hegewisch, K.C. TerraClimate, a high-resolution global dataset of monthly climate and climatic water balance from 1958–2015. Sci. Data 2018, 5, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Luo, Y.; Zhang, Z.; Li, Z.; Chen, Y.; Zhang, L.; Cao, J.; Tao, F. Identifying the spatiotemporal changes of annual harvesting areas for three staple crops in China by integrating multi-data sources. Environ. Res. Lett. 2020, 15, 074003. [Google Scholar] [CrossRef]
- Van Diepen, C.v.; Wolf, J.v.; Van Keulen, H.; Rappoldt, C. WOFOST: A simulation model of crop production. Soil Use Manag. 1989, 5, 16–24. [Google Scholar] [CrossRef]
- Tanaka, S.; Kawamura, K.; Maki, M.; Muramoto, Y.; Yoshida, K.; Akiyama, T. Spectral index for quantifying leaf area index of winter wheat by field hyperspectral measurements: A case study in Gifu Prefecture, Central Japan. Remote Sens. 2015, 7, 5329–5346. [Google Scholar] [CrossRef]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.-Y. LightGBM: A Highly Efficient Gradient Boosting Decision Tree. In Proceedings of the NIPS’17 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 1–9. [Google Scholar]
- Cao, J.; Zhang, Z.; Tao, F.; Zhang, L.; Luo, Y.; Han, J.; Li, Z. Identifying the contributions of multi-source data for winter wheat yield prediction in China. Remote Sens. 2020, 12, 750. [Google Scholar] [CrossRef]
- Mutanga, O.; Skidmore, A.K. Narrow band vegetation indices overcome the saturation problem in biomass estimation. Int. J. Remote Sens. 2004, 25, 3999–4014. [Google Scholar] [CrossRef]
- Delegido, J.; Verrelst, J.; Meza, C.; Rivera, J.; Alonso, L.; Moreno, J. A red-edge spectral index for remote sensing estimation of green LAI over agroecosystems. Eur. J. Agron. 2013, 46, 42–52. [Google Scholar] [CrossRef]
- Kimm, H.; Guan, K.; Jiang, C.; Miao, G.; Wu, G.; Suyker, A.E.; Ainsworth, E.A.; Bernacchi, C.J.; Montes, C.M.; Berry, J.A. A physiological signal derived from sun-induced chlorophyll fluorescence quantifies crop physiological response to environmental stresses in the US Corn Belt. Environ. Res. Lett. 2021, 16, 124051. [Google Scholar] [CrossRef]
- Lecerf, R.; Ceglar, A.; López-Lozano, R.; Van Der Velde, M.; Baruth, B. Assessing the information in crop model and meteorological indicators to forecast crop yield over Europe. Agric. Syst. 2019, 168, 191–202. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, Z.; Tao, F.; Wang, P.; Wei, X. Spatio-temporal patterns of winter wheat yield potential and yield gap during the past three decades in North China. Field Crops Res. 2017, 206, 11–20. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, P.; Chen, Y.; Song, X.; Wei, X.; Shi, P. Global warming over 1960–2009 did increase heat stress and reduce cold stress in the major rice-planting areas across China. Eur. J. Agron. 2014, 59, 49–56. [Google Scholar] [CrossRef]
- Huang, J.; Sedano, F.; Huang, Y.; Ma, H.; Li, X.; Liang, S.; Tian, L.; Zhang, X.; Fan, J.; Wu, W. Assimilating a synthetic Kalman filter leaf area index series into the WOFOST model to improve regional winter wheat yield estimation. Agric. For. Meteorol. 2016, 216, 188–202. [Google Scholar] [CrossRef]
- Zhu, P.; Jin, Z.; Zhuang, Q.; Ciais, P.; Bernacchi, C.; Wang, X.; Makowski, D.; Lobell, D. The important but weakening maize yield benefit of grain filling prolongation in the US Midwest. Glob. Change Biol. 2018, 24, 4718–4730. [Google Scholar] [CrossRef]
- Wu, S.; Yang, P.; Ren, J.; Chen, Z.; Liu, C.; Li, H. Winter wheat LAI inversion considering morphological characteristics at different growth stages coupled with microwave scattering model and canopy simulation model. Remote Sens. Environ. 2020, 240, 111681. [Google Scholar] [CrossRef]
| precip a | sr b | tmean c | tmax d | t_key e | t_percent f | |
|---|---|---|---|---|---|---|
| mm | W/m2 | °C | °C | days | ||
| mean | 175.46 | 231.12 | 14.89 | 30.69 | 44.14 | 0.32 |
| min | 66 | 187.95 | 9.4 | 22.8 | 28 | 0.16 |
| max | 482 | 251 | 17.53 | 35.6 | 60 | 0.59 |
| std | 69.17 | 10.84 | 1.41 | 2.26 | 7.67 | 0.10 |
| OLS | RF | LightGBM | |||||
|---|---|---|---|---|---|---|---|
| R2 | RMSE | R2 | RMSE | R2 | RMSE | ||
| Vis a only | GCVI | 0.31 | 396 | 0.35 | 384 | 0.42 | 365 |
| NDVI | 0.15 | 438 | 0.35 | 384 | 0.42 | 365 | |
| EVI | 0.18 | 430 | 0.35 | 384 | 0.42 | 365 | |
| Climate b only | 0.23 | 411 | 0.26 | 402 | 0.26 | 401 | |
| VIs + Climate | GCVI | 0.51 | 326 | 0.57 | 307 | 0.57 | 307 |
| NDVI | 0.44 | 349 | 0.57 | 307 | 0.57 | 307 | |
| EVI | 0.46 | 343 | 0.57 | 307 | 0.57 | 307 | |
| VIs + Phe c | GCVI | 0.39 | 362 | 0.40 | 359 | 0.45 | 345 |
| NDVI | 0.23 | 407 | 0.40 | 359 | 0.45 | 345 | |
| EVI | 0.26 | 397 | 0.40 | 359 | 0.45 | 345 | |
| VIs + Climate + Phe | GCVI | 0.56 | 312 | 0.60 | 295 | 0.58 | 301 |
| NDVI | 0.46 | 343 | 0.60 | 295 | 0.58 | 301 | |
| EVI | 0.49 | 335 | 0.60 | 295 | 0.58 | 301 | |
| OLS | RF | LightGBM | ||||
|---|---|---|---|---|---|---|
| R2 | RMSE | R2 | RMSE | R2 | RMSE | |
| Climate’ a only | 0.00 | 467 | 0.14 | 436 | 0.16 | 431 |
| GCVI + Climate’ | 0.44 | 351 | 0.55 | 315 | 0.55 | 317 |
| GCVI + Climate’ + Phe | 0.51 | 328 | 0.60 | 296 | 0.58 | 304 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Huang, J.; Xiao, G.; Huang, H.; Sun, Z.; Li, X. Improved Winter Wheat Yield Estimation by Combining Remote Sensing Data, Machine Learning, and Phenological Metrics. Remote Sens. 2024, 16, 3217. https://doi.org/10.3390/rs16173217
Li S, Huang J, Xiao G, Huang H, Sun Z, Li X. Improved Winter Wheat Yield Estimation by Combining Remote Sensing Data, Machine Learning, and Phenological Metrics. Remote Sensing. 2024; 16(17):3217. https://doi.org/10.3390/rs16173217
Chicago/Turabian StyleLi, Shiji, Jianxi Huang, Guilong Xiao, Hai Huang, Zhigang Sun, and Xuecao Li. 2024. "Improved Winter Wheat Yield Estimation by Combining Remote Sensing Data, Machine Learning, and Phenological Metrics" Remote Sensing 16, no. 17: 3217. https://doi.org/10.3390/rs16173217
APA StyleLi, S., Huang, J., Xiao, G., Huang, H., Sun, Z., & Li, X. (2024). Improved Winter Wheat Yield Estimation by Combining Remote Sensing Data, Machine Learning, and Phenological Metrics. Remote Sensing, 16(17), 3217. https://doi.org/10.3390/rs16173217









