Radar Anti-Jamming Performance Evaluation Based on Logistic Fusion of Multi-Stage SIR Information
Abstract
1. Introduction
2. Logistic Fusion Model and the MCMC Fusion Method
2.1. Definition of the Logistic Fusion Model
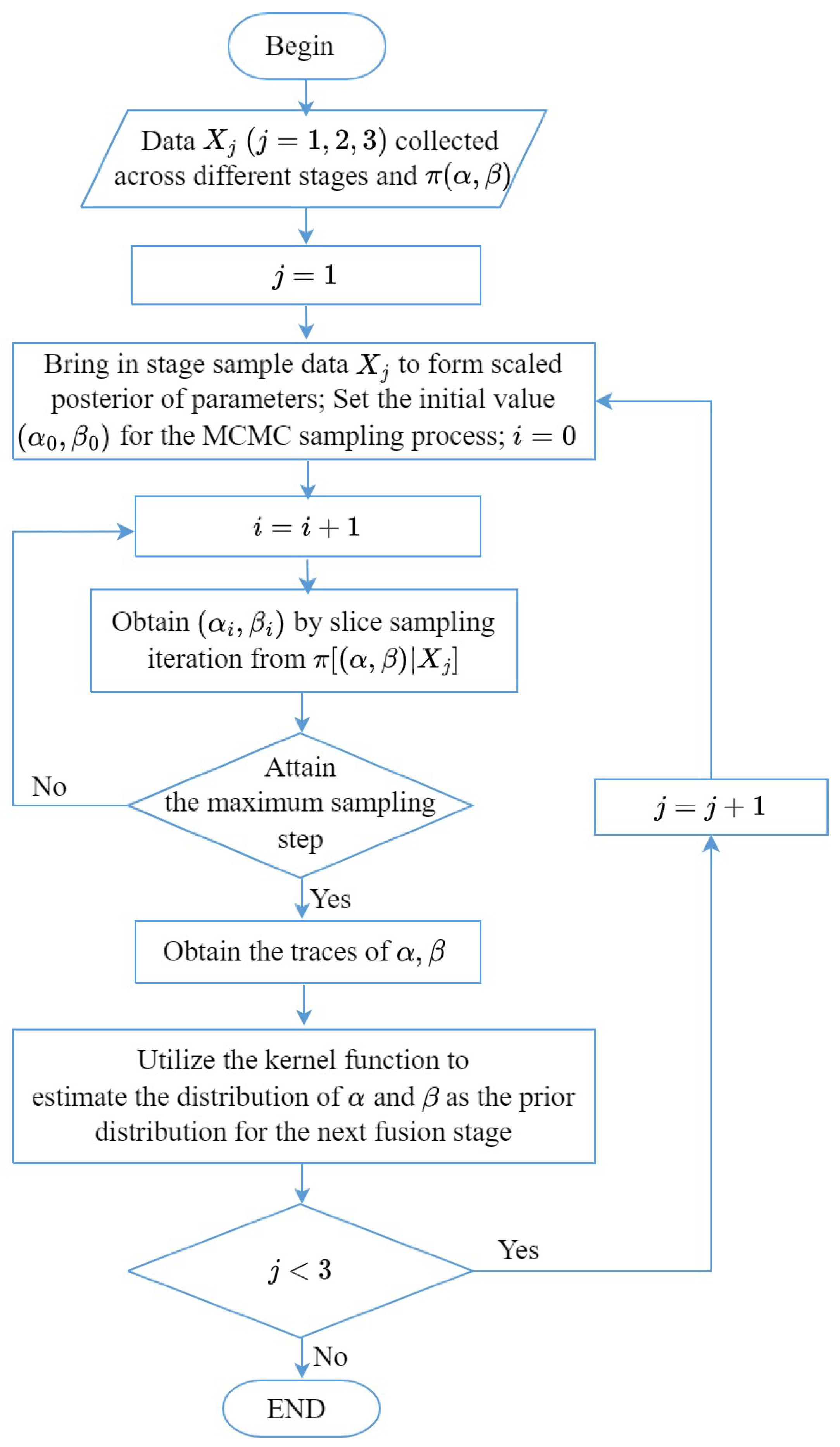
2.2. MCMC Sampling Process
- Sample slice variable: Choose a value z uniformly from the interval .
- Update parameters: Update by sampling a new point from the slice defined by . This involves iteratively sampling along the slice until a suitable point is found.
- Repeat: Repeat the above steps for a sufficient number of iterations to obtain a representative sample from the posterior distribution .
2.3. Multi-Stage Bayesian Fusion Process
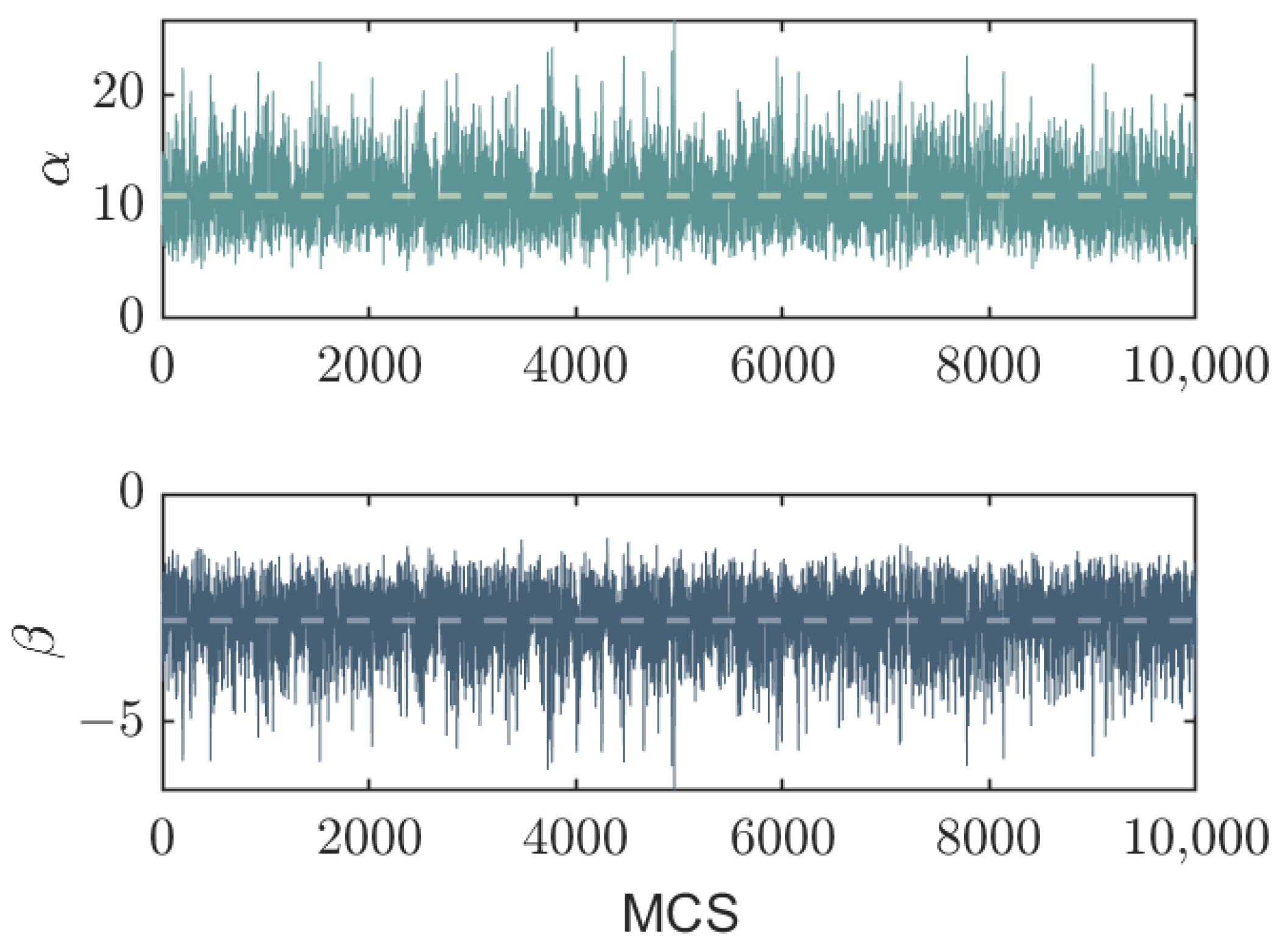
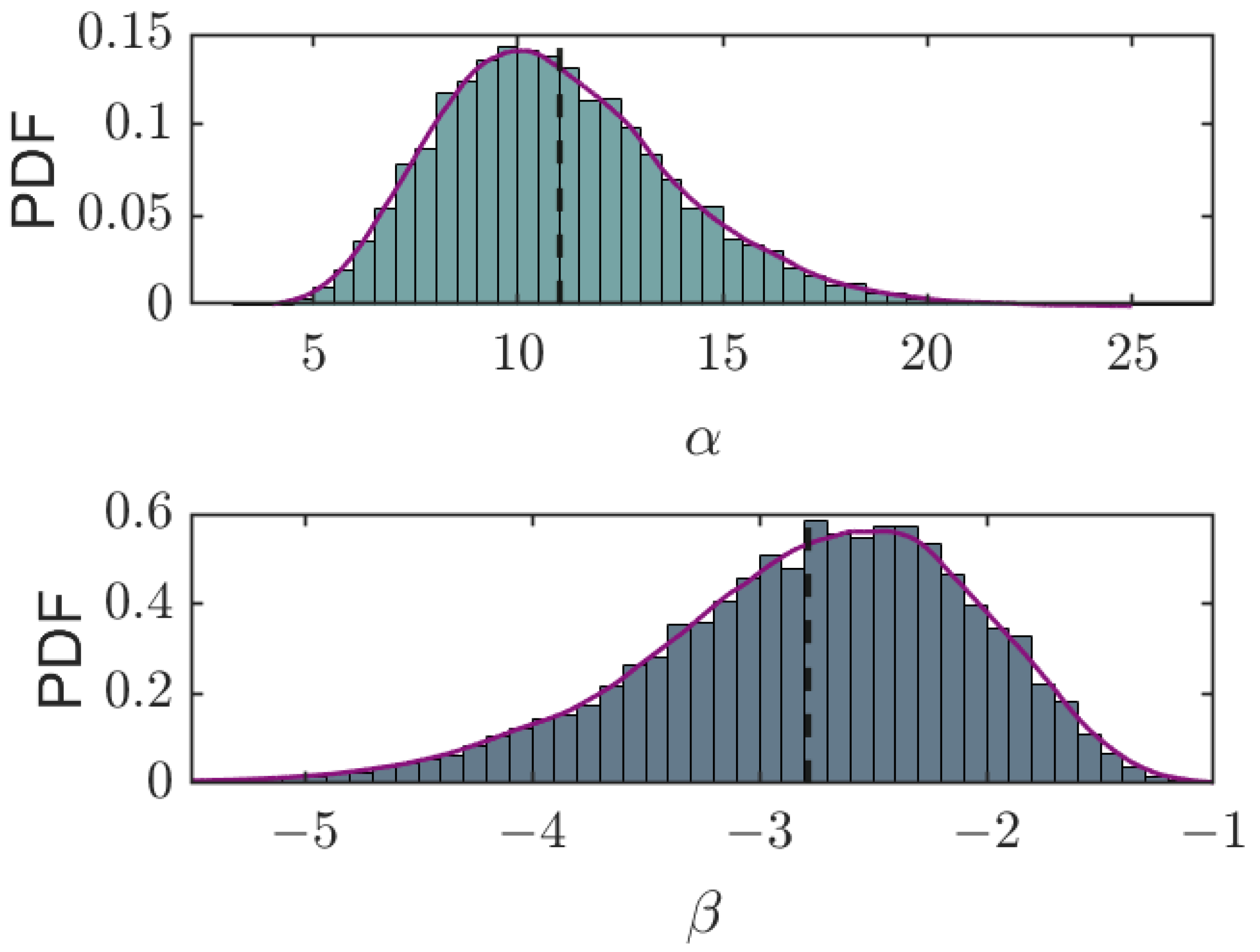
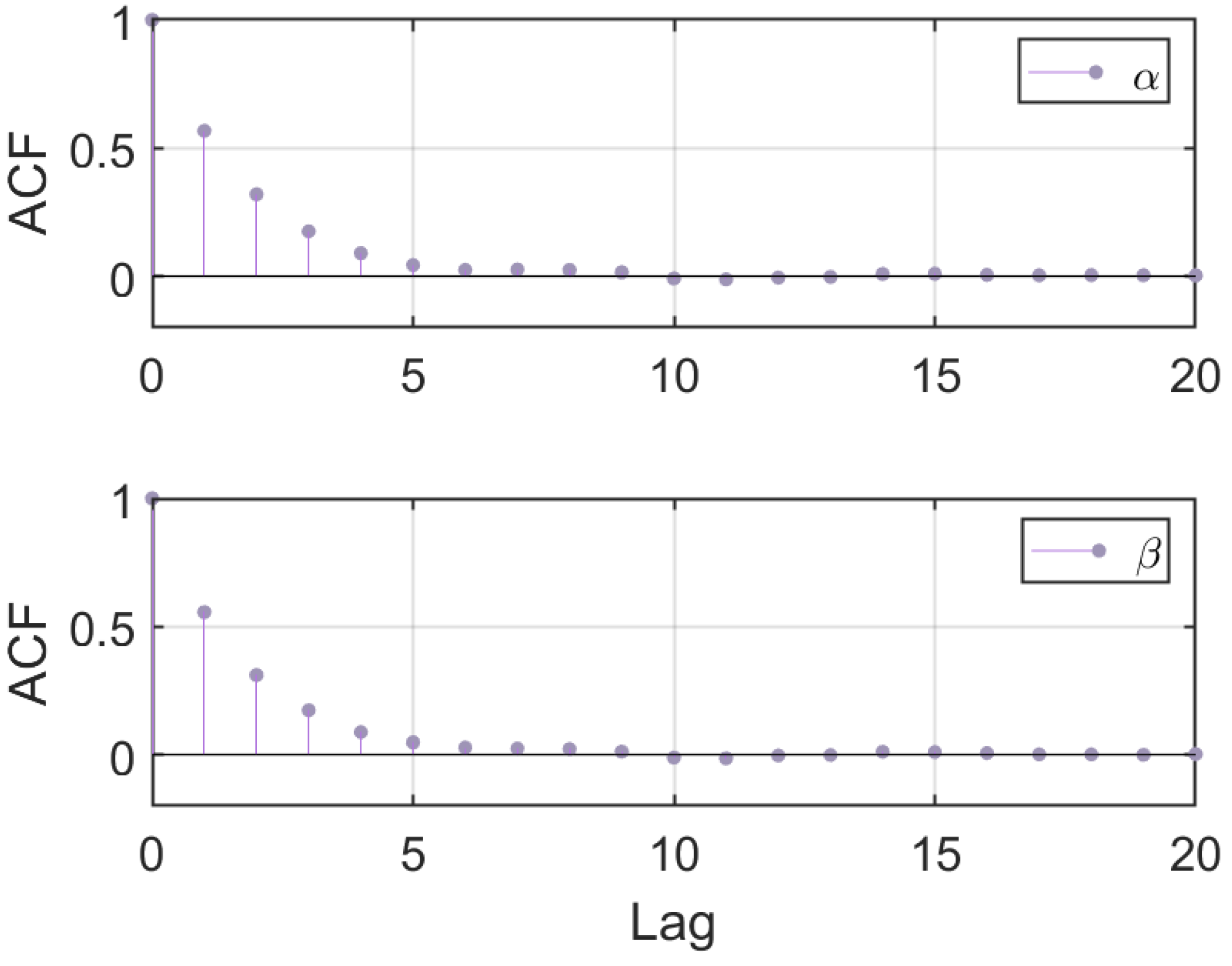
3. Fusion Results
3.1. Data Generation Scheme
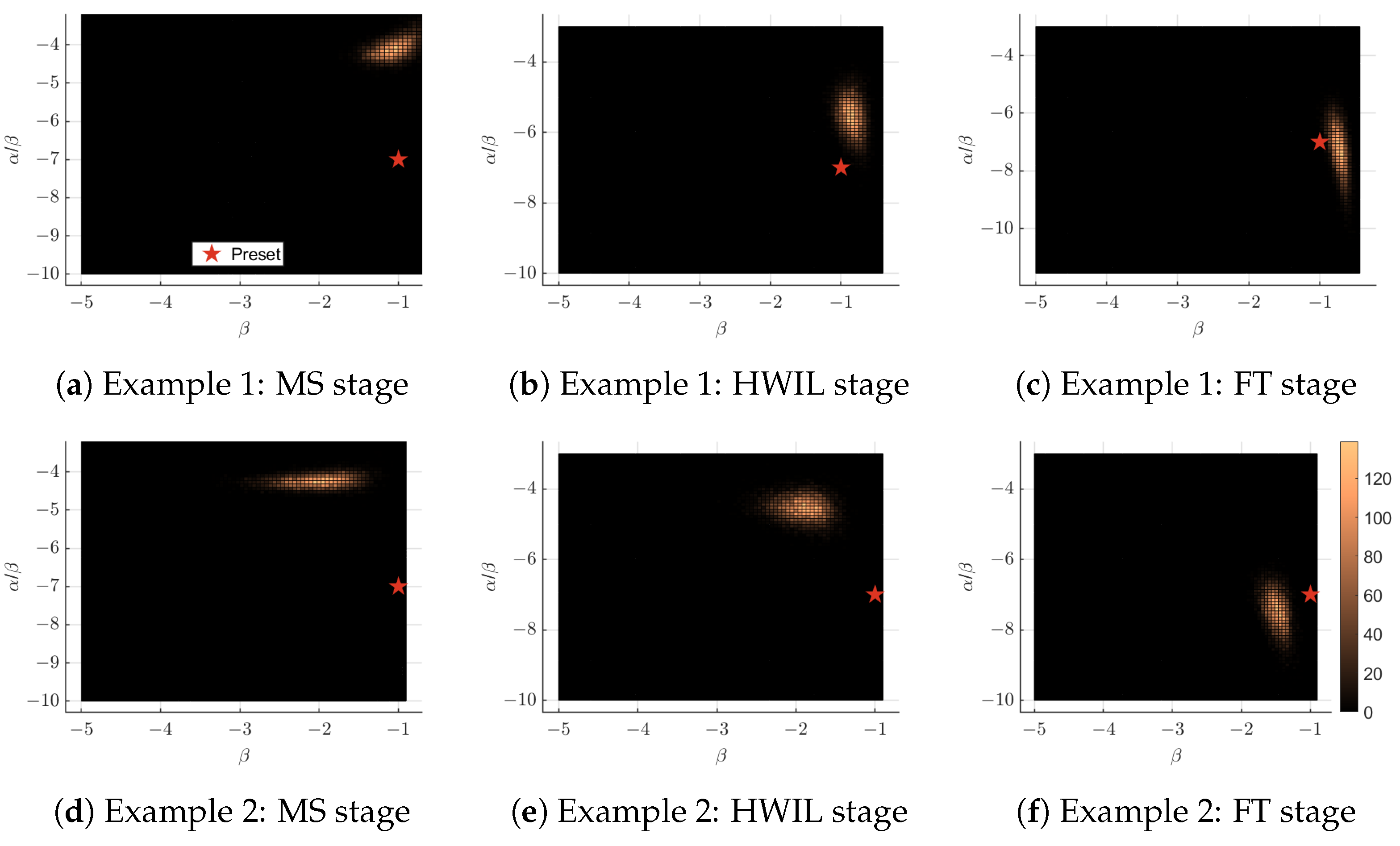
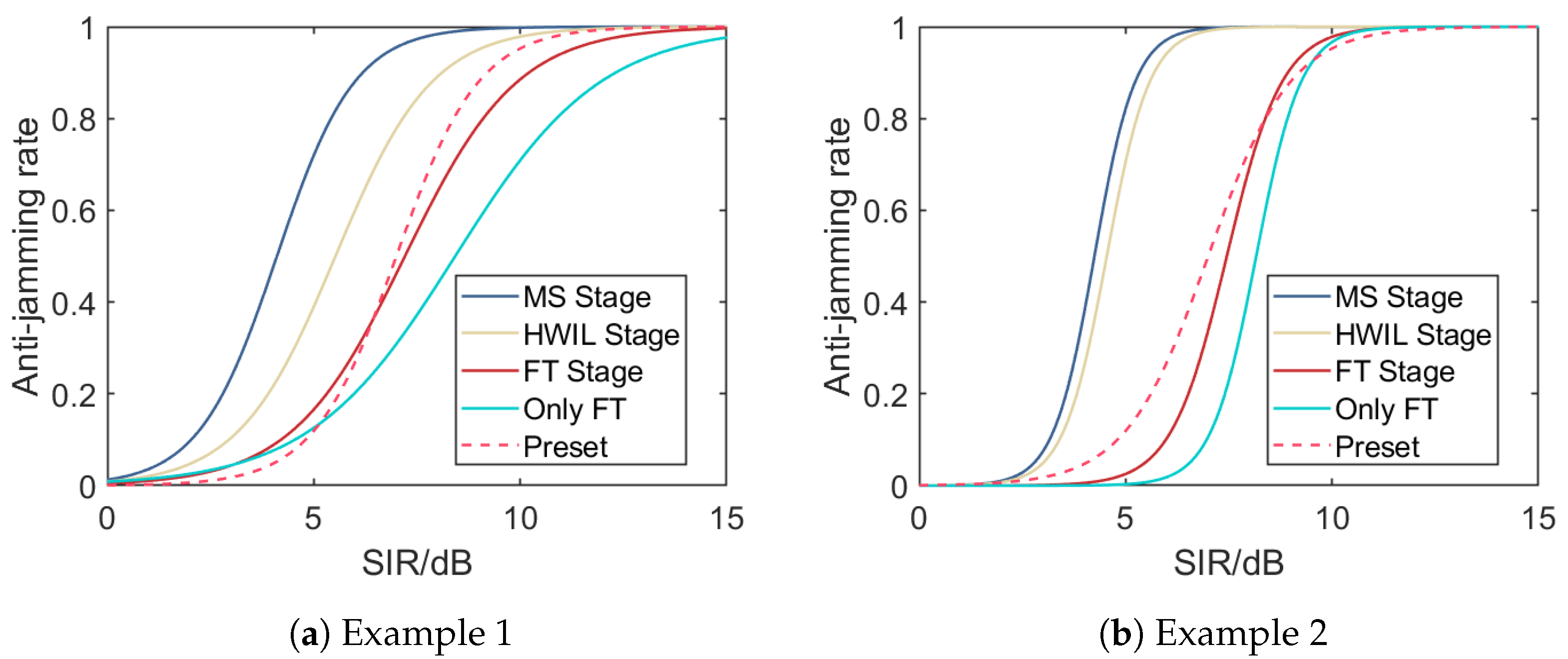
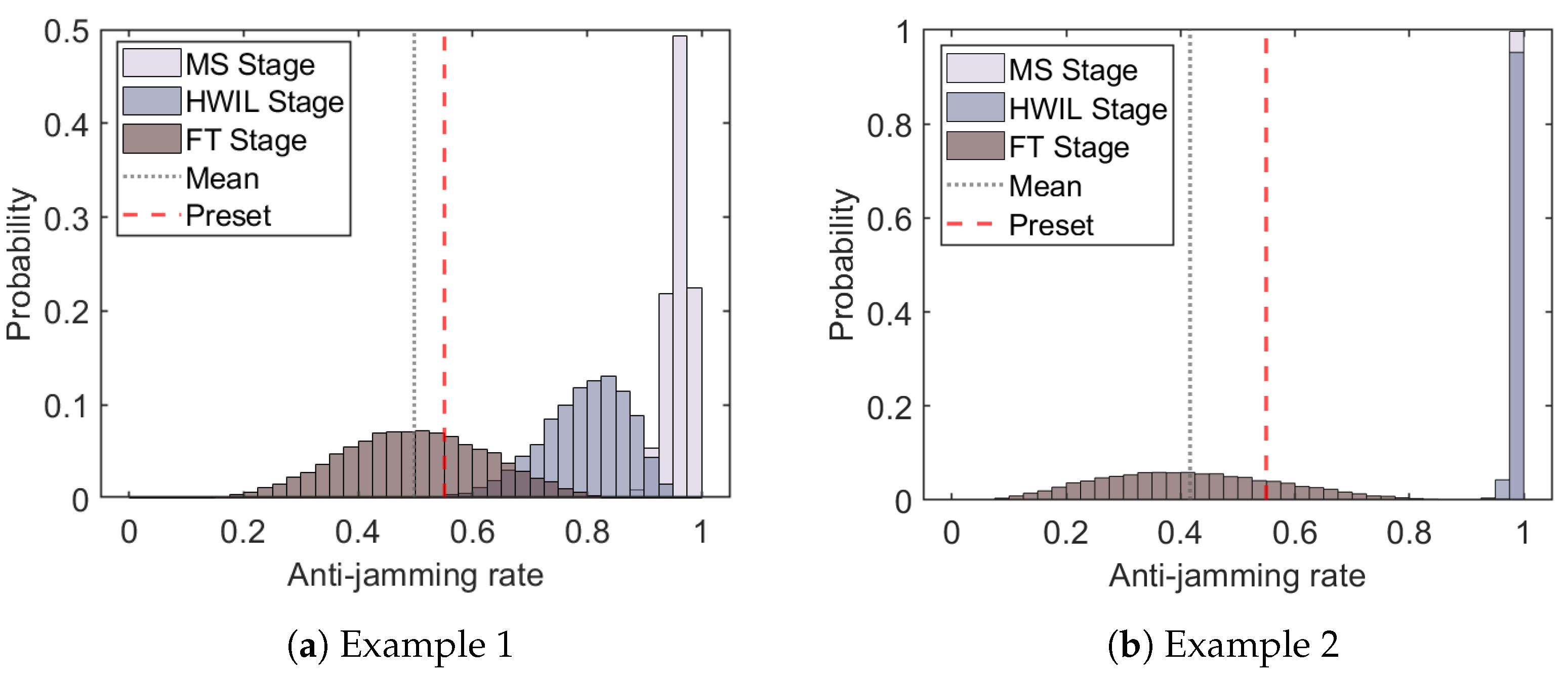
3.2. Fusion Examples
- —
- For the MS stage, samples are generated with SIR increments of within the interval , reflecting the abundance of samples in this stage.
- —
- For the HWIL stage, samples are generated with SIR increments of within the interval , representing a moderate sample size.
- —
- For the FT stage, samples are generated with SIR increments of 1 within the interval , reflecting the scarcity of samples in this stage.
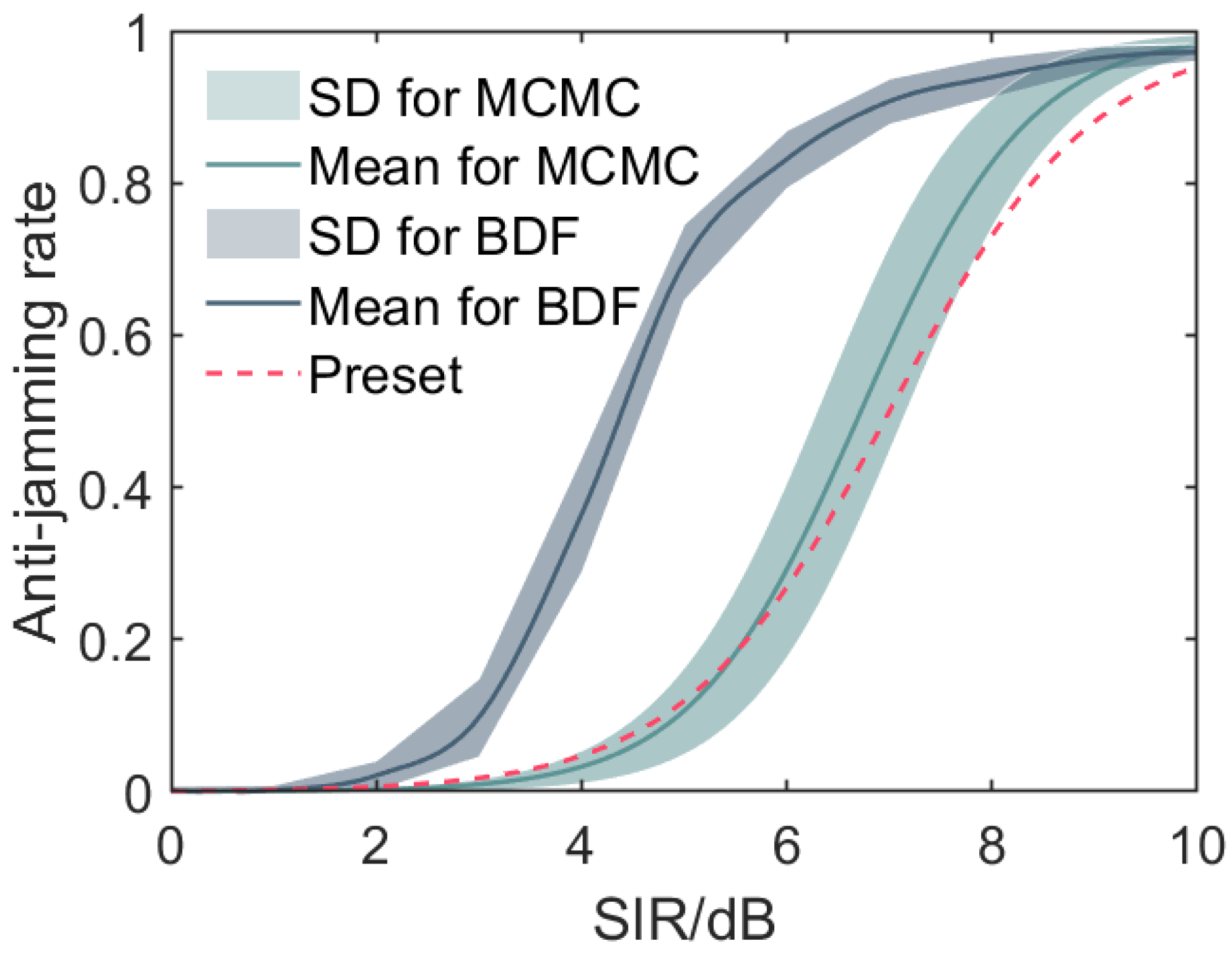
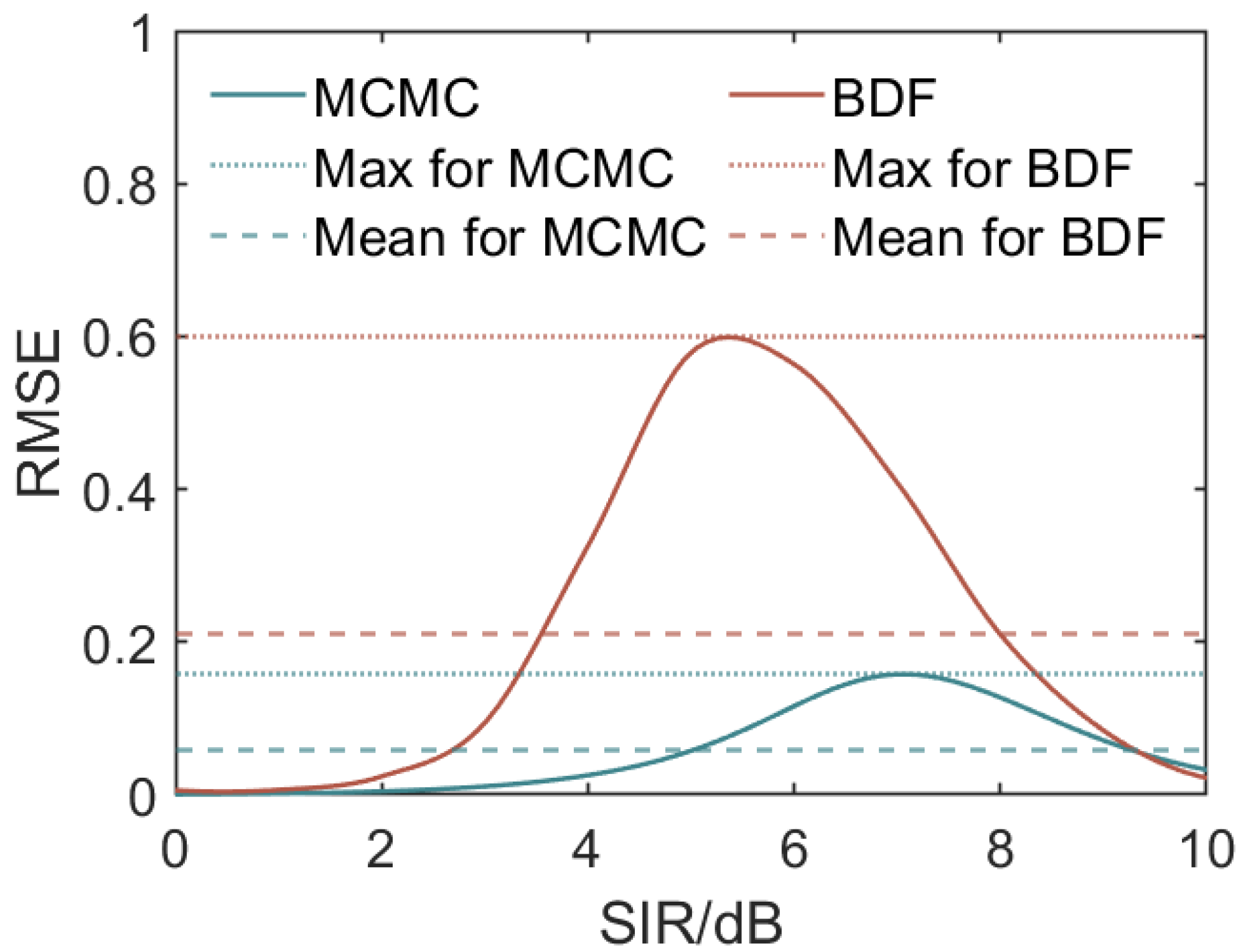
3.3. Comparison with the Other Fusion Models
3.4. Limitations of the Model
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SIR | Signal-to-interference ratio |
| MCMC | Monte Carlo Markov chain |
| MS | Mathematical simulation |
| HWIL | Hardware-in-the-loop |
| FT | Field test |
| ACF | Autocorrelation function |
| ROC | Receiver operating characteristic |
| TPR | True positive rate |
| FPR | False positive rate |
| AUC | Area under the ROC curve |
| BDF | Beta distribution fusion |
| RMSE | Root mean square error |
References
- Claassen, G.; du Plessis, W.P. Time-Interleaved Noise Jamming. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 3359–3367. [Google Scholar] [CrossRef]
- Wei, J.; Wei, Y.; Yu, L.; Xu, R. Radar Anti-Jamming Decision-Making Method Based on DDPG-MADDPG Algorithm. Remote Sens. 2023, 15, 4046. [Google Scholar] [CrossRef]
- Pourranjbar, A.; Kaddoum, G.; Aghababaiyan, K. Deceiving-Based Anti-Jamming Against Single-Tone and Multitone Reactive Jammers. IEEE Trans. Commun. 2022, 70, 6133–6148. [Google Scholar] [CrossRef]
- Liu, X.; Yang, J.; Lu, J.; Liu, G.; Geng, Z. Application of AHP and D-S evidential theory in radar seeker anti-interference performance evaluation. J. Eng. 2019, 2019, 7977–7980. [Google Scholar] [CrossRef]
- Shuang, B.; Jun, H.; Zhiyong, N. Research on Evaluation Method of Radar Anti-jamming Effectiveness Based on Experimental Big Data. In Proceedings of the 2020 6th International Conference on Big Data and Information Analytics (BigDIA), Shenzhen, China, 4–6 December 2020; pp. 392–395. [Google Scholar] [CrossRef]
- Sun, H.; Xie, X. Threat evaluation method of warships formation air defense based on AR(p)-DITOPSIS. J. Syst. Eng. Electron. 2019, 30, 297–307. [Google Scholar]
- Yang, M.; Chen, J.; Niu, Y. An evaluation method of anti-jamming capability to communication system based on cloud-evidence theory. In Proceedings of the 2017 First International Conference on Electronics Instrumentation & Information Systems (EIIS), Harbin, China, 3–5 June 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Bu, F.; He, J.; Li, H.; Fu, Q. Radar seeker anti-jamming performance prediction and evaluation method based on the improved grey wolf optimizer algorithm and support vector machine. In Proceedings of the 2020 IEEE 3rd International Conference on Electronics Technology (ICET), Chengdu, China, 8–12 May 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 704–710. [Google Scholar]
- Deting, H.; Zongfeng, Q.; Teng, J.; Minpeng, Z. Effectiveness evaluation method for warning radar in jamming environment. In Proceedings of the 2018 Chinese Control And Decision Conference (CCDC), Shenyang, China, 9–11 June 2018; pp. 1755–1760. [Google Scholar]
- Li, C.; Liu, J.; Liu, X.; Kang, X.; Li, S. Combining Time-Series Variation Modeling and Fuzzy Spatiotemporal Feature Fusion: A novel Approach for unsupervised Flood Mapping using Dual-polarized Sentinel-1 SAR Images. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–15. [Google Scholar] [CrossRef]
- Peng, J.; Sun, W.; Li, H.C.; Li, W.; Meng, X.; Ge, C.; Du, Q. Low-rank and sparse representation for hyperspectral image processing: A review. IEEE Geosci. Remote Sens. Mag. 2021, 10, 10–43. [Google Scholar] [CrossRef]
- Vivone, G. Multispectral and hyperspectral image fusion in remote sensing: A survey. Inf. Fusion 2023, 89, 405–417. [Google Scholar] [CrossRef]
- Shiraki, N.; Honma, N.; Murata, K.; Nakayama, T.; Iizuka, S. Experimental Evaluation of Multi-Target Localization Accuracy Using Multistatic MIMO Radar. IEEE Sens. J. 2023, 23, 28863–28871. [Google Scholar] [CrossRef]
- Mahler, R.P. Advances in Statistical Multisource-Multitarget Information Fusion; Artech House: Norwood, MA, USA, 2014. [Google Scholar]
- Yang, Y.; Da, K.; Zhu, Y.; Xiang, S.; Fu, Q. Consensus based target tracking against deception jamming in distributed radar networks. IET Radar Sonar Navig. 2023, 17, 683–700. [Google Scholar] [CrossRef]
- Zhao, S.; Zhang, L.; Zhou, Y.; Liu, N.; Liu, J. Discrimination of active false targets in multistatic radar using spatial scattering properties. IET Radar Sonar Navig. 2016, 10, 817–826. [Google Scholar] [CrossRef]
- Ling, Q.; Huang, P.; Wang, D.; Xu, H.; Wang, L.; Liu, X.; Liao, G.; Sun, Y. Range Deception Jamming Performance Evaluation for Moving Targets in a Ground-Based Radar Network. Electronics 2023, 12, 1614. [Google Scholar] [CrossRef]
- Liu, X.; Yang, J.; Hou, B.; Lu, J.; Yao, Z. Radar seeker performance evaluation based on information fusion method. SN Appl. Sci. 2020, 2, 674. [Google Scholar] [CrossRef]
- Yang, C.; Feng, L.; Zhang, H.; He, S.; Shi, Z. A novel data fusion algorithm to combat false data injection attacks in networked radar systems. IEEE Trans. Signal Inf. Process. Networks 2018, 4, 125–136. [Google Scholar] [CrossRef]
- Qiao, S.; Fan, Y.; Zhang, H. An Improved Multi-Radar Track Weighted Data Fusion Algorithm. In Proceedings of the 2023 42nd Chinese Control Conference (CCC), Tianjin, China, 24–26 July 2023; pp. 3152–3156. [Google Scholar] [CrossRef]
- Han, L.; Ning, Q.; Chen, B.; Lei, Y.; Zhou, X. Ground threat evaluation and jamming allocation model with Markov chain for aircraft. IET Radar, Sonar Navig. 2020, 14, 1039–1045. [Google Scholar] [CrossRef]
- Zhao, L.; Yan, L.; Duan, X.; Wang, Z. A Bayesian Multistage Fusion Model for Radar Antijamming Performance Evaluation. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 729–740. [Google Scholar] [CrossRef]
- Seng, C.H.; Bouzerdoum, A.; Amin, M.G.; Phung, S.L. Two-Stage Fuzzy Fusion with Applications to Through-the-Wall Radar Imaging. IEEE Geosci. Remote Sens. Lett. 2012, 10, 687–691. [Google Scholar] [CrossRef]
- Molin, R.D.; Rosa, R.A.; Bayer, F.M.; Pettersson, M.I.; Machado, R. A Change Detection Algorithm for Sar Images Based on Logistic Regression. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1514–1517. [Google Scholar]
- Shao, F.; Xing, H. Logistic regression prediction based on fractal characteristics of sea surface targets. In Proceedings of the 2019 14th IEEE International Conference on Electronic Measurement & Instruments (ICEMI), Changsha, China, 1–3 November 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 545–550. [Google Scholar]
- Kou, L.; Tang, J.; Wang, Z.; Jiang, Y.; Chu, Z. An Adaptive Rainfall Estimation Algorithm for Dual-Polarization Radar. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Araveeporn, A.; Klomwises, Y. The estimated parameter of logistic regression model by Markov Chain Monte Carlo method with multicollinearity. Stat. J. IAOS 2020, 36, 1253–1259. [Google Scholar] [CrossRef]
- Al-Khairullah, N.A.; Al-Baldawi, T.H. Bayesian Computational Methods of the Logistic Regression Model. J. Phys. Conf. Ser. 2021, 1804, 012073. [Google Scholar] [CrossRef]
- van Ravenzwaaij, D.; Cassey, P.; Brown, S.D. A simple introduction to Markov Chain Monte–Carlo sampling. Psychon. Bull. Rev. 2018, 25, 143–154. [Google Scholar] [CrossRef]
- Neal, R.M. Slice sampling. Ann. Stat. 2003, 31, 705–767. [Google Scholar] [CrossRef]
- Epanechnikov, V.A. Non-Parametric Estimation of a Multivariate Probability Density. Theory Probab. Its Appl. 1969, 14, 153–158. [Google Scholar] [CrossRef]
- Joo, H.; Choi, C.; Kim, J.; Kim, D.; Kim, S.; Kim, H.S. A Bayesian Network-Based Integrated for Flood Risk Assessment (InFRA). Sustainability 2019, 11, 3733. [Google Scholar] [CrossRef]
- Zheng, Y.J. Research on combat effectiveness evaluation of radar EW system based on Bayesian network. Adv. Mater. Res. 2011, 204, 1697–1700. [Google Scholar] [CrossRef]
- Pearl, J. Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Hao, H.; Duan, Z. Tracking With Sequentially Fused Radar and Acoustic Sensor Data With Propagation Delay. IEEE Sens. J. 2023, 23, 7345–7361. [Google Scholar] [CrossRef]
- Saaty, R.W. The analytic hierarchy process—What it is and how it is used. Math. Model. 1987, 9, 161–176. [Google Scholar] [CrossRef]



| Metric | Dataset Size | Gaussian Samples | Exponential Samples | Beta Samples | |||
|---|---|---|---|---|---|---|---|
| KernelE | KernelG | KernelE | KernelG | KernelE | KernelG | ||
| 1000 | 3.74 | 11.39 | 4.01 | 12.02 | 4.23 | 14.56 | |
| Time (ms) | 10,000 | 27.60 | 66.56 | 27.15 | 64.10 | 27.07 | 66.76 |
| 100,000 | 96.09 | 456.70 | 85.61 | 383.03 | 86.12 | 351.05 | |
| 1000 | 0.0103 | 0.0179 | 0.0080 | 0.0107 | 0.0576 | 0.0901 | |
| RMSE | 10,000 | 0.0042 | 0.0074 | 0.0059 | 0.0077 | 0.0233 | 0.0391 |
| 100,000 | 0.0016 | 0.0028 | 0.0044 | 0.0058 | 0.0099 | 0.0160 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, L.; Yan, L.; Duan, X.; Wang, Z. Radar Anti-Jamming Performance Evaluation Based on Logistic Fusion of Multi-Stage SIR Information. Remote Sens. 2024, 16, 3214. https://doi.org/10.3390/rs16173214
Zhao L, Yan L, Duan X, Wang Z. Radar Anti-Jamming Performance Evaluation Based on Logistic Fusion of Multi-Stage SIR Information. Remote Sensing. 2024; 16(17):3214. https://doi.org/10.3390/rs16173214
Chicago/Turabian StyleZhao, Linqi, Liang Yan, Xiaojun Duan, and Zhengming Wang. 2024. "Radar Anti-Jamming Performance Evaluation Based on Logistic Fusion of Multi-Stage SIR Information" Remote Sensing 16, no. 17: 3214. https://doi.org/10.3390/rs16173214
APA StyleZhao, L., Yan, L., Duan, X., & Wang, Z. (2024). Radar Anti-Jamming Performance Evaluation Based on Logistic Fusion of Multi-Stage SIR Information. Remote Sensing, 16(17), 3214. https://doi.org/10.3390/rs16173214







