A Denoising Method Based on DDPM for Radar Emitter Signal Intra-Pulse Modulation Classification
Abstract
1. Introduction
2. Materials and Methods
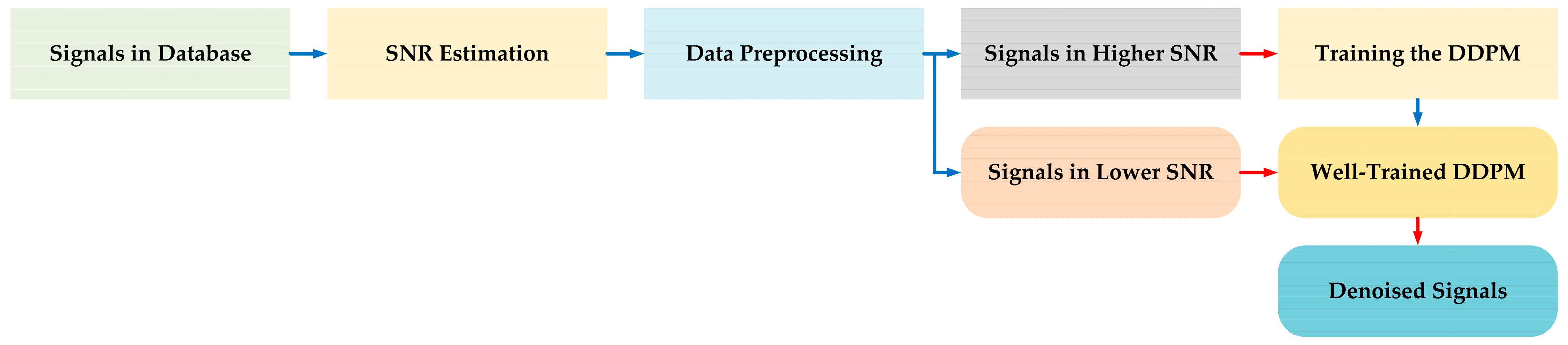
2.1. Denoising Method Based on DDPM
2.2. Structure of the U-Net Model for Denoising
2.3. SNR Estimation
2.4. Data Preprocessing
3. Dataset and Experimental Settings
3.1. Radar Emitter Signal Intra-Pulse Modulation Dataset
3.2. Description of the Experiments with Different Conditions
3.3. Baseline DNN Classification Models for Classification
3.4. CDAE Model
4. Experiment
4.1. Parameter Setting for Denoising U-Net Model
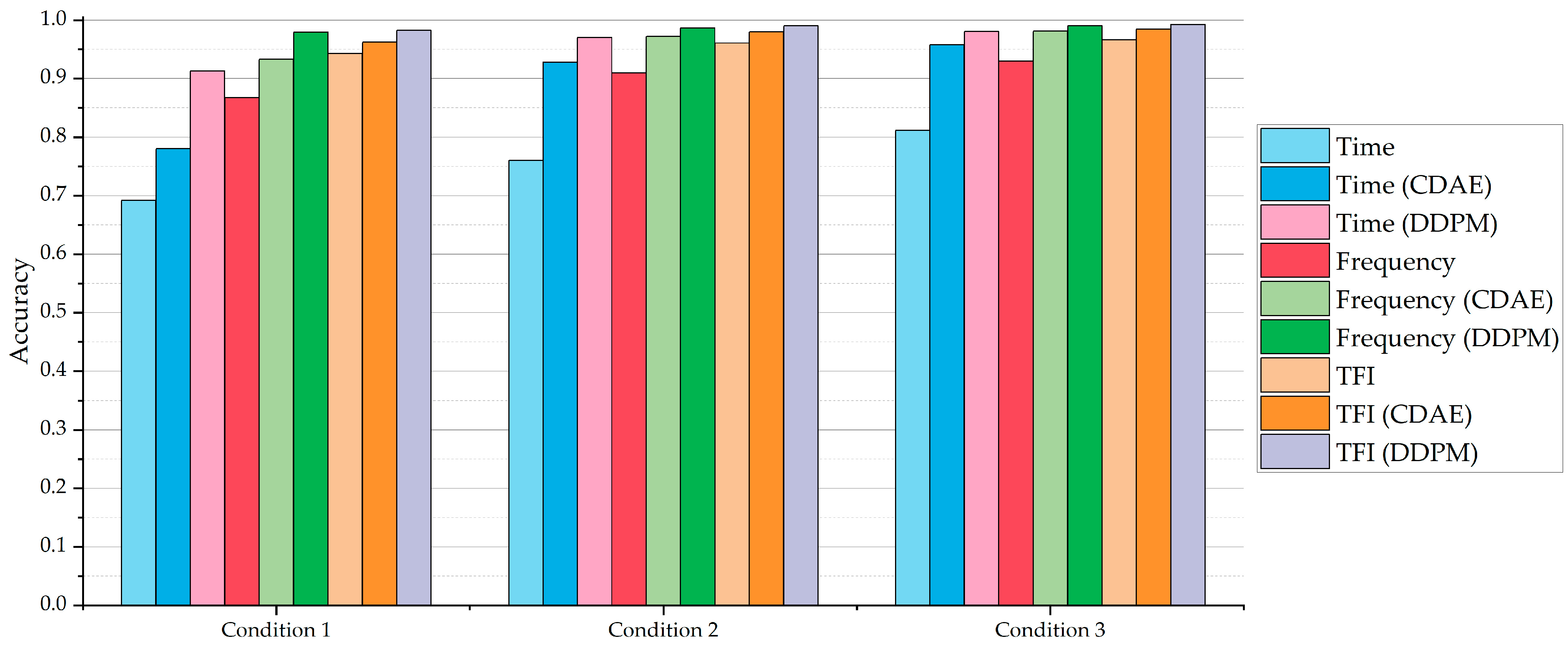
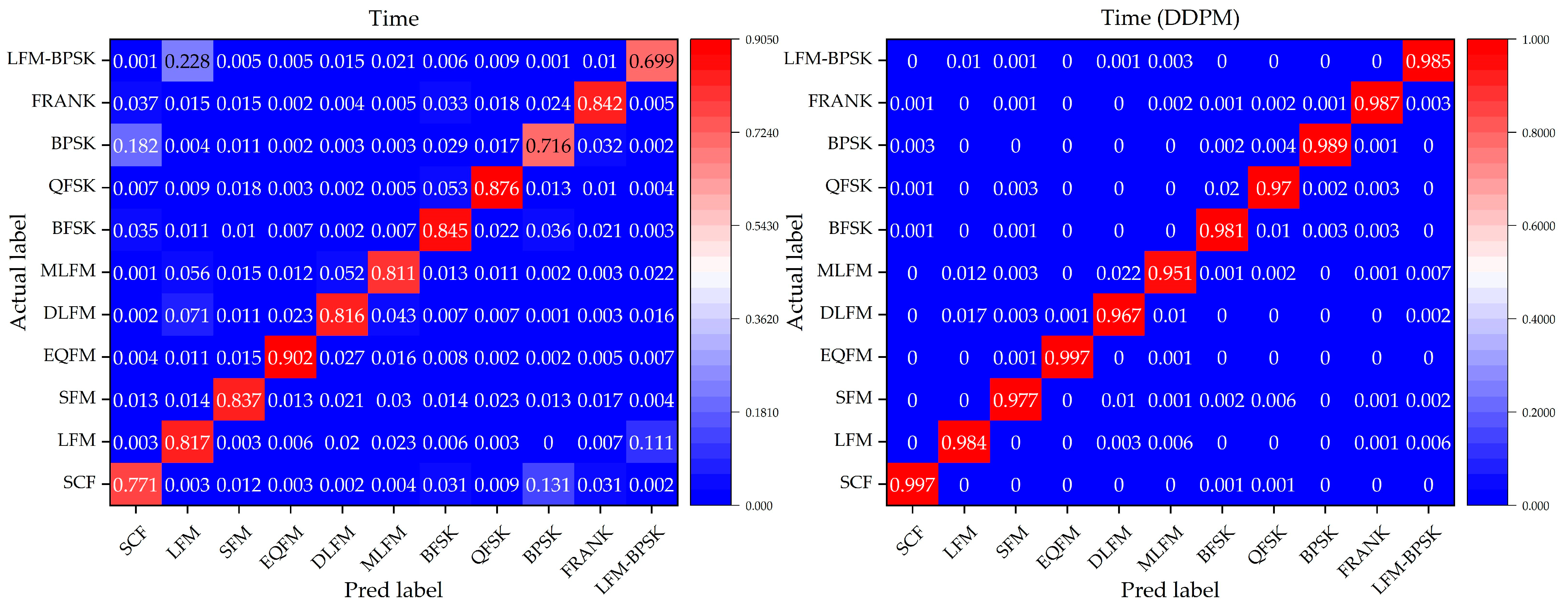
4.2. Classification Results
5. Discussion
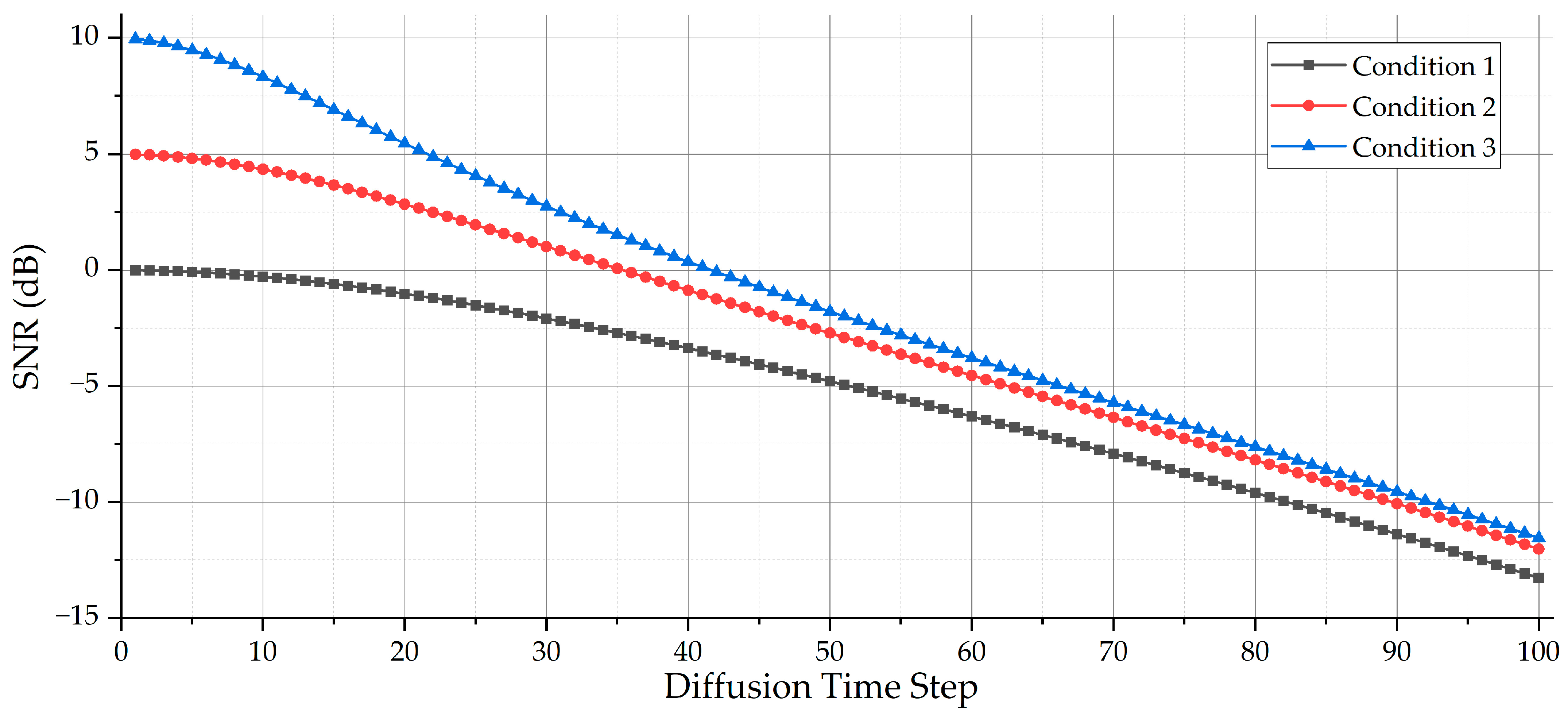
5.1. Ablation Study on the Max Time Step of Forward Process
5.2. Potential Application Scenarios
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| SNR/dB | Condition 1 | Condition 2 | Condition 3 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Time | Frequency | TFI | Time | Frequency | TFI | Time | Frequency | TFI | |
| −10 | 0.4473 | 0.6436 | 0.7491 | 0.3145 | 0.6382 | 0.7600 | 0.2745 | 0.6309 | 0.7209 |
| −9 | 0.5245 | 0.7173 | 0.8464 | 0.4118 | 0.7218 | 0.8273 | 0.3409 | 0.7118 | 0.8145 |
| −8 | 0.6164 | 0.7636 | 0.8982 | 0.4855 | 0.7718 | 0.9109 | 0.4673 | 0.7745 | 0.8927 |
| −7 | 0.6800 | 0.8182 | 0.9491 | 0.5855 | 0.8273 | 0.9373 | 0.5582 | 0.8364 | 0.9300 |
| −6 | 0.7245 | 0.8736 | 0.9691 | 0.6682 | 0.8664 | 0.9718 | 0.6364 | 0.8664 | 0.9682 |
| −5 | 0.7427 | 0.9100 | 0.9773 | 0.7309 | 0.9045 | 0.9882 | 0.7191 | 0.9000 | 0.9800 |
| −4 | 0.7691 | 0.9355 | 0.9927 | 0.7755 | 0.9418 | 0.9918 | 0.7736 | 0.9382 | 0.9882 |
| −3 | 0.7682 | 0.9527 | 0.9982 | 0.8273 | 0.9573 | 0.9982 | 0.8264 | 0.9618 | 0.9973 |
| −2 | 0.7918 | 0.9645 | 0.9955 | 0.8500 | 0.9755 | 0.9964 | 0.8664 | 0.9582 | 0.9982 |
| −1 | 0.7800 | 0.9791 | 0.9982 | 0.8782 | 0.9891 | 0.9991 | 0.9045 | 0.9845 | 1.0000 |
| 0 | 0.7673 | 0.9864 | 0.9982 | 0.8873 | 0.9864 | 0.9991 | 0.9145 | 0.9900 | 0.9991 |
| 1 | — | — | — | 0.9373 | 0.9900 | 0.9991 | 0.9500 | 0.9936 | 1.0000 |
| 2 | — | — | — | 0.9427 | 0.9945 | 0.9964 | 0.9573 | 0.9964 | 0.9973 |
| 3 | — | — | — | 0.9500 | 0.9955 | 0.9982 | 0.9773 | 0.9955 | 1.0000 |
| 4 | — | — | — | 0.9509 | 0.9973 | 0.9991 | 0.9836 | 0.9991 | 1.0000 |
| 5 | — | — | — | 0.9600 | 0.9991 | 1.0000 | 0.9782 | 1.0000 | 0.9991 |
| 6 | — | — | — | — | — | — | 0.9864 | 0.9982 | 1.0000 |
| 7 | — | — | — | — | — | — | 0.9818 | 0.9991 | 1.0000 |
| 8 | — | — | — | — | — | — | 0.9809 | 0.9991 | 0.9991 |
| 9 | — | — | — | — | — | — | 0.9827 | 0.9991 | 1.0000 |
| 10 | — | — | — | — | — | — | 0.9891 | 1.0000 | 0.9991 |
| AA | 0.6920 | 0.8677 | 0.9429 | 0.7597 | 0.9098 | 0.9608 | 0.8119 | 0.9301 | 0.9659 |
| SNR/dB | Condition 1 | Condition 2 | Condition 3 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Time | Frequency | TFI | Time | Frequency | TFI | Time | Frequency | TFI | |
| −10 | 0.6482 | 0.8009 | 0.8018 | 0.7218 | 0.8300 | 0.8409 | 0.7309 | 0.8300 | 0.8555 |
| −9 | 0.6973 | 0.8645 | 0.9018 | 0.8245 | 0.9082 | 0.9264 | 0.8373 | 0.9155 | 0.9191 |
| −8 | 0.7509 | 0.8964 | 0.9418 | 0.8555 | 0.9364 | 0.9573 | 0.8891 | 0.9391 | 0.9509 |
| −7 | 0.7755 | 0.9236 | 0.9782 | 0.8982 | 0.9655 | 0.9818 | 0.9355 | 0.9618 | 0.9818 |
| −6 | 0.7909 | 0.9391 | 0.9864 | 0.9264 | 0.9782 | 0.9909 | 0.9627 | 0.9891 | 0.9918 |
| −5 | 0.8018 | 0.9591 | 0.9882 | 0.9264 | 0.9855 | 0.9936 | 0.9545 | 0.9909 | 0.9927 |
| −4 | 0.8109 | 0.9636 | 0.9927 | 0.9464 | 0.9909 | 0.9955 | 0.9655 | 0.9927 | 0.9964 |
| −3 | 0.8209 | 0.9736 | 0.9973 | 0.9591 | 0.9882 | 0.9982 | 0.9782 | 0.9945 | 0.9973 |
| −2 | 0.8236 | 0.9773 | 0.9991 | 0.9564 | 0.9945 | 0.9991 | 0.9791 | 0.9964 | 0.9973 |
| −1 | 0.8373 | 0.9827 | 0.9991 | 0.9618 | 0.9982 | 1.0000 | 0.9827 | 0.9982 | 0.9991 |
| 0 | 0.8236 | 0.9818 | 0.9982 | 0.9764 | 0.9982 | 1.0000 | 0.9855 | 0.9991 | 1.0000 |
| 1 | — | — | — | 0.9709 | 0.9964 | 1.0000 | 0.9900 | 1.0000 | 0.9991 |
| 2 | — | — | — | 0.9809 | 0.9964 | 0.9973 | 0.9882 | 0.9982 | 0.9991 |
| 3 | — | — | — | 0.9764 | 0.9964 | 0.9973 | 0.9900 | 1.0000 | 0.9991 |
| 4 | — | — | — | 0.9836 | 0.9982 | 0.9991 | 0.9891 | 0.9991 | 1.0000 |
| 5 | — | — | — | 0.9864 | 0.9982 | 0.9991 | 0.9945 | 1.0000 | 1.0000 |
| 6 | — | — | — | — | — | — | 0.9927 | 0.9973 | 1.0000 |
| 7 | — | — | — | — | — | — | 0.9918 | 1.0000 | 1.0000 |
| 8 | — | — | — | — | — | — | 0.9955 | 1.0000 | 1.0000 |
| 9 | — | — | — | — | — | — | 0.9918 | 1.0000 | 1.0000 |
| 10 | — | — | — | — | — | — | 0.9873 | 0.9991 | 1.0000 |
| AA | 0.7801 | 0.9330 | 0.9622 | 0.9282 | 0.9724 | 0.9798 | 0.9577 | 0.9810 | 0.9847 |
| SNR/dB | Condition 1 | Condition 2 | Condition 3 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Time | Frequency | TFI | Time | Frequency | TFI | Time | Frequency | TFI | |
| −10 | 0.8282 | 0.8991 | 0.8936 | 0.8500 | 0.8945 | 0.9136 | 0.8636 | 0.8991 | 0.9164 |
| −9 | 0.8982 | 0.9527 | 0.9564 | 0.9209 | 0.9509 | 0.9564 | 0.9291 | 0.9564 | 0.9618 |
| −8 | 0.9100 | 0.9755 | 0.9736 | 0.9482 | 0.9718 | 0.9827 | 0.9473 | 0.9673 | 0.9791 |
| −7 | 0.9318 | 0.9900 | 0.9945 | 0.9782 | 0.9873 | 0.9918 | 0.9809 | 0.9918 | 0.9945 |
| −6 | 0.9518 | 0.9973 | 0.9991 | 0.9791 | 0.9973 | 0.9991 | 0.9882 | 0.9945 | 0.9982 |
| −5 | 0.9291 | 0.9945 | 0.9982 | 0.9873 | 0.9918 | 0.9964 | 0.9918 | 0.9964 | 0.9991 |
| −4 | 0.9382 | 0.9945 | 0.9973 | 0.9882 | 0.9973 | 0.9991 | 0.9918 | 0.9991 | 1.0000 |
| −3 | 0.9364 | 0.9955 | 0.9991 | 0.9891 | 1.0000 | 0.9991 | 0.9945 | 0.9991 | 0.9991 |
| −2 | 0.9227 | 0.9936 | 0.9982 | 0.9882 | 1.0000 | 1.0000 | 0.9909 | 0.9991 | 1.0000 |
| −1 | 0.9136 | 0.9964 | 0.9982 | 0.9955 | 1.0000 | 1.0000 | 0.9945 | 1.0000 | 1.0000 |
| 0 | 0.8864 | 0.9864 | 0.9973 | 0.9836 | 0.9991 | 1.0000 | 0.9936 | 0.9982 | 1.0000 |
| 1 | — | — | — | 0.9900 | 0.9991 | 1.0000 | 0.9936 | 1.0000 | 0.9991 |
| 2 | — | — | — | 0.9882 | 1.0000 | 0.9982 | 0.9945 | 1.0000 | 0.9982 |
| 3 | — | — | — | 0.9791 | 0.9973 | 1.0000 | 0.9927 | 0.9991 | 0.9991 |
| 4 | — | — | — | 0.9818 | 0.9973 | 1.0000 | 0.9936 | 1.0000 | 1.0000 |
| 5 | — | — | — | 0.9791 | 0.9991 | 1.0000 | 0.9936 | 1.0000 | 1.0000 |
| 6 | — | — | — | — | — | — | 0.9909 | 1.0000 | 0.9991 |
| 7 | — | — | — | — | — | — | 0.9936 | 1.0000 | 1.0000 |
| 8 | — | — | — | — | — | — | 0.9936 | 1.0000 | 1.0000 |
| 9 | — | — | — | — | — | — | 0.9873 | 0.9991 | 1.0000 |
| 10 | — | — | — | — | — | — | 0.9900 | 0.9991 | 1.0000 |
| AA | 0.9133 | 0.9796 | 0.9823 | 0.9704 | 0.9864 | 0.9898 | 0.9805 | 0.9904 | 0.9926 |
Appendix B
| SNR/dB | Condition 1 | Condition 2 | Condition 3 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Time | Frequency | TFI | Time | Frequency | TFI | Time | Frequency | TFI | |
| −10 | 0.6936 | 0.8400 | 0.8282 | 0.8291 | 0.8845 | 0.8155 | 0.8336 | 0.8855 | 0.8182 |
| −9 | 0.8218 | 0.9273 | 0.9191 | 0.8927 | 0.9300 | 0.9027 | 0.9191 | 0.9473 | 0.9136 |
| −8 | 0.8536 | 0.9609 | 0.9418 | 0.9382 | 0.9782 | 0.9573 | 0.9455 | 0.9736 | 0.9473 |
| −7 | 0.8536 | 0.9755 | 0.9545 | 0.9718 | 0.9900 | 0.9800 | 0.9782 | 0.9945 | 0.9800 |
| −6 | 0.8909 | 0.9864 | 0.9736 | 0.9782 | 0.9945 | 0.9882 | 0.9864 | 0.9982 | 0.9909 |
| −5 | 0.8845 | 0.9900 | 0.9582 | 0.9864 | 0.9973 | 0.9855 | 0.9873 | 0.9945 | 0.9909 |
| −4 | 0.8809 | 0.9927 | 0.9718 | 0.9809 | 0.9964 | 0.9909 | 0.9955 | 0.9991 | 0.9882 |
| −3 | 0.8745 | 0.9909 | 0.9764 | 0.9909 | 0.9982 | 0.9900 | 0.9945 | 0.9982 | 0.9864 |
| −2 | 0.8591 | 0.9855 | 0.9573 | 0.9873 | 0.9982 | 0.9927 | 0.9936 | 0.9982 | 0.9918 |
| −1 | 0.8573 | 0.9900 | 0.9491 | 0.9900 | 1.0000 | 0.9873 | 0.9900 | 0.9991 | 0.9964 |
| 0 | 0.8355 | 0.9855 | 0.9409 | 0.9882 | 0.9982 | 0.9891 | 0.9927 | 1.0000 | 0.9927 |
| 1 | — | — | — | 0.9855 | 0.9991 | 0.9882 | 0.9973 | 1.0000 | 0.9955 |
| 2 | — | — | — | 0.9827 | 0.9973 | 0.9864 | 0.9955 | 1.0000 | 0.9945 |
| 3 | — | — | — | 0.9764 | 0.9991 | 0.9791 | 0.9927 | 0.9991 | 0.9918 |
| 4 | — | — | — | 0.9791 | 0.9991 | 0.9809 | 0.9936 | 1.0000 | 0.9909 |
| 5 | — | — | — | 0.9845 | 0.9991 | 0.9809 | 0.9955 | 1.0000 | 0.9909 |
| 6 | — | — | — | — | — | — | 0.9955 | 1.0000 | 0.9945 |
| 7 | — | — | — | — | — | — | 0.9900 | 1.0000 | 0.9936 |
| 8 | — | — | — | — | — | — | 0.9945 | 1.0000 | 0.9945 |
| 9 | — | — | — | — | — | — | 0.9945 | 0.9982 | 0.9873 |
| 10 | — | — | — | — | — | — | 0.9909 | 0.9991 | 0.9909 |
| AA | 0.8460 | 0.9659 | 0.9428 | 0.9651 | 0.9849 | 0.9684 | 0.9789 | 0.9897 | 0.9772 |
| SNR/dB | Condition 1 | Condition 2 | Condition 3 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Time | Frequency | TFI | Time | Frequency | TFI | Time | Frequency | TFI | |
| −10 | 0.7973 | 0.8591 | 0.8891 | 0.8300 | 0.8800 | 0.8536 | 0.8427 | 0.8618 | 0.8664 |
| −9 | 0.8691 | 0.9509 | 0.9591 | 0.9118 | 0.9409 | 0.9391 | 0.9209 | 0.9364 | 0.9418 |
| −8 | 0.9109 | 0.9673 | 0.9791 | 0.9491 | 0.9727 | 0.9745 | 0.9682 | 0.9718 | 0.9627 |
| −7 | 0.9445 | 0.9891 | 0.9845 | 0.9709 | 0.9909 | 0.9864 | 0.9864 | 0.9891 | 0.9936 |
| −6 | 0.9555 | 0.9927 | 0.9964 | 0.9809 | 0.9982 | 0.9973 | 0.9909 | 0.9936 | 0.9927 |
| −5 | 0.9309 | 0.9927 | 0.9900 | 0.9855 | 0.9973 | 0.9964 | 0.9927 | 0.9955 | 0.9964 |
| −4 | 0.9418 | 0.9936 | 0.9945 | 0.9882 | 0.9991 | 0.9991 | 0.9936 | 0.9973 | 1.0000 |
| −3 | 0.9300 | 0.9945 | 0.9918 | 0.9918 | 0.9973 | 0.9991 | 0.9955 | 0.9964 | 0.9982 |
| −2 | 0.9127 | 0.9909 | 0.9855 | 0.9836 | 0.9991 | 0.9991 | 0.9982 | 0.9991 | 0.9991 |
| −1 | 0.9245 | 0.9918 | 0.9927 | 0.9882 | 1.0000 | 0.9991 | 0.9973 | 1.0000 | 1.0000 |
| 0 | 0.8955 | 0.9855 | 0.9818 | 0.9845 | 0.9991 | 0.9982 | 0.9955 | 0.9991 | 0.9991 |
| 1 | — | — | — | 0.9909 | 0.9982 | 0.9991 | 0.9973 | 1.0000 | 1.0000 |
| 2 | — | — | — | 0.9891 | 0.9973 | 0.9982 | 0.9982 | 0.9991 | 1.0000 |
| 3 | — | — | — | 0.9827 | 0.9982 | 0.9982 | 0.9945 | 0.9982 | 1.0000 |
| 4 | — | — | — | 0.9709 | 0.9964 | 0.9991 | 0.9945 | 0.9991 | 1.0000 |
| 5 | — | — | — | 0.9827 | 0.9991 | 0.9991 | 0.9973 | 0.9991 | 1.0000 |
| 6 | — | — | — | — | — | — | 1.0000 | 0.9982 | 1.0000 |
| 7 | — | — | — | — | — | — | 0.9973 | 1.0000 | 1.0000 |
| 8 | — | — | — | — | — | — | 0.9964 | 0.9982 | 1.0000 |
| 9 | — | — | — | — | — | — | 0.9982 | 0.9991 | 0.9991 |
| 10 | — | — | — | — | — | — | 0.9964 | 0.9991 | 0.9991 |
| AA | 0.9102 | 0.9735 | 0.9768 | 0.9676 | 0.9852 | 0.9835 | 0.9834 | 0.9871 | 0.9880 |
| SNR/dB | Condition 1 | Condition 2 | Condition 3 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Time | Frequency | TFI | Time | Frequency | TFI | Time | Frequency | TFI | |
| −10 | 0.8282 | 0.8891 | 0.9045 | 0.8155 | 0.8536 | 0.9064 | 0.8182 | 0.8664 | 0.8936 |
| −9 | 0.9191 | 0.9591 | 0.9645 | 0.9027 | 0.9391 | 0.9536 | 0.9136 | 0.9418 | 0.9564 |
| −8 | 0.9418 | 0.9791 | 0.9855 | 0.9573 | 0.9745 | 0.9836 | 0.9473 | 0.9627 | 0.9809 |
| −7 | 0.9545 | 0.9845 | 0.9945 | 0.9800 | 0.9864 | 0.9918 | 0.9800 | 0.9936 | 0.9955 |
| −6 | 0.9736 | 0.9964 | 0.9973 | 0.9882 | 0.9973 | 0.9991 | 0.9909 | 0.9927 | 0.9982 |
| −5 | 0.9582 | 0.9900 | 0.9973 | 0.9855 | 0.9964 | 0.9973 | 0.9909 | 0.9964 | 0.9964 |
| −4 | 0.9718 | 0.9945 | 0.9964 | 0.9909 | 0.9991 | 0.9991 | 0.9882 | 1.0000 | 0.9973 |
| −3 | 0.9764 | 0.9918 | 0.9991 | 0.9900 | 0.9991 | 1.0000 | 0.9864 | 0.9982 | 0.9991 |
| −2 | 0.9573 | 0.9855 | 0.9973 | 0.9927 | 0.9991 | 0.9991 | 0.9918 | 0.9991 | 0.9991 |
| −1 | 0.9491 | 0.9927 | 0.9991 | 0.9873 | 0.9991 | 1.0000 | 0.9964 | 1.0000 | 1.0000 |
| 0 | 0.9409 | 0.9818 | 0.9982 | 0.9891 | 0.9982 | 1.0000 | 0.9927 | 0.9991 | 1.0000 |
| 1 | — | — | — | 0.9882 | 0.9991 | 1.0000 | 0.9955 | 1.0000 | 1.0000 |
| 2 | — | — | — | 0.9864 | 0.9982 | 0.9991 | 0.9945 | 1.0000 | 0.9991 |
| 3 | — | — | — | 0.9791 | 0.9982 | 0.9991 | 0.9918 | 1.0000 | 1.0000 |
| 4 | — | — | — | 0.9809 | 0.9991 | 0.9991 | 0.9909 | 1.0000 | 1.0000 |
| 5 | — | — | — | 0.9809 | 0.9991 | 1.0000 | 0.9909 | 1.0000 | 1.0000 |
| 6 | — | — | — | — | — | — | 0.9945 | 1.0000 | 1.0000 |
| 7 | — | — | — | — | — | — | 0.9936 | 1.0000 | 1.0000 |
| 8 | — | — | — | — | — | — | 0.9945 | 1.0000 | 1.0000 |
| 9 | — | — | — | — | — | — | 0.9873 | 0.9991 | 1.0000 |
| 10 | — | — | — | — | — | — | 0.9909 | 0.9991 | 1.0000 |
| AA | 0.9428 | 0.9768 | 0.9849 | 0.9684 | 0.9835 | 0.9892 | 0.9772 | 0.9880 | 0.9912 |
References
- Richards, M.A. Fundamentals of Radar Signal Processing, 2nd ed.; McGraw-Hill Education: New York, NY, USA, 2005. [Google Scholar]
- Barton, D.K. Radar System Analysis and Modeling; Artech: London, UK, 2004. [Google Scholar]
- Wiley, R.G.; Ebrary, I. ELINT: The Interception and Analysis of Radar Signals; Artech: London, UK, 2006. [Google Scholar]
- Zhao, G. Principle of Radar Countermeasure, 2nd ed.; Xidian University Press: Xi’an, China, 2012. [Google Scholar]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 2012, 60, 84–90. [Google Scholar] [CrossRef]
- Wu, B.; Yuan, S.; Li, P.; Jing, Z.; Huang, S.; Zhao, Y. Radar Emitter Signal Recognition Based on One-Dimensional Convolutional Neural Network with Attention Mechanism. Sensors 2020, 20, 6350. [Google Scholar] [CrossRef]
- Zhang, S.; Pan, J.; Han, Z.; Guo, L. Recognition of Noisy Radar Emitter Signals Using a One-Dimensional Deep Residual Shrinkage Network. Sensors 2021, 21, 7973. [Google Scholar] [CrossRef] [PubMed]
- Yuan, S.; Wu, B.; Li, P. Intra-Pulse Modulation Classification of Radar Emitter Signals Based on a 1-D Selective Kernel Convolutional Neural Network. Remote Sens. 2021, 13, 2799. [Google Scholar] [CrossRef]
- Yuan, S.; Li, P.; Wu, B.; Li, X.; Wang, J. Semi-Supervised Classification for Intra-Pulse Modulation of Radar Emitter Signals Using Convolutional Neural Network. Remote Sens. 2022, 14, 2059. [Google Scholar] [CrossRef]
- Qu, Z.; Mao, X.; Deng, Z. Radar Signal Intra-Pulse Modulation Recognition Based on Convolutional Neural Network. IEEE Access 2018, 6, 43874–43884. [Google Scholar] [CrossRef]
- Si, W.; Wan, C.; Deng, Z. Intra-Pulse Modulation Recognition of Dual-Component Radar Signals Based on Deep Convolutional Neural Network. IEEE Commun. Lett. 2021, 25, 3305–3309. [Google Scholar] [CrossRef]
- Tan, M.; Le, Q. EfficientNet: Rethinking model scaling for convolutional neural networks. Proc. Int. Conf. Mach. Learn. 2019, 97, 6105–6114. [Google Scholar]
- Yu, Z.; Tang, J.; Wang, Z. GCPS: A CNN Performance Evaluation Criterion for Radar Signal Intrapulse Modulation Recognition. IEEE Commun. Lett. 2021, 25, 2290–2294. [Google Scholar] [CrossRef]
- Yuan, S.; Li, P.; Wu, B. Radar Emitter Signal Intra-Pulse Modulation Open Set Recognition Based on Deep Neural Network. Remote Sens. 2024, 16, 108. [Google Scholar] [CrossRef]
- Zhang, M.; Diao, M.; Guo, L. Convolutional Neural Networks for Automatic Cognitive Radio Waveform Recognition. IEEE Access 2017, 5, 11074–11082. [Google Scholar] [CrossRef]
- Dong, W.; Wang, P.; Yin, W.; Shi, G.; Wu, F.; Lu, X. Denoising Prior Driven Deep Neural Network for Image Restoration. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 41, 2305–2318. [Google Scholar] [CrossRef]
- Cao, X.; Fu, X.; Xu, C.; Meng, D. Deep Spatial-Spectral Global Reasoning Network for Hyperspectral Image Denoising. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5504714. [Google Scholar] [CrossRef]
- Li, K.; Zhou, W.; Li, H.; Anastasio, M.A. Assessing the Impact of Deep Neural Network-Based Image Denoising on Binary Signal Detection Tasks. IEEE Trans. Med. Imaging 2021, 40, 2295–2305. [Google Scholar] [CrossRef] [PubMed]
- Zhang, K.; Zuo, W.; Chen, Y.; Meng, D.; Zhang, L. Beyond a Gaussian Denoiser: Residual Learning of Deep CNN for Image Denoising. IEEE Trans. Image Process. 2017, 26, 3142–3155. [Google Scholar] [CrossRef]
- Zou, H.; Lan, R.; Zhong, Y.; Liu, Z.; Luo, X. EDCNN: A Novel Network for Image Denoising. In Proceedings of the 2019 IEEE International Conference on Image Processing (ICIP), Taipei, Taiwan, 22–25 September 2019; pp. 1129–1133. [Google Scholar] [CrossRef]
- Qu, Z.; Wang, W.; Hou, C.; Hou, C. Radar Signal Intra-Pulse Modulation Recognition Based on Convolutional Denoising Autoencoder and Deep Convolutional Neural Network. IEEE Access 2019, 7, 112339–112347. [Google Scholar] [CrossRef]
- Ho, J.; Jain, A.; Abbeel, P. Denoising diffusion probabilistic models. Proc. Adv. Neural Inf. Process. Syst. 2020, 33, 6840–6851. [Google Scholar]
- Hoang, L.M.; Kim, M.; Kong, S.-H. Automatic Recognition of General LPI Radar Waveform Using SSD and Supplementary Classifier. IEEE Trans. Signal Process. 2019, 67, 3516–3530. [Google Scholar] [CrossRef]
- Lugmayr, A.; Danelljan, M.; Romero, A.; Yu, F.; Timofte, R.; Van Gool, L. RePaint: Inpainting using Denoising Diffusion Probabilistic Models. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022; pp. 11451–11461. [Google Scholar] [CrossRef]
- Choi, J.; Kim, S.; Jeong, Y.; Gwon, Y.; Yoon, S. ILVR: Conditioning Method for Denoising Diffusion Probabilistic Models. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 11–17 October 2021; pp. 14347–14356. [Google Scholar] [CrossRef]
- Saharia, C.; Ho, J.; Chan, W.; Salimans, T.; Fleet, D.J.; Norouzi, M. Image Super-Resolution via Iterative Refinement. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 4713–4726. [Google Scholar] [CrossRef]
- Liu, L.; Chen, B.; Chen, H.; Zou, Z.; Shi, Z. Diverse Hyperspectral Remote Sensing Image Synthesis with Diffusion Models. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5532616. [Google Scholar] [CrossRef]
- Dhariwal, P.; Nichol, A. Diffusion models beat GANs on image synthesis. Proc. Int. Conf. Neural Inf. Process. Syst. 2021, 34, 8780–8794. [Google Scholar]
- Nichol, A.Q.; Dhariwal, P. Improved denoising diffusion probabilistic models. Proc. Int. Conf. Mach. Learn. 2021, 139, 8162–8171. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; Springer: Cham, Switzerland, 2015; pp. 234–241. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef]
- Klambauer, G.; Unterthiner, T.; Mayr, A.; Hochreiter, S. Self-normalizing neural networks. Adv. Neural Inf. Process. Syst. 2017, 30, 972–981. [Google Scholar]
- Ba, J.L.; Kiros, J.R.; Hinton, G.E. Layer Normalization. arXiv 2016, arXiv:1607.06450. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. In Proceedings of the 3rd International Conference on Learning Representations (ICLR 2015), San Diego, CA, USA, 7–9 May 2015; pp. 1–14. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. arXiv 2015, arXiv:1502.03167. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]







| Type | Carrier Frequency | Parameters | Details |
|---|---|---|---|
| SCF | 10 MHz–90 MHz | None | None |
| LFM | 10 MHz–90 MHz | Bandwidth: 10 MHz–70 MHz | 1. Both up LFM and down LFM are included; 2. Both max value and min value of the instantaneous frequency for LFM range from 10 MHz to 90 MHz. |
| SFM | 10 MHz–90 MHz | Bandwidth: 10 MHz–70 MHz | Both max value and min value of the instantaneous frequency for SFM range from 10 MHz to 90 MHz. |
| EQFM | 10 MHz–90 MHz | Bandwidth: 10 MHz–70 MHz | 1. The instantaneous frequency increases first and then decreases, or decreases first and then increases; 2. Both max value and min value of the instantaneous frequency for EQFM range from 10 MHz to 90 MHz. |
| DLFM | 10 MHz–90 MHz | Bandwidth: 10 MHz–70 MHz | 1. The instantaneous frequency increases first and then decreases, or decreases first and then increases; 2. Both max value and min value of the instantaneous frequency for DLFM range from 10 MHz to 90 MHz. |
| MLFM | 10 MHz–90 MHz 10 MHz–90 MHz | Bandwidth: 10 MHz–70 MHz Bandwidth: 10 MHz–70 MHz Segment ratio: 20%–80% | 1. Up LFM and down LFM are included in each of the two parts; 2. Both max value and min value of the instantaneous frequency for each part of the MLFM range from 10 MHz to 90 MHz; 3. The distance of the instantaneous frequency at the end of first part and the instantaneous frequency at the start of last part is more than 10 MHz. |
| BFSK | 10 MHz–90 MHz 10 MHz–90 MHz | 5-, 7-, 11-, and 13-bit Barker code | The distance of two sub-carrier frequency is more than 10 MHz. |
| QFSK | 10 MHz–90 MHz 10 MHz–90 MHz 10 MHz–90 MHz 10 MHz–90 MHz | 16-bit Frank code | The distance of each two sub-carrier frequency is more than 10 MHz. |
| BPSK | 10 MHz–90 MHz | 5-, 7-, 11-, and 13-bit Barker code | None. |
| FRANK | 10 MHz–90 MHz | Phase number: 6, 7, and 8 | None. |
| LFM-BPSK | 10 MHz–90 MHz | Bandwidth: 10 MHz–70 MHz 5-, 7-, 11-, and 13-bit Barker code | 1. Both up LFM and down LFM are included; 2. Both max value and min value of the instantaneous frequency for LFM-BPSK range from 10 MHz to 90 MHz. |
| SNR/dB | −10 | −9 | −8 | −7 | −6 | −5 | −4 | −3 | −2 | −1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Condition 1 | 82 | 77 | 71 | 64 | 58 | 51 | 45 | 37 | 29 | 20 | — | — | — | — | — | — | — | — | — | — | — |
| Condition 2 | 90 | 84 | 79 | 74 | 68 | 63 | 57 | 52 | 46 | 41 | 35 | 30 | 25 | 19 | 13 | — | — | — | — | — | — |
| Condition 3 | 92 | 87 | 82 | 77 | 71 | 66 | 61 | 56 | 51 | 46 | 42 | 37 | 33 | 29 | 25 | 22 | 18 | 15 | 11 | 7 | — |
| DNN Classification Model | Condition 1 | Condition 2 | Condition 3 |
|---|---|---|---|
| Time | N/A | 1 dB | −1 dB |
| Time (CDAE) | N/A | −6 dB | −7 dB |
| Time (DDPM) | −8 dB | −9 dB | −9 dB |
| Frequency | −5 dB | −5 dB | −5 dB |
| Frequency (CDAE) | −7 dB | −9 dB | −9 dB |
| Frequency (DDPM) | −9 dB | −9 dB | −9 dB |
| TFI | −7 dB | −8 dB | −7 dB |
| TFI (CDAE) | −9 dB | −9 dB | −9 dB |
| TFI (DDPM) | −9 dB | −10 dB | −10 dB |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, S.; Li, P.; Zhou, X.; Chen, Y.; Wu, B. A Denoising Method Based on DDPM for Radar Emitter Signal Intra-Pulse Modulation Classification. Remote Sens. 2024, 16, 3215. https://doi.org/10.3390/rs16173215
Yuan S, Li P, Zhou X, Chen Y, Wu B. A Denoising Method Based on DDPM for Radar Emitter Signal Intra-Pulse Modulation Classification. Remote Sensing. 2024; 16(17):3215. https://doi.org/10.3390/rs16173215
Chicago/Turabian StyleYuan, Shibo, Peng Li, Xu Zhou, Yingchao Chen, and Bin Wu. 2024. "A Denoising Method Based on DDPM for Radar Emitter Signal Intra-Pulse Modulation Classification" Remote Sensing 16, no. 17: 3215. https://doi.org/10.3390/rs16173215
APA StyleYuan, S., Li, P., Zhou, X., Chen, Y., & Wu, B. (2024). A Denoising Method Based on DDPM for Radar Emitter Signal Intra-Pulse Modulation Classification. Remote Sensing, 16(17), 3215. https://doi.org/10.3390/rs16173215






