Abstract
The long convergence time and non-robust positioning accuracy are the main factors limiting the application of precision single-point positioning (PPP) in kinematic vehicle navigation. Therefore, a dual/triple-frequency multi-constellation PPP-RTK method with atmospheric augmentation is proposed to achieve cm-level reliable kinematic positioning. The performance was assessed using a set of static station and kinematic vehicle positioning experiments conducted in Wuhan. In the static experiments, instantaneous convergence within 1 s and centimeter-level positioning accuracy were achieved for PPP-RTK using dual-frequency observation. For the kinematic experiments, instantaneous convergence was also achieved for dual-frequency PPP-RTK in open areas, with RMS of 2.6 cm, 2.6 cm, and 7.5 cm in the north, east, and up directions, respectively, with accuracy similar to short-baseline real-time kinematic positioning (RTK). Horizontal positioning errors of less than 0.1 m and 3D positional errors of less than 0.2 m were 99.54% and 98.46%, respectively. Additionally, after the outage of GNSS and during satellite reduction in obstructed environments, faster reconvergence and greater accuracy stability were realized compared with PPP without atmospheric enhancement. Triple-frequency PPP-RTK was able to further enhance the robustness and accuracy of positioning, with RMS of 2.2 cm, 2.0 cm, and 7.3 cm, respectively. In summary, a performance similar to RTK was achieved based on dual-frequency PPP-RTK, demonstrating that PPP-RTK has the potential for lane-level navigation.
1. Introduction
Precision single-point positioning (PPP) can achieve centimeter-level positioning accuracy through the use of a single station without the need for direct or explicit reference stations [1]. However, due to slow changes in spatial geometric structures and high noise in code observation, PPP requires a longer convergence time [2]. PPP with ambiguity resolution (PPP-AR) can effectively shorten the convergence time and improve positioning accuracy [3]. Nonetheless, even with multi-frequency and multi-system designs, PPP-AR still takes several minutes to achieve correct ambiguity resolution; furthermore, signal loss requires a prolonged reconvergence time [4,5]. The timeliness and reliability of PPP-AR remain inferior to traditional relative positioning techniques, limiting its application in kinematic positioning. Real-time kinematic positioning (RTK) is a phase-based and widely applied relatively precise positioning technique [6]. However, RTK requires a dense network to provide correction information. This creates a heavy communication burden between the reference stations and the rover and limits user capacity.
PPP-RTK was first proposed by [7]; it fully integrates the advantages of rapid ambiguity resolution for RTK and flexibility for PPP. At the same time, it avoids their drawbacks, such as heavy communication burdens and low positioning efficiency [8]. PPP-RTK is based on precise satellite orbit, clock, signal bias, and optional atmospheric products estimated through the use of a regional reference station network. Currently, PPP-RTK can achieve ambiguity resolution via the calibration of satellite phase bias products via different methods [9,10,11]. Considering that atmospheric error is the key factor affecting the convergence of PPP, using precise atmospheric products, such as ionospheric delay and tropospheric conditions provided by the ground station network, the convergence time of PPP-RTK can be further shortened [12,13].
PPP-RTK can provide unified and seamless positioning services, placing it at the forefront of research. For example, [14] proposed a PPP-RTK model that reparametrizes network parameters, such as phase biases and atmospheric delays, which are then applied to correct observations for users to achieve ambiguity resolution. A PPP–RTK model using undifferenced augmentation corrections was proposed by [9,15]. In this method, the precise satellite orbit and clock, phase bias, and atmospheric enhancement corrections are generated at the undifferenced level. With the development of multi-GNSS, PPP-RTK research has progressed from an ionosphere-free model to undifferenced and uncombined models [16,17], single systems to multi-systems [12,18,19], and single-frequency or dual-frequency designs to multi-frequency designs [20,21]. Building on the progress made in theoretical research, multiple research institutions and commercial companies have developed PPP-RTK service systems to provide real-time precise positioning services on a global scale. For example, Japan has established a regional PPP-RTK service, the Centimeter-Level Augmentation Service (CLAS), which is based on the L6D signal of the Quasi-Zenith Satellite System (QZSS) [22]. Additionally, several commercial companies have begun offering PPP-RTK services, including Trimble with its RTX service, NovAtel with the TerraStar-X service, and GEO++ with the SSRPOST service.
The use of multi-constellation GNSS augmented with precise atmospheric corrections could reduce the PPP-RTK convergence time to several seconds or even make it instantaneous [12]. However, current research mainly focuses on the static scenario, such as in the case of [23,24], who evaluated the performance of commercial PPP-RTK services in static scenarios. Although the positioning accuracy of PPP-RTK has also been evaluated in kinematic scenarios for vehicles [25] and inland waterway vessels [26], those studies only used GPS and Galileo without analyzing the improvements in terms of convergence time and positioning accuracy with the addition of BDS. Indeed, BDS can significantly increase the number of available satellites and improve geometric configurations, which is particularly noticeable in the Asia–Pacific region [27]. Other researchers have analyzed the PPP-RTK positioning performance of GPS/Galileo/BDS [28,29]; however, the benefits derived from the precise atmospheric correction products still need further refinement. Additionally, RTK is still the method commonly used for vehicle navigation [30], and there is a lack of real experimental analysis on whether PPP-RTK can replace RTK for high-precision positioning in kinematic scenarios.
In summary, the goal of this research was to implement a high-precision GPS/Galileo/BDS PPP-RTK method based on undifferenced GNSS observations with a fast convergence of a few seconds as well as centimeter-level positioning accuracy to support kinematic vehicle navigation, similar to RTK but without requiring dense ground reference station networks [31]. In the manuscript, PPP Float represents floating precision point positioning. PPP-AR represents OSB correction based on PPP Float, and PPP-RTK refers to atmospheric constraints based on PPP-AR. Performance with and without atmospheric augmentation products was evaluated. In the following section, the mathematical model of PPP-RTK we used is described in detail. This is followed by the analysis of the accuracy and convergence time for a set of static positioning and vehicle kinematic positioning experiments in the urban area of Wuhan. Finally, the conclusions are drawn.
2. Methods
2.1. Undifferenced Uncombined Observation Equation
The undifferenced and uncombined (UDUC) observation equation for the -th epoch is as follows:
In the formula, , , , and () represent the GNSS receiver, satellite, constellation, and observation frequency points, respectively; represents expectation; and and , respectively, represent the observed minus calculated (OMC) values. The observed values include code and phase observations, while the computed values are the sums of GNSS corrections. These corrections incorporate the a priori zenith tropospheric delay (ZTD) values and the geometric distance derived from the known satellite and station coordinates, with the Sagnac effect, solid earth tide, polar tides, antenna phase center offsets (PCOs), antenna phase center variations (PCVs) corrections, and phase wind-up corrections applied; here, ( is the three-dimensional increment of the k-epoch coordinates; H is the receiver-to-satellite unit direction vector; is the speed of light in vacuum; and represent the epoch clock offset parameters at the receiver and satellite ends, respectively; and represents the residual delay in the troposphere corrected by prior models. Due to the high accuracy of prior zenith hydrostatic delay (ZHD), the remaining part is mainly composed of zenith wet delay (ZWD); is the mapping function of ZWD; is the first-order ionospheric delay at the -th frequency; is the ionospheric delay conversion coefficient at the -th frequency; and are the receiver and satellite code hardware biases, respectively; are the receiver and satellite carrier phase hardware biases, respectively; is the wavelength of frequency ; and is the ambiguity of frequency . The form of the random model is as follows: .
By utilizing products such as precise satellite orbits, clock bias, uncalibrated phase delay (UPD), or observable-specific signal bias (OSB), errors in the observation equations can be corrected to estimate accurate integer ambiguity parameters. Once the reference station ambiguities are resolved, precise estimates of the ionosphere and troposphere can be obtained. Due to corrections in the tropospheric model, it is necessary to incorporate the prior tropospheric model values and partially restore the model to its original state. The ionospheric data can then be converted to various frequencies through frequency relationships to achieve accurate ionospheric observations.
2.2. Regional Atmospheric Enhancement Rapid Precise Positioning System
The architecture of the regional atmospheric enhancement rapid precise positioning system is illustrated in Figure 1. It is divided into three parts: server side, atmosphere product generation, and user side. Among these, accurate atmospheric correction information is crucial for achieving fast and accurate PPP-RTK ambiguity resolution. After fixing the ambiguity at the reference station, the atmospheric information at the reference station can be accurately determined. This allows the atmospheric information at the user station to be derived through atmospheric modeling of the reference station, thereby improving the speed of ambiguity resolution at the user station.
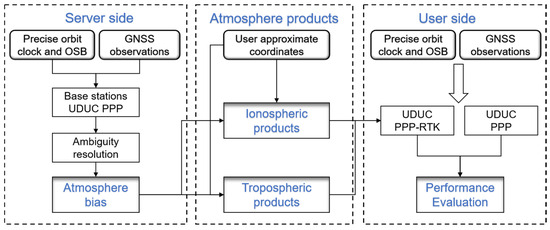
Figure 1.
The architecture of the regional atmospheric enhancement rapid precise positioning system.
The atmospheric enhancement at the rover is performed using inverse distance interpolation. Assuming there are three reference stations around the rover, the process for inverse distance interpolation is as follows [32]:
where is the ionospheric error of satellite on rover station ; represents the distances from the three reference stations to the rover; and is the sum of the reciprocal distances from the rover to the three reference stations. In this way, it can effectively ensure that the interpolation coefficient is 1, ensuring that the code hardware biases of the satellite and receiver ends included in the ionosphere at the rover remain unchanged. Therefore, the code hardware biases in the ionosphere of the rover can still be absorbed by clock bias or eliminated by a single difference from the satellite; thus, the fixed ambiguity of the rover is not affected.
The inverse distance weighting method is also used for interpolation of tropospheric delay; however, due to the strong correlation between tropospheric errors and height, the influence of height on the troposphere needs to be considered when performing tropospheric interpolation. When there is a significant difference in height between the reference stations and the rover, it is necessary to convert the tropospheric height before interpolation. The GPT3 (Global Pressure and Temperature 3) model can be used to solve the tropospheric error between different heights and perform height correction; alternatively, the vertical reduction coefficient can be used for height conversion [33]. In this article, the vertical reduction coefficient is used. Yao et al. (2013) used years of reprocessed atmospheric data to fit and obtain a prior exponential function model as follows [34]:
In the formula, . By inputting the height of the troposphere with the target height, the conversion of tropospheric height can be completed.
The interpolated tropospheric and ionospheric products have high accuracy, but there are still centimeter-level errors, and even after correction, parameter estimation is still necessary. If correction is directly made in the observation equation, it leads to inaccurate stochastic models and causes problems in parameter estimation. To avoid this issue, the influence of ionospheric and tropospheric correction is added numerically to the original observation equation in the form of constraint equations, as follows:
where and are the ionospheric and tropospheric error corrections obtained via interpolation at the reference stations, respectively; and represent the difference between the correction number and the true atmospheric delay, both of which are zero mean white noise processes with variances of and . The PPP model with atmospheric constraint equations can effectively weaken the influence of atmospheric errors and accelerate the convergence of ambiguity. On this basis, after correcting the phase deviation through OSB, the final fixed ambiguity is achieved.
3. Results
3.1. Data and Experiments
To verify the positioning performance of the PPP-RTK algorithm, a vehicle equipped with GNSS and INS measuring instruments was used to collect 78 min of on-board kinematic data in Wuhan on 28 May 2024. The continuously operating reference station (CORS) in Wuhan was utilized to generate atmospheric products and their accuracy information for the rover.
In Figure 2, the left side of the panel shows the reference station network in the Wuhan region, comprising a total of five reference stations: HBA2, HBB0, HBF7, HBE0, and HBH8. The maximum distance between adjacent reference stations was 84 km, with an average distance of 62 km. This network was used to generate atmospheric information for the rover. To obtain the interpolated atmospheric accuracy information for the rover, HBA1 was also used to verify atmospheric accuracy. HBA1, a reference station closer to the user station, was utilized to calculate the precise atmospheric conditions at HBA1. This allowed the determination of the approximate accuracy of atmospheric interpolation within the network. At the same time, in order to verify the static stations’ performance in terms of PPP-RTK, HBA1 was used for static experiments imitating kinematic solutions. The position of the reference station shown in the left panel was the kinematic starting point, and a reference station was set up at this position.
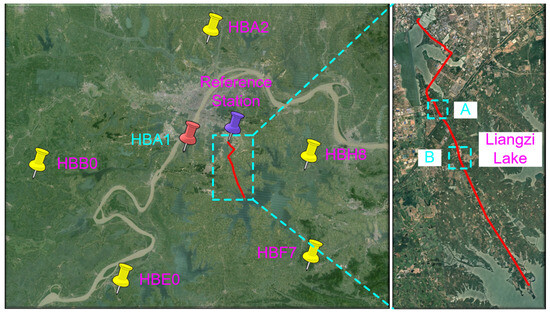
Figure 2.
CORS distribution in Wuhan region and vehicle driving trajectory. HBA2, HBB0, HBF7, HBE0, and HBH8 were reference stations used to generate atmospheric correction information, while HBA1 was used to verify the atmospheric accuracy of PPP-RTK and conduct static imitating kinematic convergence experiments on PPP-RTK.
The figure shows the measurement of the vehicle’s kinematic trajectory, with a data collection time ranging from 06:57:15 to 09:02:12 GPST. The total length of the vehicle’s journey was approximately 48 km. The vehicles passed through complex road conditions involving trees, tunnels, and elevated bridges. At locations A and B, as shown in the right-hand side of the figure, GNSS locking was lost due to the vehicle passing over the elevated bridge. The positioning performance of PPP-RTK was evaluated using high-precision GNSS data processing software, Novatel Waypoing 8.9, to calculate the smoothed RTK/INS tight combination solution as a reference.
The algorithm implementation was based on POSGO (position based on graph optimization) software [35]. Table 1 details the strategy employed for the PPP-RTK positioning system. The TurboEdit algorithm [36] and LLI flag were used for data quality control. The final WUM products from the Wuhan University Analysis Center of International GNSS Service Multi-GNSS Experiments were used [37]. The extraction and validation of precise atmospheric products were performed via localization using an UDUC function model. The carrier phase noise at each frequency for all constellations was set to 2 cm with an empirical code-to-carrier ratio of 100:1 [38,39]. To weaken the multipath effect of low-elevation observations, we adopted an elevation-dependent function for weighting, i.e., for satellites with elevations lower than 30° and 1.0 for those above 30 degrees. The mask elevation was set to 10 degrees. We employed PPP-AR to extract ionosphere and troposphere products from the reference stations, utilizing raw observations at the GPS L1/L2, Galileo E1/E5a, and BDS B1I/B3I frequencies, with a sampling interval of 5 s. The station coordinates remained fixed during the extraction of atmospheric products, and ambiguity resolution was accomplished based on the WUM final code and phase OSB. To eliminate receiver-related biases, single-difference ambiguities were formed before performing PPP-AR, and a cascading integer resolution method, similar to the approach used by Tao [38], was employed. In order to improve the ambiguity fixing rate, partial ambiguity resolution (PAR) was applied, with detailed information available in the work of Xu et al. [39]. The slant ionospheric parameters were treated as white noise, and only satellites with ambiguity resolution contributed to the estimation of ionospheric products. The ZWD parameter was modeled as a random walk, and only fixed epochs were used for ZWD extraction. The sampling interval for the vehicle-borne experiment was 1 s, and the coordinates were estimated as white noise with a priori accuracy of 500 m. The atmospheric products from the server were sampled at 5 s intervals and interpolated using linear interpolation to obtain high-precision atmospheric corrections for each epoch and to constrain the normal equations. The constraint accuracies for the slant ionosphere delay and ZWD were 0.1 m and 0.05 m, respectively.

Table 1.
Summary of the data processing strategy.
3.2. Accuracy Assessment of Atmospheric Corrections
At CORS HBA1, a high-precision coordinate was utilized. The reference station UDUC solution model was applied to HBA1 to determine its true ZWD once ambiguities were resolved. Similarly, ZWD calculations using stations HBA2, HBB0, HBF7, HBE0, and HBH8 were conducted. Interpolation via inverse distance was then employed across the reference station network to estimate ZWD at HBA1. This interpolated value was compared with the true ZWD at HBA1 to assess the accuracy of tropospheric conditions. Additionally, UDUC PPP-AR enabled the calculation of true slant path ionospheric delays for each satellite visible at HBA1. Interpolation was also used to derive slant path ionospheric delays, facilitating further evaluation in this context.
The slant path ionospheric and ZTD deviation time series on the HBA1 are shown in Figure 3. The ionospheric errors from different systems were similar, with a maximum error of around 5 cm due to afternoon ionospheric activity and satellite elevation angle variations in the Wuhan area. The RMS errors for GPS, Galileo, and BDS were 3.2 cm, 2.6 cm, and 3.8 cm, respectively, which are acceptable for PPP-RTK calculations. From the ZTD error time series shown in Figure 3, it can be seen that the ZTD error was relatively stable, with values ranging between −2.5 cm and 2.5 cm, and the RMS of ZTD was only 1.8 cm. This difference may be attributed to the larger ionospheric isolation error and the stronger activity influenced by various factors, leading to greater errors in ionospheric interpolation.
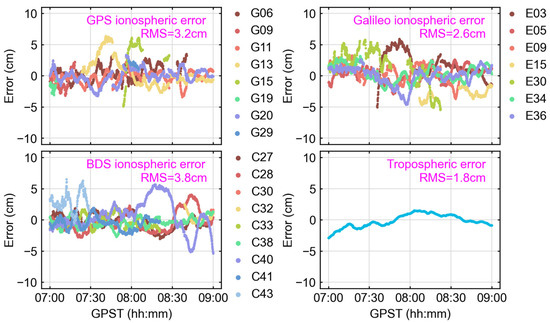
Figure 3.
Slant path ionospheric delay and ZTD errors for HBA1, both obtained by subtracting the PPP-AR estimated values (true values) from the interpolated values. The bottom right corner shows the ZTD error time series graph, while the other three sub graphs show the ionospheric errors of GPS, Galileo, and BDS, respectively.
3.3. Positioning Results of Static Experiments
To verify the reconvergence performance of PPP-RTK, a reconvergence experiment was conducted using the HBA1 station. The PPP-RTK solution utilized HBA1 observations from 04:00:00 to 12:00:00 GPST, with reconvergence performed every hour. The convergence speed and accuracy of float PPP, PPP-AR, and PPP-RTK were compared and analyzed for both the BDS single system and the combined GPS (G), Galileo (E), and BDS (C) system. In this study, once the horizontal and vertical positioning errors were less than 10 cm and 20 cm [30], respectively, and this lasted more than 5 min, the positioning was viewed as convergence. The TTFF was defined as the time difference between the beginning epoch and the epoch when a fixed solution of less than 10 cm in the horizontal and 20 cm in the vertical components was achieved and lasted for at least 5 min. The success rate of ambiguity resolution was defined as follows:
where represents the total number of epochs; represents those that do not pass the ratio test; denotes the number of epochs fixed successfully; indicates the number of epochs that pass the ratio test but that have horizontal or vertical positioning errors that exceed 10 or 20 cm, respectively.
Figure 4 shows the time series of the positioning error in the north, earth, and up directions during the convergence experiment. Similar to [40], it was evident that the performance of the GEC constellations of the three positioning methods was significantly better than that of the single BDS system. Under single BDS positioning conditions, it was observed that the float PPP solution required a long convergence time. PPP-AR significantly improved the convergence speed, but it still took a considerable amount of time to achieve full convergence. PPP-RTK demonstrated the best performance, achieving rapid convergence within a few seconds. Under multi-constellation conditions, similar conclusions were drawn as with the single BDS system. The convergence speed of the PPP-AR solution was significantly improved compared with the float PPP solution, and the positioning accuracy was also further improved. The PPP-RTK demonstrated the fastest convergence speed, achieving instantaneous fixation and the highest accuracy in all four reconvergence experiments.
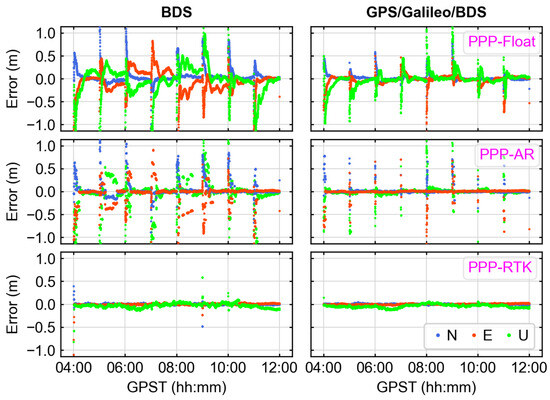
Figure 4.
PPP/PPP-AR/PPP-RTK reconvergence experiment E, N, U error time series. Reconvergence was performed every half hour for a total of four times.
Table 2 shows the statistical values of convergence time and positioning errors for PPP, PPP-AR, and PPP-RTK. It was observed that the PPP-RTK solution showed 25.22% positioning accuracy improvement in horizontal components for the single BDS scheme, compared with the PPP-AR. The TTFF decreased from 1039 s to only 25 s. In the GEC scheme, PPP-AR showed a significant enhancement in horizontal accuracy by 70.45% and vertical accuracy by 49.4% compared with the conventional PPP solution. However, in comparison to PPP-AR, the improvement in horizontal positioning accuracy with PPP-RTK was only 2.80%, along with a 11.78% enhancement in vertical accuracy. On the other hand, when compared with single BDS PPP-RTK, the utilization of multi-constellations improved horizontal accuracy by 19.19% and vertical accuracy by 44.61%. Overall, multi-constellation observations improved the positioning performance of dual-frequency PPP-RTK and increased the accuracy and stability of PPP-RTK solutions, which enabled instantaneous ambiguity resolution for static stations.

Table 2.
The statistical values of convergence time and positioning error for PPP-Float, PPP-AR, and PPP-RTK, respectively.
3.4. Positioning Results of Vehicle Kinematic Experiments
In the vehicle-mounted kinematic experiment based in Wuhan, PPP-RTK performance was assessed alongside PPP-AR and RTK using dual-frequency PPP and GEC constellations. The definitions of convergence time and TTFF were the same as used in the static experiments. Figure 5 displays the positioning error sequences of dual-frequency PPP, PPP-AR, PPP-RTK, and RTK. Table 3 provides the corresponding RMS values of the positioning error, success rate of ambiguity resolution (AR), and the convergency time. From Figure 5, it is evident that PPP had a long initialization time and slow reconvergence speed after occlusion. The positioning accuracies in the north, east, and up directions were measured at 10.8 cm, 10.8 cm, and 30.9 cm, respectively, with a convergence time of more than 20 min. PPP-AR had reduced convergence time, but it still took more than 10 min. However, the GNSS signals from fast-moving carriers tend to be noisy, increasing the possibility of incorrect ambiguity resolution and reducing positioning availability. The overall accuracies in the respective directions were 11.5 cm, 11.6 cm, and 29.3 cm. The reduced accuracy of PPP-AR may have been due to error-fixed narrow-lane (NL) ambiguity. In contrast, PPP-RTK, with high-precision atmospheric product constraints, had a significantly reduced convergence time compared with PPP and achieved improved positioning accuracies of 2.6 cm, 2.6 cm, and 7.5 cm. These accuracies represent a more than 75% improvement compared with float PPP. Additionally, the successful fix rate was enhanced from 75.50% in PPP-AR to 97.96%. Unlike PPP-RTK, the RTK algorithm mitigates errors in the observation domain, enabling rapid and high-precision positioning. In the vehicle-mounted experiment, a base station was established at the starting position, supporting a baseline length of up to 20 km. Throughout the experiment, the RTK achieved positioning accuracies of 3.1 cm, 4.3 cm, and 6.3 cm in the three respective directions. The successful fix rate of RTK was slightly higher than that of PPP-RTK. Overall, both RTK and PPP-RTK can achieve instantaneous fixing of ambiguity in open environments. Dual-frequency multi-constellation PPP-RTK demonstrated better horizontal positioning accuracy compared with RTK; however, there was a slight decrease in vertical accuracy. This could be attributed to the presence of unmodeled errors in the line-of-sight direction.
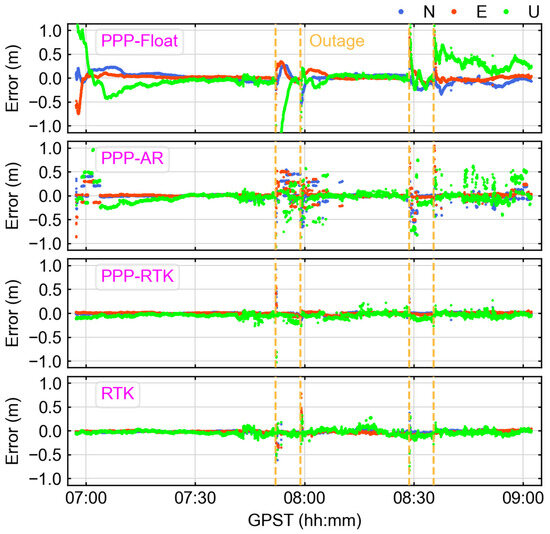
Figure 5.
The time series of positioning errors for PPP-Float, PPP-AR, PPP-RTK, and RTK solutions in the north, east, and up directions, respectively. The yellow dashed lines represent outages of GNSS.

Table 3.
The statistical values of convergence time and positioning error for four algorithms for vehicle kinematic positioning, tested in the Wuhan area.
Figure 6 shows the distribution of 3D positioning errors for the three dual-frequency schemes. Due to the long convergence time of PPP-Float, the accuracy distribution was relatively dispersed, and about half of the epochs could only achieve decimeter-level accuracy. PPP-AR achieved centimeter-level positioning accuracy in most cases, but in kinematic scenarios, the ambiguity-fixing reliability was relatively low, leading to incorrect solutions and reducing the positioning accuracy [40]. The accuracy of PPP-RTK was generally greater than 0.2 m, demonstrating a high reliability and stability similar to that of RTK. The percentages of 3D positioning errors within 0.2 m for the three schemes were 60.67%, 80.97%, and 98.46%, respectively. PPP-RTK improved by 37.79% and 17.49% compared to PPP-Float and PPP-AR, respectively. In summary, PPP-RTK exhibited a remarkably high level of position availability and was able to meet the requirements for decimeter-level lane positioning.
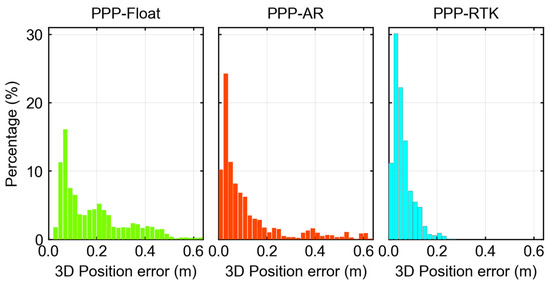
Figure 6.
The 3D position error distribution histogram for the kinematic positioning experiment with the three algorithms.
The cumulative distribution functions (CDFs) of the horizontal and vertical positioning errors for the three schemes are depicted in Figure 7. The percentages of horizontal positioning errors better than 0.1 m for the three schemes were 64.50%, 82.86%, and 99.54%, respectively. It is evident that the CDF of PPP outperformed that of PPP-AR when the horizontal positioning error was below 0.2 m. This discrepancy can be attributed to the NL ambiguity fixing error, highlighting the lower robustness of dual-frequency PPP-AR in dynamic data. Compared with the horizontal positioning error, the vertical positioning accuracy was comparatively poorer. However, PPP-RTK continued to demonstrate superior positioning accuracy and availability, with more than 99% of positioning errors within 0.2 m. On the other hand, both PPP and PPP-AR exhibited significantly lower availability in terms of vertical positioning.
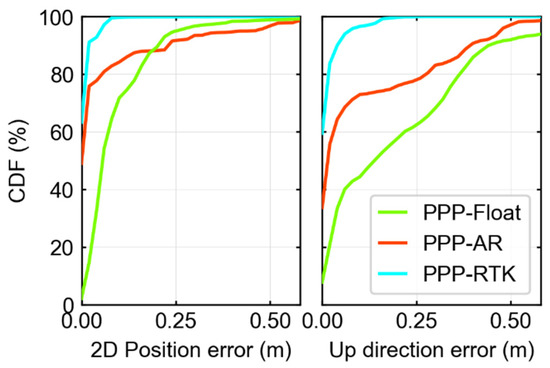
Figure 7.
Cumulative distribution function of 2D and up direction positioning error in kinematic experiments, for PPP-Float/PPP-AR/PPP-RTK.
Another advantage of PPP-RTK is its ability to achieve rapid convergence after signal loss or the blocking of GNSS. Figure 8 and Figure 9 show the positioning errors and satellite number of the three algorithms in regions A and B in Figure 2. Figure 8 shows that on Route (1), the receiver experienced a brief loss of lock for 6 s while the vehicle passed through the tunnel. It is evident that PPP had relatively large positioning errors, with RMS values of 0.57 m, 0.37 m, and 1.21 m in the north, east, and up directions, respectively. PPP-AR required a longer convergence time, and the positioning accuracy fluctuated significantly. PPP-RTK demonstrated outstanding positioning performance, swiftly achieving precise ambiguity resolution once a sufficient number of satellites were reacquired. The RMS statistical values for the north, east, and up directions were 0.18 m, 0.19 m, and 0.68 m, respectively. Route (2) also experienced a 5 s outage. Even after normal tracking was restored, PPP and PPP-AR continued to exhibit slower and less stable convergence. Fortunately, the PPP-RTK solution achieved reconvergence with high reliability, demonstrating accuracies of 0.03 m, 0.03 m, and 0.1 m in the three directions.
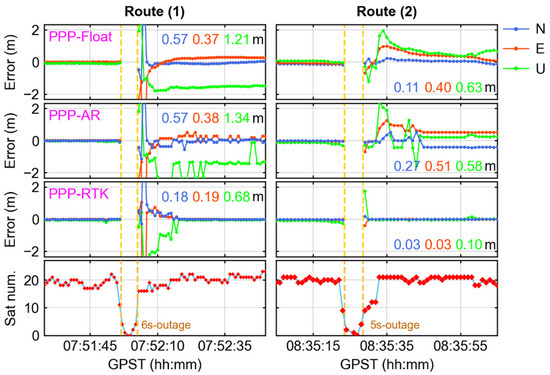
Figure 8.
The positioning errors for vehicles passing through tunnels. From top to bottom, the PPP, PPP-AR, PPP-RTK, and satellite numbers. From left to right, vehicles traveling from north to south (route 1) and from south to north (route 2) in Region A (In Figure 1), respectively.
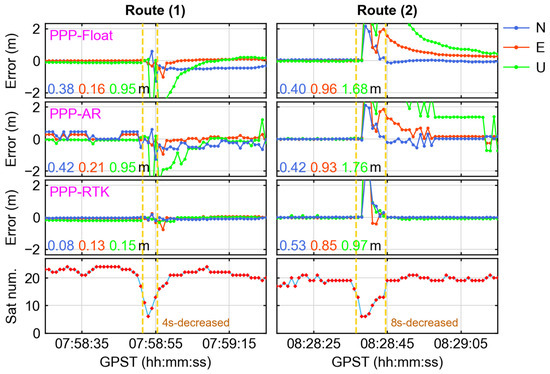
Figure 9.
The positioning error for vehicles passing through tunnels. From top to bottom, the numbers of PPP Float, PPP-AR, and PPP-RTK satellites, and from left to right, vehicles traveling from north to south (Route 1) and from south to north (Route 2) in Region B (in Figure 2), respectively.
From Figure 9, it can be observed that in Region B, the tunnel crosses the railway, leading to a gradual decrease in satellite lock. Although the three algorithms continued to provide positioning, significant fluctuations in error were also noted. The duration of the sharp change in the number of satellites on Route (1) lasted for 4 s, whereas the entire process in Route (2) lasted for 8 s. Similar to Region A, the PPP-RTK positioning was still the best and quickly reconverged after satellite observation returned to normal. The positioning accuracies were 0.08 m, 0.13 m, and 0.15 m in the north, east and up directions, respectively, for Route (1), and 0.53 m, 0.85 m, and 0.97 m for Route (2), respectively.
4. Discussion
The improved positioning accuracy and convergence time of PPP and PPP-RTK when using triple-frequency observations is an interesting topic. The time series of the positioning error statistical results of the triple-frequency scheme are shown in Figure 10 and Table 4, respectively. It is evident from Figure 10 that PPP-RTK exhibited significantly improved positioning performance compared with PPP-AR. For triple-frequency PPP-RTK, remarkable improvements of 76.13% in horizontal positioning accuracy and 69.83% in vertical positioning accuracy were observed when compared with PPP-AR. Comparing Figure 10 and Figure 5, it is evident that the disparity in positioning accuracy between the dual-frequency and triple-frequency solutions of PPP-RTK was relatively minor. In contrast, PPP-AR exhibited a substantial difference in complex environments. Compared with dual-frequency PPP-AR, triple-frequency PPP-AR demonstrated improvements of 23.84% in horizontal accuracy and 17.41% in elevation accuracy. Unfortunately, triple-frequency PPP-AR is still unable to achieve stable and reliable positioning. Compared with dual-frequency PPP-RTK, triple-frequency PPP-RTK exhibited improvements of 19.61% in the horizontal direction and 2.67% in the elevation direction. Since dual-frequency PPP-RTK demonstrated outstanding performance, the contribution of multi-frequency observations appears to have been less pronounced.
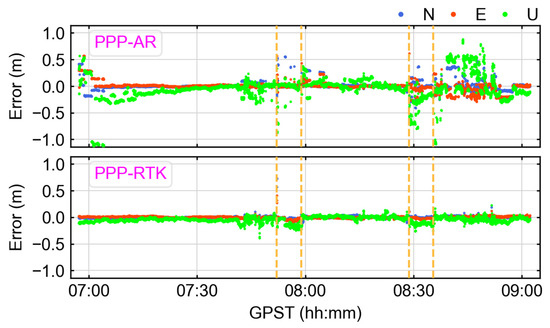
Figure 10.
The time series of positioning errors for PPP-AR and PPP-RTK triple-frequency solutions in the north, east, and up directions. The yellow dashed line represents the outage of GNSS.

Table 4.
The statistical values of convergence time and positioning error for two triple-frequency algorithms for vehicle kinematic positioning, tested in the Wuhan area.
Table 5 presents the positioning availability of dual-frequency and triple-frequency PPP-RTK. Compared with the dual-frequency scheme, the percentage of horizontal positioning errors less than 5 cm improved from 92.83% to 96.36%, and the percentage of errors less than 10 cm improved from 99.69% to 99.89%. Similarly, the percentage of elevation positioning errors less than 10 cm increased from 96.46% to 98.83%, and the percentage of errors less than 20 cm increased from 99.61% to 99.93%. Multi-frequency PPP-RTK can significantly enhance accuracy, particularly for users who demand centimeter-level 3D positioning accuracy. In such scenarios, multi-frequency PPP-RTK demonstrates exceptional performance. However, for users with slightly lower accuracy requirements who prioritize reliability, the benefits of employing multi-frequency observations may not be readily apparent.

Table 5.
Dual-frequency and triple-frequency PPP-RTK positioning availability.
5. Conclusions
A dual/triple-frequency multi-constellation PPP-RTK method with atmospheric augmentation is proposed, to shorten convergence time and improve positioning accuracy, especially for kinematic positioning. The performance of PPP-Float, PPP-AR, PPP-RTK, and short-baseline RTK was assessed in a set of experiments conducted in Wuhan. The positioning results indicate that dual-frequency PPP-RTK achieved a performance similar to short-baseline RTK, demonstrating that PPP-RTK has the potential for lane-level navigation.
For static positioning experiments, the accuracies of ionospheric and tropospheric interpolation products were within 2–4 cm and better than 2 cm, respectively. Both multi-system dual-frequency PPP-AR and PPP-RTK achieved centimeter-level positioning accuracy, with horizontal RMS of 1.43 cm and 1.39 cm and vertical RMS of 2.97 cm and 2.62 cm, respectively. Furthermore, the convergence time of PPP-RTK was reduced from 166 s in PPP-AR to just 1 s, achieving instantaneous ambiguity resolution in open areas. The addition of atmospheric products provided a more significant improvement in terms of accuracy and convergence time for BDS only.
For vehicle kinematic experiments, the positioning accuracy of dual-frequency PPP-RTK in the north, east, and up directions was 2.6 cm, 2.6 cm, and 7.6 cm, respectively, and the success rate of ambiguity resolution was 97.96%. Moreover, PPP-RTK demonstrated excellent positioning availability of over 99%, and it was able to achieve fast ambiguity resolution within several seconds after outage and blocking. Compared with PPP-Float and PPP-AR, the improvements in terms of positioning accuracy were 75.9%, 75.9%, and 75.7%, and 77.4%, 77.6%, and 74.4% in the three directions, respectively. In addition, the performances of triple-frequency PPP-AR and PPP-RTK were also evaluated. The results showed that compared with the dual-frequency designs, the positioning accuracy of PPP-AR underwent an 18.9% improvement, while the improvement for PPP-RTK was not significant. Triple-frequency PPP-RTK can further enhance the robustness and accuracy of positioning. In summary, PPP-RTK also had better performance and shorter convergence time in terms of kinematic positioning.
Author Contributions
Conceptualization, Z.L.; methodology, Z.-F.S. and D.-W.G.; validation, Z.-Y.Q. and S.-Y.X.; data curation, S.-Y.X. and X.-T.L.; writing—original draft preparation, Z.-F.S. and D.-W.G.; writing—review and editing, S.-Y.X. and X.-T.L.; project administration, Z.L.; funding acquisition, Z.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
Author Zi-Yang Qu was employed by the company Kepler Satellite Orbit Science & Technology (Wuhan) Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Zumberge, J.; Heflin, M.; Jefferson, D.; Watkins, M.; Webb, F.H. Precise point positioning for the efficient and robust analysis of GPS data from large networks. J. Geophys. Res. Solid Earth 1997, 102, 5005–5017. [Google Scholar] [CrossRef]
- Bisnath, S.; Gao, Y. Current state of precise point positioning and future prospects and limitations. In Observing Our Changing Earth; Springer: Berlin/Heidelberg, Germany, 2009; pp. 615–623. [Google Scholar]
- Ge, M.; Gendt, G.; Rothacher, M.; Shi, C.; Liu, J. Resolution of GPS carrier-phase ambiguities in precise point positioning (PPP) with daily observations. J. Geod. 2008, 82, 389–399. [Google Scholar] [CrossRef]
- Li, X.; Li, X.; Liu, G.; Feng, G.; Yuan, Y.; Zhang, K.; Ren, X. Triple-frequency PPP ambiguity resolution with multi-constellation GNSS: BDS and Galileo. J. Geod. 2019, 93, 1105–1122. [Google Scholar] [CrossRef]
- Chen, L.; Zhao, Q.; Hu, Z.; Jiang, X.; Geng, C.; Ge, M.; Shi, C. vGNSS global real-time augmentation positioning: Real-time precise satellite clock estimation, prototype system construction and performance analysis. Adv. Space Res. Off. J. Comm. Space Res. (COSPAR) 2018, 61, 367–384. [Google Scholar] [CrossRef]
- Teunissen, P.J.G.; Odolinski, R.; Odijk, D. Instantaneous BeiDou+GPS RTK positioning with high cut-off elevation angles. J. Geod. 2014, 88, 335–350. [Google Scholar] [CrossRef]
- Wabbena, G.; Schmitz, M.; Bagge, A. PPP-RTK: Precise point positioning using state-space representation in RTK networks. In Proceedings of the 18th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2005), Long Beach, CA, USA, 13–16 September 2005; pp. 2584–2594. [Google Scholar]
- Teunissen, P.; Khodabandeh, A. Review and principles of PPP-RTK methods. J. Geod. 2015, 89, 217–240. [Google Scholar] [CrossRef]
- Li, X.; Zhang, X.; Ge, M. Regional reference network augmented precise point positioning for instantaneous ambiguity resolution. J. Geod. 2011, 85, 151–158. [Google Scholar] [CrossRef]
- Laurichesse, D.; Mercier, F.; Berthias, J.-P.; Broca, P.; Cerri, L. Integer ambiguity resolution on undifferenced GPS phase measurements and its application to PPP and satellite precise orbit determination. Navigation 2014, 56, 135–149. [Google Scholar] [CrossRef]
- Zhang, B.; Chen, Y.; Yuan, Y. PPP-RTK based on undifferenced and uncombined observations: Theoretical and practical aspects. J. Geod. 2019, 93, 1011–1024. [Google Scholar] [CrossRef]
- Li, X.; Huang, J.; Li, X.; Lyu, H.; Wang, B.; Xiong, Y.; Xie, W. Multi-constellation GNSS PPP instantaneous ambiguity resolution with precise atmospheric corrections augmentation. GPS Solut. 2021, 25, 107. [Google Scholar] [CrossRef]
- Zha, J.; Zhang, B.; Liu, T.; Hou, P. Ionosphere-weighted undifferenced and uncombined PPP-RTK: Theoretical models and experimental results. GPS Solut. 2021, 25, 135. [Google Scholar] [CrossRef]
- Teunissen, P.J.; Odijk, D.; Zhang, B. PPP-RTK: Results of CORS network-based PPP with integer ambiguity resolution. J. Aeronaut. Astronaut. Aviat. Ser. A 2010, 42, 223–230. [Google Scholar]
- Li, X.; Dick, G.; Ge, M.; Heise, S.; Wickert, J.; Bender, M. Real-time GPS sensing of atmospheric water vapor: Precise point positioning with orbit, clock, and phase delay corrections. Geophys. Res. Lett. 2014, 41, 3615–3621. [Google Scholar] [CrossRef]
- Geng, J.; Bock, Y. Triple-frequency GPS precise point positioning with rapid ambiguity resolution. J. Geod. 2013, 87, 449–460. [Google Scholar] [CrossRef]
- Odijk, D.; Zhang, B.; Khodabandeh, A.; Odolinski, R.; Teunissen, P.J. On the estimability of parameters in undifferenced, uncombined GNSS network and PPP-RTK user models by means of S-system theory. J. Geod. 2016, 90, 15–44. [Google Scholar] [CrossRef]
- Li, Z.; Chen, W.; Ruan, R.; Liu, X. Evaluation of PPP-RTK based on BDS-3/BDS-2/GPS observations: A case study in Europe. GPS Solut. 2020, 24, 38. [Google Scholar] [CrossRef]
- Ma, H.; Zhao, Q.; Verhagen, S.; Psychas, D.; Liu, X. Assessing the performance of multi-GNSS PPP-RTK in the local area. Remote Sens. 2020, 12, 3343. [Google Scholar] [CrossRef]
- Odijk, D.; Teunissen, P.J.; Zhang, B. Single-frequency integer ambiguity resolution enabled GPS precise point positioning. J. Surv. Eng. 2012, 138, 193–202. [Google Scholar] [CrossRef]
- Li, X.; Wang, B.; Li, X.; Huang, J.; Lyu, H.; Han, X. Principle and performance of multi-frequency and multi-GNSS PPP-RTK. Satell. Navig. 2022, 3, 7. [Google Scholar] [CrossRef]
- Cabinet Office (2021) Quasi-Zenith Satellite System Interface Specification: Centimeter Level Augmentation Service (Specification No. IS-QZSS-L6-004). Available online: https://qzss.go.jp/en/technical/download/pdf/ps-is-qzss/is-qzss-l6-004.pdf (accessed on 3 August 2024).
- Nardo, A.; Drescher, R.; Brandl, M.; Chen, X.; Landau, H.; Rodriguez-Solano, C.; Seeger, S.; Weinbach, U. Experiences with Trimble CenterPoint RTX with Fast Convergence; Trimble TerraSat GmbH: Hoehenkirchen, Germany, 2015; Volume 19, p. 85635. [Google Scholar]
- Hesselbarth, A.; Medina, D.; Ziebold, R.; Sandler, M.; Hoppe, M.; Uhlemann, M. Enabling assistance functions for the safe navigation of inland waterways. IEEE Intell. Transp. Syst. Mag. 2020, 12, 123–135. [Google Scholar] [CrossRef]
- Gu, S.; Dai, C.; Fang, W.; Zheng, F.; Wang, Y.; Zhang, Q.; Lou, Y.; Niu, X. Multi-GNSS PPP/INS tightly coupled integration with atmospheric augmentation and its application in urban vehicle navigation. J. Geod. 2021, 95, 64. [Google Scholar] [CrossRef]
- An, X.; Ziebold, R.; Lass, C. From RTK to PPP-RTK: Towards real-time kinematic precise point positioning to support autonomous driving of inland waterway vessels. GPS Solut. 2023, 27, 86. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, L.; Li, J.; Yang, Y.; Zhang, T.; Mao, Y.; Sun, B.; Ren, X. Featured services and performance of BDS-3. Sci. Bull. 2021, 66, 2135–2143. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Huang, J.; Li, X.; Shen, Z.; Han, J.; Li, L.; Wang, B. Review of PPP–RTK: Achievements, challenges, and opportunities. Satell. Navig. 2022, 3, 28. [Google Scholar] [CrossRef]
- Xin, S.; Geng, J.; Zhang, G.; Ng, H.-F.; Guo, J.; Hsu, L.-T. 3D-mapping-aided PPP-RTK aiming at deep urban canyons. J. Geod. 2022, 96, 78. [Google Scholar] [CrossRef]
- Li, Z.; Xu, G.; Guo, J.; Zhao, Q. A sequential ambiguity selection strategy for partial ambiguity resolution during RTK positioning in urban areas. GPS Solut. 2022, 26, 92. [Google Scholar] [CrossRef]
- Chen, L.; Zheng, F.; Gong, X.; Jiang, X. GNSS high-precision augmentation for autonomous vehicles: Requirements, solution, and technical challenges. Remote Sens. 2023, 15, 1623. [Google Scholar] [CrossRef]
- Li, B.; Shen, Y.; Feng, Y.; Gao, W.; Yang, L. GNSS ambiguity resolution with controllable failure rate for long baseline network RTK. J. Geod. 2014, 88, 99–112. [Google Scholar] [CrossRef]
- Lei, X.; Xu, X.; Tao, J.; Yang, T.; Zhao, Q.; Guo, J. High-precision tropospheric correction method for NRTK regions with significant height differences. Meas. Sci. Technol. 2024, 35, 106315. [Google Scholar] [CrossRef]
- Yao, Y.; He, C.; Zhang, B.; Xu, Q. A new global Zenith Troposphere Delay model GZTD. Chin. J. Geophys.-Chin. Ed. 2013, 56, 2218–2227. [Google Scholar] [CrossRef]
- Li, Z.; Guo, J.; Zhao, Q. POSGO: An open-source software for GNSS pseudorange positioning based on graph optimization. GPS Solut. 2023, 27, 187. [Google Scholar] [CrossRef]
- Blewitt, G. An automatic editing algorithm for GPS data. Geophys. Res. Lett. 1990, 17, 199–202. [Google Scholar] [CrossRef]
- Guo, J.; Wang, C.; Chen, G.; Xu, X.; Zhao, Q. BDS-3 precise orbit and clock solution at Wuhan University: Status and improvement. J. Geod. 2023, 97, 15. [Google Scholar] [CrossRef]
- Tao, J.; Chen, G.; Guo, J.; Zhang, Q.; Liu, S.; Zhao, Q. Toward BDS/Galileo/GPS/QZSS triple-frequency PPP instantaneous integer ambiguity resolutions without atmosphere corrections. GPS Solut. 2022, 26, 127. [Google Scholar] [CrossRef]
- Xu, S.; Yang, Q.; Du, X.; Xu, X.; Zhao, Q.; Yang, L.; Qin, Y.; Guo, J. Multi-GNSS Precise Point Positioning enhanced by the real navigation signals from CENTISPACETM LEO mission. Adv. Space Res. 2024, 73, 4175–4186. [Google Scholar] [CrossRef]
- Verhagen, S. Integer ambiguity validation: An open problem? GPS Solut. 2004, 8, 36–43. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).