Automatic Detection of Quasi-Periodic Emissions from Satellite Observations by Using DETR Method
Abstract
1. Introduction
2. Dataset and Target
2.1. CSES-01 Satellite and Dataset
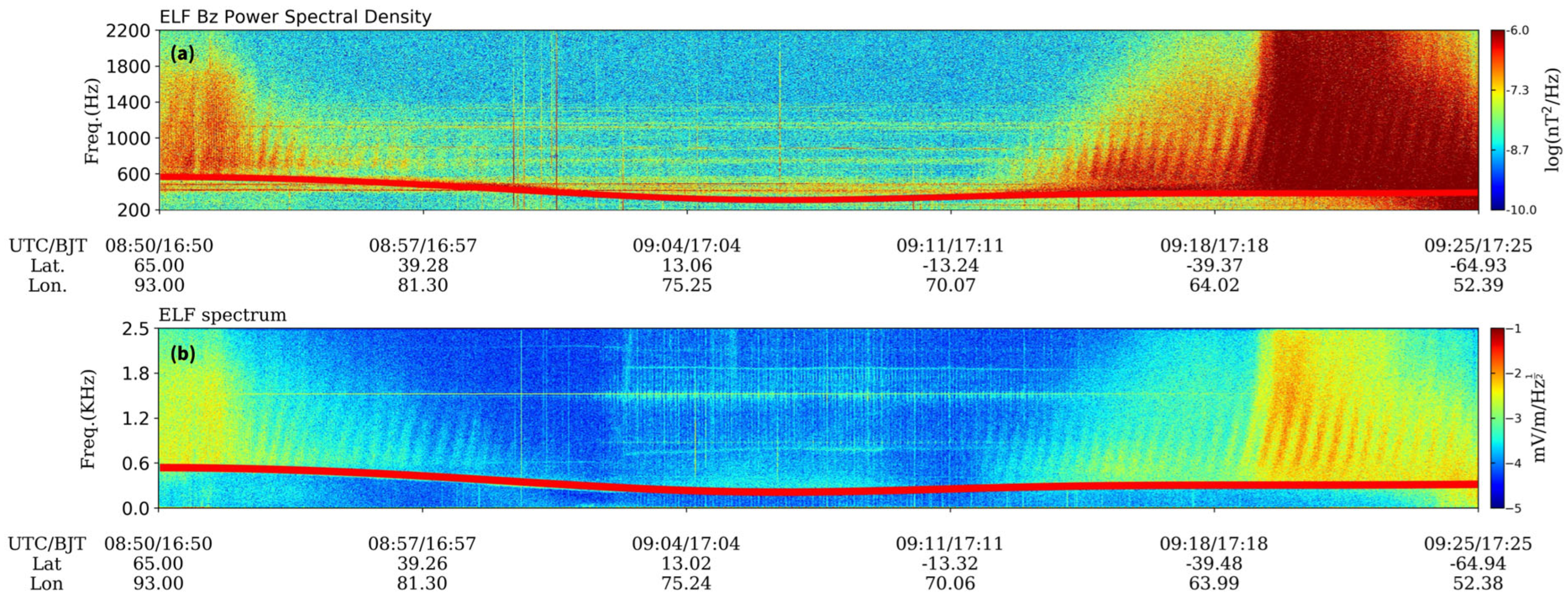
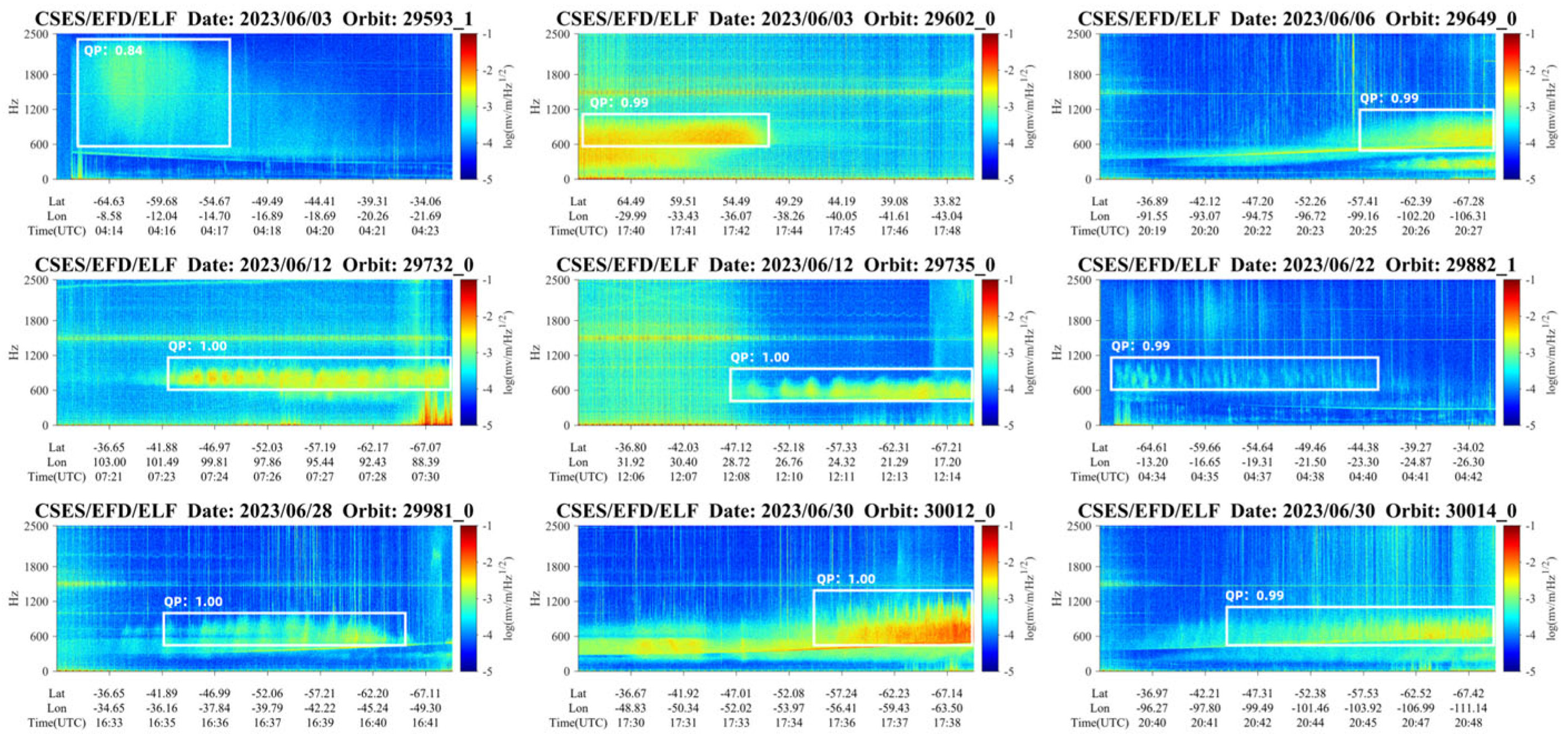
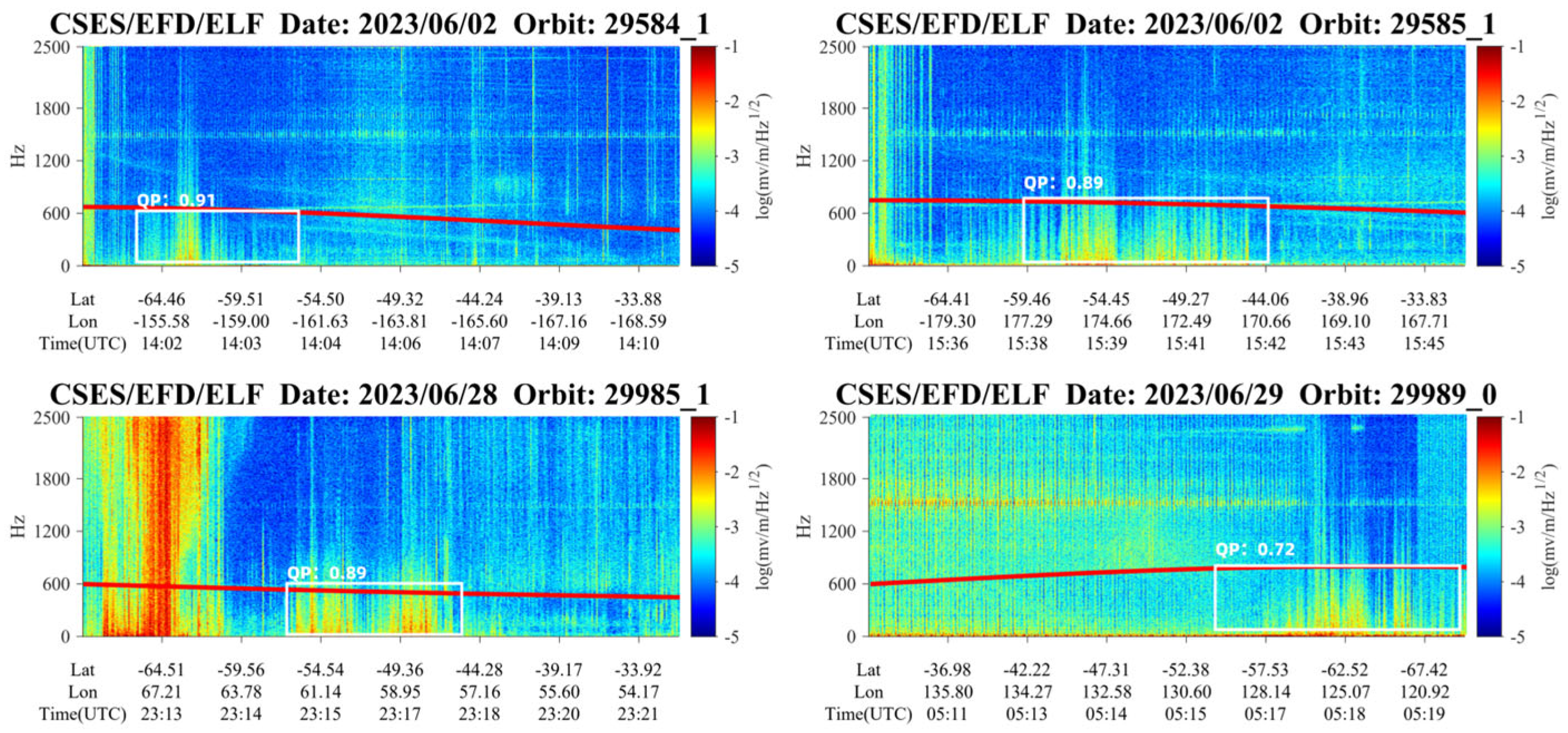
2.2. Identification and Characteristics of QP Emissions
3. Automatic Detection Method Development
3.1. QP-DETR Design
3.2. The Backbone Network Is Modified with EfficientNetV2
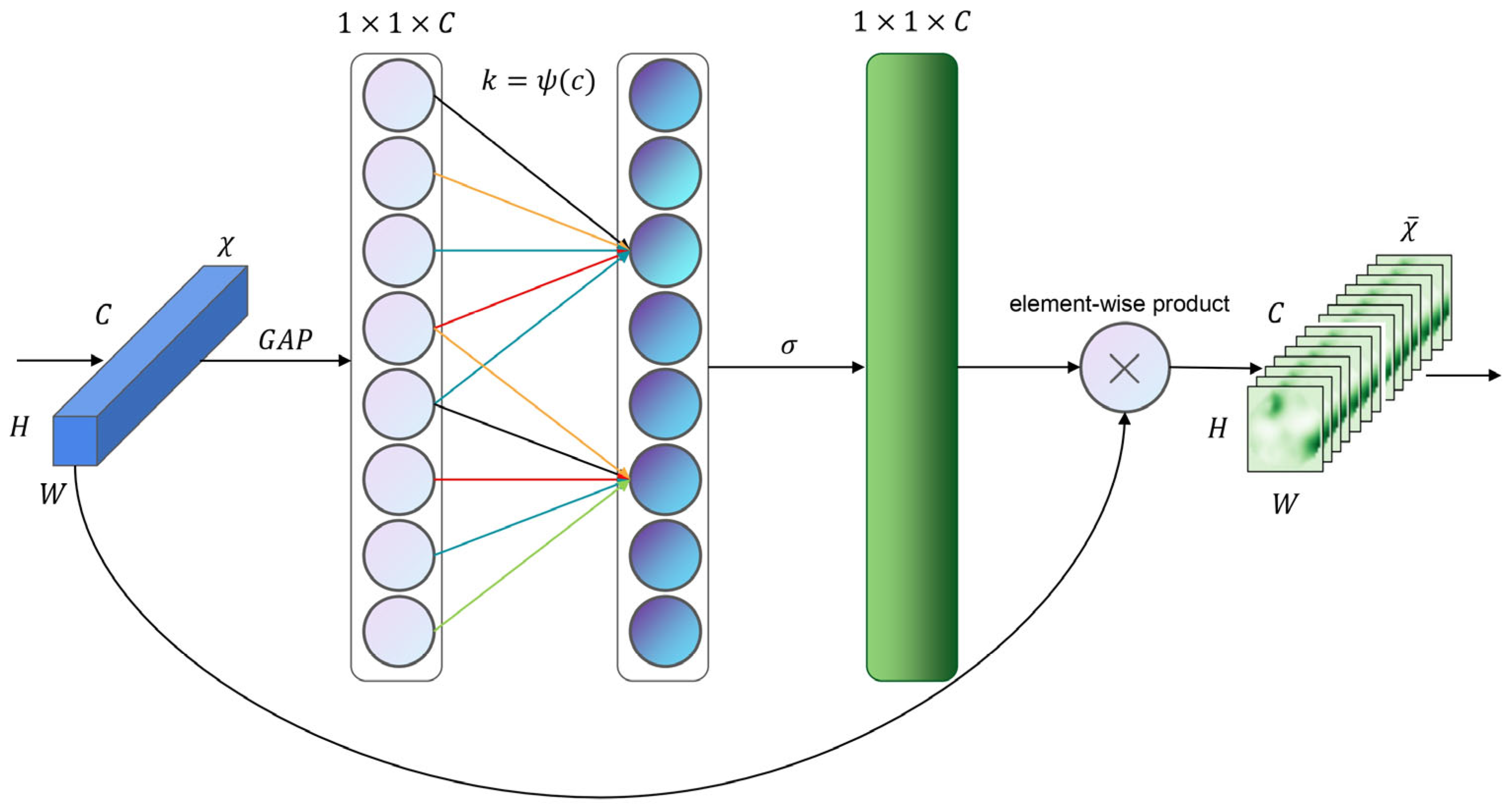
3.3. Adding Efficient Channel Attention Module
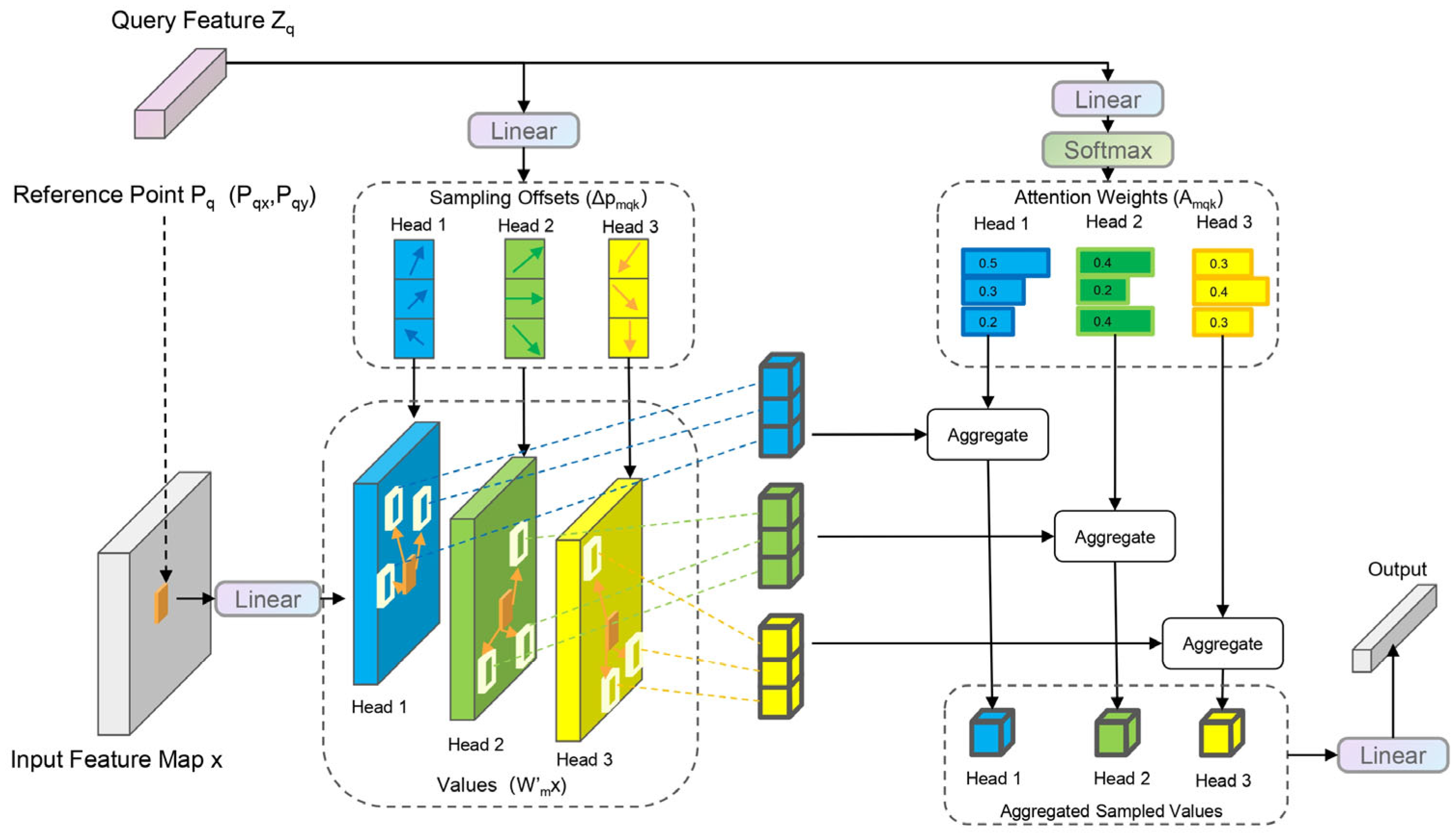
3.4. Improving Deformable Attention Mechanism
4. Results
4.1. Experimental Environment
4.2. Evaluation Indicators
4.3. Algorithm Performance Assessment
4.4. Test Set Comparison Experiment
4.5. Improvement of the Detection Stage
5. Discussions
5.1. Impacts of Other Types of Wave Activity
5.2. Neural Networks in Other Space Missions
5.3. Future Directions: Audio Feature Extraction and Model Integration
5.4. Limitations and Potential Failure Conditions
6. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sato, N.; Hayashi, K.; Kokubun, S.; Oguti, T.; Fukunishi, H. Relationships between Quasi-Periodic VLF Emission and Geomagnetic Pulsation. J. Atmos. Terr. Phys. 1974, 36, 1515–1526. [Google Scholar] [CrossRef]
- Hayosh, M.; Němec, F.; Santolík, O.; Parrot, M. Propagation Properties of Quasiperiodic VLF Emissions Observed by the DEMETER Spacecraft. Geophys. Res. Lett. 2016, 43, 1007–1014. [Google Scholar] [CrossRef]
- Zhima, Z.; Huang, J.; Shen, X.; Xia, Z.; Chen, L.; Piersanti, M.; Yang, Y.; Wang, Q.; Zeng, L.; Lei, J.; et al. Simultaneous Observations of ELF/VLF Rising-Tone Quasiperiodic Waves and Energetic Electron Precipitations in the High-Latitude Upper Ionosphere. J. Geophys. Res. Space Phys. 2020, 125, e2019JA027574. [Google Scholar] [CrossRef]
- Němec, F.; Santolík, O.; Parrot, M.; Pickett, J.; Hayosh, M.; Cornilleau-Wehrlin, N. Conjugate Observations of Quasi-Periodic Emissions by Cluster and DEMETER Spacecraft. J. Geophys. Res. Space Phys. 2013, 118, 198–208. [Google Scholar] [CrossRef]
- Hayosh, M.; Pasmanik, D.; Demekhov, A.; Santolík, O.; Parrot, M.; Titova, E. Simultaneous Observations of Quasi-Periodic ELF/VLF Wave Emissions and Electron Precipitation by DEMETER Satellite: A Case Study. J. Geophys. Res. Space Phys. 2013, 118, 4523–4533. [Google Scholar] [CrossRef]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-Cnn: Towards Real-Time Object Detection with Region Proposal Networks. Adv. Neural Inf. Process. Syst. 2015, 28. [Google Scholar] [CrossRef]
- Lin, T.-Y.; Goyal, P.; Girshick, R.; He, K.; Dollár, P. Focal Loss for Dense Object Detection. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2980–2988. [Google Scholar]
- Redmon, J.; Farhadi, A. Yolov3: An Incremental Improvement. arXiv 2018, arXiv:1804.02767. [Google Scholar] [CrossRef]
- Duan, K.; Bai, S.; Xie, L.; Qi, H.; Huang, Q.; Tian, Q. Centernet: Keypoint Triplets for Object Detection. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 6569–6578. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Lukasz, K.; Polosukhin, I. Attention Is All You Need. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar] [CrossRef]
- Carion, N.; Massa, F.; Synnaeve, G.; Usunier, N.; Kirillov, A.; Zagoruyko, S. End-to-End Object Detection with Transformers. In Proceedings of the European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2020; pp. 213–229. [Google Scholar]
- Shen, X.; Zhang, X.; Yuan, S.; Wang, L.; Cao, J.; Huang, J.; Zhu, X.; Piergiorgio, P.; Dai, J. The State-of-the-Art of the China Seismo-Electromagnetic Satellite Mission. Sci. China Technol. Sci. 2018, 61, 634–642. [Google Scholar] [CrossRef]
- Cheng, B.; Zhou, B.; Magnes, W.; Lammegger, R.; Pollinger, A. High Precision Magnetometer for Geomagnetic Exploration Onboard of the China Seismo-Electromagnetic Satellite. Sci. China Technol. Sci. 2018, 61, 659–668. [Google Scholar] [CrossRef]
- Pollinger, A.; Lammegger, R.; Magnes, W.; Hagen, C.; Ellmeier, M.; Jernej, I.; Leichtfried, M.; Kürbisch, C.; Maierhofer, R.; Wallner, R.; et al. Coupled Dark State Magnetometer for the China Seismo-Electromagnetic Satellite. Meas. Sci. Technol. 2018, 29, 095103. [Google Scholar] [CrossRef]
- Cao, J.; Zeng, L.; Zhan, F.; Wang, Z.; Wang, Y.; Chen, Y.; Meng, Q.; Ji, Z.; Wang, P.; Liu, Z.; et al. The Electromagnetic Wave Experiment for CSES Mission: Search Coil Magnetometer. Sci. China Technol. Sci. 2018, 61, 653–658. [Google Scholar] [CrossRef]
- Huang, J.; Shen, X.; Zhang, X.; Lu, H.; Tan, Q.; Wang, Q.; Yan, R.; Chu, W.; Yang, Y.; Liu, D.; et al. Application System and Data Description of the China Seismo-Electromagnetic Satellite. Earth Planet. Phys. 2018, 2, 444–454. [Google Scholar] [CrossRef]
- Zhima, Z.; Zhou, B.; Zhao, S.; Wang, Q.; Huang, J.; Zeng, L.; Lei, J.; Chen, Y.; Li, C.; Yang, D.; et al. Cross-Calibration on the Electromagnetic Field Detection Payloads of the China Seismo-Electromagnetic Satellite. Sci. China Technol. Sci. 2022, 65, 1415–1426. [Google Scholar] [CrossRef]
- Yang, D.; Zhima, Z.; Wang, Q.; Huang, J.; Wang, X.; Zhang, Z.; Zhao, S.; Guo, F.; Cheng, W.; Lu, H.; et al. Stability Validation on the VLF Waveform Data of the China-Seismo-Electromagnetic Satellite. Sci. China Technol. Sci. 2022, 65, 3069–3078. [Google Scholar] [CrossRef]
- Hu, Y.; Zhima, Z.; Huang, J.; Zhao, S.; Guo, F.; Wang, Q.; Shen, X. Algorithms and Implementation of Wave Vector Analysis Tool for the Electromagnetic Waves Recorded by the CSES Satellite. Chin. J. Geophys. 2020, 63, 1751–1765. [Google Scholar] [CrossRef]
- Yang, Y.; Zhou, B.; Hulot, G.; Olsen, N.; Wu, Y.; Xiong, C.; Stolle, C.; Zhima, Z.; Huang, J.; Zhu, X.; et al. CSES High Precision Magnetometer Data Products and Example Study of an Intense Geomagnetic Storm. J. Geophys. Res. Space Phys. 2021, 126, e2020JA028026. [Google Scholar] [CrossRef]
- Yang, Y.; Zhima, Z.; Shen, X.; Zhou, B.; Wang, J.; Magnes, W.; Pollinger, A.; Lu, H.; Guo, F.; Lammegger, R.; et al. An Improved In-Flight Calibration Scheme for CSES Magnetic Field Data. Remote Sens. 2023, 15, 4578. [Google Scholar] [CrossRef]
- Sato, N.; Fukunishi, H. Interaction between ELF-VLF Emissions and Magnetic Pulsations: Classification of Quasi-Periodic ELF-VLF Emissions Based on Frequency-Time Spectra. J. Geophys. Res. Space Phys. 1981, 86, 19–29. [Google Scholar] [CrossRef]
- Hayosh, M.; Němec, F.; Santolík, O.; Parrot, M. Statistical Investigation of VLF Quasiperiodic Emissions Measured by the DEMETER Spacecraft. J. Geophys. Res. Space Phys. 2014, 119, 8063–8072. [Google Scholar] [CrossRef]
- Tan, M.; Le, Q. Efficientnet: Rethinking Model Scaling for Convolutional Neural Networks. In Proceedings of the International Conference on Machine Learning, PMLR, Long Beach, CA, USA, 10–15 June 2019; pp. 6105–6114. [Google Scholar]
- Tan, M.; Le, Q. Efficientnetv2: Smaller Models and Faster Training. In Proceedings of the International Conference on Machine Learning, PMLR, Virtual, 18–24 July 2021; pp. 10096–10106. [Google Scholar]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-Excitation Networks. In Proceedings of the Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 7132–7141.
- Howard, A.G.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Andreetto, M.; Adam, H. MobileNets: Efficient Convolutional Neural Networks for Mobile Vision Applications. arXiv 2017, arXiv:1704.04861. [Google Scholar]
- Wang, Q.; Wu, B.; Zhu, P.; Li, P.; Zuo, W.; Hu, Q. ECA-Net: Efficient Channel Attention for Deep Convolutional Neural Networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 11534–11542. [Google Scholar] [CrossRef]
- Dai, J.; Qi, H.; Xiong, Y.; Li, Y.; Zhang, G.; Hu, H.; Wei, Y. Deformable Convolutional Networks. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 764–773. [Google Scholar]
- Zhu, X.; Su, W.; Lu, L.; Li, B.; Wang, X.; Dai, J. Deformable Detr: Deformable Transformers for End-to-End Object Detection. arXiv 2020, arXiv:2010.04159. [Google Scholar] [CrossRef]
- Bottou, L. Large-Scale Machine Learning with Stochastic Gradient Descent. In Proceedings of the COMPSTAT’2010, Paris, France, 22–27 August 2010; Lechevallier, Y., Saporta, G., Eds.; Physica-Verlag HD: Heidelberg, Germany, 2010; pp. 177–186. [Google Scholar]
- Hu, Y.; Zhima, Z.; Fu, H.; Cao, J.; Piersanti, M.; Wang, T.; Yang, D.; Sun, X.; Lv, F.; Lu, C.; et al. A Large-Scale Magnetospheric Line Radiation Event in the Upper Ionosphere Recorded by the China-Seismo-Electromagnetic Satellite. J. Geophys. Res. Space Phys. 2023, 128, e2022JA030743. [Google Scholar] [CrossRef]
- Yuan, J.; Wang, Q.; Yang, D.; Liu, Q.; Zhima, Z.; Shen, X. Automatic Recognition Algorithm of Lightning Whistlers Observed by the Search Coil Magnetometer Onboard the Zhangheng-1 Satellite. Chin. J. Geophys. 2021, 64, 3905–3924. [Google Scholar] [CrossRef]
- Zhima, Z.; Hu, Y.; Shen, X.; Chu, W.; Piersanti, M.; Parmentier, A.; Zhang, Z.; Wang, Q.; Huang, J.; Zhao, S.; et al. Storm-Time Features of the Ionospheric ELF/VLF Waves and Energetic Electron Fluxes Revealed by the China Seismo-Electromagnetic Satellite. Appl. Sci. 2021, 11, 2617. [Google Scholar] [CrossRef]
- Elie, F.; Hayakawa, M.; Parrot, M.; Pinçon, J.-L.; Lefeuvre, F. Neural Network System for the Analysis of Transient Phenomena on Board the DEMETER Micro-Satellite. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 1999, 82, 1575–1581. [Google Scholar]
- Yuan, J.; Wang, Z.; Zeren, Z.; Wang, Z.; Feng, J.; Shen, X.; Wu, P.; Wang, Q.; Yang, D.; Wang, T.; et al. Automatic Recognition Algorithm of the Lightning Whistler Waves by Using Speech Processing Technology. Chin. J. Geophys. 2022, 65, 882–897. [Google Scholar] [CrossRef]
- Wang, Z.; Yi, J.; Yuan, J.; Hu, R.; Peng, X.; Chen, A.; Shen, X. Lightning-Generated Whistlers Recognition for Accurate Disaster Monitoring in China and Its Surrounding Areas Based on a Homologous Dual-Feature Information Enhancement Framework. Remote Sens. Environ. 2024, 304, 114021. [Google Scholar] [CrossRef]





| Stage | Operator | Stride | #Channels | #Layers |
|---|---|---|---|---|
| 0 | Conv3×3 | 2 | 48 | 1 |
| 1 | Fused-MBConv1, k3×3 | 1 | 32 | 2 |
| 2 | Fused-MBConv4, k3×3 | 2 | 64 | 4 |
| 3 | Fused-MBConv4, k3×3 | 2 | 128 | 4 |
| 4 | MBConv4, k3×3 | 2 | 256 | 6 |
| 5 | MBConv6, k3×3 | 1 | 512 | 9 |
| 6 | MBConv6, k3×3 | 2 | 1024 | 15 |
| 7 | Conv1×1 and Pooling and FC | - | 2048 | 1 |
| Algorithm | Backbone | Params/M | FPS | mAP0.5:0.95 | mAP0.5 |
|---|---|---|---|---|---|
| RetinaNet | ResNet50 | 36.47 | 35.6 | 0.417 | 0.835 |
| YOLOv3 | Darknet-53 | 61.52 | 43.5 | 0.468 | 0.879 |
| Faster RCNN | ResNet50 | 41.44 | 21.2 | 0.403 | 0.763 |
| CenterNet | Hourglass-52 | 104.8 | 16.8 | 0.436 | 0.829 |
| DETR-R50 | ResNet50 | 41.28 | 28.4 | 0.458 | 0.914 |
| DETR-R101 | ResNet101 | 60.22 | 17.9 | 0.475 | 0.920 |
| QP-DETR | EfficientNetV2 | 34.27 | 39.3 | 0.480 | 0.923 |
| EfficientNetV2 | ECA | DefAttention | Ml-DefAttention | Params/M | mAP0.5:0.95 | mAP0.5 |
|---|---|---|---|---|---|---|
| - | - | - | - | 41.28 | 0.458 | 0.914 |
| √ | - | - | - | 34.27 | 0.452 | 0.916 |
| √ | √ | - | - | 34.27 | 0.467 | 0.920 |
| √ | √ | √ | - | 34.27 | 0.476 | 0.923 |
| √ | √ | √ | √ | 34.27 | 0.480 | 0.923 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ran, Z.; Lu, C.; Hu, Y.; Yang, D.; Sun, X.; Zhima, Z. Automatic Detection of Quasi-Periodic Emissions from Satellite Observations by Using DETR Method. Remote Sens. 2024, 16, 2850. https://doi.org/10.3390/rs16152850
Ran Z, Lu C, Hu Y, Yang D, Sun X, Zhima Z. Automatic Detection of Quasi-Periodic Emissions from Satellite Observations by Using DETR Method. Remote Sensing. 2024; 16(15):2850. https://doi.org/10.3390/rs16152850
Chicago/Turabian StyleRan, Zilin, Chao Lu, Yunpeng Hu, Dehe Yang, Xiaoying Sun, and Zeren Zhima. 2024. "Automatic Detection of Quasi-Periodic Emissions from Satellite Observations by Using DETR Method" Remote Sensing 16, no. 15: 2850. https://doi.org/10.3390/rs16152850
APA StyleRan, Z., Lu, C., Hu, Y., Yang, D., Sun, X., & Zhima, Z. (2024). Automatic Detection of Quasi-Periodic Emissions from Satellite Observations by Using DETR Method. Remote Sensing, 16(15), 2850. https://doi.org/10.3390/rs16152850








