Abstract
Mangrove ecosystems provide numerous ecological services and serve as vital habitats for a wide range of flora and fauna. Thus, accurate mapping and monitoring of relevant land covers in mangrove ecosystems are crucial for effective conservation and management efforts. In this study, we proposed a novel approach for mangrove ecosystem mapping using a Hybrid Selective Kernel-based Convolutional Neural Network (HSK-CNN) framework and multi-temporal Sentinel-2 imagery. A time series of the Normalized Difference Vegetation Index (NDVI) products derived from Sentinel-2 imagery was produced to capture the temporal behavior of land cover types in the dynamic ecosystem of the study area. The proposed algorithm integrated Selective Kernel-based feature extraction techniques to facilitate the effective learning and classification of multiple land cover types within the dynamic mangrove ecosystems. The model demonstrated a high Overall Accuracy (OA) of 94% in classifying eight land cover classes, including mangrove, tidal zone, water, mudflat, urban, and vegetation. The HSK-CNN demonstrated superior performance compared to other algorithms, including random forest (OA = 85%), XGBoost (OA = 87%), Three-Dimensional (3D)-DenseNet (OA = 90%), Two-Dimensional (2D)-CNN (OA = 91%), Multi-Layer Perceptron (MLP)-Mixer (OA = 92%), and Swin Transformer (OA = 93%). Additionally, it was observed that the structure of the network, such as the types of convolutional layers and patch sizes, affected the classification accuracy using the proposed model and, thus, the optimum scenarios and values of these parameters should be determined to obtain the highest possible classification accuracy. Overall, it was observed that the produced map could offer valuable insights into the distribution of different land cover types in the mangrove ecosystem, facilitating informed decision-making for conservation and sustainable management efforts.
1. Introduction
Mangrove ecosystems are critically important coastal environments that provide a wide range of ecological and socio-economic services [1]. These unique ecosystems act as natural barriers against coastal erosion and storm surges, protecting coastlines and inland communities [2]. They serve as nurseries for many fish species, supporting both local livelihoods and global fisheries [3]. In addition, these ecosystems support rich biodiversity, providing habitats for numerous species of birds, mammals, and marine life [4]. Mangroves as a constituent of these ecosystems are also significant carbon sinks, sequestering carbon at rates far exceeding those of terrestrial forests, thus playing a critical role in mitigating climate change [5,6]. It is, however, essential to recognize that mangrove ecosystems extend beyond the boundaries of the mangroves. These intricate ecosystems encompass a multitude of interrelated land cover types, such as mangroves, tidal zones, mudflats, water bodies, and barren, that impact the entire ecosystem [7]. Therefore, monitoring all relevant land covers in such an ecosystem is essential to support ecological balance preservation [8].
Mangroves live in brackish sea water and are highly salt-tolerant due to their unique ultrafiltration and biological mechanisms [9]. These valuable ecosystems provide manifold environmental, ecological, and socio-economic benefits, including water purification [10], coastal protection [11], biodiversity conservation [12], and ecotourism [13]. Furthermore, mangroves have a high potential to sequester atmospheric carbon and help mitigate climate change [14,15]. In particular, the Intergovernmental Panel on Climate Change (IPCC) reported the significance of mangroves as blue carbon sources with high carbon burial and accumulation [16]. Although mangroves offer numerous benefits, their extent has declined continuously over the past decades. For example, it has been argued that 62% of global mangroves were lost between 2000 and 2016 [17,18]. The mangroves’ losses have been associated with natural events, including tropical cyclones [19] and droughts [20], as well as anthropogenic activities, such as aquaculture development [21] and urban expansion [22]. Therefore, it is vital to establish robust workflows to monitor the mangrove ecosystems for effective conservation and avoid further degradation.
In situ data collection is a conventional approach for mapping and monitoring mangrove ecosystems. Such an approache can deliver highly accurate information about the ecosystem; however, it is resource-intensive and impractical for frequent large-scale monitoring. These issues could become more challenging because of access limitations to these ecosystems as they are tidally inundated. Consequently, employing other advanced approaches that could reduce such limitations and provide reliable information is highly imperative. For example, leveraging remote sensing technologies along with advanced Artificial Intelligence (AI) models is beneficial in overcoming these limitations and providing frequent synoptic views from mangroves anywhere in the world [23]. Furthermore, the utility of open access satellite images significantly reduces expenses and enables low-cost monitoring programs for mangrove ecosystems. Overall, remote sensing allows the accurate mapping of mangrove ecosystems, which is one of the fundamental needs for monitoring and conservation [23,24,25]. Therefore, many studies have been conducted to map mangrove ecosystems using different remote sensing datasets and AI algorithms [26,27]. For instance, multispectral [28], hyperspectral [29], Light Detection and Ranging (LiDAR) [30], and Synthetic Aperture Radar (SAR) [31] remote sensing data have been employed for mangrove mapping in different parts of the world. These datasets have been incorporated with AI algorithms, such as the Support Vector Machine (SVM), random forest, and Artificial Neural Networks (ANNs). For instance, Ghorbanian et al. [23] applied SAR and multispectral data of Sentinel-1 and Sentinel-2 to a random forest algorithm within the Google Earth Engine (GEE) platform for mangrove ecosystem mapping in Iran. Likewise, Kumar et al. [32] calculated vegetation indices using hyperspectral data from Hyperion and fed them into an SVM algorithm for mangrove mapping in India.
Previous studies have demonstrated the applicability of incorporating remote sensing data and AI algorithms for mangrove mapping. However, few studies have explored the potential of deep learning and Convolutional Neural Network (CNN) algorithms for mangrove ecosystem mapping. These algorithms have become prevalent for land cover mapping in other disciplines because of their advantages in feature extraction and hierarchical learning abilities [33]. Accordingly, scholars have started to implement such algorithms for mangrove mapping. For instance, de Souza Moreno et al. [34] used Sentinel-1 time-series data to map mangroves in the Cananéia–Iguape Estuarine Complex, Brazil. To this end, three backbones comprising the Visual Geometry Group (VGG-16), Residual Network (ResNet-101), and EfficientNet-B7 were incorporated within the UNet architecture, and their results confirmed the better performance of the EfficientNet-B7. An F-score of 85.36% was achieved using the annual time series of Sentinel-1 data (29 images) with both polarizations. Likewise, Guo et al. [35] implemented the Capsules-UNet architecture to extract mangroves along the Maritime Silk Road. They employed Landsat archive imagery from 1990, 2000, 2010, and 2015 and produced four mangrove maps with an average F-score of 73.25%. They reported a significant decline in mangrove cover (approximately 21.5%, equal to 1,356,686 ha) during the last 25 years in their study area. In another study, Sentinel-2 spectral bands and indices, such as the Normalized Difference Vegetation Index (NDVI), were fed into a modified ResNet-101 model for mangrove extraction in Hainan Island, China [36]. The ResNet-101 architecture was modified with Multiscale Context Embedding (MCE), a Boundary Fitting Unit (BFU), and a Global Attention Model (GAM) and obtained an F-score of 97.87%. Finally, Jamaluddin et al. [37] developed a Fully Convolutional Network (FCN) to map mangrove degradation after Hurricane Irma in 2017. This network applied Convolutional Long Short-Term Memory (ConvLSTM) for feature extraction from bi-temporal Sentinel-2 imagery and reported that 26.64% (i.e., around 41,000 ha) of mangroves along the southwest coasts of Florida were degraded.
Although previous studies have successfully incorporated remote sensing and deep learning algorithms for coastal land cover mapping, they considered two or three land cover classes with a focus on delineating mangrove extents [26,27,28]. Therefore, further studies are required to investigate the applicability of deep learning algorithms for detailed mangrove ecosystem mapping. The importance of considering detailed land covers is the necessity of mapping the essential components of a mangrove ecosystem (e.g., tidal zone and mudflat) for ecological balance preservation [6,38]. Moreover, the potential of the most recent CNN models for mangrove mapping has not been thoroughly investigated. Accordingly, in this study, a new Hybrid Selective Kernel-based CNN (HSK-CNN) algorithm was developed for detailed mangrove ecosystem mapping using multi-temporal open-access Sentinel-2 imagery. The Selective Kernel (SK) module allows for multiscale spatial information extraction from remote sensing imagery to improve the mapping results [39]. Furthermore, a hybrid approach was considered by combining Two-Dimensional (2D) and Three-Dimensional (3D) convolutional layers, with the advantage of injecting temporal information. The utility of temporal information was reported to be efficient for reducing water level fluctuation and inundation effects in the inter-tidal zones where mangroves grow [23]. Finally, the robustness of the proposed algorithm was validated through visual interpretation, statistical accuracy assessment, and comparing its results with other state-of-the-art algorithms.
2. Materials and Methods
2.1. Study Area
The study area (Figure 1) contains the largest mangrove ecosystems in the Persian Gulf and Oman Sea [40], which has a substantial environmental and ecological impact on nearby regions. It is located on the Khuran Strait, between the northern coast of Qeshm island and Hormorgan Province, south of Iran. The mangrove ecosystem, called the Harra by the local community, covers an area of 20 km × 20 km between latitudes of 26°43′ and 26°59′N and longitudes of 55°28′ and 55°48′E. The mangrove ecosystem is formed by a network of shallow waterways with many tidal channels, and it is a habitat for vast species of flora and fauna [41]. The semi-diurnal tidal fluctuations cause the water level to change between 0.3 m and 4.6 m [42], emphasizing the importance of considering these variations (i.e., tidal effect) for mapping studies. At high tides, only the tree canopy is visible above the water level, while trunks and aerial roots are underneath the water level and can be seen at low-tide conditions. This ecosystem is a part of Iran’s national protected areas and is under different international protection programs, such as the Ramsar Convention. Avicennia marina is the major mangrove species in this region, which grows in sediments with a small amount of dissolved oxygen and high salinity concentrations. Commercial practices, such as oil leakage, fishing, shrimp farming, tourist boat trips, and mangrove leaf cutting, are among the factors disturbing these valuable natural environments.

Figure 1.
(A) The study area and the distribution of all reference polygons within the study area, (B) the location of the study area within the Persian Gulf; (C) a zoomed image from the locations of mangroves; (D) the distribution of test samples; (E) the distribution of training samples; and (F) the distribution of validation samples.
2.2. Reference Polygons for Classification
Reference samples are required to either train supervised algorithms or evaluate their performances. In order to collect reliable reference samples, very high-resolution satellite images embedded in the Google Earth and Esri basemaps were used as the primary sources. Additionally, four other sources, false-color (NIR–Red–Green bands) satellite images of Sentinel-2, previous maps of the study area, a global mangrove extent map [43], and a global distribution of tidal flat map [44], were considered to ensure the reliability of sample collection. The reference samples were collected in Geographic Information System (GIS) polygon formats with a suitable spatial distribution over the study area (see Figure 1). Attention was paid to selecting homogenous sites for each land cover class and avoiding mixed pixels. In total, 824 reference polygons (304.83 ha) for eight major land cover classes were collected (see Table 1). These reference samples were randomly divided into test (70%) and train (30%) datasets in polygon format to ensure spatially disjoint samples in each dataset. The train dataset was further divided into training (80%, which was equal to 24% of the total reference polygons) and validation (20%, which was equal to 6% of the total reference polygons) subsets. This resulted in a final distribution of 70%, 24%, and 6% of the test, training, and validation samples, respectively.

Table 1.
The number of reference patches for different land cover classes that were divided into training, validation, and test.
In the next step, the reference polygons were converted to a raster format, where each raster cell became a sample point. These sample points then served as the center pixels for the extracted patches. For each sample point, a 7 × 7 × 12 pixel window was extracted, where 7 × 7 represents the spatial dimension in pixels and 12 represents the temporal dimension corresponding to the 12 monthly NDVI images used in our analysis. This patch size covers an area of 70 m × 70 m in the Sentinel-2 images for each time step. These patches were allowed to overlap to ensure comprehensive coverage and to capture a wide range of spatial contexts. Furthermore, it provided sufficient spatial context for the model to learn local patterns and textural characteristics of different land cover types while maintaining computational efficiency. These patches along with their corresponding class labels were finally utilized as input data to train, validate, and test the developed classification model.
2.3. Satellite Imagery
In this study, Sentinel-2 multispectral satellite images were utilized. Sentinel-2 is a European satellite launched by the European Space Agency (ESA) carrying the MultiSpectral Instrument (MSI), which is capable of covering the entire surface of Earth in 12-day cycles. In order to decrease the 12-day gap in revisiting capability, the ESA has placed two identical satellites of Sentinel-2 A/B into the same orbit, but with a 180° phase difference in their orbits, reducing the revisit time to 6 days. MSI acquires information from the Earth’s surface in 13 spectral bands with 10–60 m spatial resolutions. Here, 12 cloud-free MSI images, one in each month, captured in 2020, were utilized for the task.
2.4. Methodology
In this study, an HSK-CNN model (Figure 2) was developed for accurate mangrove ecosystem mapping. This algorithm can extract deep features from time series of Sentinel-2 images in multiple Receptive Field (RF) sizes. The HSK-CNN is composed of modules with 2D and 3D convolutional layers.
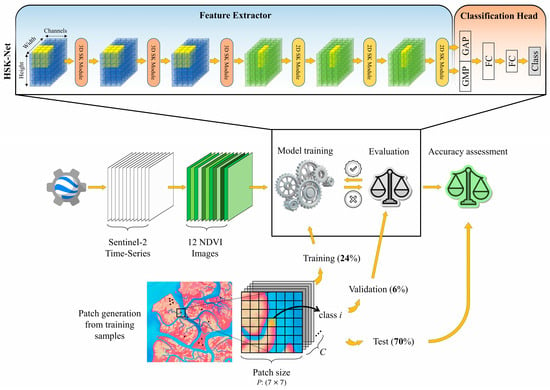
Figure 2.
General framework of the proposed HSK-CNN model for mangrove ecosystem mapping. SK, GMP, GAP, FC, and NDVI stand for Selective Kernel-based, Global Max Pooling, Global Average Pooling, Fully Connected, and Normalized Difference Vegetation Index, respectively.
2.4.1. Time-Series NDVI Products
Sentinel-2 imagery can be negatively affected by clouds or atmospheric conditions. The surface reflectance product of Sentinel-2 images (COPERNICUS/S2_SR) was utilized due to its atmospheric correction by the European Space Agency (ESA) within the Google Earth Engine (GEE) [45]. The GEE was useful in reducing the complexity of data manipulation and improved processing without the requirement to download large volumes of data. Since satellite images acquired at different times of a year improve the accuracy of mangrove ecosystem mapping and reduce the effects of seasonality and diurnal tidal variations, we utilized 12 Sentinel-2 datapoints acquired from 1 January 2020 to 28 December 2020. Using these images, the time-series NDVI (Equation (1)) products were produced.
where NIR and Red refer to the near-infrared (band 8, 842 nm) and red (band 4, 665 nm) spectral bands, respectively.
The input data were prepared in arrays over the study area, where H, W, and C indicate the height, width, and number of image channels, respectively. In our case, where we have used time-series datasets, the number of channels refers to the considered time epochs of 12 NDVI images within the year.
Patches with equal shapes were required to be fed as the input data into the network. Thus, for each pixel (i, j) from the input dataset X, a 3D patch with a size of P × P × C was extracted. This neighborhood window was fed into the proposed model acting as a mapping function that maps , where is its final corresponding land cover class for the focused pixel , is the classification map, and θ are learnable parameters of the network.
2.4.2. Convolutional Layers
After preparing the input 3D patches, i.e., time-series NDVI patches and their corresponding reference patches, they were ingested into a hybrid network of 3D and 2D convolution layers. These layers were capable of extracting meaningful features from the input dataset. Each convolution layer was followed by a ReLU activation function and a batch normalization layer. The deep feature extraction section of the proposed network was a combination of three 3D convolutional feature extractors, followed by three 2D convolutional feature extractors, where 3D/2D SK modules, along with Global Max Pooling (GMP) layers, were put between each of these layers for feature map reduction (see Figure 2).
Convolutional layers are specialized types of linear operations that were utilized as the core building blocks in the proposed HSK-CNN model. In the 2D convolution layer, the feature map () at position () on the feature layer is given by Equation (2) [46,47]:
where is the activation function; is the bias parameter; is the number of feature maps in the (l − 1)th layer; and and are the width and height of each kernel along the number of image channels, respectively. Similarly, the feature map () of the 3D convolution operation is defined as [48,49]:
in which is the activation function; is the bias parameter; is the number of feature maps in the (l − 1)th; and and are the width, height, and depth of each kernel along the number of image channels, respectively.
The generated deep features were fed into a Global Average Pooling (GAP) and GMP layers, in parallel, and the concatenated outputs were inserted into a Fully Connected (FC) layer and finally into a Softmax classifier, to be able to predict the land cover class for each input patch. It should be noted that the classification result was assigned to the central pixel of the patch.
2.4.3. Selective Kernel-Based (SK) Network Modules
The main idea behind the proposed network was to improve the accuracy and efficiency of simple CNN structures by adaptively selecting the most descriptive features using different RF sizes in the network. RF is a critical hyperparameter in designing CNNs and enables the networks to be sensitive to features with different spatial scales. Thus, utilizing fixed RFs could decrease the robustness and generality of a CNN. If the RF size was selected to be too large, fine-grained structures could be missed out, and small RF sizes could not detect overall patterns. With the SK network design, we wanted to allow the input image to be convolved with different RF sizes in different branches. The effect of these branches could be adaptively adjusted by an attention mechanism based on the input feature dataset. Taking advantage of the SK modules could help to select the most descriptive spatial/spectral feature maps through an attention mechanism based on SK layers. The attention mechanism recalibrates the weights of each feature response nonlinearly with respect to other features (i.e., channels). As demonstrated in Figure 2, the proposed HSK-CNN was composed of three 3D SK modules followed by three 2D SK modules, where each SK module followed a 3D or 2D convolutional layer. Each SK module contained three main operators of Spilt, Fuse, and Select, which are further described in the following subsections. As an example, Figure 3 provides a detailed overview of the proposed 3D SK modules in terms of layers, kernel size, and output map dimensions.
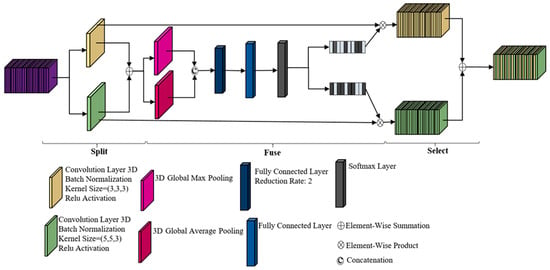
Figure 3.
The structure of the proposed 3D SK module.
Split
Multiple paths were generated by the Split operator with different kernel sizes corresponding to different neuron RF sizes. To this end, for a given input patch (), two convolution layers with different kernel sizes ( and ) were used to generate feature maps and . These feature maps in the 2D SK module were obtained by convolution layers () and () with kernel sizes () and (), respectively. Furthermore, a 3D point-wise convolution () with kernel size (), and a standard 3D convolution layer () with a kernel size () were utilized to produce the feature maps in the 3D SK module for a given 3D patch, . The feature maps were generated by convolutions followed by Batch Normalization and ReLU functions.
Fuse
This part integrated the multiscale feature maps from the multiple paths in the Spilt part to obtain a global and comprehensive representation for weight selection. This was employed using element-wise summation of feature maps. Then, GAP and GMP were performed to generate channel-wise statistics of the data. GAP reduced the dimension of feature maps to , a one-dimensional vector of a size equal to the number of channels where each element acts as a weight for that channel, by taking the average of the spatial dimension at each channel. The GAP for 2D and 3D feature maps can be defined by the following equations.
where and denote aggregation results for th element of the input feature map for 2D and 3D SK modules, respectively. The results of GAP and GMP were concatenated into a vector and fed into an FC layer, , with the ReLU activation function and Batch Normalization. The result, , was a feature vector (Equation (6)) to enable guidance for precise and adaptive selections of most descriptive features.
where , being the weights of the neurons in the Fully Connected layer, acts as a weight matrix with size . Parameter , where is the minimum value of , played an important role in the structure of the SK modules. is the reduction rate, which was considered to control the compression rate of .
Select
The Select operator integrated the feature maps from different RF sizes based on the computed weights. This was controlled by an attention mechanism, which selected the most important regions of the feature vector, . To achieve this goal, a softmax function was applied to the results of the Fuse operator using the following equations.
where and are soft attention vectors of and , respectively. This operation was the same for both 2D and 3D SK modules, with the constraint that . Finally, the output feature map was obtained using Equation (9).
2.5. Accuracy Assessment
It is important to evaluate the performance of the classification algorithms using independent reference samples and appropriate evaluation criteria. In this study, both visual and statistical accuracy assessments were conducted to evaluate the accuracy of the produced mangrove maps. Visual interpretation was conducted to evaluate the performance of the HSK-CNN compared to high-resolution satellite imagery. Statistical accuracy assessment was performed by comparing the maps with the test samples. To this end, criteria, including the Overall Accuracy (OA), Cohens Kappa Coefficient (CKC), Mathews Correlation Coefficient (MCC), and Balanced Accuracy (BA), derived from the confusion matrix were employed.
The results of HSK-CNN were also compared to those of multiple classification algorithms, such as random forest, XGBoost, 2D-CNN, MLP-Mixer [50], Swin Transformer [51], and 3D-DenseNet [52,53]. This allowed us to have a more comprehensive validation of our proposed model.
2.6. Implementation
The inputs to all algorithms were the patches extracted from the time-series NDVI images, along with the corresponding reference patches to support training, validation, and accuracy assessment steps. All of the convolutional kernel weights were randomly initialized and were trained using the back-propagation algorithm. The Adam function was selected as the optimizer and the loss was computed using the cross-entropy function. The minibatches with a size of 100 samples were utilized, and the networks were trained for 500 epochs without data augmentation. The deep learning models were implemented in the Python 3.8 environment using several libraries, such as tensorflow, gdal, and sklearn.
Each of the classification algorithms utilized different hyperparameters. To ensure a fair comparison, the algorithms were initialized with their default or best configurations, which were mentioned in their related reference studies. These hyperparameters are provided in Table 2.

Table 2.
The selected values for different hyperparameters of the classification algorithms.
3. Results
The classification maps produced using the proposed HSK-CNN model and other algorithms are illustrated in Figure 4 and Figure 5, respectively. The optical satellite image of the study area, along with the three zoomed regions, isalso provided in Figure 4 for better comparison purposes. It can be observed that different classes were correctly classified using most classification algorithms, with a superior performance for HSK-CNN. In general, the results obtained from the convolutional-based models (i.e., HSK-CNN, 2D-CNN, MLP-Mixer, Swin Transformer, and 3D-DenseNet) were smoother and contained fewer noisy pixels, which was a direct influence of using convolutional kernels in these types of algorithms. These smoother maps could be better observed in the results of the HSK-CNN and Swin Transformer algorithms. The 2D-CNN model and 3D-DenseNet models, which contained relatively fewer convolutional layers, generated more noisy outputs compared to other convolutional-based models. Overall, the random forest and XGBoost algorithms, which are pixel-based methods, resulted in the most noisy pixels.
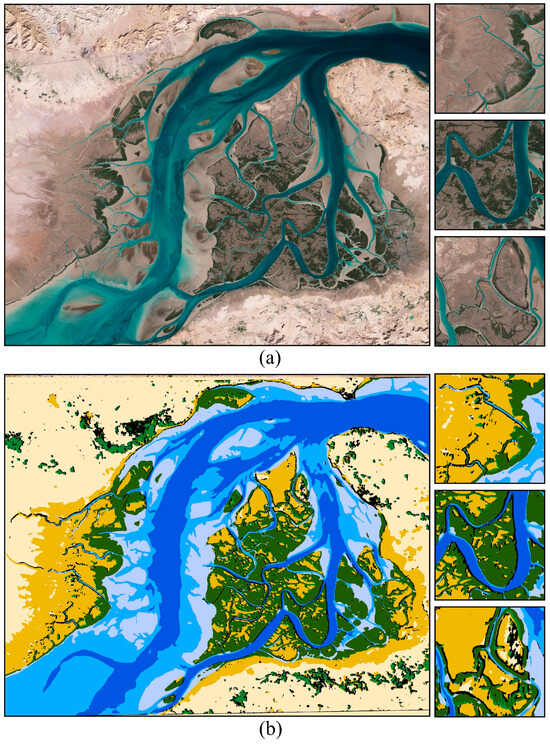
Figure 4.
(a) Study area with three zoomed regions. (b) Mangrove ecosystem map produced using the proposed HSK-CNN model (see Figure 1 for the colors of different classes).
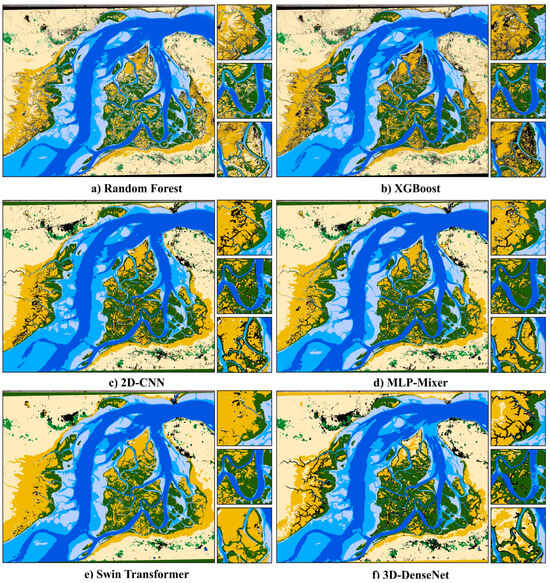
Figure 5.
The mangrove ecosystem maps produced using different classification algorithms from the study area (see Figure 1 for the colors of different classes).
Table 3 shows the accuracies of different classification algorithms for mangrove mapping in the study area. The results showed that the proposed HSK-CNN model achieved the highest performance with an OA of 94% among different methods. Other convolutional-based models also produced high accuracy (e.g., OAs were more than 90%). The non-convolutional-based models had the lowest classification accuracy, where random forest and XGBoost resulted in OAs of 85% and 87%, respectively.

Table 3.
The accuracies of different algorithms based on various accuracy measures derived from the confusion matrices. OA, CKC, MCC, and BA refer to the Overall Accuracy, Cohens Kappa Coefficient, Mathews Correlation Coefficient, and Balanced Accuracy, respectively.
Figure 6 shows the confusion matrices of different models. The proposed HSK-CNN (Figure 6g) demonstrated the best overall performance, with higher accuracy levels across all classes and minimal misclassifications. The proposed model particularly excelled in distinguishing between tidal zones, vegetation, and water classes, which are critical for accurate mangrove ecosystem mapping.

Figure 6.
The confusion matrices of different models for mangrove ecosystem mapping: (a) Random Forest, (b) XGboost, (c) 2D-CNN, (d) MLP-Mixer, (e) Swin Transformer, (f) 3D-DeseNet, (g) Proposed HSK-CNN.
Two different complementary scenarios were investigated to provide a deeper understanding of the effect of different network structures in the proposed HSK-CNN model.
First, the effect of removing 2D or 3D convolutions on the results of the classification was studied. In this regard, the 2D or 3D convolutional layers were omitted from the feature extraction section of the network architecture, and the algorithm was trained using new architectures. The results of this investigation are presented in Table 4. It was observed that the hybrid structure of the proposed model, which included both 2D and 3D convolutional layers, provided a superior performance. Moreover, the results showed that the effect of 3D convolutional layers was higher than that of the 2D layers.

Table 4.
The effects of removing the 2D and 3D convolutional layers from the network structure of the proposed mangrove mapping model. SK, OA, CKC, MCC, and BA refer to Selective Kernel-based, Overall Accuracy, Cohens Kappa Coefficient, Mathews Correlation Coefficient, and Balanced Accuracy, respectively.
Second, the effect of utilizing various patch sizes as network inputs was studied. In this regard, three patch sizes of 7 × 7, 9 × 9, and 11 × 11 pixels were tested and the results are demonstrated in Table 5. The results showed that although higher patch sizes resulted in higher classification accuracies, there was an optimum value, after which the classification accuracy did not change. It is finally worth noting that increasing the size of the patches increases the computation time and, thus, there should be a trade-off between the accuracy level and computation time.

Table 5.
The effects of using different patch sizes in the network structure of the proposed mangrove mapping model. OA, CKC, MCC, and BA refer to Overall Accuracy, Cohens Kappa Coefficient, Mathews Correlation Coefficient, and Balanced Accuracy, respectively.
4. Discussion
This study introduced a novel HSK-CNN model for comprehensive land cover mapping in mangrove ecosystems using multi-temporal Sentinel-2 imagery. The model achieved an OA of 94%, outperforming other state-of-the-art algorithms, such as random forest (OA = 85%), XGBoost (OA = 87%), 2D-CNN (OA = 91%), MLP-Mixer (OA = 92%), Swin Transformer (OA = 93%), and 3D-DenseNet (OA = 90%). This high accuracy, especially in classifying eight different land cover classes, showed a significant advance in detailed mapping of the mangrove ecosystems.
The confusion matrices of different algorithms showed that the HSK-CNN model performed particularly well in distinguishing between mangroves and other vegetation types, a common challenge in remote sensing-based mangrove mapping. The model also showed a high accuracy in delineating water bodies and tidal zones, which is crucial for understanding the dynamics of these coastal ecosystems. Overall, the HSK-CNN model provided better accuracies of all land cover types in the mangrove ecosystems. This high level of overall classification accuracy is critical for holistic mapping and understanding of the ecosystem. The slightly lower accuracy for mangroves in our model may be due to its balanced approach to handling all classes, which may be beneficial for overall ecosystem analysis, but may slightly compromise the accuracy of any single class. While our proposed HSK-CNN model achieved the highest OA, it is important to note that some other models, specifically XGBoost, 2D-CNN, and MLP-Mixer, also showed high accuracies for the mangrove class itself (e.g., see Figure 6b–d). This showed that these models might be particularly effective at identifying mangrove classes.
The superior performance of our HSK-CNN model could be attributed to several key features that addressed the challenging task of informative feature extraction in complex mangrove ecosystems. First, the multiscale feature extraction was achieved by the SK modules, which allowed the model to adaptively capture features at different scales. This is particularly advantageous in mangrove ecosystems, where land cover types exhibit different spatial patterns and textures. Second, the integration of temporal information was another critical aspect of our model. It effectively captured seasonal variations and tidal effects in the study area using time-series NDVI datasets. This temporal aspect is critical in coastal environments where water levels and vegetation phenology can significantly affect the appearance of land covers throughout the year. Third, the hybrid 2D-3D architecture of the proposed model combined 2D and 3D convolutional layers, allowing the model to effectively process both spatial and temporal information. This approach enabled the model to learn both spatial context information and temporal patterns, which was particularly beneficial for distinguishing between spectrally similar classes, such as different water bodies or vegetation types. Fourth, our HSK-CNN employed a novel attention mechanism to focus on the most relevant features for each land cover class. This attention mechanism adaptively weighed the importance of different spatial and temporal features, improving the model’s ability to discriminate between similar land cover types.
Although the proposed model showed a high potential for land cover classification in mangrove ecosystems, it is suggested to implement and evaluate the proposed model’s performance in diverse global mangrove ecosystems and to assess its generalizability to potentially lead to a standardized global mapping tool. Additionally, it is suggested to integrate complementary data sources, such as SAR and LiDAR imagery, to further enhance the model’s capabilities. SAR data could provide insight into mangrove structure and biomass, especially in cloud-covered areas, while LiDAR could provide detailed canopy height models.
5. Conclusions
Accurately mapping and monitoring mangroves is fundamental for effective conservation and management strategies aimed at preserving these invaluable ecosystems. In this study, we introduced an innovative deep learning model, called HSK-CNN, for mapping mangroves using multi-temporal Sentinel-2 NDVI products. The proposed algorithm incorporated SK feature extraction techniques, enabling it to efficiently learn and classify mangrove areas in the input remote sensing imagery. The outcomes of our study demonstrated the superior performance of the proposed HSK-CNN model in mangrove classification, achieving an OA of 94%. This outperformed several other algorithms, including random forest, XGBoost, 3D-DenseNet, 2D-CNN, MLP-Mixer, and Swin Transformer, which recorded lower OA values ranging from 85% to 93%. Furthermore, our analysis revealed that the architecture of the neural network, such as the types of convolutional layers and patch sizes, influenced the classification accuracy. Therefore, determining the optimal scenarios and values of these parameters is crucial for maximizing classification accuracy. In conclusion, our findings underscore the importance of accurately mapping mangroves, as the resulting maps provide valuable insights into the distribution of and changes in mangrove ecosystems. This information is vital for guiding informed decision-making processes aimed at conserving and sustainably managing these critical habitats.
Author Contributions
Conceptualization, S.T.S.; data curation, S.T.S., S.A.A. and A.G.; formal analysis, S.T.S. and S.A.A.; funding acquisition, M.A.; investigation, S.T.S., S.A.A., A.G. and M.A.; methodology, S.T.S.; software, S.T.S.; validation, S.T.S. and S.A.A.; visualization, S.T.S., S.A.A. and M.A.; writing—original draft, S.T.S., S.A.A., and A.G.; writing—review and editing, S.T.S., S.A.A., A.G. and M.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
Author Meisam Amani was employed by the company WSP Canada Inc. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Getzner, M.; Islam, M.S. Ecosystem Services of Mangrove Forests: Results of a Meta-Analysis of Economic Values. Int. J. Environ. Res. Public Health 2020, 17, 5830. [Google Scholar] [CrossRef] [PubMed]
- Asari, N.; Suratman, M.N.; Mohd Ayob, N.A.; Abdul Hamid, N.H. Mangrove as a Natural Barrier to Environmental Risks and Coastal Protection. In Mangroves: Ecology, Biodiversity and Management; Rastogi, R.P., Phulwaria, M., Gupta, D.K., Eds.; Springer Singapore: Singapore, 2021; pp. 305–322. ISBN 9789811624933. [Google Scholar]
- Hutchison, J.; Spalding, M.; Zu Ermgassen, P. The Role of Mangroves in Fisheries Enhancement. Nat. Conserv. Wetl. Int. 2014, 54, 434. [Google Scholar]
- Arceo-Carranza, D.; Chiappa-Carrara, X.; Chávez López, R.; Yáñez Arenas, C. Mangroves as Feeding and Breeding Grounds. In Mangroves: Ecology, Biodiversity and Management; Rastogi, R.P., Phulwaria, M., Gupta, D.K., Eds.; Springer Singapore: Singapore, 2021; pp. 63–95. ISBN 9789811624933. [Google Scholar]
- Nyanga, C. The Role of Mangroves Forests in Decarbonizing the Atmosphere. In Carbon-Based Material for Environmental Protection and Remediation; Bartoli, M., Frediani, M., Rosi, L., Eds.; IntechOpen: London, UK, 2020. [Google Scholar]
- Lee, S.Y.; Primavera, J.H.; Dahdouh-Guebas, F.; McKee, K.; Bosire, J.O.; Cannicci, S.; Diele, K.; Fromard, F.; Koedam, N.; Marchand, C.; et al. Ecological Role and Services of Tropical Mangrove Ecosystems: A Reassessment. Glob. Ecol. Biogeogr. 2014, 23, 726–743. [Google Scholar] [CrossRef]
- Cooke, A.; Lutjeharms, J.R.E.; Vasseur, P. Marine and Coastal Ecosystems. In The Natural History of Madagascar; Goodman, S.M., Benstead, J.P., Eds.; 2003; pp. 179–208. [Google Scholar]
- De Groot, R.S.; Alkemade, R.; Braat, L.; Hein, L.; Willemen, L. Challenges in Integrating the Concept of Ecosystem Services and Values in Landscape Planning, Management and Decision Making. Ecol. Complex. 2010, 7, 260–272. [Google Scholar] [CrossRef]
- Natarajan, P.; Murugesan, A.K.; Govindan, G.; Gopalakrishnan, A.; Kumar, R.; Duraisamy, P.; Balaji, R.; Shyamli, P.S.; Parida, A.K.; Parani, M.; et al. A Reference-Grade Genome Identifies Salt-Tolerance Genes from the Salt-Secreting Mangrove Species Avicennia Marina. Commun. Biol. 2021, 4, 851. [Google Scholar] [CrossRef] [PubMed]
- Adame, M.F.; Roberts, M.E.; Hamilton, D.P.; Ndehedehe, C.E.; Reis, V.; Lu, J.; Griffiths, M.; Curwen, G.; Ronan, M. Tropical Coastal Wetlands Ameliorate Nitrogen Export during Floods. Front. Mar. Sci. 2019, 6, 671. [Google Scholar] [CrossRef]
- Raju, R.D.; Arockiasamy, M. Coastal Protection Using Integration of Mangroves with Floating Barges: An Innovative Concept. J. Mar. Sci. Eng. 2022, 10, 612. [Google Scholar] [CrossRef]
- Rahman, M.M.; Zimmer, M.; Ahmed, I.; Donato, D.; Kanzaki, M.; Xu, M. Co-Benefits of Protecting Mangroves for Biodiversity Conservation and Carbon Storage. Nat. Commun. 2021, 12, 3875. [Google Scholar] [CrossRef] [PubMed]
- Vipriyanti, N.U.; Semadi, I.; Fauzi, A. Developing Mangrove Ecotourism in Nusa Penida Sacred Island, Bali, Indonesia. Environ. Dev. Sustain. 2022, 26, 535–548. [Google Scholar] [CrossRef]
- Arifanti, V.B.; Kauffman, J.B.; Ilman, M.; Tosiani, A.; Novita, N. Contributions of Mangrove Conservation and Restoration to Climate Change Mitigation in Indonesia. Glob. Change Biol. 2022, 28, 4523–4538. [Google Scholar] [CrossRef]
- Hilmi, N.; Chami, R.; Sutherland, M.D.; Hall-Spencer, J.M.; Lebleu, L.; Benitez, M.B.; Levin, L.A. The Role of Blue Carbon in Climate Change Mitigation and Carbon Stock Conservation. Front. Clim. 2021, 3, 710546. [Google Scholar] [CrossRef]
- Pörtner, H.-O.; Roberts, D.C.; Masson-Delmotte, V.; Zhai, P.; Tignor, M.; Poloczanska, E.; Mintenbeck, K.; Nicolai, M.; Okem, A.; Petzold, J.; et al. IPCC Special Report on the Ocean and Cryosphere in a Changing Climate; IPCC Intergovernmental Panel on Climate Change: Geneva, Switzerland, 2019; Volume 1. [Google Scholar]
- Goldberg, L.; Lagomasino, D.; Thomas, N.; Fatoyinbo, T. Global Declines in Human-Driven Mangrove Loss. Glob. Change Biol. 2020, 26, 5844–5855. [Google Scholar] [CrossRef] [PubMed]
- Polidoro, B.A.; Carpenter, K.E.; Collins, L.; Duke, N.C.; Ellison, A.M.; Ellison, J.C.; Farnsworth, E.J.; Fernando, E.S.; Kathiresan, K.; Koedam, N.E.; et al. The Loss of Species: Mangrove Extinction Risk and Geographic Areas of Global Concern. PLoS ONE 2010, 5, e10095. [Google Scholar] [CrossRef] [PubMed]
- Mondal, P.; Dutta, T.; Qadir, A.; Sharma, S. Radar and Optical Remote Sensing for near Real-Time Assessments of Cyclone Impacts on Coastal Ecosystems. Remote Sens. Ecol. Conserv. 2022, 8, 506–520. [Google Scholar] [CrossRef] [PubMed]
- Mafi-Gholami, D.; Zenner, E.K.; Jaafari, A. Mangrove Regional Feedback to Sea Level Rise and Drought Intensity at the End of the 21st Century. Ecol. Indic. 2020, 110, 105972. [Google Scholar] [CrossRef]
- Nguyen, H.T.T.; Hardy, G.E.S.; Le, T.V.; Nguyen, H.Q.; Nguyen, H.H.; Nguyen, T.V.; Dell, B. Mangrove Forest Landcover Changes in Coastal Vietnam: A Case Study from 1973 to 2020 in Thanh Hoa and Nghe An Provinces. Forests 2021, 12, 637. [Google Scholar] [CrossRef]
- Moschetto, F.A.; Ribeiro, R.B.; De Freitas, D.M. Urban Expansion, Regeneration and Socioenvironmental Vulnerability in a Mangrove Ecosystem at the Southeast Coastal of São Paulo, Brazil. Ocean Coast. Manag. 2021, 200, 105418. [Google Scholar] [CrossRef]
- Ghorbanian, A.; Zaghian, S.; Asiyabi, R.M.; Amani, M.; Mohammadzadeh, A.; Jamali, S. Mangrove Ecosystem Mapping Using Sentinel-1 and Sentinel-2 Satellite Images and Random Forest Algorithm in Google Earth Engine. Remote Sens. 2021, 13, 2565. [Google Scholar] [CrossRef]
- Xue, Z.; Qian, S. Generalized Composite Mangrove Index for Mapping Mangroves Using Sentinel-2 Time Series Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 5131–5146. [Google Scholar] [CrossRef]
- Kuenzer, C.; Bluemel, A.; Gebhardt, S.; Quoc, T.V.; Dech, S. Remote Sensing of Mangrove Ecosystems: A Review. Remote Sens. 2011, 3, 878–928. [Google Scholar] [CrossRef]
- Pham, T.D.; Yokoya, N.; Bui, D.T.; Yoshino, K.; Friess, D.A. Remote Sensing Approaches for Monitoring Mangrove Species, Structure, and Biomass: Opportunities and Challenges. Remote Sens. 2019, 11, 230. [Google Scholar] [CrossRef]
- Maurya, K.; Mahajan, S.; Chaube, N. Remote Sensing Techniques: Mapping and Monitoring of Mangrove Ecosystem—A Review. Complex Intell. Syst. 2021, 7, 2797–2818. [Google Scholar] [CrossRef]
- Bihamta Toosi, N.; Soffianian, A.R.; Fakheran, S.; Pourmanafi, S.; Ginzler, C.T.; Waser, L. Land Cover Classification in Mangrove Ecosystems Based on VHR Satellite Data and Machine Learning—An Upscaling Approach. Remote Sens. 2020, 12, 2684. [Google Scholar] [CrossRef]
- Yang, G.; Huang, K.; Sun, W.; Meng, X.; Mao, D.; Ge, Y. Enhanced Mangrove Vegetation Index Based on Hyperspectral Images for Mapping Mangrove. ISPRS J. Photogramm. Remote Sens. 2022, 189, 236–254. [Google Scholar] [CrossRef]
- Wang, D.; Wan, B.; Qiu, P.; Tan, X.; Zhang, Q. Mapping Mangrove Species Using Combined UAV-LiDAR and Sentinel-2 Data: Feature Selection and Point Density Effects. Adv. Space Res. 2022, 69, 1494–1512. [Google Scholar] [CrossRef]
- Ghorbanian, A.; Ahmadi, S.A.; Amani, M.; Mohammadzadeh, A.; Jamali, S. Application of Artificial Neural Networks for Mangrove Mapping Using Multi-Temporal and Multi-Source Remote Sensing Imagery. Water 2022, 14, 244. [Google Scholar] [CrossRef]
- Kumar, T.; Mandal, A.; Dutta, D.; Nagaraja, R.; Dadhwal, V.K. Discrimination and Classification of Mangrove Forests Using EO-1 Hyperion Data: A Case Study of Indian Sundarbans. Geocarto. Int. 2019, 34, 415–442. [Google Scholar] [CrossRef]
- Ma, L.; Liu, Y.; Zhang, X.; Ye, Y.; Johnson, B.A. Deep Learning in Remote Sensing Applications: A Meta-Analysis and Review. ISPRS J. Photogramm. Remote Sens. 2019, 152, 166–177. [Google Scholar] [CrossRef]
- de Souza Moreno, G.M.; de Carvalho Júnior, O.A.; de Carvalho, O.L.F.; Andrade, T.C. Deep Semantic Segmentation of Mangroves in Brazil Combining Spatial, Temporal, and Polarization Data from Sentinel-1 Time Series. Ocean Coast. Manag. 2023, 231, 106381. [Google Scholar] [CrossRef]
- Guo, Y.; Liao, J.; Shen, G. Mapping Large-Scale Mangroves along the Maritime Silk Road from 1990 to 2015 Using a Novel Deep Learning Model and Landsat Data. Remote Sens. 2021, 13, 245. [Google Scholar] [CrossRef]
- Guo, M.; Yu, Z.; Xu, Y.; Huang, Y.; Li, C. ME-Net: A Deep Convolutional Neural Network for Extracting Mangrove Using Sentinel-2A Data. Remote Sens. 2021, 13, 1292. [Google Scholar] [CrossRef]
- Jamaluddin, I.; Thaipisutikul, T.; Chen, Y.-N.; Chuang, C.-H.; Hu, C.-L. MDPrePost-Net: A Spatial-Spectral-Temporal Fully Convolutional Network for Mapping of Mangrove Degradation Affected by Hurricane Irma 2017 Using Sentinel-2 Data. Remote Sens. 2021, 13, 5042. [Google Scholar] [CrossRef]
- Toosi, N.B.; Soffianian, A.R.; Fakheran, S.; Waser, L.T. Mapping Disturbance in Mangrove Ecosystems: Incorporating Landscape Metrics and PCA-Based Spatial Analysis. Ecol. Indic. 2022, 136, 108718. [Google Scholar] [CrossRef]
- Alipour-Fard, T.; Paoletti, M.E.; Haut, J.M.; Arefi, H.; Plaza, J.; Plaza, A. Multibranch Selective Kernel Networks for Hyperspectral Image Classification. IEEE Geosci. Remote Sens. Lett. 2020, 18, 1089–1093. [Google Scholar] [CrossRef]
- Alireza, S.M.; Mansour, J.B. Satellite based assessment of the area and changes in the Mangrove ecosystem of the QESHM island, Iran. J. Environ. Res. Develop. 2012, 7, 1052–1060. [Google Scholar]
- Sharifi, N.; Danehkar, A.; Robati, M.; Khorasani, N.A.; Rajaee, T. Developing Decision Algorithm for Determination of Protection Zones in Protected Areas (Case Study: Hara Protected Area). Int. J. Environ. Sci. Technol. 2021, 18, 2237–2250. [Google Scholar] [CrossRef]
- Vahidi, F.; Fatemi, S.M.R.; Danehkar, A.; Mashinchian Moradi, A.; Mousavi Nadushan, R. Patterns of Mollusks (Bivalvia and Gastropoda) Distribution in Three Different Zones of Harra Biosphere Reserve, the Persian Gulf, Iran. Iran. J. Fish. Sci. 2021, 20, 1336–1353. [Google Scholar]
- Bunting, P.; Rosenqvist, A.; Lucas, R.M.; Rebelo, L.-M.; Hilarides, L.; Thomas, N.; Hardy, A.; Itoh, T.; Shimada, M.; Finlayson, C.M. The Global Mangrove Watch—A New 2010 Global Baseline of Mangrove Extent. Remote Sens. 2018, 10, 1669. [Google Scholar] [CrossRef]
- Murray, N.J.; Phinn, S.R.; DeWitt, M.; Ferrari, R.; Johnston, R.; Lyons, M.B.; Clinton, N.; Thau, D.; Fuller, R.A. The Global Distribution and Trajectory of Tidal Flats. Nature 2019, 565, 222–225. [Google Scholar] [CrossRef]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-Scale Geospatial Analysis for Everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Seydi, S.T.; Arefi, H. A Comparison of Deep Learning-Based Super-Resolution Frameworks for SENTINEL-2 Imagery in Urban Areas. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2023, 10, 1021–1026. [Google Scholar] [CrossRef]
- Seydi, S.T.; Hasanolu, M.; Chanussot, J. A Novel Deep Siamese Framework for Burned Area Mapping Leveraging Mixture of Experts. Eng. Appl. Artif. Intell. 2024, 133, 108280. [Google Scholar] [CrossRef]
- Seydi, S.T.; Hasanlou, M. Binary Hyperspectral Change Detection Based on 3D Convolution Deep Learning. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, 43, 1629–1633. [Google Scholar] [CrossRef]
- Seydi, S.T.; Hasanlou, M.; Chanussot, J. DSMNN-Net: A Deep Siamese Morphological Neural Network Model for Burned Area Mapping Using Multispectral Sentinel-2 and Hyperspectral PRISMA Images. Remote Sens. 2021, 13, 5138. [Google Scholar] [CrossRef]
- Tolstikhin, I.O.; Houlsby, N.; Kolesnikov, A.; Beyer, L.; Zhai, X.; Unterthiner, T.; Yung, J.; Steiner, A.; Keysers, D.; Uszkoreit, J. Mlp-Mixer: An All-Mlp Architecture for Vision. Adv. Neural Inf. Process. Syst. 2021, 34, 24261–24272. [Google Scholar]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin Transformer: Hierarchical Vision Transformer Using Shifted Windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 10012–10022. [Google Scholar]
- Li, G.; Zhang, C.; Lei, R.; Zhang, X.; Ye, Z.; Li, X. Hyperspectral Remote Sensing Image Classification Using Three-Dimensional-Squeeze-and-Excitation-DenseNet (3D-SE-DenseNet). Remote Sens. Lett. 2020, 11, 195–203. [Google Scholar] [CrossRef]
- Zhang, C.; Li, G.; Du, S.; Tan, W.; Gao, F. Three-Dimensional Densely Connected Convolutional Network for Hyperspectral Remote Sensing Image Classification. J. Appl. Remote Sens. 2019, 13, 016519. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).