1. Introduction
Hyperspectral imagery (HSI) records numerous contiguous and narrow spectral bands, and has been extensively utilized in diverse fields such as military and industry [
1]. Nonetheless, the high redundancy of bands in HSI poses great challenges in terms of data transmission, storage, and computation, and can also lead to the Hughes phenomenon in classification, thereby reducing classification accuracy [
2,
3]. Consequently, dimensionality reduction is essential for HSI.
The dimensionality reduction in HSI can be divided into two categories: feature extraction (FE) and band selection (BS) [
4]. FE aims to project the original HSI into a lower-dimensional space, which results in the loss of HSI’s physical information due to alterations in the feature space. Conversely, BS focuses on selecting a representative band subset from HSI that preserves the physical significance and has higher interpretability, which is more preferable for practical applications [
5,
6,
7].
According to different task scenarios, BS methods can be primarily categorized into target detection-oriented methods and classification-oriented methods. The former typically considers the spectral differences between targets and backgrounds when selecting a subset of bands [
8,
9], whereas the latter selects bands that contain a large amount of information and exhibit strong discrimination capability [
10,
11]. Most of these methods are supervised and depend on prior information, such as ground truth labels, which limits their practical application. In contrast, unsupervised methods do not rely on prior information, but select the representative bands by identifying the intrinsic properties of HSIdata. It is more versatile and can be applied to downstream tasks in all scenarios, including classification [
12]. Hence, the focus of this paper is on unsupervised band selection methods which are more versatile for task scenarios.
The initial BS approaches employed the artificially designed band evaluation metrics or heuristic strategies to obtain target bands [
1]. However, the manually designed BS process was unable to account for the complex real-world factors in a comprehensive manner, resulting in unsatisfactory performance. The advent of machine learning has offered novel insights into the field of BS. The maximum-variance principal component analysis (MVPCA) [
13] and Boltzmann entropy-based band selection (BE) [
14] employ specific metrics derived from machine learning models to evaluate the equality of bands. Techniques such as fast density-peak-based clustering (E-FDPC) [
15] and graph regularized spatial–spectral subspace clustering (GRSC) [
16] utilize clustering to partition bands into multiple clusters, from which the most representative band in each cluster is selected. The sparse representation-based band selection (SpaBS) [
17] and spectral–spatial hypergraph-regularized self-representation (HyGSR) [
18] operate under the assumption that the original HSI can be represented by a linear combination of a limited number of bands, identifying the optimal band combination through iterative optimization of the sparse representation model. Those above machine learning-based BS methods attained considerable performance and can effectively reduce band redundancy.
However, those BS methods usually rely on strong assumptions to model the internal interactions within HSI [
19,
20]. In reality, the interaction between bands and pixels is complex [
21]. Due to various physical factors, the reflectance of band in a certain pixel is influenced by its surrounding pixels and bands. Thus, the predefined strong assumptions cannot cover all situations, and hence are not the optimal solution [
22,
23,
24,
25].
Neural networks possess remarkable fitting capabilities and can reveal the intricate interdependent relationships in HSI [
26,
27,
28]. The attention mechanism is effective in distinguishing the important features [
29,
30]. Networks with the attention mechanism can automatically learn the potential interrelations and distinguish the most representative bands of HSI [
31,
32]. Therefore, various attention modules are widely employed in the field of band selection. On this basis, BS-Nets [
33] is the first band selection framework that combines band attention mechanism and autoencoder. This model utilizes attention mechanism to search for important bands and applies band-wise attention weighting to the original HSI. By optimizing the model using an autoencoder, significant bands are selected according to the band attention weights.
Subsequently, various models have employed different attention mechanisms to model the spectral or spatial dimensions of HSI, and enhance the model performance. Attention-based autoencoder (AAE) [
34] generates the attention mask for each pixel. Then, the band correlations are calculated based on the attention mask and the final band subset is obtained by clustering. Non-local band attention network (NBAN) [
20] employs a global-local attention mechanism, which fully considers the nonlinear long-range dependencies of HSI in the band dimension. This approach significantly enhances the effectiveness and robustness of the attention mechanism, facilitating the automatic selection of bands. Dual-attention reconstruction network (DARecNet-BS) [
35] incorporates two independent self-attention mechanisms, one in the spectral dimension and the other in the spatial dimension. These mechanisms enhance the results of band selection by exploring the dependencies of HSI in various dimensions.
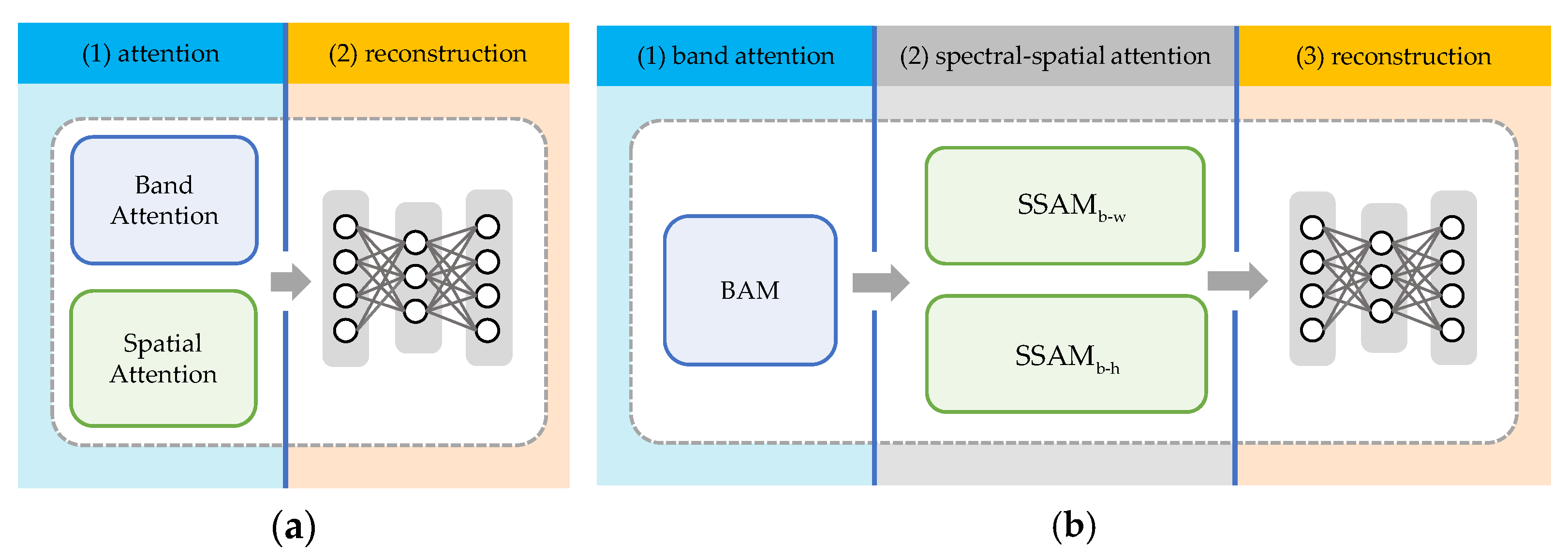
The aforementioned methods have utilized the nonlinear interaction information within HSI, yielding promising results. However, these methods solely model in the spectral or spatial dimensions independently, overlooking the potential improvement in performance achieved from considering the connections between them. Most of them are two-stage models, i.e., attention and reconstruction network, which brought new challenges. Methods such as DARecNet-BS and the triplet-attention and multi-scale reconstruction network (TAttMSRecNet) [
36] introduce spatial attention modules connected in parallel with the band attention module to mine image spatial information, as shown in
Figure 1a. The band attention module and the spatial attention modules are integrated to function in unison, thereby rendering the band attention weights unable to represent the saliency of the bands independently. Hence, these methods are incapable of selecting bands based on the converged band attention weights and must rely on calculating the entropy of the reconstructed image for band selection, a process that constrains the potential of the attention mechanism to automatically identify significant bands.
In this end, we propose a deep neural network, SSANet-BS, based on spectral–spatial cross-dimensional attention. SSANet-BS is a three-stage model, as shown in
Figure 1b and
Figure 2. This network regards BS as a reconstruction task for HSI to achieve unsupervised BS that is applicable to scenarios such as classification. Initially, a band attention module (BAM) is designed to model the spectral dimension of HSI, extracting salient band features, and outputting band attention weights. Subsequently, two spectral–spatial attention modules (SSAMs) are constructed in the band-width (b-w) and band-height (b-h) directions using the BAM-weighted image as input, to explore the complex spectral–spatial interactions within HSI, and generate SSAM weights along with SSAM-fused image. Finally, a multi-scale reconstruction network is used to reconstruct the above fused image. In the optimization process, the band attention weights obtained by BAM are gradually converged to the bands with large information and high saliency. Compared with the above two-stage methods, DARecNet-BS and TAttMSRecNet, SSANet-BS makes SSAMs compatible with BAM by the ingenious design of the three-stage structure, and fully takes advantage of the automatic convergence of the attention mechanism to the important bands during the back propagation process to achieve automatic band selection. The main contributions of this paper are as follows:
This paper proposes a deep neural network based on spectral–spatial cross-dimensional attention for hyperspectral BS, named SSANet-BS. This network employs complementary multi-dimensional attention mechanisms to automatically discover salient bands, and improves the performance of BS by exploring the complex spectral–spatial interactions in HSI.
SSANet-BS, with its three-stage structural design, addresses the issue of existing BS methods that introduce spatial modules, which compromise the independence of the band attention weights. The experimental results demonstrate that SSANet-BS is effective and stable. This offers a novel solution for the field of hyperspectral BS.
2. The Proposed Method
This section introduces the proposed method, SSANet-BS, outlines its design concept and overall structure, and presents the implementation details of every module and step.
2.1. Overview of SSANet-BS
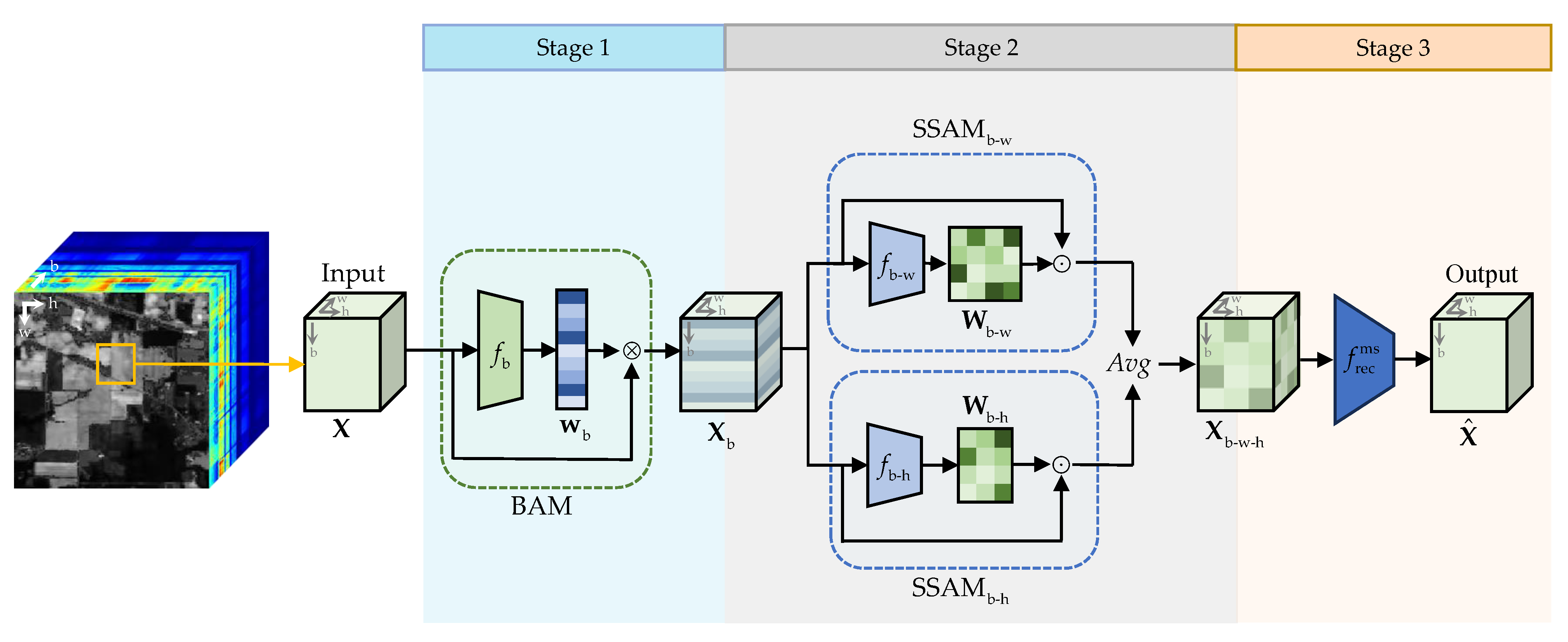
SSANet-BS treats BS as a task of band-weighted reconstruction for HSI. To enhance performance, it fully models the nonlinear interactions between pixels and bands in HSI [
37] throughout the reconstruction process. SSANet-BS is comprised of three stages, and the overall structure is shown in
Figure 2.
In the first stage, SSANet-BS inputs image patch from the original HSI multiple times as a single input with width M, height N, and number of bands L. This process ensures that SSANet-BS can read the original HSI thoroughly. Afterwards, X is fed into the band attention module (BAM) to obtain band attention weights, which are then applied proportionally. The output of BAM is a band-attention-weighted image with enhanced salient bands.
The second stage is designed to extract the spectral–spatial information of the HSI. The above BAM-weighted image is input into two spectral–spatial attention modules (SSAMs) to fully explore the complex spectral–spatial cross-dimesional interactions. This leads to the generation of spectral–spatial attention weights, which are later used to construct the SSAM-fusion image.
The third stage is the reconstruction of the attention-weighted HSI for model optimization. A multi-scale reconstruction network based on 3D convolution and transposed convolution is employed to reconstruct the aforementioned SSAM-fusion image. The loss function is defined as the residual between the reconstructed image and the original image, facilitating the optimization of SSANet-BS.
It should be noted that the existing two-stage approach employs a band attention module and other modules in the same stage. Consequently, the band attention weights are unable to represent the salience of bands independently. In contrast, the BAM of SSANet-BS is employed independently in the first stage. Therefore, the weight vector generated by the BAM represent the salience or reconstruction capability of each band in relation to the original HSI. When SSANet-BS reaches convergence, the band attention weights are sorted in descending order. The higher the band ranking, the higher its priority. Specifically, the details of each module in SSANet-BS are illustrated below.
2.2. The Band Attention Module
The BAM takes
X as input, and generates a band attention weight vector through neural network
within this module:
The
i-th element
of the vector
represents the salience of the
i-th band
in
X. A higher value of
indicates that
contributes more to the reconstruction of
X, making it more salient. The structure of
is detailed in
Figure 3 and
Table 1. Compared to using a fully connected network to extract band information from a single pixel, employing a convolutional neural network with spatial inductive bias [
33] can effectively make use of spatial information and boost modeling capabilities. Consequently, the initial layer of the network uses multiple 2D convolution kernels to extract band information, while the second layer employs max-pooling operations to reduce the feature dimension of the output of the convolutional layer. Finally, after passing through a fully connected network with a sigmoid activation function and batch normalization, the weight vector
can be obtained.
Subsequently,
X is weighted band-by-band to generate the output image
of BAM:
Here, . represents band-wise multiplication, and denotes the linear transformation operation. The regularization is imposed on the loss function of SSANet-BS, which introduces a sparse constraint on in order to reduce the redundancy of the final band subset. Therefore, some elements in may be 0 or close to 0. At this point, if is obtained through , it will inevitably lose some original band information, making it difficult for the subsequent SSAMs to fully model the spectral–spatial cross-dimensional interactions in HSI. Therefore, in this paper, the linear transformation is adopted to map each element in from the range of to without changing relative relationship of band saliency. As the input of the subsequent module, enhances the features of salient bands in X, improving the rationality of BS.
2.3. The Spectral–Spatial Attention Module
If only a single dimension such as spectral or spatial considered in HSI reconstruction, the interdependent relationship between these dimensions is ignored. In reality, proper modeling of the complex nonlinear interactions in HSI can effectively improve the performance of model [
36]. Based on this, SSANet-BS not only uses BAM to learn and model the interactions in the spectral dimension but also further introduces two spectral–spatial attention modules (SSAM) for the band-width (b-w) and band-height (b-h) directions. This approach aims at fusing the spectral–spatial information to deeply explore the complex spectral–spatial cross-dimensional dependencies in HSI.
and
are implemented in the same way, except that the directions are different. Taking the
in b-w direction as an example, the neural network
takes
as input, and generates the spectral–spatial attention weight matrix
in b-w direction:
In Equation (3), the elements in
are non-negative. The detailed structure of
is shown in
Table 1.
first performs max-pooling and average-pooling along the height direction of
to reduce its dimensionality, obtaining feature maps of salient and global information in the b-w direction. Further, by stacking the above two feature maps and passing them through a convolutional layer, a batch normalization layer and a ReLU nonlinear activation function,
and the SSAM-weighted image of the b-w direction
can be obtained:
Here,
represents the corresponding position-wise multiplication. Specifically, let
and
be the
k-th section or layer of
and
in the height direction,
, respectively. Then,
is obtained by the element-wise multiplication of
and
. Similarly, the module
outputs the SSAM-weighted image
of the b-h direction. Then,
and
are fused to generate the SSAM-fusion image
:
In this case, is the average operation. will provide spectral–spatial cross-dimensional interaction information for the adjustment of BAM weight vector and subsequent image reconstruction process, thus enabling SSANet-BS to fully utilize the spectral–spatial correlation information to select more reasonable bands and achieve performance improvement.
2.4. The Multi-Scale Reconstruction Network
3D convolutional networks can exploit spectral–spatial information and have found extensive usage in reconstructing HSI [
36,
38]. To develop a network that can model HSI’s interactions on varying scales and enhance reconstruction proficiency, this paper puts forth a multi-scale reconstruction network
inspired by MSRN [
38] that incorporates 3D convolutions and transposed convolutions with diverse kernel scales. Then, the above SSAM-fusion image
can be reconstructed by
:
The detailed implementation of
are displayed in
Table 1. The SSAM-fusion image
will be reconstructed as
using
. To ensure that bands with adjacent spectral positions are not assigned approximate attention weights and to reduce the redundancy of the band subset, the loss function of SSANet-BS is designed as:
Here, represents all trainable parameters of SSANet-BS. denotes the total number of pixel in X. represents the sparse constraint. The coefficient controls the sparsity degree of . The three-stage design of SSANet-BS enables the band attention weight of the BAM to represent the band saliency independently, thus facilitating band selection. Specifically, the average of corresponding to each X, can be treated as the ultimate salience scores of each band once the SSANet-BS has converged. The larger the i-th atom of , the more important the i-th band . Based on this, after sorting the atoms of in descending order, the bands linked to the top n values are picked as the ultimate band subset.
4. Discussion
This section discusses the quality of the selected band subset and the runtime of each method, verifies the effectiveness of two SSAM modules through ablation experiments, and concludes with the advantages and limitations of SSANet-BS.
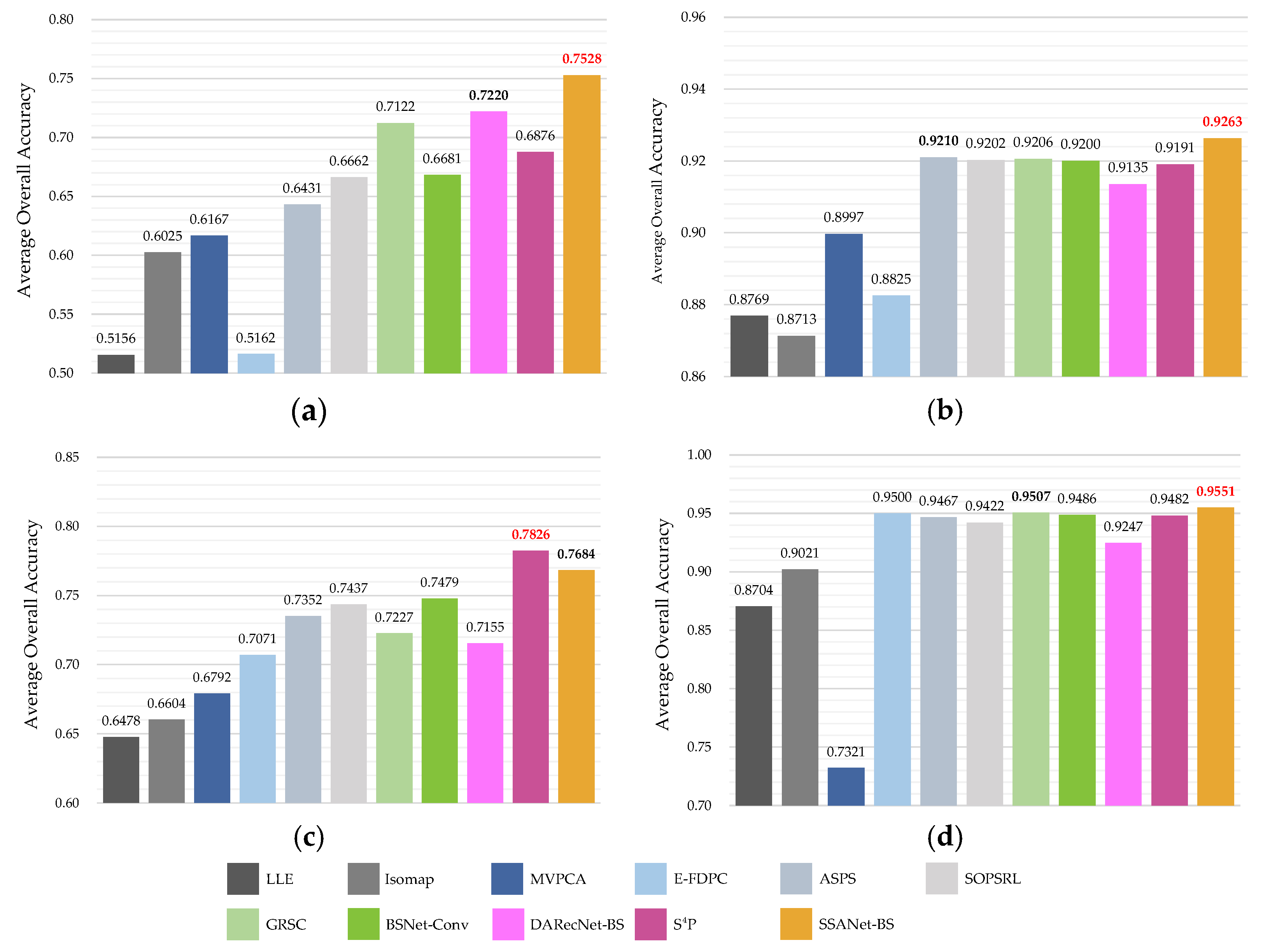
4.1. Band Quanlity
Hyperspectral band selection methods aim to select a subset of bands that are both informative and low-redundancy, while also providing a comprehensive representation of the original HSI. Consequently, the quantity of information and the degree of redundancy are pivotal metrics for evaluating the quality of the band subset selected by the BS method under examination. On the one hand, bands with greater information content exhibit higher Shannon entropy values. On the other hand, the content of adjacent bands in HSI is similar and tends to be redundant [
44], which means that the distribution of bands can reflect the redundancy of the band subsets.
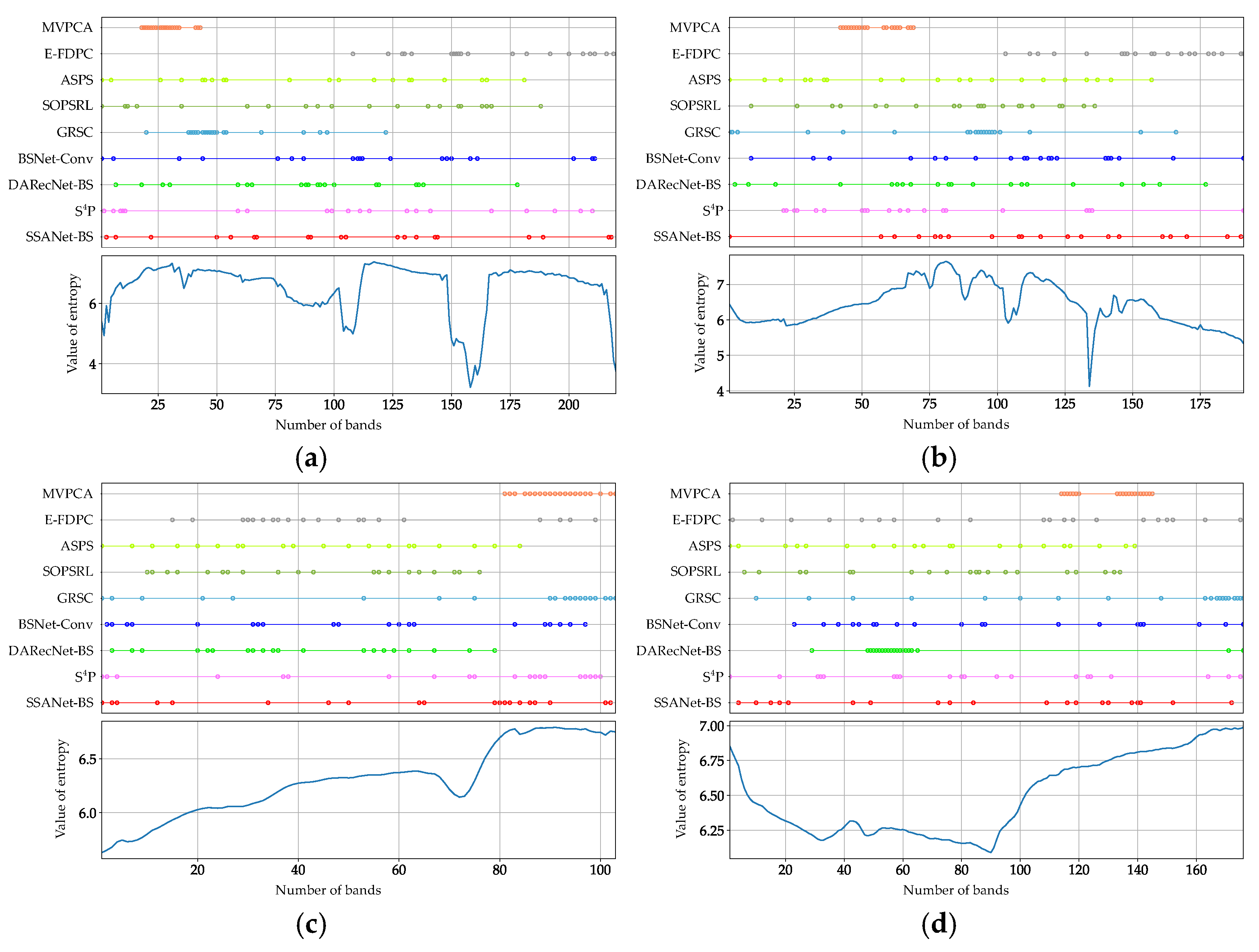
It can be observed in
Figure 11 that bands with high entropy exhibit greater clarity in the features of ground objects. Conversely, bands with low entropy, such as
Figure 11c, are noisy bands, which can have a detrimental impact on subsequent classification tasks. In order to assess the quality of the selected band for each method,
Figure 12 further plots the distribution of the selected bands (top for each subplot), and the entropy values for all bands (bottom for each subplot) for the IP220 dataset. All subplots of
Figure 12 indicates that the distribution of selected bands for MVPCA is concentrated in comparison to other methods. Although the selected bands of MVPCA are concentrated in the region of higher entropy, the classification performance is unsatisfactory. In contrast, methods such as EFDPC, ASPS, SOPSRL, BSNet-Conv and
, select bands that exhibit greater dispersion but inevitably fall within the low entropy range. The sparse constraints imposed on SSANet-BS result in a uniform distribution of bands across the four datasets. The selected bands are spaced further apart with lower redundancy and superior quality. This demonstrates the effectiveness of SSANet-BS.
4.2. Computation Time
This section mainly focuses on the computation time of SSANet-BS. Deep learning-based methods can be accelerated by GPU, so SSANet-BS, DARecNet-BS, and BSNet-Conv run on GPU, while the others run on CPU.
Table 7 shows the computation time of different methods for selecting 30 bands on the IP220 dataset. Compared to other methods, deep learning-based methods take more time. Among the three deep learning methods, DARecNet-BS requires a significantly longer processing time than BSNet-Conv and SSANet-BS. The reason is that the band attention weights of DARecNet-BS can not represent the band saliency in its entirety. Consequently, DARecNet-BS is only able to select bands by calculating the entropy of the reconstructed image, which introduces additional computational cost. This disadvantage becomes more pronounced as the image size increases. Conversely, the three-stage structure of SSANet-BS enables the selection of bands from the converged band attention weights directly as in BSNet-Conv, thereby reducing the computational costs. This represents a distinct advantage of the three-stage structure of SSANet-BS.
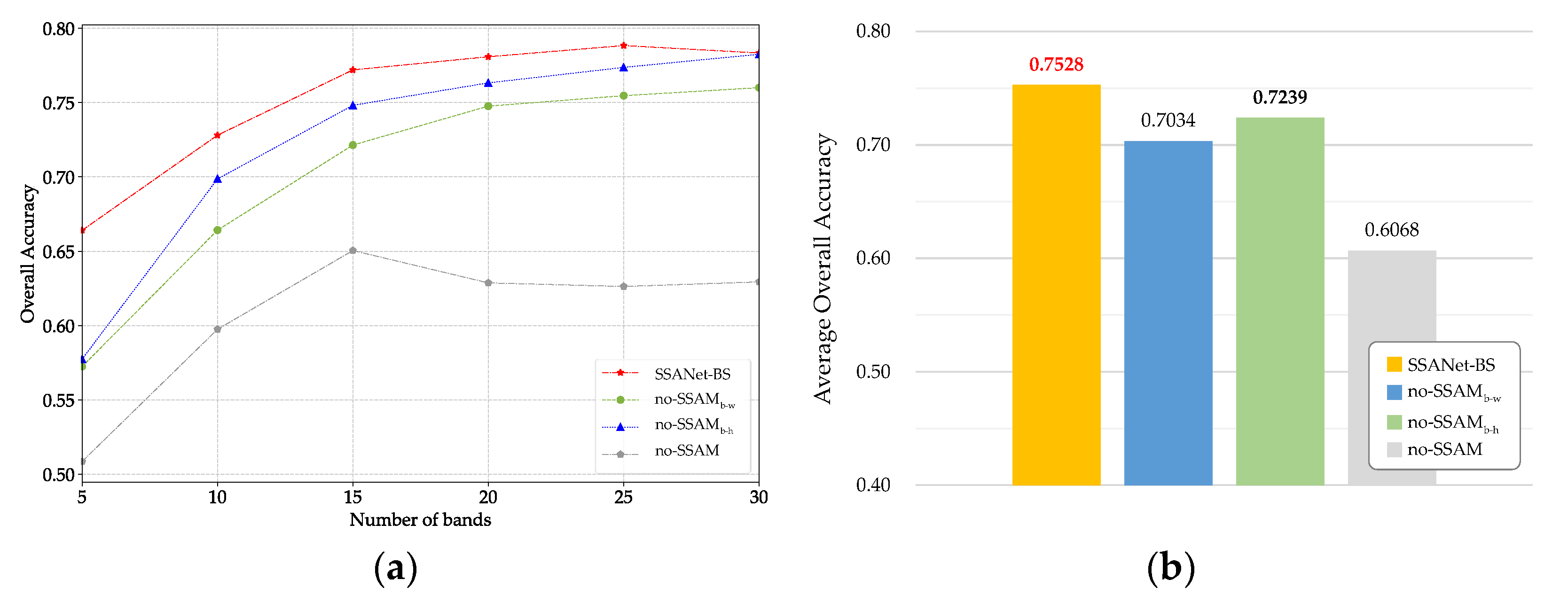
4.3. Ablation Study for SSAMs
In this section, three variants of the SSANet-BS model are constructed to verify the effectiveness of SSAM. This is achieved by removing the
in the band-width (b-w) direction,
in band-height (b-h) direction and both of them in the SSANet-BS, respectively. The three aforementioned variants, designated as
,
, and no-SSAM, are subjected to testing on the IP220 dataset. The OA and A OA values of SSANet-BS, along with its three variants under
ranging from 5 to 30 are recorded, as shown in
Figure 13.
As can be seen in
Figure 13a, the SSANet-BS exceeds the three variants mentioned above at all
. Meanwhile, both variants lacking SSAM module in one direction, namely
and
, are superior to the variant without any SSAM module. In addition, the AOA values shown in
Figure 13b indicate that in comparison to the complete SSANet-BS, the variants lacking either any modules
or
,
, or all modules exhibited a reduction in AOA values of 2.89%, 4.94% and 14.59%, respectively. Therefore, both
and
developed in this paper can effectively improve the model’s performance. The ablation study indicates that SSANet-BS has successfully utilized SSAM to capture the spectral–spatial information of HSI during the band selection process. The three-stage structure of SSANet-BS, comprising BAM, SSAMs and reconstruction network, has been demonstrated to be effective.
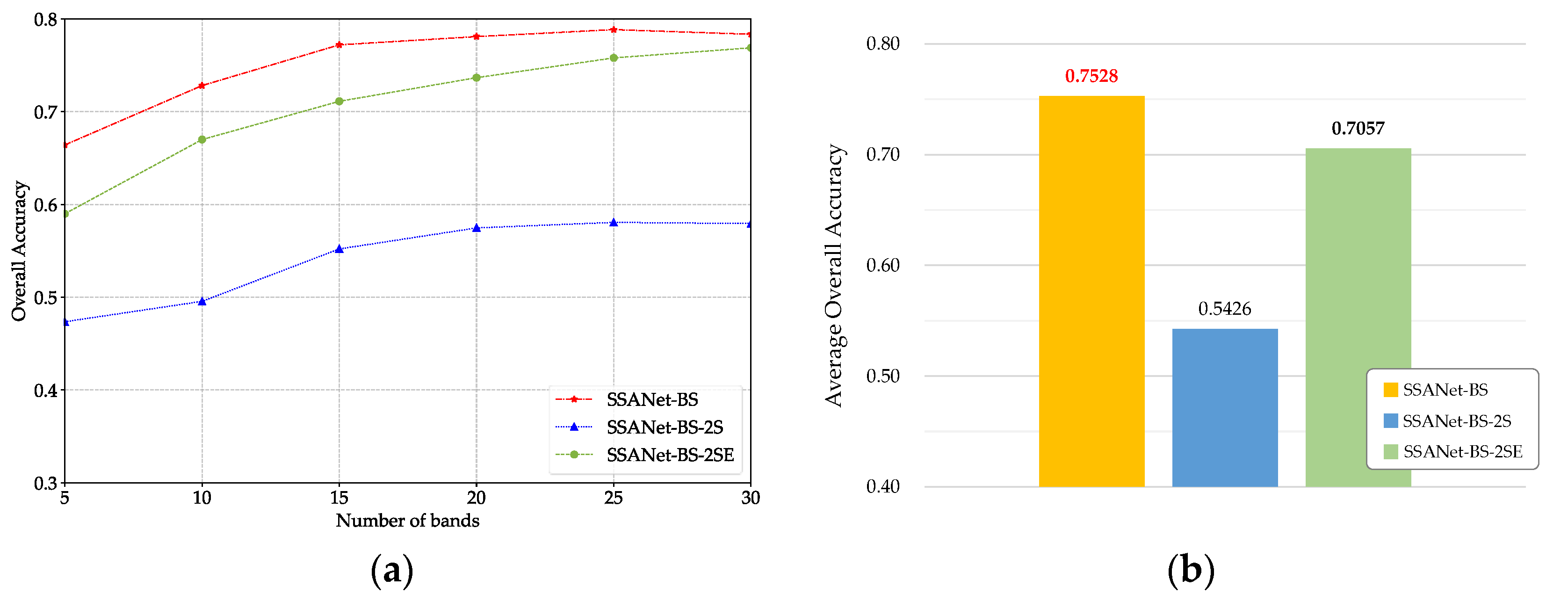
4.4. Effectiveness of the Three-Stage Structure
In order to validate the necessity and effectiveness of the three-stage structure, a variant of the SSANet-BS with two-stage has been constructed. This variant is named SSANet-BS-2S. In SSANet-BS-2S, the BAM is situated in the same stage as the two SSAMs, which are in a parallel relationship. This is in contrast to the progressive relationship in the three-stage version of SSANet-BS.
Under the optimal parameters,
Figure 14 shows that the performance of SSANet-BS-2S is markedly inferior to that of SSANet-BS, exhibiting an approximate 21% deficit in AOA. The discrepancy can be attributed to the fact that, in the variant SSANet-BS-2S which is a two-stage structure, the BAM and the two SSAMs operate in a cooperative manner, jointly modelling the HSI. Information pertaining to the significance of bands is distributed throughout the hidden features of
,
, and
. Consequently,
cannot independently and comprehensively represent the significance of bands. In contrast, within the SSANet-BS which is a three-stage structure, the BAM and SSAMs are in a progressive order. The spectral–spatial information within HSI learned by the SSAMs is used to guide the adjustment of w
b in the BAM via backpropagation, enabling
to automatically converge to the bands with high significance during the training process.
To further validate the effectiveness of the three-stage structure of SSANet-BS, we developed a variant based on SSANet-BS-2S, termed SSANet-BS-2SE. In order to address the aforementioned issues that have arisen from the introduction of spatial or spectral–spatial modules, DARecNet-BS selects bands with higher entropy value during the reconstructed process. Variant SSANet-BS-2SE implements band selection in an analogous manner.
Figure 14 illustrates that SSANet-BS-2SE demonstrates a notable enhancement in performance relative to SSANet-BS-2S. Nevertheless, it still exhibits a performance deficit when compared to SSANet-BS. This suggests that, in comparison to criteria (entropy) that have been manually designed, the automatic discovery of salient bands using attention mechanisms can effectively enhance model performance. It is evident that the two-stage structure of SSANet-BS-2SE is unable to fully capitalize on the advantages of the attention mechanism.
In conclusion, the three-stage structure of SSANet-BS guarantees that the band attention weights can independently and comprehensively represent the significance of bands. This allows the attention mechanism to automatically evaluate and select salient bands and achieve superior results. Therefore, the three-stage structure is both an effective and necessary.
4.5. Comments on Existing BS Methods and SSANet-BS
The attention mechanism can be used to learn the complex spectral–spatial interactions within HSI and enable the automated identification of significant bands. Current research on deep learning-based BS methods predominantly focuses on how to more effectively utilize attention mechanisms to enhance model performance. BS-Net [
33] is the first BS method to automatically select bands using an attention mechanism. Then, NBAN [
20] employs a non-local attention mechanism to capture long-range contextual information in the spectral dimension. Next, DARecNet-BS [
35] introduces an independent spatial attention module and TAttMSRecNet [
36] further exploits spectral–spatial information to improve model performance. By contrast, the proposed method SSANet-BS makes the SSAMs compatible with the BAM through the ingenious design of the three-stage structure, and achieves automatic band selection using the attention mechanism based on the full use of spectral–spatial information. The experimental results demonstrate that SSANet-BS is an effective and stable method.
BSNet-Conv is characterized by a straightforward structure that facilitates expeditious processing in real-world scenarios. Nonetheless, Its performance is generally mediocre. DARecNet-BS incorporates an independent spatial attention module, which offers new insights for HSI BS domain. However, the band selection process of DARecNet-BS relies on entropy, which results in a slower processing speed. SSANet-BS achieves promising results by learning the spectral–spatial information of HSIs. But according to statistics from the PyTorch framework, for the IP220 dataset (comprising 220 bands), the parameter count of SSANet-BS is about 43% higher than that of BSNet-Conv. The augmented number of parameters results in a greater requirement for GPU memory. This is less conducive to computing platforms with lower specifications, which may limit its applicability in certain contexts. However, in the context of today’s highly developed GPU hardware, the parameter volume of SSANet-BS does not present a significant bottleneck in application. With the rapid advancement of computer technology, this disadvantage is becoming mitigated.
Further, deep learning-based methods, including SSANet-BS, have the following potential issues. In contrast to domains such as CV and NLP, where models are employed in the manner of inference [
45,
46], the band selection process of existing attention-based BS methods is conducted on the training process. The existing BS model can only learn information about the target HSI, which greatly limits the potential capability of the neural network. In addition, due to the training process, the deep learning-based BS method takes tens or even hundreds of times longer than machine learning-based methods. Therefore, it is interesting to see how to make the model train on multiple HSIs, and implement BS on target HSI in the manner of inference. The inference process of neural network is much faster than the training process, and if the training can be done on multiple HSIs, it may be possible to obtain a BS method with higher performance and comparable time to machine learning-based methods. In the future, we will fully study those above issues and improve SSANet-BS.