Abstract
The precise acquisition of phenotypic parameters for individual trees in plantation forests is important for forest management and resource exploration. The use of Light-Detection and Ranging (LiDAR) technology mounted on Unmanned Aerial Vehicles (UAVs) has become a critical method for forest resource monitoring. Achieving the accurate segmentation of individual tree crowns (ITCs) from UAV LiDAR data remains a significant technical challenge, especially in broad-leaved plantations such as rubber plantations. In this study, we designed an individual tree segmentation framework applicable to dense rubber plantations with complex canopy structures. First, the feature extraction module of PointNet++ was enhanced to precisely extract understory branches. Then, a graph-based segmentation algorithm focusing on the extracted branch and trunk points was designed to segment the point cloud of the rubber plantation. During the segmentation process, a directed acyclic graph is constructed using components generated through grey image clustering in the forest. The edge weights in this graph are determined according to scores calculated using the topologies and heights of the components. Subsequently, ITC segmentation is performed by trimming the edges of the graph to obtain multiple subgraphs representing individual trees. Four different plots were selected to validate the effectiveness of our method, and the widths obtained from our segmented ITCs were compared with the field measurement. As results, the improved PointNet++ achieved an average recall of 94.6% for tree trunk detection, along with an average precision of 96.2%. The accuracy of tree-crown segmentation in the four plots achieved maximal and minimal R2 values of 98.2% and 92.5%, respectively. Further comparative analysis revealed that our method outperforms traditional methods in terms of segmentation accuracy, even in rubber plantations characterized by dense canopies with indistinct boundaries. Thus, our algorithm exhibits great potential for the accurate segmentation of rubber trees, facilitating the acquisition of structural information critical to rubber plantation management.
1. Introduction
The rubber tree, a vital industrial crop cultivated in tropical regions worldwide, yields latex from its bark, which is collected and processed into natural rubber—an essential raw material used in the production of over 40,000 industrial products [1]. Rubber trees exhibit carbon-positive characteristics by actively absorbing and fixing CO2, thereby contributing to the mitigation of climate change in tropical forest ecosystems. In a rubber plantation, ecologically and economically viable outcomes can be produced through the precise management of quantitative tree growth parameters—such as height, crown width, crown volume, and diameter at breast height (DBH)—at the individual tree scale. These growth parameters are critical when scientifically formulating plantation management plans and approximating rubber tree carbon dynamics. Although field surveys can be performed to obtain accurate information on forest parameters, they often require cumbersome measurements and are not easily conducted within complex understory terrains. Instead, light-detection and ranging (LiDAR) techniques are often used to accurately portray spatial forest characteristics, having become mainstream forest surveying tools that minimize labor intensity. These techniques reveal the 3D structures of trees through high-resolution representations known as point clouds [2]. Therefore, designing an intelligent strategy for the detection and segmentation of individual tree crowns (ITCs) in complex rubber plantations using LiDAR data is a prerequisite for revealing new potential for rubber-tree resource inventories in heterogeneous and mixed-clone woodlands.
The methodological characterization of forest morphology is often limited by complex geometric traits and noise. As a means to address these challenges, ITC segmentation has attracted widespread attention from many research communities. ITC segmentation methods can be classified into two categories. The first category includes methods based on image processing and computer graphics algorithms, usually conducted using digital surface models (DSMs) [3], canopy height models (CHMs), or the collected point clouds themselves. For example, a local maximization algorithm [4] has been applied to DSMs and CHMs along with various smoothing filters [5,6,7] to conduct real treetop detection and spurious treetop exclusion. Meanwhile, image processing algorithms include the marker-controlled-watershed algorithm, used to simulate pouring water into pits for the accurate delineation of adjacent tree crowns [8,9]; the normalized cut algorithm method, which recursively bisects CHMs obtained from point clouds into disjoint subgraphs representing individual tree crowns [10,11,12]; the energy-function minimization-based method, which includes constraints to segment complex intersections of multiple crowns [5]; and the fishing net dragging algorithm, wherein a deformable curve moves under the external or internal forces driven by height differences between adjacent CHM pixels to measure the tree-crown drip line [13]. In addition, many related studies have employed computer graphic techniques to segment ITCs using geometric information pertaining to tree crowns. Such methods include mean shift segmentation based on the joint feature space of scanned points combined with semi-supervised classification [14,15], a subdivision strategy for the scanned points of medium density using geometric-feature-driven merging and clustering operated at a super voxel scale [16], and the verticality analysis of the scanned point distribution from high-density point clouds to locate tree trunks in conjunction with the density-based clustering of leaf points [6].
The second category of ITC segmentation methods consists of deep-learning-based methods. Previously, deep learning has attained significant pioneering achievements in many fields, including human–computer interaction and intelligent industrial applications. Deep-learning-based ITC segmentation is typically performed using one of two types of data: aerial images or point clouds. Existing methods that use aerial images include an adapted U-Net convolutional neural network (CNN) architecture [17,18] designed to fine-scale feature extraction, and the Mask R-CNN model [19,20], which generates a pixel-wise binary mask within a bounding box to complete the semantic segmentation of tree crowns. In contrast, LiDAR-based point cloud segmentation methods can be further categorized as projection-, volumetric-, or point-based. Projection-based methods [21] are typically trained on images produced from scanned points using Multiview orthographic projection strategies [22,23]. Volumetric-based methods usually vocalize point clouds into 3D grids, and then apply a 3D CNN embedded with a constant number of sampled points on the volumetric representation [24,25]. In contrast, point-based methods always employ semantic segmentation networks with pointwise direction calculations to enhance the boundary portrayal of instance-level trees [26]. Multichannel attention modules [27] and typical deep learning frameworks [28] have also been employed for automatic tree feature selection and engineering.
Although many attempts have been made to resolve the challenges of mining semantic information from unstructured 3D forest point clouds, current methods are still not sufficiently automatic or accurate enough to effectively analyze complex forest habitats and achieve fine-grained segmentation. Specifically, the following three issues are encountered most frequently:
(1) The uppermost appearance of tree crowns with uneven or blurred morphologies disrupts the decline tendency, benefiting water expansion among crown pits for boundary delineation. The geometric compactness of a tree crown can be determined by integrating trunk detection techniques with deep learning algorithms.
(2) Some tree crowns have multifoliate clumps or skewed trunks, leading to the misidentification of treetops and the center points of tree crowns. A bottom-up approach that takes the bole as the root point may provide another perspective in identifying the structural phenotypic traits of tree crowns according to ecological theories.
(3) More sophisticated tree-crown segmentation algorithms require the manual configuration of the kernel parameters. Furthermore, deep learning methods arise through proof-of-concept stages applied to specific forest point clouds, necessitating validation on various forest plot types. A universal strategy for the adaptive assignment of parameters must therefore be developed.
We propose an ITC segmentation framework that focuses on subcanopy information. First, a network based on the PointNet++ pipeline with a convolutional feature extraction block is combined with kernel density estimation to segment the trunk from the point cloud, obtaining an accurate location of the stem and avoiding false treetop detection. To avoid the use of complex canopy structures, the topological structure of the subcanopy point cloud is then used to generate gridded data through an upward projection. Finally, a graph-based segmentation method is deployed to divide the graph—which is constructed according to gridded data—into multiple subgraphs starting from the trunk location, thereby completing point cloud segmentation. Overall, we propose a novel and robust basis for the accurate acquisition of forest structure information, facilitating the scientific management and sustainable development of rubber tree cultivation.
2. Materials
2.1. Study Area
The study area is located in Danzhou City, Hainan Island, China (19°31′N, 109°29′E), a place renowned for extensive rubber production (Figure 1). Hainan has a tropical monsoon climate characterized by abundant rainfall and ample sunshine. Annual precipitation ranges from 1000 to 2600 mm, with the majority occurring between May and October, providing favorable conditions for the growth of rubber trees. Situated at an altitude of 287 m, the study area encompasses a mixed rubber forest plantation spanning approximately 1529.6 ha, consisting of various rubber tree clones. Owing to stochastic natural disturbances, such as hurricanes and chilling caused by Hainan’s tropical climate, significant biological differences were observed between tree clones in terms of stem diameter, number of branches, leaf area index (LAI), angles between branches and trunk, clear bole height, and crown morphological structure (Figure 1e–h). For this study, an experimental plot measuring approximately 3 ha (221 m long and 135 m wide) was selected (Figure 1a), encompassing four rubber tree clones—ReKen 523, ReYan 72059, ReYan 73397, and PR 107—that were 15 years old.
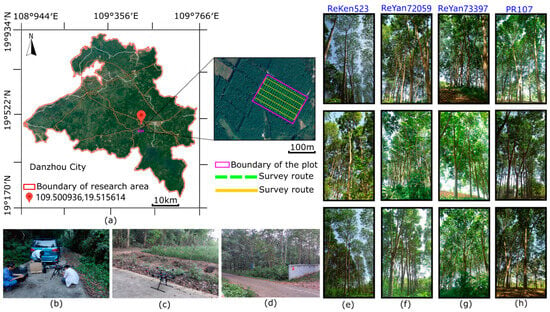
Figure 1.
General overview of the study area. (a) The location of the rubber tree plantation in Danzhou City along with the magnification level of the study plot. (b–d) Depicts UAV LiDAR data collection for the forest plot. (e–h) Showcases images specially related to the four predominant rubber tree clones present in the plot: ReKen 523, ReYan 72059, ReYan 73393, and PR107.
2.2. LiDAR Data Acquisition and Field Measurements
UAV LiDAR data were acquired on 15 July 2020, using a DJI Matrice 600 Pro drone equipped with a Velodyne HDL-32E laser scanner. The drone flew at an altitude of 70 m above ground level, maintaining a flight speed of 5 km/h and flight line side lap of 50%, as depicted in Figure 1b–d. A dual-grid flight strategy was assumed to optimize the routing of the carrying platforms, ensuring optimal LiDAR light exposure on tree trunks while capturing comprehensive details of surrounding trees. The scanner emitted a wavelength of 903 nm at a pulse repetition frequency of 21.7 kHz, providing a vertical field of view (FOV) ranging from −30.67° to 10.67° from the nadir, and a complete horizontal FOV of 360°. The Velodyne LiDAR system incorporates Simultaneous Localization and Mapping (SLAM) technology, enabling rapid scanning, point cloud registration, and real-time generation of high-density point clouds. The average ground-point density was approximately 3500 points per m2. All specifications of the LiDAR equipment used for measurements are listed in Table 1.

Table 1.
The specification of laser scanner Velodyne HDL-32E.
In the experimental plot, rubber trees of the same clone were systematically planted with a fixed spacing of 7 m between rows in a north–south orientation and 3 m between lines in an east–west orientation, facilitating efficient cultivation and harvest management. Of the represented clones, ReKen 523 is a high-yielding cultivar that exhibits a relatively thick trunk and the tallest height of the sample, with a densely packed crown and trunk bifurcation occurring at a height of approximately 10 m. The lateral branches of ReKen 523 are non-pendulous in nature. ReYan 72059 is a relatively late-maturing and fast-growing variety characterized by a large crown with trunk bifurcation at approximately 5 m. Although this variant exhibit strong wind resistance, some dead and injured trees with broken trunks were still observed within the plot. ReYan 73397 has a multi-trunk structure that competes for crown space more intensively than ReYan 72059, resulting in interlacing branches and pendulous foliage clumps on the periphery of the crown. PR107 exhibits a skewed or inclined trunk, possibly as a result of past typhoon strikes. Although this variant has a lower mortality rate than the other clones, the inclined forest canopy poses a challenge for ITC segmentation. All four clones possess an excellent water absorption capacity and nutrient uptake ability, leading to an undergrowth-free subcanopy layer where the exposed boles facilitate latex collection during rubber tapping. The specific growth properties of the four rubber tree clones are listed in Table 2, where the median and floating values were calculated using interquartile ranges.

Table 2.
The growth properties of trees in the study plot obtained from field measurements.
2.3. Data Processing
To generate training data for the deep learning model, fine-grained point clouds at individual tree scales were extracted by the voxelization of forest point clouds. To ensure that each generated voxel was likely to contain point clouds of a single tree in the equidistantly planted experimental plot, we set the voxel size to a length of 7 m, width of 3 m, and height of 30 m, which is in accordance with the fixed tree spacing. Meanwhile, we set the voxels in a consecutive order along the marshaling sequence of each tree trunk, thereby covering the point clouds of the whole forest plot. Voxelization results for the subset plots are depicted in Figure 2. We employed a machine learning algorithm [29], assisted by manual refinement, to classify leaves for the collected point clouds, with the partial segmentation results shown in Figure 3. The labeled wood and leaf points in each voxel were fed into the deep learning network for classification.
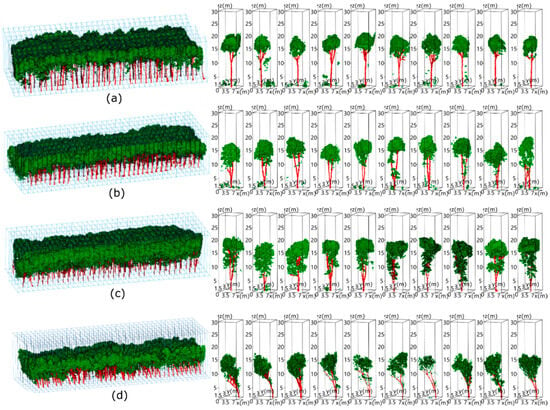
Figure 2.
Voxelization and wood-leaf point labeling performed on five subset plots containing different rubber tree clones, namely (a) Reken 523, (b) ReYan 72059, (c) ReYan 73397 and (d) PR 107 forest plot.
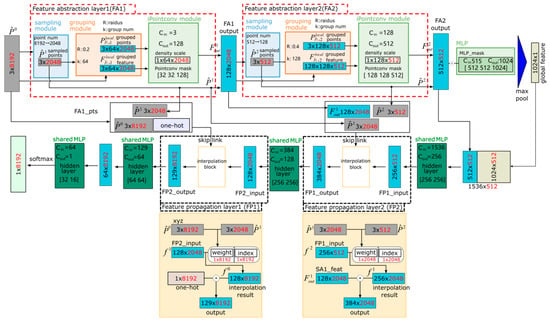
Figure 3.
The architecture framework of our deep learning network for wood-leaf point classification consists of two feature abstraction layers for salient feature abstraction and two feature propagation layers for restoring the coarse level of the point clouds to the original resolution. The red numbers represent the dimensions of the data.
3. Methods
3.1. Improved Deep Learning Network for Branch and Leaf Separation
To differentiate between the photosynthetic and non-photosynthetic parts of trees within a plot at the voxel level, we developed a deep learning network equipped with an integrated convolutional module that performs a permutation-invariant convolution on scanned points. The network’s architecture, depicted in Figure 3, comprises two layers for feature abstraction and two layers for feature propagation. The input to the deep learning network is a 3 × 8192 matrix, reflecting that 8192 points were sampled uniformly from each voxel, and the associated input features for these points are the three-dimensional spatial coordinates. The output of the network is a 2 × 8192 matrix, where each point is assigned a label of either (0,1) or (1,0), indicating whether the point corresponds to a branch or a leaf, respectively.
3.1.1. Feature Abstraction Layer
The feature abstraction layer contains three modules: a sampling module for input point clouds, a grouping module that extracts local regions centered on sampled points, and an improved point convolution (iPointConv) module that agglomerates local region features, with the input sets of points and corresponding features denoted as . The output of the feature abstraction layer is also a tensor of size , where is the subset of the input point set by the sampling module and the feature set is derived by the subsequent processing of the grouping and iPointConv modules.
To prepare central points for the grouping module, the sampling module adopts a decimation strategy based on the farthest-point sampling algorithm [30] to reduce the number of original input point clouds to the extracted number of point clouds , thereby reducing computational complexity. The farthest-point sampling algorithm ensures that any extracted points maintain geometric integrity and a semantic distribution.
The grouping module takes a point in the set as the center and generates overlapping local regions equivalent in quantity by locating neighboring points via the ball query algorithm, i.e., taking each point as the center of the sphere, and searching for neighboring points within a radius . The algorithm terminates when the number of points in the spherical region reaches . If the number of neighboring points is insufficient, the points in the spherical region are iteratively considered as . Thus, the input of the grouping module is a tensor of size , whereas its output is the three-dimensional tensor , which associates each sampled point with its neighboring points and the corresponding features.
Since point clouds are inherently unordered and do not align with regular grid structures, they cannot be processed using standard convolutional methods. To overcome this challenge, we developed the iPointConv module, which incorporates a Kernel Density Estimation (KDE) algorithm [31]. KDE is a method used to estimate the probability density function of a random variable based on its neighboring points. In theory, KDE permits an observation to be a part of an infinite number of neighborhood sets, leading to a filtering or smoothing effect on the distribution shape, similar to a convolution operation. The choice of an optimal bandwidth, akin to the size of a convolution filter, critically affects the outcomes because the density of the data varies across the support region of the distribution. To maintain a consistent kernel approximation, the bandwidth should be reduced as the sample size within the support region increases. Using an inappropriate bandwidth that is too large can lead to oversmoothing, which degrades the quality of the probability density estimation. Accordingly, we introduce the correction coefficient with a unit geometric mean. To adapt the sample point bandwidth to the density of local data, this coefficient is used as a scale factor for the global fixed bandwidth . Thus, the kernel density can be approximated as
where are the neighbor points of , represents the Euclidean distance between and , and represents kernel function. For the purposes of this study, we used the Epanechnikov kernel function [32], defined as for and 0 otherwise. The correction coefficient was defined as , where is the pilot approximation of kernel density using the fixed bandwidth and represents the neighboring points of . The initial fixed bandwidth is calculated based on the minimum of the scaled interquartile range and the standard deviation, i.e., Here, where is the number of observations on the input dataset , i.e., the neighboring points of . is the variance, and is the interquartile range of . With an adaptive bandwidth derived from the attributes of each individual case and its neighborhood, our approach can sufficiently depict the spatial heterogeneity of local tree structures.
The architecture of iPointConv is detailed in Figure 4, where denotes a multilayer perceptron, which is a type of fully connected feedforward artificial neural network. The input data for the iPointConv module consists of three main components: the 3D local positions of neighboring points, calculated by subtracting the coordinates of the local centroids; the feature set associated with these neighboring points; and the estimated kernel density for each central point, derived from its neighboring points within the defined support area. The result is a set of features that are generated for each of the sample points.
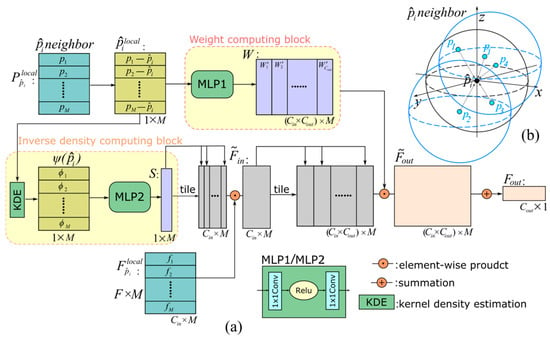
Figure 4.
Schematic diagram illustrating the architecture of the iPointConv module for convolution operation for a center point with its neighboring points. Figure (a) shows the structure of iPointConv, and figure (b) shows the calculation diagram of inverse distance-weighted interpolation of a point.
To illustrate the iPointConv structure, we may take the -th local region with the corresponding feature . First, the coordinates of any points in the local region are normalized to the central point, with the resulting set of local coordinate points fed into the MLP. A 1 × 1 convolution is then used to obtain a weight matrix with dimensions of , represented by the weight-computing block in Figure 4. Then, the local coordinate points are taken as input to calculate the point density vector by Equation (1) followed by an MLP operation in the inverse density computing block. The density vector tiles times, and element-wise production is then applied with the input feature to obtain the intermediate results , which are multiplied by the weight matrix to obtain the matrix . Finally, an output with dimensions of is obtained by adding the dimensions corresponding to .
Let the and be the number of channels for the input and output features, respectively, with representing the -th neighbor and -th channel for an input feature. The iPointConv flow in Figure 4 can be abstracted using the following formula:
where is the density vector of input points, is a vector in at index , and is the output feature at the center point of the local region. At the end of the iPointConv operation, the stack of all local region features at is sent to the next module as input or computed by the MLP to obtain global features through max pooling, as shown in Figure 3.
3.1.2. Feature Propagation Layer
The feature propagation pipeline, illustrated in the bottom half of Figure 3, maps and propagates global features by the skip-link concatenation of point features, with some points omitted by the interpolation block.
The interpolation block assigns an input feature to discarded points by inverse-distance-weighted interpolation, wherein a set of points with size is interpolated into points (with ). Letting the input of the -th FP layer be , the feature of output after interpolation can be calculated as
where is the feature corresponding to point , and the upper bound is the number of nearest neighbors centered around . Owing to the weighted global feature pipeline from the encoder, which lacks local semantic information, any feature derived via inverse distance-weighted interpolation is global. The one-hot encoding shown in Figure 3 is a process of representing categorical variables as binary vectors, where each vector represents a unique category. The skip connection shown in Figure 3 is a trick that concatenates global and local features (output of the FA layer in the encoded pipeline) to improve classification accuracy.
3.2. Graph-Based ITC Segmentation
3.2.1. Inverted CHM Generation
First, we standardize the point cloud data to reduce the impact of uneven ground on our above-ground measurements. Since rubber trees absorb a lot of water and nutrients from the soil, the plantation area is mostly covered with low-maintenance shrubs. This landscape feature causes minimal interference with our measurements, which makes it easier to filter out ground points using Cloth Simulation Filtering (CSF) [33]. Once all ground points are removed, we use the standardized point cloud to create an Inverted Canopy Height Model (Inverted CHM).
Due to their strong light-seeking behavior and rapid growth, rubber trees compete intensely for canopy space. They are similar to upper rainforest trees with a crown density of about 90%, which makes it hard to see the crown boundaries from above. As rubber trees grow, they develop small-angle branches with small leaves that extend outward, resulting in fewer leaves drooping and giving the crown an inverted cone shape. Therefore, segmenting the trees from the bottom up, based on their shape, is more effective and precise than doing it from the top down. The Inverted CHM is created from the standardized point cloud after ground points are removed, with the highest point representing the tree trunk. By projecting the point clouds onto a flat surface, we convert the inverted point cloud into a 2D raster or grid, which becomes the Inverted CHM. The cell is a uniformly distributed horizontal square of size with an assigned height value , corresponding to the maximum height of all inverted tree points within each raster.
To maintain the intricate details of the crown’s shape and prevent gaps between adjacent laser points, we determine the ideal cell size based on the point density from the laser scanning data. Given that our study area had an average point density of about 500 points per square meter and an average spacing of approximately 8 cm between points, we chose a square cell size of 10 cm to ensure that each cell contains at least five points.
These cells can be susceptible to impulse noise due to incorrect point positioning caused by electromagnetic interference. This interference might arise from synchronization issues between the inertial measurement unit (IMU) and other system components, laser instability during flight vibrations, or erroneous echoes from the laser beam striking insects. To address these challenges, we utilized digital image processing techniques, including Gaussian filtering for image smoothing and morphological operations consisting of dilation followed by erosion, to reduce noise within the cells.
3.2.2. Component Merging from Inverted CHM
A typical graph-partitioning algorithm segments objects at a piece scale using an edge weight census [34]. Here, adjacent cells with similar properties constitute a larger component , i.e., . Each cell in the DSM is regarded as a component at the algorithm’s initial state, as shown in Figure 5a. The height difference between a pair of adjacent cells is taken as a criterion to measure dissimilarity between two cells, denoted as , where and are a pair of adjacent cells with respective heights and . Then, the minimal spanning tree (MST) for each component is determined to form a path that traverses all the cells with the smallest sum of dissimilarity values between adjacent cells. Consequently, an internal difference and external difference are defined for each pair of adjacent components to determine whether the components should be merged. The internal difference of a component is calculated as follows:
where represents the maximal dissimilarity between pairs of adjacent cells and , is the number of cells in , and the hyperparameter is set to 2. Because each component initially contains only one cell, and hence the initial internal difference for each component is .
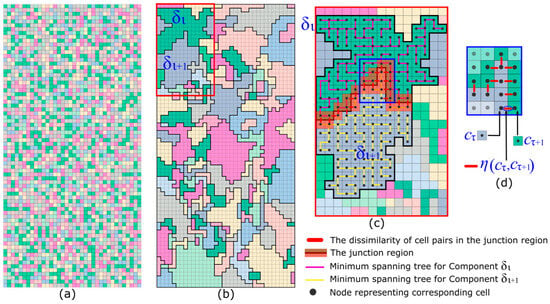
Figure 5.
Schematic diagram illustrating the process of merging components and calculating the index for internal and external differences derived from cell values in the inversed CHM. (a) Depicts the initial distribution of components in the inversed CHM, with each colored cell representing a distinct component. (b) Showcases the merging process, where all components are uniformly colored and delineated by black lines. (c) Provides a magnified view of two adjacent components highlighted by a red box in (b). The irregular pink and yellow lines traversing all cells represent generated minimal spanning trees for the two components. The vermilion transparent mask covers the junction region used for calculating external difference calculation. (d) Presents an enlarged view of the junction region in (c) demarcated by blue lines.
The external difference between two adjacent components and is assigned to the minimum value among the corresponding to pairs of adjacent cells within the region of connectivity between two adjacent components and , where and . A schematic diagram of the two components is shown in Figure 5b, with the corresponding junction region shown in Figure 5c. All cells in the region of connectivity correspond to an edge where the two adjacent components meet. In the algorithm’s initial state, the external difference of the two components equals , as each component only contains one cell. In subsequent iterations, the external difference of and is computed by the following formula:
Then, a comparison predictor associated with Int and Dif is defined to evaluate whether the adjacent components have similar enough properties to warrant merging. The equation for is as follows:
Components are fused when they satisfy the condition . Thus, as the number of iterations increases, the components increase in size while their total number decreases, as shown in Figure 5b. The algorithm terminates when the total number and size of the CHM components no longer change.
3.2.3. ITC Segmentation at Component Scale
In the inverted DSM, groups of components with similar height cells represent specific parts of a tree (Figure 6a), such as the trunk or a cluster of leaves. We constructed a digraph to concatenate all components using an adjacency relationship (Figure 6b), and subsequently segmented the graph into subgraphs to complete the inverse DSM segmentation (Figure 6c,d). For ease of understanding, we refer to any subsequent graph nodes as components, i.e., . Each component has an elevation value set by the average height value of its constituent cells. The root component is denoted as , represented in light green in Figure 6e.
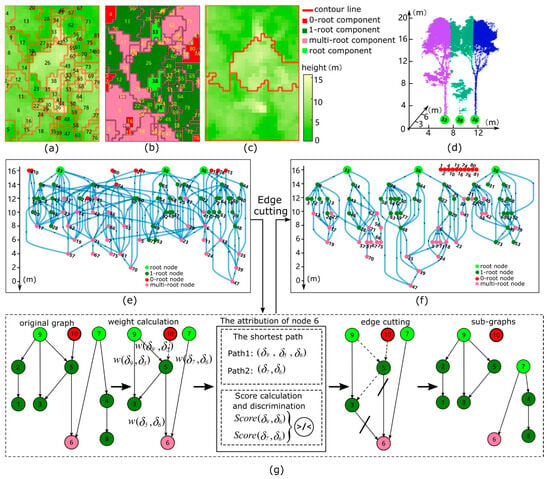
Figure 6.
Schematic diagram illustrating the DSM segmentation process based on graph theory, where the components generated by DSM are represented as nodes in the graph. (a) showcases the inverted DSM divided into multiple components using red lines, with each component assigned its own index number. (b) Illustrates the classified component determined based on their connectivity to the root component; dark green components represent 1-root structures, while pink represents multi-root structures. (c) Shows the comparison between the segmentation result (red line). (d) Exhibits the point cloud segmentation results projected from the segmented inverted DSM. (e) Displays a graph representing component connectivity, with colors and numbers corresponding to those in (b). (f) Depicts the three subgraphs divided from the graph in (e) by our algorithm, which correspond to actual trees present within the scene. (g) Illustrates the process of generating multiple subgraphs from a complete graph, wherein nodes 7 and 9 compete for local maximum node 7 according to the proximity principle.
The construction of the graph begins with prespecified root components by retrieving the tree trunk position from the inverted DSM and proceeds according to a breadth-first search (BFS)—a layer-wise traversing algorithm that explores the neighboring components of each node. Initially, components adjacent to the root are searched with a lower elevation value than the root counterclockwise, with an edge extending from the root component to the lower adjacent component. These pointed components are utilized as starting components to identify lower components in subsequent iterations. This process continues until none of the current pointed components are associated with lower neighboring components. Each edge in the digraph has a corresponding weight , which is a non-negative measure of the perimeter ratio between the two components before and after merging combined with the height difference. This value is defined as
where is the elevation difference between the two components, represents the perimeter of a component , and denotes the sum of and . The intuition behind using the perimeter ratio to measure the degree of inclusion is that the presence of an inclusion between two components indicates that one component is over-segmented [35], with more pronounced inclusions indicating a higher probability of over-segmenting.
A digraph (Figure 6f) generated in this manner has a particular topological structure that can be regarded as a mutually intersecting tree, where any components that can be reached from a root component belong to that root component. Components can be classified as 0-root, 1-root, or multi-root according to the number of roots they belong to.
Each root component in the data uniquely identifies a real-world tree. That is to say, within this topologically constructed directed graph [36], each 1-root component corresponds to an individual tree. Moreover, a 0-root component can be associated with its nearest 1-root component based on the shortest Euclidean distance between their centers, since 0-root components usually signify noise or small, hanging leaves.
Since multi-root components often represent distinct peripheral parts of the trees, merely considering their neighboring components is not adequate. Instead, it is essential to examine the topological structure of the tree as well. To do this, we evaluated the scores of multi-root components by comparing the sum of the weights along the shortest paths leading back to their respective roots. Given a multi-root component , we assume that its shortest path to a root is , where is the root component and . The subscript represents the number of components associated with the shortest path. The score from to is calculated as follows:
Figure 6g shows an example of attributing multi-root components to a specific root. Finally, the 0-point local maximum component is assigned to the nearest root component according to the proximity principle. Here, proximity is defined as the Euclidean distance between the centers of the components.
3.3. Assessment of Model Accuracy
The performance of the enhanced PointNet++ in the point cloud segmentation task was assessed using the evaluation indicators of recall, precision, F1-score, and mIoU. The number of classified points or trunks is denoted as , representing the total number of points belonging to class but predicted to be class . Specifically, represents true positives (TPs), represents false positives (FPs), and represents false negatives (FNs). The four indices are defined as follows, where is the number of categories:
The obtained crown widths in the north–south and east–west directions were compared with field data. We adopted a linear regression for qualitative assessment, and the R-squared, root-mean-squared error (RMSE), and relative root-mean-square error (rRMSE) measures for quantitative assessment, wherein the rRMSE is the ratio of the RMSE to the observed mean values [37].
4. Results
4.1. Leaf Detection
The experiment was performed on the Pytorch deep learning framework, running on Windows 10. All experiments were performed on a PC with an Intel i7-8550U CPU, 16 GB of RAM, and a NIVIDA GTX 1070 GPU. As hyperparameters, a batch size of 16, weight decay rate of 0.0001, input size of 2048, learning rate of 0.001, and the Adam optimizer were selected to balance performance with overall training time.
During training iterations, the loss curve (shown in Figure 7) converged rapidly in 81 epochs, indicating that the model was globally optimized [38]. As a standard evaluation measure of semantic segmentation, the mIoU represents the average ratio between the intersections and unions of all class points. This value was used to evaluate model performance on the test set at the end of each epoch. Initially, the fluctuation range of the mIoU was significant, as shown in Figure 7. Following loss of convergence as a consequence of multi-period training, the mIoU tended to fluctuate within 80%. When training the standard PointNet++ model, the loss and mIoU curves exhibited similar fluctuation characteristics. During the training process, the network may encounter complex samples—such as voxels with multiple trees, missing data owing to leaf occlusion, and ambiguous leaf and branch shapes—that tend to weaken the learning efficiency and lead to drastic fluctuations in the regression loss.
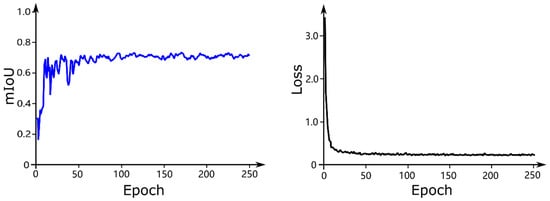
Figure 7.
Loss and mIoU chart of the improved PointNet++ during the training process, in which the horizontal axis represents the epoch, and the vertical axis is mIoU or loss.
We fed the test set into a trained network for trunk recognition and displayed the results at two different granularities according to different scales [39]: at the instance level (when the number of positive points belonging to the same tree was more significant than 75% of the ground truth), and at the point level. Results at the instance level represent the availability of trunks identified by the network in subsequent ITC segmentation tasks, whereas those at the point level represent network performance. Figure 8 illustrates the performance of the trained network in classifying randomly sampled tree trunks from the four plots, with corresponding quantitative results listed in Table 3. For the instance-level classification of the trunk, high accuracy was achieved in all four plots, with mean recall, precision, and F1-scores of 94.6%, 96.2%, and 95.4%, respectively. As shown in Figure 8a, the model can also identify smaller tree trunks that appear due to recent reseeding. Between the four plots, few differences were observed in accuracy at the instance level; however, such differences were more pronounced at the point level, where errors were concentrated in the branches. This indicates that some areas of leaves were misattributed to the trunk, or continuous branches were truncated. The mean recall, precision, and F1-scores obtained for point-level classification were 80.6%, 78.0%, and 79.2%, respectively. The high recall rates for each of the four plots indicate that recognition performance for the trunk points was relatively good [40]. However, the uneven precision also indicates that recognition varied between the tree variants: the accuracy of trunk point recognition in Plot 3, which exhibits drooping leaf plexus, was lower than that in Plot 2, which possesses a more superficial understory morphology. Furthermore, the complex tree structure in Plot 4, which can be attributed to a hurricane strike, was associated with the lowest recall among the four plots.
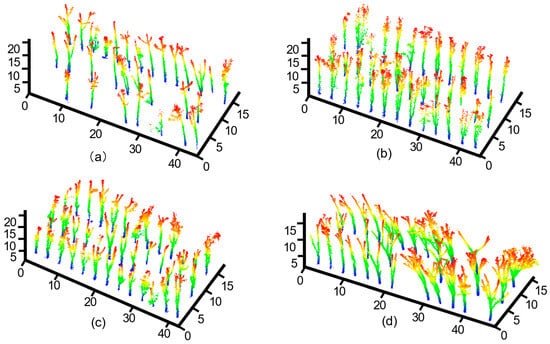
Figure 8.
The result of trunk point clouds recognition obtained from training the improved PointNet++ model. (a–d) corresponds to Plot 1–4.

Table 3.
The results of tree trunk identification obtained from the improved network at the instance and point levels in the four study plots.
4.2. Individual Tree Segmentation
The algorithm process in this study ensured that individual tree segmentation was consistent with the trunk numbers recognized by the deep learning network [35]. The tree-crown segmentation results for the four plots are shown in Figure 9. Although the uniformity of these results demonstrates the algorithm’s robustness, some unrecognized tree trunks were classified as the same tree, resulting in specific segmentation errors [28]. For example, a stump at 30 m on the horizontal axis was not recognized and remained undetected.
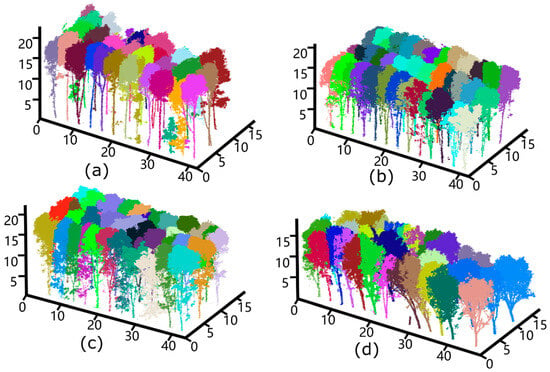
Figure 9.
The illustration of individual tree segmentation. (a–d) Corresponds to Plot 1–4.
The R2, RMSE, and rRMSE scores were measured to quantify the accuracy of crown segmentation. To interpret the algorithm’s ability to recognize tree crowns, we calculated the crown widths obtained from the segmentation results using actual crown widths of the four plots to obtain the three indicators. We randomly selected trees from the four species and calculated their corresponding evaluation indices. Figure 10 shows the least-squares regression of the approximated crown widths, comparing our method’s results with field measurements.
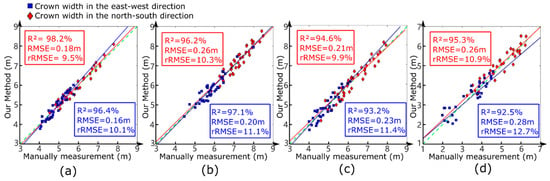
Figure 10.
The comparison results of the crown width obtained by field measurements versus our method. (a–d) Corresponds to the result of Plot 1–4. The red line in figure represents the linear regression for the magnitude of crown width of canopy trees in the east-west orientation. The blue line indicates the linear regression for the magnitude of crown width of canopy trees in the north-south orientation. The green dashed line is the 1:1 line for the linear regression.
Among the four plots, Plot 1 was associated with the highest estimation accuracy (east–west direction crown width R2 = 98.2%, RMSE = 0.18 m, rRMSE = 9.5%), which may be attributed to sparse crown distribution and a simple understory environment. Although the phenotypes of the two species were similar in Plots 2 and 3, the R2 corresponding to Plot 2 was approximately 3% higher than that of Plot 3 due to more intense inter-species competition and understory disturbances in the latter. The east–west and north–south canopy widths obtained using our method were calculated to diverge from the understory branches. These adverse factors affect the gradient calculation and crown estimation when the position of the trunk is abnormal, such as when the tilt exceeds the projection range of the crown. In Plot 4, more fallen trees were dumped into the adjacent canopy in extreme cases owing to turbulent weather. As a result, the RMSE of the east–west and north–south canopies in Plot 4 were only 0.26 m and 0.28 m, respectively.
5. Discussion
5.1. Comparison between the Two Networks
Our enhanced network performed well in the recognition task for all four plots. Because deep learning aims to hierarchically abstract and model structural features in data [3], extracting efficient features from many samples and continuously improving network performance provide machines with an extraordinary ability to identify targets [41]. The disorder, inhomogeneity, irregularity, and noise inherent to forest point clouds pose significant challenges to point cloud segmentation [27], and the accuracy of trunk identification affects the subsequent graph-based single-tree segmentation task. Furthermore, accurate branch identification also leads to the accurate identification of surrounding tissues. We compared the proposed network’s performance with that of the standard PointNet++ through qualitative and quantitative analyses. Figure 11 shows the branch recognition results of the two networks in four different plots. The tree clones in Plot 1 were excellent varieties, with few branches, a simple topological structure, and thick trunks. Compared to the other three species, the crown competition of this species was relatively low. Thus, owing to the high light transmittance of the canopy and high laser exposure of each trunk, both networks achieved accurate results. However, the standard network performed poorly in Plot 2 in terms of recall. This may be attributed to the low altitude of branch bifurcation and the massive subcanopy branch in the plot, leading to obscured tree trunks [42]. For this reason, the two networks also obtained the worst mIoU (71.1% for the improved network, and 67.4% for the standard network). However, the improved network still outperformed the standard PointNet++, with a 2.2% higher precision and 5.7% higher recall. As observed from Figure 11, the proposed network could more comprehensively identify first- and second-order branches from the main branches. The first-order branches of trees in Plot 3 were relatively low, making the area favorable for network identification. However, a large DBH difference between trees in the same field led to insufficient laser exposure on slender trunks, leading to the poor recognition of samples with sparse trunk points. As shown in Table 4, the precision gap between the two networks was 3.0% and the recall gap was 5.8%, indicating that the omission phenomenon of the original network was prominent in the sample plot. We speculate that the network’s sampling strategy led to the erroneous elimination of tree trunk points, resulting in low recall. Plot 4 had a high canopy density and large leaf area index, which made it difficult for the laser to penetrate the canopy. As shown in Table 4, the two networks achieved comparable precision, and the improved network obtained a 6.3% higher recall than the standard network. This indicates that the density of the point cloud has a greater impact on the original network, making the proposed network more effective for trunk point recognition.
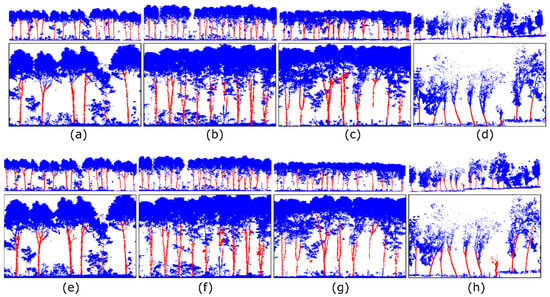
Figure 11.
Comparison of the trunk recognition results obtained from raw PointNet++ (a–d) and improved PointNet++ (e–h). Each graph showcases a row of trees and its enlarged part.

Table 4.
The tree growth properties and the accuracy assessments for trunk recognition in the four study plots.
5.2. Comparison with Existing Methods
The experimental plots in this study were high-planting-density broad-leaved forests with planting intervals of 3 m × 7 m. The plots were characterized by fuzzy treetops and crowded trees, which pose challenges to ITC segmentation [43]. We selected a marker-controlled watershed- and clustering-based algorithm [44] suitable for mixed forests as a baseline for a further comparison. The results are summarized in Table 5. In Plot 1, with a clear canopy boundary, the F1-scores of the three methods were close, indicating that all three algorithms were well-adapted to the single-wood segmentation of broad-leaved forests [45]. The marking-controlled watershed identifies the treetop by searching for the local maximum in the smoothed CHM and then performing single segmentation. However, this algorithm is limited to tree species with regular shapes [9]. The watershed algorithm performs better for trees with similar crown phenotypic characteristics—that is, trees that are neatly arranged and usually tower- or umbrella-shaped. In addition, because the watershed algorithm is not sensitive to regions with slight gradients, over-segmentation and false segmentation can easily occur. Therefore, in Plots 2 and 3 with relatively dense upper canopies, both the watershed and clustering algorithms exhibited suboptimal precision and recall. Our method achieved the highest F1-score for these plots by avoiding the dense canopy and prioritizing segmentation on the understory with a clear structure. The measurement results of ITC segmentation are achieved at the point level. The clustering algorithm assumes that treetops can be identified by analyzing the geometric space features of scanned points and subsequently combined with various distance indices to segment single trees. For Plot 4, although our algorithm outperformed the other algorithms in locating tree trunks during segmentation, it was influenced by sloping tree trunks caused by hurricane disasters, resulting in segmentation errors. Overall, the results presented in Table 5 demonstrate that the performance of our method in ITC segmentation surpasses that of the other two methods, as evidenced by its superior average accuracy across all five indices (TP, FP, FN, recall, precision, and F1-score) for all study plots.

Table 5.
The results of accuracy assessment of different methods in four plots.
6. Conclusions
In this study, we developed a point cloud segmentation framework that combines deep learning with traditional image segmentation to identify tree trunks, eliminate points corresponding to areas under the crown, and segment individual trees. The experimental results indicate that the framework ensures accurate crown edge identification even for suppressed hard-to-detect trees. The ITC segmentation algorithm, designed for the overhead segmentation of plots with moderate canopy density, was quantitatively verified to achieve accurate performance. Compared to the omission and commission errors observed in dense-canopy plots, there was a significant decline in performance under a traditional overlay angle. Owing to the uneven distribution of point clouds in the vertical direction under UAV LiDAR, the standard PointNet ++ network could not accurately identify tree trunks. Accordingly, targeted improvements were applied to the feature extraction module of PointNet ++, improving the overall mIoU of tree trunk recognition by 3.0%. Our algorithm framework especially outperformed conventional segmentation on plots with dense tree growth and unclear crown structures. With further developments in deep learning, we expect further enhancements to the algorithm modules to improve the precision of spatial structure identification for rubber plantation management.
Author Contributions
Y.Z.: Writing—original draft, and formal analysis. Y.L.: Visualization, writing—reviewing & editing. B.C.: Resources and data curation. T.Y.: Supervision, conceptualization, and methodology. X.W.: Investigation, writing—review & editing, data curation, project administration, and funding acquisition. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Opening Project Fund of State Key Laboratory Breeding Base of Cultivation and Physiology for Tropical Crops (grant number RRIKLOF202301), Central Public-interest Scientific Institution Basal Research Fund (grant number 1630032022007), National Natural Science Foundation of China (grant numbers 31770591 and 32071681), Natural Science Foundation of Jiangsu Province (BK20221337), Jiangsu Provincial Agricultural Science and Technology Independent Innovation Fund (CX(22)3048).
Data Availability Statement
The data presented in this study are available upon request from the corresponding author due to the sensitive nature of the data content.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Arias, M.; Van Dijk, P.J. What Is Natural Rubber and Why Are We Searching for New Sources? Front. Young Minds 2019, 7, 100. [Google Scholar] [CrossRef]
- Beland, M.; Parker, G.; Sparrow, B.; Harding, D.; Chasmer, L.; Phinn, S.; Antonarakis, A.; Strahler, A. On Promoting the Use of Lidar Systems in Forest Ecosystem Research. For. Ecol. Manag. 2019, 450, 117484. [Google Scholar] [CrossRef]
- Zhang, J.; Hu, X.; Dai, H.; Qu, S. DEM Extraction from ALS Point Clouds in Forest Areas via Graph Convolution Network. Remote Sens. 2020, 12, 178. [Google Scholar] [CrossRef]
- Hu, B.; Li, J.; Jing, L.; Judah, A. Improving the Efficiency and Accuracy of Individual Tree Crown Delineation from High-Density LiDAR Data. Int. J. Appl. Earth Obs. Geoinf. 2014, 26, 145–155. [Google Scholar] [CrossRef]
- Yun, T.; Jiang, K.; Li, G.; Eichhorn, M.P.; Fan, J.; Liu, F.; Chen, B.; An, F.; Cao, L. Individual Tree Crown Segmentation from Airborne LiDAR Data Using a Novel Gaussian Filter and Energy Function Minimization-Based Approach. Remote Sens. Environ. 2021, 256, 112307. [Google Scholar] [CrossRef]
- Mongus, D.; Žalik, B. An Efficient Approach to 3D Single Tree-Crown Delineation in LiDAR Data. ISPRS J. Photogramm. Remote Sens. 2015, 108, 219–233. [Google Scholar] [CrossRef]
- Dong, T.; Zhang, X.; Ding, Z.; Fan, J. Multi-Layered Tree Crown Extraction from LiDAR Data Using Graph-Based Segmentation. Comput. Electron. Agric. 2020, 170, 105213. [Google Scholar] [CrossRef]
- Reitberger, J.; Schnörr, C.; Krzystek, P.; Stilla, U. 3D Segmentation of Single Trees Exploiting Full Waveform LIDAR Data. ISPRS J. Photogramm. Remote Sens. 2009, 64, 561–574. [Google Scholar] [CrossRef]
- Yang, J.; Kang, Z.; Cheng, S.; Yang, Z.; Akwensi, P.H. An Individual Tree Segmentation Method Based on Watershed Algorithm and Three-Dimensional Spatial Distribution Analysis from Airborne LiDAR Point Clouds. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 1055–1067. [Google Scholar] [CrossRef]
- Dersch, S.; Heurich, M.; Krueger, N.; Krzystek, P. Combining Graph-Cut Clustering with Object-Based Stem Detection for Tree Segmentation in Highly Dense Airborne Lidar Point Clouds. ISPRS J. Photogramm. Remote Sens. 2021, 172, 207–222. [Google Scholar] [CrossRef]
- Dutta, A.; Engels, J.; Hahn, M. Segmentation of Laser Point Clouds in Urban Areas by a Modified Normalized Cut Method. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 41, 3034–3047. [Google Scholar] [CrossRef]
- Shi, J.; Malik, J. Normalized Cuts and Image Segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 18. [Google Scholar] [CrossRef]
- Liu, T.; Im, J.; Quackenbush, L.J. A Novel Transferable Individual Tree Crown Delineation Model Based on Fishing Net Dragging and Boundary Classification. ISPRS J. Photogramm. Remote Sens. 2015, 110, 34–47. [Google Scholar] [CrossRef]
- Dai, W.; Yang, B.; Dong, Z.; Shaker, A. A New Method for 3D Individual Tree Extraction Using Multispectral Airborne LiDAR Point Clouds. ISPRS J. Photogramm. Remote Sens. 2018, 144, 400–411. [Google Scholar] [CrossRef]
- Xiao, W.; Zaforemska, A.; Smigaj, M.; Wang, Y.; Gaulton, R. Mean Shift Segmentation Assessment for Individual Forest Tree Delineation from Airborne Lidar Data. Remote Sens. 2019, 11, 1263. [Google Scholar] [CrossRef]
- Ramiya, A.M.; Nidamanuri, R.R.; Krishnan, R. Individual Tree Detection from Airborne Laser Scanning Data Based on Supervoxels and Local Convexity. Remote Sens. Appl. Soc. Environ. 2019, 15, 100242. [Google Scholar] [CrossRef]
- Schiefer, F.; Kattenborn, T.; Frick, A.; Frey, J.; Schall, P.; Koch, B.; Schmidtlein, S. Mapping Forest Tree Species in High Resolution UAV-Based RGB-Imagery by Means of Convolutional Neural Networks. ISPRS J. Photogramm. Remote Sens. 2020, 170, 205–215. [Google Scholar] [CrossRef]
- Ioannidou, A.; Chatzilari, E.; Nikolopoulos, S.; Kompatsiaris, I. Deep Learning Advances in Computer Vision with 3D Data: A Survey. ACM Comput. Surv. 2018, 50, 1–38. [Google Scholar] [CrossRef]
- Hao, Z.; Lin, L.; Post, C.J.; Mikhailova, E.A.; Li, M.; Chen, Y.; Yu, K.; Liu, J. Automated Tree-Crown and Height Detection in a Young Forest Plantation Using Mask Region-Based Convolutional Neural Network (Mask R-CNN). ISPRS J. Photogramm. Remote Sens. 2021, 178, 112–123. [Google Scholar] [CrossRef]
- Guan, Z.; Miao, X.; Mu, Y.; Sun, Q.; Ye, Q.; Gao, D. Forest Fire Segmentation from Aerial Imagery Data Using an Improved Instance Segmentation Model. Remote Sens. 2022, 14, 3159. [Google Scholar] [CrossRef]
- Wang, J.; Chen, X.; Cao, L.; An, F.; Chen, B.; Xue, L.; Yun, T. Individual Rubber Tree Segmentation Based on Ground-Based LiDAR Data and Faster R-CNN of Deep Learning. Forests 2019, 10, 793. [Google Scholar] [CrossRef]
- Kumar, B.; Pandey, G.; Lohani, B.; Misra, S.C. A Multi-Faceted CNN Architecture for Automatic Classification of Mobile LiDAR Data and an Algorithm to Reproduce Point Cloud Samples for Enhanced Training. ISPRS J. Photogramm. Remote Sens. 2019, 147, 80–89. [Google Scholar] [CrossRef]
- Harikumar, A.; Bovolo, F.; Bruzzone, L. A Local Projection-Based Approach to Individual Tree Detection and 3-D Crown Delineation in Multistoried Coniferous Forests Using High-Density Airborne LiDAR Data. IEEE Trans. Geosci. Remote Sens. 2019, 57, 1168–1182. [Google Scholar] [CrossRef]
- Chen, X.; Jiang, K.; Zhu, Y.; Wang, X.; Yun, T. Individual Tree Crown Segmentation Directly from UAV-Borne LiDAR Data Using the PointNet of Deep Learning. Forests 2021, 12, 131. [Google Scholar] [CrossRef]
- Zhou, Y.; Tuzel, O. VoxelNet: End-to-End Learning for Point Cloud Based 3D Object Detection. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, IEEE; Salt Lake City, UT, USA: 18–23 June 2018; pp. 4490–4499.
- Luo, H.; Khoshelham, K.; Chen, C.; He, H. Individual Tree Extraction from Urban Mobile Laser Scanning Point Clouds Using Deep Pointwise Direction Embedding. ISPRS J. Photogramm. Remote Sens. 2021, 175, 326–339. [Google Scholar] [CrossRef]
- Wei, H.; Xu, E.; Zhang, J.; Meng, Y.; Wei, J.; Dong, Z.; Li, Z. BushNet: Effective Semantic Segmentation of Bush in Large-Scale Point Clouds. Comput. Electron. Agric. 2022, 193, 106653. [Google Scholar] [CrossRef]
- Xi, Z.; Hopkinson, C.; Rood, S.B.; Peddle, D.R. See the Forest and the Trees: Effective Machine and Deep Learning Algorithms for Wood Filtering and Tree Species Classification from Terrestrial Laser Scanning. ISPRS J. Photogramm. Remote Sens. 2020, 168, 1–16. [Google Scholar] [CrossRef]
- Yun, T.; An, F.; Li, W.; Sun, Y.; Cao, L.; Xue, L. A Novel Approach for Retrieving Tree Leaf Area from Ground-Based LiDAR. Remote Sens. 2016, 8, 942. [Google Scholar] [CrossRef]
- Kamousi, P.; Lazard, S.; Maheshwari, A.; Wuhrer, S. Analysis of Farthest Point Sampling for Approximating Geodesics in a Graph. Comput. Geom. 2016, 57, 1–7. [Google Scholar] [CrossRef]
- Chen, Q.; Wynne, R.J.; Goulding, P.; Sandoz, D. The Application of Principal Component Analysis and Kernel Density Estimation to Enhance Process Monitoring. Control Eng. Pract. 2000, 8, 531–543. [Google Scholar] [CrossRef]
- Flores-Garnica, J.G.; Macías-Muro, A. Bandwidth selection for kernel density estimation of forest fires. Rev. Chapingo Ser. Cienc. For. Y Del Ambiente 2018, 24, 313–327. [Google Scholar] [CrossRef]
- Zhang, W.; Cai, S.; Liang, X.; Shao, J.; Hu, R.; Yu, S.; Yan, G. Cloth Simulation-Based Construction of Pit-Free Canopy Height Models from Airborne LiDAR Data. For. Ecosyst. 2020, 7, 1. [Google Scholar] [CrossRef]
- Felzenszwalb, P.F.; Huttenlocher, D.P. Efficient Graph-Based Image Segmentation. Int. J. Comput. Vis. 2004, 59, 167–181. [Google Scholar] [CrossRef]
- Amiri, N.; Polewski, P.; Heurich, M.; Krzystek, P.; Skidmore, A.K. Adaptive Stopping Criterion for Top-down Segmentation of ALS Point Clouds in Temperate Coniferous Forests. ISPRS J. Photogramm. Remote Sens. 2018, 141, 265–274. [Google Scholar] [CrossRef]
- Han, T.S.; Endo, H.; Sasaki, M. Reliability and Secrecy Functions of the Wiretap Channel Under Cost Constraint. IEEE Trans. Inf. Theory 2014, 60, 6819–6843. [Google Scholar] [CrossRef]
- Wang, K.; Zhou, J.; Zhang, W.; Zhang, B. Mobile LiDAR Scanning System Combined with Canopy Morphology Extracting Methods for Tree Crown Parameters Evaluation in Orchards. Sensors 2021, 21, 339. [Google Scholar] [CrossRef]
- Jing, Z.; Guan, H.; Zhao, P.; Li, D.; Yu, Y.; Zang, Y.; Wang, H.; Li, J. Multispectral LiDAR Point Cloud Classification Using SE-PointNet++. Remote Sens. 2021, 13, 2516. [Google Scholar] [CrossRef]
- Li, D.; Shi, G.; Li, J.; Chen, Y.; Zhang, S.; Xiang, S.; Jin, S. PlantNet: A Dual-Function Point Cloud Segmentation Network for Multiple Plant Species. ISPRS J. Photogramm. Remote Sens. 2022, 184, 243–263. [Google Scholar] [CrossRef]
- Huo, L.; Lindberg, E.; Holmgren, J. Towards Low Vegetation Identification: A New Method for Tree Crown Segmentation from LiDAR Data Based on a Symmetrical Structure Detection Algorithm (SSD). Remote Sens. Environ. 2022, 270, 112857. [Google Scholar] [CrossRef]
- Li, Y.; Quan, C.; Yang, S.; Wu, S.; Shi, M.; Wang, J.; Tian, W. Functional Identification of ICE Transcription Factors in Rubber Tree. Forests 2022, 13, 52. [Google Scholar] [CrossRef]
- Peng, X.; Zhao, A.; Chen, Y.; Chen, Q.; Liu, H.; Wang, J.; Li, H. Comparison of Modeling Algorithms for Forest Canopy Structures Based on UAV-LiDAR: A Case Study in Tropical China. Forests 2020, 11, 1324. [Google Scholar] [CrossRef]
- Hao, Y.; Widagdo, F.R.A.; Liu, X.; Liu, Y.; Dong, L.; Li, F. A Hierarchical Region-Merging Algorithm for 3-D Segmentation of Individual Trees Using UAV-LiDAR Point Clouds. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–16. [Google Scholar] [CrossRef]
- Tusa, E.; Monnet, J.-M.; Barre, J.-B.; Mura, M.D.; Dalponte, M.; Chanussot, J. Individual Tree Segmentation Based on Mean Shift and Crown Shape Model for Temperate Forest. IEEE Geosci. Remote Sens. Lett. 2021, 18, 2052–2056. [Google Scholar] [CrossRef]
- Minařík, R.; Langhammer, J.; Lendzioch, T. Automatic Tree Crown Extraction from UAS Multispectral Imagery for the Detection of Bark Beetle Disturbance in Mixed Forests. Remote Sens. 2020, 12, 4081. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).