DDSR: Degradation-Aware Diffusion Model for Spectral Reconstruction from RGB Images
Abstract
1. Introduction
- We propose DDSR, a diffusion-based spectral reconstruction architecture that utilizes a degradation-aware correction to reduce the error caused by the prediction uncertainty in each inverse step.
- Since realistic scenarios are usually noisy, a noise-related correction method of our work, motivated by adapting the correction process to the noise level of the current image, is proposed to reduce the effect of the noise.
- JPEG compression is a common nonlinear degradation, and we propose to extend the correction further for JPEG-related scenarios.
- Quantitative experiments on various public datasets demonstrate that our method can achieve competitive performance and shows promising generalization ability.
2. Related Work
2.1. Prior-Based Methods
2.2. Data-Driven Methods
2.3. Diffusion Model for Image Restoration
3. Method
3.1. Background
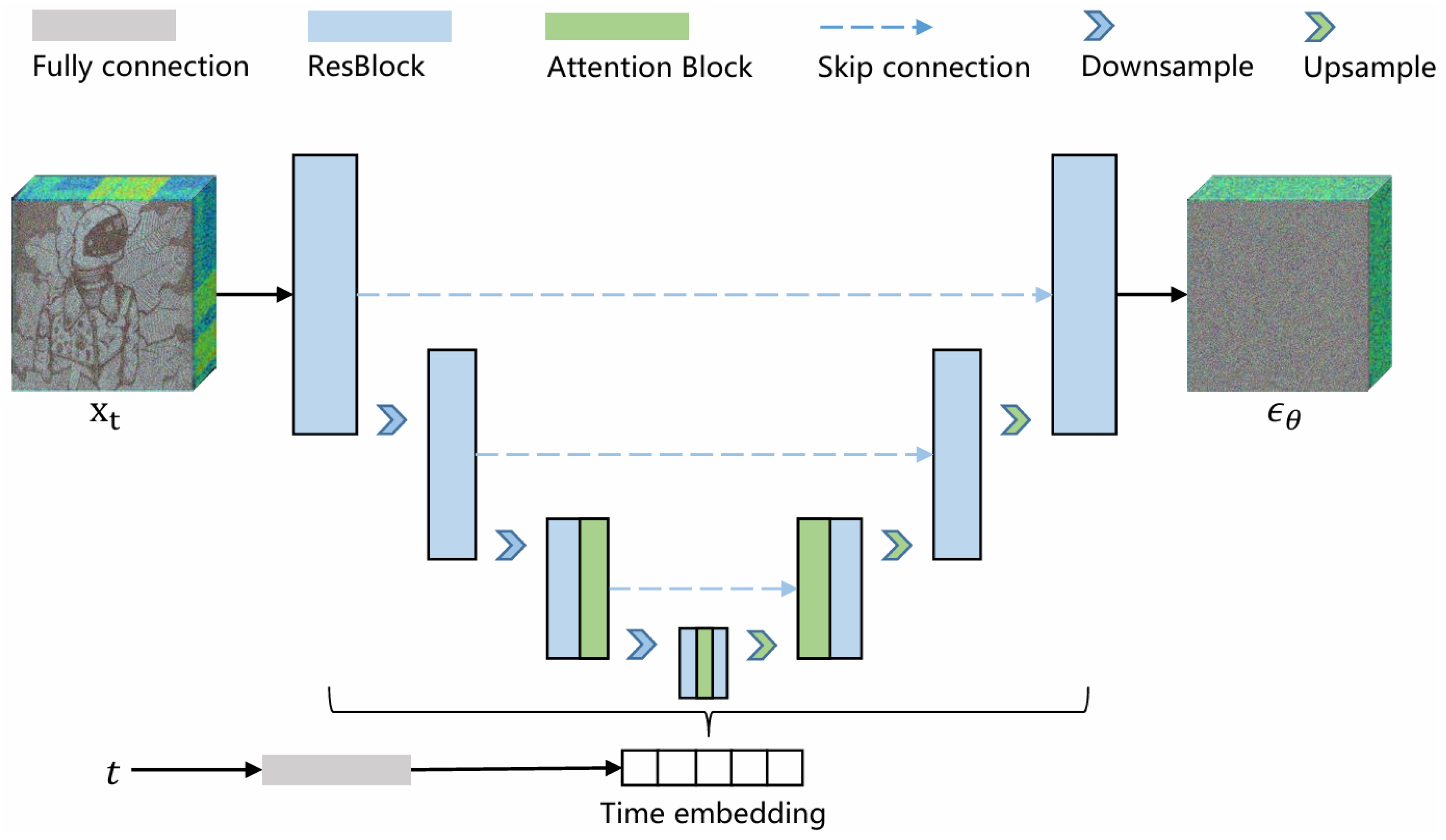
3.2. Architecture of Neural Network
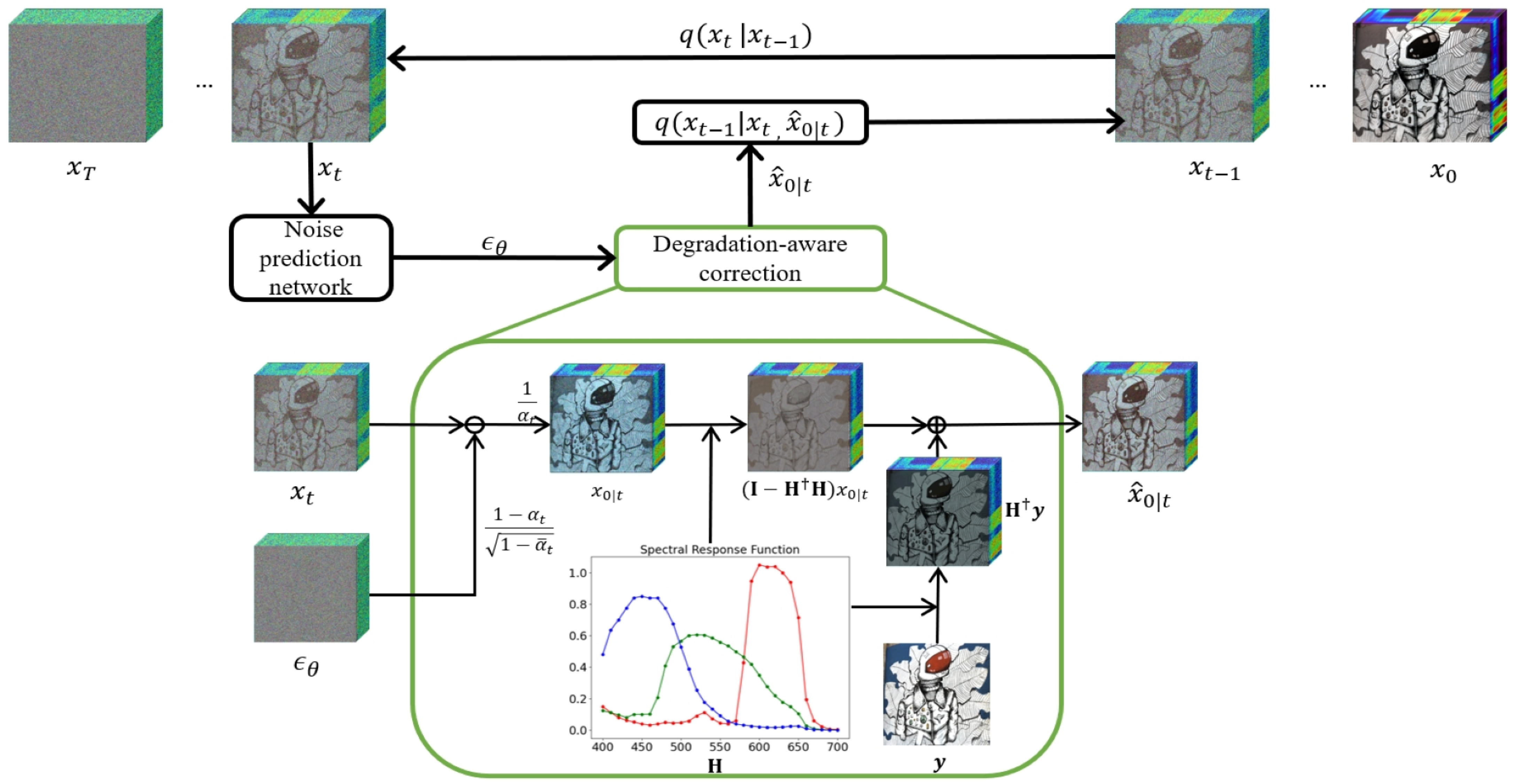
3.3. Degradation-Aware Diffusion Model
3.3.1. Degradation-Aware Correction
| Algorithm 1 Simple sampling | |
| 1: Input: , degraded image | |
| 2: Output: Reconstructed HSI | |
| 3: for do | |
| 4: | |
| 5: | ▹ update via Equation (8) |
| 6: | ▹ Equation (3) |
| 7: end for | |
| 8: return | |
3.3.2. Noise-Related Correction
| Algorithm 2 Noise-related sampling | |
| 1: Input: , degraded image | |
| 2: Output: Reconstructed HSI | |
| 3: for do | |
| 4: Update via Equation (12) | |
| 5: | |
| 6: | ▹ update via Equation (10) |
| 7: | ▹ Equation (11) |
| 8: end for | |
| 9: return | |
3.3.3. JPEG-Related Correction
4. Experiments
4.1. Dataset
4.2. Implementation Detail
4.3. Baseline
4.4. Experiment Results
4.4.1. Quantitative Result
4.4.2. Qualitative Results
4.5. Ablation Study
4.6. Generalization Ability
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Background
Appendix A.2. Training the Neural Network
| Algorithm A1 Training process |
|
References
- Khan, U.; Paheding, S.; Elkin, C.P.; Devabhaktuni, V.K. Trends in Deep Learning for Medical Hyperspectral Image Analysis. IEEE Access 2021, 9, 79534–79548. [Google Scholar] [CrossRef]
- Zhao, H.; Wang, X.; Li, J.; Zhong, Y. Class Prior-Free Positive-Unlabeled Learning with Taylor Variational Loss for Hyperspectral Remote Sensing Imagery. In Proceedings of the International Conference on Computer Vision (ICCV), Paris, France, 2–6 October 2023. [Google Scholar]
- Chen, S.; Li, X.; Yan, Y. Hyperspectral Anomaly Detection with Auto-Encoder and Independent Target. Remote. Sens. 2023, 15, 5266. [Google Scholar] [CrossRef]
- Basterretxea, K.; Martinez, V.; Echanobe, J.; Gutierrez-Zaballa, J.; Del Campo, I. HSI-Drive: A Dataset for the Research of Hyperspectral Image Processing Applied to Autonomous Driving Systems. In Proceedings of the IEEE Intelligent Vehicles Symposium (IV), Nagoya, Japan, 11–17 July 2021. [Google Scholar]
- Fu, Y.; Zhang, T.; Zheng, Y.; Zhang, D.; Huang, H. Joint Camera Spectral Sensitivity Selection and Hyperspectral Image Recovery. In Proceedings of the Computer Vision–ECCV 2018, Lecture Notes in Computer Science, Munich, Germany, 8–14 September 2018. [Google Scholar]
- Zhang, J.; Su, R.; Fu, Q.; Ren, W.; Heide, F.; Nie, Y. A survey on computational spectral reconstruction methods from RGB to hyperspectral imaging. Sci. Rep. 2022, 12, 11905. [Google Scholar] [CrossRef] [PubMed]
- Fu, J.; Liu, J.; Zhao, R.; Chen, Z.; Qiao, Y.; Li, D. Maize disease detection based on spectral recovery from RGB images. Front. Plant Sci. 2023, 13, 1056842. [Google Scholar] [CrossRef] [PubMed]
- Kong, L.; Li, L.; Yuan, J.; Zhao, Y.; Dong, L.; Liu, M.; Zhao, Y.; Lu, T.; Chu, X. High-precision hemoglobin detection based on hyperspectral reconstruction of RGB images. Biomed. Signal Process. Control 2024, 91, 105904. [Google Scholar] [CrossRef]
- Arad, B.; Ben-Shahar, O. Sparse Recovery of Hyperspectral Signal from Natural RGB Images. In Proceedings of the European Conference on Computer Vision (ECCV), Amsterdam, The Netherlands, 11–14 October 2016. [Google Scholar]
- Jia, Y.; Zheng, Y.; Gu, L.; Subpa-Asa, A.; Lam, A.; Sato, Y.; Sato, I. From RGB to Spectrum for Natural Scenes via Manifold-Based Mapping. In Proceedings of the International Conference on Computer Vision (ICCV), Zurich, Switzerland, 6–12 September 2014. [Google Scholar]
- Nguyen, R.M.H.; Prasad, D.K.; Brown, M.S. Training-Based Spectral Reconstruction from a Single RGB Image. In Proceedings of the International Conference on Computer Vision (ICCV), Zurich, Switzerland, 6–12 September 2014. [Google Scholar]
- Liao, X.; He, L.; Mao, J.; Xu, M. Spectral Superresolution Using Transformer with Convolutional Spectral Self-Attention. Remote Sens. 2024, 16, 1688. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, L.; Song, R.; Tong, Q. A General Deep Learning Point–Surface Fusion Framework for RGB Image Super-Resolution. Remote Sens. 2024, 16, 139. [Google Scholar] [CrossRef]
- Wang, L.; Sole, A.; Hardeberg, J.Y. Densely Residual Network with Dual Attention for Hyperspectral Reconstruction from RGB Images. Remote Sens. 2022, 14, 3128. [Google Scholar] [CrossRef]
- Li, J.; Wu, C.; Song, R.; Li, Y.; Liu, F. Adaptive Weighted Attention Network with Camera Spectral Sensitivity Prior for Spectral Reconstruction from RGB Images. In Proceedings of the Computer Vision and Pattern Recognition Workshops (CVPRW), Seattle, WA, USA, 14–19 June 2020. [Google Scholar]
- Shi, Z.; Chen, C.; Xiong, Z.; Liu, D.; Wu, F. HSCNN+: Advanced CNN-Based Hyperspectral Recovery from RGB Images. In Proceedings of the Computer Vision and Pattern Recognition Workshops (CVPRW), Seattle, WA, USA, 14–19 June 2020. [Google Scholar]
- Li, J.; Du, S.; Wu, C.; Leng, Y.; Song, R.; Li, Y. DRCR Net: Dense Residual Channel Re-calibration Network with Non-local Purification for Spectral Super Resolution. In Proceedings of the Computer Vision and Pattern Recognition Workshops (CVPRW), New Orleans, LA, USA, 19–20 June 2022. [Google Scholar]
- Syed Waqas, Z.; Arora, A.; Khan, S.; Hayat, M.; Khan, F.S.; Yang, M.H. Restormer: Efficient Transformer for High-Resolution Image Restoration. In Proceedings of the Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022. [Google Scholar]
- Cai, Y.; Lin, J.; Lin, Z.; Wang, H.; Zhang, Y.; Pfister, H.; Timofte, R.; Gool, L. MST++: Multi-stage Spectral-wise Transformer for Efficient Spectral Reconstruction. In Proceedings of the Computer Vision and Pattern Recognition (CVPR) Workshops, New Orleans, LA, USA, 19–20 June 2022. [Google Scholar]
- Niu, B.; Wen, W.; Ren, W.; Zhang, X.; Yang, L.; Wang, S.; Zhang, K.; Cao, X.; Shen, H. Single Image Super-Resolution via a Holistic Attention Network. In Proceedings of the European Conference on Computer Vision (ECCV), Glasgow, UK, 23–28 August 2020. [Google Scholar]
- Yao, J.; Hong, D.; Chanussot, J.; Meng, D.; Zhu, X.; Xu, Z. Cross-Attention in Coupled Unmixing Nets for Unsupervised Hyperspectral Super-Resolution. In Proceedings of the European Conference on Computer Vision (ECCV), Glasgow, UK, 23–28 August 2020. [Google Scholar]
- Saharia, C.; Ho, J.; Chan, W.; Salimans, T.; Fleet, D.J.; Norouzi, M. Image Super-Resolution via Iterative Refinement. IEEE Trans. Pattern Anal. Mach. Intell. (TPAMI) 2022, 45, 4713–4726. [Google Scholar] [CrossRef] [PubMed]
- Han, L.; Zhao, Y.; Lv, H.; Zhang, Y.; Liu, H.; Bi, G.; Han, Q. Enhancing Remote Sensing Image Super-Resolution with Efficient Hybrid Conditional Diffusion Model. Remote Sens. 2023, 15, 3452. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, N.; Li, M.; Mao, S. The Crack Diffusion Model: An Innovative Diffusion-Based Method for Pavement Crack Detection. Remote Sens. 2024, 16, 986. [Google Scholar] [CrossRef]
- Chen, J.; Luo, Y.; Wang, J.; Tang, H.; Tang, Y.; Li, J. Elimination of Irregular Boundaries and Seams for UAV Image Stitching with a Diffusion Model. Remote Sens. 2024, 16, 1483. [Google Scholar] [CrossRef]
- Chen, J.; Jia, L.; Zhang, J.; Feng, Y.; Zhao, X.; Tao, R. Super-Resolution for Land Surface Temperature Retrieval Images via Cross-Scale Diffusion Model Using Reference Images. Remote Sens. 2024, 16, 1356. [Google Scholar] [CrossRef]
- Arad, B.; Timofte, R.; Yahel, R.; Morag, N.; Bernat, A.; Cai, Y.; Lin, J.; Lin, Z.; Wang, H.; Zhang, Y.; et al. NTIRE 2022 Spectral Recovery Challenge and Data Set. In Proceedings of the Computer Vision and Pattern Recognition Workshops (CVPRW), New Orleans, LA, USA, 19–20 June 2022. [Google Scholar]
- Zhu, Z.; Liu, H.; Hou, J.; Zeng, H.; Zhang, Q. Semantic-embedded Unsupervised Spectral Reconstruction from Single RGB Images in the Wild. In Proceedings of the International Conference on Computer Vision (ICCV), Virtual Conference, 11–17 October 2021. [Google Scholar]
- Zhao, Y.; Po, L.M.; Yan, Q.; Liu, W.; Lin, T. Hierarchical Regression Network for Spectral Reconstruction from RGB Images. In Proceedings of the Computer Vision and Pattern Recognition Workshops (CVPRW), Seattle, WA, USA, 14–19 June 2020. [Google Scholar]
- Wang, Y.; Yu, J.; Zhang, J. Zero-Shot Image Restoration Using Denoising Diffusion Null-Space Model. In Proceedings of the International Conference on Learning Representations (ICLR), Virtual Event, 25–29 April 2022. [Google Scholar]
- Xiao, Y.; Yuan, Q.; Jiang, K.; He, J.; Jin, X.; Zhang, L. EDiffSR: An Efficient Diffusion Probabilistic Model for Remote Sensing Image Super-Resolution. IEEE Trans. Geosci. Remote. Sens. (TGRS) 2023, 62, 5601514. [Google Scholar] [CrossRef]
- Wu, C.; Wang, D.; Mao, H.; Li, Y. HSR-Diff:Hyperspectral Image Super-Resolution via Conditional Diffusion Models. In Proceedings of the International Conference on Computer Vision (ICCV), Paris, France, 2–3 October 2023. [Google Scholar]
- Dong, W.; Liu, S.; Xiao, S.; Qu, J.; Li, Y. ISPDiff: Interpretable Scale-Propelled Diffusion Model for Hyperspectral Image Super-Resolution. IEEE Trans. Geosci. Remote. Sens. 2024, 62, 5519614. [Google Scholar] [CrossRef]
- Ho, J.; Jain, A.; Abbeel, P. Denoising Diffusion Probabilistic Models. In Proceedings of the Neural Information Processing Systems (NIPS), Online Conference, 6–12 December 2020. [Google Scholar]
- Sohl-Dickstein, J.; Weiss, E.A.; Maheswaranathan, N.; Ganguli, S. Deep Unsupervised Learning using Nonequilibrium Thermodynamics. In Proceedings of the International Conference on Machine Learning (ICCV), Lille, France, 6–11 July 2015. [Google Scholar]
- Schwab, J.; Antholzer, S.; Haltmeier, M. Deep Null Space Learning for Inverse Problems: Convergence Analysis and Rates. Inverse Probl. 2019, 35, 025008. [Google Scholar] [CrossRef]
- Wallace, G. The JPEG still picture compression standard. IEEE Trans. Consum. Electron. 1992, 38, xviii–xxxiv. [Google Scholar] [CrossRef]
- Yasuma, F.; Mitsunaga, T.; Iso, D.; Nayar, S. Generalized Assorted Pixel Camera: Postcapture Control of Resolution, Dynamic Range, and Spectrum. IEEE Trans. Image Process. 2010, 19, 2241–2253. [Google Scholar] [CrossRef] [PubMed]
- Nascimento, S.M.; Amano, K.; Foster, D.H. Spatial distributions of local illumination color in natural scenes. Vis. Res. 2016, 120, 39–44. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Fu, Q.; Heidrich, W. Multispectral illumination estimation using deep unrolling network. In Proceedings of the International Conference on Computer Vision (ICCV), Virtual Conference, 11–17 October 2021. [Google Scholar]
- Hu, X.; Cai, Y.; Lin, J.; Wang, H.; Yuan, X.; Zhang, Y.; Timofte, R.; Gool, L. HDNet: High-resolution Dual-domain Learning for Spectral Compressive Imaging. In Proceedings of the Computer Vision and Pattern Recognition Workshops (CVPRW), New Orleans, LA, USA, 19–20 June 2022. [Google Scholar]








| Method | KAUST | NUS | ||||
|---|---|---|---|---|---|---|
| MRAE | RMSE | PSNR | MRAE | RMSE | PSNR | |
| AWAN [15] | 0.279 | 0.0894 | 22.435 | 0.192 | 0.0239 | 34.215 |
| HDNet [29] | 0.302 | 0.0878 | 22.639 | 0.201 | 0.0249 | 33.347 |
| HRNet [41] | 0.287 | 0.0867 | 22.752 | 0.204 | 0.0251 | 33.469 |
| Restormer [18] | 0.291 | 0.0856 | 22.936 | 0.212 | 0.0251 | 33.470 |
| MST++ [19] | 0.279 | 0.0855 | 23.592 | 0.205 | 0.0237 | 33.433 |
| Ours | 0.277 | 0.0797 | 24.102 | 0.191 | 0.0236 | 34.274 |
| Method | CAVE | Foster | ||||
|---|---|---|---|---|---|---|
| MRAE | RMSE | PSNR | MRAE | RMSE | PSNR | |
| AWAN [15] | 0.409 | 0.0389 | 29.333 | 0.331 | 0.0226 | 34.620 |
| HDNet [29] | 0.425 | 0.0352 | 30.132 | 0.339 | 0.0217 | 35.347 |
| HRNet [41] | 0.398 | 0.0360 | 29.757 | 0.300 | 0.0223 | 35.128 |
| Restormer [18] | 0.447 | 0.0347 | 29.867 | 0.294 | 0.0205 | 35.541 |
| MST++ [19] | 0.390 | 0.0332 | 30.485 | 0.311 | 0.0195 | 36.163 |
| Ours | 0.446 | 0.0331 | 30.496 | 0.389 | 0.0199 | 35.644 |
| Method | ARAD-1K | ICVL | ||||
|---|---|---|---|---|---|---|
| MRAE | RMSE | PSNR | MRAE | RMSE | PSNR | |
| AWAN [15] | 0.158 | 0.0222 | 34.950 | 0.201 | 0.0214 | 34.505 |
| HDNet [29] | 0.167 | 0.0224 | 35.542 | 0.196 | 0.0217 | 34.218 |
| HRNet [41] | 0.154 | 0.0224 | 34.918 | 0.188 | 0.0244 | 33.675 |
| Restormer [18] | 0.159 | 0.0207 | 36.258 | 0.215 | 0.0216 | 34.378 |
| MST++ [19] | 0.148 | 0.0219 | 35.305 | 0.198 | 0.0203 | 34.825 |
| Ours | 0.198 | 0.0215 | 35.586 | 0.213 | 0.0202 | 34.886 |
| Method | MRAE | RMSE | PSNR |
|---|---|---|---|
| SR3 [22] | 1.442 | 0.0698 | 23.456 |
| EDiffSR [31] | 0.840 | 0.0861 | 21.736 |
| Ours | 0.198 | 0.0220 | 35.586 |
| Sample Method | MRAE | RMSE | PSNR |
|---|---|---|---|
| Simple ( = 0.01) | 0.300 | 0.0219 | 34.642 |
| Simple ( = 0.005) | 0.211 | 0.0195 | 36.385 |
| Noise-related ( = 0.01) | 0.215 | 0.0191 | 36.699 |
| Noise-related ( = 0.005) | 0.178 | 0.0192 | 36.914 |
| Amount | Range | MRAE | RMSE | PSNR | Range | MRAE | RMSE | PSNR |
|---|---|---|---|---|---|---|---|---|
| 100 | (400,500) | 1.263 | 0.0792 | 22.367 | (900,1000) | 1.003 | 0.0820 | 22.965 |
| 250 | (250,500) | 0.918 | 0.0659 | 24.082 | (750,1000) | 0.770 | 0.0750 | 23.745 |
| 500 | (0,500) | 0.854 | 0.0597 | 25.802 | (500,1000) | 0.536 | 0.0529 | 26.403 |
| Sample Method | MRAE | RMSE | PSNR |
|---|---|---|---|
| Simple () | 0.558 | 0.0460 | 27.549 |
| JPEG-related () | 0.521 | 0.0452 | 27.702 |
| Simple () | 0.477 | 0.0420 | 28.327 |
| JPEG-related () | 0.456 | 0.0414 | 28.594 |
| Method | KAUST | ICVL | ||||
|---|---|---|---|---|---|---|
| MRAE | RMSE | PSNR | MRAE | RMSE | PSNR | |
| AWAN [15] | 0.301 | 0.1351 | 18.371 | 0.328 | 0.0523 | 26.650 |
| HDNet [29] | 0.304 | 0.1304 | 18.631 | 0.361 | 0.0532 | 26.534 |
| HRNet [41] | 0.324 | 0.1378 | 18.139 | 0.354 | 0.0540 | 26.348 |
| Restormer [18] | 0.303 | 0.1309 | 18.285 | 0.352 | 0.0539 | 26.312 |
| MST++ [19] | 0.296 | 0.1313 | 18.573 | 0.342 | 0.0531 | 26.485 |
| Ours | 0.204 | 0.0689 | 24.979 | 0.236 | 0.0225 | 33.936 |
| Method | CAVE | Foster | ||||
|---|---|---|---|---|---|---|
| MRAE | RMSE | PSNR | MRAE | RMSE | PSNR | |
| AWAN [15] | 0.554 | 0.0791 | 22.836 | 0.427 | 0.0393 | 30.738 |
| HDNet [29] | 0.551 | 0.0674 | 24.067 | 0.452 | 0.0388 | 30.924 |
| HRNet [41] | 0.548 | 0.0770 | 22.927 | 0.424 | 0.0406 | 30.536 |
| Restormer [18] | 0.523 | 0.0690 | 23.815 | 0.417 | 0.0404 | 30.288 |
| MST++ [19] | 0.509 | 0.0666 | 24.114 | 0.414 | 0.0391 | 31.001 |
| Ours | 0.443 | 0.0354 | 29.771 | 0.390 | 0.0217 | 35.454 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Zhang, X. DDSR: Degradation-Aware Diffusion Model for Spectral Reconstruction from RGB Images. Remote Sens. 2024, 16, 2692. https://doi.org/10.3390/rs16152692
Chen Y, Zhang X. DDSR: Degradation-Aware Diffusion Model for Spectral Reconstruction from RGB Images. Remote Sensing. 2024; 16(15):2692. https://doi.org/10.3390/rs16152692
Chicago/Turabian StyleChen, Yunlai, and Xiaoyan Zhang. 2024. "DDSR: Degradation-Aware Diffusion Model for Spectral Reconstruction from RGB Images" Remote Sensing 16, no. 15: 2692. https://doi.org/10.3390/rs16152692
APA StyleChen, Y., & Zhang, X. (2024). DDSR: Degradation-Aware Diffusion Model for Spectral Reconstruction from RGB Images. Remote Sensing, 16(15), 2692. https://doi.org/10.3390/rs16152692








