Hyperspectral Image Classification Based on Double-Branch Multi-Scale Dual-Attention Network
Abstract
1. Introduction
- High-dimensional spectral data and a small number of training samples often lead to the Hughes phenomenon, where classification accuracy first increases and then decreases as the number of participating bands increases [19].
- Spectral variability refers to changes in the spectrum caused by atmospheric effects, shadows, instrument noise, and other factors. High spectral variability in some categories makes it challenging to classify objects of the same category into the same group (“same objects with different spectra”). Conversely, low spectral variability among certain distinct classes complicates their differentiation (“different objects with the same spectra”) [23].
- The convolution-based backbone network demonstrates strong capabilities in extracting spatial structure and local context information from HSI. However, simple convolutional neural networks cannot capture global information, and hyperspectral data often yields poor classification results due to excessive redundancy. Even with the addition of an attention mechanism, extracting diagnostic spectral and spatial characteristics remains ineffective. Additionally, most current convolution-based networks focus excessively on spatial information. This focus can distort the learned spectral features, complicating the extraction of diagnostic spectral attributes [19].
- The Transformer-based backbone network has a strong capability to extract spectral information and sequence features from HSI. Despite numerous attempts to improve local information extraction by incorporating various modules [19,25,26,27,28], the linear projection operation of Transformers still interferes with local spectral-spatial information, resulting in the loss of crucial information during classification. Additionally, the utilization of spatial information is inadequate, making it challenging to distinguish and categorize cases of “same objects with different spectra” and “different objects with the same spectra”.
- Currently, most neural networks employ a patch-wise dataset division method. This approach involves selecting a center pixel and combining it with its neighboring pixels to form a patch. The network then predicts the center pixel by extracting and analyzing information from the entire patch. A sliding window strategy is subsequently used to predict the labels of all patch center pixels. While this method is simple and practical, it has drawbacks. Random sampling can cause overlap and information leakage between the training and test sets, potentially leading to overly optimistic results [29].
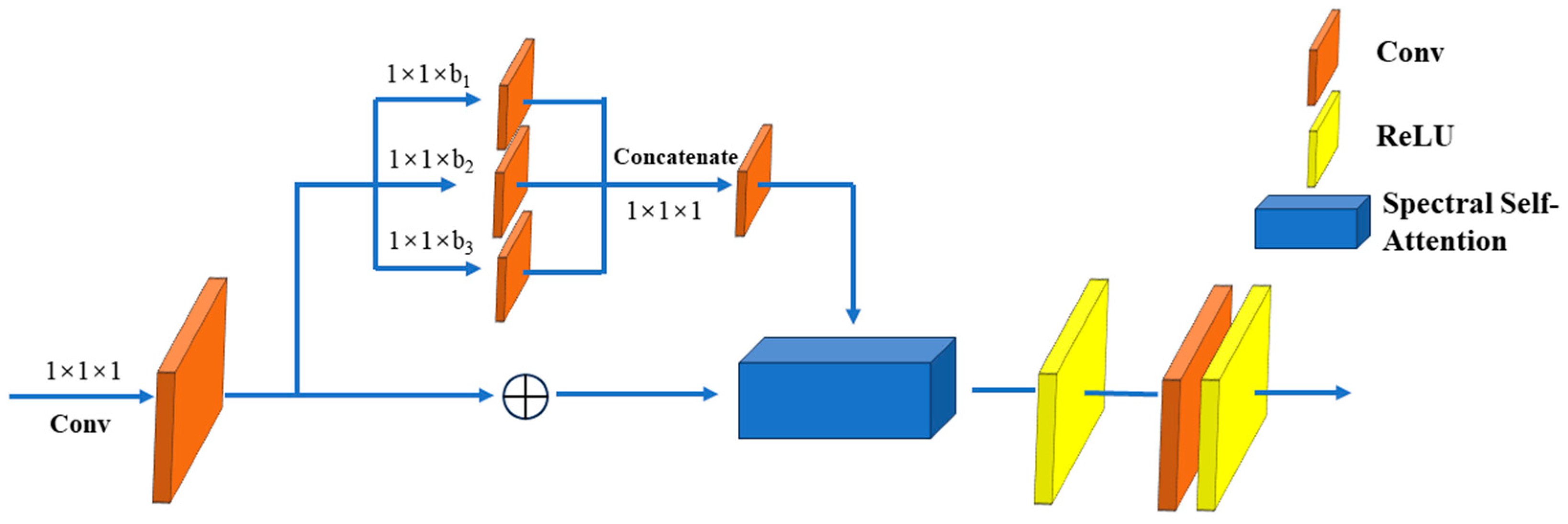
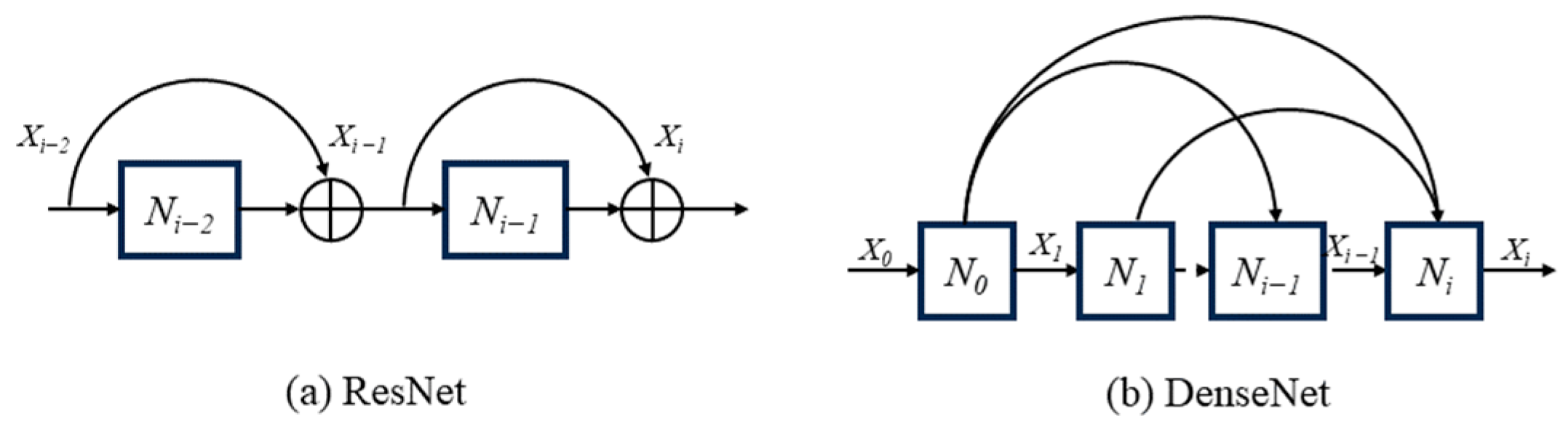
- Due to the limitations of information obtained at a single scale, this article proposes a multi-scale spectral residual self-attention (MSeRA) structure. This structure combines spectral self-attention mechanisms with multi-scale integration and utilizes residual connections to prevent gradient vanishing, effectively extracting high-dimensional complex spectral information from hyperspectral images. This module serves as a fundamental dense block unit in dense connections, enabling multiple extractions and integrations of spectral features. This enhances the transmission of spectral features and more effectively utilizes valid spectral information. It ensures the acquisition of long-distance information in the network, avoiding gradient explosion and vanishing while enhancing the extraction of spectral features. Additionally, this module extracts diagnostic features from hyperspectral images to the fullest extent, even with limited samples and sample imbalances, thereby enhancing classification accuracy.
- This article adopts a training-test set division method to prevent information leakage in the dataset. This approach enhances the utilization of limited labeled samples, ensures the accuracy of sample labels, and prevents potential information leakage between the training and test data.
- This article introduces a new hyperspectral geological lithology dataset, showcasing the benefits of the DBMSDA network in lithology recognition. It addresses the lack of deep learning methods in hyperspectral remote sensing lithology recognition and enhances the identification performance in this field. The study highlights the significant research potential and value of deep learning methods in hyperspectral remote sensing lithology identification.
2. Related Works
2.1. HSI Classification Method Based on Deep Learning
2.2. HSI Classification Method Based on Double-Branch Networks
2.3. Training–Test Set Division Method without Information Leakage
3. Materials and Methods
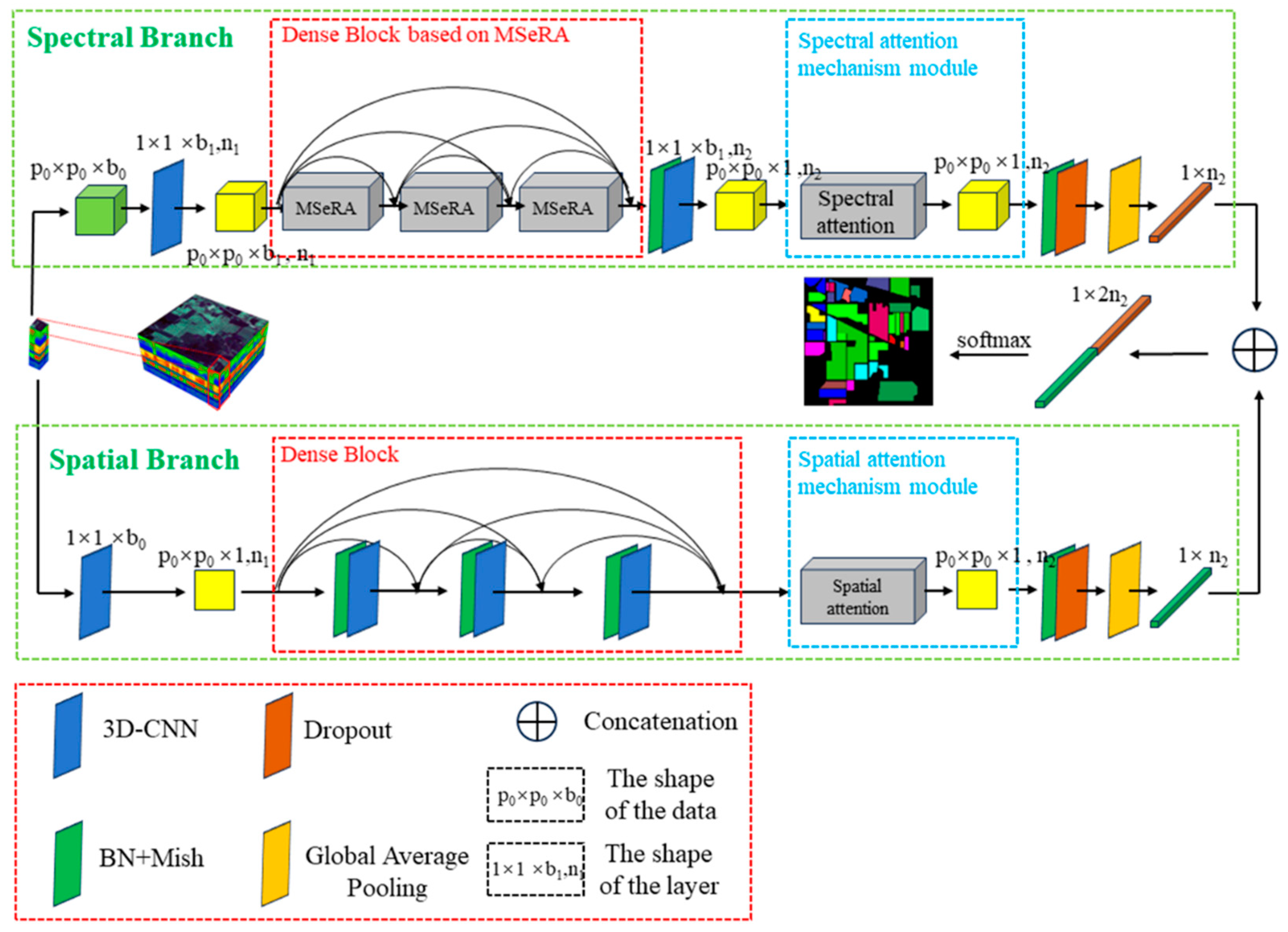
3.1. DBMSDA Network Framework
3.2. Spectral Feature Extraction Module Based on MSeRA Structure
3.2.1. MSeRA Structure
3.2.2. Dense Block Based on MSeRA
3.3. Spatial Feature Extraction Module
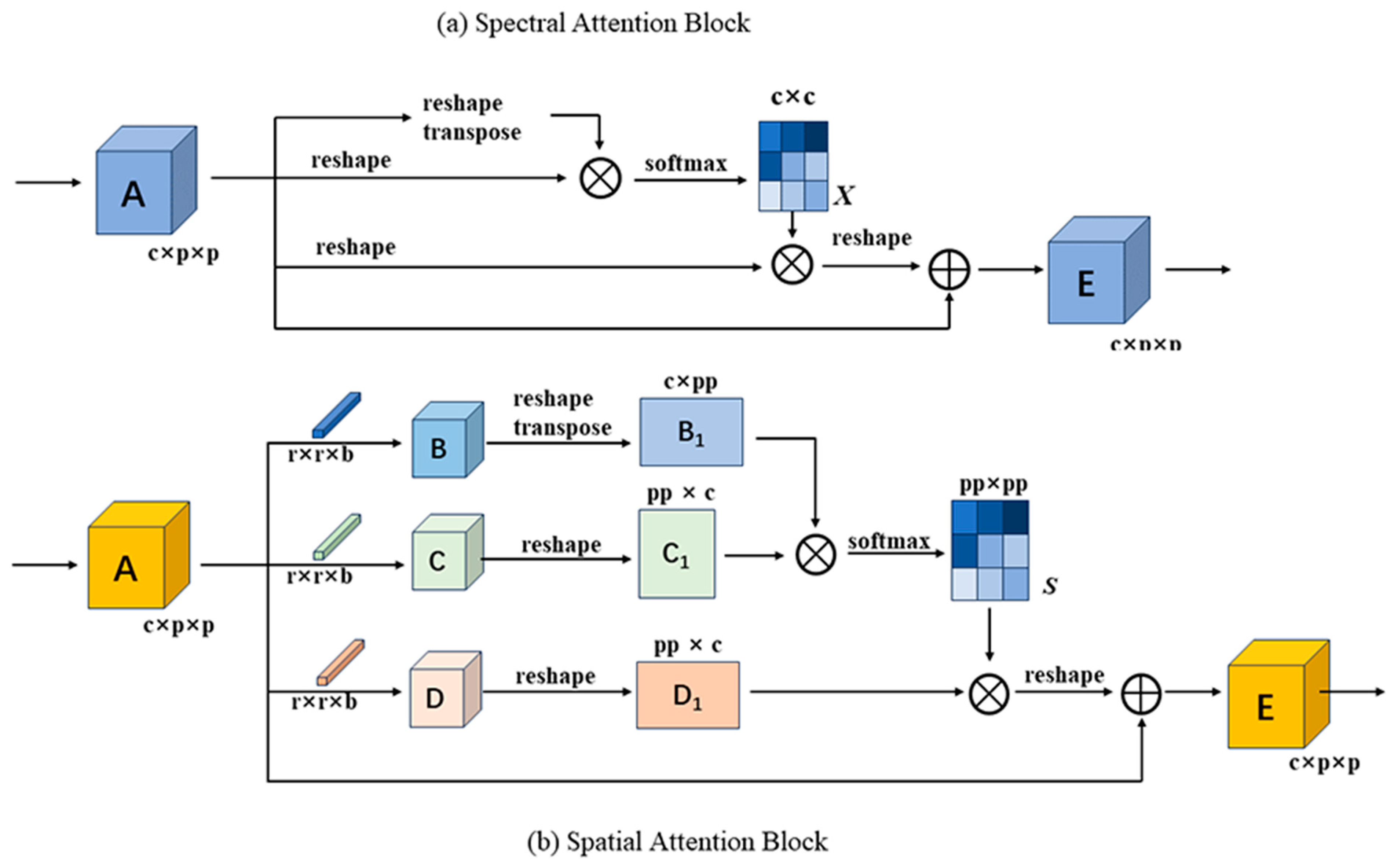
3.4. Attention Mechanism
3.4.1. Spectral Attention Module
3.4.2. Spatial Attention Module
4. Results
4.1. Datasets Description
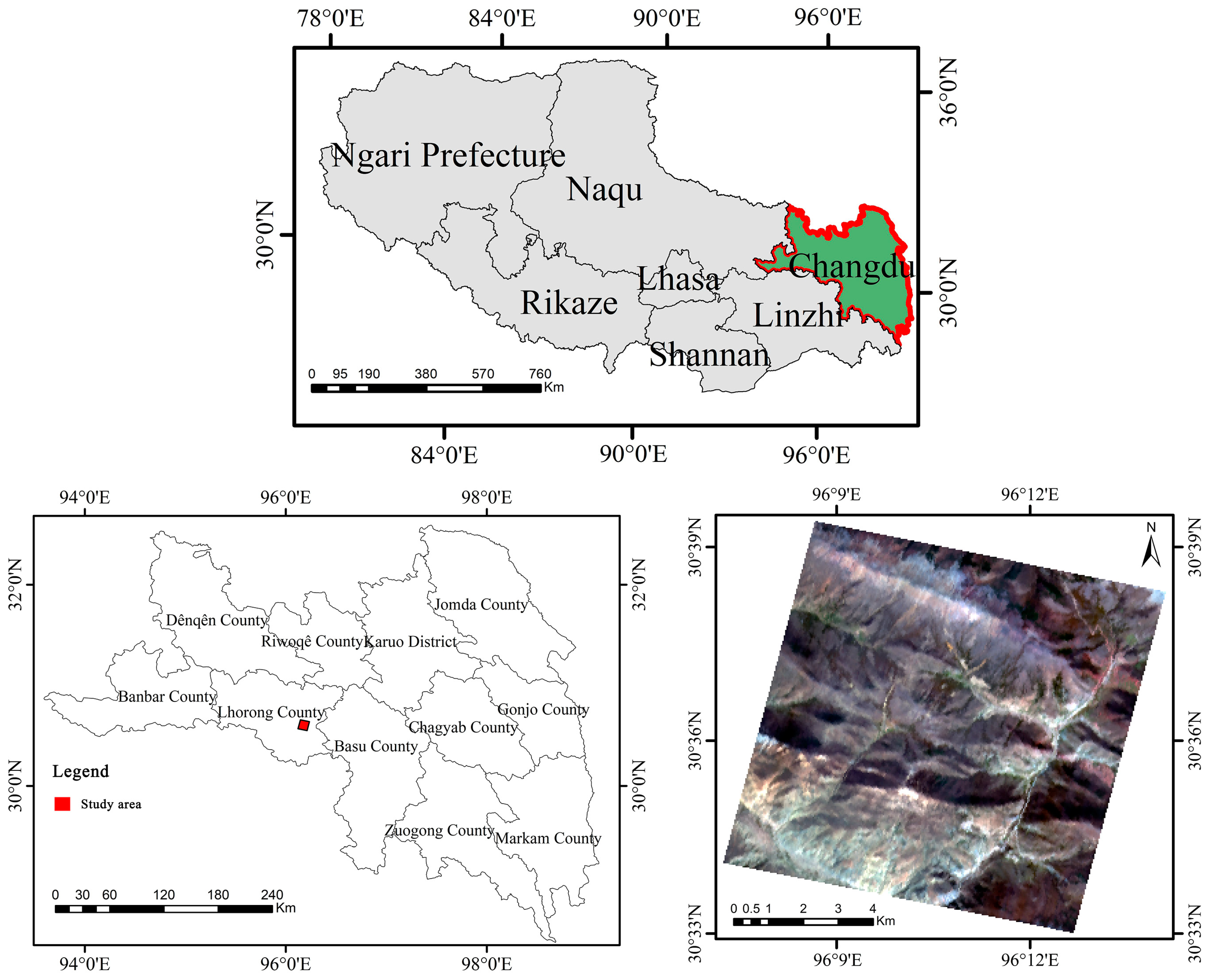
- KY dataset: This hyperspectral lithology dataset was created using ENVI 5.3 software, MATLAB R2021b software, manual interpretation, and field surveys with data from the Zhiyuan-1 remote sensing satellite. The data were collected in the eastern part of Luolong County, Changdu City, Tibet Autonomous Region, China (Figure 5). The image has a spatial resolution of 30 m. The original remote sensing image covers an area of 147 square kilometers, situated between latitudes 30°33′–30°40′N and longitudes 96°07′–96°14′E. The terrain is predominantly bare mountains. The image has spatial dimensions of 300 × 300 and consists of 166 bands. Excluding background pixels, the number of spatial pixels used for the experiment is 89,981. There are six types of real ground objects, mainly consisting of various surface lithologies such as sand and gravel, mudstone, sandstone, quartz sandstone, slate, schist, and phyllite. These represent different surface outcrop lithologies, with detailed information provided in Figure 6. There is a clear imbalance in the number of samples from different categories. The average training pixels account for 4.5% of the labeled pixels.
- Houston_2018 (Hu) dataset: This dataset was collected using an airborne hyperspectral sensor over the University of Houston campus and adjacent urban areas in 2018. The image has spatial dimensions of 601 × 2384 and consists of 50 bands. Excluding background pixels, there are 504,856 spatial pixels used for experiments. There are 20 types of ground objects, mainly buildings, vegetation, and urban ground objects. Detailed information is provided in Figure 6. There is a noticeable imbalance in the number of samples among different classes. The average training pixels account for 1% of labeled pixels.
- Indian Pines (IN) dataset: This dataset was collected using the AVIRIS sensor in the Indian Pines region of northwest India in 1992. The image has spatial dimensions of 145 × 145, consists of 220 bands, and covers a wavelength range of 200–400 nm. The spectral and spatial resolutions are 10 nm and 20 m, respectively. Excluding background pixels, there are 10,249 spatial pixels used for experiments. There are 16 types of ground objects, primarily crops and vegetation, with a small number of buildings and other objects. Detailed information is provided in Figure 6. Due to the unavailability of 20 bands, the experiment only utilizes the remaining 200 bands out of the total 220 for research. There is a noticeable imbalance in the number of samples among different classes. The average training pixels account for 11.59% of labeled pixels.
- Salinas Valley (SV) dataset: This dataset was collected using the AVIRIS sensor in Salinas Valley, California, USA in 1998. The image has spatial dimensions of 512 × 217, with a total of 224 bands. However, 20 water absorption bands were excluded, leaving 204 bands for hyperspectral image classification experiments. The spatial resolution is 1.7 m. Excluding background pixels, there are 54,129 spatial pixels used for experiments. There are 16 types of ground objects, mainly including vegetables, bare soil, and vineyards. Detailed information is provided in Figure 6. There is no imbalance in the number of samples among different classes. The average training pixels account for 4.3% of labeled pixels.
4.2. Datasets Partitioning Strategy
- First, determine the α parameter and β parameter. The α parameter represents the proportion of training pixels to all pixels in the original hyperspectral image, while the β parameter indicates the number of labeled pixels in each training block. From the above two parameters, we can know that the number of training blocks in each category is . Where i represents the category of each pixel, Fi represents the number of training blocks in the corresponding pixel category , and fi represents the total number of pixels of each category in the original hyperspectral image.
- According to the training pixel ratio α, the original hyperspectral image can be divided into two parts. One part is the training image, and the other part is the verification–test image. There is no overlap between these two images.
- According to the number of labeled pixels β in each training block, the training image is divided into two parts. One part is defined as the training image, which is guaranteed to have labeled pixels, while the other part is defined as the leaked image. Similarly, the verification–test image is divided into a verification image and a test image.
- Divide the acquired training image, leaked image, verification image and test image into blocks of W × H × B size to generate training blocks, leaked blocks, verification blocks and test blocks.
- Finally, the sliding window strategy is used to divide the training patches, verification patches, and test patches from the blocks. These patches constitute the final training set, validation set, and test set.
4.3. Experimental Settings (Evaluation Indicators, Parameter Configuration, and Networkconfiguration)
4.4. Experimental Results and Analysis
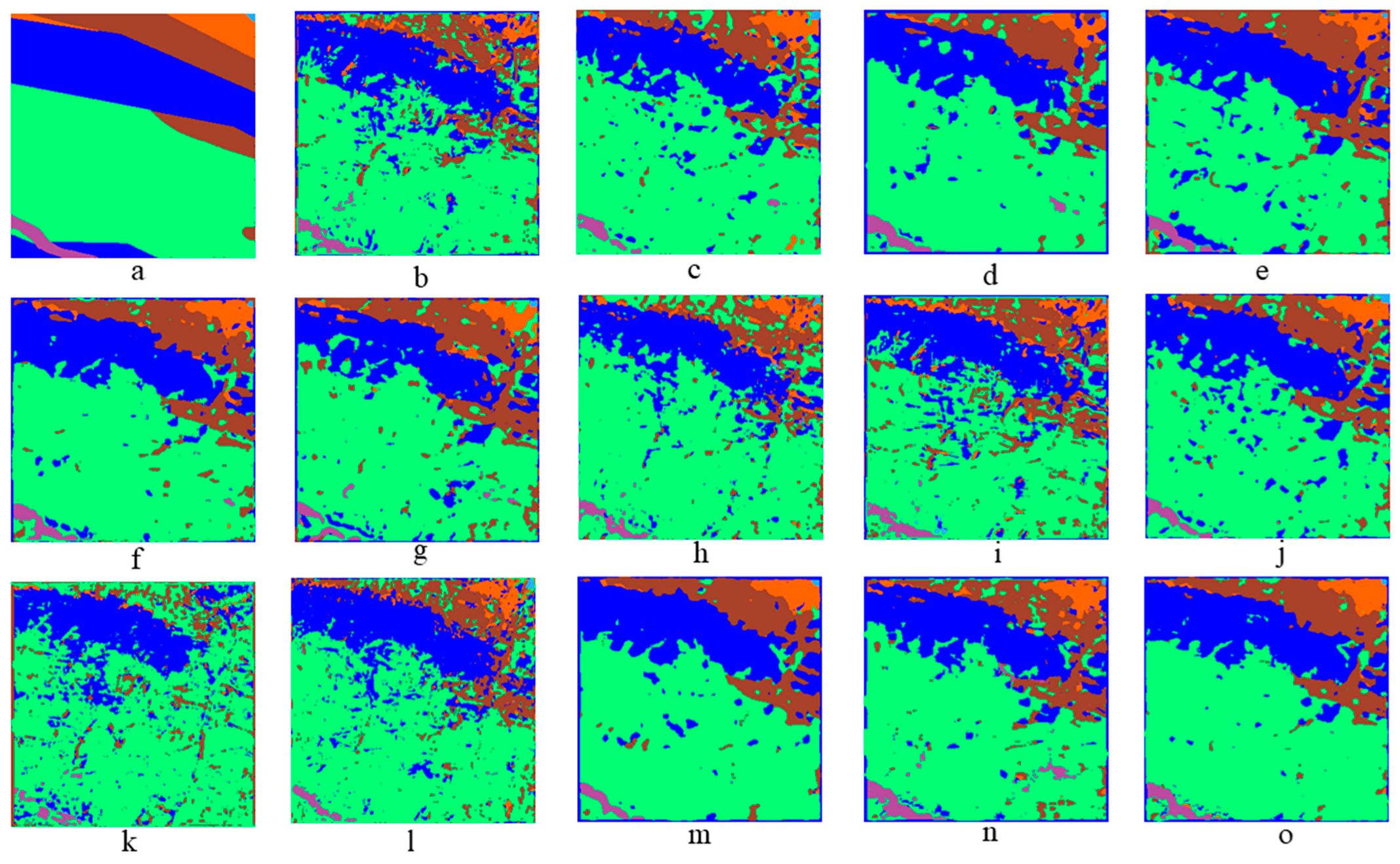
4.4.1. Classification Results of KY Dataset
4.4.2. Classification Results of Hu Dataset
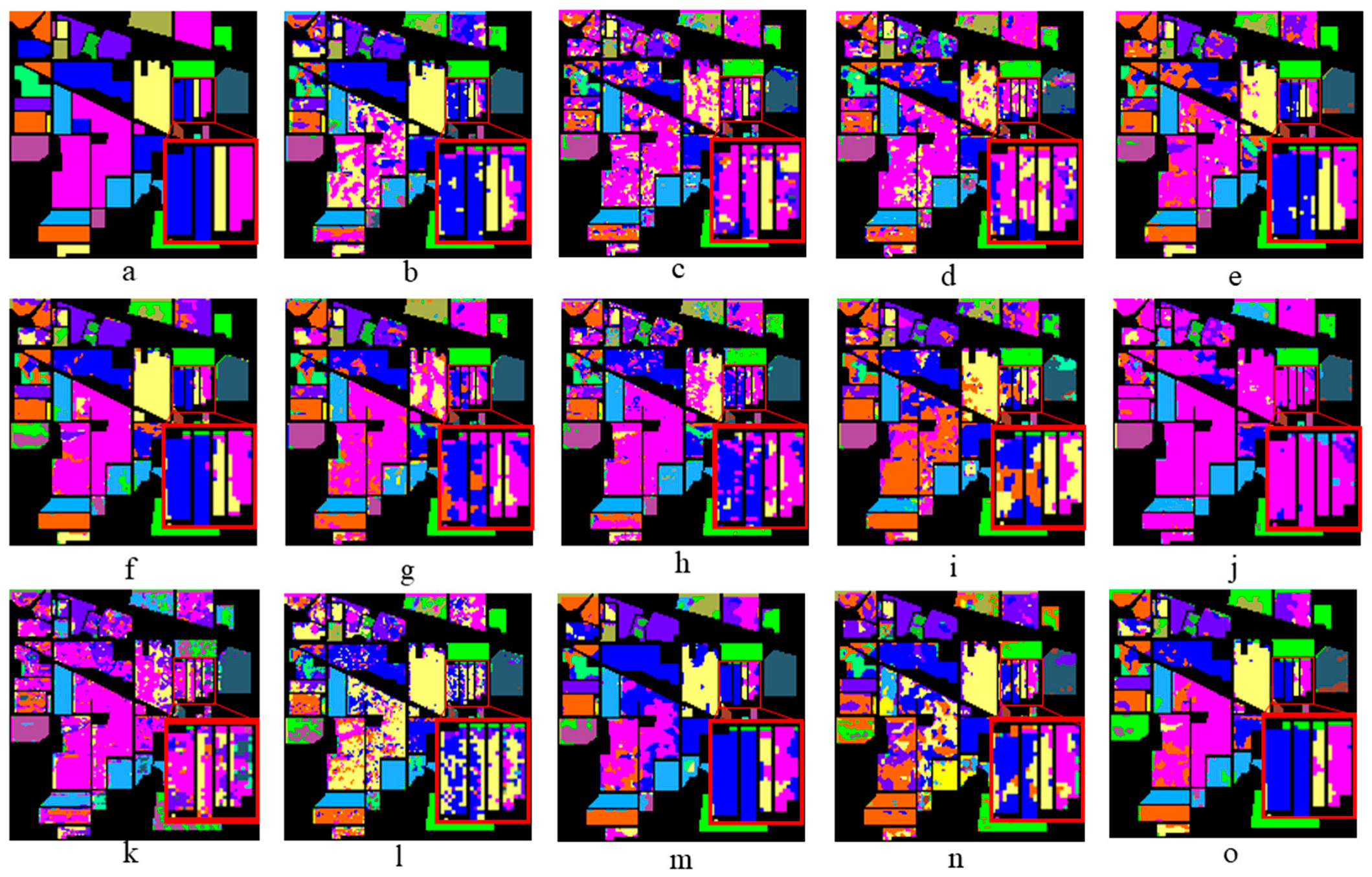
4.4.3. Classification Results of IN Dataset
4.4.4. Classification Results of SV Dataset
5. Discussion
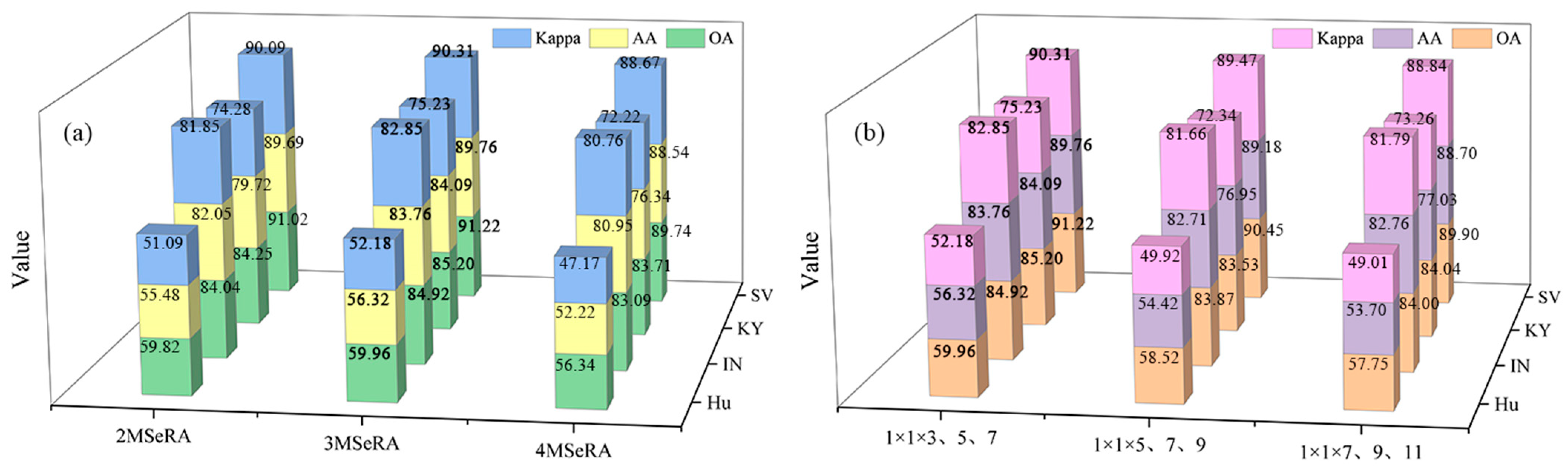
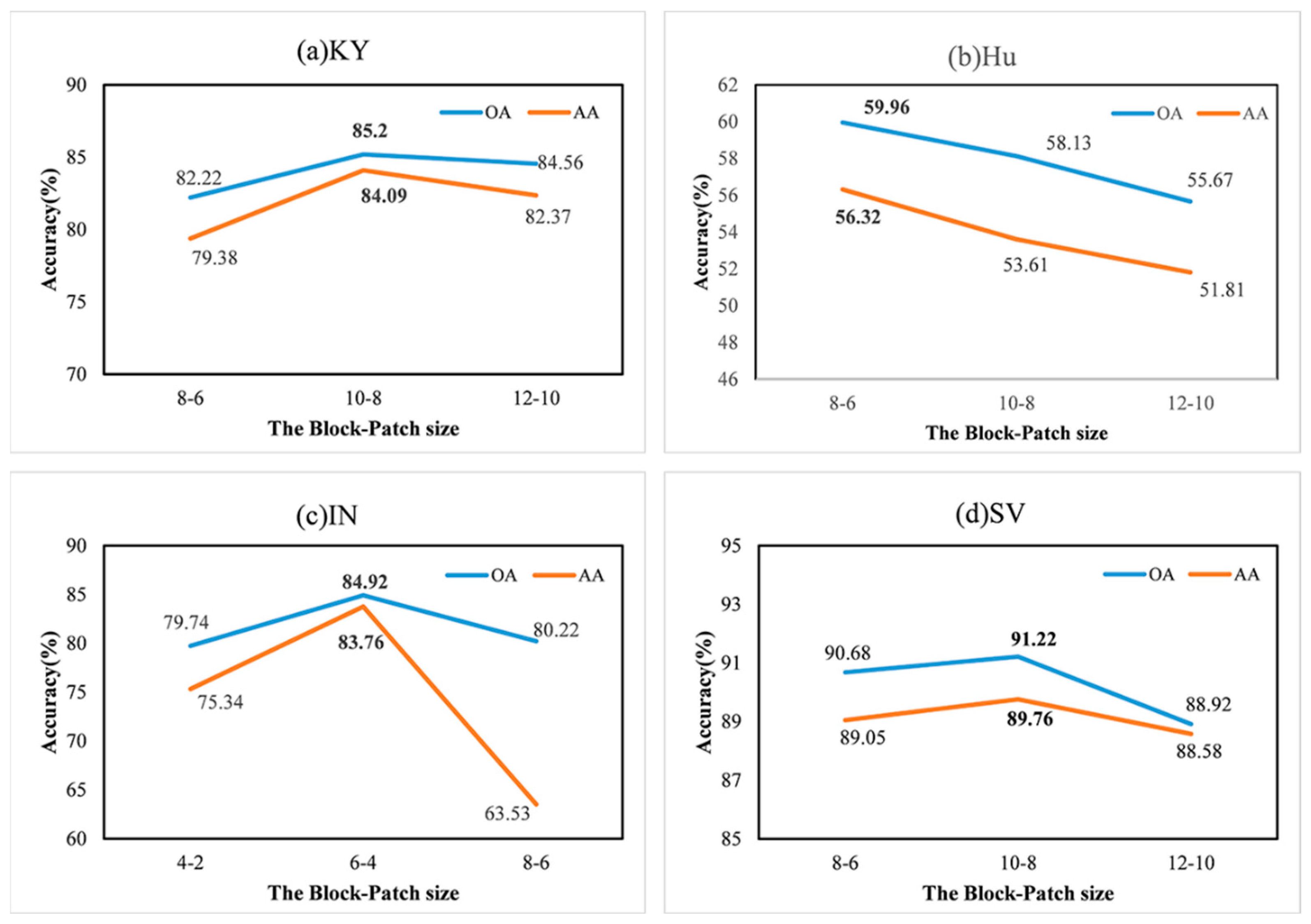
5.1. Effect of Block-Patch Size
5.2. Impact of the Number of Labeled Training Pixels
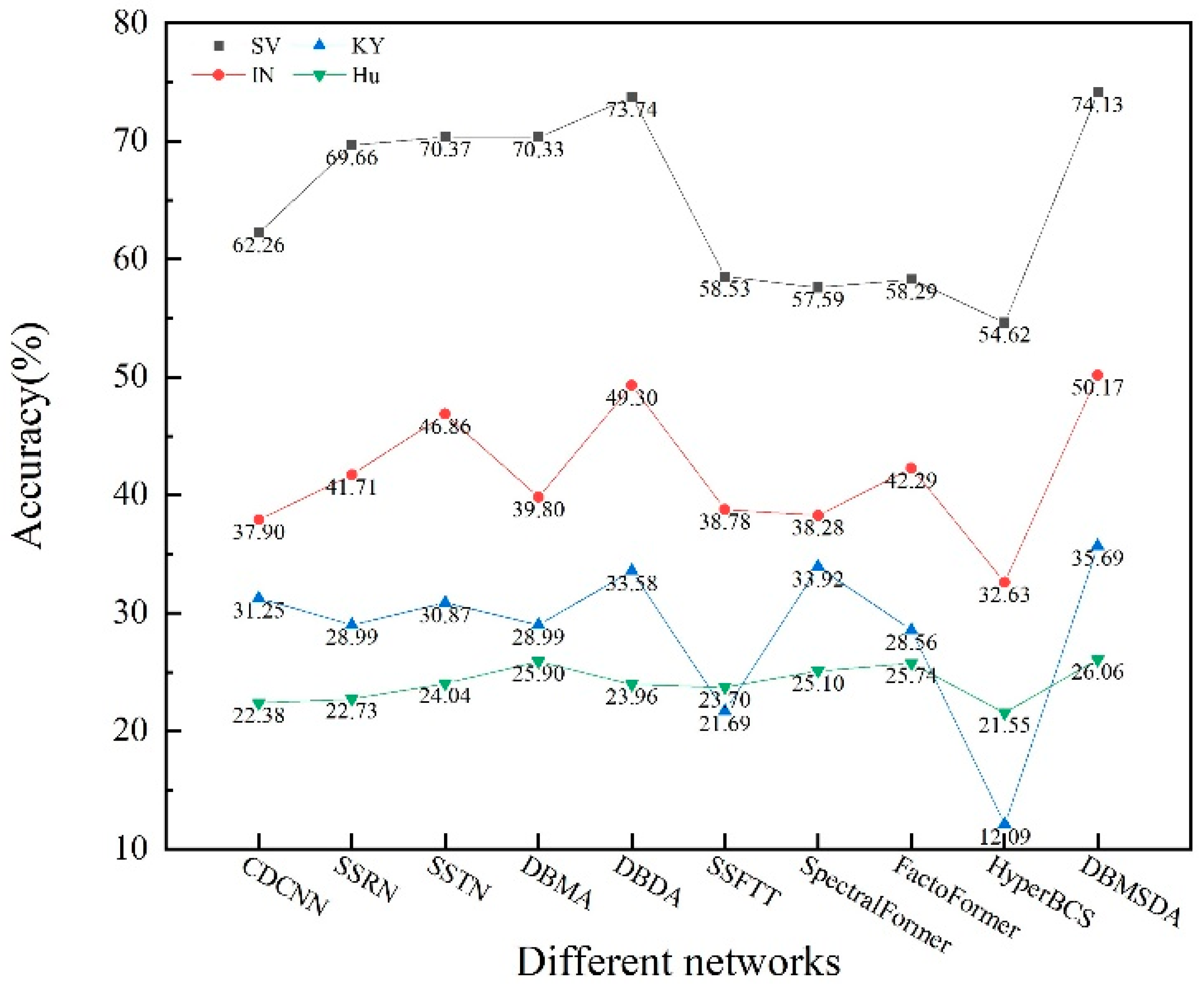
5.3. Classification Results of Networks in Minimal Sample Data
5.4. Impact of Different Network Branches and Module Combinations
5.5. Time Cost Comparison
5.6. The Effect of Having or Not Having a Dataset Segmentation Strategy
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tong, Q.; Zhang, B.; Zhang, L. Current progress of hyperspectral remote sensing in China. J. Remote Sens. 2016, 20, 689–707. [Google Scholar]
- Meyer, J.; Kokaly, R.; Holley, E. Hyperspectral remote sensing of white mica: A review of imaging and point-based spectrometer studies for mineral resources, with spectrometer design considerations. Remote Sens. Environ. 2022, 275, 113000. [Google Scholar] [CrossRef]
- Nalepa, J.; Antoniak, M.; Myller, M.; Lorenzo, P.; Marcinkiewicz, M. Towards resource-frugal deep convolutional neural networks for hyperspectral image segmentation. Microprocess. Microsyst. 2020, 73, 102994. [Google Scholar] [CrossRef]
- Kuras, A.; Brell, M.; Liland, K.; Burud, I. Multitemporal Feature-Level Fusion on Hyperspectral and LiDAR Data in the Urban Environment. Remote Sens. 2023, 15, 632. [Google Scholar] [CrossRef]
- Yang, B.; Wang, S.; Li, S.; Zhou, B.; Zhao, F.; Ali, F.; He, H. Research and application of UAV-based hyperspectral remote sensing for smart city construction. Cogn. Robot. 2022, 2, 255–266. [Google Scholar] [CrossRef]
- Arroyo-Mora, J.; Kalacska, M.; Inamdar, D.; Soffer, R.; Lucanus, O.; Gorman, J.; Naprstek, T.; Schaaf, E.; Ifimov, G.; Elmer, K.; et al. Implementation of a UAV–Hyperspectral Pushbroom Imager for Ecological Monitoring. Drones 2019, 3, 12. [Google Scholar] [CrossRef]
- Liu, H.; Wu, K.; Xu, H.; Xu, Y. Lithology Classification Using TASI Thermal Infrared Hyperspectral Data with Convolutional Neural Networks. Remote Sens. 2021, 13, 3117. [Google Scholar] [CrossRef]
- Ye, B.; Tian, S.; Cheng, Q.; Ge, Y. Application of Lithological Mapping Based on Advanced Hyperspectral Imager (AHSI) Imagery Onboard Gaofen-5 (GF-5) Satellite. Remote Sens. 2020, 12, 3990. [Google Scholar] [CrossRef]
- Lin, N.; Fu, J.; Jiang, R.; Li, G.; Yang, Q. Lithological Classification by Hyperspectral Images Based on a Two-Layer XGBoost Model, Combined with a Greedy Algorithm. Remote Sens. 2023, 15, 3764. [Google Scholar] [CrossRef]
- Zou, L.; Zhu, X.; Wu, C.; Liu, Y.; Qu, L. Spectral–Spatial Exploration for Hyperspectral Image Classification via the Fusion of Fully Convolutional Networks. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 659–674. [Google Scholar] [CrossRef]
- Qu, L.; Zhu, X.; Zheng, J.; Zou, L. Triple-Attention-Based Parallel Network for Hyperspectral Image Classification. Remote Sens. 2021, 13, 324. [Google Scholar] [CrossRef]
- Ibañez, D.; Fernandez-Beltran, R.; Pla, F.; Yokoya, N. Masked Auto-Encoding Spectral–Spatial Transformer for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5542614. [Google Scholar] [CrossRef]
- Li, N.; Wang, Z. Spatial Attention Guided Residual Attention Network for Hyperspectral Image Classification. IEEE Access 2022, 10, 9830–9847. [Google Scholar] [CrossRef]
- Tan, Y.; Lu, L.; Bruzzone, L.; Guan, R.; Chang, Z.; Yang, C. Hyperspectral Band Selection for Lithologic Discrimination and Geological Mapping. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 471–486. [Google Scholar] [CrossRef]
- Zhong, Z.; Li, Y.; Ma, L.; Li, J.; Zheng, W. Spectral–Spatial Transformer Network for Hyperspectral Image Classification: A Factorized Architecture Search Framework. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
- Mei, X.; Pan, E.; Ma, Y.; Dai, X.; Huang, J.; Fan, F.; Du, Q.; Zheng, H.; Ma, J. Spectral-Spatial Attention Networks for Hyperspectral Image Classification. Remote Sens. 2019, 11, 963. [Google Scholar] [CrossRef]
- Li, R.; Zheng, S.; Duan, C.; Yang, Y.; Wang, X. Classification of Hyperspectral Image Based on Double-Branch Dual-Attention Mechanism Network. Remote Sens. 2020, 12, 582. [Google Scholar] [CrossRef]
- Liu, Q.; Xiao, L.; Yang, J.; Chan, J. Content-Guided Convolutional Neural Network for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2020, 58, 6124–6137. [Google Scholar] [CrossRef]
- Hong, D.; Han, Z.; Yao, J.; Gao, L.; Zhang, B.; Plaza, A.; Chanussot, J. SpectralFormer: Rethinking Hyperspectral Image Classification with Transformers. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5518615. [Google Scholar] [CrossRef]
- Melgani, F.; Bruzzone, L. Classification of hyperspectral remote sensing images with support vector machines. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1778–1790. [Google Scholar] [CrossRef]
- Li, J.; Bioucas-Dias, J.; Plaza, A. Semisupervised hyperspectral image segmentation using multinomial logistic regression with active learning. IEEE Trans. Geosci. Remote Sens. 2010, 48, 4085–4098. [Google Scholar] [CrossRef]
- Du, B.; Zhang, L. Target detection based on a dynamic subspace. Pattern Recog. 2014, 47, 344–358. [Google Scholar] [CrossRef]
- He, L.; Li, J.; Liu, C.; Li, S. Recent Advances on Spectral–Spatial Hyperspectral Image Classification: An Overview and New Guidelines. IEEE Trans. Geosci. Remote Sens. 2018, 56, 1579–1597. [Google Scholar] [CrossRef]
- Song, T.; Wang, Y.; Gao, C.; Chen, H.; Li, J. MSLAN: A Two-Branch Multidirectional Spectral–Spatial LSTM Attention Network for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5528814. [Google Scholar] [CrossRef]
- Sun, L.; Zhao, G.; Zheng, Y.; Wu, Z. Spectral–Spatial Feature Tokenization Transformer for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5522214. [Google Scholar] [CrossRef]
- Zou, J.; He, W.; Zhang, H. LESSFormer: Local-Enhanced Spectral-Spatial Transformer for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5535416. [Google Scholar] [CrossRef]
- Yu, H.; Xu, Z.; Zheng, K.; Hong, D.; Yang, H.; Song, M. MSTNet: A Multilevel Spectral–Spatial Transformer Network for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5532513. [Google Scholar] [CrossRef]
- Peng, Y.; Ren, J.; Wang, J.; Shi, M. Spectral-Swin Transformer with Spatial Feature Extraction Enhancement for Hyperspectral Image Classification. Remote Sens 2023, 15, 2696. [Google Scholar] [CrossRef]
- Zou, L.; Zhang, Z.; Du, H.; Lei, M.; Xue, Y.; Wang, Z. DA-IMRN: Dual-Attention-Guided Interactive Multi-Scale Residual Network for Hyperspectral Image Classification. Remote Sens. 2022, 14, 530. [Google Scholar] [CrossRef]
- Tao, H. Smoke Recognition in Satellite Imagery via an Attention Pyramid Network with Bidirectional Multilevel Multigranularity Feature Aggregation and Gated Fusion. IEEE Internet Things J. 2024, 11, 14047–14057. [Google Scholar] [CrossRef]
- Tao, H.; Duan, Q.; Lu, M.; Hu, Z. Learning discriminative feature representation with pixel-level supervision for forest smoke recognition. Pattern Recognit. 2023, 143, 109761. [Google Scholar] [CrossRef]
- Song, W.; Li, S.; Fang, L.; Lu, T. Hyperspectral Image Classification with Deep Feature Fusion Network. IEEE Trans. Geosci. Remote Sens. 2018, 56, 3173–3184. [Google Scholar] [CrossRef]
- Ren, S.; Zhou, D.; He, S.; Feng, J.; Wang, X. Shunted self-attention via multi-scale token aggregation. In Proceedings of the IEEE/CVF Computer Vision and Pattern Recognition Conference (CVPR), New Orleans, LA, USA, 18–24 June 2022; pp. 10843–10852. [Google Scholar]
- Qiao, X.; Roy, S.; Huang, W. Multiscale neighborhood attention transformer with optimized spatial pattern for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5523815. [Google Scholar] [CrossRef]
- Shi, C.; Yue, S.; Wang, L. A Dual-Branch Multiscale Transformer Network for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5504520. [Google Scholar] [CrossRef]
- Feng, H.; Wang, Y.; Li, Z.; Zhang, N.; Zhang, Y.; Gao, Y. Information Leakage in Deep Learning-Based Hyperspectral Image Classification: A Survey. Remote Sens. 2023, 15, 3793. [Google Scholar] [CrossRef]
- Zhong, Z.; Li, J.; Luo, Z.; Chapman, M. Spectral–Spatial Residual Network for Hyperspectral Image Classification: A 3-D Deep Learning Framework. IEEE Trans. Geosci. Remote Sens. 2018, 56, 847–858. [Google Scholar] [CrossRef]
- Hang, R.; Li, Z.; Liu, Q.; Ghamisi, P.; Bhattacharyya, S. Hyperspectral Image Classification with Attention-Aided CNNs. IEEE Trans. Geosci. Remote Sens. 2021, 59, 2281–2293. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, D.; Gao, D.; Shi, G. S³Net: Spectral–Spatial–Semantic Network for Hyperspectral Image Classification with the Multiway Attention Mechanism. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5505317. [Google Scholar]
- Ma, W.; Yang, Q.; Wu, Y.; Zhao, W.; Zhang, X. Double-Branch Multi-Attention Mechanism Network for Hyperspectral Image Classification. Remote Sens. 2019, 11, 1307. [Google Scholar] [CrossRef]
- Liang, J.; Zhou, J.; Qian, Y.; Wen, L.; Bai, X.; Gao, Y. On the Sampling Strategy for Evaluation of Spectral-Spatial Methods in Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 862–880. [Google Scholar] [CrossRef]
- Li, X.; Ding, M.; Pižurica, A. Spectral Feature Fusion Networks with Dual Attention for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Cao, X.; Liu, Z.; Li, X.; Xiao, Q.; Feng, J.; Jiao, L. Nonoverlapped Sampling for Hyperspectral Imagery: Performance Evaluation and a Cotraining-Based Classification Strategy. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Cao, X.; Lu, H.; Ren, M.; Jiao, L. Non-overlapping classification of hyperspectral imagery with superpixel segmentation. Appl. Soft Comput. 2019, 83, 105630. [Google Scholar] [CrossRef]
- Wang, W.; Dou, S.; Jiang, Z.; Sun, L. A Fast Dense Spectral–Spatial Convolution Network Framework for Hyperspectral Images Classification. Remote Sens. 2018, 10, 1068. [Google Scholar] [CrossRef]
- Shi, H.; Cao, G.; Ge, Z.; Zhang, Y.; Fu, P. Double-Branch Network with Pyramidal Convolution and Iterative Attention for Hyperspectral Image Classification. Remote Sens. 2021, 13, 1043. [Google Scholar] [CrossRef]
- Huang, G.; Liu, Z.; Maaten, L.; Weinberger, K. Densely Connected Convolutional Networks. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 2261–2269. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Fu, J.; Liu, J.; Tian, H.; Li, Y.; Bao, Y.; Fang, Z.; Lu, H. Dual Attention Network for Scene Segmentation. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 3141–3149. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Proceedings of the Annual Conference on Neural Information Processing Systems 2017, Long Beach, CA, USA, 4–9 December 2017; Volume 30, pp. 5998–6008. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An image is worth 16x16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Li, X.; Liu, B.; Zhang, K.; Chen, H.; Cao, W.; Liu, W.; Tao, D. Multi-view learning for hyperspectral image classification: An overview. Neurocomputing 2022, 500, 499–517. [Google Scholar] [CrossRef]
- Lee, H.; Kwon, H. Going Deeper with Contextual CNN for Hyperspectral Image Classification. IEEE Trans. Image Process. 2017, 26, 4843–4855. [Google Scholar] [CrossRef] [PubMed]
- Meng, Z.; Zhao, F.; Liang, M.; Xie, W. Deep Residual Involution Network for Hyperspectral Image Classification. Remote Sens. 2021, 13, 3055. [Google Scholar] [CrossRef]
- Mohamed, S.; Haghighat, M.; Fernando, T.; Sridharan, S.; Fookes, C.; Moghadam, P. FactoFormer: Factorized Hyperspectral Transformers with Self-Supervised Pretraining. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5501614. [Google Scholar] [CrossRef]
- Luo, J.; He, Z.; Lin, H.; Wu, H. Biscale Convolutional Self-Attention Network for Hyperspectral Coastal Wetlands Classification. IEEE Geosci. Remote Sens. Lett. 2024, 21, 6002705. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, X.; Wen, X.; Li, X.; Dong, H.; Zang, S. Learning a 3-D-CNN and Convolution Transformers for Hyperspectral Image Classification. IEEE Geosci. Remote Sens. Lett. 2024, 21, 5504505. [Google Scholar] [CrossRef]




| Network Name | Backbone Structure |
|---|---|
| CDCNN | 2D-CNN + ResNet |
| SSRN | 3D-CNN + ResNet |
| SSTN | 3D-CNN + Transformer |
| DBMA | Parallel network + CBAM attention + DenseNet |
| DBDA | Parallel network + Self − attention + DenseNet |
| DRIN | Involution + ResNet |
| SSFTT | 3D-CNN + Transformer + Gaussian − weighted feature tokenizer |
| SpectralFormer | CAF + GSE + Transformer, Based on ViT |
| FactoFormer | Factorized Transformers, Based on ViT |
| HyperBCS | 3D-CNN + BSAM + CSM |
| 3DCT | 3D-CNN + ViT |
| DBMSDA | Parallel network + Self-attention + DenseNet + multi-scale feature extraction |
| Method | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Class | CDCNN | SSRN | SSTN | DBMA | DBDA | DRIN | SSFTT | Spectral Former | Facto Former | Hyper BCS | 3DCT | DBMSDA (sub-1) | DBMSDA (sub-2) | DBMSDA |
| C1 | 53.63 | 64.41 | 73.33 | 72.35 | 73.17 | 65.58 | 59.83 | 54.28 | 55.49 | 32.32 | 61.59 | 74.92 | 71.85 | 74.45 |
| C2 | 69.84 | 68.99 | 67.70 | 74.13 | 73.77 | 67.11 | 61.93 | 68.92 | 68.63 | 54.90 | 63.31 | 75.56 | 69.56 | 76.35 |
| C3 | 47.46 | 53.14 | 66.36 | 57.77 | 63.62 | 56.19 | 51.34 | 45.64 | 57.95 | 4.55 | 36.36 | 64.30 | 63.17 | 67.72 |
| C4 | 82.39 | 89.05 | 89.78 | 89.70 | 93.19 | 92.46 | 91.65 | 84.12 | 88.13 | 83.74 | 87.48 | 92.14 | 91.59 | 93.73 |
| C5 | 45.51 | 54.21 | 66.31 | 72.91 | 69.61 | 63.36 | 54.34 | 38.54 | 70.59 | 52.94 | 47.06 | 62.23 | 69.81 | 74.07 |
| C6 | 91.67 | 50.00 | 75.00 | 66.67 | 100.00 | 100.00 | 50.00 | 50.00 | 100.00 | 100.00 | 100.00 | 100.00 | 75.00 | 100.00 |
| OA | 73.44 | 78.49 | 80.34 | 81.73 | 83.83 | 80.27 | 77.31 | 74.03 | 77.23 | 65.96 | 75.12 | 83.89 | 81.59 | 85.20 |
| AA | 65.08 | 63.30 | 73.08 | 72.25 | 78.89 | 74.12 | 61.51 | 56.91 | 73.46 | 54.74 | 65.97 | 78.18 | 73.49 | 84.09 |
| Kappa | 0.60 | 0.64 | 0.67 | 0.70 | 0.73 | 0.66 | 0.61 | 0.56 | 0.62 | 0.40 | 0.58 | 0.73 | 0.69 | 0.75 |
| Method | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Class | CDCNN | SSRN | SSTN | DBMA | DBDA | DRIN | SSFTT | Spectral Former | Facto Former | Hyper BCS | 3DCT | DBMSDA (sub-1) | DBMSDA (sub-2) | DBMSDA |
| C1 | 44.09 | 51.79 | 46.85 | 57.01 | 55.90 | 60.25 | 55.40 | 32.65 | 28.34 | 39.95 | 52.16 | 52.36 | 51.68 | 52.40 |
| C2 | 63.89 | 63.26 | 61.90 | 67.31 | 68.25 | 61.34 | 72.90 | 68.11 | 66.03 | 62.58 | 66.91 | 68.60 | 60.98 | 71.10 |
| C3 | 88.13 | 58.54 | 75.29 | 89.17 | 93.69 | 61.36 | 62.26 | 94.91 | 84.02 | 81.45 | 86.39 | 77.64 | 86.70 | 93.08 |
| C4 | 50.01 | 46.06 | 45.67 | 58.62 | 58.01 | 67.41 | 63.25 | 48.00 | 49.38 | 37.23 | 64.32 | 52.00 | 50.56 | 61.22 |
| C5 | 29.44 | 21.28 | 31.11 | 37.51 | 43.84 | 25.70 | 36.20 | 23.94 | 20.43 | 14.39 | 35.12 | 35.18 | 36.73 | 35.28 |
| C6 | 40.58 | 35.75 | 40.32 | 41.29 | 46.63 | 48.20 | 30.93 | 33.75 | 41.57 | 27.17 | 39.38 | 43.63 | 42.41 | 47.63 |
| C7 | 33.41 | 33.81 | 31.65 | 34.09 | 34.55 | 25.45 | 22.05 | 31.19 | 32.73 | 28.73 | 31.93 | 42.78 | 30.63 | 36.99 |
| C8 | 59.69 | 41.26 | 53.18 | 66.25 | 67.40 | 63.39 | 59.96 | 58.61 | 62.33 | 50.03 | 57.56 | 57.71 | 55.40 | 71.02 |
| C9 | 82.16 | 84.21 | 83.06 | 85.15 | 86.87 | 62.68 | 79.97 | 82.20 | 82.94 | 82.25 | 84.40 | 86.43 | 85.14 | 85.96 |
| C10 | 25.23 | 21.61 | 24.85 | 23.74 | 24.92 | 30.14 | 27.28 | 23.87 | 22.32 | 22.94 | 25.47 | 28.45 | 26.05 | 29.97 |
| C11 | 30.78 | 27.18 | 29.53 | 31.57 | 36.68 | 33.47 | 31.95 | 23.05 | 24.97 | 23.88 | 29.19 | 32.56 | 30.84 | 34.53 |
| C12 | 3.49 | 0.93 | 4.04 | 2.08 | 1.79 | 1.95 | 1.57 | 3.67 | 2.54 | 1.28 | 1.30 | 2.88 | 2.49 | 2.11 |
| C13 | 34.36 | 38.51 | 44.74 | 49.25 | 49.09 | 60.48 | 41.10 | 34.65 | 43.57 | 43.67 | 35.72 | 59.50 | 40.52 | 54.40 |
| C14 | 36.76 | 28.57 | 52.04 | 48.72 | 54.95 | 4.35 | 39.72 | 27.99 | 33.38 | 30.76 | 36.19 | 51.35 | 50.70 | 51.25 |
| C15 | 47.96 | 43.61 | 47.23 | 65.03 | 64.02 | 29.39 | 66.41 | 28.51 | 43.70 | 32.60 | 66.78 | 56.49 | 52.89 | 70.70 |
| C16 | 30.29 | 27.85 | 36.11 | 47.79 | 51.71 | 34.26 | 28.75 | 25.20 | 26.33 | 21.06 | 37.85 | 48.20 | 37.70 | 51.08 |
| C17 | 55.55 | 78.88 | 71.86 | 80.66 | 76.50 | 50.00 | 52.90 | 28.67 | 55.98 | 41.70 | 64.05 | 90.34 | 74.73 | 89.70 |
| C18 | 48.75 | 41.04 | 58.92 | 64.40 | 66.02 | 36.00 | 24.86 | 38.98 | 30.05 | 23.36 | 30.57 | 64.17 | 54.79 | 73.65 |
| C19 | 40.91 | 45.82 | 65.57 | 63.44 | 62.90 | 22.30 | 30.89 | 30.69 | 41.29 | 22.97 | 31.95 | 61.74 | 61.09 | 57.97 |
| C20 | 42.58 | 43.28 | 51.06 | 54.09 | 56.82 | 50.92 | 37.30 | 49.13 | 29.49 | 43.70 | 41.67 | 57.51 | 56.53 | 56.40 |
| OA | 52.17 | 50.09 | 53.36 | 57.01 | 58.95 | 48.93 | 53.13 | 49.83 | 51.02 | 48.68 | 53.30 | 58.13 | 54.53 | 59.96 |
| AA | 44.40 | 41.66 | 47.74 | 53.35 | 55.03 | 42.45 | 43.28 | 39.38 | 41.07 | 36.58 | 45.95 | 53.47 | 49.43 | 56.32 |
| Kappa | 0.42 | 0.39 | 0.44 | 0.49 | 0.51 | 0.41 | 0.44 | 0.39 | 0.41 | 0.36 | 0.43 | 0.50 | 0.45 | 0.52 |
| Method | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Class | CDCNN | SSRN | SSTN | DBMA | DBDA | DRIN | SSFTT | Spectral Former | Facto Former | Hyper BCS | 3DCT | DBMSDA (sub-1) | DBMSDA (sub-2) | DBMSDA |
| C1 | 33.33 | 45.14 | 40.14 | 33.47 | 81.67 | 39.45 | 18.06 | 15.19 | 23.96 | 0.00 | 11.67 | 77.92 | 52.08 | 88.33 |
| C2 | 64.32 | 69.79 | 76.87 | 72.34 | 78.32 | 71.31 | 47.74 | 65.10 | 73.11 | 29.49 | 57.98 | 80.90 | 69.75 | 80.45 |
| C3 | 63.10 | 64.31 | 74.50 | 71.28 | 75.74 | 70.02 | 53.00 | 60.84 | 66.89 | 27.05 | 43.74 | 77.83 | 67.78 | 79.05 |
| C4 | 48.48 | 31.26 | 50.75 | 50.31 | 54.29 | 50.53 | 26.56 | 42.54 | 56.98 | 17.25 | 25.13 | 48.45 | 51.74 | 53.67 |
| C5 | 66.78 | 70.94 | 72.95 | 70.42 | 73.25 | 68.56 | 68.34 | 55.72 | 63.55 | 65.98 | 64.56 | 75.53 | 72.69 | 73.60 |
| C6 | 83.33 | 89.39 | 83.62 | 86.73 | 89.10 | 77.98 | 81.43 | 80.39 | 85.40 | 58.56 | 88.15 | 93.41 | 83.33 | 92.85 |
| C7 | 25.00 | 100.00 | 100.00 | 100.00 | 100.00 | 83.33 | 58.33 | 38.89 | 37.50 | 0.00 | 20.00 | 100.00 | 100.00 | 100.00 |
| C8 | 90.62 | 94.82 | 94.31 | 94.09 | 97.62 | 95.18 | 88.64 | 82.36 | 96.02 | 83.88 | 94.29 | 99.00 | 96.18 | 99.67 |
| C9 | 66.67 | 70.83 | 54.17 | 58.33 | 83.33 | 75.00 | 62.50 | 33.44 | 56.25 | 30.00 | 20.00 | 58.33 | 66.67 | 79.17 |
| C10 | 60.06 | 71.55 | 71.58 | 74.25 | 77.41 | 72.53 | 52.71 | 68.98 | 68.65 | 37.70 | 60.24 | 90.11 | 73.84 | 87.77 |
| C11 | 76.87 | 78.69 | 79.27 | 83.93 | 89.59 | 67.50 | 67.72 | 67.28 | 74.26 | 55.07 | 74.19 | 86.27 | 84.88 | 89.17 |
| C12 | 46.49 | 55.02 | 63.21 | 64.99 | 73.42 | 59.11 | 32.42 | 53.68 | 57.35 | 22.69 | 36.93 | 76.01 | 66.34 | 75.23 |
| C13 | 88.79 | 85.85 | 89.15 | 84.72 | 90.08 | 87.90 | 81.35 | 76.60 | 86.01 | 55.39 | 84.23 | 90.08 | 90.08 | 90.08 |
| C14 | 87.55 | 90.69 | 94.04 | 91.71 | 92.59 | 89.44 | 88.31 | 82.38 | 88.05 | 85.09 | 93.39 | 92.20 | 92.57 | 93.42 |
| C15 | 70.30 | 71.07 | 61.87 | 63.98 | 75.50 | 63.75 | 46.63 | 51.13 | 65.02 | 17.92 | 44.07 | 74.91 | 68.02 | 74.98 |
| C16 | 75.48 | 86.67 | 63.37 | 74.48 | 74.72 | 84.17 | 59.72 | 70.60 | 46.90 | 37.24 | 74.14 | 84.72 | 66.31 | 86.94 |
| OA | 71.01 | 75.03 | 77.45 | 77.77 | 82.76 | 72.39 | 62.32 | 75.01 | 73.40 | 47.60 | 66.39 | 84.26 | 77.73 | 84.92 |
| AA | 65.45 | 73.50 | 73.11 | 73.44 | 81.66 | 72.23 | 58.34 | 66.09 | 65.36 | 38.95 | 55.79 | 81.60 | 75.11 | 83.76 |
| Kappa | 0.67 | 0.72 | 0.74 | 0.75 | 0.80 | 0.69 | 0.57 | 0.72 | 0.70 | 0.40 | 0.61 | 0.82 | 0.75 | 0.83 |
| Method | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Class | CDCNN | SSRN | SSTN | DBMA | DBDA | DRIN | SSFTT | Spectral Former | Facto Former | Hyper BCS | 3DCT | DBMSDA (sub-1) | DBMSDA (sub-2) | DBMSDA |
| C1 | 85.55 | 96.06 | 95.84 | 95.25 | 95.62 | 94.21 | 91.85 | 84.21 | 82.98 | 100.00 | 90.05 | 97.99 | 97.21 | 97.21 |
| C2 | 80.21 | 88.34 | 89.75 | 88.71 | 90.42 | 85.63 | 84.16 | 79.46 | 57.54 | 72.00 | 83.54 | 95.42 | 89.94 | 93.17 |
| C3 | 77.94 | 93.38 | 94.28 | 90.92 | 94.49 | 84.68 | 77.31 | 81.69 | 69.91 | 57.14 | 82.74 | 96.32 | 91.84 | 95.09 |
| C4 | 91.67 | 95.46 | 92.93 | 97.48 | 92.43 | 86.37 | 90.66 | 90.28 | 79.62 | 65.71 | 89.39 | 91.42 | 92.93 | 93.44 |
| C5 | 86.48 | 83.85 | 87.83 | 82.88 | 86.56 | 91.96 | 87.90 | 81.47 | 85.17 | 92.00 | 89.27 | 85.15 | 86.61 | 84.11 |
| C6 | 97.66 | 97.00 | 97.89 | 97.45 | 96.77 | 98.00 | 93.80 | 95.83 | 88.63 | 81.33 | 93.60 | 95.07 | 95.10 | 95.53 |
| C7 | 83.28 | 88.87 | 88.45 | 86.79 | 88.64 | 87.45 | 84.21 | 84.96 | 82.15 | 84.93 | 89.02 | 93.59 | 88.80 | 91.09 |
| C8 | 84.73 | 85.50 | 86.99 | 86.60 | 91.93 | 89.23 | 85.91 | 84.05 | 82.19 | 90.45 | 85.35 | 95.46 | 88.28 | 94.03 |
| C9 | 90.45 | 86.18 | 98.96 | 97.70 | 98.82 | 94.20 | 94.51 | 89.29 | 88.66 | 81.51 | 92.97 | 99.58 | 97.90 | 99.08 |
| C10 | 73.57 | 80.60 | 82.55 | 81.77 | 83.46 | 81.25 | 79.17 | 75.26 | 77.67 | 53.73 | 79.96 | 82.81 | 80.99 | 83.07 |
| C11 | 71.62 | 74.74 | 75.45 | 72.34 | 78.91 | 79.68 | 78.68 | 65.31 | 71.11 | 41.67 | 73.80 | 85.21 | 79.62 | 81.73 |
| C12 | 82.90 | 83.41 | 81.49 | 83.80 | 86.84 | 79.71 | 87.50 | 79.74 | 70.18 | 81.58 | 84.23 | 89.51 | 82.94 | 89.49 |
| C13 | 82.66 | 81.23 | 82.04 | 81.66 | 83.19 | 82.40 | 85.71 | 79.03 | 84.84 | 52.38 | 82.37 | 82.45 | 83.90 | 82.42 |
| C14 | 80.00 | 83.21 | 84.30 | 84.96 | 82.49 | 81.09 | 71.05 | 80.40 | 72.16 | 68.18 | 81.64 | 84.30 | 84.36 | 82.16 |
| C15 | 58.65 | 80.69 | 76.60 | 72.18 | 82.71 | 52.28 | 66.93 | 61.04 | 66.07 | 9.32 | 55.03 | 85.37 | 69.91 | 83.86 |
| C16 | 80.00 | 88.33 | 89.29 | 86.90 | 87.62 | 87.62 | 88.57 | 78.25 | 84.89 | 84.85 | 79.57 | 94.76 | 85.71 | 90.00 |
| OA | 81.55 | 87.76 | 88.30 | 86.98 | 90.10 | 84.37 | 84.39 | 81.04 | 78.28 | 70.73 | 82.85 | 92.30 | 87.34 | 91.22 |
| AA | 81.71 | 87.30 | 87.79 | 86.71 | 88.80 | 84.74 | 84.24 | 80.64 | 77.73 | 69.79 | 83.28 | 90.90 | 87.25 | 89.76 |
| Kappa | 0.80 | 0.87 | 0.87 | 0.86 | 0.89 | 0.83 | 0.83 | 0.79 | 0.76 | 0.68 | 0.81 | 0.92 | 0.86 | 0.90 |
| Branch | Spectral branch | ✓ | ✓ | |||||
| Spatial branch | ✓ | ✓ | ||||||
| Module | MSeRA | ✓ | ✓ | ✓ | ✓ | |||
| MSaRA | ✓ | |||||||
| Spectral attention | ✓ | ✓ | ✓ | |||||
| Spatial attention | ✓ | ✓ | ✓ | |||||
| Data | KY | 83.9 | 81.6 | 85.2 | 83.7 | 83.7 | 85.2 | 82.6 |
| Hu | 58.1 | 54.5 | 60.0 | 59.7 | 58.6 | 60.0 | 59.1 | |
| IN | 84.3 | 77.7 | 84.9 | 84.1 | 84.1 | 84.9 | 83.1 | |
| SV | 92.3 | 87.3 | 91.2 | 90.7 | 90.6 | 91.2 | 89.5 |
| Methods | KY | Hu | IN | SV | ||||
|---|---|---|---|---|---|---|---|---|
| Train. (m) | Test (s) | Train. (m) | Test (s) | Train. (m) | Test (s) | Train. (m) | Test (s) | |
| CDCNN | 0.36 | 0.07 | 0.26 | 0.51 | 0.25 | 0.02 | 0.26 | 0.05 |
| SSRN | 2.70 | 0.20 | 0.49 | 0.94 | 3.40 | 0.05 | 2.10 | 0.20 |
| SSTN | 0.62 | 0.08 | 0.50 | 1.10 | 0.44 | 0.04 | 0.43 | 0.08 |
| DBMA | 4.05 | 0.38 | 0.73 | 1.39 | 1.24 | 0.08 | 3.13 | 0.37 |
| DBDA | 4.06 | 0.32 | 0.76 | 1.32 | 1.19 | 0.07 | 3.14 | 0.33 |
| DRIN | 0.51 | 0.09 | 0.38 | 1.10 | 0.32 | 0.03 | 0.36 | 0.08 |
| SSFTT | 0.48 | 0.06 | 0.31 | 0.73 | 0.26 | 0.02 | 0.35 | 0.05 |
| SpectralFormer | 1.68 | 0.15 | 0.62 | 1.27 | 1.53 | 0.08 | 1.33 | 0.15 |
| FactoFormer | 2.16 | 0.16 | 0.88 | 1.57 | 1.78 | 0.08 | 1.65 | 0.16 |
| HyperBCS | 655.20 | 74.00 | 19.20 | 66.00 | 24.58 | 2.00 | 656.52 | 105.00 |
| 3DCT | 0.66 | 0.07 | 0.37 | 0.64 | 0.31 | 0.22 | 0.47 | 0.08 |
| DBMSDA (sub-1) | 172.82 | 5.60 | 4.17 | 9.08 | 11.66 | 0.50 | 170.68 | 7.42 |
| DBMSDA (sub-2) | 0.26 | 0.06 | 0.20 | 0.53 | 0.17 | 0.02 | 0.19 | 0.05 |
| DBMSDA | 172.89 | 5.62 | 4.23 | 9.22 | 11.64 | 0.51 | 174.07 | 7.59 |
| Class | Dataset Segmentation Strategy | No Dataset Segmentation Strategy |
|---|---|---|
| C1 | 77.44 | 98.70 |
| C2 | 70.59 | 98.11 |
| C3 | 68.18 | 93.62 |
| C4 | 94.39 | 99.18 |
| C5 | 94.12 | 100.00 |
| C6 | 100.00 | 100.00 |
| OA | 84.66 | 98.61 |
| AA | 84.12 | 98.27 |
| Kappa | 0.743 | 0.978 |
 |  |  |
| GT | Dataset segmentation strategy | No dataset segmentation strategy |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Liu, H.; Yang, R.; Wang, W.; Luo, Q.; Tu, C. Hyperspectral Image Classification Based on Double-Branch Multi-Scale Dual-Attention Network. Remote Sens. 2024, 16, 2051. https://doi.org/10.3390/rs16122051
Zhang H, Liu H, Yang R, Wang W, Luo Q, Tu C. Hyperspectral Image Classification Based on Double-Branch Multi-Scale Dual-Attention Network. Remote Sensing. 2024; 16(12):2051. https://doi.org/10.3390/rs16122051
Chicago/Turabian StyleZhang, Heng, Hanhu Liu, Ronghao Yang, Wei Wang, Qingqu Luo, and Changda Tu. 2024. "Hyperspectral Image Classification Based on Double-Branch Multi-Scale Dual-Attention Network" Remote Sensing 16, no. 12: 2051. https://doi.org/10.3390/rs16122051
APA StyleZhang, H., Liu, H., Yang, R., Wang, W., Luo, Q., & Tu, C. (2024). Hyperspectral Image Classification Based on Double-Branch Multi-Scale Dual-Attention Network. Remote Sensing, 16(12), 2051. https://doi.org/10.3390/rs16122051






