Improved ISAL Imaging Based on RD Algorithm and Image Translation Network Cascade
Abstract
1. Introduction
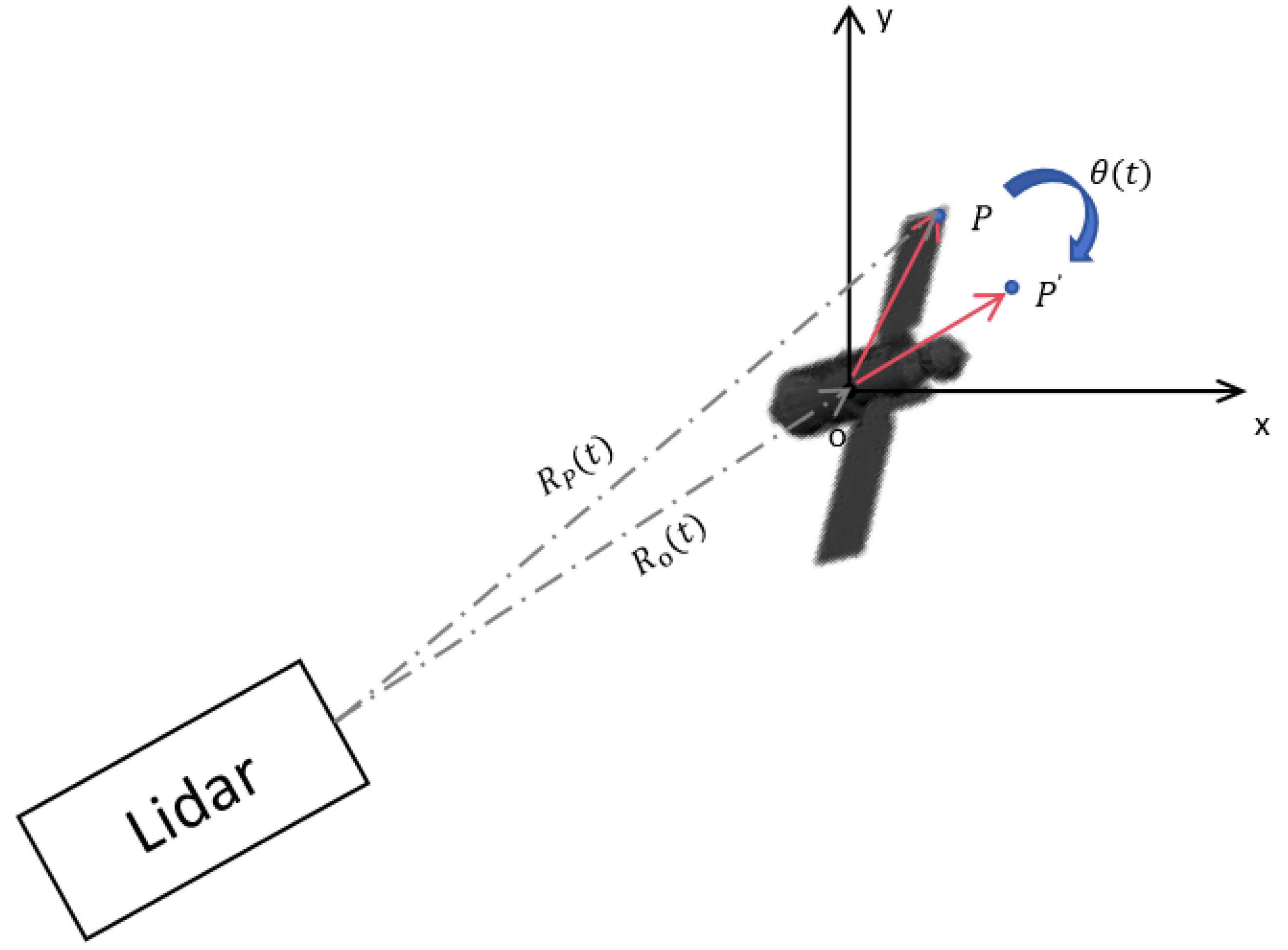
2. Signal Model of ISAL
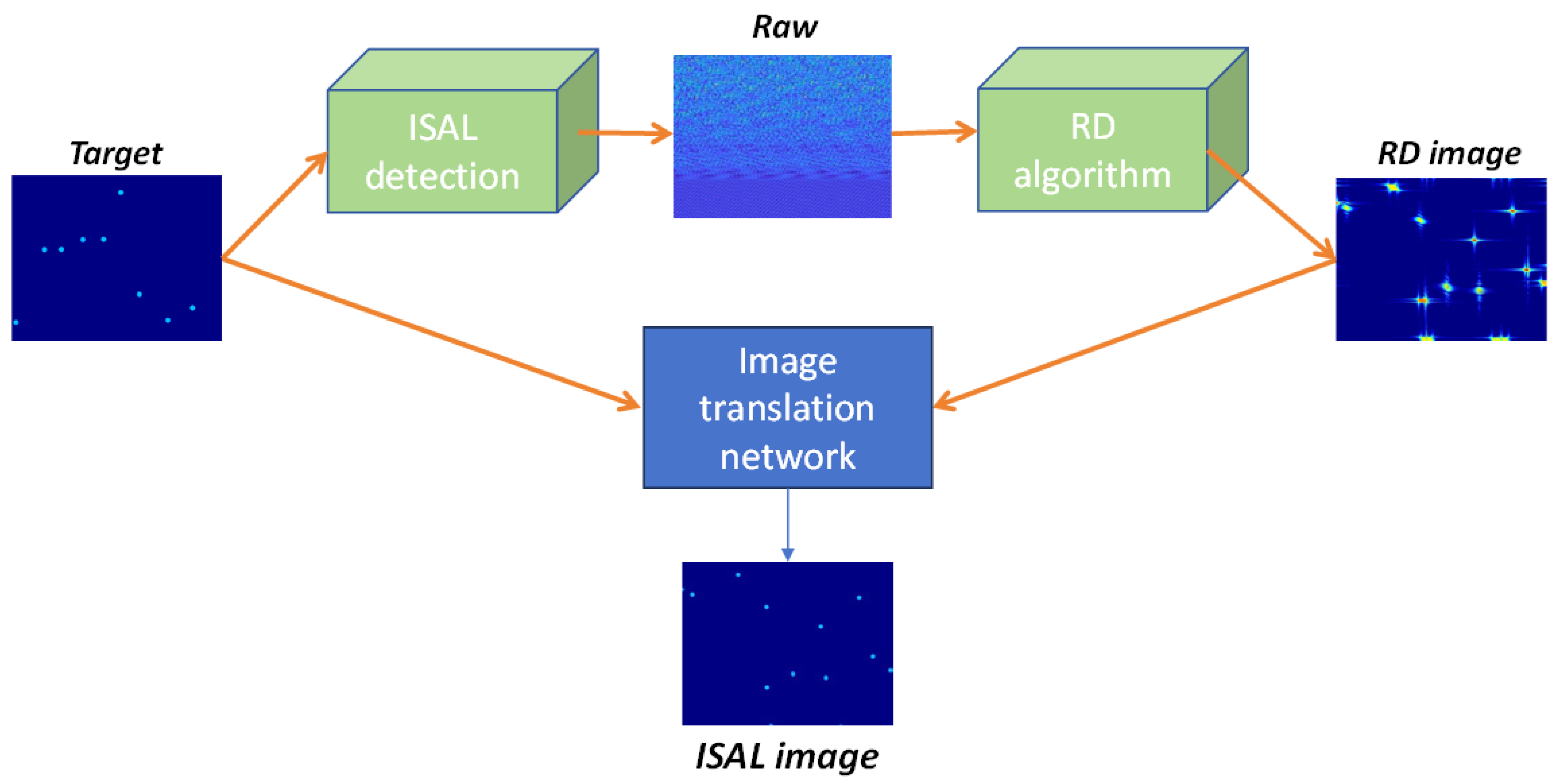
3. Structure of Proposed Network
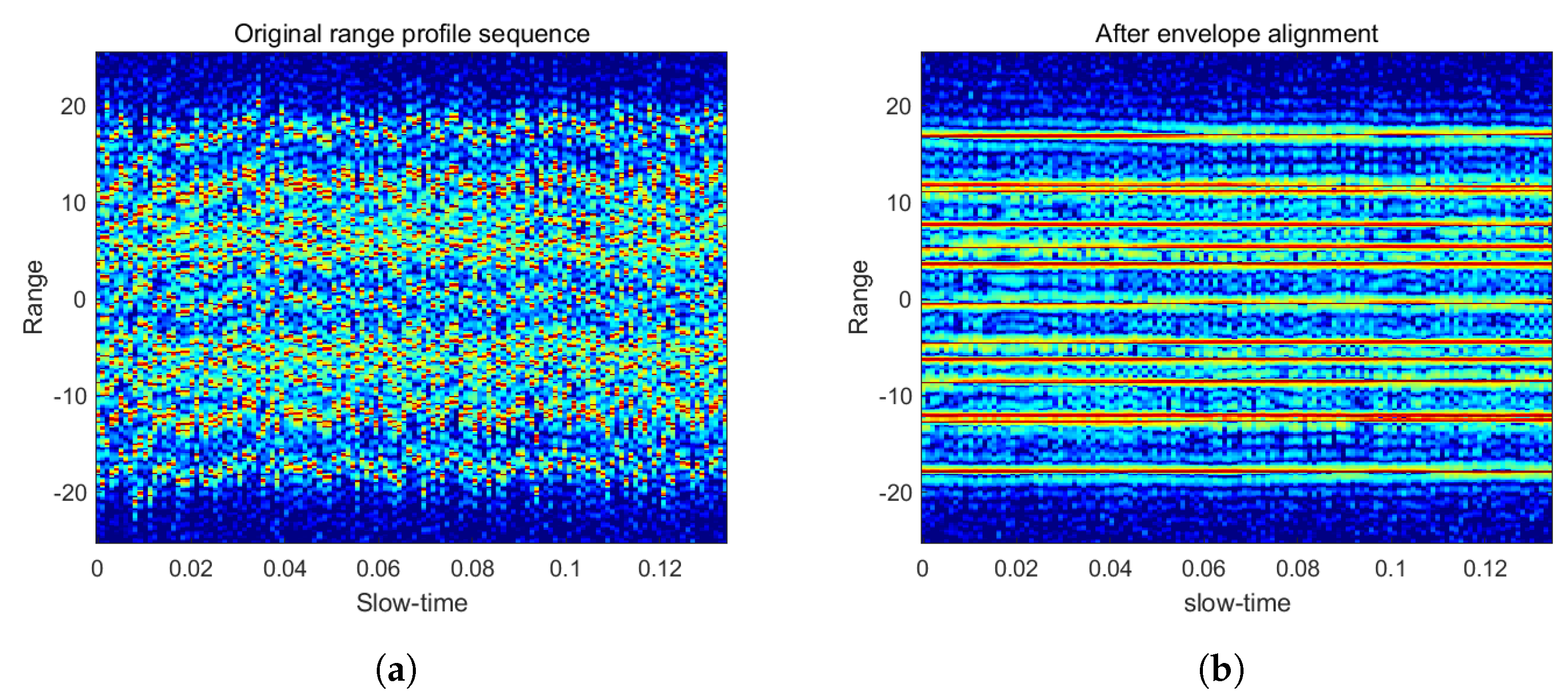
3.1. Range-Doppler Algorithm
| Algorithm 1 The RD algorithm |
|
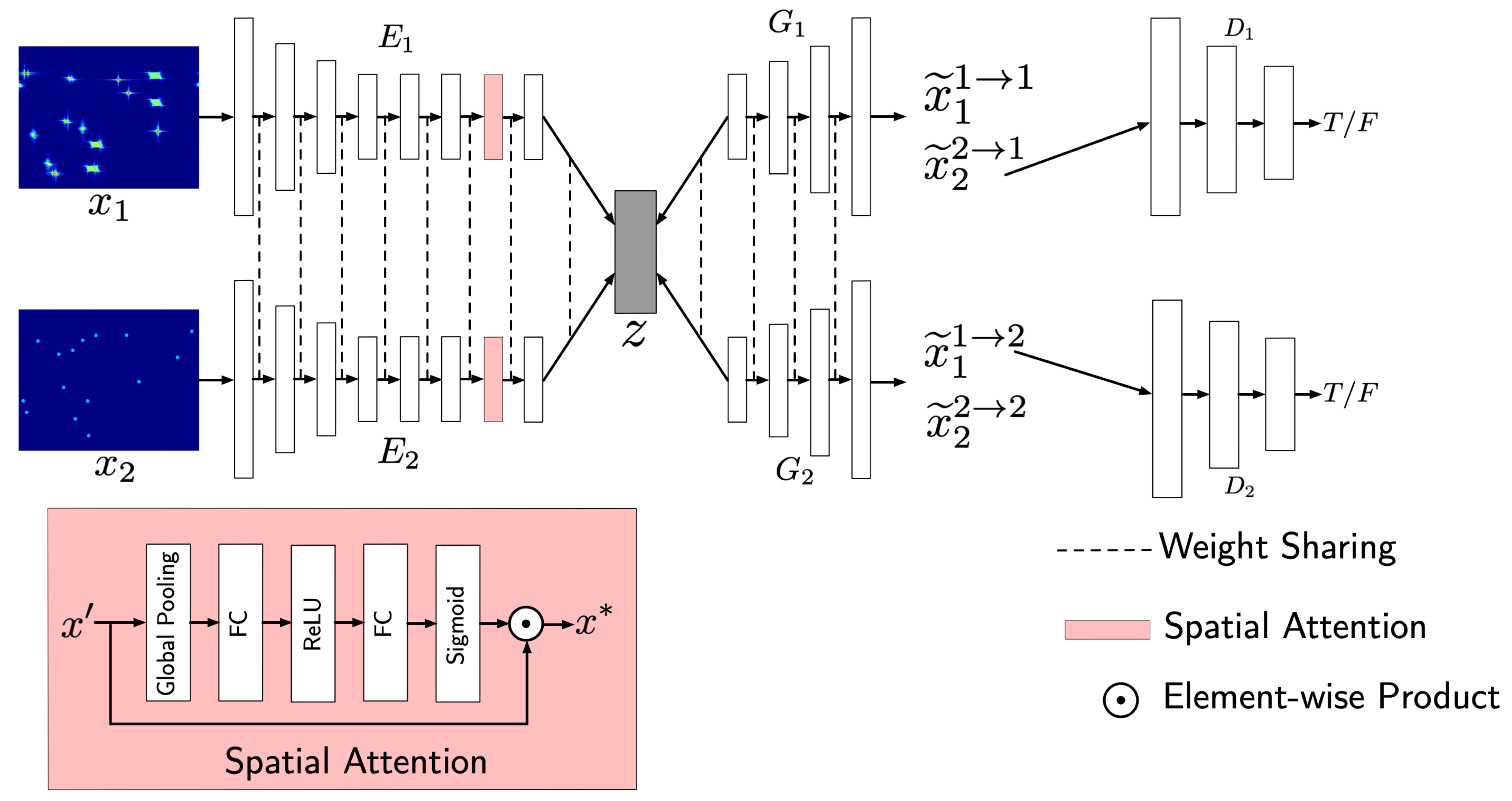
3.2. Network Module and Proposed Construction
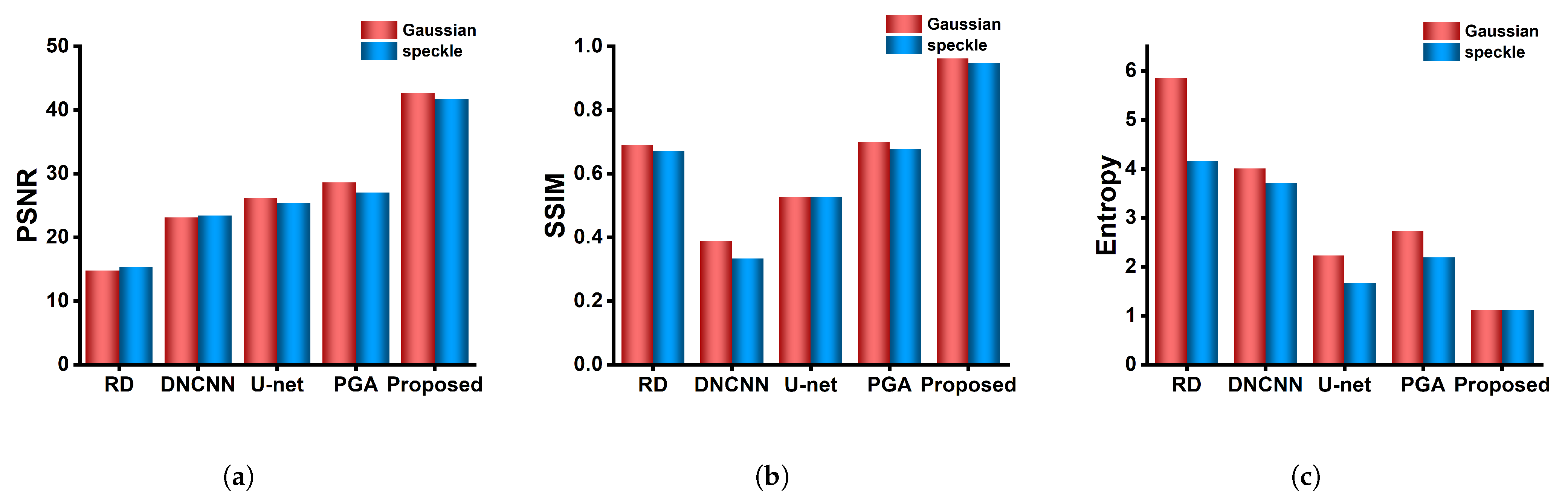
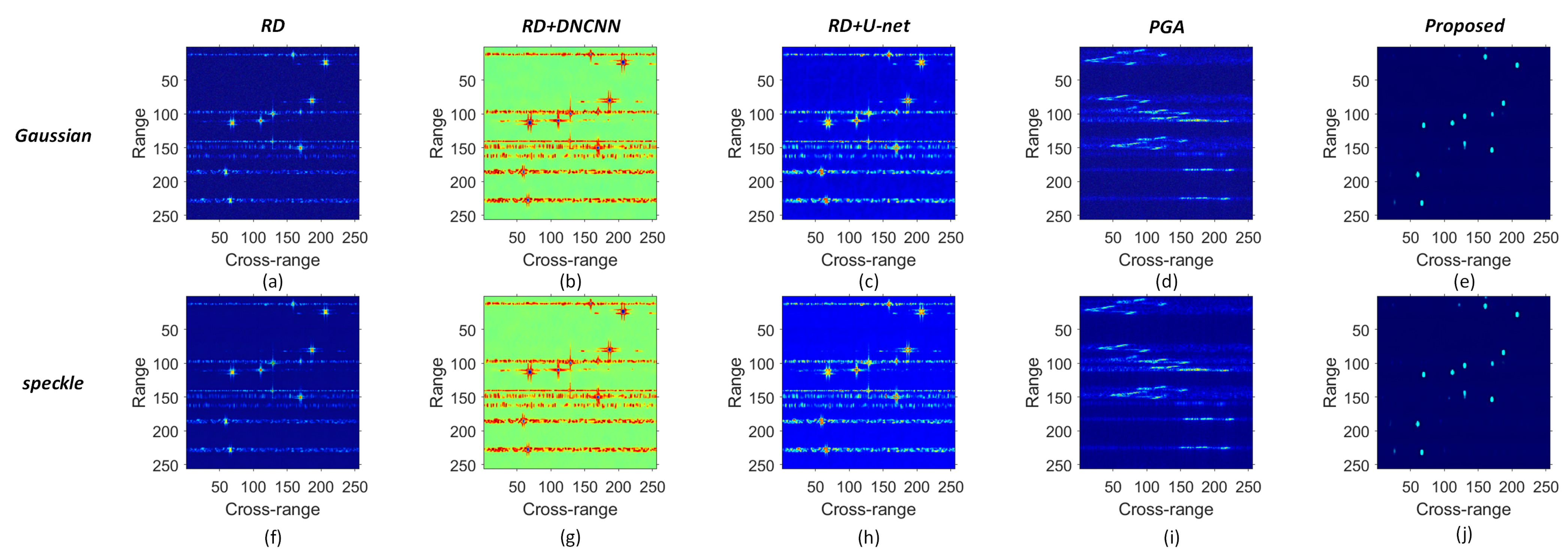
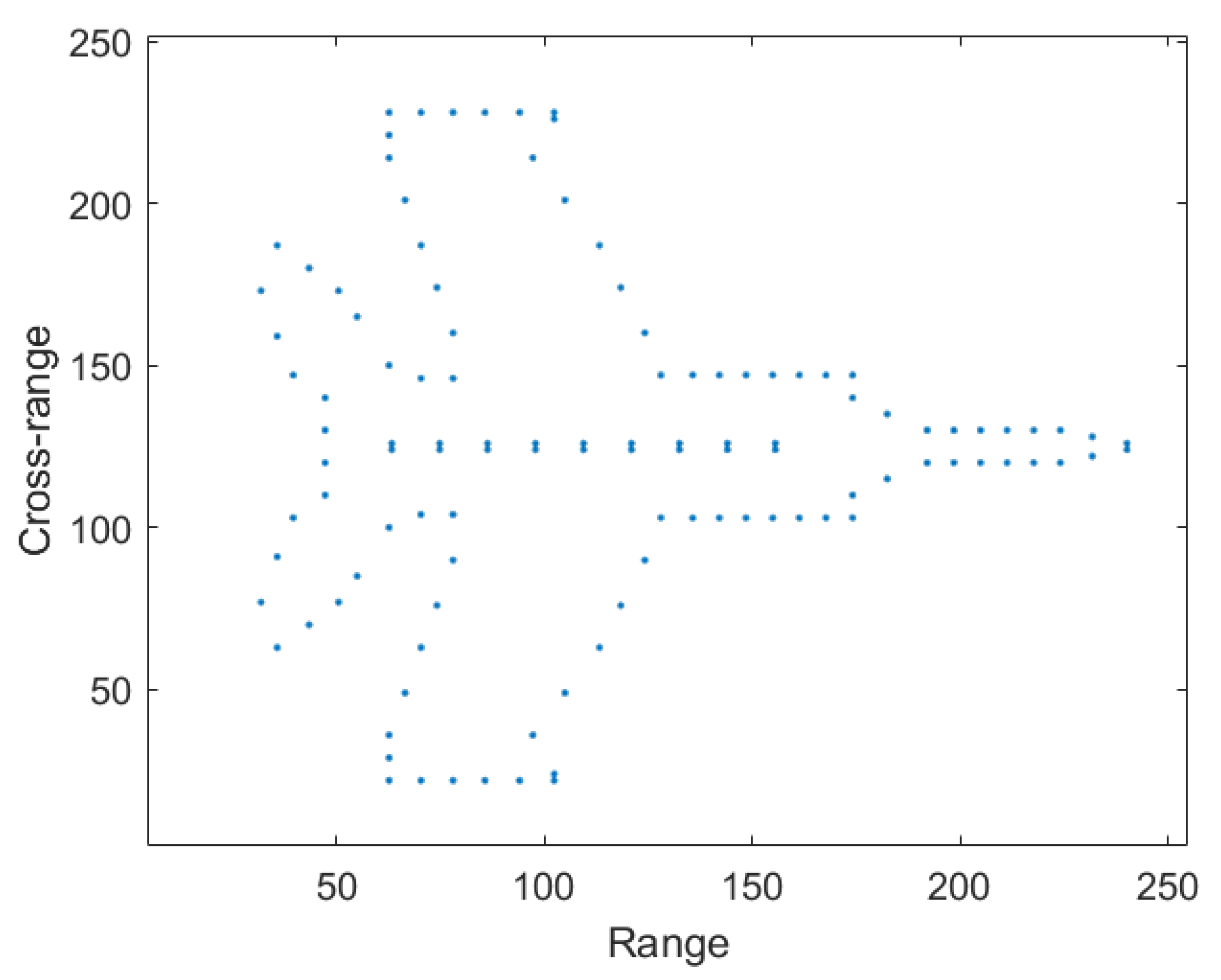
4. Experimental Results and Discussion
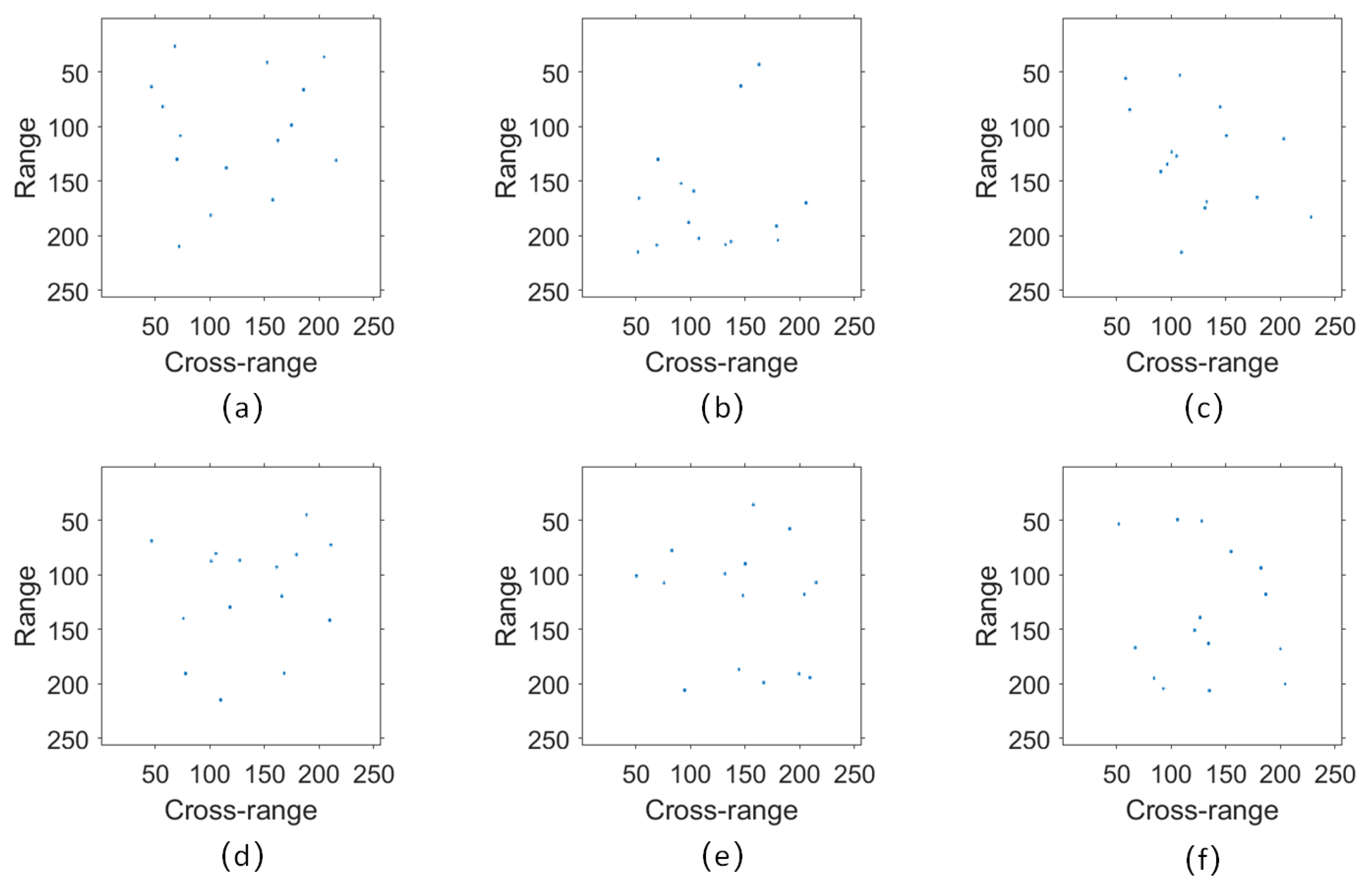
4.1. Dataset
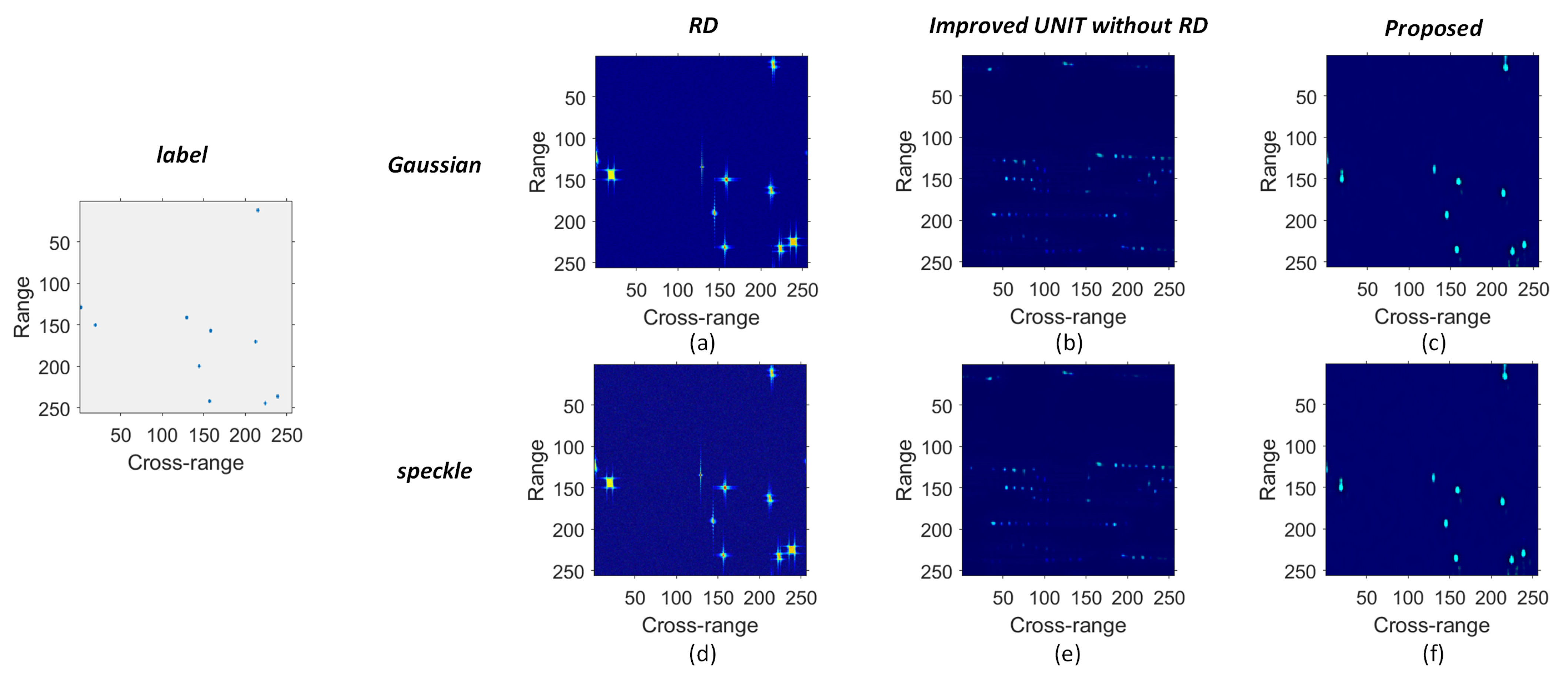
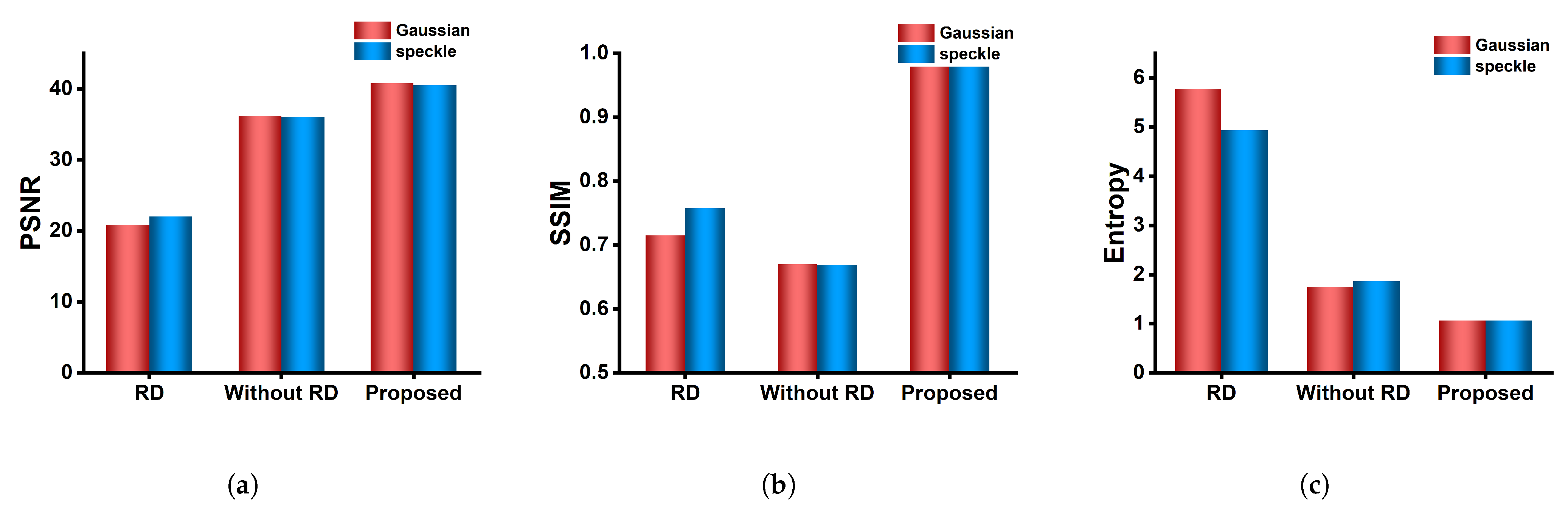
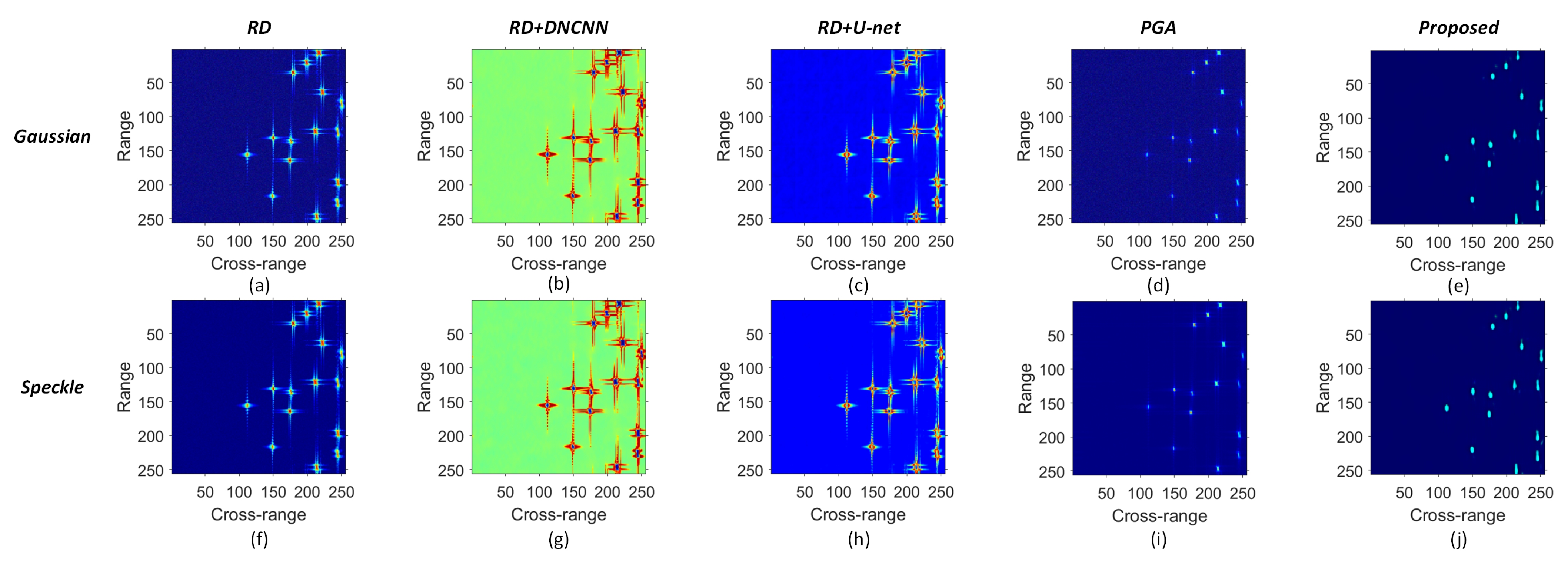
4.2. Experiment Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hong, K.; Jin, K.; Song, A.; Xu, C.; Li, M. Low sampling rate digital dechirp for Inverse Synthetic Aperture Ladar imaging processing. Opt. Commun. 2023, 540, 129482. [Google Scholar] [CrossRef]
- Wang, N.; Wang, R.; Mo, D.; Li, G.; Zhang, K.; Wu, Y. Inverse synthetic aperture LADAR demonstration: System structure, imaging processing, and experiment result. Appl. Opt. 2018, 57, 230–236. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Fu, H.; Wei, K.; Zhang, Y. Jointly compensated imaging algorithm of inverse synthetic aperture lidar based on Nelder-Mead simplex method. Acta Opt. Sin. 2018, 38, 0711002. [Google Scholar]
- Abdukirim, A.; Ren, Y.; Tao, Z.; Liu, S.; Li, Y.; Deng, H.; Rao, R. Effects of Atmospheric Coherent Time on Inverse Synthetic Aperture Ladar Imaging through Atmospheric Turbulence. Remote Sens. 2023, 15, 2883. [Google Scholar] [CrossRef]
- Berizzi, F.; Martorella, M.; Haywood, B.; Dalle Mese, E.; Bruscoli, S. A survey on ISAR autofocusing techniques. In Proceedings of the 2004 International Conference on Image Processing, Singapore, 24–27 October 2004; ICIP ’04. Volume 1, pp. 9–12. [Google Scholar] [CrossRef]
- Shakya, P.; Raj, A.B. Inverse Synthetic Aperture Radar Imaging Using Fourier Transform Technique. In Proceedings of the 2019 1st International Conference on Innovations in Information and Communication Technology (ICIICT), Chennai, India, 25–26 April 2019; pp. 1–4. [Google Scholar]
- Chen, V.C. Reconstruction of inverse synthetic aperture radar image using adaptive time-frequency wavelet transform. In Proceedings of the Wavelet Applications II, SPIE, Orlando, FL, USA, 17–21 April 1995; Volume 2491, pp. 373–386. [Google Scholar]
- Li, J.; Wu, R.; Chen, V. Robust autofocus algorithm for ISAR imaging of moving targets. IEEE Trans. Aerosp. Electron. Syst. 2001, 37, 1056–1069. [Google Scholar] [CrossRef]
- Xing, M.; Wu, R.; Bao, Z. High resolution ISAR imaging of high speed moving targets. IEE Proc.-Radar Sonar Navig. 2005, 152, 58–67. [Google Scholar] [CrossRef]
- Zhao, L.; Wang, L.; Bi, G.; Yang, L. An Autofocus Technique for High-Resolution Inverse Synthetic Aperture Radar Imagery. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6392–6403. [Google Scholar] [CrossRef]
- Wang, X.; Guo, L.; Li, Y.; Han, L.; Xu, Q.; Jing, D.; Li, L.; Xing, M. Noise-Robust Vibration Phase Compensation for Satellite ISAL Imaging by Frequency Descent Minimum Entropy Optimization. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–17. [Google Scholar] [CrossRef]
- Xue, J.; Cao, Y.; Wu, Z.; Li, Y.; Zhang, G.; Yang, K.; Gao, R. Inverse synthetic aperture lidar imaging and compensation in slant atmospheric turbulence with phase gradient algorithm compensation. Opt. Laser Technol. 2022, 154, 108329. [Google Scholar] [CrossRef]
- Li, J.; Jin, K.; Xu, C.; Song, A.; Liu, D.; Cui, H.; Wang, S.; Wei, K. Adaptive motion error compensation method based on bat algorithm for maneuvering targets in inverse synthetic aperture LiDAR imaging. Opt. Eng. 2023, 62, 093103. [Google Scholar] [CrossRef]
- Lan, R.; Zou, H.; Pang, C.; Zhong, Y.; Liu, Z.; Luo, X. Image denoising via deep residual convolutional neural networks. Signal Image Video Process. 2021, 15, 1–8. [Google Scholar] [CrossRef]
- Shan, H.; Fu, X.; Lv, Z.; Xu, X.; Wang, X.; Zhang, Y. Synthetic aperture radar images denoising based on multi-scale attention cascade convolutional neural network. Meas. Sci. Technol. 2023, 34, 085403. [Google Scholar] [CrossRef]
- Lin, W.; Gao, X. Feature fusion for inverse synthetic aperture radar image classification via learning shared hidden space. Electron. Lett. 2021, 57, 986–988. [Google Scholar] [CrossRef]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely connected convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4700–4708. [Google Scholar]
- Krichen, M. Generative Adversarial Networks. In Proceedings of the 2023 14th International Conference on Computing Communication and Networking Technologies (ICCCNT), Delhi, India, 6–8 July 2023; pp. 1–7. [Google Scholar] [CrossRef]
- Yuan, Y.; Luo, Y.; Ni, J.; Zhang, Q. Inverse Synthetic Aperture Radar Imaging Using an Attention Generative Adversarial Network. Remote Sens. 2022, 14, 3509. [Google Scholar] [CrossRef]
- Yuan, H.; Li, H.; Zhang, Y.; Wang, Y.; Liu, Z.; Wei, C.; Yao, C. High-Resolution Refocusing for Defocused ISAR Images by Complex-Valued Pix2pixHD Network. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Xiao, C.; Gao, X.; Zhang, C. Deep Convolution Network with Sparse Prior for Sparse ISAR Image Enhancement. In Proceedings of the 2021 2nd Information Communication Technologies Conference (ICTC), Nanjing, China, 7–9 May 2021; pp. 54–59. [Google Scholar] [CrossRef]
- Liu, M.Y.; Breuel, T.; Kautz, J. Unsupervised Image-to-Image Translation Networks. In Proceedings of the Advances in Neural Information Processing Systems; Guyon, I., Luxburg, U.V., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2017; Volume 30. [Google Scholar]
- Giusti, E.; Martorella, M. Range Doppler and image autofocusing for FMCW inverse synthetic aperture radar. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 2807–2823. [Google Scholar] [CrossRef]
- Othman, M.A.B.; Belz, J.; Farhang-Boroujeny, B. Performance Analysis of Matched Filter Bank for Detection of Linear Frequency Modulated Chirp Signals. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 41–54. [Google Scholar] [CrossRef]
- Chen, V.C.; Martorella, M. Inverse Synthetic Aperture Radar Imaging: Principles, Algorithms and Applications; The Institution of Engineering and Technology: London, UK, 2014. [Google Scholar]
- Zhang, S.S.; Zeng, T.; Long, T.; Yuan, H.P. Dim target detection based on keystone transform. In Proceedings of the IEEE International Radar Conference, Arlington, VA, USA, 9–12 May 2005; pp. 889–894. [Google Scholar] [CrossRef]
- Zhang, K.; Zuo, W.; Chen, Y.; Meng, D.; Zhang, L. Beyond a gaussian denoiser: Residual learning of deep cnn for image denoising. IEEE Trans. Image Process. 2017, 26, 3142–3155. [Google Scholar] [CrossRef] [PubMed]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. arXiv 2015, arXiv:cs.CV/1505.04597. [Google Scholar]
- Fu, T.; Gao, M.; He, Y. An improved scatter selection method for phase gradient autofocus algorithm in SAR/ISAR autofocus. In Proceedings of the International Conference on Neural Networks and Signal Processing, Nanjing, China, 14–17 December 2003; Volume 2, pp. 1054–1057. [Google Scholar] [CrossRef]





| Parameter | Value |
|---|---|
| Carrier frequency () | 193.5 THz |
| Bandwidth (B) | 10 GHz |
| Pulse width () | 25 s |
| Pulse repetition frequency (PRF) | 100 kHz |
| Laser wavelength () | 1550 nm |
| Configuration | Parameter |
|---|---|
| CPU | Intel(R) Core(TM) i9-13900K |
| GPU | NVIDIA GeForce RTX 4090 |
| Accelerated environment | CUDA11.8 CUDNN9.2.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Wang, B.; Wang, X. Improved ISAL Imaging Based on RD Algorithm and Image Translation Network Cascade. Remote Sens. 2024, 16, 2635. https://doi.org/10.3390/rs16142635
Li J, Wang B, Wang X. Improved ISAL Imaging Based on RD Algorithm and Image Translation Network Cascade. Remote Sensing. 2024; 16(14):2635. https://doi.org/10.3390/rs16142635
Chicago/Turabian StyleLi, Jiarui, Bin Wang, and Xiaofei Wang. 2024. "Improved ISAL Imaging Based on RD Algorithm and Image Translation Network Cascade" Remote Sensing 16, no. 14: 2635. https://doi.org/10.3390/rs16142635
APA StyleLi, J., Wang, B., & Wang, X. (2024). Improved ISAL Imaging Based on RD Algorithm and Image Translation Network Cascade. Remote Sensing, 16(14), 2635. https://doi.org/10.3390/rs16142635







