Intrapulse Modulation Radar Signal Recognition Using CNN with Second-Order STFT-Based Synchrosqueezing Transform
Abstract
1. Introduction
- A new intrapulse modulation radar signal recognition method is proposed and verified by simulations to achieve a high recognition rate under low SNR.
- The second-order STFT-based synchrosqueezing transform is introduced to feature extraction to generate TFIs for radar signal recognition, which has a strong anti-noise effect.
- An efficient convolution module named MeNet is designed, which combines residual structure, depthwise (dw) convolution, and pointwise (pw) convolution to reduce the complexity of the model and improve the recognition rate by fully learning the informative features.
2. Intrapulse Modulation Radar Signal Model
3. Proposed Intrapulse Modulation Recognition Method Using CNN with FSST2
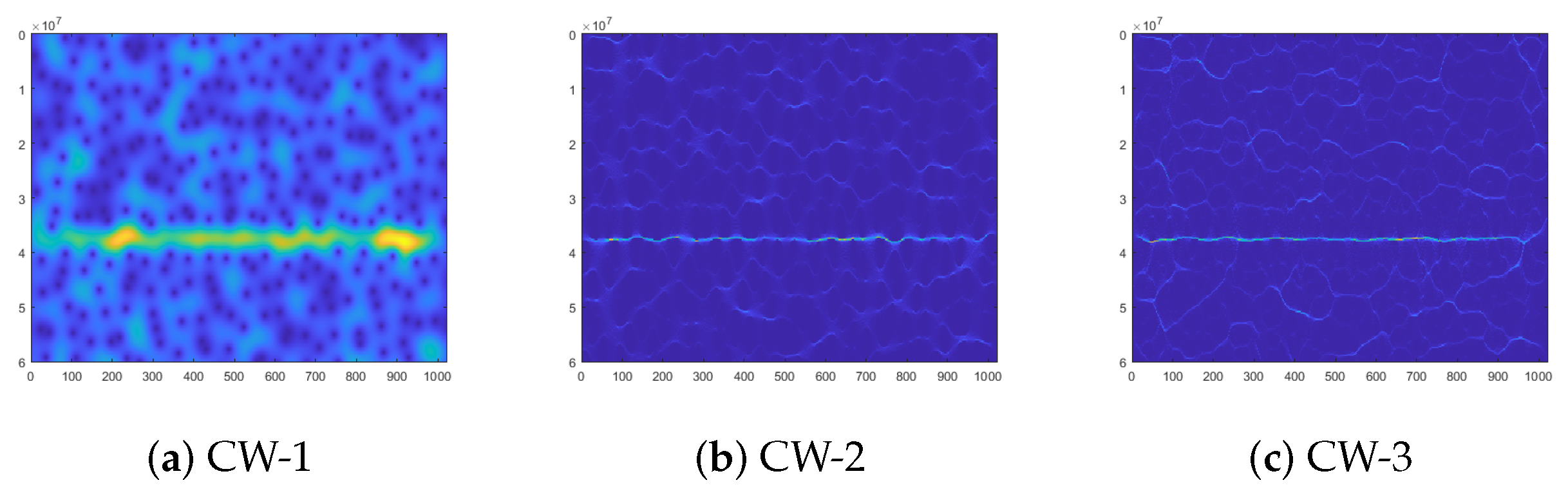
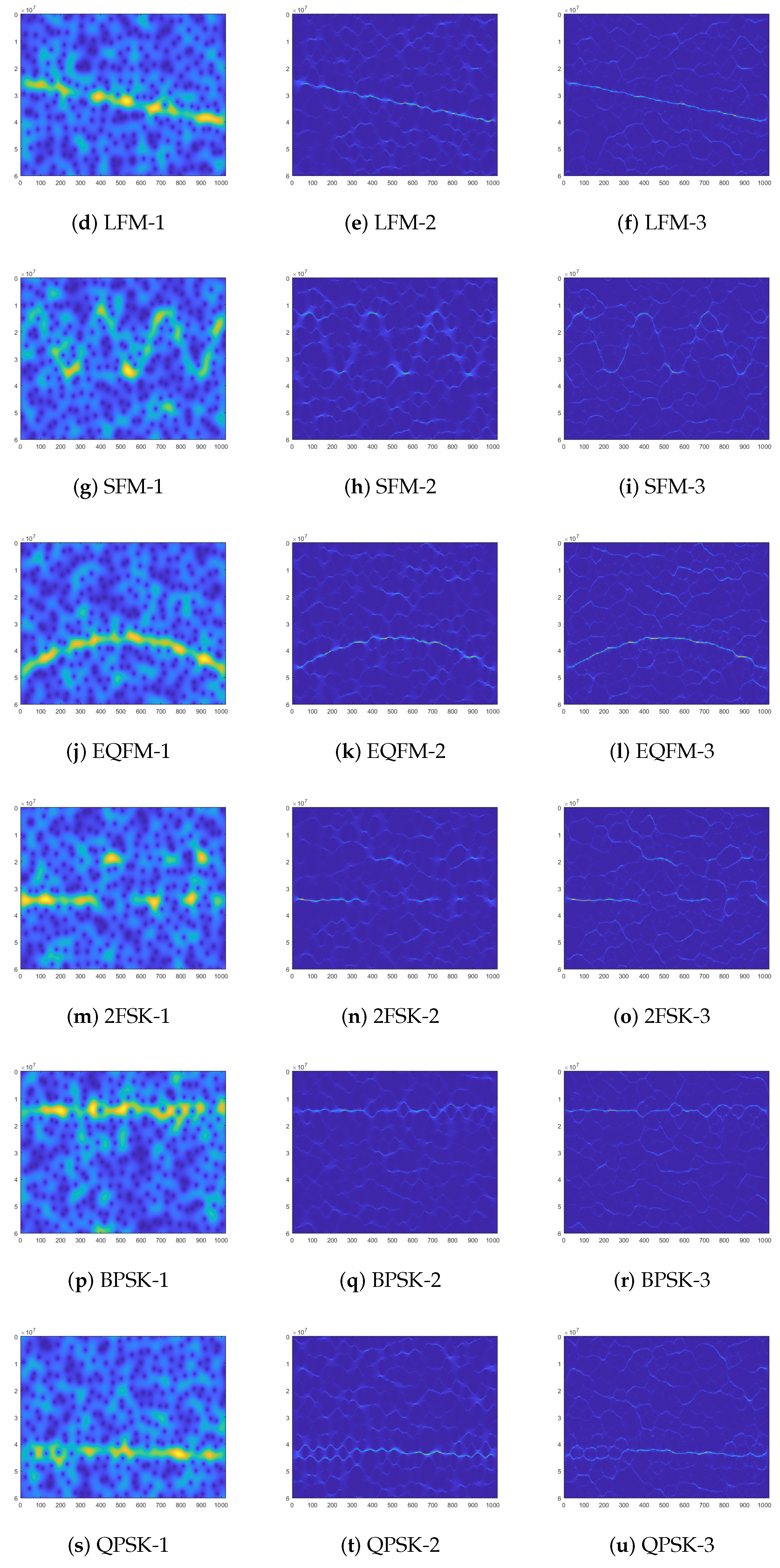
3.1. Time–Frequency Analysis
3.2. Data Preprocessing
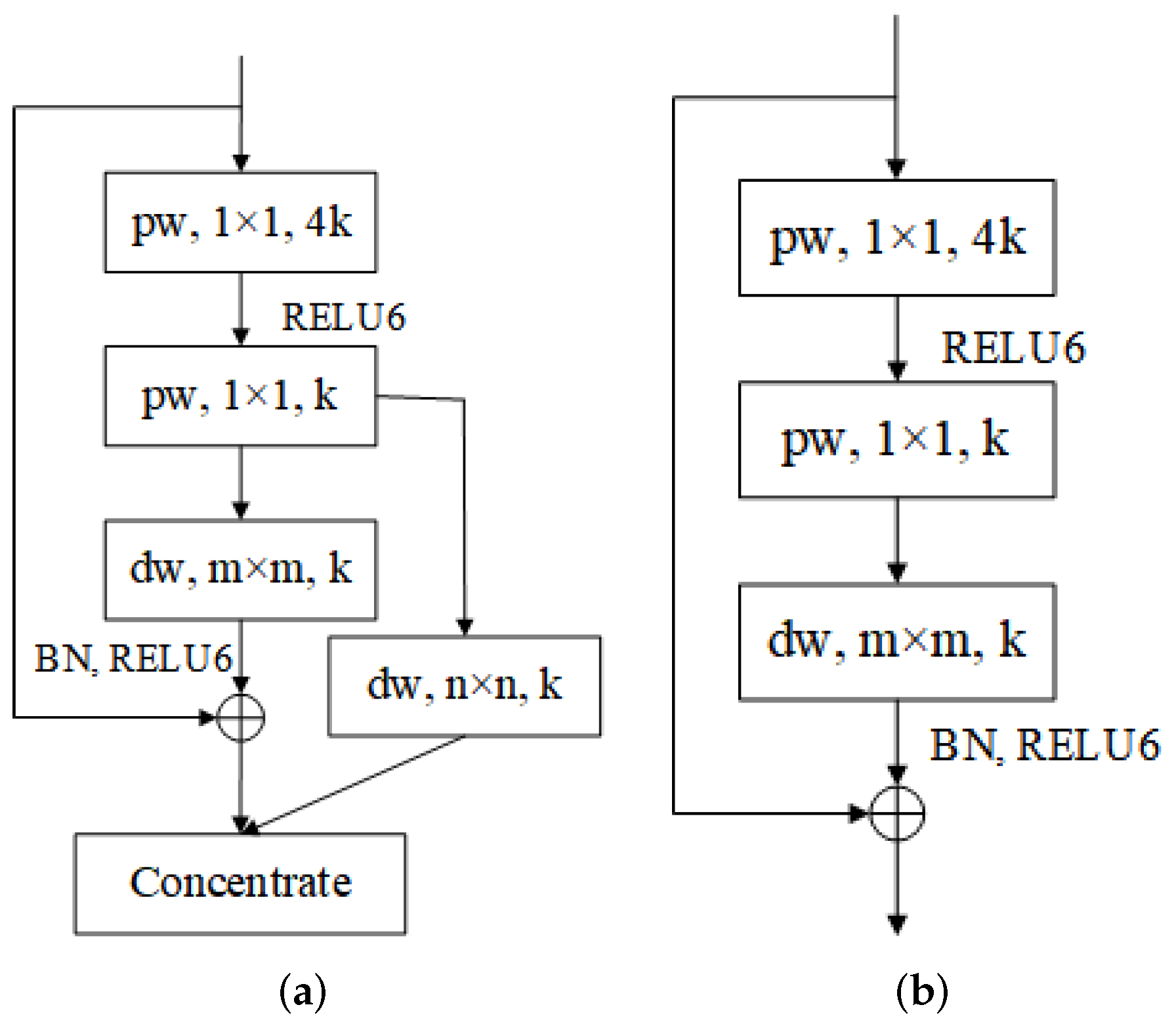
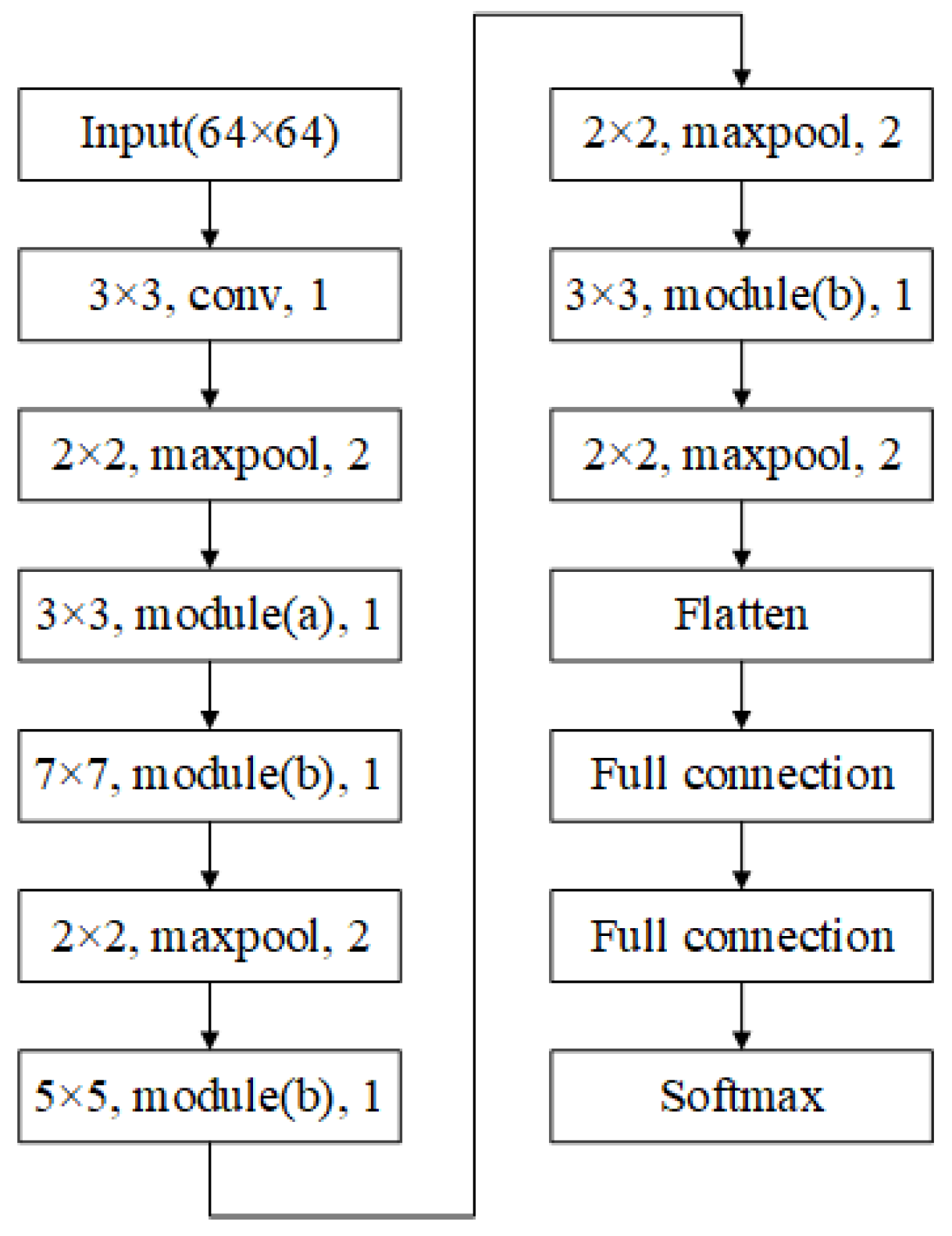
3.3. Network Construction
4. Simulation Results
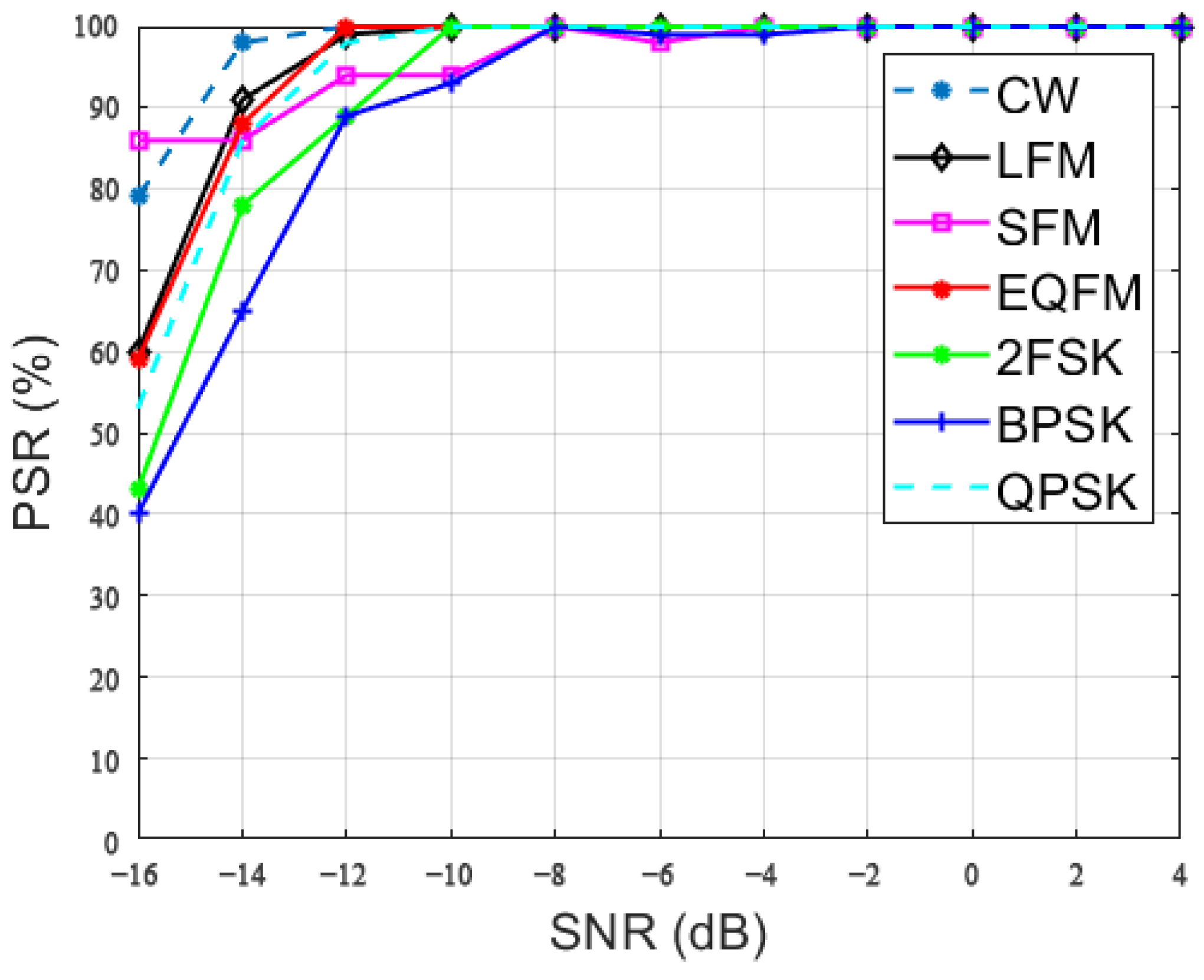
4.1. Recognition Rate vs. SNR
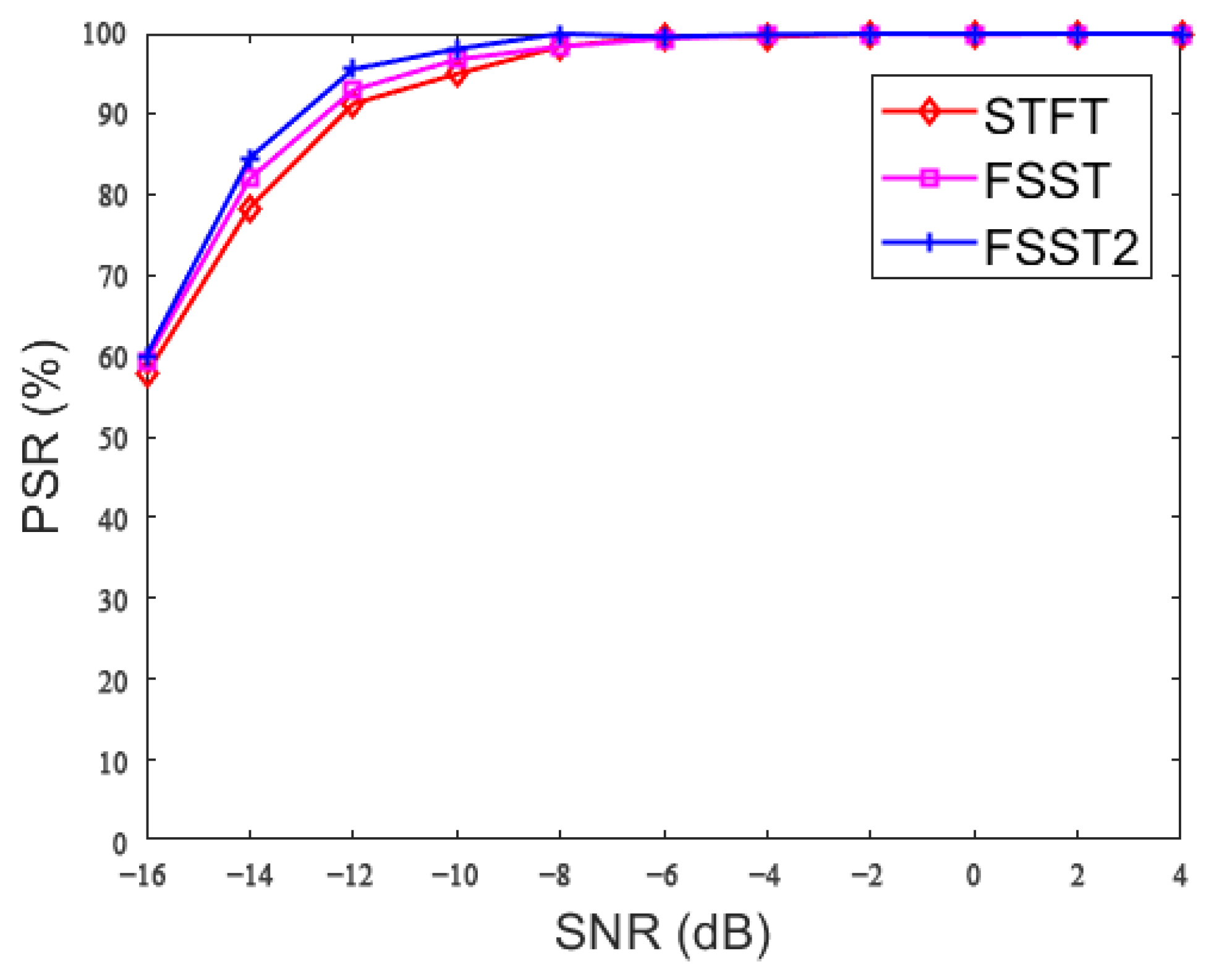
4.2. Comparison of Different TFIs
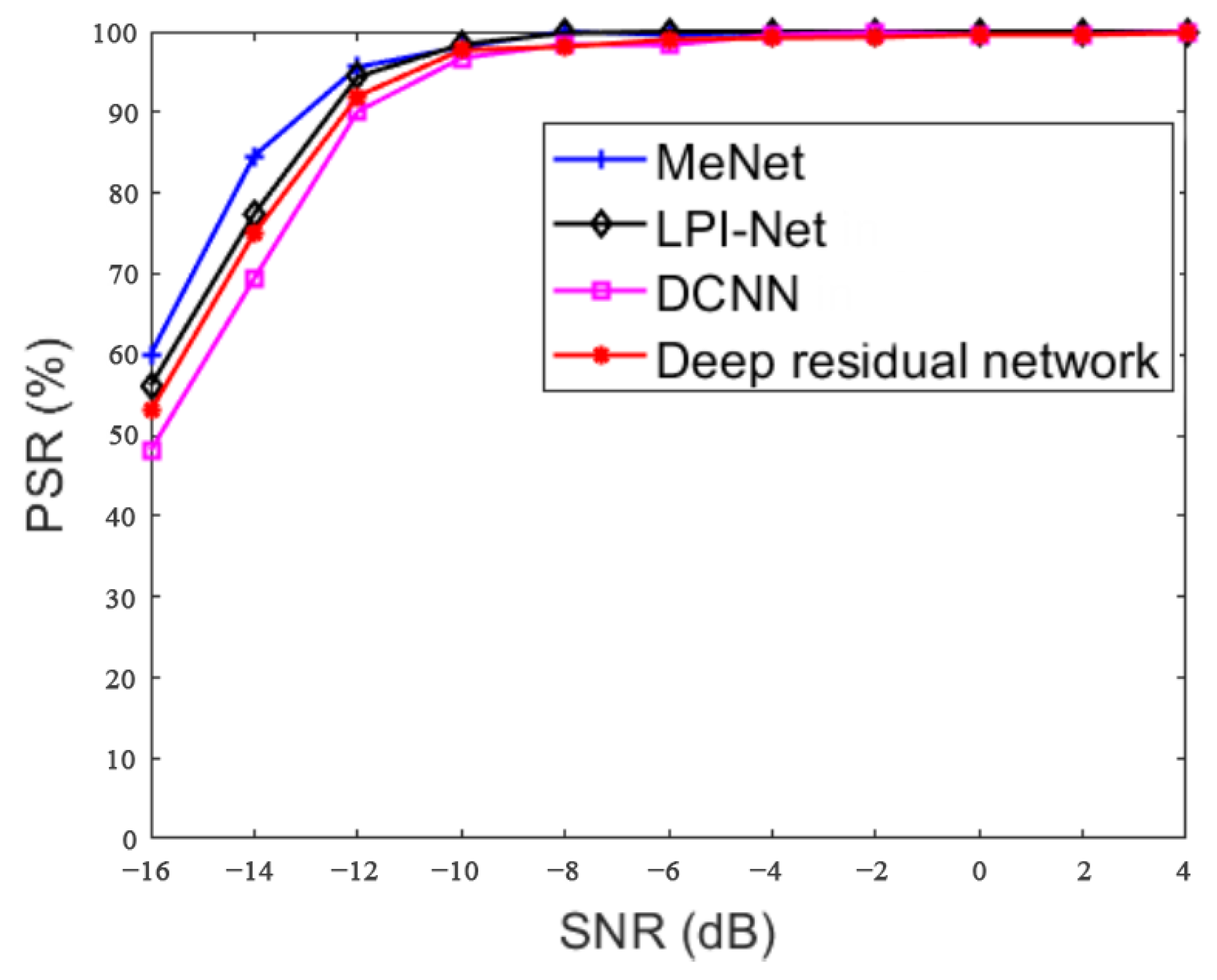
4.3. Comparison of Different Networks
4.4. Ablation Study for MeNet
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kawalec, A.; Owczarek, R. Radar emitter recognition using intrapulse data. In Proceedings of the 15th International Conference on Microwaves, Radar and Wireless Communications (IEEE Cat. No.04EX824), Warsaw, Poland, 17–19 May 2004; pp. 435–438. [Google Scholar]
- Yuan, S.; Wu, B.; Li, P. Intra-pulse modulation classification of radar emitter signals based on a 1-D selective rernel convolutional neural network. Remote Sens. 2021, 13, 2799. [Google Scholar] [CrossRef]
- Gao, L.; Zhang, X.; Gao, J.; You, S. Fusion image based radar signal feature extraction and modulation recognition. IEEE Access 2019, 7, 13135–13148. [Google Scholar] [CrossRef]
- Zhang, M.; Liu, L.; Diao, M. LPI radar waveform recognition based on time–frequency distribution. Sensors 2016, 16, 1682. [Google Scholar] [CrossRef] [PubMed]
- Wei, S.; Qu, Q.; Zeng, X.; Liang, J.; Shi, J.; Zhang, X. Self-attention bi-LSTM networks for radar signal modulation recognition. IEEE Trans. Microw. Theory Techn. 2021, 69, 5160–5172. [Google Scholar] [CrossRef]
- Qu, Q.; Wei, S.; Wu, Y.; Wang, M. ACSE networks and autocorrelation features for PRI modulation recognition. IEEE Commun. Lett. 2020, 24, 1729–1733. [Google Scholar] [CrossRef]
- Chen, S.; Zheng, S.; Yang, L.; Yang, X. Deep learning for large-scale real-world ACARS and ADS-B radio signal classification. IEEE Access 2019, 7, 89256–89264. [Google Scholar] [CrossRef]
- Wei, S.; Qu, Q.; Wu, Y.; Wang, M.; Shi, J. PRI modulation recognition based on squeeze-and-excitation networks. IEEE Commun. Lett. 2020, 24, 1047–1051. [Google Scholar] [CrossRef]
- Chen, K.; Zhu, L.; Chen, S.; Zhang, S.; Zhao, H. Deep residual learning in modulation recognition of radar signals using higher-order spectral distribution. Measurement 2021, 185, 109945. [Google Scholar] [CrossRef]
- Jin, X.; Ma, J.; Ye, F. Radar signal recognition based on deep residual network with attention mechanism. In Proceedings of the 2021 IEEE 4th International Conference on Electronic Information and Communication Technology (ICEICT), Xi’an, China, 18–20 August 2021; pp. 428–432. [Google Scholar]
- Huynh-The, T.; Doan, V.-S.; Hua, C.-H.; Pham, Q.-V.; Nguyen, T.-V.; Kim, D.-S. Accurate LPI radar waveform recognition with CWD-TFA for deep convolutional network. IEEE Wireless Commun. Lett. 2021, 10, 1638–1642. [Google Scholar] [CrossRef]
- Wang, F.; Yang, C.; Huang, S.; Wang, H. Automatic modulation classification based on joint feature map and convolutional neural network. IET Radar Sonar Navig. 2019, 13, 998–1003. [Google Scholar] [CrossRef]
- Chen, K.; Zhang, S.; Zhu, L.; Chen, S.; Zhao, H. Modulation recognition of radar signals based on adaptive singular value reconstruction and deep residual learning. Sensors 2019, 21, 449. [Google Scholar] [CrossRef] [PubMed]
- Lang, P.; Fu, X.; Martorella, M.; Dong, J.; Qin, R.; Feng, C.; Zhao, C. RRSARNet: A novel network for radar radio sources adaptive recognition. IEEE Trans. Veh. Technol. 2021, 70, 11483–11498. [Google Scholar] [CrossRef]
- Huynh-The, T.; Pham, Q.-V.; Nguyen, T.-V.; da Costa, D.B.; Kim, D.-S. RaComNet: High-performance deep network for waveform recognition in coexistence radar-communication systems. In Proceedings of the IEEE International Conference on Communications (ICC), Seoul, Republic of Korea, 16–20 May 2022; pp. 1–6. [Google Scholar]
- Auger, F.; Flandrin, P.; Lin, Y.-T.; McLaughlin, S.; Meignen, S.; Oberlin, T.; Wu, H.-T. Time-frequency reassignment and synchrosqueezing: An overview. IEEE Signal Process. Mag. 2013, 30, 32–41. [Google Scholar] [CrossRef]
- Oberlin, T.; Meignen, S.; Perrier, V. Second-order synchrosqueezing transform or invertible reassignment? Towards ideal time-frequency representations. IEEE Trans. Signal Process. 2015, 63, 1335–1344. [Google Scholar] [CrossRef]

| Modulation Type | Signal Expression |
|---|---|
| CW | |
| LFM | |
| SFM | |
| EQFM | |
| 2FSK | |
| BPSK | |
| QPSK |
| Signal | Parameter | Range |
|---|---|---|
| CW | 0.05–0.3 | |
| LFM | 0.05–0.3 | |
| B | 0.05–0.2 | |
| SFM | 0.05–0.3 | |
| B | 0.05–0.2 | |
| EQFM | 0.05–0.3 | |
| B | 0.05–0.2 | |
| 2FSK | 0.05–0.3 | |
| 0.05–0.2 | ||
| BPSK | 0.05–0.3 | |
| Barker codes | [7,11,13] | |
| QPSK | 0.05–0.3 | |
| Frank codes | [16] |
| Method to Generate TFIs | Computation Time (sec.) |
|---|---|
| STFT | 42,074 |
| FSST | 39,461 |
| FSST2 | 48,259 |
| Network | Training Time (sec.) | Test Time (sec.) |
|---|---|---|
| LPI-Net in [11] | 622.14 | 6.21 |
| DCNN in [12] | 224.69 | 3.01 |
| Deep residual network in [13] | 797.34 | 10.48 |
| MeNet | 468.25 | 6.07 |
| Experiment Group | Module (a) | Module (b) | Recognition Rate | F1 Value |
|---|---|---|---|---|
| 1 | 91.28% | 91.14% | ||
| 2 | ✓ | 92.85% | 92.83% | |
| 3 | ✓ | 94.16% | 94.13% | |
| 4 | ✓ | ✓ | 95.57% | 95.56% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, N.; Jiang, H.; Liu, Y.; Zhang, J. Intrapulse Modulation Radar Signal Recognition Using CNN with Second-Order STFT-Based Synchrosqueezing Transform. Remote Sens. 2024, 16, 2582. https://doi.org/10.3390/rs16142582
Dong N, Jiang H, Liu Y, Zhang J. Intrapulse Modulation Radar Signal Recognition Using CNN with Second-Order STFT-Based Synchrosqueezing Transform. Remote Sensing. 2024; 16(14):2582. https://doi.org/10.3390/rs16142582
Chicago/Turabian StyleDong, Ning, Hong Jiang, Yipeng Liu, and Jingtao Zhang. 2024. "Intrapulse Modulation Radar Signal Recognition Using CNN with Second-Order STFT-Based Synchrosqueezing Transform" Remote Sensing 16, no. 14: 2582. https://doi.org/10.3390/rs16142582
APA StyleDong, N., Jiang, H., Liu, Y., & Zhang, J. (2024). Intrapulse Modulation Radar Signal Recognition Using CNN with Second-Order STFT-Based Synchrosqueezing Transform. Remote Sensing, 16(14), 2582. https://doi.org/10.3390/rs16142582








