A Semi-Automatic Approach for Tree Crown Competition Indices Assessment from UAV LiDAR
Abstract
1. Introduction
2. Materials
3. Methods
3.1. Crown Features
3.2. Differentiation Dimensional Indices
3.3. Statistical Analysis
4. Results
4.1. Single Tree Manual Segmentation
4.2. Tree-Neighbors Selection
4.3. Crown Projected Area and Crown Volume
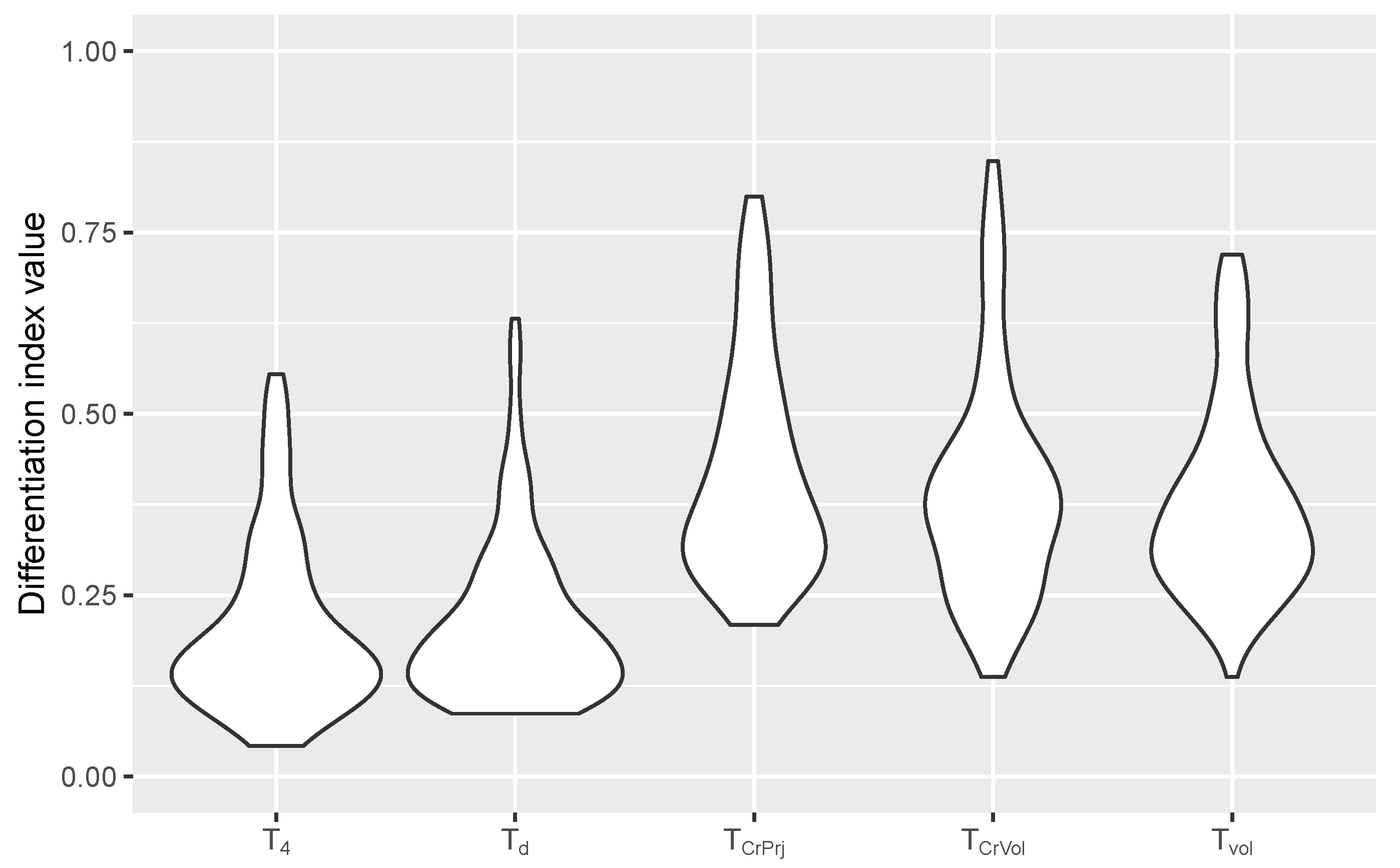
4.4. Indices Statistic Analysis
5. Discussion
6. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dial, R.; Bloodworth, B.; Lee, A.; Boyne, P.; Heys, J. The Distribution of Free Space and Its Relation to Canopy Composition at Six Forest Sites. For. Sci. 2004, 50, 312–325. [Google Scholar] [CrossRef]
- Hildebrand, M.; Perles-Garcia, M.D.; Kunz, M.; Härdtle, W.; Von Oheimb, G.; Fichtner, A. Tree-tree interactions and crown complementarity: The role of functional diversity and branch traits for canopy packing. Basic Appl. Ecol. 2021, 50, 217–227. [Google Scholar] [CrossRef]
- Verkerk, P.J.; Fitzgerald, J.B.; Datta, P.; Dees, M.; Hengeveld, G.M.; Lindner, M.; Zudin, S. Spatial distribution of the potential forest biomass availability in Europe. For. Ecosyst. 2019, 6, 5. [Google Scholar] [CrossRef]
- Aalto, I.; Aalto, J.; Hancock, S.; Valkonen, S.; Maeda, E.E. Quantifying the impact of management on the three-dimensional structure of boreal forests. For. Ecol. Manag. 2023, 535, 120885. [Google Scholar] [CrossRef]
- Pretzsch, H.; Dieler, J. Evidence of variant intra- and interspecific scaling of tree crown structure and relevance for allometric theory. Oecologia 2012, 169, 637–649. [Google Scholar] [CrossRef]
- Pretzsch, H. The Effect of Tree Crown Allometry on Community Dynamics in Mixed-Species Stands versus Monocultures. A Review and Perspectives for Modeling and Silvicultural Regulation. Forests 2019, 10, 810. [Google Scholar] [CrossRef]
- Seidel, D.; Leuschner, C.; Müller, A.; Krause, B. Crown plasticity in mixed forests—Quantifying asymmetry as a measure of competition using terrestrial laser scanning. For. Ecol. Manag. 2011, 261, 2123–2132. [Google Scholar] [CrossRef]
- Hui, G.; Gadow, K. Das Winkelmass—Herleitung des optimalen Standardwinkels. Allg. Forst Jagdztg. 2002, 173, 173–176. [Google Scholar]
- Pommerening, A. Evaluating structural indices by reversing forest structural analysis. For. Ecol. Manag. 2006, 224, 266–277. [Google Scholar] [CrossRef]
- Zhang, M.; Wang, J.; Kang, X. Spatial distribution pattern of dominant tree species in different disturbance plots in the Changbai Mountain. Sci. Rep. 2022, 12, 14161. [Google Scholar] [CrossRef]
- Pommerening, A.; Wang, H.; Zhao, Z. Global woodland structure from local interactions: New nearest-neighbour functions for understanding the ontogenesis of global forest structure. For. Ecosyst. 2020, 7, 22. [Google Scholar] [CrossRef]
- Disney, M. Terrestrial LiDAR: A three-dimensional revolution in how we look at trees. New Phytol. 2019, 222, 1736–1741. [Google Scholar] [CrossRef] [PubMed]
- Torresan, C.; Berton, A.; Carotenuto, F.; Chiavetta, U.; Miglietta, F.; Zaldei, A.; Gioli, B. Development and Performance Assessment of a Low-Cost UAV Laser Scanner System (LasUAV). Remote Sens. 2018, 10, 1094. [Google Scholar] [CrossRef]
- Puletti, N.; Innocenti, S.; Guasti, M. A co-registration approach between terrestrial and UAV laser scanning point clouds based on ground and trees features. Ann. Silvic. Res. 2024, 49, 4466. [Google Scholar] [CrossRef]
- Torresan, C.; Pelleri, F.; Manetti, M.; Becagli, C.; Castaldi, C.; Notarangelo, M.; Chiavetta, U. Comparison of TLS against traditional surveying method for stem taper modelling. A case study in European beech (Fagus sylvatica L.) forests of mount Amiata. Ann. Silvic. Res. 2021, 46, 128–140. [Google Scholar]
- Szmyt, J.; Korzeniewicz, R. Do natural processes at the juvenile stage of stand development differentiate the spatial structure of trees in artificially established forest stands? For. Res. Pap. 2014, 75, 171–179. [Google Scholar] [CrossRef]
- Owen, H.J.F.; Flynn, W.R.M.; Lines, E.R. Competitive drivers of interspecific deviations of crown morphology from theoretical predictions measured with Terrestrial Laser Scanning. J. Ecol. 2021, 109, 2612–2628. [Google Scholar] [CrossRef]
- Cutini, A.; Chianucci, F.; Giannini, T.; Manetti, M.C.; Salvati, L. Is anticipated seed cutting an effective option to accelerate transition to high forest in European beech (Fagus sylvatica L.) coppice stands? Ann. For. Sci. 2015, 72, 631–640. [Google Scholar] [CrossRef]
- Fattorini, L.; Puletti, N.; Chirici, G.; Corona, P.; Gazzarri, C.; Mura, M.; Marchetti, M. Checking the performance of point and plot sampling on aerial photoimagery of a large-scale population of trees outside forests. Can. J. For. Res. 2016, 46, 1264–1274. [Google Scholar] [CrossRef]
- Puletti, N.; Grotti, M.; Ferrara, C.; Chianucci, F. Lidar-based estimates of aboveground biomass through ground, aerial, and satellite observation: A case study in a Mediterranean forest. J. Appl. Remote. Sens. 2020, 14, 044501. [Google Scholar] [CrossRef]
- Diara, F.; Roggero, M. Quality Assessment of DJI Zenmuse L1 and P1 LiDAR and Photogrammetric Systems: Metric and Statistics Analysis with the Integration of Trimble SX10 Data. Geomatics 2022, 2, 254–281. [Google Scholar] [CrossRef]
- Štroner, M.; Urban, R.; Línková, L. A New Method for UAV Lidar Precision Testing Used for the Evaluation of an Affordable DJI ZENMUSE L1 Scanner. Remote. Sens. 2021, 13, 4811. [Google Scholar] [CrossRef]
- Roussel, J.R.; Auty, D.; Coops, N.C.; Tompalski, P.; Goodbody, T.R.; Meador, A.; Bourdon, J.; De Boissieu, F.; Achim, A. lidR: An R package for analysis of Airborne Laser Scanning (ALS) data. Remote. Sens. Environ. 2020, 251, 112061. [Google Scholar] [CrossRef]
- Keren, S.; Svoboda, M.; Janda, P.; Nagel, T.A. Relationships between Structural Indices and Conventional Stand Attributes in an Old-Growth Forest in Southeast Europe. Forests 2019, 11, 4. [Google Scholar] [CrossRef]
- Team, R.C. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2023. [Google Scholar]
- Juchheim, J.; Ammer, C.; Schall, P.; Seidel, D. Canopy space filling rather than conventional measures of structural diversity explains productivity of beech stands. For. Ecol. Manag. 2017, 395, 19–26. [Google Scholar] [CrossRef]
- Keren, S.; Diaci, J.; Motta, R.; Govedar, Z. Stand structural complexity of mixed old-growth and adjacent selection forests in the Dinaric Mountains of Bosnia and Herzegovina. For. Ecol. Manag. 2017, 400, 531–541. [Google Scholar] [CrossRef]
- Parobeková, Z.; Pittner, J.; Kucbel, S.; Saniga, M.; Filípek, M.; Sedmáková, D.; Vencurik, J.; Jaloviar, P. Structural Diversity in a Mixed Spruce-Fir-Beech Old-Growth Forest Remnant of the Western Carpathians. Forests 2017, 2018, 379. [Google Scholar] [CrossRef]
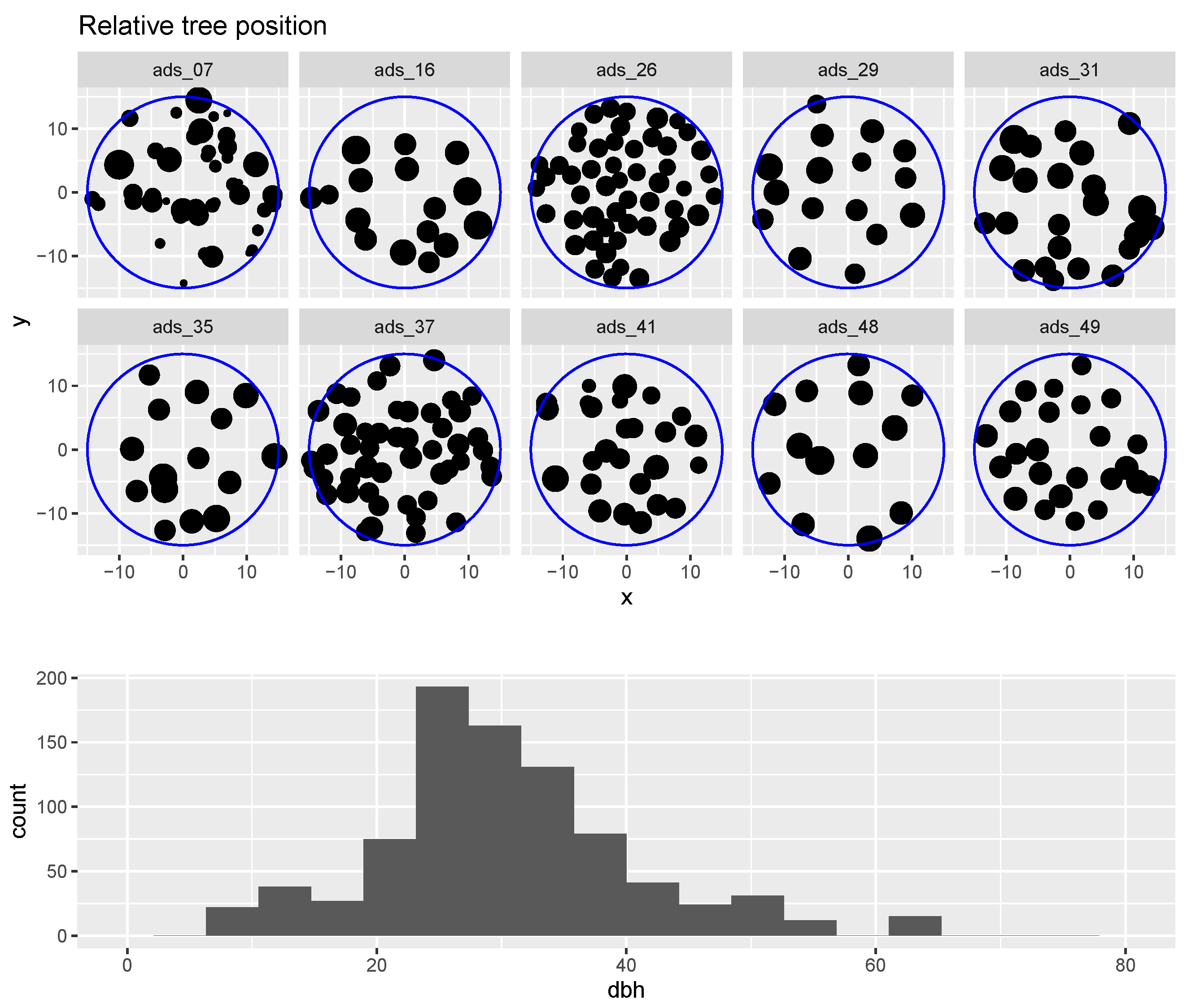

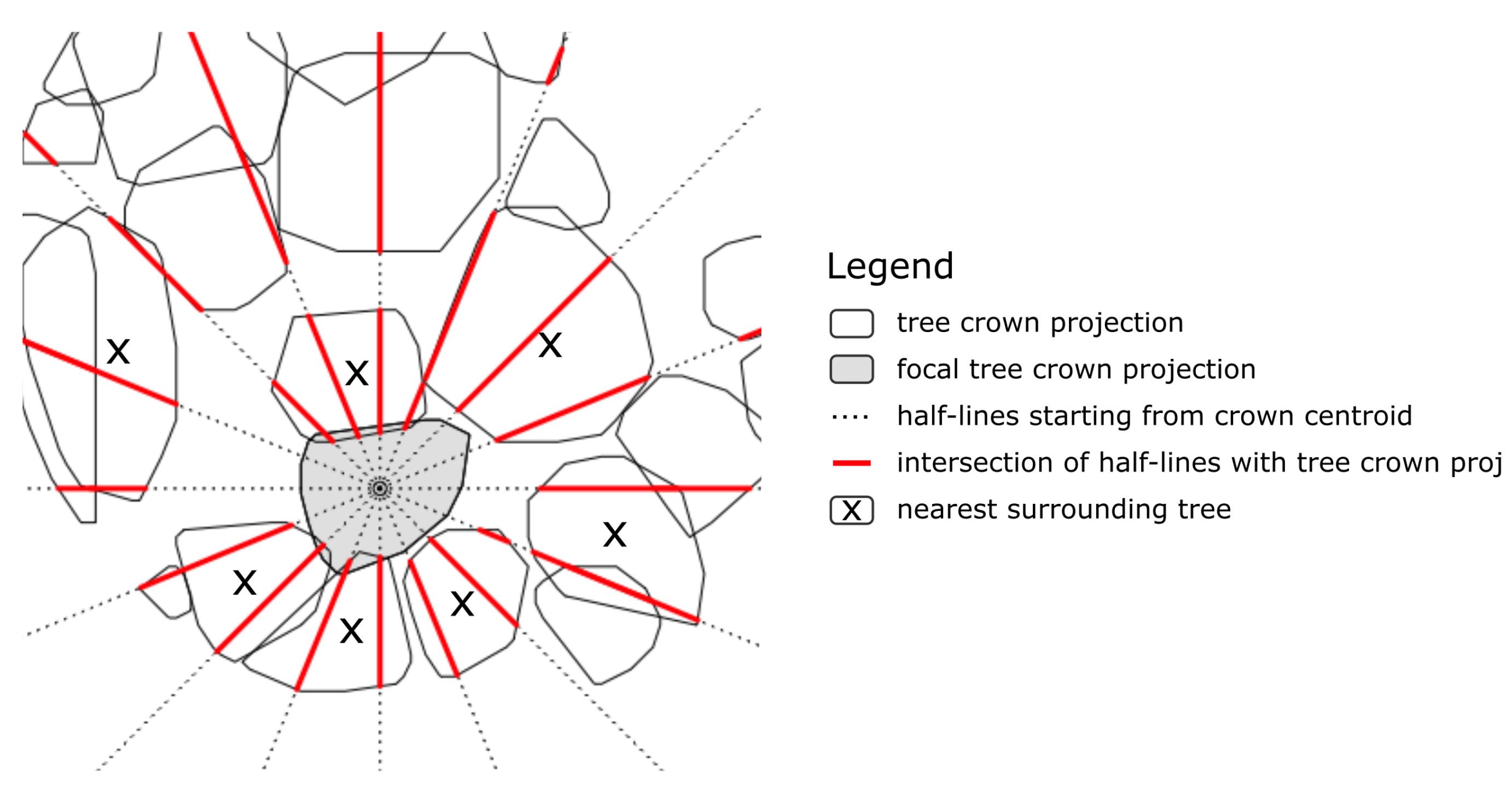
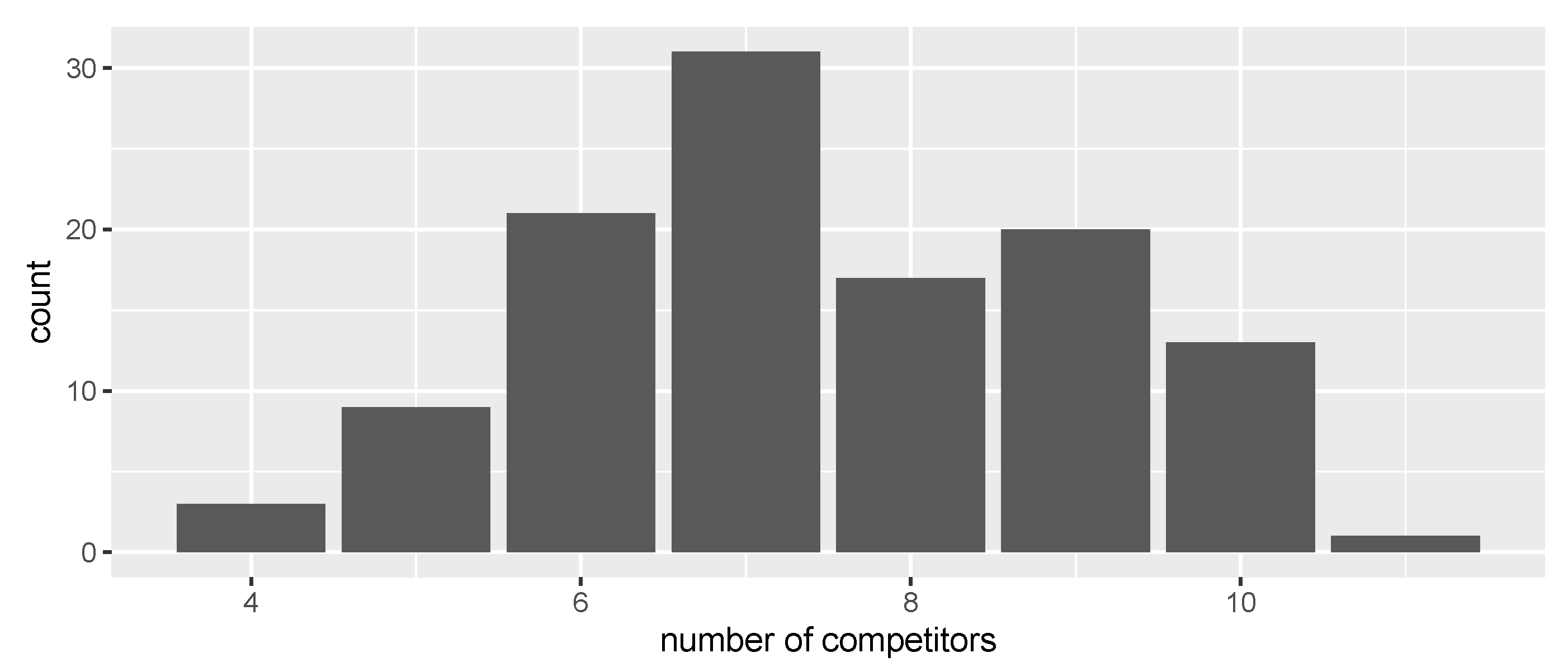
| ads id | N ha−1 | DBH | TH | vol |
|---|---|---|---|---|
| ads_07 | 679.1 | 21.6 (13.4) | 23.9 (3.8) | 0.7 (0.9) |
| ads_16 | 226.4 | 44 (10.9) | 23.1 (1.4) | 1.7 (1) |
| ads_26 | 735.6 | 25.4 (3.8) | 15.4 (1.9) | 0.3 (0.1) |
| ads_29 | 226.4 | 38.4 (9.3) | 21.5 (1.8) | 1.5 (0.8) |
| ads_31 | 325.4 | 42.8 (9.3) | 21.8 (1.6) | 1 (0.5) |
| ads_34 | 127.3 | 48.9 (21.5) | 23.1 (1.3) | 1.9 (1.5) |
| ads_35 | 212.2 | 43.3 (9.7) | 25.1 (1.4) | 1.4 (0.6) |
| ads_37 | 679.1 | 30.2 (4.2) | 22.4 (1.7) | 0.7 (0.2) |
| ads_41 | 382.0 | 32.1 (8.7) | 21.1 (1.7) | 1 (0.8) |
| ads_48 | 183.9 | 44.3 (8.5) | 27.5 (1) | 2.3 (0.8) |
| ads_49 | 339.5 | 33.6 (5.7) | 25.3 (1.3) | 0.9 (0.3) |
| Total | 411.7 | 32.5 (12.2) | 21.8 (4) | 0.9 (0.8) |
| ads id | N ha−1 | CrPrj | CrVol |
|---|---|---|---|
| ads_07 | 679.1 | 10.3 (13.6) | 26.1 (34.2) |
| ads_16 | 226.4 | 27.9 (19.9) | 79.4 (55.1) |
| ads_26 | 735.6 | 7.8 (4.2) | 17.9 (8.2) |
| ads_29 | 226.4 | 28.8 (15.1) | 79.6 (47) |
| ads_31 | 325.4 | 21.9 (13.2) | 53.3 (31.3) |
| ads_34 | 127.3 | 33.9 (22) | 85.9 (49.6) |
| ads_35 | 212.2 | 25.4 (9.9) | 53.9 (29.6) |
| ads_37 | 679.1 | 8.2 (4.2) | 22.8 (10.1) |
| ads_41 | 382.0 | 15.3 (13) | 39.8 (33.9) |
| ads_48 | 183.9 | 27.9 (11.2) | 92.1 (37.7) |
| ads_49 | 339.5 | 15.6 (6.3) | 35 (13.6) |
| Total | 411.7 | 15.6 (13.8) | 40.4 (37.5) |
| 1 | ||||
| 7.60 × | 2.73 × | |||
| 3.89 × | 1.47 × | 0.19 | ||
| 1.39 × | 1.43 × | 1.69 × | 0.62 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Puletti, N.; Guasti, M.; Innocenti, S.; Cesaretti, L.; Chiavetta, U. A Semi-Automatic Approach for Tree Crown Competition Indices Assessment from UAV LiDAR. Remote Sens. 2024, 16, 2576. https://doi.org/10.3390/rs16142576
Puletti N, Guasti M, Innocenti S, Cesaretti L, Chiavetta U. A Semi-Automatic Approach for Tree Crown Competition Indices Assessment from UAV LiDAR. Remote Sensing. 2024; 16(14):2576. https://doi.org/10.3390/rs16142576
Chicago/Turabian StylePuletti, Nicola, Matteo Guasti, Simone Innocenti, Lorenzo Cesaretti, and Ugo Chiavetta. 2024. "A Semi-Automatic Approach for Tree Crown Competition Indices Assessment from UAV LiDAR" Remote Sensing 16, no. 14: 2576. https://doi.org/10.3390/rs16142576
APA StylePuletti, N., Guasti, M., Innocenti, S., Cesaretti, L., & Chiavetta, U. (2024). A Semi-Automatic Approach for Tree Crown Competition Indices Assessment from UAV LiDAR. Remote Sensing, 16(14), 2576. https://doi.org/10.3390/rs16142576








