Estimating Brazilian Amazon Canopy Height Using Landsat Reflectance Products in a Random Forest Model with Lidar as Reference Data
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area and Data
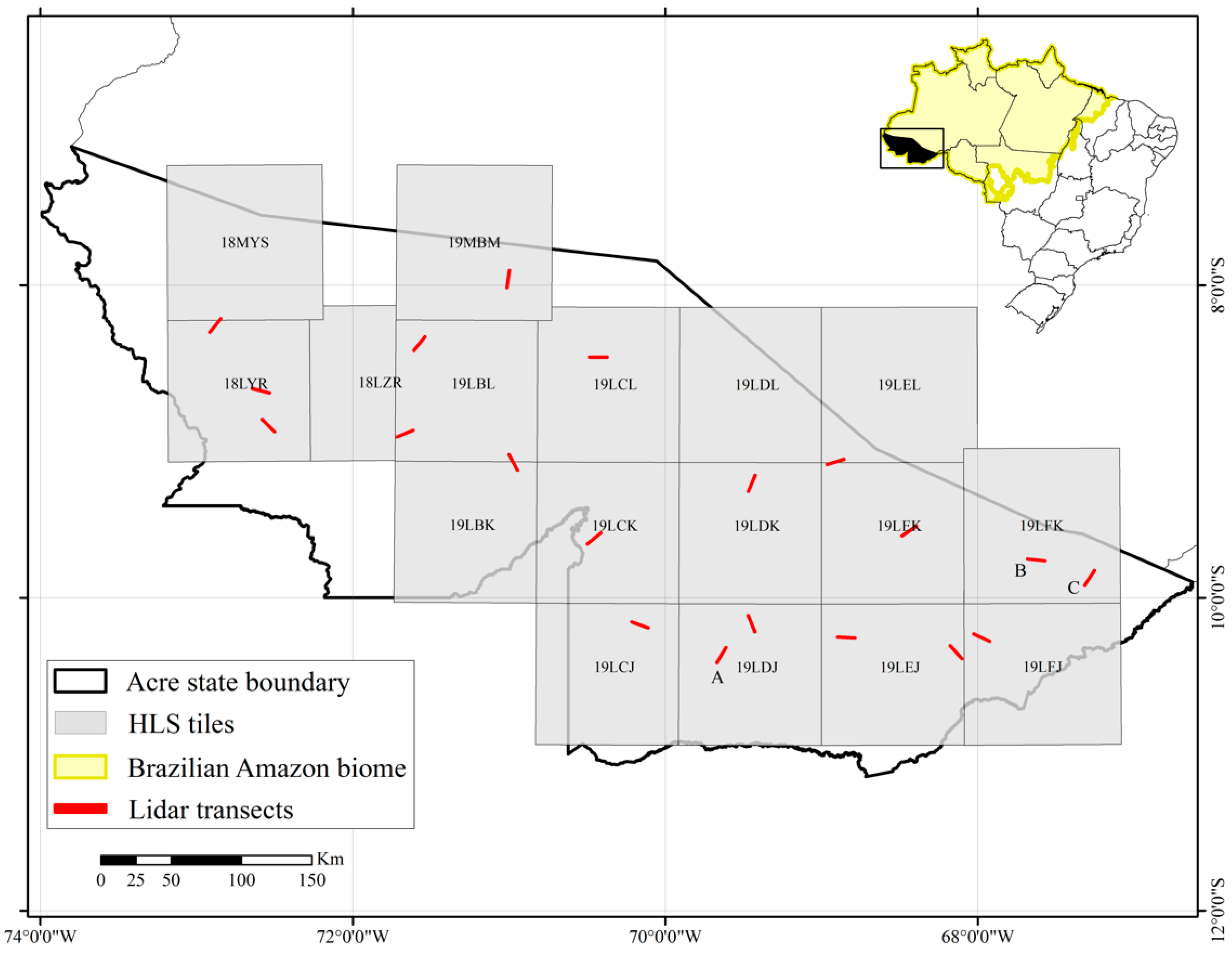
2.1.1. Study Area
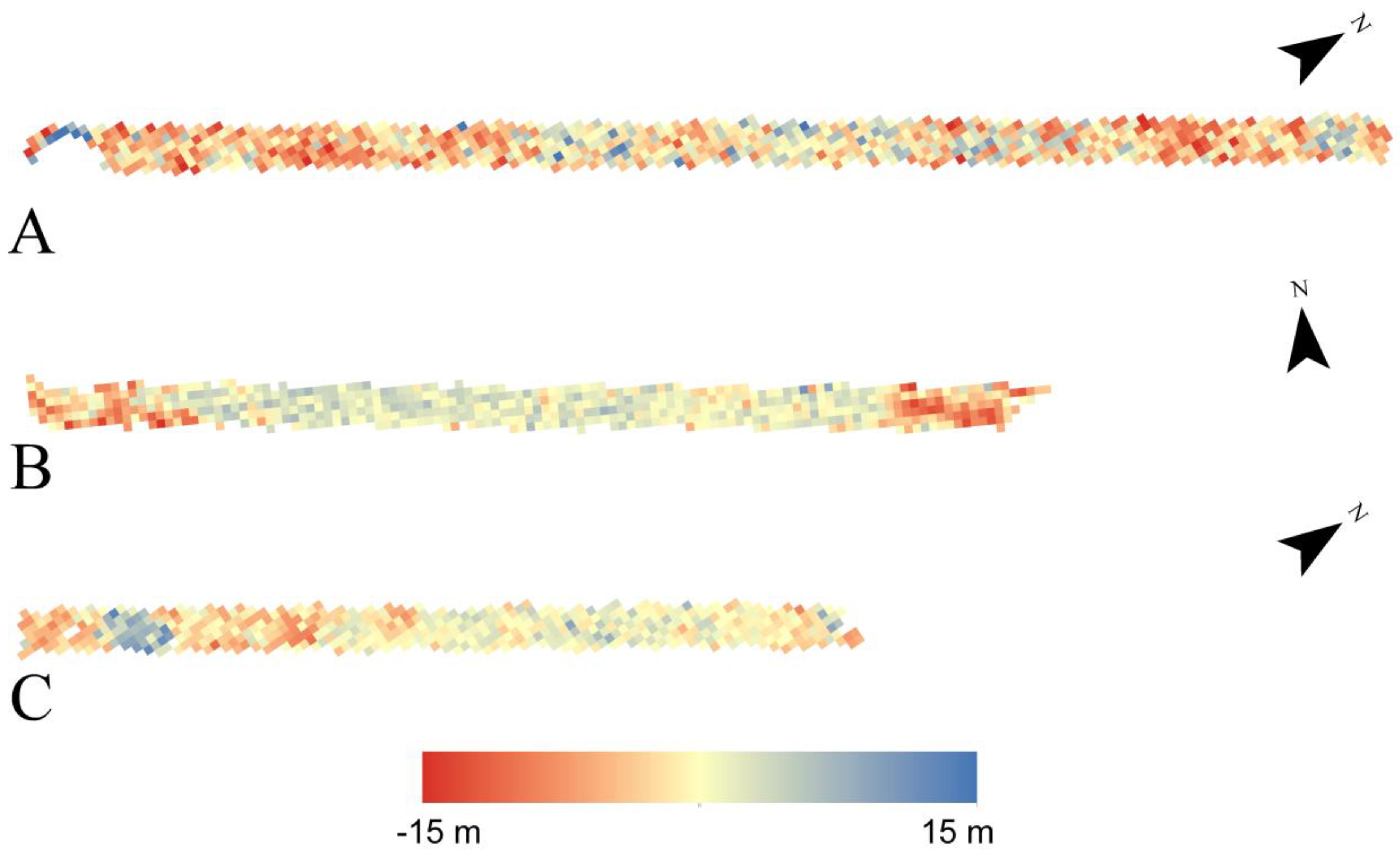
2.1.2. Airborne Lidar Transect Data
2.1.3. Landsat Reflectance Products
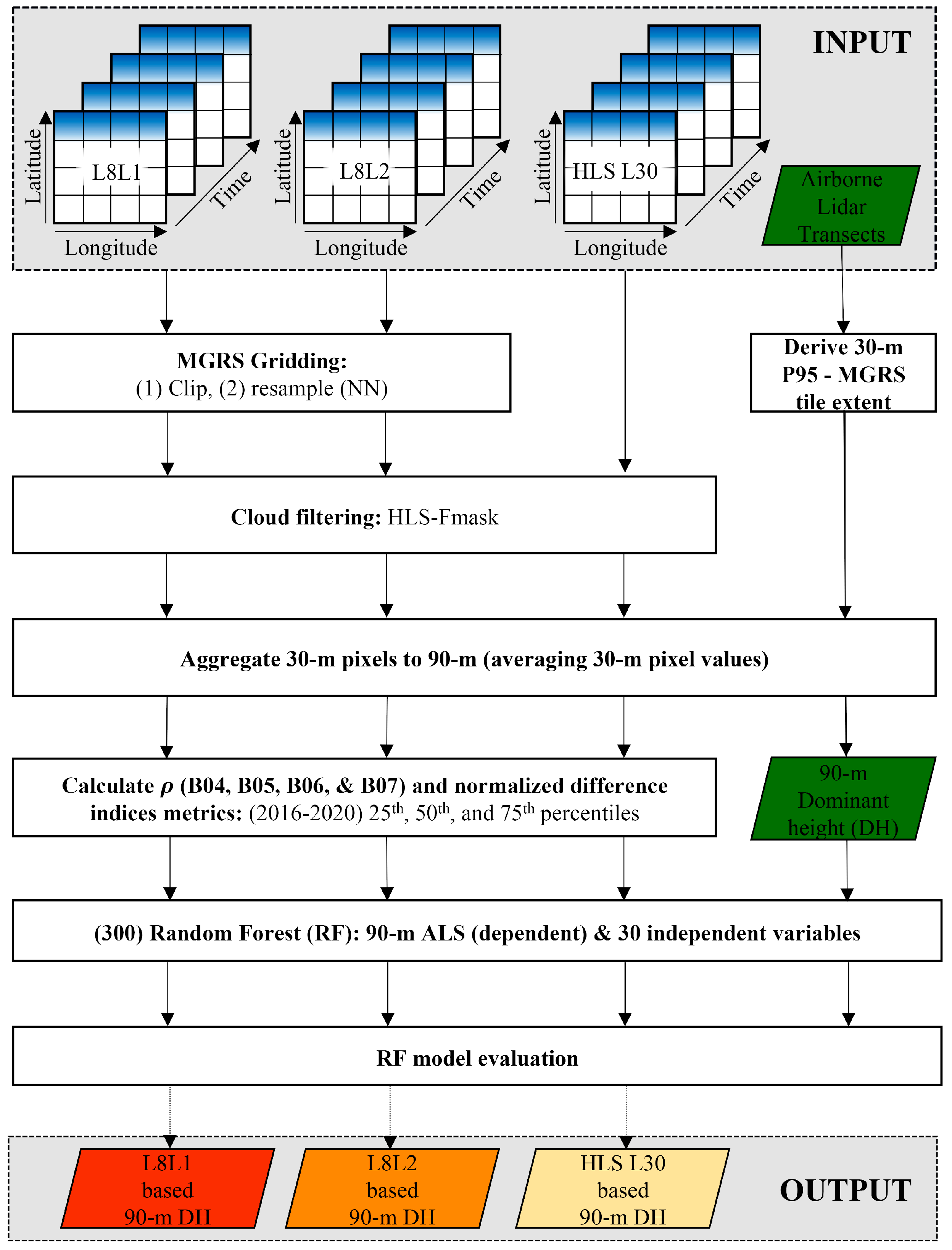
2.2. Methods
2.2.1. Image Data Pre-Processing
2.2.2. Temporal Metric Extraction for Multi-Year Observations
2.2.3. Lidar Data Pre-Processing and 90 m Dominant Canopy Height Estimation
2.2.4. Random Forest DH Prediction Experiments
2.2.5. Random Forest DH Prediction Spatial Autocorrelation Quantification Experiments
3. Results
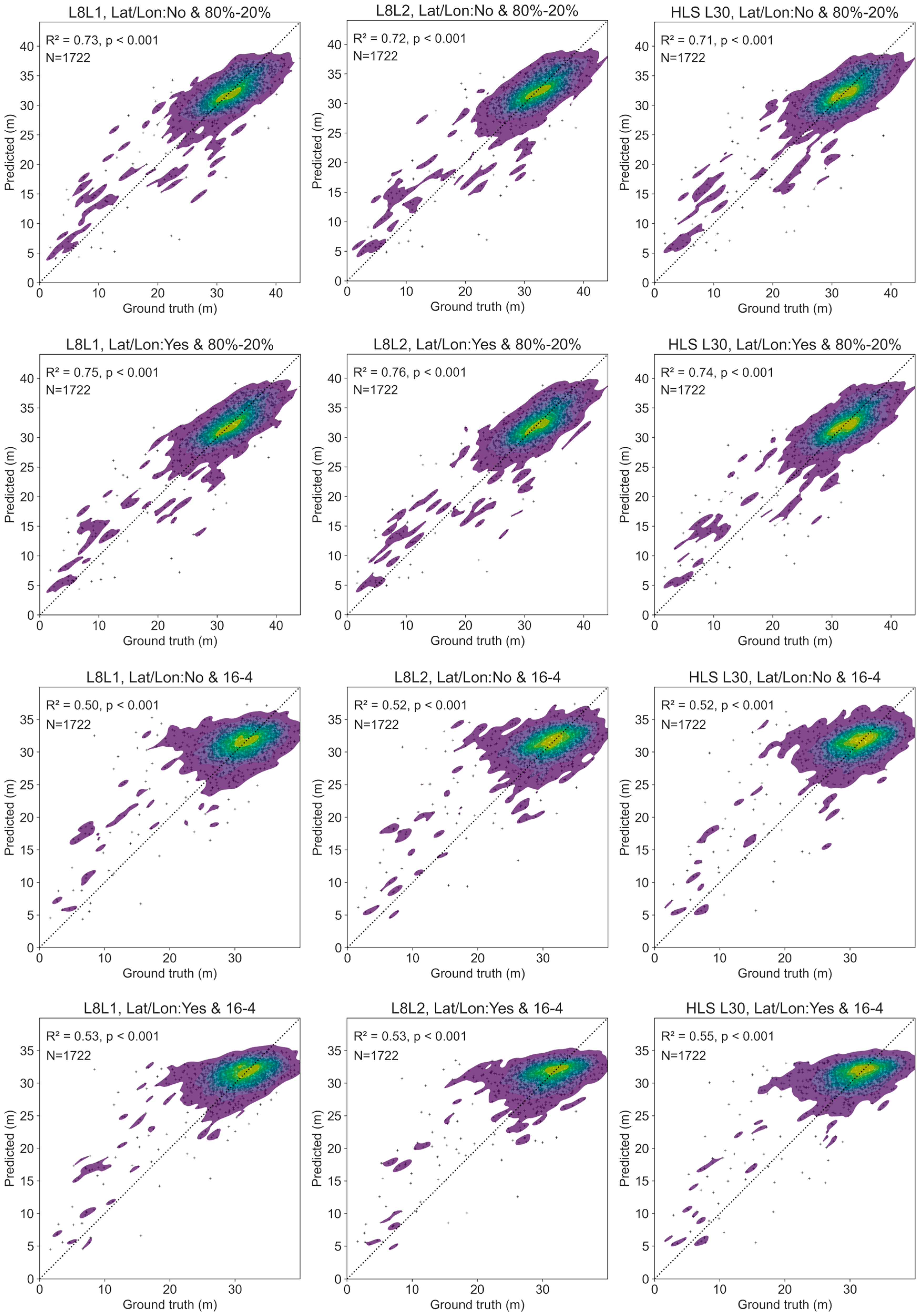
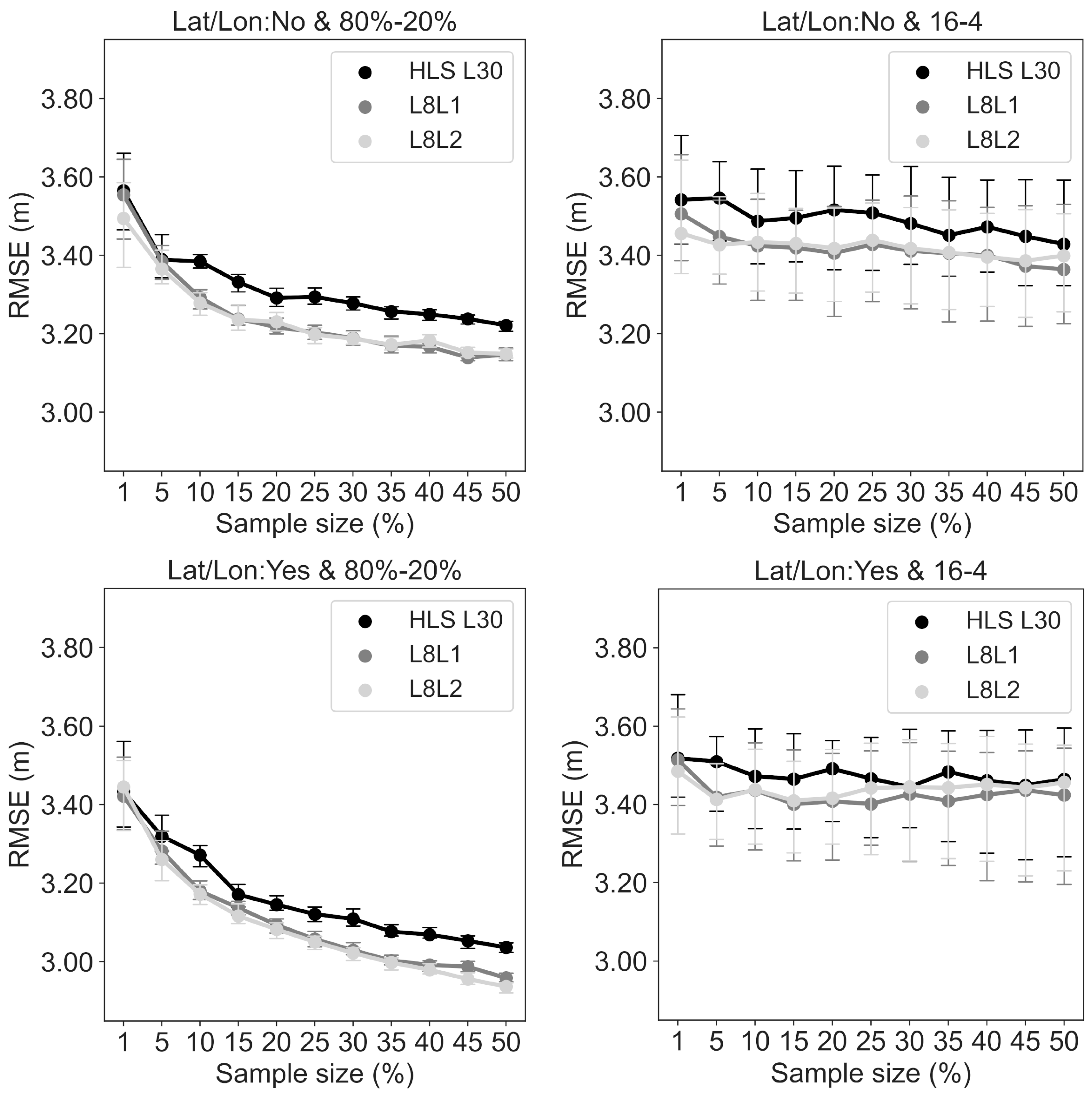
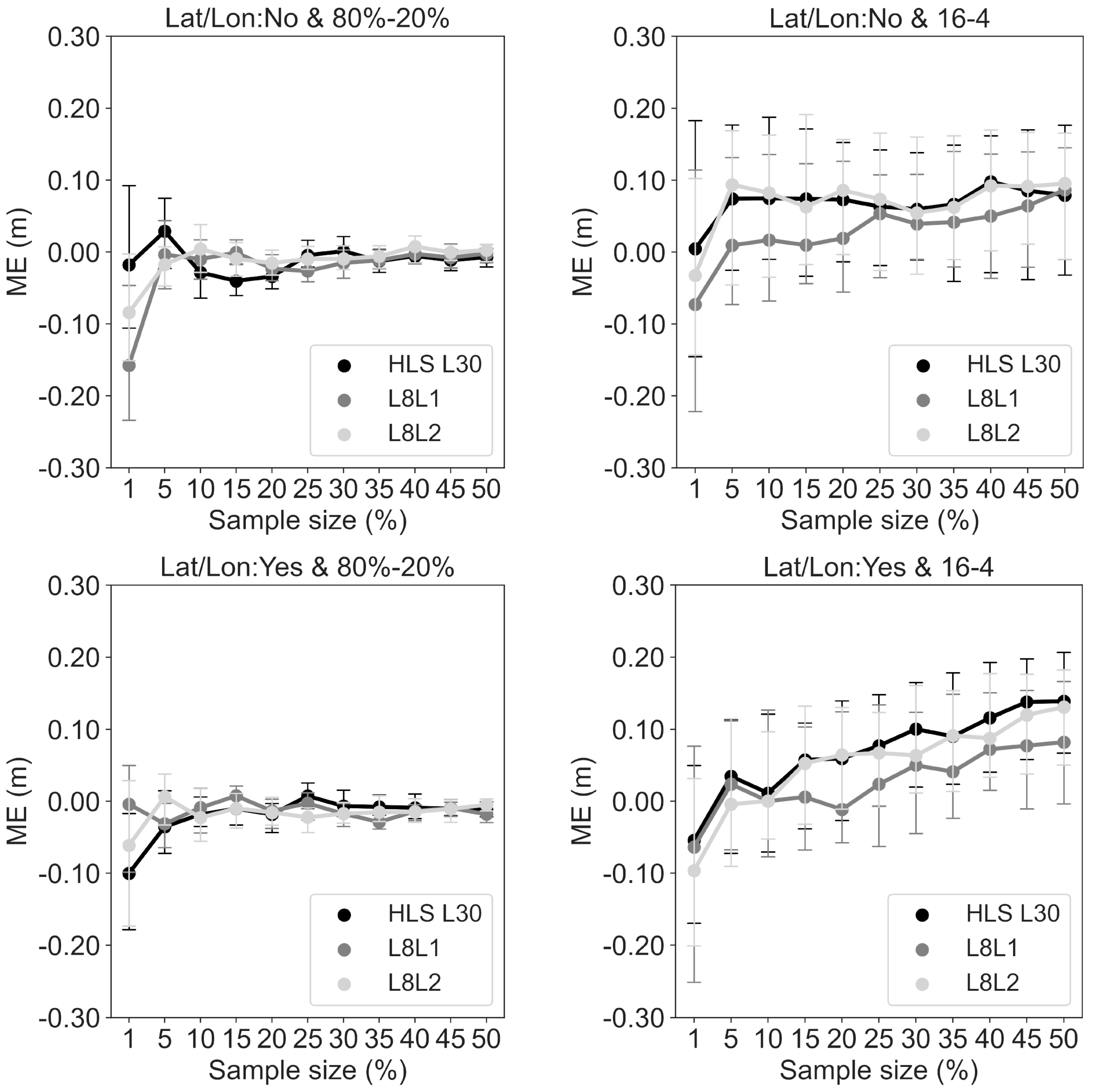
3.1. Sensitivity of Random Forest DH Prediction to the Three Landsat Reflectance Products and Sampling Strategies
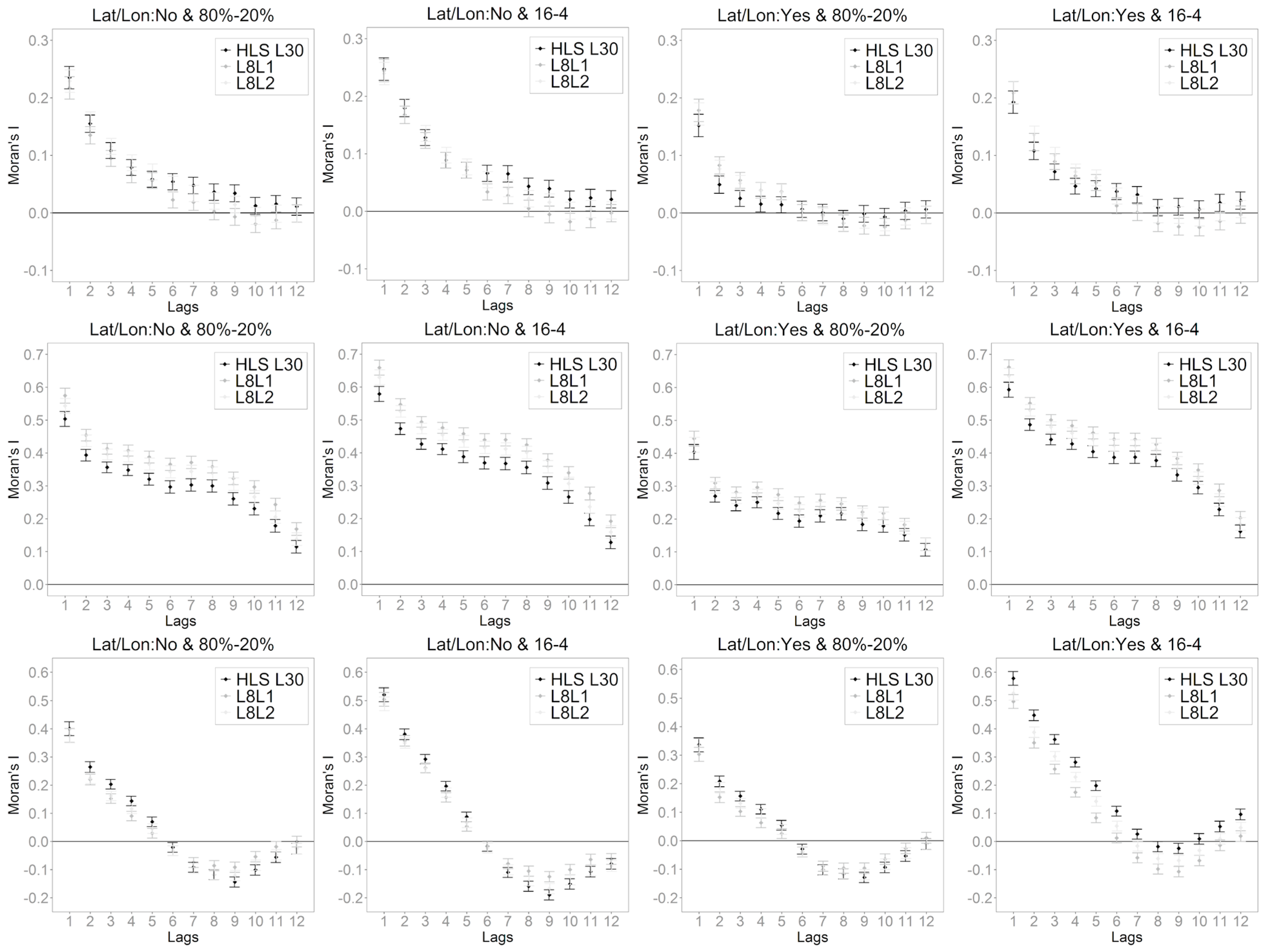
3.2. Impacts of Sample Spatial Autocorrelation on Random Forest DH Predictions
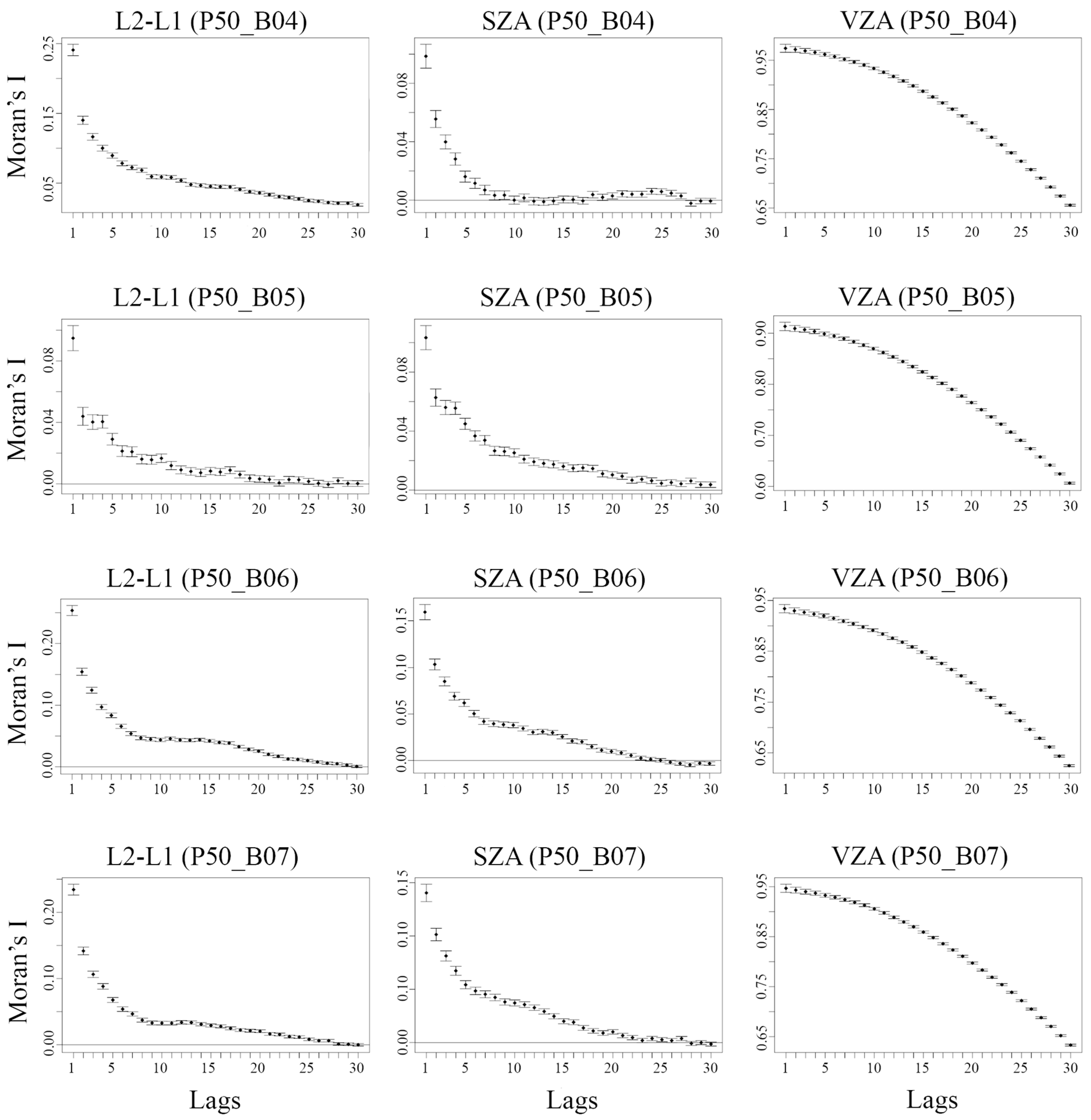
3.3. Important Independent Variables in Random Forest
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gibbs, H.K.; Brown, S.; Niles, J.O.; Foley, J.A. Monitoring and Estimating Tropical Forest Carbon Stocks: Making REDD a Reality. Environ. Res. Lett. 2007, 2, 045023. [Google Scholar] [CrossRef]
- Ometto, J.P.; Aguiar, A.P.; Assis, T.; Soler, L.; Valle, P.; Tejada, G.; Lapola, D.M.; Meir, P. Amazon Forest Biomass Density Maps: Tackling the Uncertainty in Carbon Emission Estimates. Clim. Chang. 2014, 124, 545–560. [Google Scholar] [CrossRef]
- Ometto, J.P.; Gorgens, E.B.; de Souza Pereira, F.R.; Sato, L.; de Assis, M.L.R.; Cantinho, R.; Longo, M.; Jacon, A.D.; Keller, M. A biomass map of the Brazilian Amazon from multisource remote sensing. Sci. Data 2023, 10, 668. [Google Scholar] [CrossRef] [PubMed]
- Aragão, L.E.O.C.; Anderson, L.O.; Fonseca, M.G.; Rosan, T.M.; Vedovato, L.B.; Wagner, F.H.; Silva, C.V.J.; Silva Junior, C.H.L.; Arai, E.; Aguiar, A.P.; et al. 21st Century Drought-Related Fires Counteract the Decline of Amazon Deforestation Carbon Emissions. Nat. Commun. 2018, 9, 536. [Google Scholar] [CrossRef] [PubMed]
- Fearnside, P.M. Greenhouse gases from deforestation in Brazilian Amazonia: Net committed emissions. Clim. Chang. 1997, 35, 321–360. [Google Scholar] [CrossRef]
- Foley, J.A.; Asner, G.P.; Costa, M.H.; Coe, M.T.; DeFries, R.; Gibbs, H.K.; Howard, E.A.; Olson, S.; Patz, J.; Ramankutty, N.; et al. Amazonia revealed: Forest degradation and loss of ecosystem goods and services in the Amazon Basin. Front. Ecol. Environ. 2007, 5, 25–32. [Google Scholar] [CrossRef]
- Nogueira, E.M.; Myanai, A.; Fonseca, F.O.R.; Fearnside, P.M. Carbon Stock Loss from Deforestation through 2013 in Brazilian Amazonia. Glob. Chang. Biol. 2015, 21, 1271–1292. [Google Scholar] [CrossRef] [PubMed]
- Chave, J.; Réjou-Méchain, M.; Búrquez, A.; Chidumayo, E.; Colgan, M.S.; Delitti, W.B.C.; Duque, A.; Eid, T.; Fearnside, P.M.; Goodman, R.C.; et al. Improved Allometric Models to Estimate the Aboveground Biomass of Tropical Trees. Glob. Chang. Biol. 2014, 20, 3177–3190. [Google Scholar] [CrossRef] [PubMed]
- Jucker, T.; Caspersen, J.; Chave, J.; Antin, C.; Barbier, N.; Bongers, F.; Dalponte, M.; van Ewijk, K.Y.; Forrester, D.I.; Haeni, M.; et al. Allometric equations for integrating remote sensing imagery into forest monitoring programmes. Glob. Chang. Biol. 2017, 23, 177–190. [Google Scholar] [CrossRef]
- Disney, M.; Boni Vicari, M.; Burt, A.; Calders, K.; Lewis, S.L.; Raumonen, P.; Wilkes, P. Weighing trees with lasers: Advances, challenges and opportunities. Interface Focus 2018, 8, 20170048. [Google Scholar] [CrossRef]
- Duncanson, L.; Kellner, J.R.; Armston, J.; Dubayah, R.; Minor, D.M.; Hancock, S.; Healey, S.P.; Patterson, P.L.; Saarela, S.; Marselis, S.; et al. Aboveground Biomass Density Models for NASA’s Global Ecosystem Dynamics Investigation (GEDI) Lidar Mission. Remote Sens. Environ. 2022, 270, 112845. [Google Scholar] [CrossRef]
- Silva, C.A.; Duncanson, L.; Hancock, S.; Neuenschwander, A.; Thomas, N.; Hofton, M.; Fatoyinbo, L.; Simard, M.; Marshak, C.Z.; Armston, J.; et al. Fusing Simulated GEDI, ICESat-2 and NISAR Data for Regional Aboveground Biomass Mapping. Remote Sens. Environ. 2021, 253, 112234. [Google Scholar] [CrossRef]
- Lang, N.; Kalischek, N.; Armston, J.; Schindler, K.; Dubayah, R.; Wegner, J.D. Global Canopy Height Regression and Uncertainty Estimation from GEDI LIDAR Waveforms with Deep Ensembles. Remote Sens. Environ. 2022, 268, 112760. [Google Scholar] [CrossRef]
- Lefsky, M.A. A Global Forest Canopy Height Map from the Moderate Resolution Imaging Spectroradiometer and the Geoscience Laser Altimeter System. Geophys. Res. Lett. 2010, 37, L15401. [Google Scholar] [CrossRef]
- Simard, M.; Pinto, N.; Fisher, J.B.; Baccini, A. Mapping Forest Canopy Height Globally with Spaceborne Lidar. J. Geophys. Res. Biogeosci. 2011, 116, G04021. [Google Scholar] [CrossRef]
- Los, S.O.; Rosette, J.A.B.; Kljun, N.; North, P.R.J.; Chasmer, L.; Suárez, J.C.; Hopkinson, C.; Hill, R.A.; Van Gorsel, E.; Mahoney, C.; et al. Vegetation Height and Cover Fraction between 60° S and 60° N from ICESat GLAS Data. Geosci. Model Dev. 2012, 5, 413–432. [Google Scholar] [CrossRef]
- Schutz, B.E.; Zwally, H.J.; Shuman, C.A.; Hancock, D.; DiMarzio, J.P. Overview of the ICESat Mission. Geophys. Res. Lett. 2005, 32, L21S01. [Google Scholar] [CrossRef]
- Ahmed, O.S.; Franklin, S.E.; Wulder, M.A.; White, J.C. Characterizing Stand-Level Forest Canopy Cover and Height Using Landsat Time Series, Samples of Airborne LiDAR, and the Random Forest Algorithm. ISPRS J. Photogramm. Remote Sens. 2015, 101, 89–101. [Google Scholar] [CrossRef]
- Hansen, M.C.; Potapov, P.V.; Goetz, S.J.; Turubanova, S.; Tyukavina, A.; Krylov, A.; Kommareddy, A.; Egorov, A. Mapping Tree Height Distributions in Sub-Saharan Africa Using Landsat 7 and 8 Data. Remote Sens. Environ. 2016, 185, 221–232. [Google Scholar] [CrossRef]
- Ota, T.; Ahmed, O.S.; Franklin, S.E.; Wulder, M.A.; Kajisa, T.; Mizoue, N.; Yoshida, S.; Takao, G.; Hirata, Y.; Furuya, N.; et al. Estimation of Airborne Lidar-Derived Tropical Forest Canopy Height Using Landsat Time Series in Cambodia. Remote Sens. 2014, 6, 10750–10772. [Google Scholar] [CrossRef]
- Potapov, P.V.; Turubanova, S.A.; Hansen, M.C.; Adusei, B.; Broich, M.; Altstatt, A.; Mane, L.; Justice, C.O. Quantifying Forest Cover Loss in Democratic Republic of the Congo, 2000-2010, with Landsat ETM+ Data. Remote Sens. Environ. 2012, 122, 106–116. [Google Scholar] [CrossRef]
- Cliff, A.D.; Ord, J.K. Spatial Processes: Models & Applications; Pion: London, UK, 1981. [Google Scholar]
- Legendre, P. Spatial Autocorrelation: Trouble or New Paradigm? Ecology 1993, 74, 1659–1673. [Google Scholar] [CrossRef]
- Lennon, J.J. Red-Shifts and Red Herrings in Geographical Ecology. Ecography 2000, 23, 101–113. [Google Scholar] [CrossRef]
- Mascaro, J.; Asner, G.P.; Knapp, D.E.; Kennedy-Bowdoin, T.; Martin, R.E.; Anderson, C.; Higgins, M.; Chadwick, K.D. A Tale of Two “Forests”: Random Forest Machine Learning Aids Tropical Forest Carbon Mapping. PLoS ONE 2014, 9, e85993. [Google Scholar] [CrossRef]
- Xu, L.; Saatchi, S.S.; Yang, Y.; Yu, Y.; White, L. Performance of Non-Parametric Algorithms for Spatial Mapping of Tropical Forest Structure. Carbon Balance Manag. 2016, 11, 18–20. [Google Scholar] [CrossRef] [PubMed]
- Karasiak, N.; Dejoux, J.F.; Monteil, C.; Sheeren, D. Spatial Dependence between Training and Test Sets: Another Pitfall of Classification Accuracy Assessment in Remote Sensing. Mach. Learn. 2022, 111, 2715–2740. [Google Scholar] [CrossRef]
- IBGE. Manual Técnico da Vegetação Brasileira, 2nd ed.; IBGE: Rio de Janeiro, Brazil, 2012; ISBN 9788524042720. [Google Scholar]
- Saleska, S.R.; Wu, J.; Guan, K.Y.; Araujo, A.C.; Huete, A.; Nobre, A.D.; Restrepo-Coupe, N. Dry-season greening of Amazon forests. Nature 2016, 531, E4–E5. [Google Scholar] [CrossRef] [PubMed]
- Ometto, J.P.; Gorgens, B.G.; Assis, M.; Cantinho, R.Z.; Pereira, F.R.d.S.; Sato, L.Y. L3A—Summary of Airborne LiDAR Transects Collected by EBA in the Brazilian Amazon (Version 20210616) [Data Set]. Zenodo 2021. Available online: https://zenodo.org/records/4968706 (accessed on 25 June 2024). [CrossRef]
- Kotchenova, S.Y.; Vermote, E.F.; Matarrese, R.; Klemm, F.J. Validation of a Vector Version of the 6S Radiative Transfer Code for Atmospheric Correction of Satellite Data. Part I: Path Radiance. Appl. Opt. 2006, 45, 6762–6774. [Google Scholar] [CrossRef] [PubMed]
- Asner, G.P. Cloud cover in Landsat observations of the Brazilian Amazon. Int. J. Remote Sens. 2001, 22, 3855–3862. [Google Scholar] [CrossRef]
- Crawford, C.J.; Roy, D.P.; Arab, S.; Barnes, C.; Vermote, E.; Hulley, G.; Gerace, A.; Choate, M.; Engebretson, C.; Micijevic, E.; et al. The 50-Year Landsat Collection 2 Archive. Sci. Remote Sens. 2023, 8, 100103. [Google Scholar] [CrossRef]
- Roy, D.P.; Zhang, H.K.; Ju, J.; Gomez-Dans, J.L.; Lewis, P.E.; Schaaf, C.B.; Sun, Q.; Li, J.; Huang, H.; Kovalskyy, V. A General Method to Normalize Landsat Reflectance Data to Nadir BRDF Adjusted Reflectance. Remote Sens. Environ. 2016, 176, 255–271. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, H.K.; Roy, D.P. Investigation of Sentinel-2 bidirectional reflectance hot-spot sensing conditions. IEEE Trans. Geosci. Remote Sens. 2018, 57, 3591–3598. [Google Scholar] [CrossRef]
- Masek, J.; Ju, J.; Roger, J.; Skakun, S.; Vermote, E.; Claverie, M.; Dungan, J.; Yin, Z.; Freitag, B.; Justice, C. HLS Operational Land Imager Surface Reflectance and TOA Brightness Daily Global 30m (v2.0) [Data Set]. NASA EOSDIS Land Processes DAAC 2021. Available online: https://lpdaac.usgs.gov/products/hlsl30v002/ (accessed on 25 June 2024). [CrossRef]
- Qiu, S.; Zhu, Z.; He, B. Fmask 4.0: Improved Cloud and Cloud Shadow Detection in Landsats 4–8 and Sentinel-2 Imagery. Remote Sens. Environ. 2019, 231, 111205. [Google Scholar] [CrossRef]
- DeFries, R.; Hansen, M.; Townshend, J. Global Discrimination of Land Cover Types from Metrics Derived from AVHRR Pathfinder Data. Remote Sens. Environ. 1995, 54, 209–222. [Google Scholar] [CrossRef]
- Zhang, H.K.; Roy, D.P. Using the 500 m MODIS land cover product to derive a consistent continental scale 30 m Landsat land cover classification. Remote Sens. Environ. 2017, 197, 15–34. [Google Scholar] [CrossRef]
- McGaughey, R.J. FUSION/LDV: Software for LIDAR Data Analysis and Visualization v. 4.50; United States Department of Agriculture: Seattle, WA, USA, 2023.
- Kraus, K.; Pfeifer, N. Determination of Terrain Models in Wooded Areas with Airborne Laser Scanner Data. ISPRS J. Photogramm. Remote Sens. 1998, 53, 193–203. [Google Scholar] [CrossRef]
- Coops, N.C.; Hilker, T.; Wulder, M.A.; St-Onge, B.; Newnham, G.; Siggins, A.; Trofymow, J.A. Estimating Canopy Structure of Douglas-Fir Forest Stands from Discrete-Return LiDAR. Trees -Struct. Funct. 2007, 21, 295–310. [Google Scholar] [CrossRef]
- Cochran, W.G. Sampling Techniques, 3rd ed.; John Wiley & Sons: New York, NY, USA, 1977. [Google Scholar]
- Foody, G.M. Status of Land Cover Classification Accuracy Assessment. Remote Sens. Environ. 2002, 80, 185–201. [Google Scholar] [CrossRef]
- Rogan, J.; Franklin, J.; Stow, D.; Miller, J.; Woodcock, C.; Roberts, D. Mapping Land-Cover Modifications over Large Areas: A Comparison of Machine Learning Algorithms. Remote Sens. Environ. 2008, 112, 2272–2283. [Google Scholar] [CrossRef]
- Yan, L.; Roy, D.P. Improved Time Series Land Cover Classification by Missing-Observation-Adaptive Nonlinear Dimensionality Reduction. Remote Sens. Environ. 2015, 158, 478–491. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Legendre, P.; Legendre, L. Numerical Ecology, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Diniz-Filho, J.A.F.; Bini, L.M.; Hawkins, B.A. Spatial Autocorrelation and Red Herrings in Geographical Ecology. Glob. Ecol. Biogeogr. 2003, 12, 53–64. [Google Scholar] [CrossRef]
- Lyons, M.B.; Keith, D.A.; Phinn, S.R.; Mason, T.J.; Elith, J. A Comparison of Resampling Methods for Remote Sensing Classification and Accuracy Assessment. Remote Sens. Environ. 2018, 208, 145–153. [Google Scholar] [CrossRef]
- Schratz, P.; Muenchow, J.; Iturritxa, E.; Richter, J.; Brenning, A. Hyperparameter Tuning and Performance Assessment of Statistical and Machine-Learning Algorithms Using Spatial Data. Ecol. Modell. 2019, 406, 109–120. [Google Scholar] [CrossRef]
- Miller, J.; Franklin, J.; Aspinall, R. Incorporating Spatial Dependence in Predictive Vegetation Models. Ecol. Modell. 2007, 202, 225–242. [Google Scholar] [CrossRef]
- Getis, A.; Ord, J.K. The Analysis of Spatial Association by Use of Distance Statistics. Geogr. Anal. 1992, 24, 189–206. [Google Scholar] [CrossRef]
- Wulder, M.; Boots, B. Local Spatial Autocorrelation Characteristics of Remotely Sensed Imagery Assessed with the Getis Statistic. Int. J. Remote Sens. 1998, 19, 2223–2231. [Google Scholar] [CrossRef]
- Ghimire, B.; Rogan, J.; Miller, J. Contextual Land-Cover Classification: Incorporating Spatial Dependence in Land-Cover Classification Models Using Random Forests and the Getis Statistic. Remote Sens. Lett. 2010, 1, 45–54. [Google Scholar] [CrossRef]
- Borcard, D.; Legendre, P. All-Scale Spatial Analysis of Ecological Data by Means of Principal Coordinates of Neighbour Matrices. Ecol. Modell. 2002, 153, 51–68. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Yun, T.; Li, J.; Ma, L.; Zhou, J.; Wang, R.; Eichhorn, M.P.; Zhang, H. Status, advancements and prospects of deep learning methods applied in forest studies. Int. J. Appl. Earth Obs. Geoinf. 2024, 131, 103938. [Google Scholar] [CrossRef]
- Gorgens, E.B.; Nunes, M.H.; Jackson, T.; Coomes, D.; Keller, M.; Reis, C.R.; Valbuena, R.; Rosette, J.; de Almeida, D.R.A.; Gimenez, B.; et al. Resource Availability and Disturbance Shape Maximum Tree Height across the Amazon. Glob. Chang. Biol. 2021, 27, 177–189. [Google Scholar] [CrossRef] [PubMed]

| Transect | Count | Mean | Std | Min | P25 | P50 | P75 | Max |
|---|---|---|---|---|---|---|---|---|
| 1 | 877 | 36.30 | 2.61 | 27.95 | 34.59 | 36.20 | 37.97 | 45.30 |
| 2 | 872 | 35.45 | 2.44 | 25.00 | 33.91 | 35.42 | 37.08 | 43.17 |
| 3 | 781 | 33.39 | 4.25 | 4.03 | 32.41 | 34.13 | 35.58 | 40.68 |
| 4 | 888 | 30.99 | 2.83 | 19.74 | 29.47 | 31.11 | 32.89 | 38.47 |
| 5 * | 849 | 30.95 | 2.82 | 14.19 | 29.28 | 30.96 | 32.77 | 40.08 |
| 6 | 890 | 31.42 | 3.09 | 22.30 | 29.48 | 31.52 | 33.60 | 40.56 |
| 7 | 856 | 30.53 | 4.53 | 3.69 | 29.06 | 31.24 | 33.16 | 39.20 |
| 8 | 892 | 30.87 | 2.66 | 22.15 | 29.16 | 30.76 | 32.66 | 39.48 |
| 9 | 902 | 30.48 | 3.12 | 21.00 | 28.43 | 30.62 | 32.65 | 39.22 |
| 10 | 902 | 32.17 | 4.18 | 7.70 | 30.38 | 32.78 | 34.86 | 41.28 |
| 11 | 864 | 24.90 | 10.77 | 1.79 | 16.46 | 29.07 | 33.46 | 40.47 |
| 12 | 855 | 31.32 | 2.75 | 20.84 | 29.52 | 31.28 | 33.19 | 39.09 |
| 13 | 837 | 27.48 | 8.86 | 1.64 | 23.46 | 30.78 | 33.83 | 39.67 |
| 14 ** | 819 | 22.42 | 9.71 | 1.51 | 14.88 | 25.97 | 30.19 | 37.63 |
| 15 *** | 641 | 28.64 | 5.99 | 2.88 | 26.57 | 30.03 | 32.29 | 38.46 |
| 16 | 900 | 31.11 | 3.23 | 9.23 | 29.26 | 31.42 | 33.24 | 39.26 |
| 17 | 893 | 30.46 | 4.18 | 5.31 | 28.91 | 30.92 | 32.98 | 40.78 |
| 18 | 919 | 33.44 | 2.44 | 18.44 | 31.93 | 33.50 | 35.02 | 40.86 |
| 19 | 848 | 32.65 | 2.65 | 25.58 | 30.85 | 32.57 | 34.36 | 43.56 |
| 20 | 918 | 35.58 | 4.43 | 8.09 | 33.94 | 36.14 | 38.20 | 44.45 |
| All | 12,212 | 31.10 | 5.93 | 1.51 | 29.45 | 32.05 | 34.47 | 45.30 |
| Sample Size | NTotal | NTrain | NTest |
|---|---|---|---|
| 1% | 172 | 137 | 35 |
| 5% | 861 | 688 | 173 |
| 10% | 1721 | 1376 | 345 |
| 15% | 2582 | 2065 | 517 |
| 20% | 3442 | 2753 | 689 |
| 25% | 4303 | 3442 | 861 |
| 30% | 5164 | 4131 | 1033 |
| 35% | 6024 | 4819 | 1205 |
| 40% | 6885 | 5508 | 1377 |
| 45% | 7745 | 6196 | 1549 |
| 50% | 8606 | 6884 | 1772 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oliveira, P.V.C.; Zhang, H.K.; Zhang, X. Estimating Brazilian Amazon Canopy Height Using Landsat Reflectance Products in a Random Forest Model with Lidar as Reference Data. Remote Sens. 2024, 16, 2571. https://doi.org/10.3390/rs16142571
Oliveira PVC, Zhang HK, Zhang X. Estimating Brazilian Amazon Canopy Height Using Landsat Reflectance Products in a Random Forest Model with Lidar as Reference Data. Remote Sensing. 2024; 16(14):2571. https://doi.org/10.3390/rs16142571
Chicago/Turabian StyleOliveira, Pedro V. C., Hankui K. Zhang, and Xiaoyang Zhang. 2024. "Estimating Brazilian Amazon Canopy Height Using Landsat Reflectance Products in a Random Forest Model with Lidar as Reference Data" Remote Sensing 16, no. 14: 2571. https://doi.org/10.3390/rs16142571
APA StyleOliveira, P. V. C., Zhang, H. K., & Zhang, X. (2024). Estimating Brazilian Amazon Canopy Height Using Landsat Reflectance Products in a Random Forest Model with Lidar as Reference Data. Remote Sensing, 16(14), 2571. https://doi.org/10.3390/rs16142571









