Combining LiDAR and Spaceborne Multispectral Data for Mapping Successional Forest Stages in Subtropical Forests
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data Collection and Processing
2.2.1. LiDAR Data
2.2.2. Description of the Multispectral Satellite Data
2.2.3. Preprocessing Satellite Images
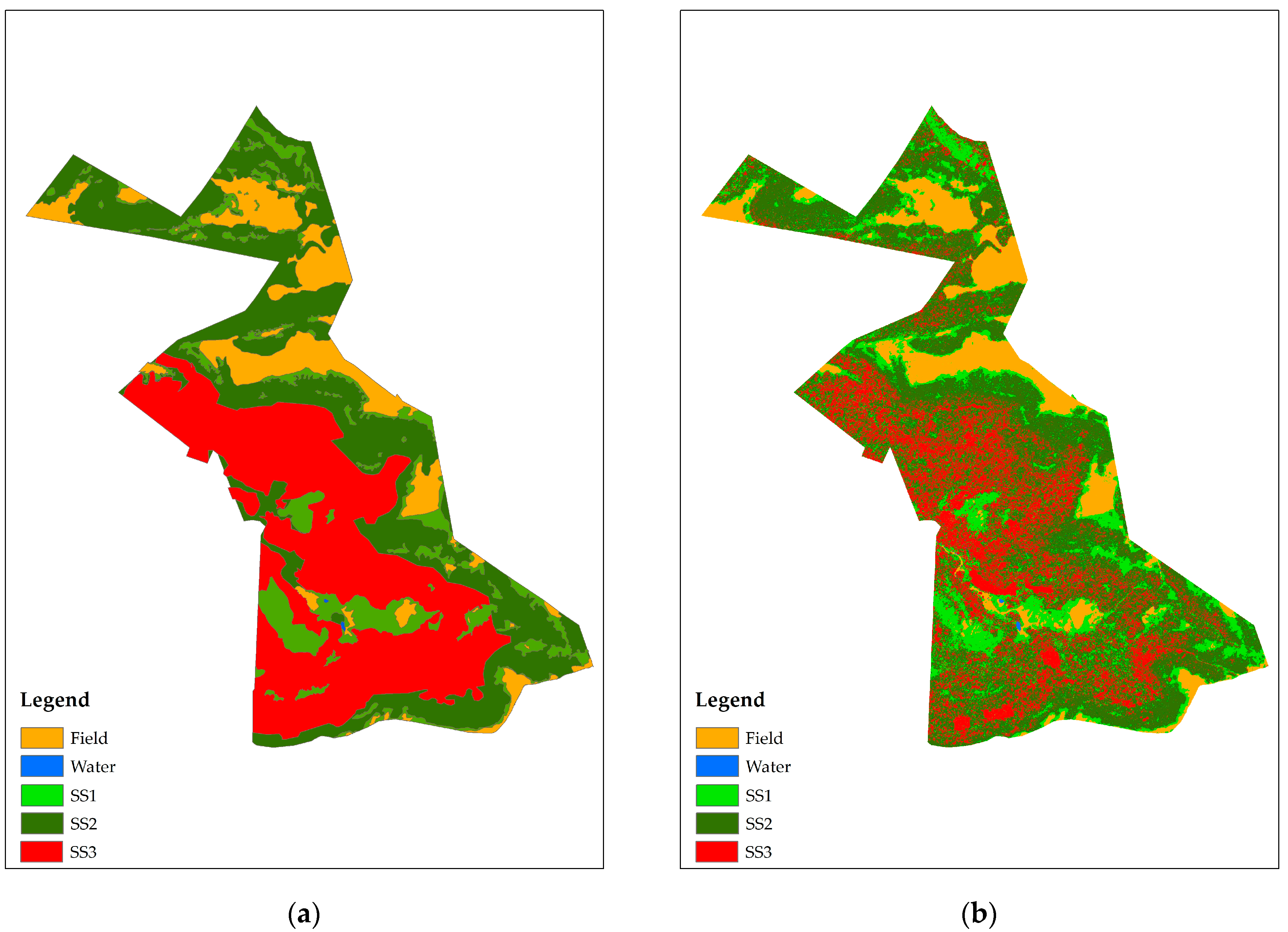
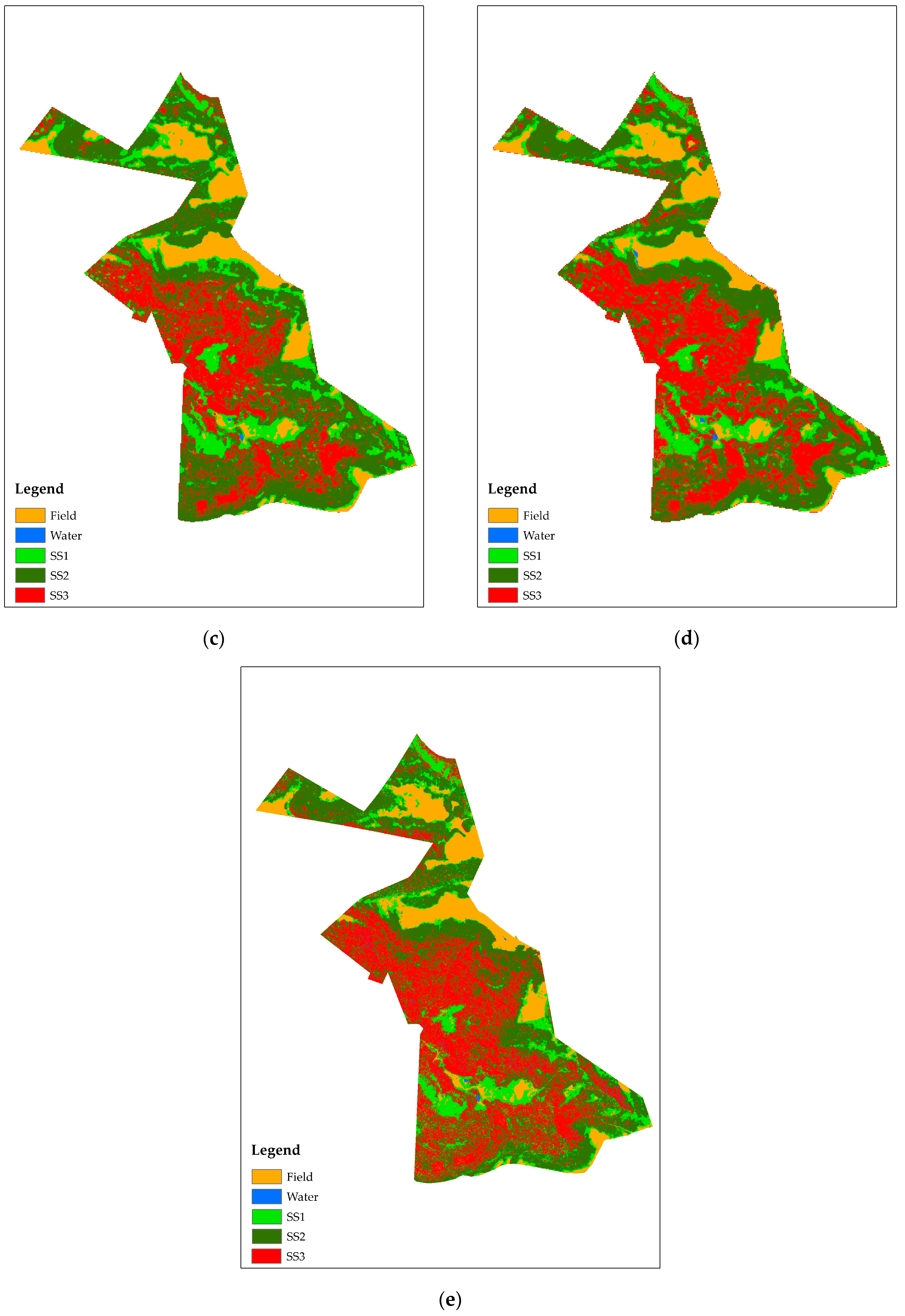
2.2.4. Reference Classification
2.2.5. Unmanned Aerial Vehicle (UAV)
2.2.6. Datasets Creation
2.3. Image Classification
2.3.1. Sampling
2.3.2. Supervised Classification
2.4. Accuracy Assessment
3. Results
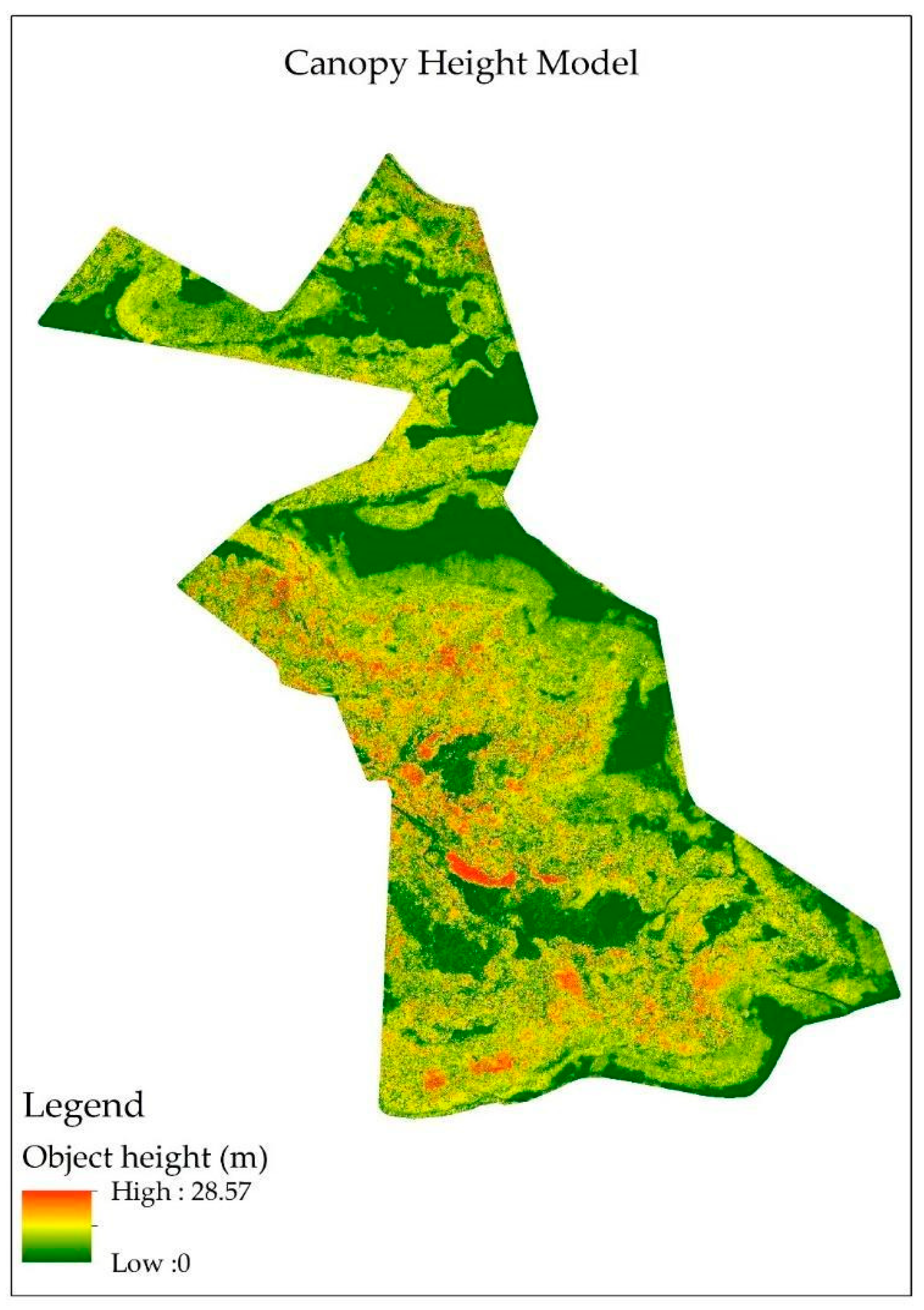
3.1. Canopy Height Model
3.2. Classification of the Vegetation Succession Stages
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A


References
- Andersen, H.E.; Reutebuch, S.E.; Mcgaughey, R.J. Active remote sensing. In Computer Applications in Sustainable Forest Management; Shao, G., Reynolds, K., Shao, G., Eds.; Springer: Dordrecht, The Netherlands, 2006; pp. 43–66. [Google Scholar]
- Rezende, C.L.; Scarano, F.R.; Assad, E.D.; Joly, C.A.; Metzger, J.P.; Strassburg, B.B.N.; Tabarelli, M.; Fonse, G.A.; Mittermeier, R.A. From hotspot to hopespot: An opportunity for the Brazilian Atlantic Forest. Perspect. Ecol. Conserv. 2018, 16, 208–214. [Google Scholar] [CrossRef]
- Joly, C.A.; Metzger, J.P.; Tabarelli, M. Experiences from the Brazilian Atlantic forest: Ecological findings and conservation initiatives. New Phytol. 2014, 204, 459–473. [Google Scholar] [CrossRef]
- Kageyama, P.Y.; Brito, M.A.; Baptiston, I.C. Estudo do mecanismo de reprodução de espécies da mata natural. In Estudo para Implantação de Matas Ciliares de Proteção na Bacia Hidrográfica do Passa Cinco, Piracicaba, SP; Kageyama, P.Y., Ed.; DAEE/USP/FEALQ: Piracicaba, Brasil, 1986; p. 236. [Google Scholar]
- Sevegnani, L.; Uhlmann, A.; Gasper, A.L.; Vibrans, A.C.; Stival-Santos, A.; Verdi, M.; Dreveck, S. Estádios sucessionais da Floresta Ombrófila Mista em Santa Catarina. In Inventário Florístico Florestal de Santa Catarina; Vibrans, A.C., Sevegnani, L., Gasper, A.L., Lingner, D.V., Eds.; Edifurb: Blumenau, Brasil, 2012; Volume 3, pp. 255–271, cap. 9. [Google Scholar]
- Shugart, H.H. Importance of Structure in the Longer-Term Dynamics of Landscapes. J. Geophys. Res. Atmos. 2000, 105, 20065–20075. [Google Scholar] [CrossRef]
- Cabral, R.P.; da Silva, G.F.; de Almeida, A.Q.; Bonilla-Bedoya, S.; Dias, H.M.; De Mendonça, A.R.; Rodrigues, N.M.M.; Valente, C.C.A.; Oliveira, K.; Gonçalves, F.G.; et al. Mapping of the Successional Stage of a Secondary Forest Using Point Clouds Derived from UAV Photogrammetry. Remote Sens. 2023, 15, 509. [Google Scholar] [CrossRef]
- Cintra, D.P.; Oliveira, R.R.; Rego, L.F.G. Classificação dos Estágios Sucessionais Florestais Através de Imagens Ikonos No Parque Estadual Da Pedra Branca. XIII Simpósio Bras. Sensoriamento Remoto 2007, 13, 1627–1629. [Google Scholar]
- Jensen, J.R. Sensoriamento Remoto Do Ambiente: Uma Perspectiva Em Recursos Terrestres (Tradução Da Segunda Edição). Inf. Syst. 2009, 336–409. [Google Scholar]
- Reutebuch, S.E.; Andersen, H.E.; McGaughey, R.J. Light Detection and Ranging (LIDAR): An Emerging Tool for Multiple Resource Inventory. J. For. 2005, 103, 286–292. [Google Scholar] [CrossRef]
- Tiede, D.; Hochleitner, G.; Blaschke, T. A Full GIS-Based Workflow for Tree Identification and Tree Crown Delineation Using Laser Scanning. In ISPRS Workshop CMRT; ISPRS: Baton Rouge, LA, USA, 2005; Volume XXXVI, pp. 9–14. [Google Scholar]
- Falkowski, M.J.; Evans, J.S.; Martinuzzi, S.; Gessler, P.E.; Hudak, A.T. Characterizing Forest Succession with LiDAR Data: An Evaluation for the Inland Northwest, USA. Remote Sens. Environ. 2009, 113, 946–956. [Google Scholar] [CrossRef]
- Castillo, M.; Rivard, B.; Sánchez-Azofeifa, A.; Calvo-Alvarado, J.; Dubayah, R. LIDAR remote sensing for secondary tropical dry forest identification. Remote Sens. Environ. 2012, 121, 132–143. [Google Scholar] [CrossRef]
- Bispo, P.D.C.; Pardini, M.; Papathanassiou, K.P.; Kugler, F.; Balzter, H.; Rains, D.; dos Santos, J.R.; Rizaev, I.G.; Tansey, K.; dos Santos, M.N.; et al. Mapping forest successional stages in the Brazilian Amazon using forest heights derived from TanDEM-X SAR interferometry. Remote. Sens. Environ. 2019, 232, 111194. [Google Scholar] [CrossRef]
- Kolecka, N.; Kozak, J.; Kaim, D.; Dobosz, M.; Ginzler, C.; Psomas, A. Mapping Secondary Forest Succession on Abandoned Agricultural Land with LiDAR Point Clouds and Terrestrial Photography. Remote Sens. 2015, 7, 8300–8322. [Google Scholar] [CrossRef]
- Lefsky, M.A.; Cohen, W.B.; Harding, D.J.; Parker, G.G.; Acker, S.A.; Gower, S.T. LiDAR Remote Sensing of Above-Ground Biomass in Three Biomes. Glob. Ecol. Biogeogr. 2002, 11, 393–399. [Google Scholar] [CrossRef]
- Næsset, E. Practical Large-Scale Forest Stand Inventory Using a Small-Footprint Airborne Scanning Laser. Scand. J. For. Res. 2004, 19, 164–179. [Google Scholar] [CrossRef]
- Asner, G.P.; Powell, G.V.N.; Mascaro, J.; Knapp, D.E.; Clark, J.K.; Jacobson, J.; Kennedy-Bowdoin, T.; Balaji, A.; Paez-Acosta, G.; Victoria, E.; et al. High-Resolution Forest Carbon Stocks and Emissions in the Amazon. Proc. Natl. Acad. Sci. USA. 2010, 107, 16738–16742. [Google Scholar] [CrossRef]
- Kennaway, T.A.; Helmer, E.H.; Lefsky, M.A.; Brandeis, T.A.; Sherrill, K.R. Mapping Land Cover and Estimating Forest Structure Using Satellite Imagery and Coarse Resolution LiDAR in the Virgin Islands. J. Appl. Remote Sens. 2008, 2, 023551. [Google Scholar] [CrossRef]
- Asner, G.P.; Knapp, D.E.; Kennedy-Bowdoin, T.; Jones, M.O.; Martin, R.E.; Boardman, J.; Hughes, R.F. Invasive Species Detection in Hawaiian Rainforests Using Airborne Imaging Spectroscopy and LiDAR. Remote Sens. Environ. 2008, 112, 1942–1955. [Google Scholar] [CrossRef]
- van Ewijk, K.Y.; Treitz, P.M.; Scott, N.A. Characterizing Forest Succession in Central Ontario Using LiDAR-Derived Indices. Photogramm. Eng. Remote Sens. 2011, 77, 261–269. [Google Scholar] [CrossRef]
- Gu, Z.; Cao, S.; Sanchez-Azofeifa, G.A. Using LiDAR Waveform Metrics to Describe and Identify Successional Stages of Tropical Dry Forests. Int. J. Appl. Earth Obs. Geoinf. 2018, 73, 482–492. [Google Scholar] [CrossRef]
- Caughlin, T.T.; Barber, C.; Asner, G.P.; Glenn, N.F.; Bohlman, S.A.; Wilson, C.H. Monitoring Tropical Forest Succession at Landscape Scales despite Uncertainty in Landsat Time Series. Ecol. Appl. 2021, 31, e02208. [Google Scholar] [CrossRef] [PubMed]
- Sothe, C.; Liesenberg, V.; De Almeida, C.M.; Schimalski, M.B. Abordagens Para Classificação Do Estádio Sucessional Da Vegetação Do Parque Nacional de São Joaquim Empregando Imagens Landsat-8 e Rapideye. Bol. Ciências Geodésicas 2017, 23, 389–404. [Google Scholar] [CrossRef]
- Szostak, M.; Likus-Cieślik, J.; Pietrzykowski, M. Planetscope Imageries and LiDAR Point Clouds Processing for Automation Land Cover Mapping and Vegetation Assessment of a Reclaimed Sulfur Mine. Remote Sens. 2021, 13, 2717. [Google Scholar] [CrossRef]
- Miranda, M.S.; de Santiago, V.A.; Körting, T.S.; Leonardi, R.; de Freitas, M.L. Deep Convolutional Neural Network for Classifying Satellite Images with Heterogeneous Spatial Resolutions. In Proceedings of the International Conference on Computational Science and Its Applications—ICCSA 2019, Saint Petersburg, Russia, 1–4 July 2019; Springer: Cham, Switzerland, 2021; Volume 12955, pp. 519–530. [Google Scholar] [CrossRef]
- Sothe, C.; de Almeida, C.M.; Liesenberg, V.; Schimalski, M.B. Evaluating Sentinel-2 and Landsat-8 Data to Map Sucessional Forest Stages in a Subtropical Forest in Southern Brazil. Remote Sens. 2017, 9, 838. [Google Scholar] [CrossRef]
- Quesada, M.; Sanchez-Azofeifa, G.A.; Alvarez-Añorve, M.; Stoner, K.E.; Avila-Cabadilla, L.; Calvo-Alvarado, J.; Castillo, A.; Espírito-Santo, M.M.; Fagundes, M.; Fernandes, G.W.; et al. Succession and Management of Tropical Dry Forests in the Americas: Review and New Perspectives. For. Ecol. Manag. 2009, 258, 1014–1024. [Google Scholar] [CrossRef]
- Liu, W.T.H. Aplicações de Sensoriamento Remoto, 2nd ed.; Oficina de Textos: São Paulo, Brasil, 2015; pp. 1–539. [Google Scholar]
- Puliti, S.; Breidenbach, J.; Schumacher, J.; Hauglin, M.; Klingenberg, T.F.; Astrup, R. Above-ground biomass change estimation using national forest inventory data with Sentinel-2 and Landsat. Remote Sens. Environ. 2021, 265, 112644. [Google Scholar] [CrossRef]
- Howe, A.A.; Parks, S.A.; Harvey, B.J.; Saberi, S.J.; Lutz, J.A.; Yocom, L.L. Comparing Sentinel-2 and Landsat 8 for Burn Severity Mapping in Western North America. Remote Sens. 2022, 14, 5249. [Google Scholar] [CrossRef]
- Pinto, F.M. Classificação do Estágio Sucessional da Vegetação em Áreas de Florest Ombrófila Mista (Fom) Com Emprego de Imagens Digitais Obtidas Por Vant (Veículo Aéreo Não Tripulado). Master’s Thesis, Universidade do Estado de Santa Catarina, Florianópolis, Brazil, 2018. [Google Scholar]
- Berveglieri, A.; Imai, N.N.; Tommaselli, A.M.G.; Casagrande, B.; Honkavaara, E. Successional Stages and Their Evolution in Tropical Forests Using Multi-Temporal Photogrammetric Surface Models and Superpixels. ISPRS J. Photogramm. Remote Sens. 2018, 146, 548–558. [Google Scholar] [CrossRef]
- Lu, D.; Weng, Q. A Survey of Image Classification Methods and Techniques for Improving Classification Performance. Int. J. Remote Sens. 2007, 28, 823–870. [Google Scholar] [CrossRef]
- Szostak, M.; Hawryło, P.; Piela, D. Using of Sentinel-2 Images for Automation of the Forest Succession Detection. Eur. J. Remote Sens. 2018, 51, 142–149. [Google Scholar] [CrossRef]
- Finlayson, C.M.; van der Valk, A.G. Wetland Classification and Inventory: A Summary. Vegetatio 1995, 118, 185–192. [Google Scholar] [CrossRef]
- Guo, M.; Li, J.; Sheng, C.; Xu, J.; Wu, L. A Review of Wetland Remote Sensing. Sensors 2017, 17, 777. [Google Scholar] [CrossRef]
- Mountrakis, G.; Im, J.; Ogole, C. Support Vector Machines in Remote Sensing: A Review. ISPRS J. Photogramm. Remote Sens. 2011, 66, 247–259. [Google Scholar] [CrossRef]
- Hosaki, G.Y.; Ribeiro, D.F. Deep Learning: Ensinando a Aprender. Rev. Gestão Estratégia 2021, 3, 1–15. [Google Scholar]
- Maxwell, A.E.; Warner, T.A.; Fang, F. Implementation of Machine-Learning Classification in Remote Sensing: An Applied Review. Int. J. Remote Sens. 2018, 39, 2784–2817. [Google Scholar] [CrossRef]
- Semolini, R. Support Vector Machines, Inferência Transdutiva e o Problema de Classificação. Master’s Thesis, Universidade Estadual de Campinas, Campinas, Brazil, 2002. [Google Scholar]
- Izbicki, R.; Santos, T.M. Dos Machine Learning Sob a Ótica Estatística; Ufscar/Insper: São Paulo, Brazil, 2018. [Google Scholar]
- Musial, J.P.; Bojanowski, J.S. Comparison of the Novel Probabilistic Self-Optimizing Vectorized Earth Observation Retrieval Classifier with Common Machine Learning Algorithms. Remote Sens. 2022, 14, 378. [Google Scholar] [CrossRef]
- Leite, E.F.; Rosa, R. Análise Do Uso, Ocupação E Cobertura Da Terra Na Bacia Hidrográfica Do Rio Formiga, Tocantins. Rev. Eletrônica De Geogr. 2012, 4, 90–106. [Google Scholar]
- Köppen, W. Climatologia, Con un Estudio de los Climas de la Tierra; Fondo de Cultura Economica: Mexico City, Mexico, 1948; 496p. [Google Scholar]
- IBGE. Manual Técnico da Vegetação Brasileira; Fundação Instituto Brasileiro de Geografia e Estatística: Rio de Janeiro, Brazil, 1992; 92p. [Google Scholar]
- Kumar, V. Forestry Inventory Parameters and Carbon Mapping from Airborne LiDAR. Master’s Thesis, University of Twente, Enschede, The Netherlands, 2014. [Google Scholar]
- Pereira, J.P.; Schimalski, M.B. LiDAR Aplicado a Florestas Naturais; Novas Edições Acadêmicas: Chisinau, Moldova, 2014. [Google Scholar]
- Congedo, L. Semi-Automatic Classification Plugin Documentation Release 7.9.5.1 User Man. 2021, 1–225. Available online: https://readthedocs.org/projects/semiautomaticclassificationmanual/downloads/pdf/latest/ (accessed on 17 April 2024).
- Arcgis. Available online: https://desktop.arcgis.com/en/arcmap/latest/tools/data-management-toolbox/compute-pansharpen-weights.htm (accessed on 17 April 2024).
- Laben, C.A.; Brower, B.V. Process for Enhancing the Spatial Resolution of Multispectral Imagery Using Pan-Sharpening. US Patent 6,011,875, 4 January 2000. [Google Scholar]
- Rouse, J.W., Jr.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring vegetation systems in the great plains with ERTS. Remote Sensingcenter 1973, 351, 309–317. [Google Scholar] [CrossRef]
- Justice, C.O.; Vermote, E.; Townshend, J.R.G.; Defries, R.; Roy, D.P.; Hall, D.K.; Salomonson, V.V.; Privette, J.L.; Riggs, G.; Strahler, A.; et al. The Moderate Resolution Imaging Spectroradiometer (MODIS): Land Remote Sensing for Global Change Research. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1228–1249. [Google Scholar] [CrossRef]
- Hunt, E.R., Jr.; Doraiswamy, P.C.; McMurtrey, J.E.; Daughtry, C.S.T.; Perry, E.M. A Visible Band Index for Remote Sensing Leaf Chlorophyll Content at the Canopy Scale. Int. J. Appl. Earth Obs. Geoinf. 2013, 21, 103–112. [Google Scholar] [CrossRef]
- Huete, A.R. A Soil-Adjusted Vegetation Index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Kaufman, Y.J.; Stark, R.; Rundquist, D. Novel Algorithms for Remote Estimation of Vegetation Fraction. Remote Sens. Environ. 2002, 80, 76–87. [Google Scholar] [CrossRef]
- Arcgis. Available online: https://pro.arcgis.com/en/pro-app/latest/help/analysis/raster-functions/grayscale-function.htm. (accessed on 17 April 2024).
- Haralick, R.M.; Shanmugam, K.; Disntein, I. Textural Features for Image Classification. IEEE Trans. Syst. Man Cybern. 1973, 6, 610–621. [Google Scholar] [CrossRef]
- Blaschke, T.; Hay, G.J.; Kelly, M.; Lang, S.; Hofmann, P.; Addink, E.; Feitosa, R.Q.; van der Meer, F.; van derWerff, H.; van Coillie, F.; et al. Geographic object-based image analysis—Towards a new paradigm. ISPRS J. Photogramm. Remote Sens. 2014, 87, 180–191. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Zhou, Y.; Ge, Y.; An, R.; Chen, Y. Enhancing Land Cover Mapping through Integration of Pixel-Based and Object-Based Classifications from Remotely Sensed Imagery. Remote Sens. 2018, 10, 77. [Google Scholar] [CrossRef]
- Wang, L.; Sousa, W.P.; Gong, P. Integration of object-based and pixel-based classification for mapping mangroves with ikonos imagery. Int. J. Remote Sens. 2004, 25, 5655–5668. [Google Scholar] [CrossRef]
- Liu, D.; Xia, F. Assessing object-based classification: Advantages and limitations. Remote Sens. Lett. 2010, 1, 187–194. [Google Scholar] [CrossRef]
- The Orfeo Team. The Orfeo Toolbox Cookbook, a Guide for Non-Developers Updated for OTB-5.4.0; Orfeo Toolbox: San Diego, CA, USA, 2022. [Google Scholar]
- Miller, G.A.; Nicely, P.E. An Analysis of Perceptual Confusions Among Some English Consonants. J. Acoust. Soc. Am. 1955, 27, 338–352. [Google Scholar] [CrossRef]
- Cohen, J. Weighted Kappa: Nominal Scale Agreement Provision for Scaled Disagreement or Partial Credit. Psychol. Bull. 1968, 70, 213–220. [Google Scholar] [CrossRef] [PubMed]
- Ma, Z.; Redmond, R.L. Tau Coefficients for Accuracy Assessment of Classification of Remote Sensing Data. Photogramm. Eng. Remote Sens. 1995, 61, 435–439. [Google Scholar] [CrossRef] [PubMed]
- Landis, J.R.; Koch, G.G. An Application of Hierarchical Kappa-Type Statistics in the Assessment of Majority Agreement among Multiple Observers Author. Biometrics 1977, 33, 363–374. [Google Scholar] [CrossRef]
- Oh, S.; Jung, J.; Shao, G.; Shao, G.; Gallion, J.; Fei, S. High-Resolution Canopy Height Model Generation and Validation Using USGS 3DEP LiDAR Data in Indiana, USA. Remote Sens. 2022, 14, 935. [Google Scholar] [CrossRef]
- Kotivuori, E.; Korhonen, L.; Packalen, P. Nationwide Airborne Laser Scanning Based Models for Volume, Biomass and Dominant Height in Finland. Silva Fenn. 2016, 50, 1567. [Google Scholar] [CrossRef]
- Puletti, N.; Chianucci, F.; Castaldi, C. Use of Sentinel-2 for Forest Classification in Mediterranean Environments. Ann. Silvic. Res. 2018, 42, 32–38. [Google Scholar] [CrossRef]
- Sothe, C. Classificação do Estádio Sucessional da Vegetação em Áreas de Floresta Ombrófila Mista Empregando Análise Baseada em Objetos e Ortoimagens. Master’s Thesis, Universidade do Estado de Santa Catarina, Florianópolis, Brazil, 2015. [Google Scholar]
- Silva, G.O. Extração de Variáveis Ecológicas da Floresta Ombrófila Mista Empregando Dados Obtidos por Vant. Master’s Thesis, Universidade do Estado de Santa Catarina, Florianópolis, Brazil, 2020. [Google Scholar]
- Xie, G.; Niculescu, S. Mapping and Monitoring of Land Cover/Land Use (LCLU) Changes in the Crozon Peninsula (Brittany, France) from 2007 to 2018 by Machine Learning Algorithms (Support Vector Machine, Random Forest, and Convolutional Neural Network) and by Post-Classification Comparison (PCC). Remote Sens. 2021, 13, 3899. [Google Scholar] [CrossRef]
- Jamali, A. Land Use Land Cover Mapping Using Advanced Machine Learning Classifiers. Ekológia 2021, 40, 286–300. [Google Scholar] [CrossRef]
- Sothe, C.; De Almeida, C.M.; Schimalski, M.B.; Liesenberg, V. Integration of WorldView-2 and LiDAR Data to Map a Subtropical Forest Area: Comparison of Machine Learning Algorithms. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 6207–6210. [Google Scholar] [CrossRef]
- Dalponte, M.; Bruzzone, L.; Gianelle, D. Tree Species Classification in the Southern Alps Based on the Fusion of Very High Geometrical Resolution Multispectral/Hyperspectral Images and LiDAR Data. Remote Sens. Environ. 2012, 123, 258–270. [Google Scholar] [CrossRef]
- Cho, M.A.; Mathieu, R.; Asner, G.P.; Naidoo, L.; van Aardt, J.; Ramoelo, A.; Debba, P.; Wessels, K.; Main, R.; Smit, I.P.J.; et al. Mapping Tree Species Composition in South African Savannas Using an Integrated Airborne Spectral and LiDAR System. Remote Sens. Environ. 2012, 125, 214–226. [Google Scholar] [CrossRef]
- Tassetti, A.N.; Malinverni, E.S.; Hahn, M. Texture Analysis to Improve Supervised Classification in IKONOS Imagery. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci.-ISPRS Arch. 2010, 38, 245–250. [Google Scholar]
- Sannigrahi, S.; Basu, B.; Basu, A.S.; Pilla, F. Development of Automated Marine Floating Plastic Detection System Using Sentinel-2 Imagery and Machine Learning Models. Mar. Pollut. Bull. 2022, 178, 113527. [Google Scholar] [CrossRef] [PubMed]
- Pinho, C.; Feitosa, F.; Kux, H. Classificação Automática de Cobertura Do Solo Urbano Em Imagem IKONOS: Comparação Entre a Abordagem Pixel-a-Pixel e Orientada a Objetos. Simpósio Bras. Sensoriamento Remoto 2005, 12, 4217–4224. [Google Scholar]
- Piazza, G.A.; Vibrans, A.C.; Liesenberg, V.; Refosco, J.C. Object-oriented and pixel-based classification approaches to classify tropical successional stages using airborne high–spatial resolution images. GIScience & Rem. Sens. 2015, 53, 206–226. [Google Scholar] [CrossRef]
- Silva, V.V.; Nicoletti, M.F.; Dobner, M., Jr.; Vaz, D.R.; Oliveira, G.S. Fragments of Mixed Ombrophilous Forest in different successional stages: Dendrometric characterization and determination of biomass and carbon (In Portuguese). Rev. Ciênc. Agrovet. 2023, 22, 695–704. [Google Scholar] [CrossRef]

| LiDAR | Optech ALTM Gemini |
|---|---|
| Wavelength | 1064 nm |
| Acquisition date | 8 October 2019 |
| Flight height | 800 m |
| Average flight speed | 184 km/h |
| Scanning angle | ±10° |
| Laser scanner repeat | 70 kHz |
| Scanning frequency | 70 Hz |
| Return number | 1–4 |
| Intensity | 12 bits |
| Average density of points | 15.38 points/m2 |
| CBERS-4A/WPM | LANDSAT-8/OLI | Sentinel-2/MSI | PlanetScope |
|---|---|---|---|
| 0.45–0.52 µm (B) | 0.45–0.51 µm (B) | 0.46–0.52 µm (B) | 0.45–0.51 µm (B) |
| 0.52–0.59 µm (G) | 0.53–0.59 µm (G) | 0.54–0.58 µm (G) | 0.50–0.59 µm (G) |
| 0.63–0.69 µm (R) | 0.64–0.67 µm (R) | 0.65–0.68 µm (R) | 0.59–0.67 µm (R) |
| 0.77–0.89 µm (NIR) | 0.85–0.88 µm (NIR) | 0.78–0.89 µm (NIR) | 0.78–0.86 µm (NIR) |
| 0.45–0.90 µm (PAN) | 1.57–1.65 µm (SWIR1) | 0.70–0.71 µm (Red Edge 1) | |
| 2.11–2.29 µm (SWIR2) | 0.73–0.75 µm (Red Edge 2) | ||
| 0.50–0.68 µm (PAN) | 0.77–0.79 µm (Red Edge 3) | ||
| 0.85–0.87 µm (Red Edge 4) | |||
| 1.57–1.66 µm (SWIR1) | |||
| 2.11–2.29 µm (SWIR 2) |
| Vegetation Index | Equation | Reference |
|---|---|---|
| NDVI | (NIR − R)/(NIR + R) | [52] |
| EVI | 2.5 (NIR − R)/(L1 + NIR + C1 ×R − C2 × B + 1) | [53] |
| TGI | −0.5 × (190 × (R − G) − 120 ×(R − B)) | [54] |
| SAVI | (NIR − R)/(NIR + R + L2) × (1 + L2) | [55] |
| VARI | (G − R)/(G + R − B) | [56] |
| UAV | Parrot Blue Grass |
|---|---|
| Camera | Parrot Sequoia e RGB 16 MP |
| Flight autonomy (min) | 25 |
| Weight (g) | 1850 |
| Multispectral sensor | Green, Red, RedEdge, and NIR |
| Navigation sensors | GPS + GLONASS |
| Spatial resolution | 2 cm |
| Datasets | Number of the Rasters in Each Dataset | ||||
|---|---|---|---|---|---|
| CBERS-4A | Landsat-8 | Sentinel-2 | PlanetScope | ||
| 1 | Satellite bands | 4 | 6 | 10 | 4 |
| 2 | Satellite bands +CHM (LiDAR) | 5 | 7 | 11 | 5 |
| 3 | Satellite bands +CHM (LiDAR) + intensity (LiDAR) | 6 | 8 | 12 | 6 |
| 4 | Satellite bands +CHM (LiDAR) + intensity (LiDAR) + NDVI | 7 | 9 | 13 | 7 |
| 5 | Satellite bands +CHM (LiDAR) + intensity (LiDAR) + EVI | 7 | 9 | 13 | 7 |
| 6 | Satellite bands +CHM (LiDAR) + intensity (LiDAR) + TGI | 7 | 9 | 13 | 7 |
| 7 | Satellite bands +CHM (LiDAR) + intensity (LiDAR) + SAVI | 7 | 9 | 13 | 7 |
| 8 | Satellite bands +CHM (LiDAR) + intensity (LiDAR) + VARI | 7 | 9 | 13 | 7 |
| 9 | Satellite bands +CHM (LiDAR) + intensity (LiDAR) + GLCM 3 × 3 | 13 | 15 | 19 | 13 |
| 10 | Satellite bands +CHM (LiDAR) + intensity (LiDAR) + GLCM 5 × 5 | 13 | 15 | 19 | 13 |
| 11 | Satellite bands +CHM (LiDAR) + intensity (LiDAR) + GLCM 7 × 7 | 13 | 15 | 19 | 13 |
| Class | Area (ha) |
|---|---|
| Field | 125.8 |
| Water | 0.3 |
| SS1 | 118.1 |
| SS2 | 349.6 |
| SS3 | 378.9 |
| Total | 972.7 |
| Samples | |||
|---|---|---|---|
| Class | Training | Validate | Total |
| Field | 164,410 | 85,816 | 250,226 |
| Water | 975 | 788 | 1763 |
| SS1 | 82,332 | 39,157 | 121,489 |
| SS2 | 144,005 | 67,030 | 211,035 |
| SS3 | 97,036 | 49,120 | 146,156 |
| Plot | Mean Height by Forest Inventory (m) | Mean Height by CHM (m) |
|---|---|---|
| 1 | 10.05 | 12.05 |
| 2 | 10.46 | 9.9 |
| 3 | 10.94 | 12.05 |
| 4 | 6.89 | 6.25 |
| 5 | 8.72 | 9.9 |
| 6 | 6.12 | 8 |
| 7 | 8.63 | 9.9 |
| CBERS-4A | Sentinel-2 | PlanetScope | Landsat-8 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Dataset | RT | SVM | MLC | RT | SVM | MLC | RT | SVM | MLC | RT | SVM | MLC |
| 1 | 0.79 | 0.80 | 0.76 | 0.81 | 0.90 | 0.88 | 0.65 | 0.68 | 0.63 | 0.88 | 0.92 | 0.93 |
| 2 | 0.85 | 0.88 | 0.85 | 0.85 | 0.90 | 0.90 | 0.79 | 0.84 | 0.81 | 0.91 | 0.93 | 0.94 |
| 3 | 0.87 | 0.86 | 0.88 | 0.86 | 0.93 | 0.91 | 0.81 | 0.84 | 0.83 | 0.90 | 0.94 | 0.92 |
| 4 | 0.85 | 0.88 | 0.85 | 0.86 | 0.91 | 0.92 | 0.82 | 0.84 | 0.79 | 0.89 | 0.95 | 0.82 |
| 5 | 0.87 | 0.88 | 0.86 | 0.84 | 0.93 | 0.92 | 0.84 | 0.84 | 0.81 | 0.89 | 0.95 | 0.91 |
| 6 | 0.87 | 0.87 | 0.82 | 0.86 | 0.91 | 0.90 | 0.83 | 0.82 | 0.82 | 0.92 | 0.94 | 0.83 |
| 7 | 0.88 | 0.88 | 0.86 | 0.84 | 0.91 | 0.89 | 0.83 | 0.85 | 0.80 | 0.91 | 0.94 | 0.81 |
| 8 | 0.88 | 0.87 | 0.87 | 0.86 | 0.89 | 0.90 | 0.83 | 0.84 | 0.82 | 0.91 | 0.95 | 0.74 |
| 9 | 0.86 | 0.86 | 0.59 | 0.86 | 0.91 | 0.65 | 0.84 | 0.84 | 0.83 | 0.87 | 0.90 | 0.84 |
| 10 | 0.88 | 0.86 | 0.52 | 0.84 | 0.91 | 0.61 | 0.87 | 0.84 | 0.85 | 0.90 | 0.87 | 0.48 |
| 11 | 0.88 | 0.85 | 0.49 | 0.85 | 0.91 | 0.60 | 0.84 | 0.84 | 0.85 | 0.81 | 0.89 | 0.90 |
| Class | Field | Water | SS1 | SS2 | SS3 | Total | UA |
|---|---|---|---|---|---|---|---|
| Field | 355 | 0 | 0 | 0 | 0 | 355 | 1 |
| Water | 0 | 9 | 0 | 0 | 1 | 10 | 0.90 |
| SS1 | 0 | 0 | 162 | 6 | 11 | 179 | 0.91 |
| SS2 | 0 | 0 | 8 | 253 | 51 | 312 | 0.81 |
| SS3 | 0 | 0 | 1 | 9 | 140 | 150 | 0.93 |
| Total | 355 | 9 | 171 | 268 | 203 | 1006 | |
| PA | 1 | 1 | 0.95 | 0.94 | 0.69 |
| Class | Field | Water | SS1 | SS2 | SS3 | Total | UA |
|---|---|---|---|---|---|---|---|
| Field | 355 | 0 | 0 | 0 | 0 | 355 | 1 |
| Water | 0 | 10 | 0 | 0 | 0 | 10 | 1 |
| SS1 | 0 | 0 | 162 | 20 | 4 | 186 | 0.87 |
| SS2 | 0 | 0 | 2 | 249 | 22 | 273 | 0.91 |
| SS3 | 0 | 0 | 1 | 6 | 175 | 182 | 0.96 |
| Total | 355 | 10 | 165 | 275 | 201 | 1006 | |
| PA | 1 | 1 | 0.96 | 0.93 | 0.92 |
| Class | Field | Water | SS1 | SS2 | SS3 | Total | UA |
|---|---|---|---|---|---|---|---|
| Field | 355 | 0 | 0 | 0 | 0 | 355 | 1 |
| Water | 0 | 10 | 0 | 0 | 0 | 10 | 1 |
| SS1 | 0 | 0 | 162 | 1 | 2 | 165 | 0.98 |
| SS2 | 0 | 0 | 7 | 267 | 17 | 291 | 0.92 |
| SS3 | 0 | 0 | 2 | 5 | 178 | 185 | 0.96 |
| Total | 355 | 10 | 171 | 273 | 197 | 1006 | |
| PA | 1 | 1 | 0.90 | 0.97 | 0.94 |
| Class | Field | Water | SS1 | SS2 | SS3 | Total | UA |
|---|---|---|---|---|---|---|---|
| Field | 355 | 0 | 1 | 0 | 0 | 356 | 0.99 |
| Water | 0 | 6 | 0 | 0 | 4 | 10 | 0.60 |
| SS1 | 0 | 0 | 151 | 4 | 26 | 181 | 0.83 |
| SS2 | 0 | 0 | 6 | 237 | 21 | 264 | 0.90 |
| SS3 | 0 | 0 | 4 | 31 | 159 | 194 | 0.82 |
| Total | 355 | 6 | 162 | 272 | 210 | 1005 | |
| PA | 1 | 1 | 0.86 | 0.83 | 0.87 |
| Sensor | Classifier | Dataset | Weighted Kappa | Standard Deviation | Minimum | Maximum |
|---|---|---|---|---|---|---|
| CBERS-4A | SVM | 2* | 0.88 | 0.0119 | 0.8603 | 0.9068 |
| Sentinel-2 | SVM | 3* | 0.93 | 0.0097 | 0.9066 | 0.9446 |
| Landsat-8 | SVM | 4* | 0.95 | 0.0077 | 0.9387 | 0.9691 |
| PlanetScope | RT | 10* | 0.87 | 0.0125 | 0.8441 | 0.8931 |
| Sensor | Datasets | Z | Critical Value |
|---|---|---|---|
| CBERS-4A | SVM2 *—RT11 * | 0.3122 | 1.96 |
| SVM2 *—MLC3 * | 0.2175 | ||
| Sentinel-2 | SVM3 *—RT8 * | 5.3904 | |
| SVM3 *—MLC5 * | 0.7511 | ||
| Landsat-8 | SVM4 *—RT6 * | 3.8575 | |
| SVM4 *—MLC2 * | 2.1378 | ||
| PlanetScope | RT10 *—SVM7 * | 1.6503 | |
| RT10 *—MLC11 * | 1.0931 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ziegelmaier Neto, B.H.; Schimalski, M.B.; Liesenberg, V.; Sothe, C.; Martins-Neto, R.P.; Floriani, M.M.P. Combining LiDAR and Spaceborne Multispectral Data for Mapping Successional Forest Stages in Subtropical Forests. Remote Sens. 2024, 16, 1523. https://doi.org/10.3390/rs16091523
Ziegelmaier Neto BH, Schimalski MB, Liesenberg V, Sothe C, Martins-Neto RP, Floriani MMP. Combining LiDAR and Spaceborne Multispectral Data for Mapping Successional Forest Stages in Subtropical Forests. Remote Sensing. 2024; 16(9):1523. https://doi.org/10.3390/rs16091523
Chicago/Turabian StyleZiegelmaier Neto, Bill Herbert, Marcos Benedito Schimalski, Veraldo Liesenberg, Camile Sothe, Rorai Pereira Martins-Neto, and Mireli Moura Pitz Floriani. 2024. "Combining LiDAR and Spaceborne Multispectral Data for Mapping Successional Forest Stages in Subtropical Forests" Remote Sensing 16, no. 9: 1523. https://doi.org/10.3390/rs16091523
APA StyleZiegelmaier Neto, B. H., Schimalski, M. B., Liesenberg, V., Sothe, C., Martins-Neto, R. P., & Floriani, M. M. P. (2024). Combining LiDAR and Spaceborne Multispectral Data for Mapping Successional Forest Stages in Subtropical Forests. Remote Sensing, 16(9), 1523. https://doi.org/10.3390/rs16091523











