DBI-Attack:Dynamic Bi-Level Integrated Attack for Intensive Multi-Scale UAV Object Detection
Abstract
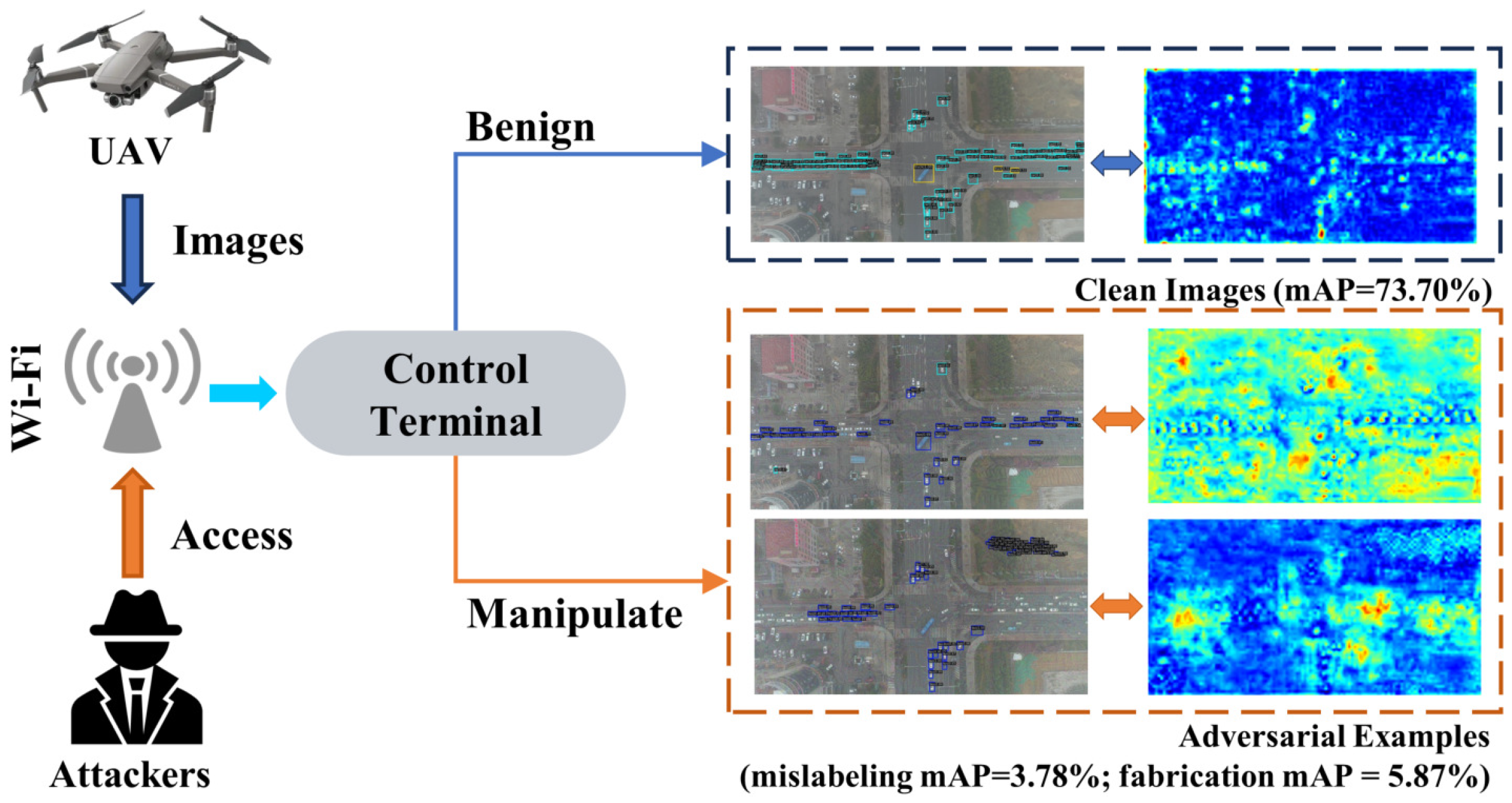
1. Introduction
- The white-box attack module DIA employs the guidance of classification loss to generate primary adversarial examples from the internal feature space of the bounding box to deceive the classifier, which avoids the iteration stopping and skipping extreme points problem caused by the fixed step sizes.
- The white-box attack module BAAM further improves the performance of adversarial examples at the decision level by using the RPN classification loss of the two-stage model and the multi-class confidence loss of the one-stage model to improve the attack capability of the model.
- The black-box attack module IBAM integrates the weight balance and weight optimization modules to combine the perturbations obtained from the white-box model for the black-box model without gradient information. The predefined perturbations generated by the agent white-box model improve the transfer performance of the black-box attack model.
- The proposed model can fully consider the performance of the white-box attack and improve the effect of black-box attacks. Hence, DBI-Attack does not need to design proprietary adversarial examples for different black-box target detection models. Our attack combines query with transfer to improve the applicability of the white-box attack integrations on the black-box models.
2. Related Work
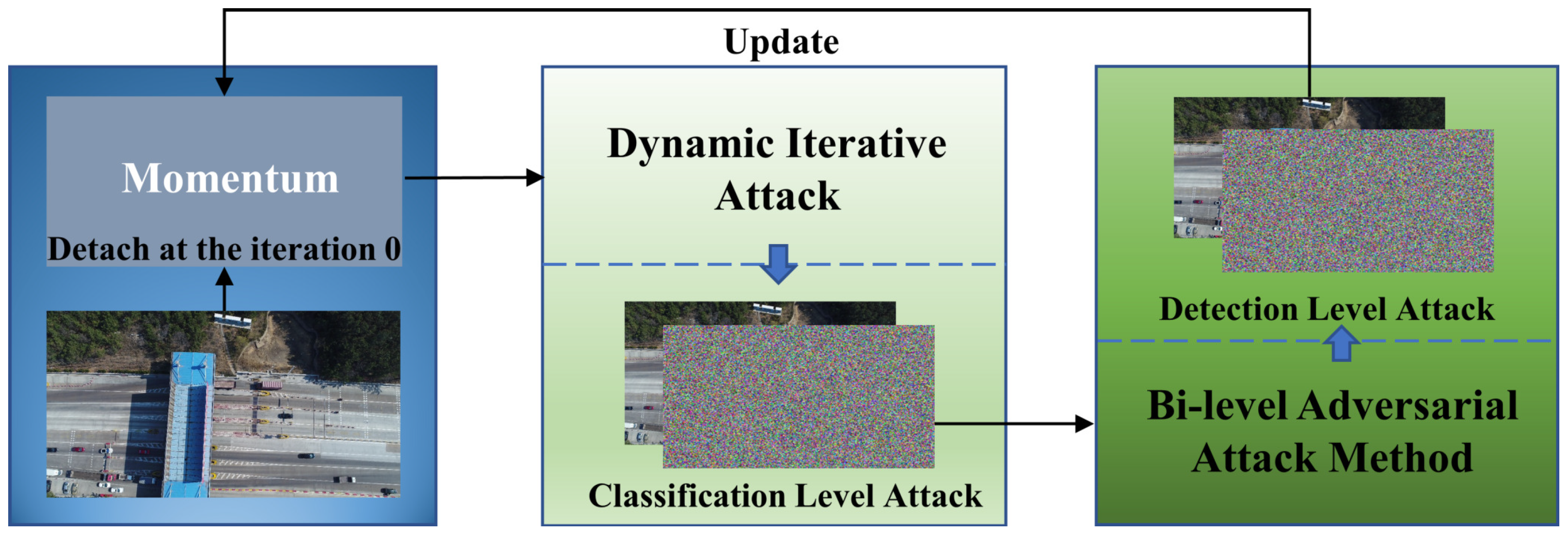
3. Methodology
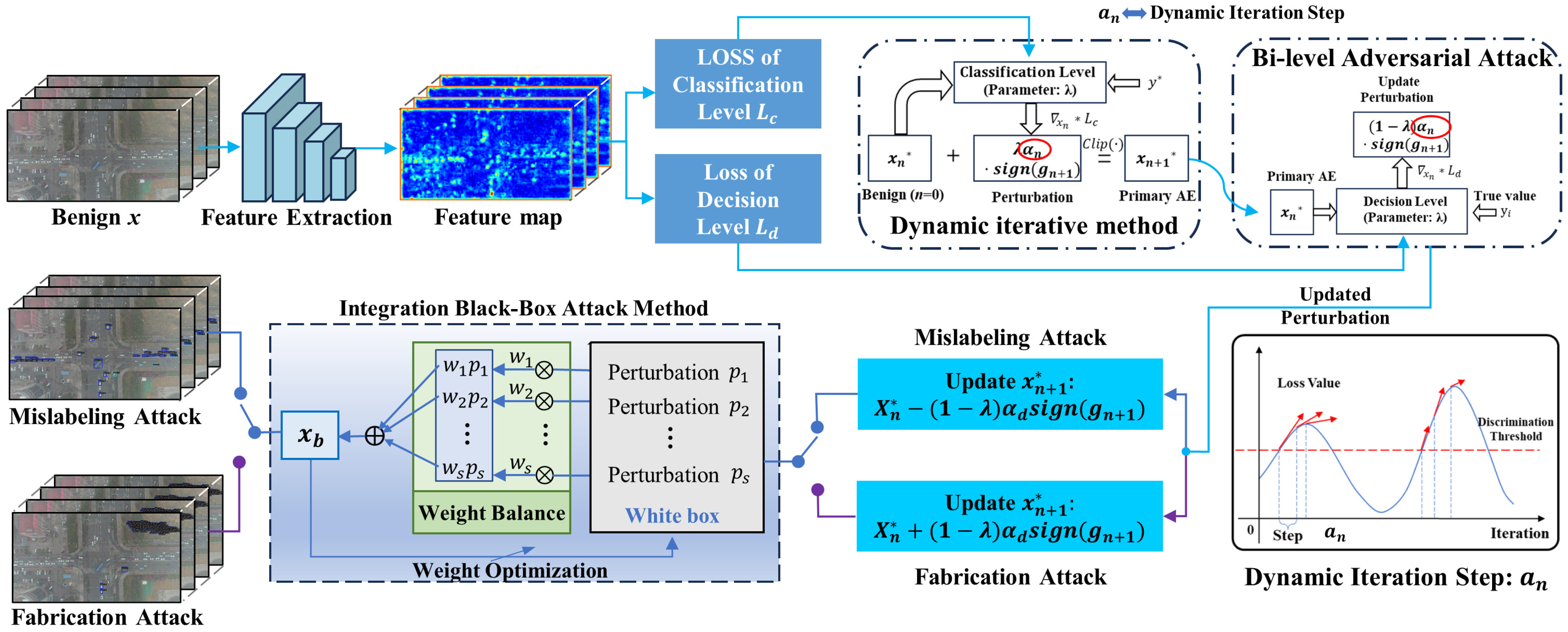
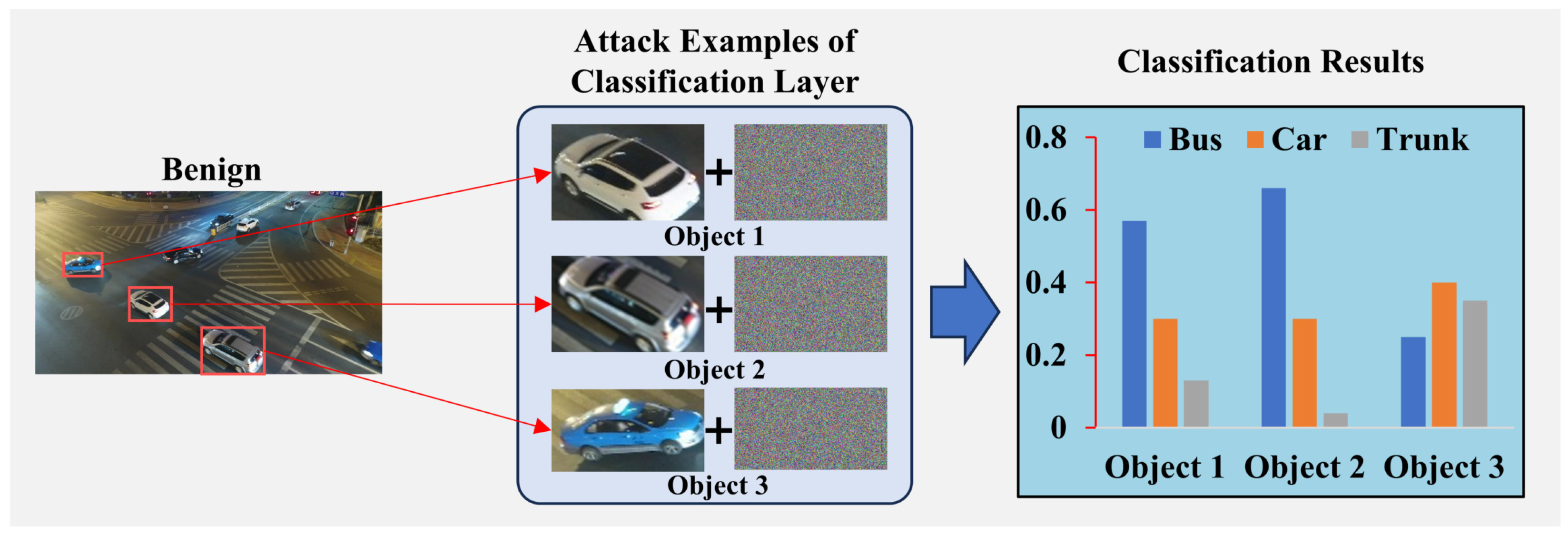
3.1. Momentum Iterative Fast Gradient Sign Method
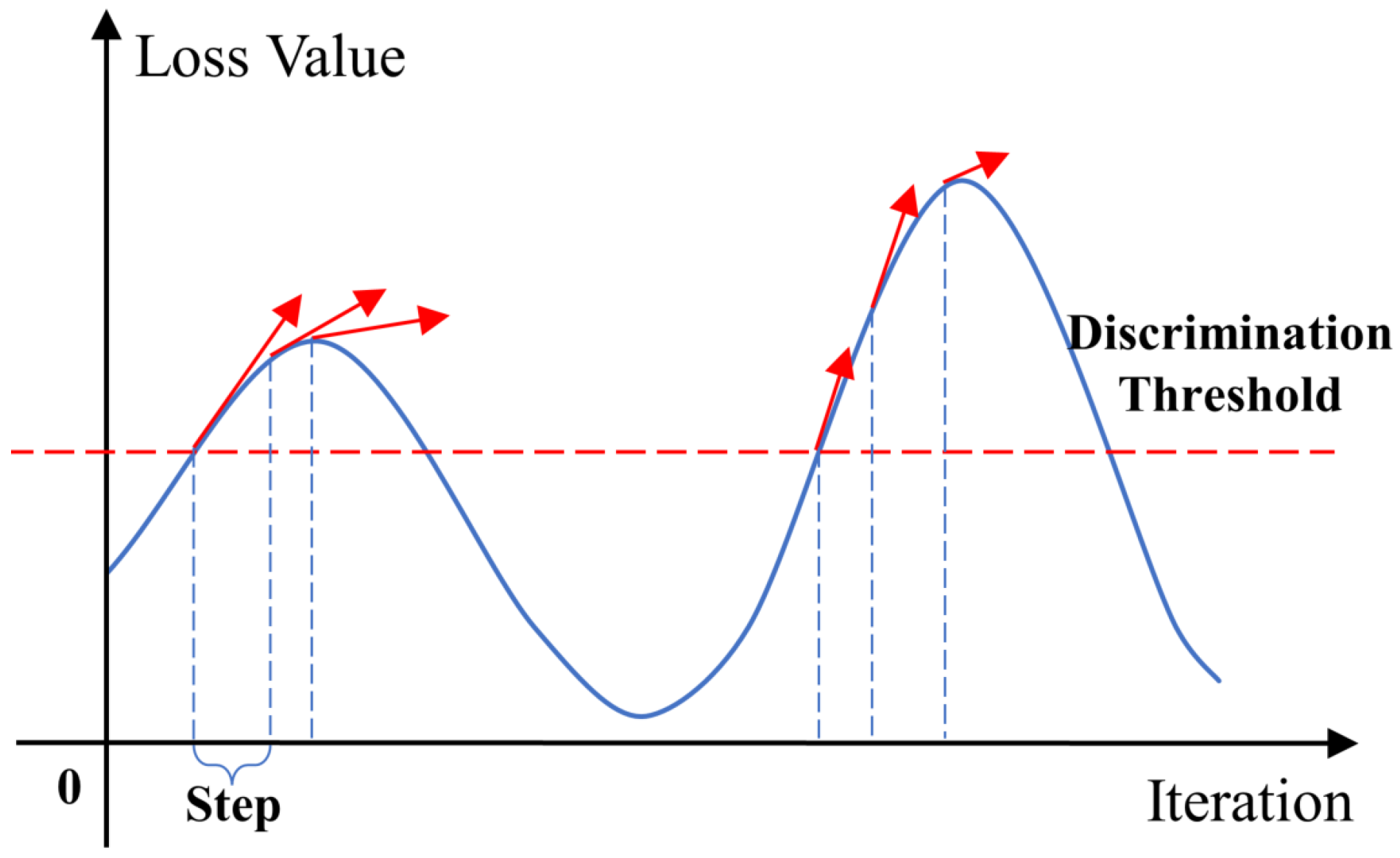
3.2. Dynamic Iterative Attack
3.3. Bi-Level Adversarial Attack Method
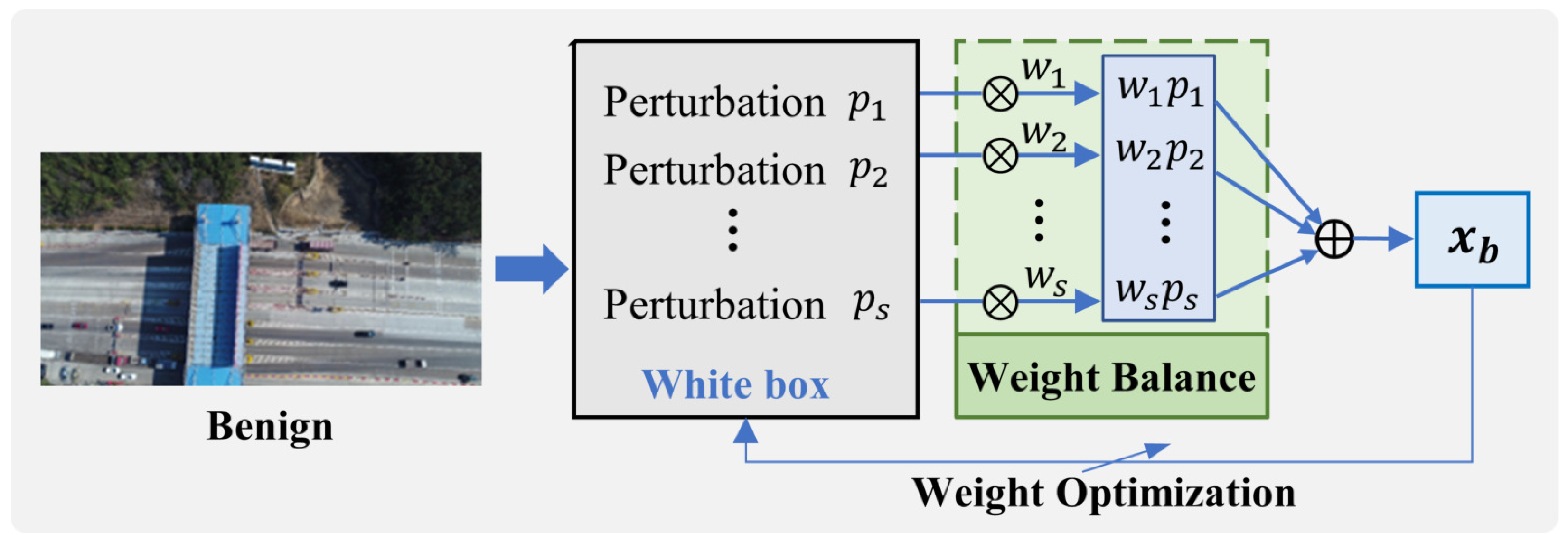
3.4. Integration Black-Box Attack Method
| Algorithm 1 Dynamic bi-level integrated attack. |
| Input: Original signal object x; GT label l; GT bounding box; loss function of the classifier; loss function of decision level in agent model; loss function of decision level in victim model. Input: Number of iteration N; number of agent models s; weight of agent models ; perturbation constraint ; number of inner iterations decay factor ; classification level perturbation factor . Output: An adversarial example with . 1: ; ; 2: for to S do 3: for to do 4: Input to the classifier, calculate the according to Equation (5), and determine the direction of the classification level perturbation according to Equation (7); 5: Calculate the perturbation size of each iteration by Equation (7); 6: Update the confrontation by Equation (8); 7: Calculate the decision loss according to Equation (9), and determine the direction of the double level perturbation according to Equations (12) and (13); 8: Calculate the final adversary sample by solving the optimization problem as ; 9: Weight balance and optimization by Equations (17) and (18); 10: end for 11: end for 12: return |
4. Experiments and Analysis
4.1. Dataset
4.2. Implement Details
4.3. Criteria
4.4. Parameter Discussion
4.5. Experimental Results
4.6. Ablation Study
4.7. Compare with State-of-Art Methods
4.7.1. Compared with Other White-Box Attack Methods
4.7.2. Compared with Other Black-Box Methods
4.8. Adversarial Training
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, A.; Ni, S.; Chen, Y.; Chen, J. Cross-Modal Object Detection Via UAV. IEEE Trans. Veh. Technol. 2023, 72, 10894–10905. [Google Scholar] [CrossRef]
- Lu, Z.; Sun, H.; Xu, Y. Adversarial Robustness Enhancement of UAV-Oriented Automatic Image Recognition Based on Deep Ensemble Models. Remote Sens. 2020, 21, 3007. [Google Scholar] [CrossRef]
- Lu, Z.; Sun, H.; Ji, K.; Kuang, G. Adversarial Robust Aerial Image Recognition Based on Reactive-Proactive Defense Framework with Deep Ensembles. Remote Sens. 2023, 15, 4660. [Google Scholar] [CrossRef]
- Messenger, R.; Islam, M.; Whitlock, M. Real-Time Traffic End-of-Queue Detection and Tracking in UAV Video. J. Syst. Eng. Electron. 2023, 21, 493–505. [Google Scholar] [CrossRef]
- Li, X.; Wu, J. Developing a More Reliable Framework for Extracting Traffic Data from a UAV Video. IEEE Trans. Intell. Transp. Syst. 2023, 24, 12272–12283. [Google Scholar] [CrossRef]
- Ren, H.; Huang, T.; Yan, H. Adversarial examples: Attacks and defenses in the physical world. Int. J. Mach. Learn. Cybern. 2021, 12, 3325–3336. [Google Scholar]
- Wei, X.; Guo, Y.; Yu, J. Adversarial Sticker: A Stealthy Attack Method in the Physical World. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 2711–2725. [Google Scholar] [CrossRef] [PubMed]
- Sun, X.; Cheng, G.; Pei, L.; Li, H.; Han, J. Threatening patch attacks on object detection in optical remote sensing images. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–10. [Google Scholar] [CrossRef]
- Sun, L.; Chang, J.; Zhang, J.; Fan, B.; He, Z. Adaptive image dehazing and object tracking in UAV videos based on the template updating siamese network. IEEE Sens. J. 2023, 23, 12320–12333. [Google Scholar] [CrossRef]
- Xu, Y.; Sun, H.; Chen, J.; Lei, L.; Kuang, G.; Ji, K. Robust remote sensing scene classification by adversarial self-supervised learning. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; pp. 4936–4939. [Google Scholar]
- Xu, Y.; Sun, H.; Chen, J.; Lei, L.; Ji, K.; Kuang, G. Adversarial Self-Supervised Learning for Robust SAR Target Recognition. Remote Sens. 2021, 13, 4158. [Google Scholar] [CrossRef]
- Zhao, S.; Wang, W.; Du, Z.; Chen, J.; Duan, Z. A Black-Box Adversarial Attack Method via Nesterov Accelerated Gradient and Rewiring Towards Attacking Graph Neural Networks. IEEE Trans. Big Data 2023, 9, 1586–1597. [Google Scholar] [CrossRef]
- Zhou, S.; Liu, C.; Ye, D.; Zhu, T.; Zhou, W.; Yu, P.S. Adversarial attacks and defenses in deep learning: From a perspective of cybersecurity. ACM Comput. Surv. 2022, 55, 1–39. [Google Scholar] [CrossRef]
- Cai, Z.; Tan, Y.; Asif, M.S. Ensemble-based blackbox attacks on dense prediction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Vancouver, BC, Canada, 18–22 June 2023; pp. 4045–4055. [Google Scholar]
- Wei, X.; Yuan, M. Adversarial pan-sharpening attacks for object detection in remote sensing. Pattern Recognit. 2023, 139, 109466–109471. [Google Scholar] [CrossRef]
- Tian, J.; Wang, B.; Guo, R.; Wang, Z.; Cao, K.; Wang, X. Adversarial attacks and defenses for deep-learning-based unmanned aerial vehicles. IEEE Internet Things J. 2022, 9, 22399–22409. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, K.; Zhu, Z.; Wang, F.-Y. Adversarial attacks on faster RCNN object detector. Neurocomputing 2020, 382, 87–95. [Google Scholar] [CrossRef]
- Mumcu, F.; Yilmaz, Y. Sequential architecture-agnostic black-box attack design and analysis. Pattern Recognit. 2023, 15, 110066–110072. [Google Scholar] [CrossRef]
- Tian, J.; Shen, C.; Wang, B.; Xia, X.; Zhang, M.; Lin, C.; Li, Q. LESSON: Multi-Label Adversarial False Data Injection Attack for Deep Learning Locational Detection. In IEEE Transactions on Dependable and Secure Computing; IEEE: Piscataway, NJ, USA, 2024. [Google Scholar]
- Kuang, X.; Gao, X.; Wang, L.; Zhao, G.; Ke, L.; Zhang, Q. A discrete cosine transform-based query efficient attack on black-box object detectors. Inf. Sci. 2021, 546, 596–607. [Google Scholar] [CrossRef]
- Shibly, K.H.; Hossain, M.D.; Inoue, H.; Taenaka, Y.; Kadobayashi, Y. Towards autonomous driving model resistant to adversarial attack. Appl. Artif. Intell. 2023, 37, 2193461–2193470. [Google Scholar] [CrossRef]
- Zhu, H.; Zhu, Y.; Zheng, H.; Ren, Y.; Jiang, W. LIGAA: Generative adversarial attack method based on low-frequency information. Comput. Secur. 2023, 125, 103057–103070. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, C. Attacking object detector by simultaneously learning perturbations and locations. Neural Process. Lett. 2023, 55, 2761–2776. [Google Scholar] [CrossRef]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards real-time object detection with region proposal networks. Adv. Neural Inf. Process. Syst. 2015, 28, 112–118. [Google Scholar] [CrossRef] [PubMed]
- Redmon, J.; Farhadi, A. YOLOv3: An incremental improvement. arXiv 2018, arXiv:1804.02767. [Google Scholar]
- Lin, T.-Y.; Goyal, P.; Girshick, R.; He, K.; Dollár, P. Focal loss for dense object detection. In Proceedings of the IEEE International Conference on Computer Vision (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 2980–2988. [Google Scholar]
- Liu, W.; Anguelov, D.; Erhan, D.; Szegedy, C.; Reed, S.; Fu, C.Y.; Berg, A.C. SSD: Single shot multibox detector. In Computer Vision ECCV 2016: 14th European Conference, Proceedings, Part I, Amsterdam, The Netherlands, 11–14 October 2016; Springer: Berlin/Heidelberg, Germany, 2016; pp. 21–37. [Google Scholar]
- Sun, P.; Zhang, R.; Jiang, Y.; Kong, T.; Xu, C.; Zhan, W.; Tomizuka, M.; Li, L.; Yuan, Z.; Wang, C.; et al. Sparse R-CNN: End-to-end object detection with learnable proposals. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 14454–14463. [Google Scholar]
- Madry, A.; Makelov, A.; Schmidt, L.; Tsipras, D.; Vladu, A. Towards deep learning models resistant to adversarial attacks. arXiv 2017, arXiv:1706.06083. [Google Scholar]
- Xie, C.; Wang, J.; Zhang, Z.; Zhou, Y.; Xie, L.; Yuille, A. Adversarial examples for semantic segmentation and object detection. In Proceedings of the IEEE International Conference on Computer Vision (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 1369–1378. [Google Scholar]
- Wei, X.; Liang, S.; Chen, N.; Cao, X. Transferable adversarial attacks for image and video object detection. arXiv 2018, arXiv:1811.12641. [Google Scholar]
- Du, M.; Bi, D.; Du, M.; Xu, X.; Wu, Z. ULAN: A universal local adversarial network for SAR target recognition based on layer-wise relevance propagation. Remote Sens. 2022, 15, 21. [Google Scholar] [CrossRef]
- Wang, D.; Yao, W.; Jiang, T.; Chen, X. Improving Transferability of Universal Adversarial Perturbation with Feature Disruption. IEEE Trans. Image Process. 2024, 33, 722–737. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Tian, D.; Chang, M.; Bian, X.; Lyu, S. Robust adversarial perturbation on deep proposal-based models. arXiv 2018, arXiv:1809.05962. [Google Scholar]
- Wu, H.; Rowlands, S.; Wahlstrom, J. A Man-in-the-Middle Attack against Object Detection Systems. arXiv 2024, arXiv:2208.07174. [Google Scholar]
- Chow, K.H.; Liu, L.; Loper, M.; Bae, J.; Gursoy, M.E.; Truex, S.; Wei, W.; Wu, Y. Adversarial objectness gradient attacks in real-time object detection systems. In Proceedings of the 2020 Second IEEE International Conference on Trust, Privacy and Security in Intelligent Systems and Applications (TPS-ISA), Atlanta, GA, USA, 28–31 October 2020; pp. 263–272. [Google Scholar]
- Zhang, X.; Sun, C.; Han, H. Object-fabrication Targeted Attack for Object Detection. arXiv 2022, arXiv:2212.06431. [Google Scholar]
- Zhang, H.; Zhou, W.; Li, H. Contextual adversarial attacks for object detection. In Proceedings of the 2020 IEEE International Conference on Multimedia and Expo (ICME), London, UK, 6–10 July 2020; pp. 1–6. [Google Scholar]
- Wang, Y.; Tan, Y.; Zhang, W.; Zhao, Y.; Kuang, X. An adversarial attack on DNN-based black-box object detectors. J. Netw. Comput. Appl. 2020, 161, 102634. [Google Scholar] [CrossRef]
- Li, Y.; Xu, X.; Xiao, J.; Li, S.; Shen, H.T. Adaptive square attack: Fooling autonomous cars with adversarial traffic signs. IEEE Internet Things J. 2020, 8, 6337–6347. [Google Scholar] [CrossRef]
- Dong, Y.; Liao, F.; Pang, T.; Su, H.; Zhu, J.; Hu, X.; Li, J. Boosting adversarial attacks with momentum. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 9185–9193. [Google Scholar]
- Wang, S.; Liu, W.; Chang, C.-H. A new lightweight in situ adversarial sample detector for edge deep neural network. IEEE J. Emerg. Sel. Top. Circuits Syst. 2021, 11, 252–266. [Google Scholar] [CrossRef]
- Yin, M.; Li, S.; Cai, Z.; Song, C.; Asif, M.S.; Roy-Chowdhury, A.K.; Krishnamurthy, S.V. Exploiting multi-object relationships for detecting adversarial attacks in complex scenes. In Proceedings of the IEEE/CVF International Conference on Computer Vision (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 7858–7867. [Google Scholar]
- Shin, D.; Kim, G.; Jo, J.; Park, J. Low Complexity Gradient Computation Techniques to Accelerate Deep Neural Network Training. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 5743–5759. [Google Scholar] [CrossRef]
- Zhang, F.; Meng, T.; Xiang, D.; Ma, F.; Sun, X.; Zhou, Y. Adversarial deception against SAR target recognition network. IEEE J. Select.Top. Appl. Earth Obs. Remote Sens. 2022, 15, 4507–4520. [Google Scholar] [CrossRef]
- Shih, K.-H.; Chiu, C.-T.; Lin, J.-A.; Bu, Y.-Y. Real-time object detection with reduced region proposal network via multi-feature concatenation. IEEE Trans. Neural Netw. Learn. Syst. 2019, 31, 2164–2173. [Google Scholar] [CrossRef]
- Ma, X.; Niu, Y.; Gu, L.; Wang, Y.; Zhao, Y.; Bailey, J.; Lu, F. Understanding adversarial attacks on deep learning based medical image analysis systems. Pattern Recognit. 2021, 110, 107332. [Google Scholar] [CrossRef]
- Liu, M.; Zhang, Z.; Chen, Y.; Ge, J.; Zhao, N. Adversarial attack and defense on deep learning for air transportation communication jamming. IEEE Trans. Intell. Transp. Syst. 2023, 25, 973–986. [Google Scholar] [CrossRef]
- Jing, C.; Wu, Y.; Cui, C. Ensemble dynamic behavior detection method for adversarial malware. Future Gener. Comput. Syst. 2022, 130, 193–206. [Google Scholar] [CrossRef]
- Li, D.; Zhang, J.; Huang, K. Universal adversarial perturbations against object detection. Pattern Recognit. 2021, 110, 107584. [Google Scholar] [CrossRef]
- Li, X.; Li, X.; Li, Z.; Xiong, X.; Khyam, M.O.; Sun, C. Robust vehicle detection in high-resolution aerial images with imbalanced data. IEEE Trans. Artif. Intell. 2021, 2, 238–250. [Google Scholar] [CrossRef]
- Wu, H.; He, Z.; Gao, M. Gcevt: Learning global context embedding for vehicle tracking in unmanned aerial vehicle videos. IEEE Geosci. Remote Sens. Lett. 2022, 20, 1–5. [Google Scholar] [CrossRef]
- Xu, J.; Li, Y.; Wang, S. AdaZoom: Towards scale-aware large scene object detection. IEEE Trans. Multimed. 2022, 25, 4598–4609. [Google Scholar] [CrossRef]
- Zhang, Y.; Zheng, Y. Object tracking in UAV videos by multi-feature correlation filters with saliency proposals. IEEE J. Select. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 5538–5548. [Google Scholar] [CrossRef]
- Yuan, Y.; Zhang, Y. OLCN: An optimized low coupling network for small objects detection. IEEE Geosci. Remote Sens. Lett. 2021, 19, 1–5. [Google Scholar] [CrossRef]
- Li, Y.; Pang, Y.; Cao, J.; Shen, J.; Shao, L. Improving single shot object detection with feature scale unmixing. IEEE Trans. Image Process. 2021, 30, 2708–2721. [Google Scholar] [CrossRef]
- Wang, W.; Li, F.; Ng, M.K. Structural similarity-based nonlocal variational models for image restoration. IEEE Trans. Image Process. 2019, 28, 4260–4272. [Google Scholar] [CrossRef]
- Zhou, Z.; Sun, Y.; Sun, Q.; Li, C.; Ren, Z. Only once attack: Fooling the tracker with adversarial template. IEEE Trans. Circuits Syst. Video Technol. 2023, 33, 3173–3184. [Google Scholar] [CrossRef]
- Lanfredi, B.; Schroeder, J.; Tasdizen, T. Quantifying the preferential direction of the model gradient in adversarial training with projected gradient descent. Pattern Recognit. 2023, 139, 109430. [Google Scholar] [CrossRef]
- Chen, C.; Ye, D.; He, Y.; Tang, L.; Xu, Y. Improving adversarial robustness with adversarial augmentations. IEEE Internet Things J. 2024, 11, 5105–5117. [Google Scholar] [CrossRef]
- Huang, Z.; Fan, Y.; Liu, C.; Zhang, W.; Zhang, Y.; Salzmann, M.; Süsstrunk, S.; Wang, J. Fast adversarial training with adaptive step size. IEEE Trans. Image Process. 2023, 32, 6102–6114. [Google Scholar] [CrossRef] [PubMed]
- de Araujo-Filho, P.F.; Kaddoum, G.; Ben Nasr, M.C.; Arcoverde, H.F.; Campelo, D.R. Defending Wireless Receivers Against Adversarial Attacks on Modulation Classifiers. IEEE Internet Things J. 2023, 10, 19153–19162. [Google Scholar] [CrossRef]
- Li, Z.; Xia, P.; Tao, R.; Niu, H.; Li, B. A new perspective on stabilizing GANs training: Direct adversarial training. IEEE Trans. Emerg. Top. Comput. Intell. 2023, 7, 178–189. [Google Scholar] [CrossRef]
- Jia, X.; Zhang, Y.; Wu, B.; Wang, J.; Cao, X. Boosting fast adversarial training with learnable Adversarial Initialization. IEEE Trans. Image Process. 2022, 31, 4417–4430. [Google Scholar] [CrossRef]
- Dong, J.; Yang, L.; Wang, Y.; Xie, X.; Lai, J. Toward intrinsic adversarial robustness through probabilistic training. IEEE Trans. Image Process. 2023, 32, 3862–3872. [Google Scholar] [CrossRef]
- Ni, S.; Li, J.; Yang, M.; Kao, H.-Y. DropAttack: A random dropped weight attack adversarial training for natural language understanding. IEEE/ACM Trans. Audio Speech Language Process. 2024, 32, 364–373. [Google Scholar] [CrossRef]
- Xu, M.; Zhang, T.; Li, Z.; Zhang, D. InfoAT: Improving adversarial training using the information bottleneck principle. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 1255–1264. [Google Scholar] [CrossRef]






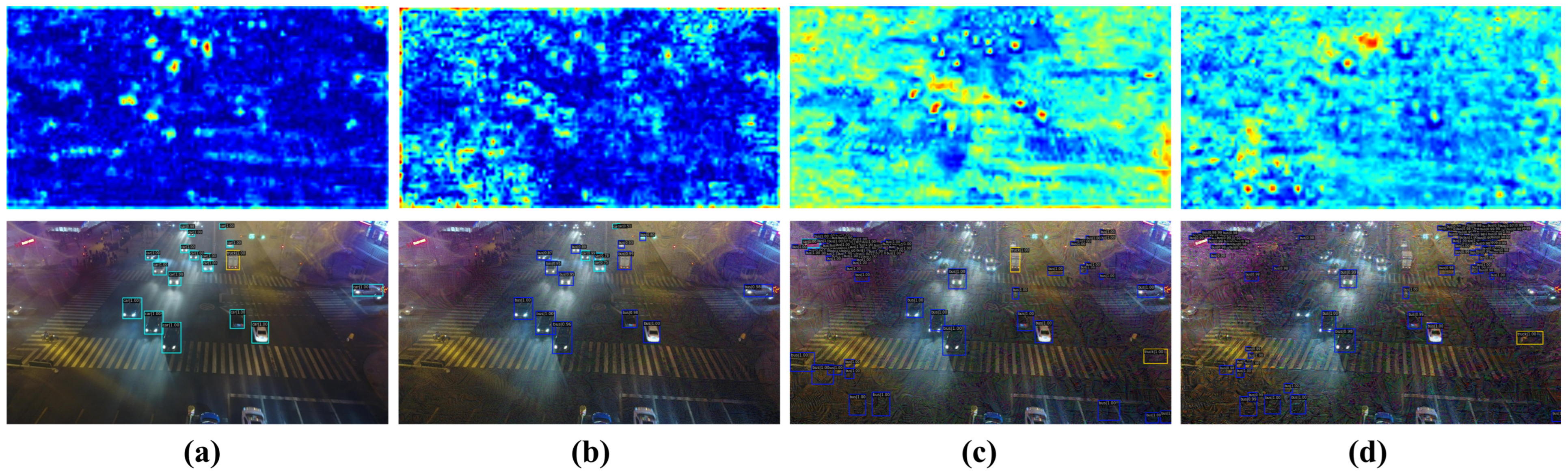

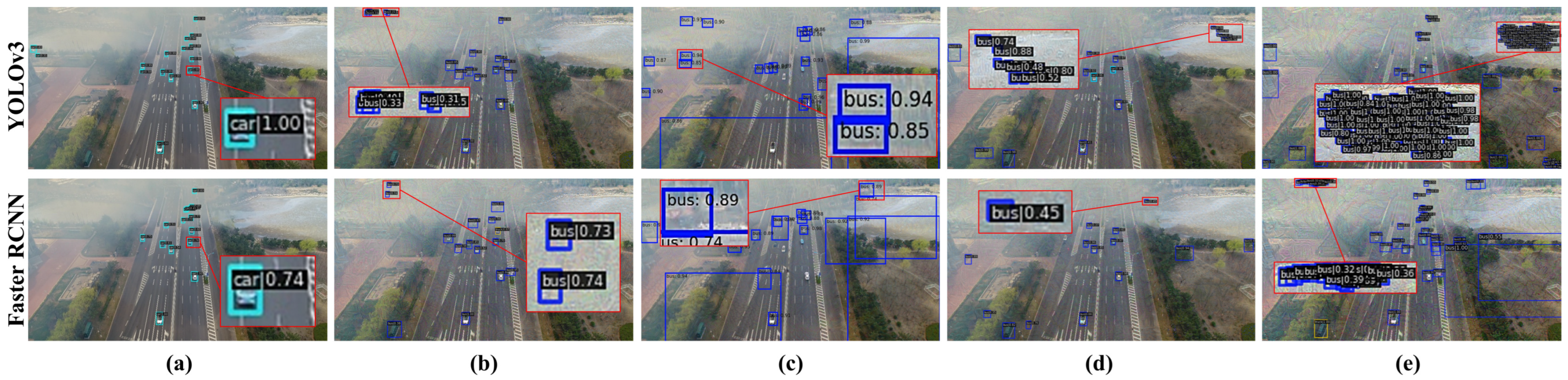

| Method | Reference | White-Box | Black-Box | Mislabeling | Fabrication |
|---|---|---|---|---|---|
| PGD | Madry et al. [29] | ✓ | ✓ | ||
| DAG | Xie et al. [30] | ✓ | ✓ | ||
| UAE | Wei et al. [31] | ✓ | ✓ | ||
| ULAN | Du et al. [32] | ✓ | ✓ | ||
| UAP | Qin et al. [33] | ✓ | ✓ | ||
| RAP | Li et al. [34] | ✓ | ✓ | ||
| PCB | Wu et al. [35] | ✓ | ✓ | ✓ | |
| TOG | Chow et al. [36] | ✓ | ✓ | ✓ | |
| TFA | Zhang et al. [37] | ✓ | ✓ | ✓ | |
| CAP | Zhang et al. [38] | ✓ | ✓ | ||
| WSOD | Kuang et al. [20] | ✓ | ✓ | ||
| EA | Wang et al. [39] | ✓ | ✓ | ||
| ASA | Li et al. [40] | ✓ | ✓ | ||
| EBAD | Cai et al. [14] | ✓ | ✓ |
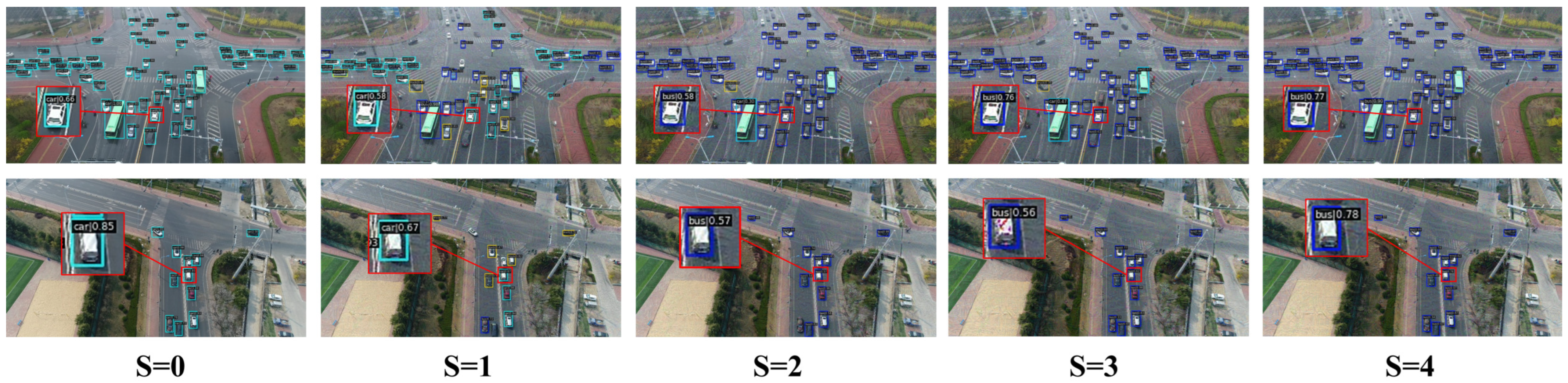
| Function | Metric | S = 0 | S = 1 | S = 2 | S = 3 | S = 4 |
|---|---|---|---|---|---|---|
| Mislabeling Attack | mAP (%) | |||||
| Time Cost (s) | ||||||
| Fabrication Attack | mAP (%) | |||||
| Time Cost (s) |
| Type | Models | mAP (%) | Time Cost (s) | SSIM | ||
|---|---|---|---|---|---|---|
| Benign | Adv. | Benign | Adv. | |||
| Agent Models (White Box) | YOLOV3 | 73.70 | 3.78 | 0.11 | 2.17 | 0.848 |
| Faster RCNN | 69.23 | 1.96 | 0.32 | 3.87 | 0.817 | |
| Victim Models (Black-Box) | RetinaNet | 67.61 | 7.69 | 0.10 | 4.24 | 0.879 |
| SSD | 71.68 | 5.27 | 0.12 | 4.04 | 0.868 | |
| Sparse RCNN | 69.33 | 5.52 | 0.27 | 6.99 | 0.844 | |
| Type | Models | mAP (%) | Time Cost (s) | SSIM | ||
|---|---|---|---|---|---|---|
| Benign | Adv. | Benign | Adv. | |||
| Agent Models (White Box) | YOLOV3 | 73.70 | 5.87 | 0.11 | 2.34 | 0.799 |
| Faster RCNN | 69.23 | 7.31 | 0.32 | 3.92 | 0.786 | |
| Victim Models (Black-Box) | RetinaNet | 67.61 | 11.56 | 0.10 | 4.85 | 0.831 |
| SSD | 71.68 | 8.45 | 0.12 | 5.17 | 0.833 | |
| Sparse RCNN | 69.33 | 6.68 | 0.27 | 7.29 | 0.815 | |
| Clean | MIM | DIA | BAAM | IBAM | SSD |
|---|---|---|---|---|---|
| mAP (%) | |||||
| A | - | - | - | - | 71.68 |
| A | A | - | - | A | 61.57 |
| A | A | A | - | A | 12.23 |
| A | A | A | A | A | 5.27 |
| Clean | MIM | DIA | BAAM | IBAM | SSD |
|---|---|---|---|---|---|
| mAP (%) | |||||
| A | - | - | - | - | 71.68 |
| A | A | - | - | A | 66.98 |
| A | A | A | - | A | 16.52 |
| A | A | A | A | A | 8.45 |
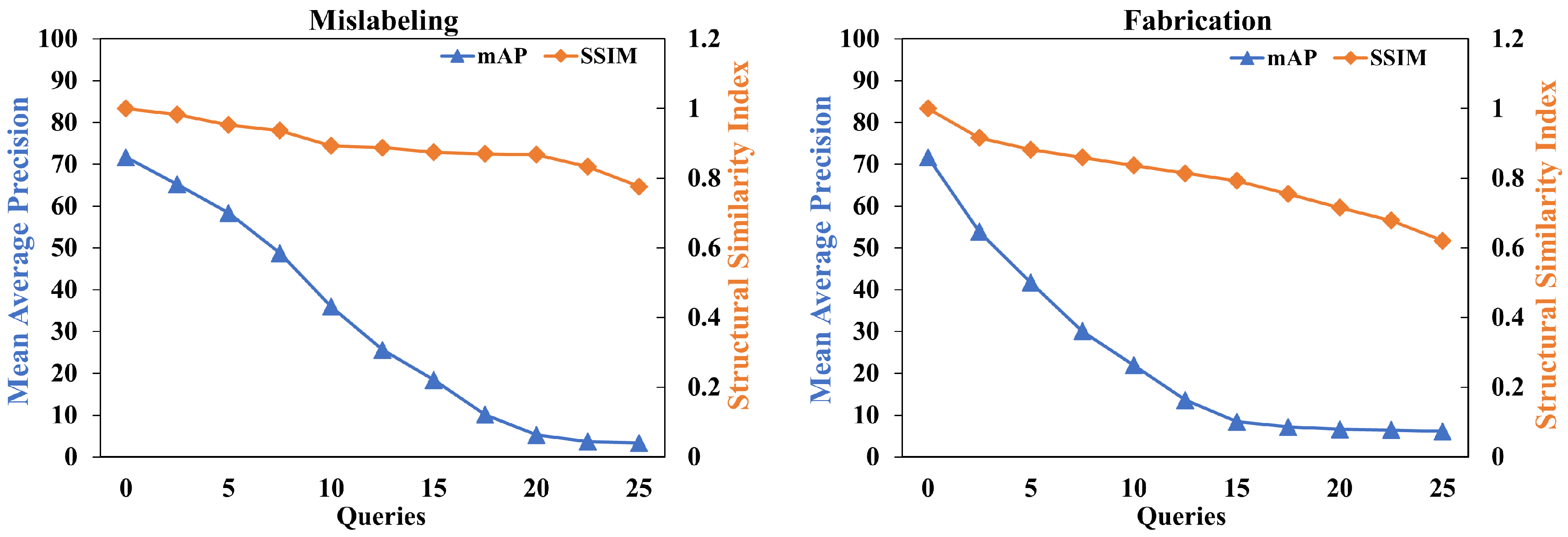
| Attack | Method | mAP | Time Cost (s) | SSIM | Queries |
|---|---|---|---|---|---|
| Clean Model | YOLOv3 | 73.70 | 0.11 | 1.000 | 0 |
| Faster RCNN | 69.23 | 0.32 | 1.000 | 0 | |
| TOG-Mislabel | YOLOv3 | 4.46 | 0.92 | 0.834 | 30 |
| Faster RCNN | 3.74 | 1.25 | 0.828 | 30 | |
| DAG | YOLOv3 | 71.65 | 9.37 | 0.936 | 160 |
| Faster RCNN | 8.43 | 9.49 | 0.941 | 160 | |
| PGD | YOLOv3 | 4.16 | 6.28 | 0.879 | 40 |
| Faster RCNN | 5.59 | 6.44 | 0.856 | 40 | |
| DBI-Attack (White Box) | YOLOv3 | 3.78 | 2.17 | 0.845 | 20 |
| Faster RCNN | 1.96 | 3.87 | 0.817 | 20 |
| Attack | Method | mAP | Time Cost (s) | FA | SSIM | Queries |
|---|---|---|---|---|---|---|
| Clean Model | YOLOv3 | 73.70 | 0.11 | 0.000 | 1.000 | 0 |
| Faster RCNN | 69.23 | 0.32 | 0.000 | 1.000 | 0 | |
| PCB | YOLOv3 | 3.39 | 0.78 | 0.112 | 0.862 | 10 |
| Faster RCNN | 3.65 | 1.09 | 0.077 | 0.835 | 10 | |
| TOG-Fabrication | YOLOv3 | 2.36 | 0.67 | 0.146 | 0.849 | 30 |
| Faster RCNN | 2.43 | 0.88 | 0.138 | 0.836 | 30 | |
| TFA-Fabrication | YOLOv3 | 2.49 | 0.83 | 0.237 | 0.830 | 30 |
| Faster RCNN | 2.93 | 1.47 | 0.051 | 0.844 | 30 | |
| DBI-Attack (White Box) | YOLOv3 | 5.87 | 2.34 | 0.671 | 0.799 | 15 |
| Faster RCNN | 7.31 | 3.92 | 0.310 | 0.774 | 15 |
| Attack | Method | mAP | Time Cost (s) | SSIM | Queries |
|---|---|---|---|---|---|
| Clean Model | RetinaNet | 67.61 | 0.10 | 1.00 | 0 |
| SSD | 71.68 | 0.12 | 1.00 | 0 | |
| Sparse RCNN | 69.33 | 0.27 | 1.00 | 0 | |
| RAP+IBAM | RetinaNet | 53.58 | 3.09 | 0.803 | 30 |
| SSD | 51.12 | 3.37 | 0.797 | 30 | |
| Sparse RCNN | 18.67 | 6.74 | 0.790 | 30 | |
| EBAD | RetinaNet | 26.23 | 3.14 | 0.833 | 10 |
| SSD | 19.24 | 3.26 | 0.860 | 10 | |
| Sparse RCNN | 24.19 | 4.51 | 0.827 | 10 | |
| TFA-Mislabeling +IBAM | RetinaNet | 11.92 | 12.26 | 0.874 | 40 |
| SSD | 12.11 | 14.87 | 0.883 | 40 | |
| Sparse RCNN | 14.67 | 15.79 | 0.821 | 40 | |
| DBI-Attack (Black-Box) | RetinaNet | 7.69 | 4.24 | 0.879 | 20 |
| SSD | 5.27 | 4.04 | 0.868 | 20 | |
| Sparse RCNN | 5.52 | 6.99 | 0.834 | 20 |
| Attack | Method | mAP | Time Cost (s) | FR | SSIM | Queries |
|---|---|---|---|---|---|---|
| Clean Model | RetinaNet | 67.61 | 0.10 | 0.000 | 1.000 | 0 |
| SSD | 71.68 | 0.12 | 0.000 | 1.000 | 0 | |
| Sparse RCNN | 69.33 | 0.27 | 0.000 | 1.000 | 0 | |
| PCB+IBAM | RetinaNet | 7.24 | 1.59 | 0.021 | 0.876 | 10 |
| SSD | 8.33 | 1.33 | 0.043 | 0.866 | 10 | |
| Sparse RCNN | 6.16 | 2.84 | 0.059 | 0.829 | 10 | |
| TOG-Fabrication +IBAM | RetinaNet | 6.26 | 2.29 | 0.122 | 0.838 | 30 |
| SSD | 7.38 | 2.57 | 0.109 | 0.826 | 30 | |
| Sparse RCNN | 6.57 | 5.04 | 0.128 | 0.821 | 30 | |
| TFA-Fabrication +IBAM | RetinaNet | 5.95 | 4.72 | 0.169 | 0.824 | 30 |
| SSD | 6.31 | 4.59 | 0.214 | 0.817 | 30 | |
| Sparse RCNN | 7.18 | 6.30 | 0.036 | 0.837 | 30 | |
| DBI-Attack (Black-Box) | RetinaNet | 11.56 | 4.85 | 0.397 | 0.791 | 15 |
| SSD | 8.45 | 5.17 | 0.587 | 0.773 | 15 | |
| Sparse RCNN | 6.68 | 7.29 | 0.337 | 0.755 | 15 |
| Queries | 5 | 10 | 15 | 20 | 25 | |
|---|---|---|---|---|---|---|
| Mislabeling | No Defense | 58.34 | 35.92 | 18.43 | 5.27 | 3.35 |
| AT | 61.49 | 39.82 | 26.17 | 18.83 | 17.62 | |
| Fabrication | No Defense | 41.68 | 21.92 | 8.45 | 6.62 | 6.13 |
| AT | 46.29 | 27.71 | 18.26 | 17.55 | 18.48 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Z.; Wang, B.; Wang, Z.; Yao, X. DBI-Attack:Dynamic Bi-Level Integrated Attack for Intensive Multi-Scale UAV Object Detection. Remote Sens. 2024, 16, 2570. https://doi.org/10.3390/rs16142570
Zhao Z, Wang B, Wang Z, Yao X. DBI-Attack:Dynamic Bi-Level Integrated Attack for Intensive Multi-Scale UAV Object Detection. Remote Sensing. 2024; 16(14):2570. https://doi.org/10.3390/rs16142570
Chicago/Turabian StyleZhao, Zhengyang, Buhong Wang, Zhen Wang, and Xuan Yao. 2024. "DBI-Attack:Dynamic Bi-Level Integrated Attack for Intensive Multi-Scale UAV Object Detection" Remote Sensing 16, no. 14: 2570. https://doi.org/10.3390/rs16142570
APA StyleZhao, Z., Wang, B., Wang, Z., & Yao, X. (2024). DBI-Attack:Dynamic Bi-Level Integrated Attack for Intensive Multi-Scale UAV Object Detection. Remote Sensing, 16(14), 2570. https://doi.org/10.3390/rs16142570







