Using Multi-Source National Forest Inventory Data for the Prediction of Tree Lists of Individual Stands for Long-Term Simulation
Abstract
1. Introduction
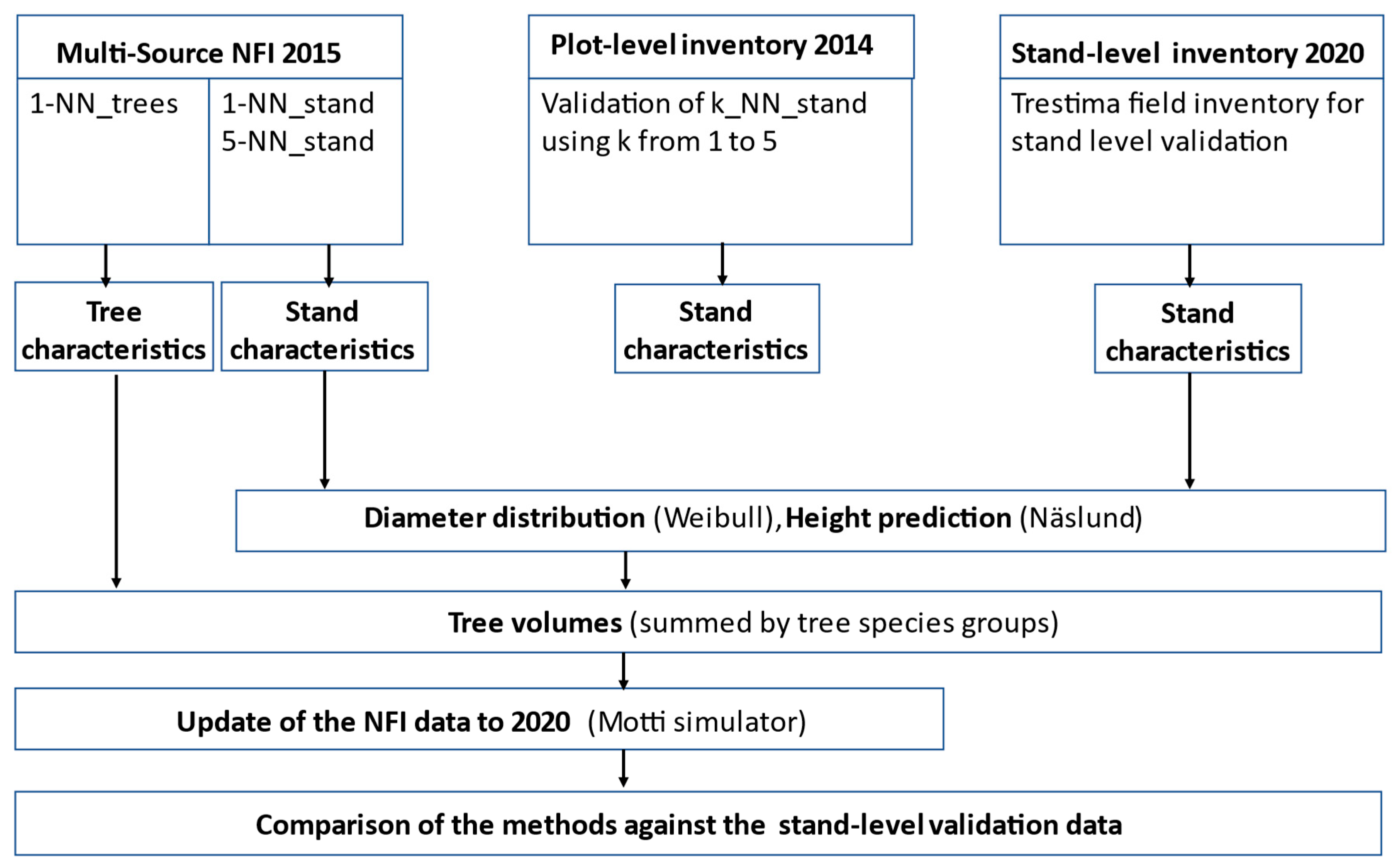
2. Material and Methods
2.1. The Plot and Stand-Level Validation Data Sets
2.2. The Multi-Source NFI Data
2.3. The k-NN Estimation Method Used in the MS-NFI
2.4. The Alternative Prediction Methods
- (1)
- k-NN_stand: stand characteristics of the k NFI plots for predicting the grid-level stand characteristics using k from 1 to 5 for the plot-level (2014 measured data) validation (criteria stand characteristics and dbh distributions).
- (2)
- k-NN_stand: combining species-specific stand characteristics from the two best performed k (1 or 5) NFI plots to grid-level stand characteristics for stand-level (2020 inventory) validation (criteria total and species-wise volumes).
- (3)
- 1-NN_trees: using the measured trees of the nearest neighbor NFI plot per grid cell for stand-level validation (criteria total and species-wise volumes).
2.5. Comparison of the Methods
3. Results
3.1. Plot-Level Results with Varying k
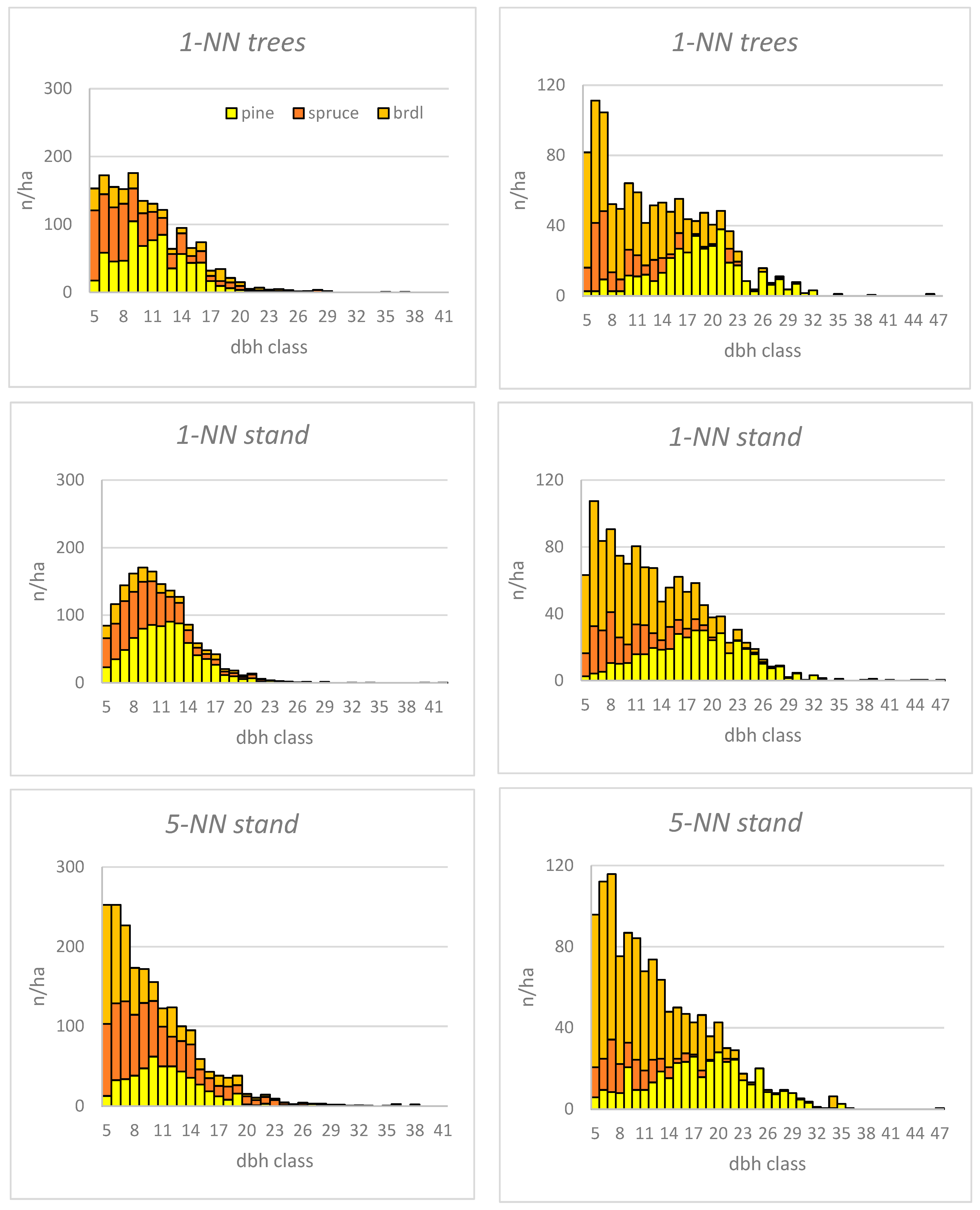
3.2. Differences in the Dbh Distributions between the Methods
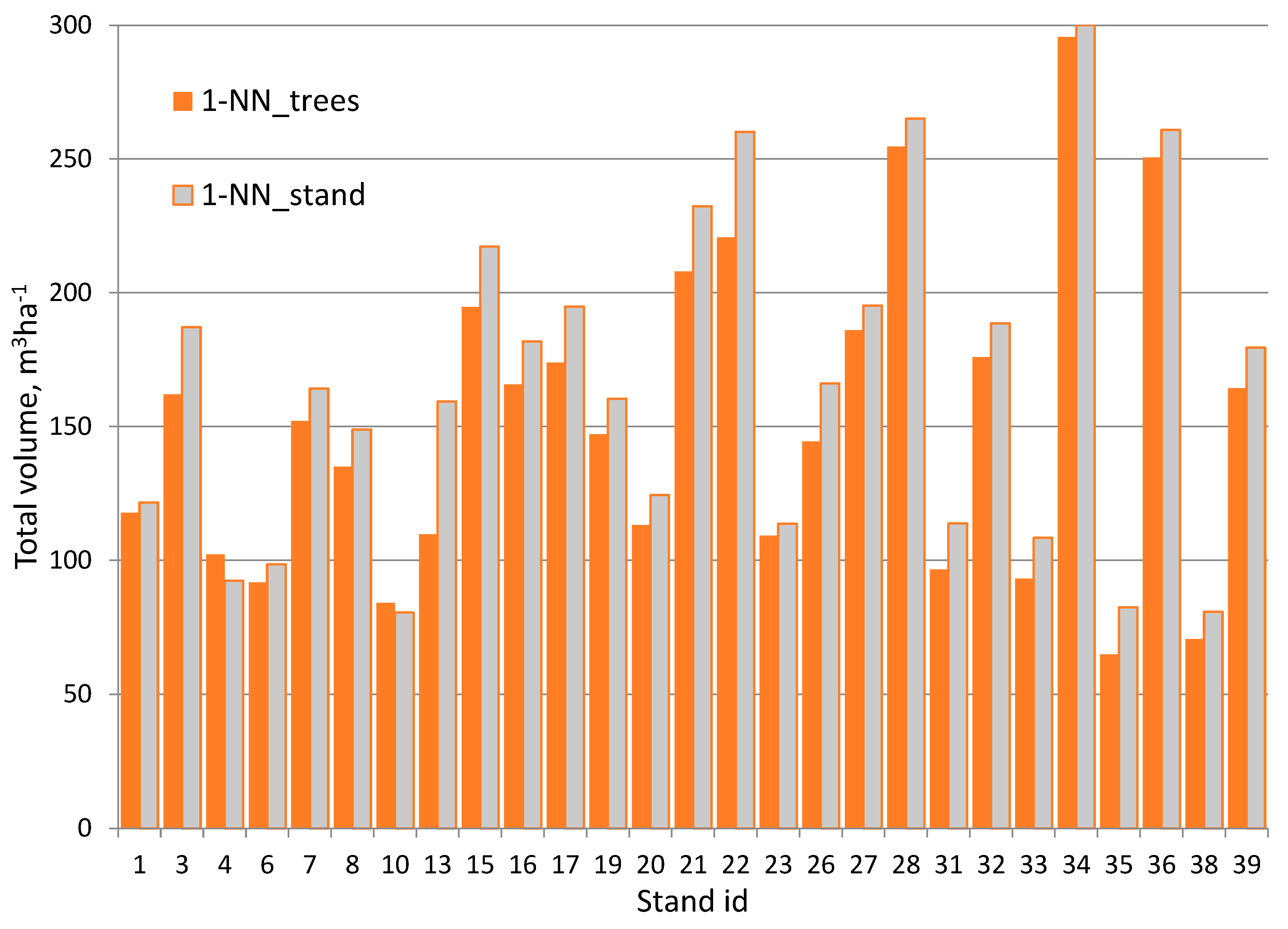
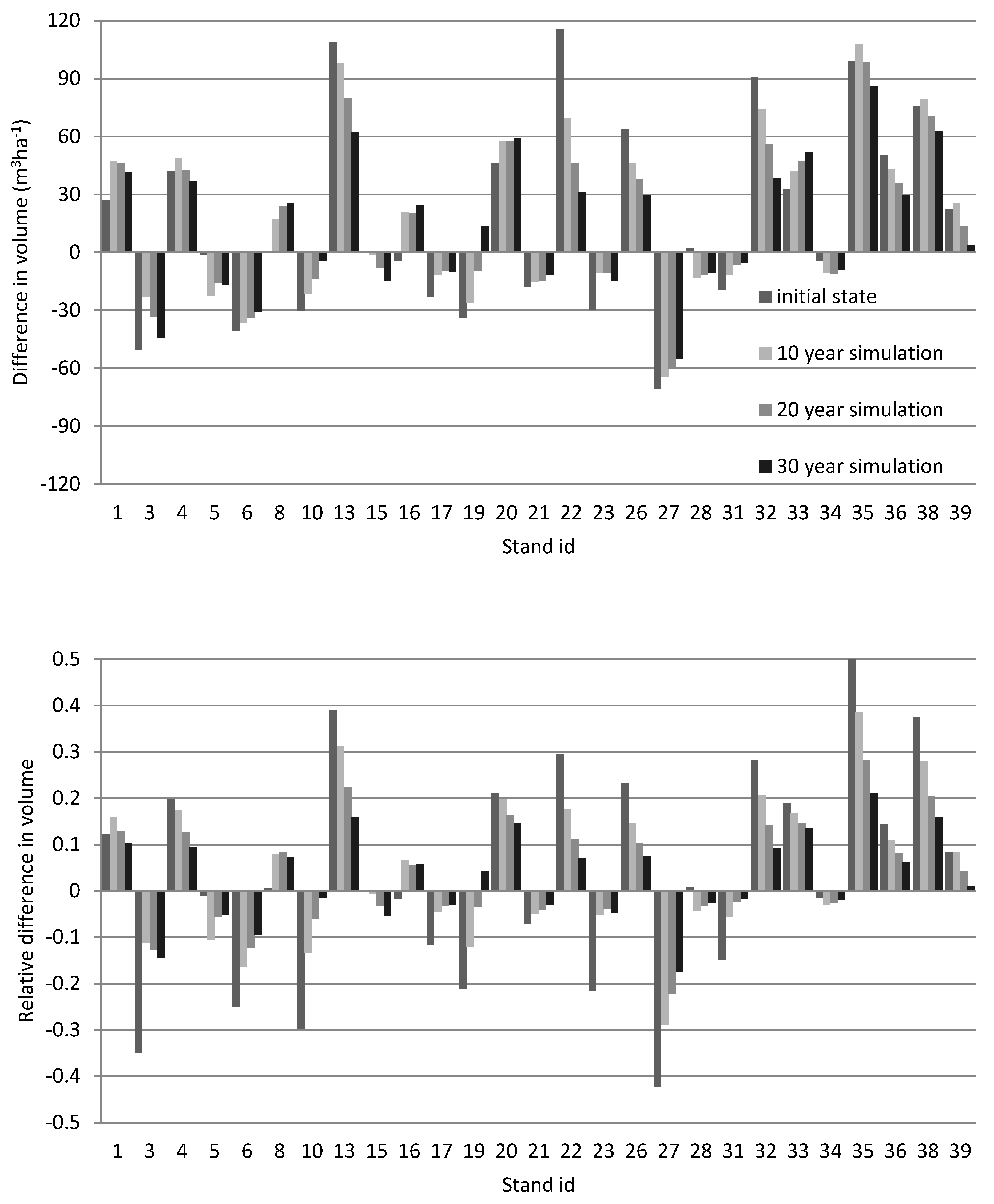
3.3. The Accuracy in the Initial Stand Volume and That after 30-Year Simulation
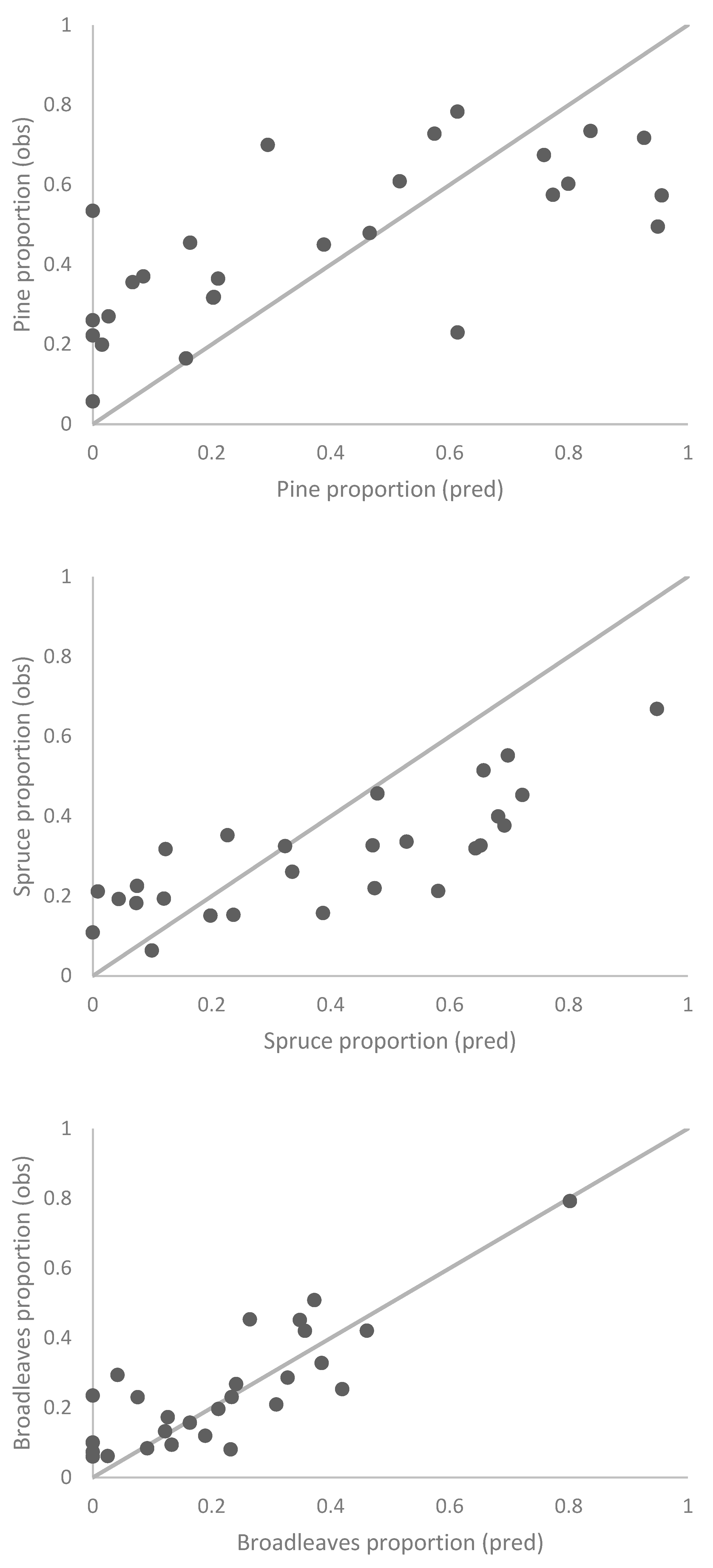
3.4. Species Proportion
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tomppo, E. Satellite image-based National Forest Inventory of Finland. Photogramm. J. Finl. 1990, 12, 115–120. [Google Scholar]
- Tomppo, E.; Haakana, M.; Katila, M.; Peräsaari, J. Multi-Source National Forest Inventory: Methods and Applications; Springer Science & Business Media: Dodrecht, The Netherlands, 2008. [Google Scholar]
- Mäkisara, K.; Katila, M.; Peräsaari, J. The Multi-Source National Forest Inventory of Finland—Methods and Results 2015. Natural Resources and Bioeconomy Studies 8/2019, Natural Resources Institute Finland. 2019. 57p. Available online: https://urn.fi/URN:ISBN:978-952-326-711-4 (accessed on 1 July 2024).
- Maltamo, M.; Kangas, A. Methods based on k-nearest neighbor regression in the prediction of basal area diameter distribution. Can. J. For. Res. 1998, 28, 1107–1115. [Google Scholar] [CrossRef]
- Næsset, E. Estimating timber volume of forest stands using airborne laser scanner data. Remote Sens. Environ. 1997, 61, 246–253. [Google Scholar] [CrossRef]
- Næsset, E. Predicting forest stand characteristics with airborne scanning laser using a practical two-stage procedure and field data. Remote Sens. Environ. 2002, 80, 88–99. [Google Scholar] [CrossRef]
- Næsset, E. Practical large-scale forest stand inventory using a small-footprint airborne laser scanning. Scand. J. For. Res. 2004, 19, 164–179. [Google Scholar] [CrossRef]
- Kangas, A.; Astrup, R.; Breidenbach, J.; Fridman, J.; Gobakken, T.; Korhonen, K.T.; Maltamo, M.; Nilsson, M.; Nord-larsen, T.; Næsset, E.; et al. Remote Sensing and Forest Inventories in Nordic Countries—Roadmap for the Future. Scand. J. For. Res. 2018, 33, 397–412. [Google Scholar] [CrossRef]
- Holmgren, P.; Thuresson, T. Satellite remote sensing for forestry planning—A review. Scand. J. For. Res. 1998, 13, 90–110. [Google Scholar] [CrossRef]
- Packalén, P.; Maltamo, M. Estimation of species-specific diameter distributions using airborne laser scanning and aerial photographs. Can. J. For. Res. 2008, 38, 1750–1760. [Google Scholar] [CrossRef]
- Peuhkurinen, J.; Maltamo, M.; Malinen, J. Estimating species-specific diameter distributions and saw log recoveries of boreal forests from airborne laser scanning data and aerial photographs: A distribution-based approach. Silva Fenn. 2008, 42, 625–641. [Google Scholar] [CrossRef]
- Barrett, F.; McRoberts, R.E.; Tomppo, E.; Cienciala, E.; Waser, L.T. A questionnaire-based review of the operational use of remotely sensed data by national forest inventories. Remote Sens. Environ. 2016, 174, 279–289. [Google Scholar] [CrossRef]
- Nilsson, M. Estimation of Forest Variables Using Satellite Image Data and Airborne Lidar. Ph.D. Thesis, Swedish University of Agricultural Sciences, The Department of Forest Resource Management and Geomatics, Acta Universitas Agriculture Sueciae, Uppsala, Sweden, 1997; 84p. [Google Scholar]
- Næsset, E.; Gobakken, T.; Holmgren, J.; Hyyppä, H.; Hyyppä, J.; Maltamo, M.; Nilsson, M.; Olsson, H.; Persson, Å.; Söderman, U. Laser scanning of forest resources: The Nordic experience. Scand. J. For. Res. 2004, 19, 482–499. [Google Scholar] [CrossRef]
- Maltamo, M.; Packalén, P.; Peuhkurinen, J.; Suvanto, A.; Pesonen, A.; Hyyppä, J. Experiences and possibilities of ALS based forest inventory in Finland. In Proceedings of the ISPRS Workshop on Laser Scanning 2007 and SilviLaser 2007, Espoo, Finland, 12–14 September 2007; pp. 270–279. [Google Scholar]
- McRoberts, R.E.; Cohen, W.B.; Næsset, E.; Stehman, S.V.; Tomppo, E.O. Using remotely sensed data to construct and assess forest attribute maps and related spatial products. Scand. J. For. Res. 2010, 25, 340–367. [Google Scholar] [CrossRef]
- Maltamo, M.; Packalen, P. Species-Specific Management Inventory in Finland. In Forestry Applications of Airborne Laser Scanning. Managing Forest Ecosystems; Maltamo, M., Næsset, E., Vauhkonen, J., Eds.; Springer: Dordrecht, The Netherlands, 2014; Volume 27. [Google Scholar] [CrossRef]
- Fassnacht, F.E.; White, J.C.; Wulder, M.A.; Næsset, E. Remote sensing in forestry: Current challenges, considerations and directions. Forestry 2024, 97, 11–37. [Google Scholar] [CrossRef]
- Wulder, M.A.; Hermosilla, T.; White, J.C.; Bater, C.W.; Hobart, G.; Bronson, S.C. Development and implementation of a stand-level satellite-based forest inventory for Canada. Forestry 2024, 1, cpad065. [Google Scholar] [CrossRef]
- Zhang, J.; Foody, G.M. A fuzzy classification of sub-urban land cover from remotely sensed imagery. Int. J. Remote Sens. 1998, 19, 2721–2738. [Google Scholar] [CrossRef]
- Wikström, P. Effect of decision variable definition and data aggregation on search process applied to a single-tree simulator. Can. J. For. Res. 2001, 31, 1057–1066. [Google Scholar] [CrossRef]
- Ahtikoski, A.; Siipilehto, J.; Salminen, H.; Lehtonen, M.; Hynynen, J. Effect of stand structure and number of sample trees on optimal management for Scots pine: A model-based study. Forests 2018, 9, 750. [Google Scholar] [CrossRef]
- Maltamo, M. Basal Area Diameter Distribution in Estimating the Quantity and Structure of Growing Stock. Doctoral Dissertation, University of Joensuu, Faculty of Forestry, Joensuu, Finland, 1998. [Google Scholar]
- Mehtätalo, L. Predicting Stand Characteristics Using Limited Measurements. Finnish Forest Research Institute, Research Papers 929. 2004. 39p. Available online: http://urn.fi/URN:ISBN:951-40-1934-2 (accessed on 1 July 2024).
- Packalén, P. Using airborne laser scanning data and digital aerial photographs to estimate growing stock by tree species. Diss. For. 2009, 77, 41. [Google Scholar] [CrossRef]
- Siipilehto, J. Methods and applications for improving parameter prediction models for stand structures in Finland. Diss. For. 2011, 124, 56. [Google Scholar] [CrossRef][Green Version]
- Räty, J. Prediction of diameter distributions in boreal forests using remotely sensed data. Diss. For. 2020, 294, 47. [Google Scholar] [CrossRef]
- Bailey, R.L.; Dell, T.R. Quantifying diameter distributions with the Weibull function. For. Sci. 1973, 19, 97–104. [Google Scholar]
- Siipilehto, J.; Mehtätalo, L. Parameter recovery vs. parameter prediction for the Weibull distribution validated for Scots pine stands in Finland. Silva Fenn. 2013, 47, 1–22. [Google Scholar] [CrossRef]
- Moeur, M.; Stage, A.R. Most similar neighbor: An improved sampling inference procedure for natural resource planning. For. Sci. 1995, 41, 337–359. [Google Scholar] [CrossRef]
- Maltamo, M.; Malinen, J.; Kangas, A.; Härkönen, S.; Pasanen, A.-M. Most similar neighbor-based stand variable estimation for use in inventory by compartments in Finland. Forestry 2003, 76, 449–463. [Google Scholar] [CrossRef]
- Fix, E.; Hodges, J.L. Discriminatory Analysis: Nonparametric Discrimination: Consistency Properties; USAF School of Aviation Medicine: Randolf Field, TX, USA, 1951. [Google Scholar]
- Chirici, G.; Mura, M.; McInerney, D.; Py, N.; Tomppo, E.; Waser, L.T.; Travaglini, D.; McRoberts, R.E. A meta-analysis and review of the literature on the k-nearest neighbors technique for forestry applications that use remotely sensed data. Remote Sens. Environ. 2016, 176, 282–294. [Google Scholar] [CrossRef]
- Rouvinen, T. Kuvia metsästä. [Photos from forest]. Metsätieteen Aikakauskirja 2014, 2, 119–122. [Google Scholar] [CrossRef]
- Trestima. Forest Inventory System. User Manual v.1.4. 2020. Available online: https://www.trestima.com/w/wp-content/uploads/2020/02/TRESTIMA_user_guide_en_v1.4.pdf (accessed on 1 July 2024).
- Tomppo, E.; Kuusinen, N.; Mäkisara, K.; Katila, M.; McRoberts, R.E. Effect of field plot configuration on the uncertainties of ALS-assisted forest resource estimates. Scand. J. For. Res. 2017, 32, 488–500. [Google Scholar] [CrossRef]
- Cajander, A.K. Forest types and their significance. Acta For. Fenn. 1949, 56, 1–69. [Google Scholar] [CrossRef]
- Salminen, H.; Lehtonen, M.; Hynynen, J. Reusing legacy FORTRAN in MOTTI growth and yield simulator. Comput. Electron. Agr. 2005, 49, 105–113. [Google Scholar] [CrossRef]
- Hynynen, J.; Salminen, H.; Ahtikoski, A.; Huuskonen, S.; Ojansuu, R.; Siipilehto, J.; Lehtonen, M.; Eerikäinen, K. Long-term impacts of forest management on biomass supply and forest resource development: A scenario analysis for Finland. Eur. J. For. Res. 2015, 134, 415–431. [Google Scholar] [CrossRef]
- Rogers, W.H. Some Convergence Properties of k-Nearest Neighbor Estimates; Department of Statistics, Stanford University: Palo Alto, CA, USA, 1978. [Google Scholar]
- Tomppo, E.; Halme, M. Using coarse scale forest variables as ancillary information and weighting of variables in k-NN estimation: A genetic algorithm approach. Remote Sens. Environ. 2004, 92, 1–20. [Google Scholar] [CrossRef]
- Siipilehto, J.; Lindeman, H.; Vastaranta, M.; Yu, X.; Uusitalo, J. Reliability of the predicted stand structure for clear-cut stands using optional methods: Airborne laser scanning-based methods, smartphone-based forest inventory application Trestima and pre-harvest measurement tool EMO. Silva Fenn. 2016, 50, 1568. [Google Scholar] [CrossRef]
- Geman, S.; Bienenstock, E.; Doursat, R. Neural networks and the bias/variance dilemma. Neural Comput. 1992, 4, 1–58. [Google Scholar] [CrossRef]
- Holopainen, M.; Tuominen, S.; Karjalainen, M.; Hyyppä, J.; Vastaranta, M.; Hyyppä, H. Korkearesoluutioisten E-SAR-tutkakuvien tarkkuus puustotunnusten koealatason estimoinnissa. Metsätieteen Aikakauskirja 2009, 4, 309–323. [Google Scholar] [CrossRef]
- Siipilehto, J.; Kangas, A. Näslundin pituuskäyrä ja siihen perustuvia malleja läpimitta-pituus riippuvuudesta suomalaisissa talousmetsissä. [Näslund’s hight curve models for the dbh-height relationship in Finnish commercial forests.]. Metsätieteen Aikakauskirja 2015, 4, 215–236. [Google Scholar] [CrossRef][Green Version]
- Laasasenaho, J. Taper curve and volume functions for pine, spruce and birch. Commun. Inst. For. Fenn. 1982, 108, 1–74. [Google Scholar]
- Tuominen, S.; Balazs, A.; Honkavaara, E.; Pölönen, I.; Saari, H.; Hakala, T.; Viljanen, N. Hyperspectral UAV-imagery and photogrammetric canopy height model in estimating forest stand variables. Silva Fenn. 2017, 51, 7721. [Google Scholar] [CrossRef]
- Hudak, A.T.; Crookston, N.L.; Evans, J.S.; Hall, D.E.; Falkowski, M.J. Nearest neighbor imputation of species-level, plot-scale forest structure attributes from LiDAR data. Remote Sens. Environ. 2008, 112, 2232–2245. [Google Scholar] [CrossRef]
- McRoberts, R.E.; Næsset, E.; Gobakken, T. Optimizing the k-Nearest Neighbors technique for estimating forest aboveground biomass using airborne laser scanning data. Remote Sens. Environ. 2015, 163, 13–22. [Google Scholar] [CrossRef]
- Vastaranta, M.; Gonzalez Latorre, E.; Luoma, V.; Saarinen, N.; Holopainen, M.; Hyyppä, J. Evaluation of a smartphone app for forest sample plot measurements. Forests 2015, 6, 1179–1194. [Google Scholar] [CrossRef]
- Ruusunen, P. Trestiman Puustotulkinnan Tarkkuus Tarkkaan Mitatuilla Puukarttakoealoilla. [Trestima’s Accuracy in Accurately Measured Tree Map Plots]. Häme University of Applied Sciences. 2020. 41p. Available online: https://urn.fi/URN:NBN:fi:amk-202004165202 (accessed on 1 July 2024).
- Dunaeva, T. Preharvest Efficiency of Trestima, Airborne Laser Scanning and Forest Management Plan Data Validated by Actual harvesting Results and Forest Engineer Preharvest Estimation. Bachelor’s Thesis, Yrkehögskolan NOVIA, Raseborg, Finland, 2017; 98p. [Google Scholar]
- Mäkelä, H.; Pekkarinen, A. Estimation of forest stand volumes by Landsat TM imagery and stand-level field-inventory data. For. Ecol. Manag 2004, 196, 245–255. [Google Scholar] [CrossRef]
- Hyyppä, J.; Hyyppä, H.; Inkinen, M.; Engdahl, M.; Linko, S.; Zhu, Y.-H. Accuracy comparison of various remote sensing data sources in the retrieval of forest stand attributes. For. Ecol. Manag. 2000, 128, 109–120. [Google Scholar] [CrossRef]
- Hyvönen, P. Kuvioittaisten puustotunnusten ja toimenpide-ehdotusten estimointi k-lähimmän naapurin menetelmällä Landsat TM -satelliittikuvan, vanhan inventointitiedon ja kuviotason tukiaineiston avulla. Metsätieteen Aikakauskirja 2002, 3, 363–379. (In Finnish) [Google Scholar] [CrossRef][Green Version]
- Muukkonen, P.; Heiskanen, J. Estimating biomass for boreal forests using ASTER satellite data combined with standwise forest inventory data. Remote Sens. Environ. 2005, 99, 434–447. [Google Scholar] [CrossRef]
- Astola, H.; Häme, T.; Sirro, L.; Molinier, M.; Kilpi, J. Comparison of Sentinel-2 and Landsat 8 imagery for forest variable prediction in boreal region. Remote Sens. Environ. 2019, 223, 257–273. [Google Scholar] [CrossRef]
- Nink, S.; Hill, J.; Buddenbaum, H.; Stoffels, J.; Sachtleber, T.; Langshausen, J. Assessing the Suitability of Future Multi- and Hyperspectral Satellite Systems for Mapping the Spatial Distribution of Norway Spruce Timber Volume. Remote Sens. 2015, 7, 12009–12040. [Google Scholar] [CrossRef]
- Esteban, J.; McRoberts, R.E.; Fernández-Landa, A.; Tomé, J.L.; Næsset, E. Estimating Forest Volume and Biomass and Their Changes Using Random Forests and Remotely Sensed Data. Remote Sens. 2019, 11, 1944. [Google Scholar] [CrossRef]
- Holopainen, M.; Haapanen, R.; Tuominen, S.; Viitala, R. Performance of airborne laser scanning- and aerial photograph-based statistical and textural features in forest variable estimation. In Proceedings of the SilviLaser, Edinburgh, UK, 17–19 September 2008. [Google Scholar]
- Hovi, A.; Raitio, P.; Rautiainen, M. A spectral analysis of 25 boreal tree species. Silva Fenn. 2017, 51, 7753. [Google Scholar] [CrossRef]
- Tomppo, E.; Gagliano, C.; De Natale, F.; Katila, M.; McRoberts, R.E. Predicting categorical forest variables using an improved k-Nearest Neighbour estimator and Landsat imagery. Remote Sens. Environ. 2009, 113, 500–517. [Google Scholar] [CrossRef]
- Persson, M.; Lindberg, E.; Reese, H. Tree classification with Multi-Temporal Sentinel-2 data. Remote Sens. 2018, 10, 1794. [Google Scholar] [CrossRef]
- Breidenbach, J.; Waser, L.T.; Debella-Gilo, M.; Schumacher, J.; Rahlf, J.; Hauglin, M.; Puliti, S.; Astrup, R. National mapping and estimation of forest area by dominant tree species using Sentinel-2 data. Can. J. For. Res. 2020, 51, 365–379. [Google Scholar] [CrossRef]
- Maltamo, M.; Packalén, P.; Suvanto, A.; Korhonen, K.T.; Mehtätalo, L.; Hyvönen, P. Combining ALS and NFI training data for forest management planning: A case study in Kuortane, Western Finland. Eur. J. For. Res. 2009, 128, 305–317. [Google Scholar] [CrossRef]
- Tuominen, S.; Pitkänen, J.; Balazs, A.; Korhonen, K.T.; Hyvönen, P.; Muinonen, E. NFI plots as complementary reference data in forest inventory based on airborne laser scanning and aerial photography in Finland. Silva Fenn. 2014, 48, 983. [Google Scholar] [CrossRef]
- Packalén, P.; Maltamo, M. The k-MSN method for the prediction of species-specific stand attributes using airborne laser scanning and aerial photographs. Remote Sens. Environ. 2007, 109, 328–341. [Google Scholar] [CrossRef]
- Holopainen, M.; Vastaranta, M.; Rasinmäki, J.; Kalliovirta, J.; Mäkinen, A.; Haapanen, R.; Melkas, T.; Yu, X.; Hyyppä, J. Uncertainty in timber assortment estimates predicted from forest inventory data. Eur. J. For. Res. 2010, 129, 1131–1142. [Google Scholar] [CrossRef]
- Lee, D.; Siipilehto, J.; Hynynen, J. Models for diameter distribution and tree height in hybrid aspen plantations in southern Finland. Silva Fenn. 2021, 55, 10612. [Google Scholar] [CrossRef]
- Maltamo, M. Comparing basal area diameter distributions estimated by tree species and for the entire growing stock in a mixed stand. Silva Fenn. 1997, 31, 53–65. [Google Scholar] [CrossRef]
- Siipilehto, J. Improving the accuracy of predicted basal-area diameter distribution in advanced stands by determining stem number. Silva Fenn. 1999, 33, 281–301. [Google Scholar] [CrossRef]
- Kangas, A.; Maltamo, M. Calibrating predicted diameter distribution with additional information in growth and yield predictions. Can. J. For. Res. 2003, 33, 430–434. [Google Scholar] [CrossRef]
- Mäkinen, A.; Holopainen, M.; Kangas, A.; Rasinmäki, J. Propagating the errors of initial forest variables through stand- and tree-level growth simulators. Eur. J. For. Res. 2010, 129, 887–897. [Google Scholar] [CrossRef]

| Variable | Mean | Stdev | Min | Max |
|---|---|---|---|---|
| Plot-level characteristics (in 2014) | ||||
| Basal area, m2ha−1 | 23.1 | 8.5 | 9.1 | 42.0 |
| Stem number, ha−1 | 2200 | 1006 | 430. | 4619 |
| DG * (all species), cm | 15.1 | 5.6 | 7.7 | 28.9 |
| Stand-level characteristics (in 2020) | ||||
| Age, years | 46.7 | 22.6 | 19 | 110 |
| Dominant height, m | 18.5 | 3.2 | 12.7 | 25.2 |
| Basal area, m2ha−1 | 26.6 | 7.6 | 16.2 | 45 |
| Stem number, ha−1 | 1279 | 623 | 439 | 2348 |
| DG * (all species), cm | 20.8 | 4.8 | 13.7 | 30 |
| Total stem volume (V), m3ha−1 | 213.6 | 72.7 | 101.4 | 390.5 |
| V * for Scots pine, m3ha−1 | 74.8 | 64.0 | 0.0 | 209.5 |
| V for Norway spruce, m3ha−1 | 93.0 | 79.6 | 0.0 | 278.9 |
| V for broadleaves, m3ha−1 | 45.7 | 35.7 | 0.0 | 116.7 |
| G, m2ha−1 | N, ha−1 | DG, cm | G, m2ha−1 | N, ha−1 | DG, cm | ||
|---|---|---|---|---|---|---|---|
| 1-NN_stand | |||||||
| bias | 2.47 | 904.7 | −3.75 | RMSE | 8.83 | 1368.4 | 5.26 |
| bias% | 10.67 | 41.1 | −24.8 | RMSE% | 43.11 | 110.8 | 27.52 |
| 2-NN_stand | |||||||
| bias | 0.85 | 857.9 | −4.08 | RMSE | 8.04 | 1323.2 | 5.30 |
| bias% | 3.69 | 39.0 | −26.97 | RMSE% | 36.19 | 103.0 | 27.21 |
| 3-NN_stand | |||||||
| bias | 1.14 | 862.3 | −3.93 | RMSE | 8.05 | 1314.4 | 5.09 |
| bias% | 4.93 | 39.2 | −25.98 | RMSE% | 36.74 | 102.6 | 26.34 |
| 4-NN_stand | |||||||
| bias | 0.36 | 842.2 | −4.01 | RMSE | 7.71 | 1303.7 | 5.26 |
| bias% | 1.57 | 38.3 | −26.53 | RMSE% | 33.91 | 100.1 | 27.1 |
| 5-NN_stand | |||||||
| bias | 0.49 | 846.9 | −4.10 | RMSE | 7.36 | 1313.6 | 5.32 |
| bias% | 2.12 | 38.5 | −27.10 | RMSE% | 32.55 | 101.4 | 27.3 |
| Stand | 1-NN_stand | 3-NN_stand | 4-NN_stand | 5-NN_stand |
|---|---|---|---|---|
| average | 0.930 | 0.917 | 0.895 | 0.883 |
| rejected | 7 | 8 | 9 | 7 |
| proportion | 0.241 | 0.276 | 0.310 | 0.241 |
| best fit | 5 | 4 | 7 | 13 |
| worst fit | 8 | 7 | 9 | 4 |
| Initial State of Stands | After 30-Year Simulation with Motti | |||||
|---|---|---|---|---|---|---|
| 1-NN Trees | 1-NN Stand | 5-NN Stand | 1-NN_Trees | 1-NN_Stand | 5-NN_ Stand | |
| Total | ||||||
| difference, m3ha−1 | 30.6 | 30.0 | 16.7 | 21.56 | 20.35 | 8.53 |
| difference, % | 14.3 | 14.1 | 7.8 | 5.8 | 5.5 | 2.3 |
| RMSE | 63.0 | 65.9 | 52.8 | 42.4 | 41.4 | 35.1 |
| RMSE% | 29.5 | 30.8 | 24.7 | 11.4 | 11.1 | 9.4 |
| Scots pine | ||||||
| difference, m3ha−1 | −7.9 | −7.5 | −12.5 | −4.5 | −3.3 | −8.8 |
| difference, % | −10.6 | −10.0 | −16.7 | −2.9 | −2.1 | −5.6 |
| RMSE | 50.4 | 51.7 | 48.9 | 96.6 | 101.8 | 93.0 |
| RMSE% | 67.4 | 69.1 | 65.4 | 61.4 | 64.7 | 59.1 |
| Norway spruce | ||||||
| difference, m3ha−1 | 32.9 | 34.2 | 29.1 | 36.4 | 36.4 | 28.7 |
| difference, % | 35.3 | 36.7 | 31.3 | 21.8 | 21.8 | 17.2 |
| RMSE | 61.9 | 64.4 | 60.8 | 84.2 | 86.1 | 82.7 |
| RMSE% | 66.5 | 69.3 | 65.3 | 50.4 | 51.5 | 49.5 |
| Broadleaves | ||||||
| difference, m3ha−1 | 5.7 | 3.7 | 0.1 | 8.3 | 5.4 | 6.4 |
| difference, % | 12.4 | 8.0 | 0.1 | 9.1 | 5.9 | 7.0 |
| RMSE | 29.6 | 30.1 | 27.9 | 37.1 | 38.1 | 35.5 |
| RMSE% | 64.8 | 65.8 | 60.9 | 40.7 | 41.9 | 39.0 |
| Predicted | Observed Main Tree Species | ||||
|---|---|---|---|---|---|
| Main Species | Pine | Spruce | Broadleaves | Total | Accuracy |
| Pine | 11 | 3 | 0 | 14 | 0.79 |
| Spruce | 0 | 7 | 0 | 7 | 1.00 |
| Broadleaves | 1 | 3 | 2 | 6 | 0.33 |
| Total | 12 | 13 | 2 | 27 | |
| Accuracy | 0.92 | 0.54 | 1.00 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Siipilehto, J.; Henttonen, H.M.; Katila, M.; Mäkinen, H. Using Multi-Source National Forest Inventory Data for the Prediction of Tree Lists of Individual Stands for Long-Term Simulation. Remote Sens. 2024, 16, 2513. https://doi.org/10.3390/rs16142513
Siipilehto J, Henttonen HM, Katila M, Mäkinen H. Using Multi-Source National Forest Inventory Data for the Prediction of Tree Lists of Individual Stands for Long-Term Simulation. Remote Sensing. 2024; 16(14):2513. https://doi.org/10.3390/rs16142513
Chicago/Turabian StyleSiipilehto, Jouni, Helena M. Henttonen, Matti Katila, and Harri Mäkinen. 2024. "Using Multi-Source National Forest Inventory Data for the Prediction of Tree Lists of Individual Stands for Long-Term Simulation" Remote Sensing 16, no. 14: 2513. https://doi.org/10.3390/rs16142513
APA StyleSiipilehto, J., Henttonen, H. M., Katila, M., & Mäkinen, H. (2024). Using Multi-Source National Forest Inventory Data for the Prediction of Tree Lists of Individual Stands for Long-Term Simulation. Remote Sensing, 16(14), 2513. https://doi.org/10.3390/rs16142513






