Spatial Prediction of Diameter Distributions for the Alpine Protection Forests in Ebensee, Austria, Using ALS/PLS and Spatial Distributional Regression Models
Abstract
1. Introduction
2. Materials and Methods
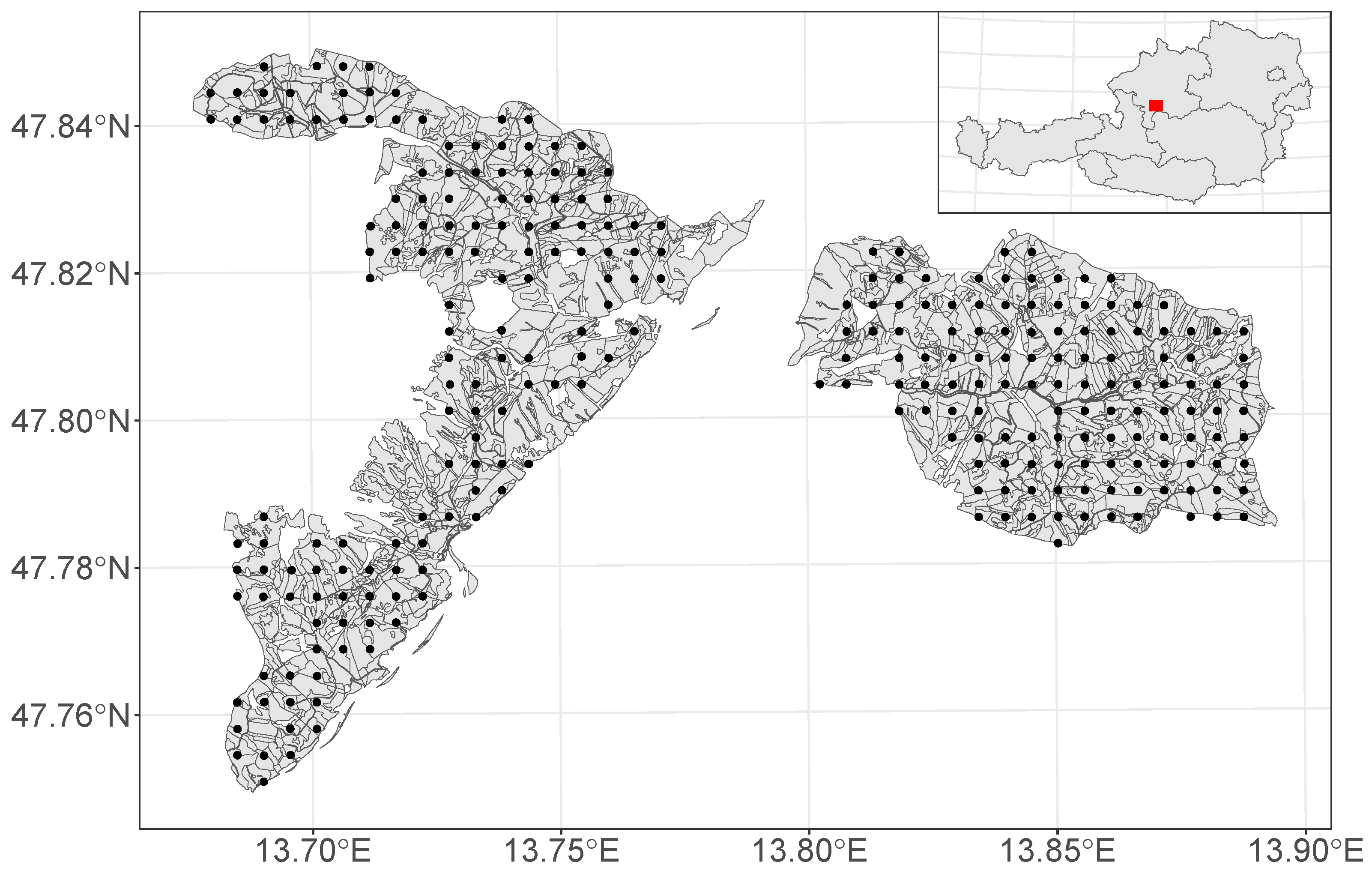
2.1. Study Region and Model Data
2.2. Model Construction
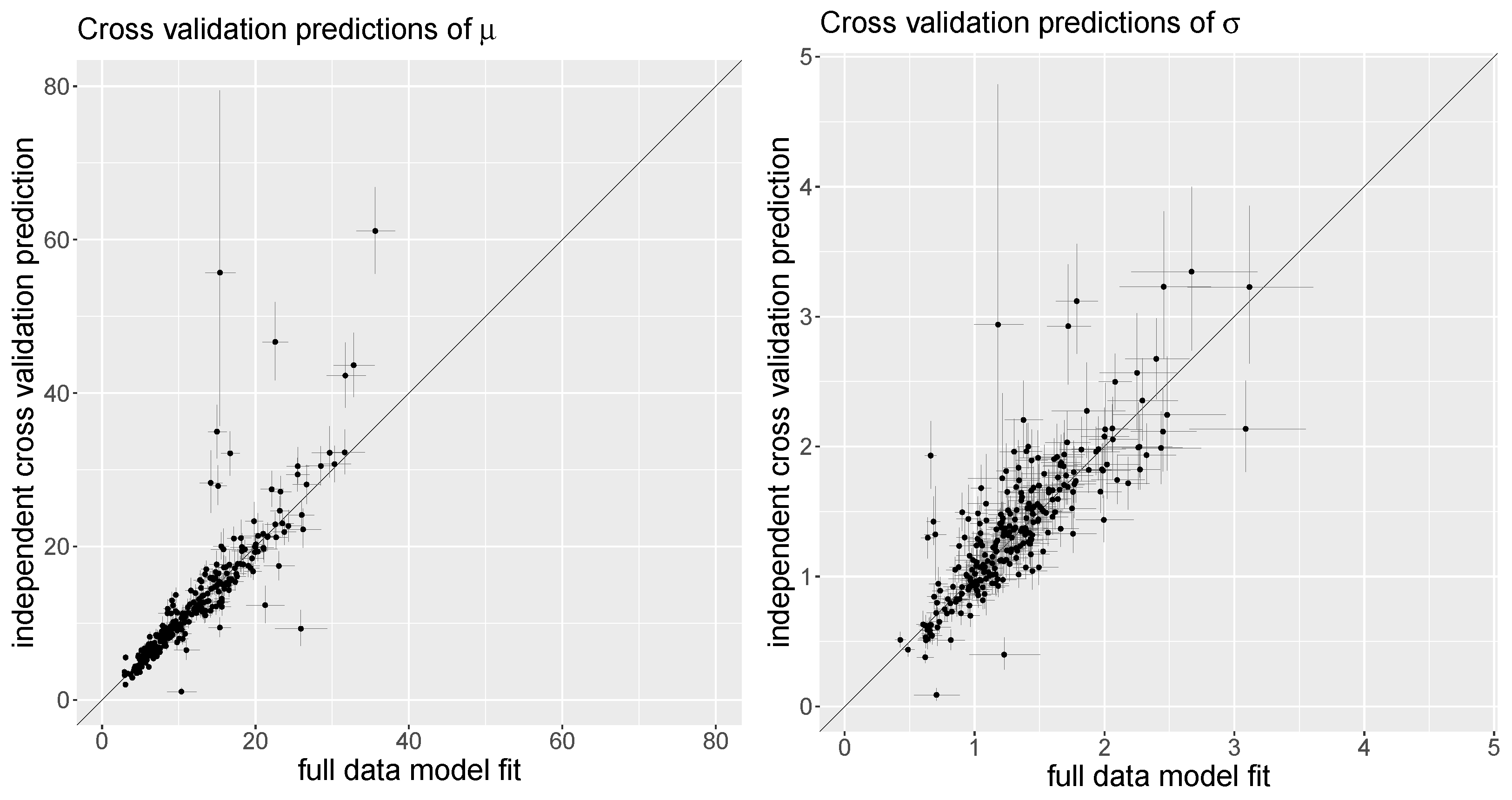
2.3. Model Validation
2.4. Prediction
3. Results
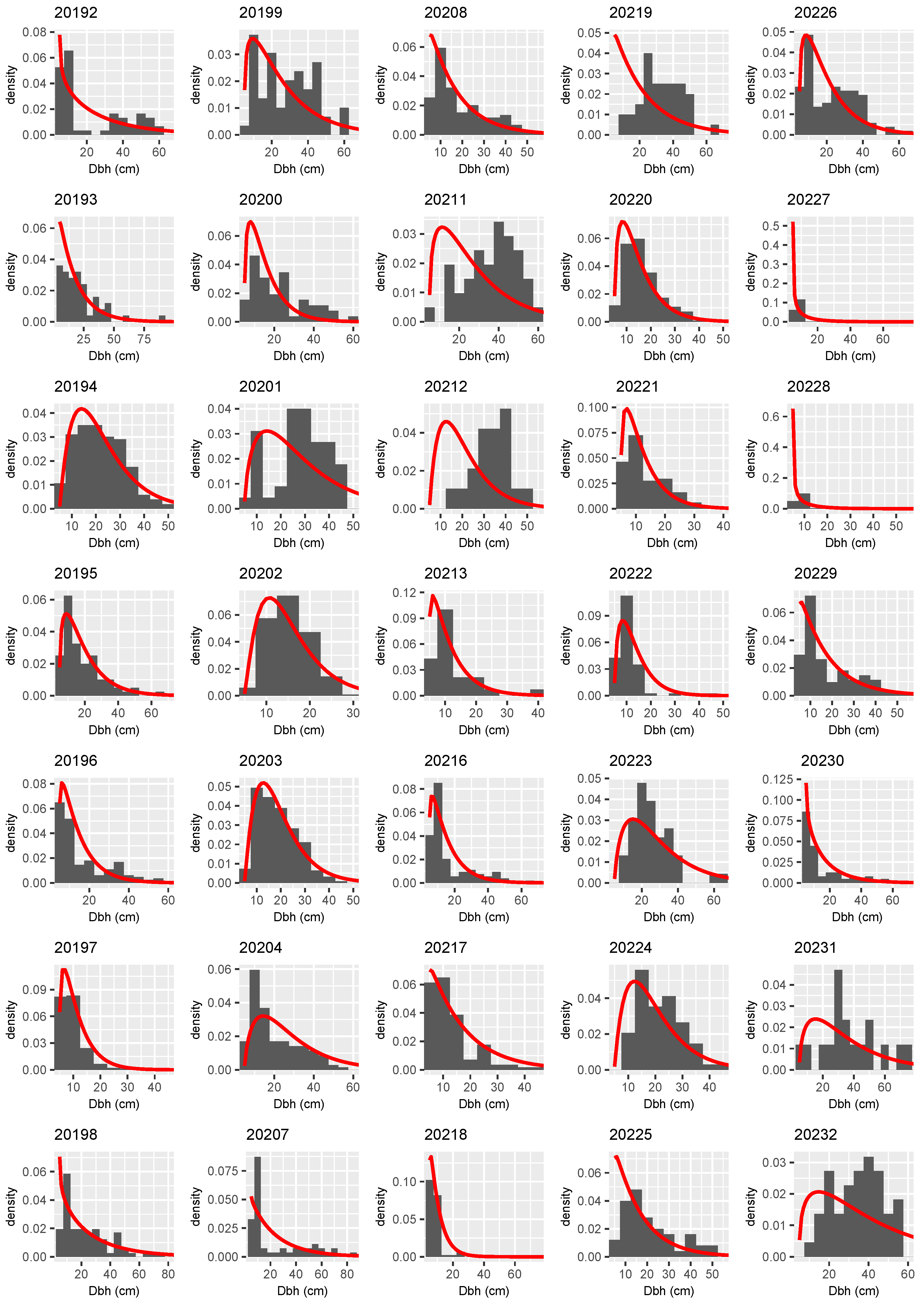
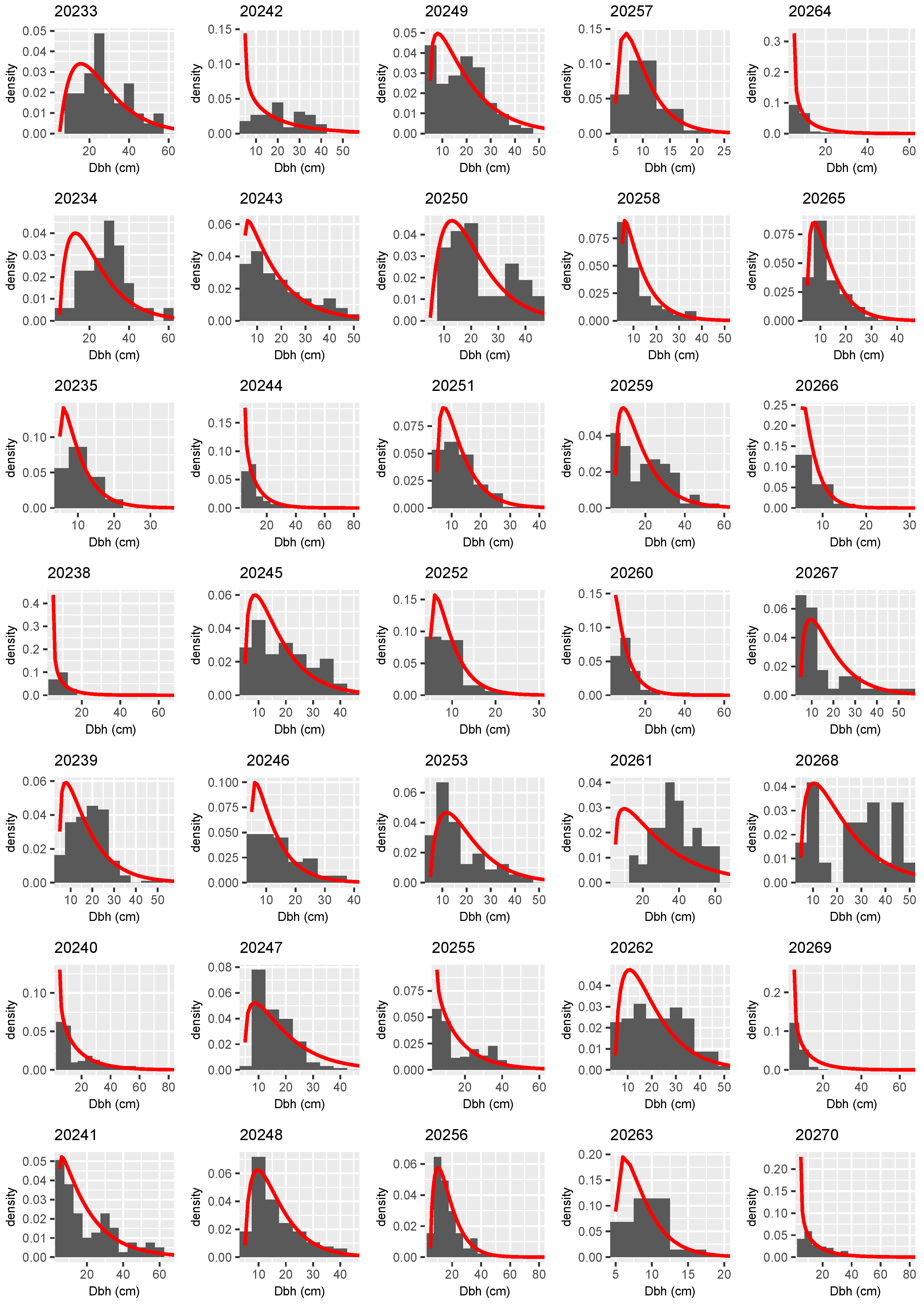
3.1. Candidate Models
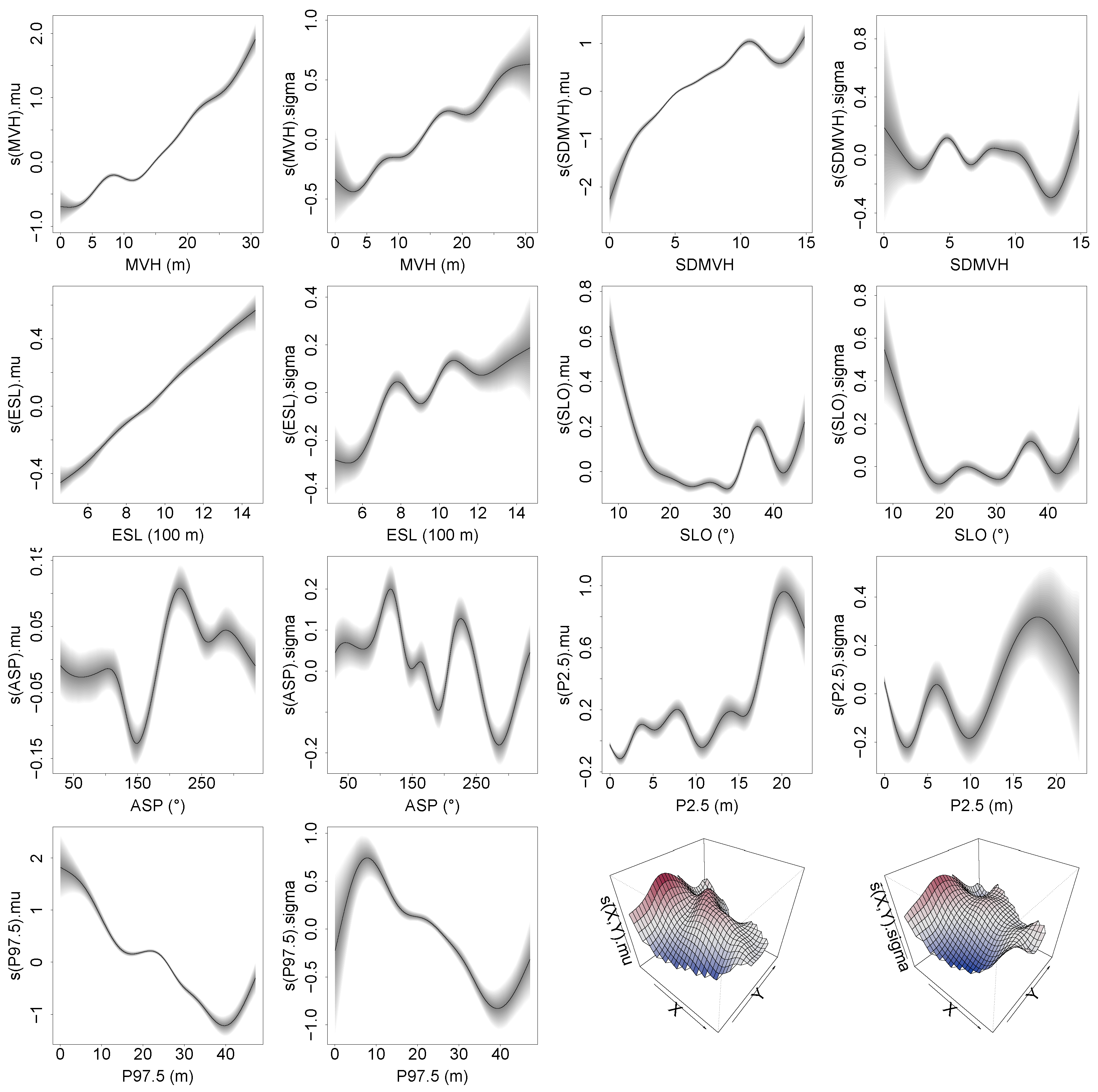
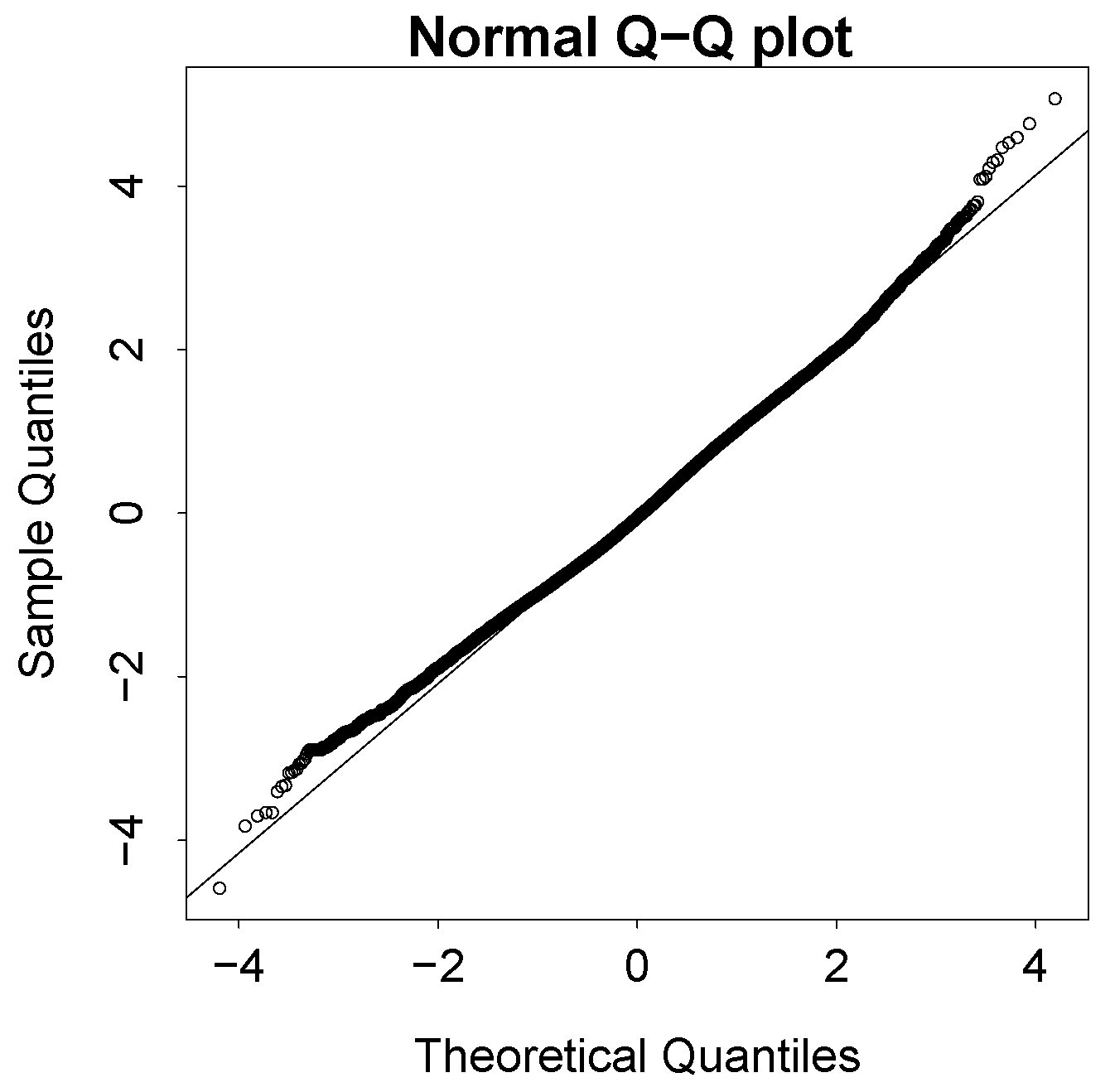
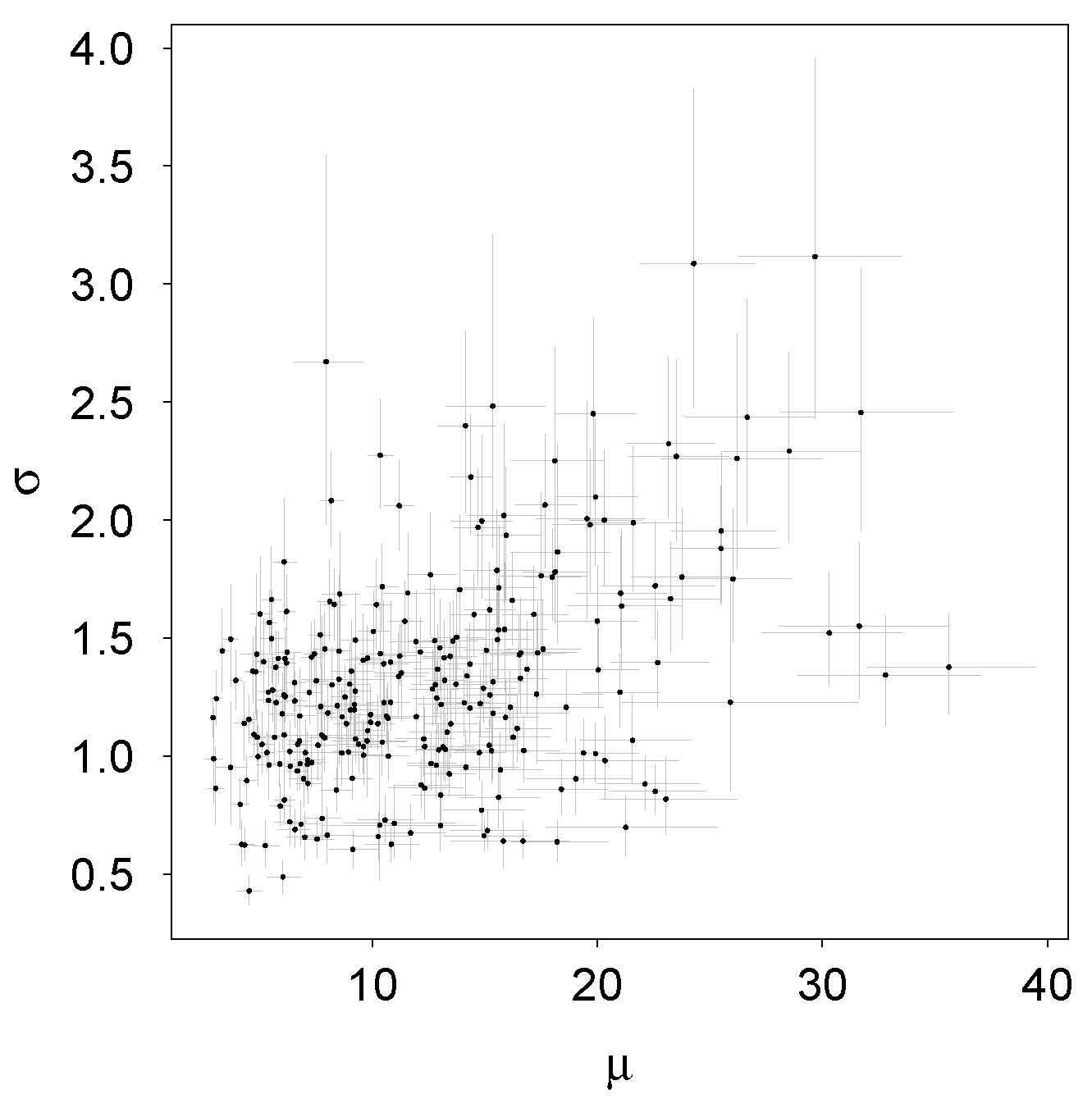
3.2. Analysis and Inference of the Best Model
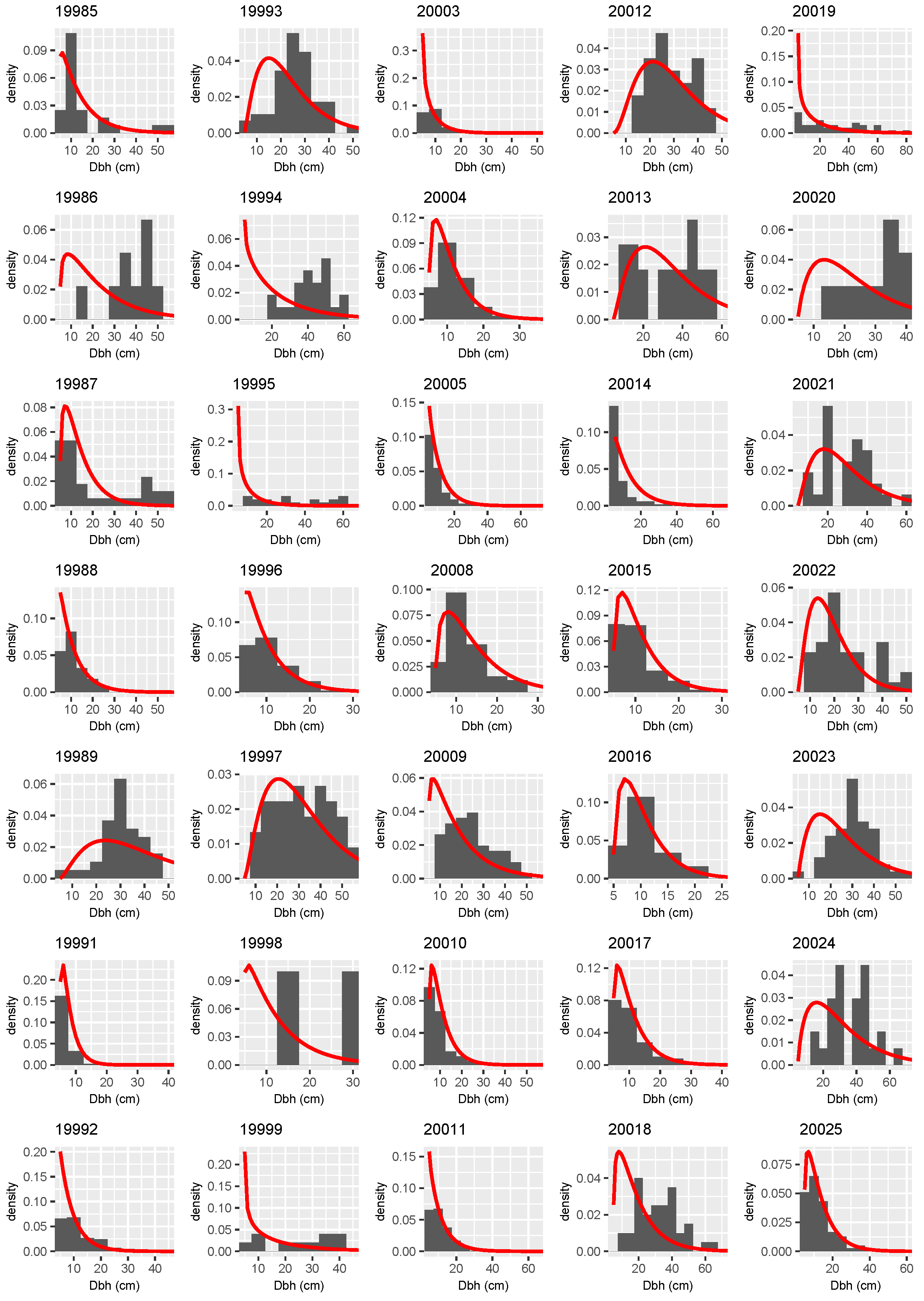
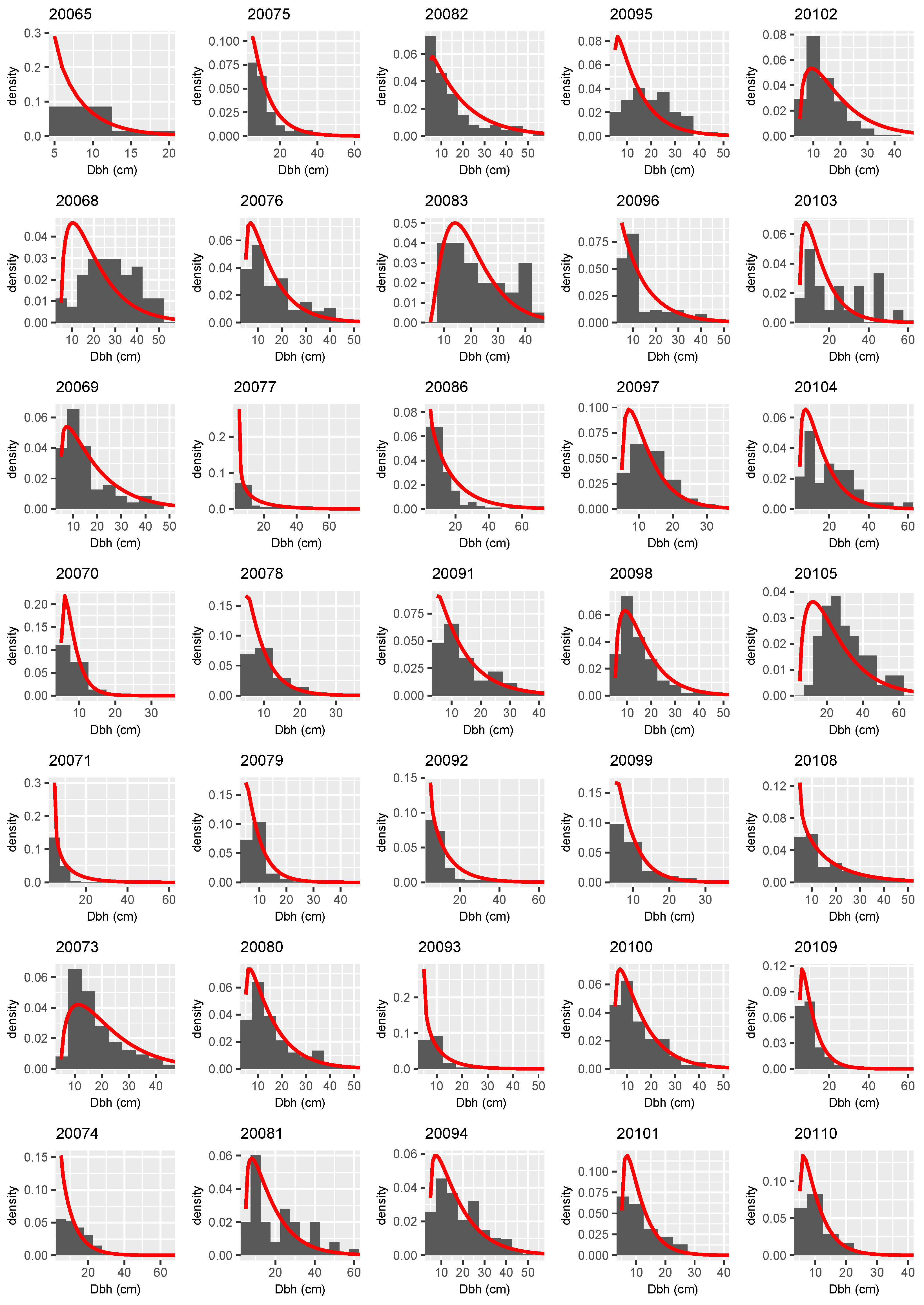
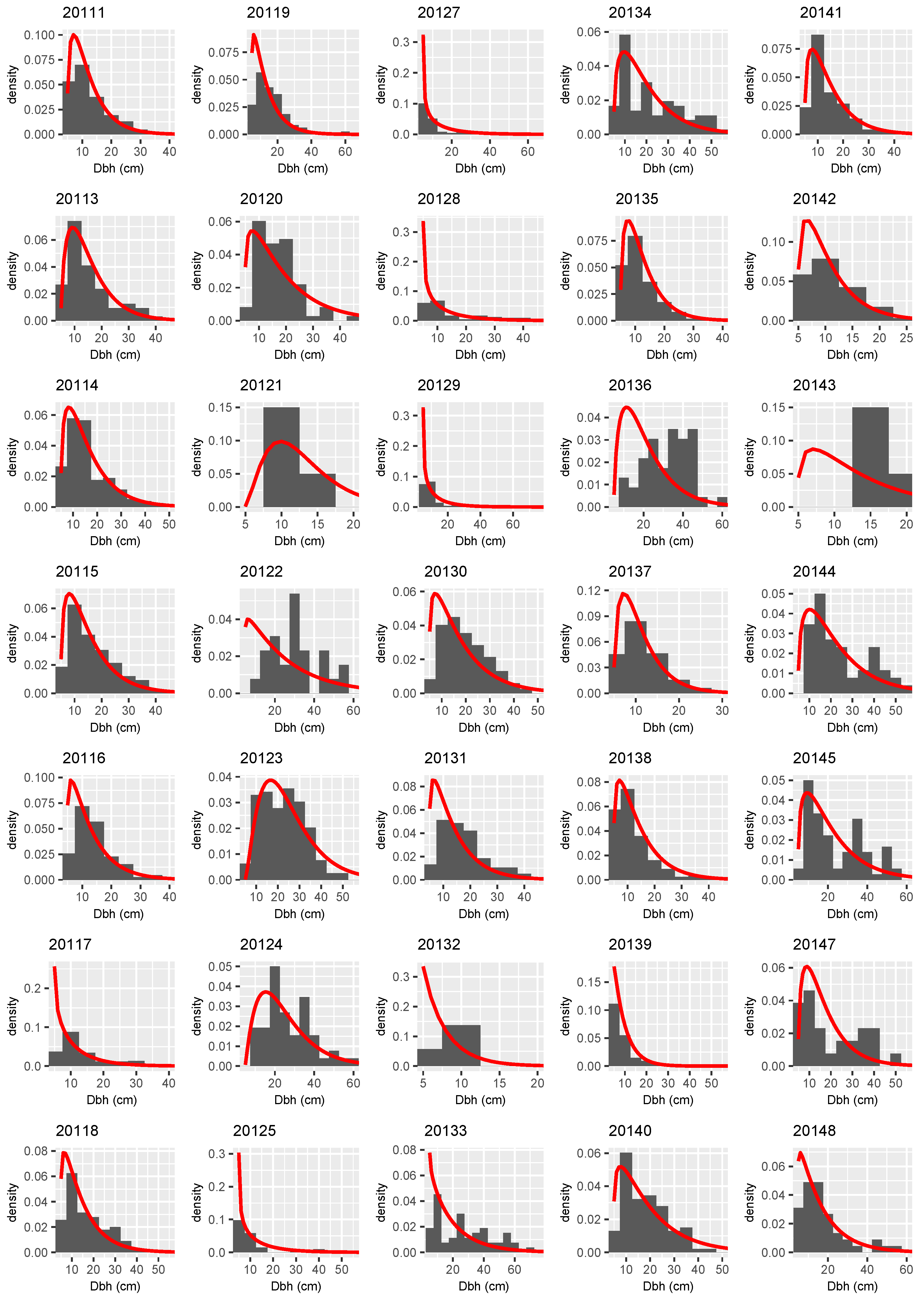
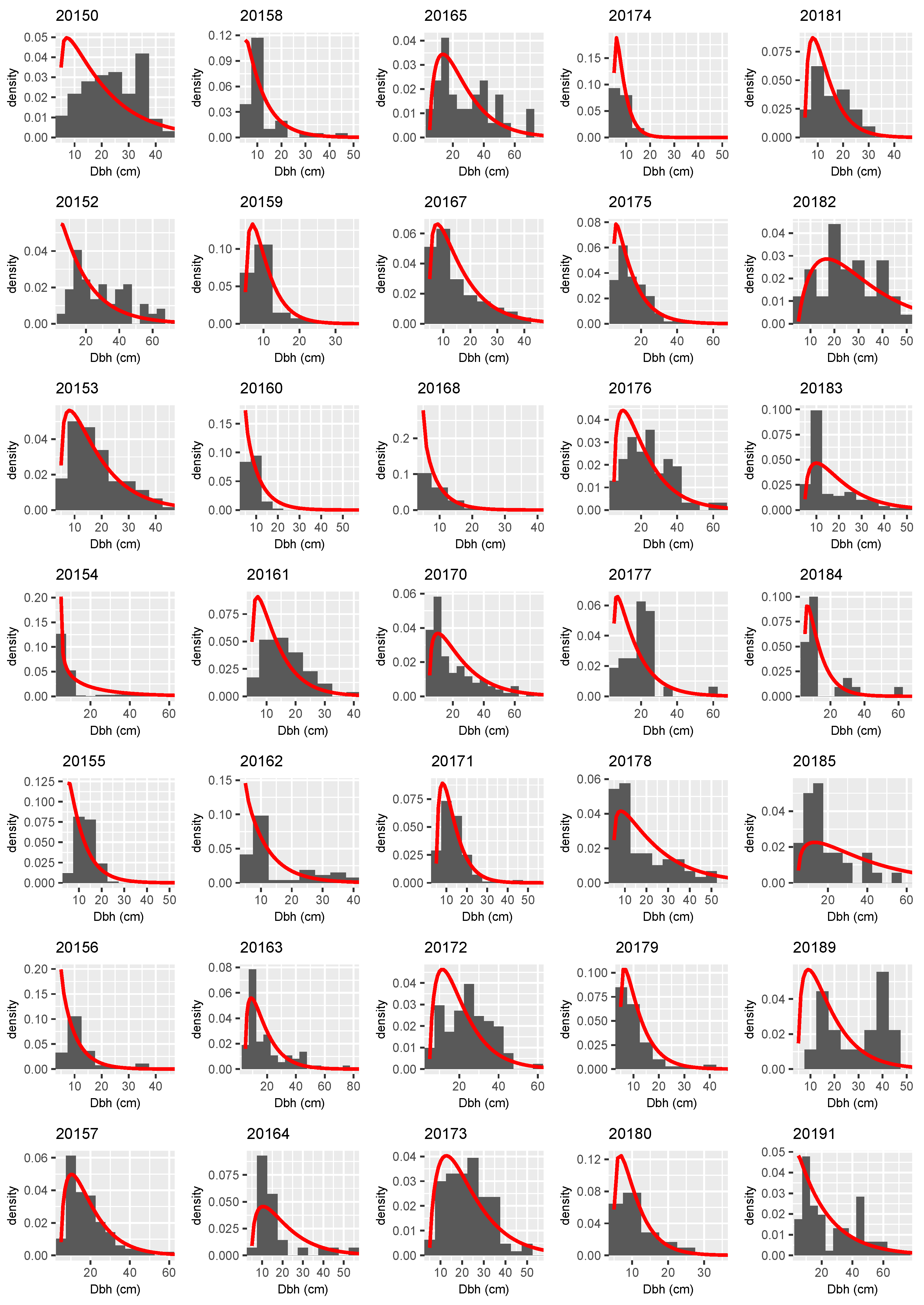
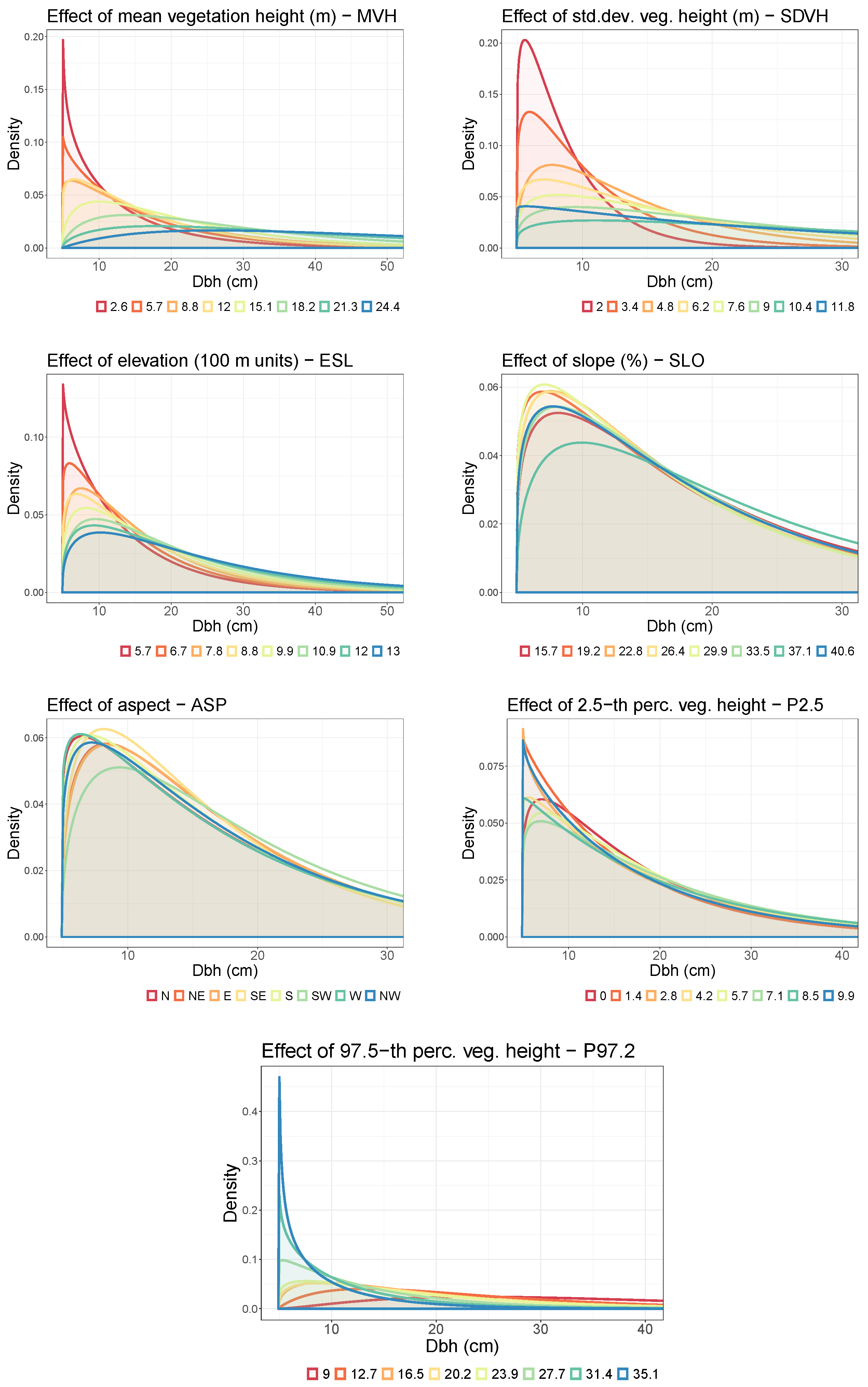
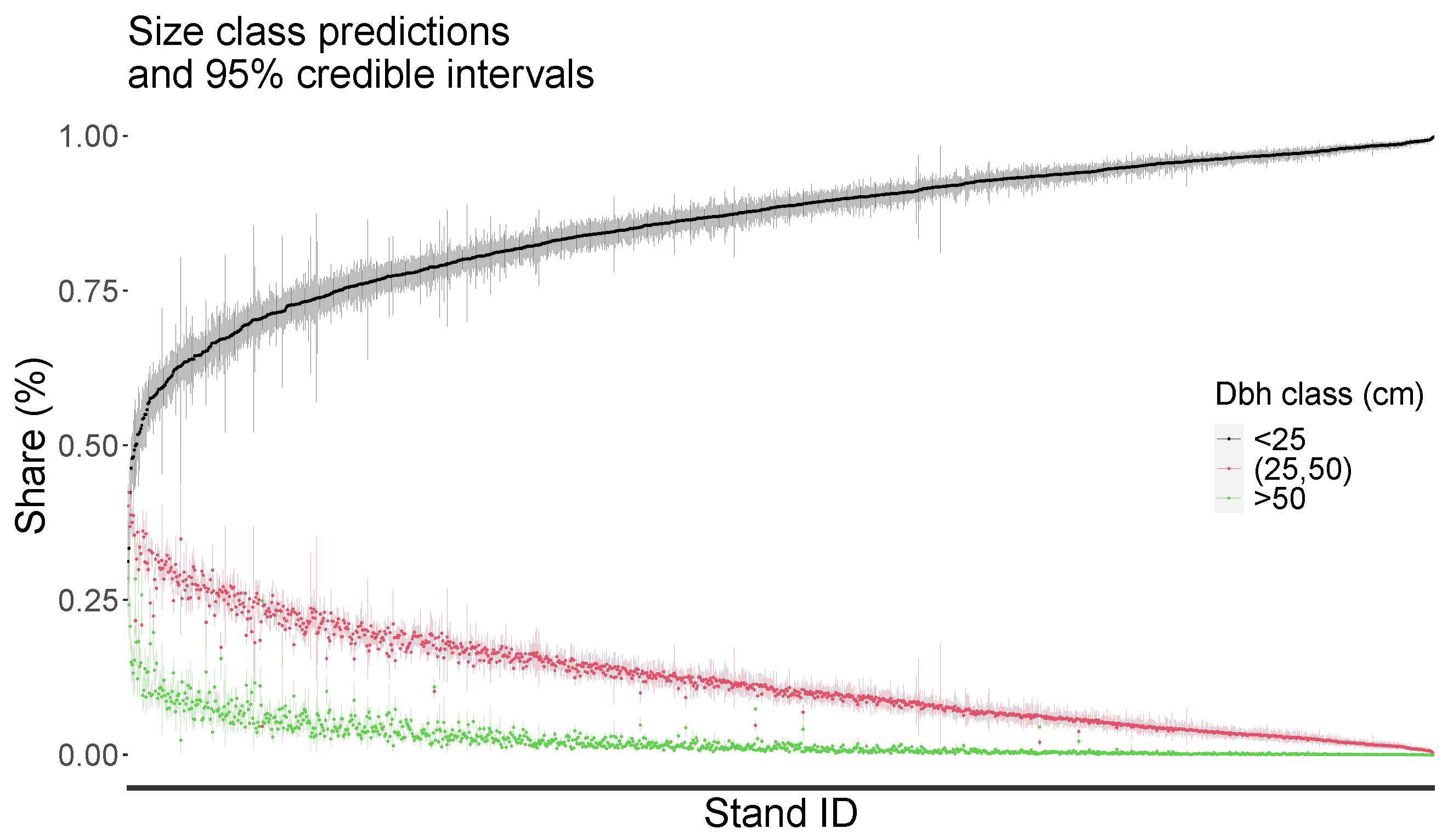
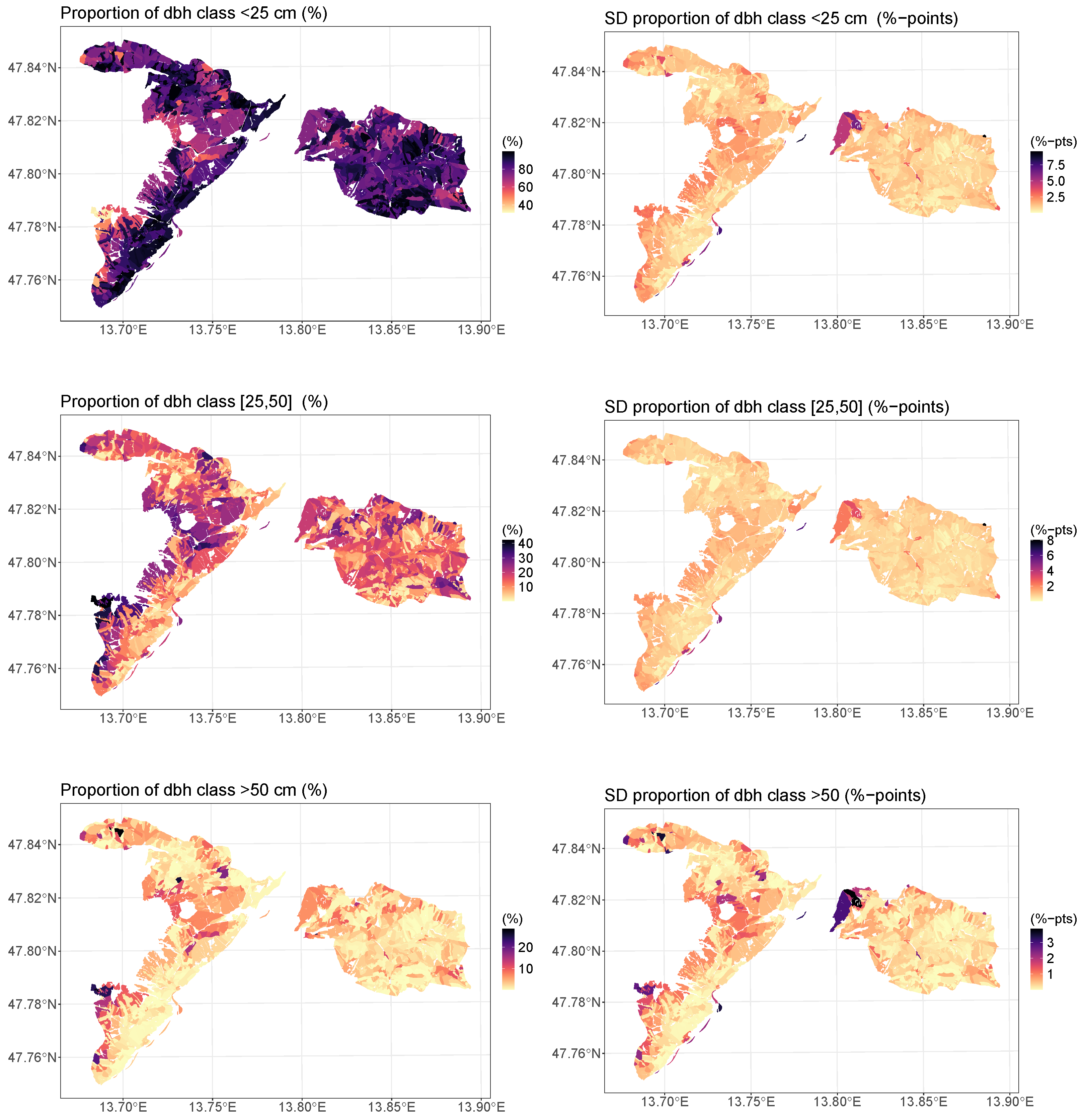
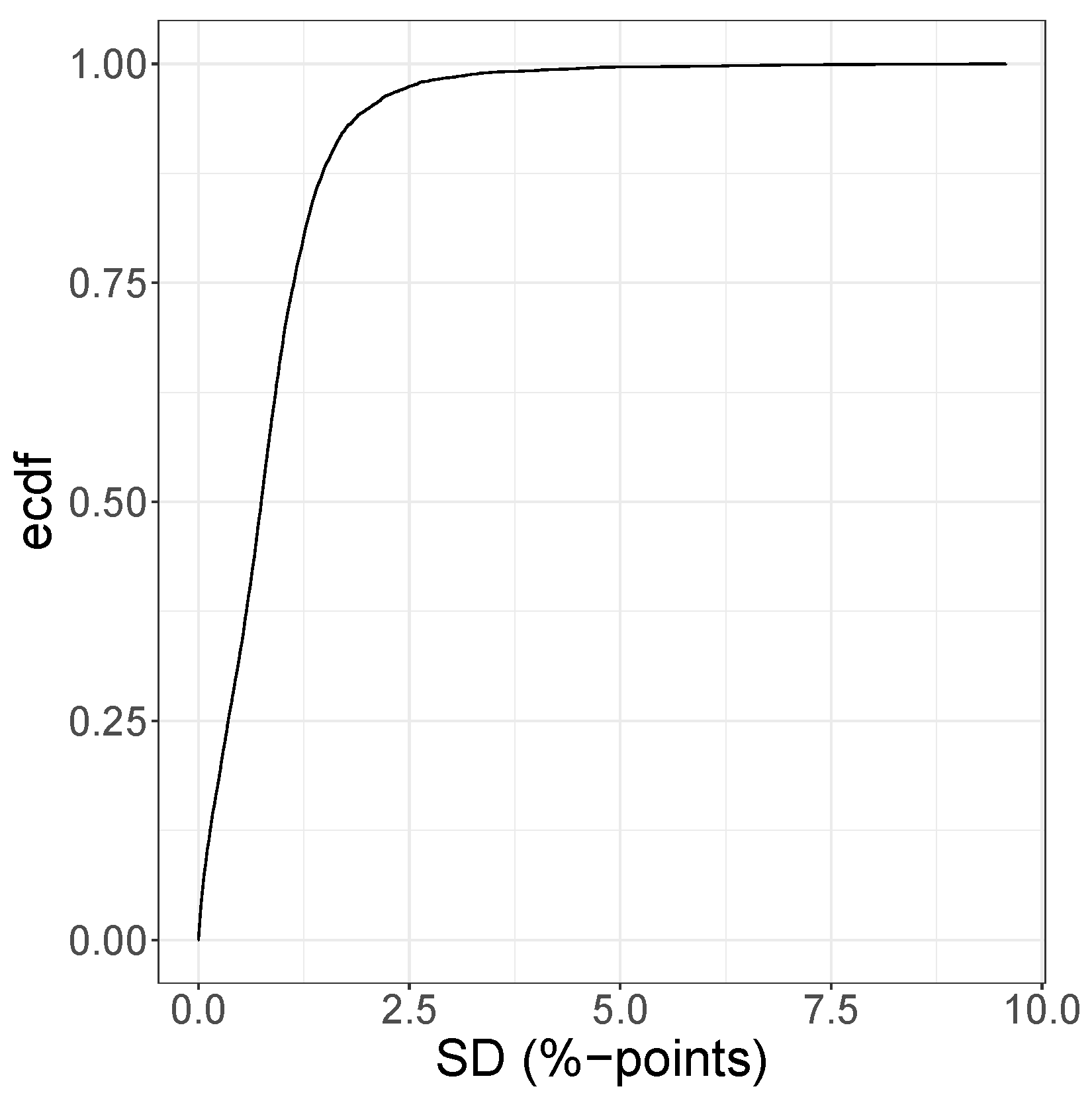
3.3. Distributional Prediction
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A


References
- Brang, P. Resistance and elasticity: Promising concepts for the management of protection forests in the European Alps. For. Ecol. Manag. 2001, 145, 107–119. [Google Scholar] [CrossRef]
- Perzl, F.; Huber, A.; Fromm, R.; Hagen, K.; Rössel, M.; Outer, J.D. Wald mit Steinschlag-Objektschutzfunktion in Österreich. Bedeut. Und Herausforderung. Bfw-Praxisinformation 2017, 45, 8–12. [Google Scholar]
- BML Zahlen und Fakten 2022. Booklet, Österreichisches Bundesministerium für Land- und Forstwirtschaft, Regionen und Wasserwirtschaft, Abt. Präs. 5 sowie Fachsektionen und Fachabteilungen des BML, Wien. 2022. Available online: https://info.bml.gv.at/dam/jcr:d108c97d-0e16-42fc-92fb-360280464006/BML_Broschuere_Zahlen_und_Fakten_DE_2022_Barrierefrei%20(002).pdf (accessed on 10 June 2024).
- Dorren, L.K.; Berger, F.; le Hir, C.; Mermin, E.; Tardif, P. Mechanisms, effects and management implications of rockfall in forests. For. Ecol. Manag. 2005, 215, 183–195. [Google Scholar] [CrossRef]
- Teich, M.; Bebi, P. Evaluating the benefit of avalanche protection forest with GIS-based risk analyses—A case study in Switzerland. For. Ecol. Manag. 2009, 257, 1910–1919. [Google Scholar] [CrossRef]
- Bebi, P.; Kienast, F.; Schönenberger, W. Assessing structures in mountain forests as a basis for investigating the forests’ dynamics and protective function. For. Ecol. Manag. 2001, 145, 3–14. [Google Scholar] [CrossRef]
- Köhl, M.; Magnussen, S.; Marchetti, M. Sampling Methods, Remote Sensing and GIS Multiresource Forest Inventory; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar] [CrossRef]
- Adnan, S.; Maltamo, M.; Coomes, D.A.; García-Abril, A.; Malhi, Y.; Manzanera, J.A.; Butt, N.; Morecroft, M.; Valbuena, R. A simple approach to forest structure classification using airborne laser scanning that can be adopted across bioregions. For. Ecol. Manag. 2019, 433, 111–121. [Google Scholar] [CrossRef]
- Yao, W.; Krzystek, P.; Heurich, M. Tree species classification and estimation of stem volume and DBH based on single tree extraction by exploiting airborne full-waveform LiDAR data. Remote Sens. Environ. 2012, 123, 368–380. [Google Scholar] [CrossRef]
- Schütz, J.P. Silvicultural tools to develop irregular and diverse forest structures. For. Int. J. For. Res. 2002, 75, 329–337. [Google Scholar] [CrossRef]
- D’Amato, A.W.; Bradford, J.B.; Fraver, S.; Palik, B.J. Forest management for mitigation and adaptation to climate change: Insights from long-term silviculture experiments. For. Ecol. Manag. 2011, 262, 803–816. [Google Scholar] [CrossRef]
- Gough, C.M.; Atkins, J.W.; Fahey, R.T.; Hardiman, B.S. High rates of primary production in structurally complex forests. Ecology 2019, 100, e02864. [Google Scholar] [CrossRef] [PubMed]
- Schütz, J.P. Opportunities and strategies of transforming regular forests to irregular forests. For. Ecol. Manag. 2001, 151, 87–94. [Google Scholar] [CrossRef]
- Morgenroth, J.; Nowak, D.J.; Koeser, A.K. DBH Distributions in America’s Urban Forests—An Overview of Structural Diversity. Forests 2020, 11, 135. [Google Scholar] [CrossRef]
- Hyink, D.M.; Moser, J.W. A Generalized Framework for Projecting Forest Yield and Stand Structure Using Diameter Distributions. For. Sci. 1983, 29, 85–95. [Google Scholar] [CrossRef]
- Knoebel, B.R.; Burkhart, H.E. A Bivariate Distribution Approach to Modeling Forest Diameter Distributions at Two Points in Time. Biometrics 1991, 47, 241–253. [Google Scholar] [CrossRef]
- Finley, A.O.; Banerjee, S.; Weiskittel, A.R.; Babcock, C.; Cook, B.D. Dynamic spatial regression models for space-varying forest stand tables. Environmetrics 2014, 25, 596–609. [Google Scholar] [CrossRef]
- Rigby, R.A.; Stasinopoulos, D.M. Generalized additive models for location, scale and shape. J. R. Stat. Soc. Ser. 2005, 54, 507–554. [Google Scholar] [CrossRef]
- Klein, N.; Kneib, T.; Lang, S.; Sohn, A. Bayesian structured additive distributional regression with an application to regional income inequality in Germany. Ann. Appl. Stat. 2015, 9, 1024–1052. [Google Scholar] [CrossRef]
- Klein, N.; Kneib, T.; Lang, S. Bayesian Generalized Additive Models for Location, Scale, and Shape for Zero-Inflated and Overdispersed Count Data. J. Am. Stat. Assoc. 2015, 110, 405–419. [Google Scholar] [CrossRef]
- Klein, N.; Kneib, T.; Klasen, S.; Lang, S. Bayesian structured additive distributional regression for multivariate responses. J. R. Stat. Soc. Ser. 2015, 64, 569–591. [Google Scholar] [CrossRef]
- Umlauf, N.; Klein, N.; Zeileis, A. BAMLSS: Bayesian Additive Models for Location, Scale and Shape (and Beyond). J. Comput. Graph. Stat. 2018, 27, 612–627. [Google Scholar] [CrossRef]
- Umlauf, N.; Klein, N.; Simon, T.; Zeileis, A. bamlss: A Lego Toolbox for Flexible Bayesian Regression (and Beyond). J. Stat. Softw. 2021, 100, 1–53. [Google Scholar] [CrossRef]
- Kneib, T.; Silbersdorff, A.; Säfken, B. Rage Against the Mean—A Review of Distributional Regression Approaches. Econom. Stat. 2023, 26, 99–123. [Google Scholar] [CrossRef]
- Gollob, C.; Ritter, T.; Wassermann, C.; Nothdurft, A. Influence of Scanner Position and Plot Size on the Accuracy of Tree Detection and Diameter Estimation Using Terrestrial Laser Scanning on Forest Inventory Plots. Remote Sens. 2019, 11, 1602. [Google Scholar] [CrossRef]
- Gollob, C.; Ritter, T.; Nothdurft, A. Forest Inventory with Long Range and High-Speed Personal Laser Scanning (PLS) and Simultaneous Localization and Mapping (SLAM) Technology. Remote Sens. 2020, 12, 1509. [Google Scholar] [CrossRef]
- Tockner, A.; Gollob, C.; Kraßnitzer, R.; Ritter, T.; Nothdurft, A. Automatic tree crown segmentation using dense forest point clouds from Personal Laser Scanning (PLS). Int. J. Appl. Earth Obs. Geoinf. 2022, 114, 103025. [Google Scholar] [CrossRef]
- Ritter, T.; Schwarz, M.; Tockner, A.; Leisch, F.; Nothdurft, A. Automatic Mapping of Forest Stands Based on Three-Dimensional Point Clouds Derived from Terrestrial Laser-Scanning. Forests 2017, 8, 265. [Google Scholar] [CrossRef]
- Ritter, T.; Gollob, C.; Nothdurft, A. Towards an Optimization of Sample Plot Size and Scanner Position Layout for Terrestrial Laser Scanning in Multi-Scan Mode. Forests 2020, 11, 1099. [Google Scholar] [CrossRef]
- Pollanschütz, J. Eine neue Methode der Formzahl- und Massenbestimmung stehender Stämme-Neue Form-bzw. Kubierungsfunkionen und ihre Anwendung—A new method for the estimation of stem forms. Technical Report 68, Forstliche Bundesversuchsanstalt Mariabrunn, 1965.
- Land Oberösterreich. Digital Surface Model 40704. Available online: https://e-gov.ooe.gv.at/at.gv.ooe.intramapgem/dop/downloads/40704/40704_DOM_tif.zip (accessed on 7 August 2023).
- Land Oberösterreich. Digital Terrain Model 40704. Available online: https://e-gov.ooe.gv.at/at.gv.ooe.intramapgem/dop/downloads/40704/40704_DGM_tif.zip (accessed on 7 August 2023).
- Stasinopoulos, R.R.M.; Heller, G.; Bastiani, F.D. Distributions for Modeling Location, Scale, and Shape: Using GAMLSS in R; Chapman & Hall/CRC: Boca Raton, FL, USA, 2019. [Google Scholar]
- Wood, S.N. Thin Plate Regression Splines. J. R. Stat. Soc. Ser. Stat. Methodol. 2003, 65, 95–114. [Google Scholar] [CrossRef]
- Kammann, E.E.; Wand, M.P. Geoadditive Models. J. R. Stat. Soc. Ser. Appl. Stat. 2003, 52, 1–18. [Google Scholar] [CrossRef]
- Spiegelhalter, D.J.; Best, N.G.; Carlin, B.P.; Van Der Linde, A. Bayesian Measures of Model Complexity and Fit. J. R. Stat. Soc. Ser. 2002, 64, 583–639. [Google Scholar] [CrossRef]
- Gelman, A.; Hwang, J.; Vehtari, A. Understanding predictive information criteria for Bayesian models. Stat. Comput. 2014, 24, 997–1016. [Google Scholar] [CrossRef]
- Zhou, R.; Wu, D.; Zhou, R.; Fang, L.; Zheng, X.; Lou, X. Estimation of DBH at Forest Stand Level Based on Multi-Parameters and Generalized Regression Neural Network. Forests 2019, 10, 778. [Google Scholar] [CrossRef]
- Nothdurft, A.; Gollob, C.; Kraßnitzer, R.; Erber, G.; Ritter, T.; Stampfer, K.; Finley, A.O. Estimating timber volume loss due to storm damage in Carinthia, Austria, using ALS/TLS and spatial regression models. For. Ecol. Manag. 2021, 502, 119714. [Google Scholar] [CrossRef]
- Roussel, J.R.; Auty, D.; Coops, N.C.; Tompalski, P.; Goodbody, T.R.; Meador, A.S.; Bourdon, J.F.; de Boissieu, F.; Achim, A. lidR: An R package for analysis of Airborne Laser Scanning (ALS) data. Remote Sens. Environ. 2020, 251, 112061. [Google Scholar] [CrossRef]
- Roussel, J.R.; Auty, D. R Package, version 4.0.4. Airborne LiDAR Data Manipulation and Visualization for Forestry Applications. 2023. Available online: https://cran.r-project.org/package=lidR (accessed on 9 June 2024).
| m_1 | m_2 | m_3 | m_4 | m_5 | m_6 | m_7 | m_8 | m_9 | m_10 | m_11 | m_12 | m_13 | m_14 | m_15 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MVH | p | s | s | s | s | p | p | s | s | s | s | s | s | s | s |
| SDVH | p | s | s | s | s | p | p | s | s | s | s | s | s | s | s |
| P2.5 | p | s | p | p | s | s | |||||||||
| P97.5 | p | s | p | p | s | s | |||||||||
| ESL | p | s | s | s | s | p | p | s | s | s | s | s | s | s | s |
| SLO | s | s | s | s | s | s | s | s | s | ||||||
| ASP | s(cc) | s(cc) | s(cc) | s(cc) | s(cc) | s(cc) | s(cc) | s(cc) | s(cc) | ||||||
| XY | s(gp) | te | s(gp) | te | s(gp) | te | s(gp) | te | s(gp) | te | |||||
| DIC | 231.268 | 229.278 | 228.321 | 228.087 | 227.304 | 230.008 | 230.235 | 228.347 | 228.460 | 227.577 | 227.630 | 227.214 | 227.236 | 226.486 | 226.526 |
| edf | 8.1 | 53.2 | 85.8 | 87.3 | 114.2 | 62.6 | 51.2 | 107.9 | 94.4 | 137.6 | 129.4 | 139.1 | 132.1 | 166.1 | 158.1 |
| WAIC1 | 231.269 | 229.277 | 228.319 | 228.086 | 227.302 | 230.005 | 230.233 | 228.343 | 228.458 | 227.574 | 227.627 | 227.211 | 227.234 | 226.484 | 226.524 |
| WAIC2 | 231.269 | 229.278 | 228.321 | 228.088 | 227.305 | 230.006 | 230.234 | 228.346 | 228.460 | 227.577 | 227.631 | 227.215 | 227.238 | 226.489 | 226.529 |
| p1 | 8.4 | 52.7 | 83.9 | 85.7 | 112.2 | 60.0 | 49.7 | 104.3 | 91.9 | 134.5 | 126.9 | 135.9 | 129.9 | 163.8 | 156.6 |
| p2 | 8.4 | 53.3 | 84.8 | 86.7 | 113.7 | 60.5 | 50.1 | 105.6 | 93.0 | 136.4 | 128.5 | 137.8 | 131.7 | 166.6 | 159.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nothdurft, A.; Tockner, A.; Witzmann, S.; Gollob, C.; Ritter, T.; Kraßnitzer, R.; Stampfer, K.; Finley, A.O. Spatial Prediction of Diameter Distributions for the Alpine Protection Forests in Ebensee, Austria, Using ALS/PLS and Spatial Distributional Regression Models. Remote Sens. 2024, 16, 2181. https://doi.org/10.3390/rs16122181
Nothdurft A, Tockner A, Witzmann S, Gollob C, Ritter T, Kraßnitzer R, Stampfer K, Finley AO. Spatial Prediction of Diameter Distributions for the Alpine Protection Forests in Ebensee, Austria, Using ALS/PLS and Spatial Distributional Regression Models. Remote Sensing. 2024; 16(12):2181. https://doi.org/10.3390/rs16122181
Chicago/Turabian StyleNothdurft, Arne, Andreas Tockner, Sarah Witzmann, Christoph Gollob, Tim Ritter, Ralf Kraßnitzer, Karl Stampfer, and Andrew O. Finley. 2024. "Spatial Prediction of Diameter Distributions for the Alpine Protection Forests in Ebensee, Austria, Using ALS/PLS and Spatial Distributional Regression Models" Remote Sensing 16, no. 12: 2181. https://doi.org/10.3390/rs16122181
APA StyleNothdurft, A., Tockner, A., Witzmann, S., Gollob, C., Ritter, T., Kraßnitzer, R., Stampfer, K., & Finley, A. O. (2024). Spatial Prediction of Diameter Distributions for the Alpine Protection Forests in Ebensee, Austria, Using ALS/PLS and Spatial Distributional Regression Models. Remote Sensing, 16(12), 2181. https://doi.org/10.3390/rs16122181










