Abstract
Accurate land surface temperature (LST) retrieval from satellite data is pivotal in environmental monitoring and scientific research. This study addresses the impact of variability in the effective wavelengths used for LST retrieval from the Thermal Infrared Sensor (TIRS) data of Landsat 8. We conduct a detailed analysis comparing the effective wavelengths reported by Yu et al. (2014) and those derived from data provided by the USGS. Our analysis reveals significant variability in the effective wavelengths for bands 10 and 11 of Landsat 8. By applying Planck’s Law and utilizing the K1 and K2 coefficients available in the metadata of Landsat 8 products, we derive the effective wavelengths for bands 10 and 11. We also rederive the effective wavelength by integrating the spectral response function of the TIRS1 sensor. Our findings indicate that the effective wavelength for band 10 is 10.814 μm, aligning with the USGS data, while the effective wavelength for band 11 is 12.013 μm. We discuss the implications of these corrected effective wavelengths on the accuracy of LST retrieval algorithms, particularly the single channel algorithm (SC) and the radiative transfer equation (RT) employed by Yu et al. The importance of using precise effective wavelengths in satellite-based temperature retrieval is emphasized, to ensure the reliability and consistency of results. This analysis underscores the critical role of accurate spectral calibration parameters in remote sensing studies and provides valuable insights in the field of land surface temperature retrieval from Landsat 8 TIRS data.
1. Introduction
I would like to thank the authors for their commentary on the publication “Land Surface Temperature Retrieval from Landsat 8 TIRS—Comparison between Radiative Transfer Equation-Based Method, Split Window Algorithm and Single Channel Method” []. I value this opportunity to address the points raised in the commentary, and to engage in a communication that can hopefully enrich the collective understanding of the methods for land surface temperature retrieval and their applications in environmental and climatic studies. Satellite-based remote sensing plays a pivotal role in environmental monitoring and scientific research, offering valuable insights into land surface temperature (LST) dynamics, which are crucial to various applications, such as climate modeling, agricultural management, and urban heat island studies. Among satellite platforms, Landsat 8 stands out with its Thermal Infrared Sensor (TIRS), which captures thermal radiation emitted by the Earth’s surface.
In their study, Yu et al. [] discussed the retrieval of the LST from Landsat 8 TIRS data, presenting effective wavelengths of 10.896 μm for band 10 and 12.006 μm for band 11. However, this contradicts the data provided by the United States Geological Survey (USGS), commonly included in the Landsat 8 metadata file.
This discrepancy underscores the importance of scrutinizing spectral calibration parameters in satellite-based remote sensing studies. In this analysis, we aim to address this inconsistency by comparing the effective wavelengths reported by Yu et al. [] with the data provided by USGS. By reconciling this discrepancy, we seek to enhance the accuracy and reliability of LST retrieval from Landsat 8 TIRS data, thereby contributing to the advancement of remote sensing research in environmental monitoring and beyond.
2. Comments about the Results and Correction
Firstly, regarding the derivation of the effective wavelength based on physical constants, the metadata that come with Landsat 8 images include key parameters known as K1 and K2. These parameters are crucial to the process of converting the thermal electromagnetic radiation captured at the top of the atmosphere in bands 10 and 11 of Landsat 8 into the brightness temperature (BT) [].
This conversion relies on applying Planck’s Law, which is a fundamental principle in physics. It defines the relationship between the thermal radiation emitted by a black body at a specific wavelength and its corresponding temperature.
When working with satellite data, we use Planck’s equation, which relates the intensity of thermal radiation measured at the top of the atmosphere (considering the Earth as a black body) with the temperature measured at the top of the atmosphere, as follows []:
where is the ground radiance, Ts is the land surface temperature (k), is the TOA radiance (thermal radiation measured at the top of the atmosphere), BT is the brightness temperature (K), c is the light speed (c = 2.99792458 × m/s), h is the Planck constant (h = 6.62607015 × J·s), k is the Boltzmann constant (k = 1.380649 × J/K), and is the effective band wavelength for band i.
We consider that
where C1 = 1.191042972 × and C2 = 14,387.76878 (μm·k).
Equation (2) can be written in the following form:
In addition, we consider that
where the coefficients K1 and K2 are as they are found in the Metadata for Landsat 8:
- K1_CONSTANT_BAND_10 = 774.8853 (W·m−2·μm−1)
- K2_CONSTANT_BAND_10 = 1321.0789 (K)
- K1_CONSTANT_BAND_11 = 480.8883 (W·m−2·μm−1)
- K2_CONSTANT_BAND_11 = 1201.1442 (K)
We obtain the simple equation:
Now, we can obtain the relationship between the effective wavelength and the numerical factor K2 and K1
where
Applying Equation (7), we obtain the effective wavelength , as presented in Table 1.

Table 1.
The effective wavelength from Equation (7).
Applying Equation (8), we obtain the effective wavelength , as presented in Table 2.

Table 2.
The effective wavelength from Equation (8).
Yu et al. [] did not use any of the wavelengths shown in Table 1 and Table 2, which we calculated based on the data provided by the USGS. They did not mention the method used to obtain the effective wavelength.
Despite the impossibility of finding a true constant value for the effective wavelength in order to accurately calculate K1 and K2, according to Equation (5), and it being impossible to deny the validity of Equation (5) itself, we pose this question to the USGS, seeking a proper explanation.
Secondly, the paper relies on the spectral response function ,
where is the spectral response function for the corresponding band. and are the lower and upper boundary of .
Figure 1 represents the spectral response function for each of the thermal bands in Landsat 8.
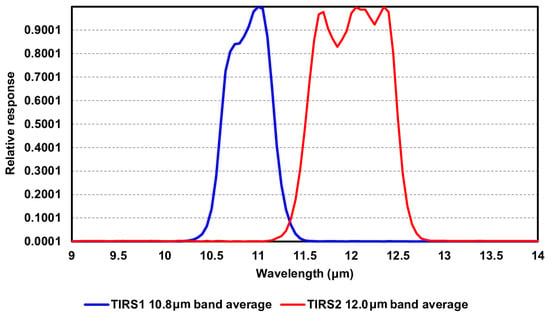
Figure 1.
TIRS relative spectral response.
We can access the relative spectral response (RSR) values through the Spectral Characteristics Viewer provided by USGS at the following link: Spectral Characteristics Viewer [].
We refer to the first spectral range of the thermal sensor TIRS (Band 10), where
λ1 (lower) = 10.602 μm and λ1 (upper) = 11.19 μm
Figure 2 and Figure 3 illustrate the spectral response function and the standard deviation for band 10 in Landsat 8.
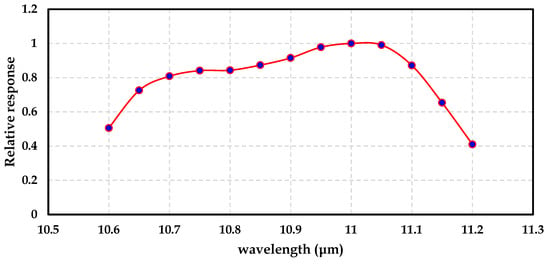
Figure 2.
Spectral response function for Landsat 8 product (B10).
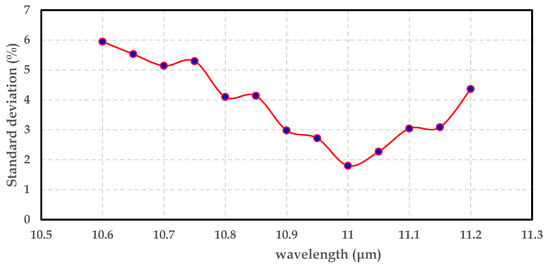
Figure 3.
Standard deviation for Landsat 8 product (B10).
Figure 3 shows the standard deviation as a percentage of the relative spectral response values for band 10. Within the wavelengths from 10.8 to 10.9, the data exhibit a deviations ranging between 3 and 4%.
In the second spectral range of the thermal sensor TIRS (Band 11),
λ1 (lower) = 11.5 μm and λ1 (upper) = 12.511 μm
Figure 4 and Figure 5 illustrate the spectral response function and the standard deviation for the band 11 in Landsat 8.
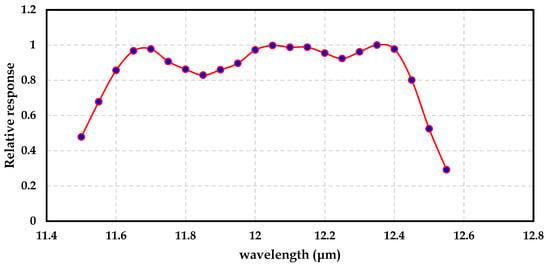
Figure 4.
Spectral response function for Landsat 8 product (B11).
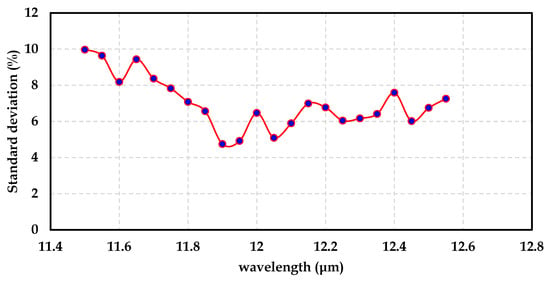
Figure 5.
Standard deviation for Landsat 8 product (B11).
Within the wavelength range from 11.5 to 12.511, the data show deviations ranging between 4 and 10%.
Thirdly, using cubic interpolation in Python 3.12.4., we formed the spectral response function based on the discrete, non-continuous data provided by USGS. The function is the result of cubic interpolation, which involves dividing the data into segments, each represented by a separate cubic function. This interpolated function consists of interconnected cubic functions, ensuring the continuity of the function and its first and second derivatives at the data points.
We experimented with several interpolation methods to construct the spectral response functions but did not achieve any alignment with the literature cited by the reviewers.
Therefore, the effective band wavelengths are 10.904 μm and 12.003 μm, respectively, for bands 10 and 11.
Applying Equation (9), we obtain the effective wavelength , as presented in Table 3.

Table 3.
The effective wavelength from Equation (9).
Figure 6 and Figure 7 explain the relative spectral response functions for bands 10 and 11 obtained via cubic interpolation.
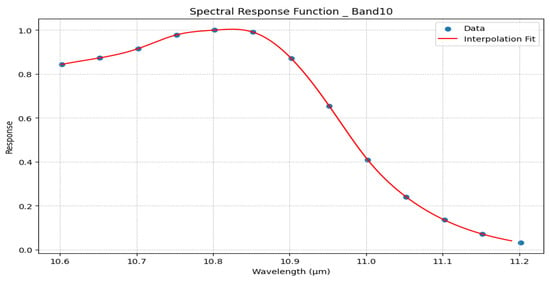
Figure 6.
The relative spectral response function for band 10 using cubic interpolation.
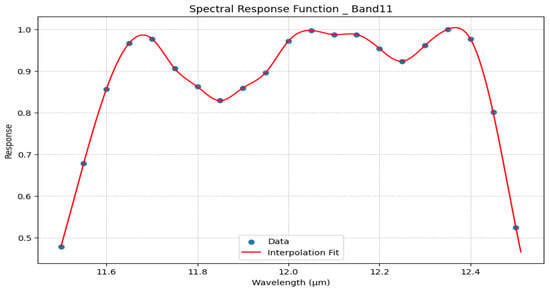
Figure 7.
The relative spectral response function for band 11 using cubic interpolation.
Fourthly, the radiative transfer equation used by Yu et al. [] is
where
- is the thermal radiance measured at the top of the atmosphere;
- is the atmospheric transmittance for specific wavelengths;
- is the surface emissivity at specific wavelengths;
- are the downwelling and upwelling radiance, respectively, at specific wavelengths (the contribution of the atmosphere);
- is the thermal radiance at the Earth’s surface.
Yu et al. [] used the effective wavelength directly to derive the surface temperature in Equation (4) (in their paper), although they could express the equation in terms of K1 and K2 from the metadata file (using Equations (3) and (5) as presented in this comment). This introduces variability in the effective wavelength and may lead to discussions regarding the obtained results.
Fifthly, considering the application of the Split Window (SW) algorithm, researchers should use the calibration parameters provided by USGS to convert digital number (DN) values to the TOA radiance and brightness temperature, ensuring that the results presented are robust and less open to debate.
Sixthly, regarding the Single-Channel algorithm, Jiménez-Muñoz et al. [] introduced a revision of the single channel algorithm (SCA) to retrieve the LST from Landsat TIR data. Considering the SCA, LST (Ts) can be computed using the following general equation:
According to the method proposed by Jiménez-Muñoz et al. [] for estimating atmospheric functions, ,
The parameters , ξ, χ, and φ are related to the effective band wavelength, and is the water vapor in cm (Table 4) [].

Table 4.
The parameters related to the effective band wavelength.
The results obtained by the researchers are closely related to the effective wavelength used.
Seventhly, regarding errors in the equations presented in the research, Equation (13) in the paper contains a typographical error, and the correct form is
Equation number 33 and its accompanying description in the paper by Yu et al. [] are incorrect, and the correct form is
is the relative humidity (%) observed from the SURFRAD site; is the water content (g/m2) near the ground; Rw(0) is the ratio of near-ground water vapor to the total-column water vapor, which was adapted from []; is the converting factor between Pascal and the water column content, which is 1.0197, calculated by (Equation number 32 in the paper).
3. Conclusions
In conclusion, our analysis has highlighted a critical discrepancy in the effective wavelengths used for land surface temperature (LST) retrieval from Landsat 8 Thermal Infrared Sensor (TIRS) data. By comparing the reported effective wavelengths with the data provided by the United States Geological Survey (USGS), we have identified the correct values that should have been utilized for accurate LST calculations.
This discrepancy has significant implications for the accuracy of LST retrieval algorithms, particularly the Single-Channel (SC) algorithm and the Radiative Transfer Equation (RT). The incorrect effective wavelengths utilized by the researcher would lead to entirely inaccurate results, undermining the reliability of the findings.
Moving forward, it is imperative for researchers and practitioners in the field of remote sensing to ensure the meticulous consideration of spectral calibration parameters, such as effective wavelengths, to uphold the accuracy and reliability of LST retrieval from satellite data. By adhering to standardized procedures and utilizing accurate metadata, we can enhance the robustness of LST retrieval algorithms and facilitate more precise environmental monitoring and research endeavors.
Overall, this analysis underscores the importance of rigorous quality control measures in remote sensing studies and contributes to advancing the accuracy of LST retrieval methodologies from Landsat 8 TIRS data.
Author Contributions
Conceptualization, A.A.E.A. and B.Z.; methodology, A.A.E.A. and B.Z.; software, A.A.E.A. and B.Z.; validation, A.A.E.A. and B.Z.; formal analysis, A.A.E.A. and B.Z.; investigation, A.A.E.A. and B.Z.; resources, A.A.E.A. and B.Z.; data curation, A.A.E.A. and B.Z.; writing—original draft preparation, A.A.E.A. and B.Z.; writing—review and editing, A.A.E.A. and B.Z.; visualization, A.A.E.A. and B.Z.; supervision, A.A.E.A. and B.Z.; project administration, A.A.E.A. and B.Z.; funding acquisition, A.A.E.A. and B.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data supporting this study’s findings are available from the corresponding author, BZ, upon reasonable request.
Acknowledgments
The authors thank Algeria’s Directorate General for Scientific Research and Technological Development. We would also like to express our gratitude to Xiaolei Yu, the author of the paper ‘Land Surface Temperature Retrieval from Landsat 8 TIRS—Comparison between Radiative Transfer Equation-Based Method, Split Window Algorithm and Single Channel Method,’ for their invaluable assistance during the preparation of this comment paper.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Yu, X.; Guo, X.; Wu, Z. Land Surface Temperature Retrieval from Landsat 8 TIRS—Comparison between Radiative Transfer Equation-Based Method, Split Window Algorithm and Single Channel Method. Remote Sens. 2014, 6, 9829–9852. [Google Scholar] [CrossRef]
- United States Geological Survey (USGS). Available online: https://www.usgs.gov/landsat-missions/using-usgs-landsat-level-1-data-product (accessed on 5 January 2023).
- MAO, K.; Qin, Z.; Shi, J.; Gong, P. The research of split-window algorithm on the MODIS. Geomat. Inf. Sci. Wuhan Univ. 2005, 30, 703–707. [Google Scholar]
- Spectral Characteristics Viewer. Available online: https://landsat.usgs.gov/spectral-characteristics-viewer (accessed on 15 June 2023).
- Jiménez-Muñoz, J.C.; Sobrino, J.A. A Generalized Single-Channel Method for Retrieving Land Surface Temperature from Remote Sensing Data. J. Geophys. Res. Atmos. 2003, 109, 8112. [Google Scholar] [CrossRef]
- Qin, Z.; Karnieli, A.; Berliner, P. A mono-window algorithm for retrieving land surface temperature from Landsat TM data and its application to the Israel-Egypt border region. Int. J. Remote Sens. 2001, 22, 3719–3746. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).