Abstract
Infrared (IR) small target detection in sky scenes is crucial for aerospace, border security, and atmospheric monitoring. Most current works are typically designed for generalized IR scenes, which may not be optimal for the specific scenario of sky backgrounds, particularly for detecting small and dim targets at long ranges. In these scenarios, the presence of heavy clouds usually causes significant false alarms due to factors such as strong edges, streaks, large undulations, and isolated floating clouds. To address these challenges, we propose an infrared dim and small target detection algorithm based on morphological filtering with dual-structure elements. First, we design directional dual-structure element morphological filters, which enhance the grayscale difference between the target and the background in various directions, thus highlighting the region of interest. The grayscale difference is then normalized in each direction to mitigate the interference of false alarms in complex cloud backgrounds. Second, we employ a dynamic scale awareness strategy, effectively preventing the loss of small targets near cloud edges. We enhance the target features by multiplying and fusing the local response values in all directions, which is followed by threshold segmentation to achieve target detection results. Experimental results demonstrate that our method achieves strong detection performance across various complex cloud backgrounds. Notably, it outperforms other state-of-the-art methods in detecting targets with a low signal-to-clutter ratio (MSCR ≤ 2). Furthermore, the algorithm does not rely on specific parameter settings and is suitable for parallel processing in real-time systems.
1. Introduction
With the growing demand for long-range target detection in both civil and military fields, and the limitations of radar detection in long-range detection scenarios, optoelectronic detection is receiving increasing attention [1,2,3]. Infrared (IR) target detection technology has been widely used in road monitoring, pest control, industrial instrument fault location, search and rescue due to its nature of being unaffected by obstacles, weather, time and other external factors [4,5,6].
IR small target detection in sky scenes plays a critical role in aerospace, border security, and atmospheric environment monitoring. Unlike the ground scenes, the sky background has a relatively fixed clutter morphology and changes slowly over time with observations significantly influenced by meteorological conditions. The observation interference of the ground background mainly comes from human factors such as occlusion and environment. Therefore, the difficulty and focus of small target detection in the sky background lies in the background suppression technique and the capture of high-speed moving targets, whereas detection in ground backgrounds often emphasizes target identification and scene understanding. However, for long-distance detection, small targets in the sky background tend to move slowly in the time domain, exhibit small imaging sizes, and they have very low signal-to-noise ratios. The information in the time dimension is challenging to utilize effectively, making single-frame-based infrared dim and small target detection methods crucial.
Research on small targets has developed rapidly over the past few years, but the literature on weak target detection in cloud backgrounds is scarce. High-performance detection methods for small targets in cloud backgrounds based on single frames are especially needed. For example, Liu et al. [7] described the sky scene as a fractal random field and simulated the infrared small target signal using the generalized Gaussian intensity model, which has a better suppression effect on the complex cloud background, although its real-time performance is limited. Wu et al. [8] proposed a fast detection algorithm based on saliency and scale space, which improves real-time performance. However, the detection rate needs enhancement for targets with a low signal-to-noise ratio. Deng et al. [9] proposed a weighted local difference measure (WLDM)-based scheme for detecting small targets against various complex cloudy–sky backgrounds. Other works [10,11,12,13,14] detect moving targets in cloud backgrounds by incorporating time-domain information. While there are fewer methods specifically focusing on small target detection in cloud backgrounds, numerous methods exist for generalized complex backgrounds, ground–air backgrounds, and sea–sky backgrounds. These methods provide valuable insights for small target detection amidst heavy clouds.
Single-frame-based methods can be classified into model-driven and data-driven approaches. Despite the great potential of data-driven methods, the substantial distribution shift between different datasets and real-world scenarios, along with the lack of large-scale datasets, hinders their practical deployment [15,16,17,18,19,20,21,22,23]. Consequently, model-driven methods still hold significant value in deployment. Among the model-driven approaches, those based on the infrared patch-image model (IPI) [24] and the infrared tensor model (IPT) [25] are hot research topics. Although these methods perform well in complex ground scenes, they lack significant advantages when dealing with cloud backgrounds characterized by simple morphological structures. Moreover, their time-consuming optimization limits their potential for engineering applications. Efficient approaches such LCM [26] and MPCM [27] rely on target characterization. These methods are straightforward and effective when the target is bright and are widely used in engineering. However, their performance declines noticeably as the target grayscale decreases. Several studies have shown that incorporating prior knowledge constraints into the model for specific scenarios can yield significant performance gains [28,29], indicating the value of this theory. In addition, background-based modeling is a classical and crucial method for small target detection in sky backgrounds. The core of the background-based modeling approach is to extract background features that distinguish the target, thereby suppressing the background [30,31,32]. Designing these features manually is very challenging for complex backgrounds, and achieving a generalized background is highly impractical. Despite these challenges, modeling background features remains an effective and important technique for cloud backgrounds.
To effectively suppress false alarms and highlight weak targets in complex cloud backgrounds, it is crucial to fully utilize the spatial properties of target and background clutter signals. In the infrared small target detection problem under complex sky backgrounds, bright and sparse cloud edges, isolated small cloud clusters near weak targets, and undulating thick cloud tips all pose significant challenges. To address these issues, we propose a novel and effective detection strategy called Multi-scale and Multidirectional Local Z-score Top-hat (MMDLTH). The main contributions of this work are as follows:
- We introduce center-invariant rotating dual-structure elements as background suppression templates, which can effectively distinguish small targets from cloud backgrounds with multiple morphological structures.
- We employ a dynamically aware neighborhood scaling strategy to address the limitations of traditional methods that use predefined consistent neighborhood sizes, which often result in the loss of targets near clouds.
- We use a sub-region local normalization method similar to the Z-score to transform the global absolute grayscale difference to a relative grayscale difference. This method effectively suppresses anisotropic and high-variation clouds, highlighting extremely weak targets in homogeneous regions. Compared to traditional linear normalization methods, it is more robust in assessing background clutter complexity and is less affected by outliers, reducing their interference with algorithm performance.
The rest of the paper is organized as follows: Section 2 briefly reviews related work on small target detection. Section 3 details the proposed methodology. Section 4 presents experiments demonstrating the validity of our approach. Section 5 discusses future work. Section 6 concludes the paper. Additional experimental results are provided in Appendix A and Appendix B.
2. Related Work
In this section, we briefly review single-frame-based model-driven methods for infrared small target detection, all of which are instructive for the method proposed in this paper. There are three main approaches for single-frame-based methods: (1) methods based on background modeling, (2) methods based on target saliency, and (3) methods based on the assumptions of low-rank background and sparse targets.
2.1. Methods Based on Background Modeling
Constructing an appropriate background model is very challenging when dealing with complex backgrounds. Single-frame methods, although scarce, are crucial for sky backgrounds. Morphology-based methods are classical approaches [30,32]. The NWTH method [33] enhances the difference between target and background regions using a hollow structure to improve the performance. MRWTH [34] incorporates directional information to more accurately characterize various homogeneous features of the target. Sun et al. utilized wavelet transform to decompose the image into time and frequency domains to extract features, addressing sea and sky background modeling [35]. The difference of Gaussian (DOG) filter predicts the background to detect points of interest [36]. Kernel regression is used to estimate complex clutter backgrounds, offering better performance improvement for complex scenes [31]. Generally, background feature-based methods are simple, efficient, and valuable for engineering applications. Most current research focuses on generalized scenes, often overlooking these methods due to perceived ineffectiveness for complex scenes. However, for sky scenes, their performance can be comparable to other methods.
2.2. Methods Based on Target Saliency
Han et al. [37] conducted an in-depth study on the LCM model and proposed a multiscale detection algorithm utilizing Relative Local Contrast Measurement (RLCM), which can simultaneously suppress all types of interference. Subsequently, the TLLCM and SLCM models were developed to enhance performance by incorporating shape information of the target and fusing weighting functions [38,39]. To avoid the “expansion effect” caused by multiscale technology, Lv et al. [40] proposed a novel algorithm (NSM), which performs well in detecting weak point targets (MSCR < 1). Wu et al. [41] used a fixed scale to detect small targets of different sizes (DNGM). Cui et al. [42] introduced a weighting function into the TLLCM framework (WTLLCM), which can adapt to different scale targets. Mahdi [43] distinguished between targets and false alarms by analyzing the variance of different layers of neighboring patch-images (VARD). Chen et al. [44]. proposed an improved fuzzy C-means (IFCM) clustering framework that fuses multiple features (IFCM-MF) to suppress backgrounds, effectively handling heterogeneous backgrounds and arbitrary noise. Du et al. [45] primarily used local contrast and homogeneity features to detect small targets (HWLCM), which supports parallel computing. Both STLDM and STLCM construct 3D feature models in the spatio-temporal domain, which, while not strictly single-frame methods, are useful for feature extraction [46,47].
2.3. Methods Based on Low Rank and Sparse Assumption
The infrared patch-image (IPI) model is constructed based on the low-rank assumption, exploiting the non-local self-correlation of the infrared background [24]. Its advantage lies in not needing to preset the size and shape of the target, making it highly adaptable to different scenes. However, its iterative process affects real-time performance. Additionally, due to the limitations of sparse characterization, dim targets are often over-shrunk, or strong cloud edges remain in the target image. To further suppress false alarms caused by strong edges, both WIPI and NIPPS introduce priors to improve the accuracy of model constraints, enhancing false alarm suppression [48,49,50]. In addition, the construction of the IPI model can destroy the local self-correlation of the image, which can lead to the loss of prior knowledge. To address this, Dai et al. proposed the Reweighted Infrared Patch-Tensor (RIPT) model, which can utilize both local and non-local priors simultaneously and appropriately [25]. The PSTNN model with a joint weighted L1 norm showed great performance and significantly reduced the complexity of the ADMM solver [51]. Guan et al. introduced a local contrast energy feature into the IPT framework to weight the target tensor, forming a novel detection model via non-convex tensor rank surrogate joint local contrast energy (NTRS) [52]. Kong et al. focused on a more reasonable representation of the background rank and robustness against noise, introducing multi-modal t-SVD and tensor fibered nuclear norm based on the Log operator (LogTFNN) [53]. A novel Group IPT (GIPT) model was proposed using different weights to constrain and differentiate line structures from point structures [54]. Additionally, algorithms for dim and small infrared target detection that fuse time–space domain features with the IPT model have also gained attention recently [14,55,56,57,58,59].
3. Proposed Method
The flowchart of the proposed algorithm is shown in Figure 1. We propose an infrared dim and small target detection algorithm based on morphological filtering with dual-structure elements. First, we design a directional dual-structure element morphological filter. Subsequently, we perform multidirectional morphological filtering and local Z-score normalization at each scale. Finally, we dynamically identify the scale with the highest response in each direction and maximize the enhancement of the target by fusing the results from all directions.
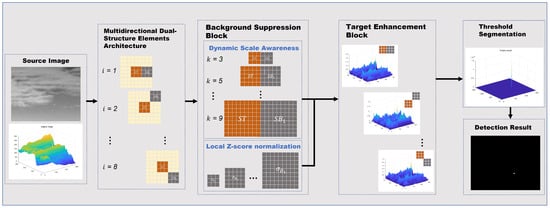
Figure 1.
Flowchart of the proposed MMDLTH method.
3.1. Background Suppression Based on Multidirectional Dual-Structure Elements Top Hat
Compared to ground backgrounds, cloud backgrounds are relatively homogeneous in morphology and slow in intensity change despite their complexity. We aim to use a simpler and more effective method to suppress the cloud background and highlight weak targets, ensuring that the algorithm remains robust.
The classical Top-hat filter is based on a single structural element, which is designed according to the size and shape of the target to be detected. This means the Top-hat filter primarily considers the characteristics of small targets. When dealing with homogeneous backgrounds, it can effectively highlight bright targets smaller than the structural element. For our dual-structure elements, an additional structural element is introduced to further characterize background features and obtain additional prior knowledge. This approach improves the local contrast between the target and the background but does not account for the orientation differences in background features.
Cloud edges and thin strips of cloud can easily form false alarms due to their large gradient changes from their neighbors. However, unlike targets, which vary from their neighbors in all directions, these cloud features differ from the background only in certain directions and remain continuous in at least one direction. Therefore, we use directional dual-structure elements as the basic components of the morphological filter for better background clutter suppression.
Figure 2 illustrates the dual-structure elements of size 3 in 8 directions. The first is a rectangular structural element representing the target region and marked in orange. Its size is related to the size of the target to be detected. The second structural element represents the background region centered on and is marked in dark gray. We split the background structural element into 8 directions . The size of in the i-th direction is the same as that of . We then perform eight filtering operations, which are each based on a dual-structure element in a different direction.
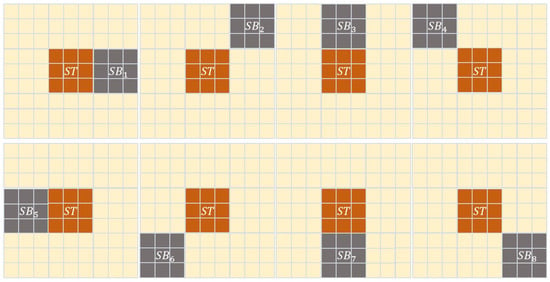
Figure 2.
Illustration of dual-structure elements in eight directions.
The Top-hat method [30] predicts the background using an opening operation, which first erodes the original image and then dilates it with the same structural element. In our scheme, a closing operation is used to predict the background. For each direction, is used for dilation and is used for erosion. Therefore, the predicted backgrounds in different directions are as follows:
where I is the original infrared image, is the first structural element denoting the target region, and is the second structural element representing the i-th background of . is the predicted background using the i-th dual-structure element. The operation symbol “⊕” refers to the dilation operation in morphological processing, which takes the maximum value of the region covered by the structural element. Similarly, the symbol “⊖” refers to the erosion operation, which takes the minimum value of the region of the defined structural element.
Due to the characteristics of infrared radiation, small infrared targets will only be local maxima, meaning that infrared targets are bright targets. Therefore, the predicted background value at the location of the small target should be less than the original image, so the result of background suppression can be expressed as shown below:
where identifies the bright regions in the i-th direction, i.e., the candidate regions for infrared small targets. Given a non-negative constraint, the infrared small target detection model based on multi-directional dual-structure elements morphological filtering can be defined as follows:
3.2. Target Enhancement Based on Multi-Directional Fusion
With the morphological filtering based on dual-structure elements, we have obtained results for background suppression in eight directions. False alarms from structures such as strip clouds and cloud edges have been suppressed as much as possible. However, if the target is weak enough, it can still be drowned out by complex background clutter. Therefore, additional features need to be extracted to further enhance the targets.
Since the responses of the target are strong in all directions, while the backgrounds are not, we can fuse them by multiplication. The formula is defined as follows:
The target will be significantly enhanced by the fusion, as shown in Figure 3. It can be seen that the cloud background suppression and small target enhancement based on multidirectional dual-structure elements lead to promising detection performance. However, there are still some challenging cases that need further improvement.
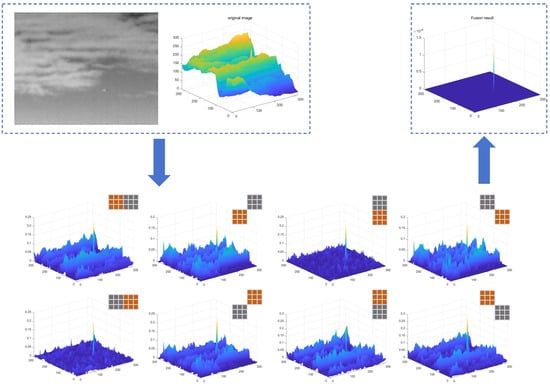
Figure 3.
Fusion of multidirectional background suppression result.
3.3. Local Z-Score Normalization
In the sky background, clouds are major contributors to false alarms because they are the main radiation source aside from the target. Despite suppressing false alarms that are inconsistent with the target’s directional characteristics, anisotropic cloud false alarms remain. In regions with large areas of cloud, there are significant grayscale variations; the difference in grayscale between peaks and adjacent areas is much greater than in regions without clouds. In the operations described above, when the target’s grayscale is low and the cloud clutter is strong, it is difficult to highlight the target using absolute grayscale features.
As shown in Figure 4, the blue box on the left contains a very weak target in a uniform background, which exhibits noticeable grayscale variation from the surrounding background and is identifiable as a target to the human eye. In contrast, the red box on the right contains a false alarm in non-homogeneous clouds, which appears as a continuous background to the human eye. However, based on the numerical values obtained from the calculation of absolute grayscale features, these false alarms are more likely to be identified as candidate targets. We need a more effective strategy for calculating feature differences to avoid interference from the undulating background region.

Figure 4.
Schematic representation of the grayscale distribution of a weak target and clouds.
To address this problem, relative grayscale differences should be introduced in place of absolute grayscale differences. Z-score normalization is employed, and the formula for Z-score normalization is defined as follows:
where X is the raw data, u is the mean value of the raw data X, and is the standard deviation of X. Z is the normalized data, i.e., the normalized score. It indicates the position of the raw data relative to the mean value, which is expressed as a multiple of the standard deviation. Applied to the task in this paper, u and are statistical values from the background region, and X is the value of the target region.
This approach is consistent with the definition of the signal-to-clutter ratio in IR target detection. With this normalization, the Z-score value of the target in Figure 4 will be greater than that of the cloud false alarms. This method allows different data to be unified under the same scale for easy comparison and further analysis, and it better resists the interference of outliers compared to other normalization methods.
Z-score normalization is further applied to subregions to more accurately describe the complexity of the background. This comes from the fact that if the variance of the background around the target localization is calculated directly, it does not correctly reflect the fluctuations of the background in some specific cases; even the normalization step leads to the missing of some targets. As shown in Figure 5, the variance value is larger when the target is at a boundary position. However, the subregions are homogeneous, indicating that the model is inaccurate.
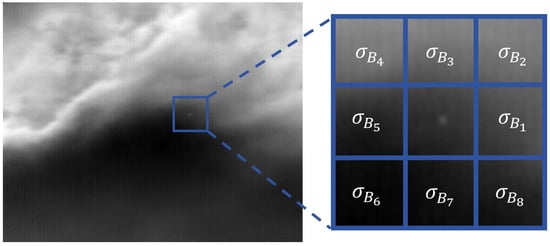
Figure 5.
Schematic representation of local variance in local Z-score.
To address this, local Z-score normalization of subregions is introduced to improve the model’s accuracy. The values of u and will be computed in each of the 8 subregions. In our model, the mean value u of the subregion background is replaced with the predicted value of the background from morphological filtering. The subregion’s range of and u are consistent with the second structure element in the background suppression described above. The improved local , named the model, can be expressed as follows:
where denotes the standard deviation of the i-th direction background as shown in Figure 5, and is set to 0.5 according to the experiments. This formula provides the residual results after normalization in each direction, where the differences between the target and background are normalized for each direction.
This grayscale difference quantification method can more accurately reflect the local significance of the target. The local multidirectional standard deviation of subregions can more reasonably describe background fluctuations, preventing excessive background suppression due to large variances at cloud edges. In homogeneous backgrounds, the standard deviation tends to be small or even less than 1. As a result, the computed local difference is closer to, or even larger than, the grayscale differences themselves. This means that when the background variance is minimal, the target can be greatly enhanced. This is a critical step in combating interference from heavy clouds.
As can be seen in Figure 6, the mean signal-to-clutter ratio (MSCR), as defined in Section 4.1, is 0.469. The grayscale value difference between the target and its neighbors is less than 10, as shown in the bottom right subfigure. In fact, experiments show that its grayscale difference is 5, making it difficult to detect with the human eye and not very prominent in the local region. This frequently ignored target can be detected correctly by our method. Moreover, as shown in Figure 7, the extremely dim target is highlighted, and heavy clouds are well suppressed compared to the results without local Z-score normalization.
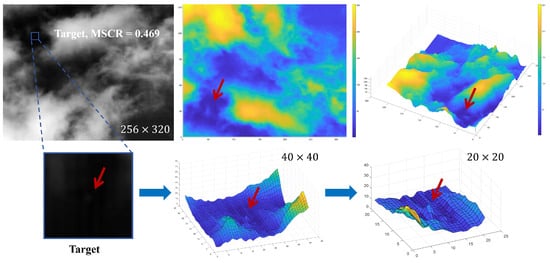
Figure 6.
A dim target and 3D maps of the neighborhood size of and centered locally on it.

Figure 7.
Three-dimensional (3D) display before and after cloud suppression by local Z-score normalization.
3.4. Dynamic Awareness of Scale Strategy
Multiscale models are widely used for IR target detection, focusing on identifying the scale layer where the characteristic feature response is maximized. However, the maximum characteristic response of the target in different directions does not always come from the same scale of filters. As shown in Figure 5, when the target is close to the cloud boundary, the background area around the target in 8 directions does not present a high response at the same scale. In such cases, if the target is dim enough, it is likely to be missed.
If the target boundary is 7 pixels from the cloud boundary and a structural element size of 9 is used, the response in that direction will be low. However, if the size of the structural elements is 3, the target features are preserved and highly responsive in that direction. This indicates that the response of the target in different directions may come from different scales. Therefore, we dynamically determine the reasonable scales in different directions to solve this problem. According to the Society of Photo-Optical Instrumentation Engineers (SPIE), the size of a small infrared target is less than [1]. We use four different sizes of filter templates: , and , respectively. Thus, the dynamic multiscale model can be expressed as
where k represents the side length of the square template. As analyzed above, there is a high probability that the targets will have a high response in all directions. The final fusion result of responses in 8 directions is given similarly to Equation (4), and can be expressed as
3.5. Threshold Segmentation
After the above set of operations, the dim targets are greatly enhanced. Experimentally, we verified that the target can be extracted by simply using adaptive threshold segmentation. The threshold can be expressed as
where and denote the mean value and the standard deviation of . is a factor ranging from 1 to 60 based on the experiments. The operator symbol “·” stands for multiplication.
4. Experimental Results and Analysis
In this section, we present the details of our experiments. We first introduce the evaluation metrics, baseline methods, and datasets. To illustrate the performance of the algorithm, we demonstrate its capability for background suppression and target detection across different scenarios, varying signal-to-clutter ratios of targets, and the presence of multiple targets.
4.1. Evaluation Metrics
To illustrate the performance of our proposed algorithm, the signal-to-clutter ratio (SCR) is introduced to represent the difficulty of small target detection. It is defined as follows:
where and denote the mean value of the target region and its surrounding background region, as shown in Figure 8, and is the standard deviation of the background. Here, the SCR is calculated using the mean value of the target region; hence, it is also known as the mean signal-to-clutter ratio (MSCR). Similarly, we can measure the ratio of the intensity of the peak signal of the target to the background clutter by replacing the mean value with the maximum value in the target region in Equation (10), which is known as the peak signal-to-clutter ratio (PSCR).

Figure 8.
Schematic of the target and its local background.
In our experiments, the values of a and b are the height and width of the external rectangle of the infrared small targets. d is the computational range representing the background region, which is centered and symmetric to the target region. To facilitate comparative experiments, we set , which is the same as in paper [49]. In general, the higher the signal-to-clutter ratio, the easier it is to detect the target.
The metrics MSCR and PSCR reflect the difficulty of detecting the target. The ability to enhance small and dim targets and suppress complex backgrounds directly determines the overall performance of the detection algorithm. Therefore, the gain of the signal-to-clutter ratio (SCRG) and the background suppression factor (BSF) are common evaluation metrics used. SCRG is defined as follows:
where the suffixes “in” and “out” represent the original image and the processed image, respectively. The definition of BSF is as follows:
where and represent the standard deviations of the background before and after the detection algorithm, respectively. Higher SCRG and BSF values are desired, as they indicate better detection capability.
To further evaluate the performance of the proposed method, the receiver operating characteristic (ROC) curve is used as a key evaluation metric. It shows the relationship between the true positive rate (TPR) and the false positive rate (FPR). The TPR and FPR in infrared small target detection are defined as follows:
According to the definition of the ROC curve, the closer the curve is to the upper left corner, the better the algorithm performs.
4.2. Baseline Methods
To validate the effectiveness of the proposed method, we compare it against several classical methods. Firstly, the classical Top-hat method is used as a baseline. Our approach is inspired by MNWTH [33] and MDRTH [34], and our experimental results will be compared with these methods. Among methods based on human visual systems, LCM [26] and MCPM [27] are highly representative; thus, both are included in our comparison. Additionally, methods based on low-rank and sparse decomposition can be categorized into matrix decomposition and tensor decomposition. In this work, IPI [24] and NRAM [49] are used as baseline methods for low-rank matrix factorization. Furthermore, we select RIPT [25] and PSTNN [51] as baseline methods, which are widely followed by researchers. The parameters used for these baseline algorithms during experimentation are provided in Table 1.

Table 1.
Detailed parameter settings for the ten methods.
4.3. Datasets
Our experimental data include two parts. The first part is the public dataset of SIRST [17], which contains 315 images of sky scenes required for our experiments. Both homogeneous and non-homogeneous backgrounds are included. According to the literature [34], the maximum resolution of the target is 78 pixels, and the minimum is 4 pixels. A few images contain more than two targets.
To further validate the algorithm’s detection ability in low SCR and complex backgrounds, we also use real backgrounds superimposed on simulated targets to obtain additional datasets. A detailed description of the data is presented in Table 2. The MSCR and PSCR of targets for each dataset are shown in Figure 9. For clarity, each curve is arranged in order of MSCR from smallest to largest, making the MSCR and PSCR ranges of targets in each sequence clearly visible. Except for the public SIRST dataset, the MSCR of small targets in our datasets are all lower.

Table 2.
Detailed description of the six real sequences.
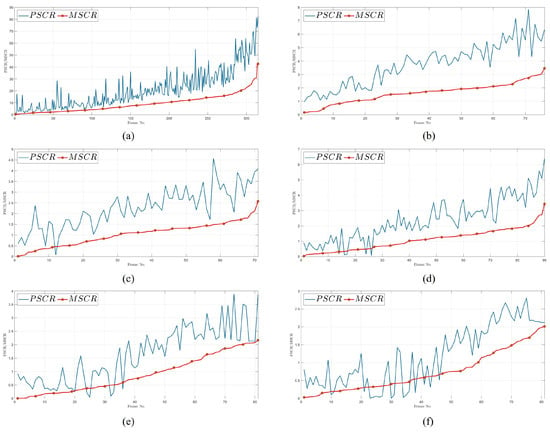
Figure 9.
The PSCR and MSCR of the six tested sequences are presented in Table 2. (a–f) correspond to Seq1–Seq6, respectively.
Let be the peak value of the target, and let and be the mean values of the target and background regions, respectively. For small targets, the relationship typically holds in most cases, leading to PSCR being greater than MSCR. However, when the target is extremely weak, the relationship may occur, causing MSCR to be less than PSCR when taking the absolute value in Equation (10). As shown in Figure 9, most of the data we used contain very weak targets, highlighting the challenge for detection.
4.4. Qualitative Evaluation
4.4.1. Robustness to Various Scenes
First, we verified the background suppression ability in different kinds of sky scenes. In Figure 10 and Figure 11, we show the results after background suppression and target enhancement operations in uniform and complex backgrounds, respectively. Both sets of image data are from the SIRST dataset. In Figure 10, it can be seen that the targets under a uniform sky background without clouds in the ten images are relatively more significant, and the background clutter interference is not serious. Therefore, the backgrounds are better suppressed, and the targets are highlighted by the method proposed in this paper.
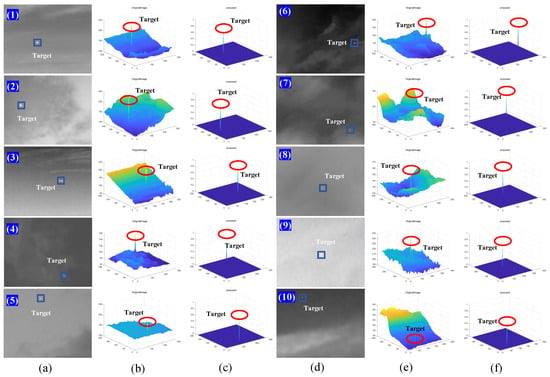
Figure 10.
Background suppression ability on homogenized sky backgrounds. (a) Original infrared images (1)–(5); (b) 3D display of original images; (c) 3D display of background suppression results; (d) original infrared images (6)–(10); (e) 3D display of original images; (f) 3D display of background suppression results.
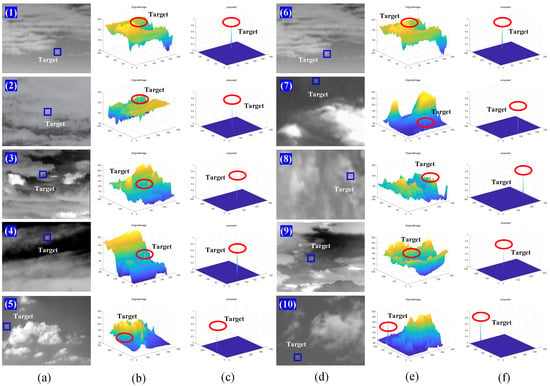
Figure 11.
Background suppression ability on complex sky backgrounds with heavy clouds. (a) Original infrared images (1)–(5); (b) 3D display of original image; (c) 3D display of background suppression results; (d) original infrared images (6)–(10); (e) 3D display of original image; (f) 3D display of background suppression results.
In Figure 11, we use another 10 sets of data to illustrate the robustness of our algorithm in complex sky scenes. These data are also from the SIRST dataset. As shown in the 3D display of the original images in columns (b) and (e), compared to the previous set of data in Figure 10, the overall undulation of the image background is larger, the prominence of the targets is greatly diminished, and some targets are even submerged in the background. However, as seen in (c) and (f), our method still maintains excellent background suppression, and the targets are greatly highlighted, making it easier to separate the background from the targets subsequently.
4.4.2. Robustness to Multiple Targets
If multiple targets exist simultaneously, the detection becomes more challenging due to the uncertainty of target information, such as different sizes, signal-to-noise ratios, and shapes. This can lead to the loss of targets if the priors are not fully utilized. In Figure 12, 10 sets of examples with multiple targets are presented. The number of targets in the images varies from two to six, and the locations of the targets are either close together or scattered.
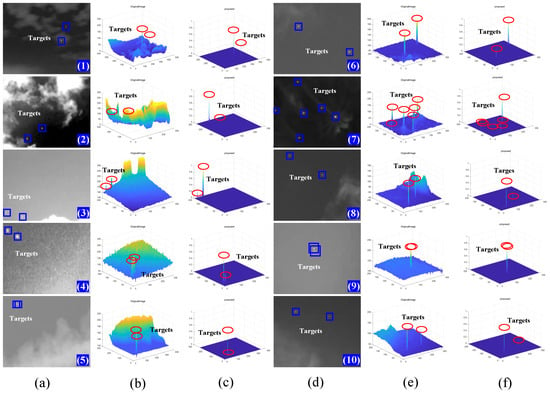
Figure 12.
Background suppression ability on sky backgrounds with the presence of multiple targets. (a) Original infrared image (1)–(5); (b) 3D display of original image; (c) 3D display of background suppression results; (d) original infrared image (6)–(10); (e) 3D display of original image; (f) 3D display of background suppression results.
In Figure 12, we see examples with thin or thick clouds in the sky backgrounds. Despite these challenging conditions, all the targets are highlighted simultaneously, and the background is well suppressed. Our method shows good adaptability for scenes with multiple targets.
4.4.3. Robustness to Low SCR Targets
To verify the detection performance of the algorithms for weaker targets, we add simulated weak targets in different real sky backgrounds. These targets follow Gaussian distributions. Figure 13 and Figure 14 show the experimental results for targets with MSCR between 1 and 2 and MSCR below 1, respectively. The MSCR is calculated using Equation (10), where the neighboring background sizes of the targets take the value of according to the IPI method.
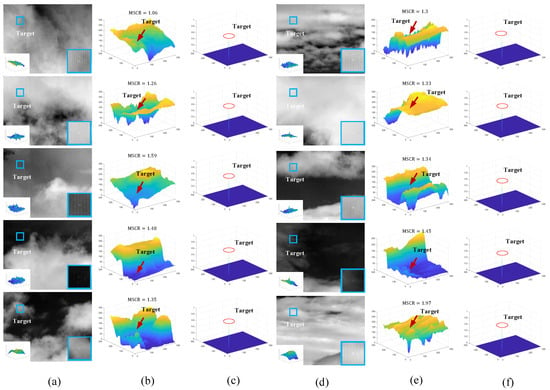
Figure 13.
Background suppression ability on sky backgrounds with low SCR (1 < MSCR < 2, d = 20) of small targets. (a) Original infrared image; (b) 3D display of original image; (c) 3D display of background suppression results; (d) original infrared image; (e) 3D display of original image; (f) 3D display of background suppression results.
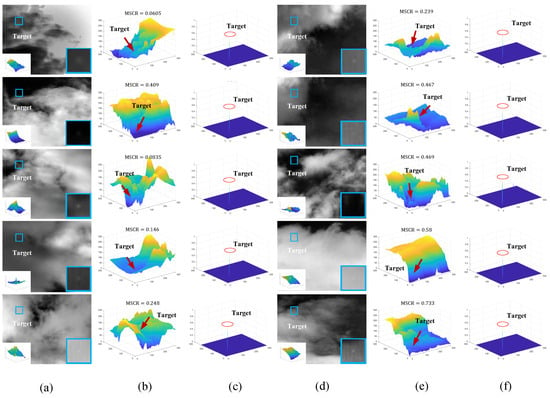
Figure 14.
Background suppression ability on sky backgrounds with low SCR (MSCR < 1, d = 20) of small targets. (a) Original infrared image; (b) 3D display of original image; (c) 3D display of background suppression results; (d) original infrared image; (e) 3D display of original image; (f) 3D display of background suppression results.
Since the targets are very weak, they are difficult to discriminate in the original image or its 3D display. Therefore, the local regions of the targets are shown in the lower right corner of the original image in (a) and (d) with a corresponding local 3D display of the targets in the lower left corner. The targets are all located in the upper left corner of the image. As seen in the experimental results (c) and (f), the targets are greatly emphasized with a sufficiently large difference from the background.
4.4.4. Visual Comparison with Baselines
To further visualize the performance of all the competing methods, we present the detection results of four representative infrared images compared to the baseline methods. The four original images are shown in Figure 15 along with their 3D images. The target locations and MSCR values are also noted in the figure. As seen from the 3D representations of the original images, the targets are difficult to recognize even with the human eye. The MSCRs of the four targets are all less than 3.
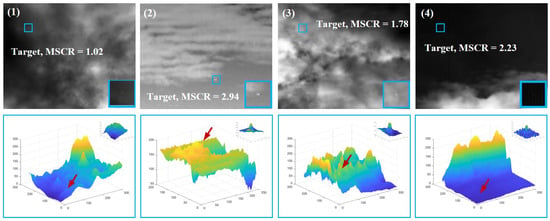
Figure 15.
Four representative infrared images with low SCR targets.
Figure 16 presents the experimental results of the proposed method compared with nine baseline methods. The red circle indicates the target’s location. If the red circle is not marked, it signifies that the target was not detected. The results demonstrate that for the four images with complex backgrounds and weak targets, the proposed algorithm maintains robust detection performance. It exhibits strong background suppression capabilities, effectively distinguishing target features from background features.
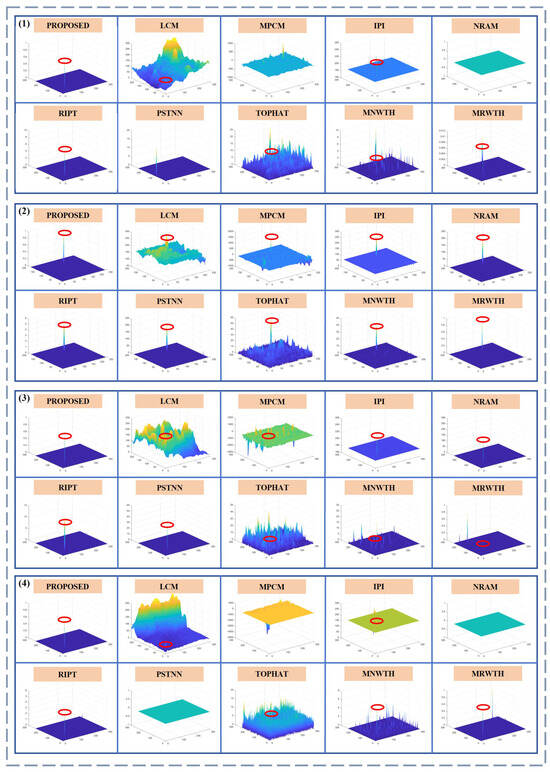
Figure 16.
The detection results of the proposed algorithm and 9 baseline methods of images from Figure 15.
4.5. Quantitative Evaluation
In addition to visually demonstrating the robustness of our method through single-frame detection results of targets with different backgrounds and signal-to-noise ratios, we also provide quantitative evaluations using the signal-to-clutter gain (SCRG), background suppression factor (BSF), and ROC curves. Table 3 lists the experimental results for all 10 methods across sequences 1–6. Note that INF (i.e., infinity) indicates that the entire background is completely suppressed to zero.

Table 3.
SCRG and BSF of the six real sequences.
For the methods IPI, RIPT, and PSTNN, the local background regional variance and global background variance of the target are 0 or infinitesimally small, so the value of SCRG is denoted as INF. Similarly, for the method proposed in this paper, the target’s local background variance is also generally infinitesimal, resulting in SCRG values recorded as INF. The NRAM method frequently resulted in target loss during experiments with no false alarms present; in these cases, the outputs were all 0, and therefore, no statistics were available for SCRG and BSF. The BSF value of our method is notably high, demonstrating the algorithm’s ability to distinguish features of weak targets from clutter. As shown in Table 3, compared with other methods, the proposed method exhibits an excellent enhancement of weak targets and suppression of complex cloud backgrounds.
In addition, we plot the ROC curves for the six test sequences. As shown in Figure 17, the curves for our method are consistently close to the upper left corner across all six representative sequences, indicating superior overall performance.
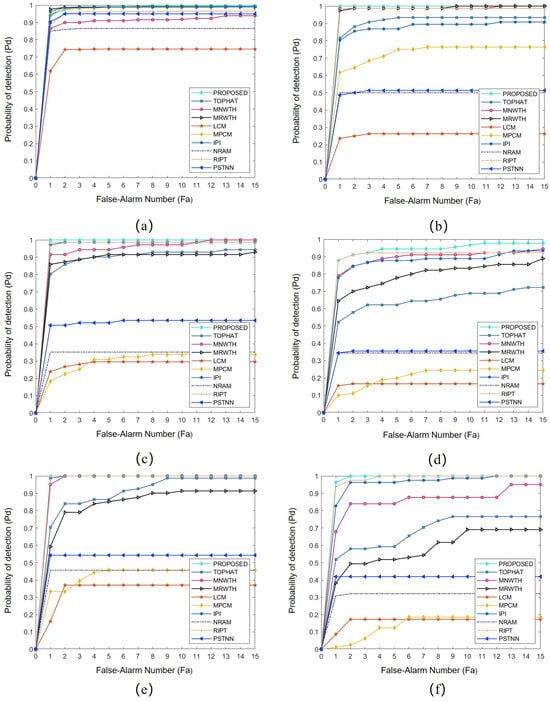
Figure 17.
ROC curves of different algorithms in Table 2. (a–f) correspond to Seq1–Seq6, respectively.
5. Discussion
Infrared weak target detection methods are a significant research area that has garnered much attention. The detection performance of many methods diminishes significantly under strong clutter interference. This is mainly because the complex background feature information is not sufficiently utilized, and the target information is poor and not well enhanced. However, we note that robust small target detection methods in generalized scenarios are difficult to achieve. In practical applications, there is an urgent demand for high-accuracy small target detection methods tailored to specific scenarios. Only by leveraging specific scenario priors of the background clutter and small targets can stable performance be achieved. Therefore, we explore and focus on the most common sky background, aiming to propose a framework for small target detection that can be applied in real-world scenarios with robust detection performance.
Mainstream state-of-the-art methods based on low-rank and sparse assumptions effectively detect very small targets but face challenges in practical application due to iterative optimization and parameter selection. Target saliency methods have potential but struggle at low signal-to-clutter ratios. Filtering-based methods are simple and easy to implement but perform poorly in complex scenarios.
To balance performance metrics, we draw on both target saliency-based and filtering-based ideas. We use morphological filtering methods suitable for parallel computation to achieve background suppression in multiple directions and at multiple scales. Then, we normalize the global differences using the local standard deviation, which is similar to computing local contrast in HSV. Finally, we fuse the local differences of the entire image to maximize target enhancement, leveraging the feature that the target has significant differences from the local background in all directions.
Compared with the baseline algorithms, we discuss the performance of different methods under four conditions.
As image 1 shown in Figure 18, when the background is homogeneous and the absolute grayscale of the target varies widely, all methods can detect the target well with few false alarms.

Figure 18.
Four representative images with different features.
As image 2 shown in Figure 18, when the background is homogeneous and the absolute grayscale difference of the target is small, especially when the target grayscale is lower than the background variance, making it difficult to see with the human eye, only our method and the MDRTH method maintain stable performance.
As image 3 shown in Figure 18, when the background is complex with heavy clouds and the target is prominent in the local region, the performance of IPI, NRAM, RIPT, PSTNN, MDRTH, and our method is promising. However, TOPHAT and MNWTH struggle to suppress the complex background well due to the simplicity of their models. LCM and MPCM enhance the contrast of the target but introduce some false alarms with similar characteristics to the target, weakening detection performance.
As image 4 shown in Figure 18, when the background is complex with heavy clouds and the absolute grayscale difference of the target is small, TOPHAT, MNWTH, LCM, and MPCM perform unsatisfactorily. Methods based on the low-rank assumption are affected by convergence conditions, leading to a significant increase in algorithm time consumption. Since MDRTH uses global differences, the small absolute grayscale differences of the targets result in many highly responsive false alarms in undulating background areas. Promisingly, our method performs a normalization operation and thus still performs well in such extremely complex scenes.
Although our method significantly outperforms other baseline methods in detecting small targets under complex sky backgrounds in the test datasets, it has some limitations. One of the more noticeable drawbacks is the loss of some edge pixels from the target after segmentation. This problem can be mitigated by increasing the size of the filtering template, but doing so also leads to an increase in false alarms, which is an issue worth optimizing in the future. Additionally, whether the method can be applied to other types of backgrounds warrants further exploration.
6. Conclusions
In long-range infrared detection, targets are imaged weakly, especially in complex sky scenes where drastic cloud changes make dim target detection more difficult. To effectively solve the problems of cloud clutter suppression and infrared small target detection, we introduce a center-invariant rotating dual-structure element template as a background suppression template, which can effectively distinguish small targets from cloud backgrounds with multiple morphological structures. Meanwhile, we use a dynamically-aware neighborhood scaling strategy to address the problem of using predefined consistent neighborhood sizes in traditional methods, which tends to result in the loss of targets close to clouds. Finally, a subregion normalization method similar to Z-score is used to transform the global absolute grayscale difference into a more accurate subdivided relative grayscale difference, which can effectively suppress the isotropic anisotropy and high-variation clouds while highlighting some very weak targets in the smoothing region. Experimental results show that our method performs well in different SCR. In particular, when MSCR , it has fewer false alarms than other tested methods for the same detection rate. Our method has higher background suppression and target enhancement capabilities and has the potential of parallel computing, which is promising to be applied in practice in the future.
Author Contributions
Conceptualization, L.P.; methodology, L.P. and Z.L.; validation, L.P.; formal analysis, L.P.; investigation, L.P.; original draft preparation, L.P.; review and editing, L.P., Z.L., T.L. and P.J.; funding acquisition, Z.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China under Grant 62302471, the Postdoctoral Fellowship Program of CPSF under Grant GZC20232565 and the fellowship of the China Postdoctoral Science Foundation under Grant 2023M743401.
Data Availability Statement
Seq1 dataset can be found here: https://github.com/YimianDai/sirst (accessed on 10 September 2023), Seq2–Seq6 datasets are not available to public.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
As shown in Figure A1 and Figure A2, these are the detection results for 16 images not shown in the main body of this paper.
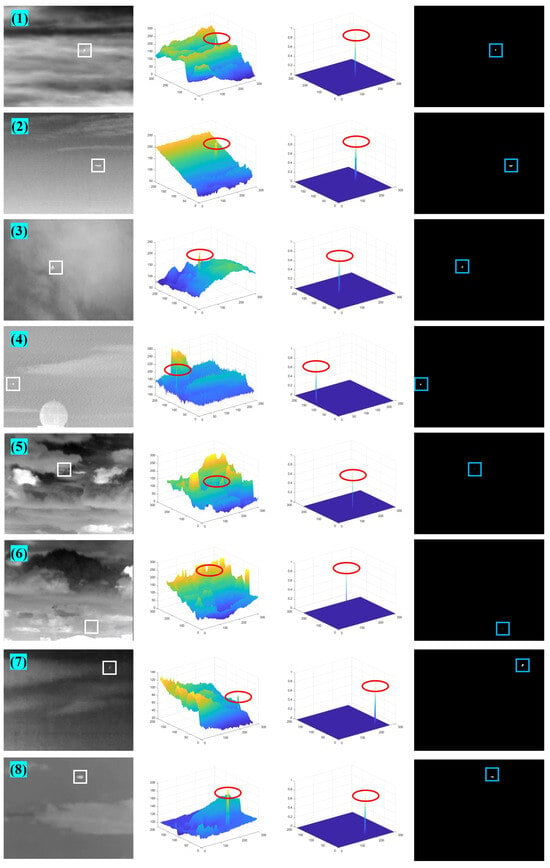
Figure A1.
The detection results of the first group of 8 images.
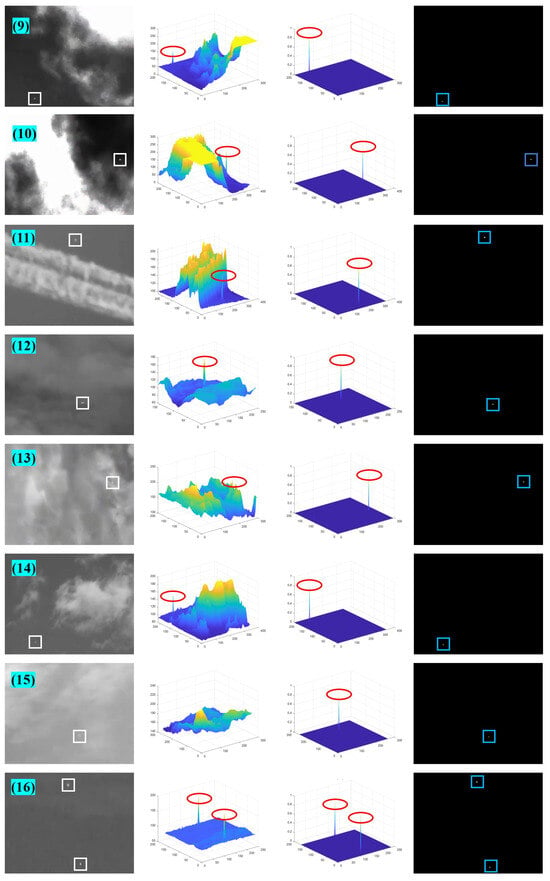
Figure A2.
The detection results of the second group of 8 images.
Appendix B
To further illustrate the capability of our method, Figure A3, Figure A4 and Figure A5 give the detection results of nine images not shown in the main text, while the MSCR of the target is labeled in the figures. Figure A6, Figure A7 and Figure A8 show the results of the 3D map of the proposed algorithm in this paper compared to other baseline algorithms.
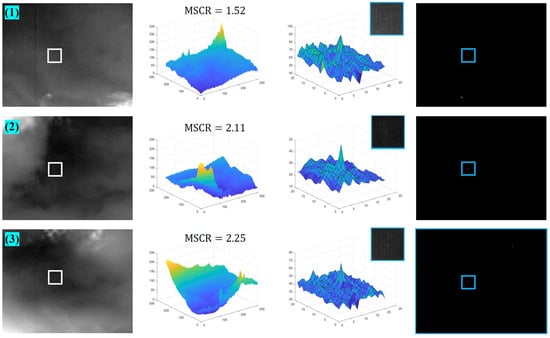
Figure A3.
The detection results of images (1) to (3).
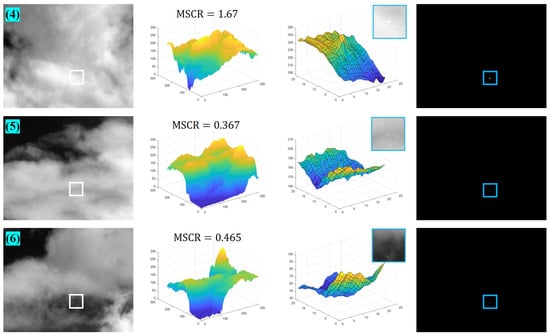
Figure A4.
The detection results of images (4) to (6).
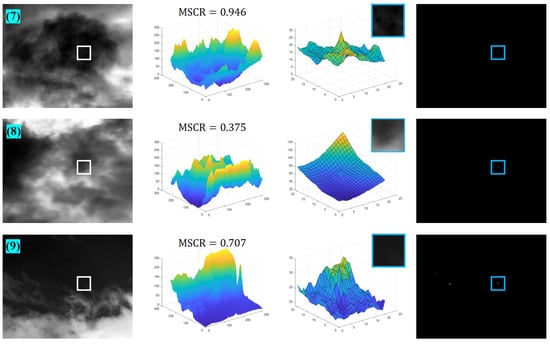
Figure A5.
The detection results of images (7) to (9).
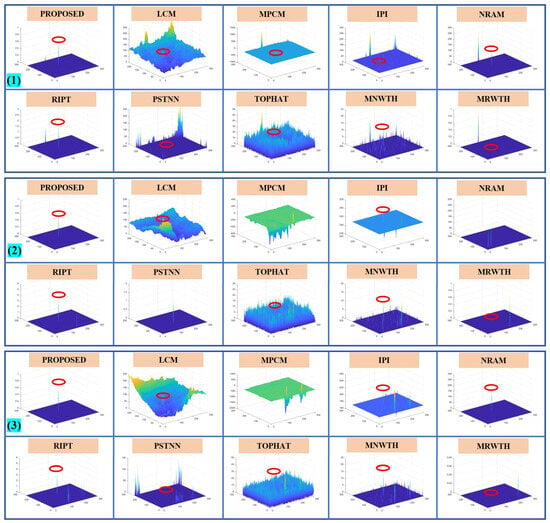
Figure A6.
The 3D map of the proposed algorithm and 9 baseline methods for images (1) to (3).
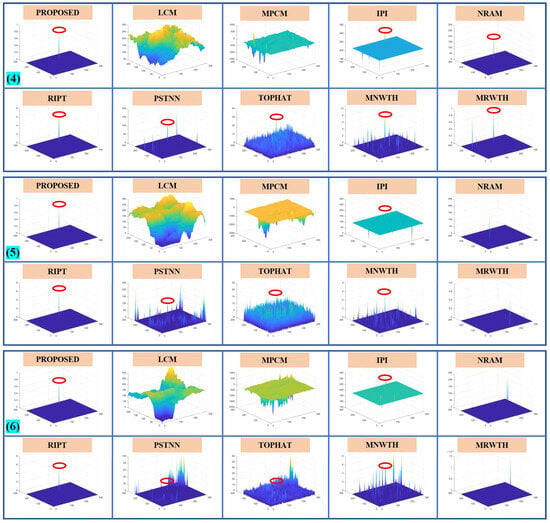
Figure A7.
The 3D map of the proposed algorithm and 9 baseline methods for images (4) to (6).
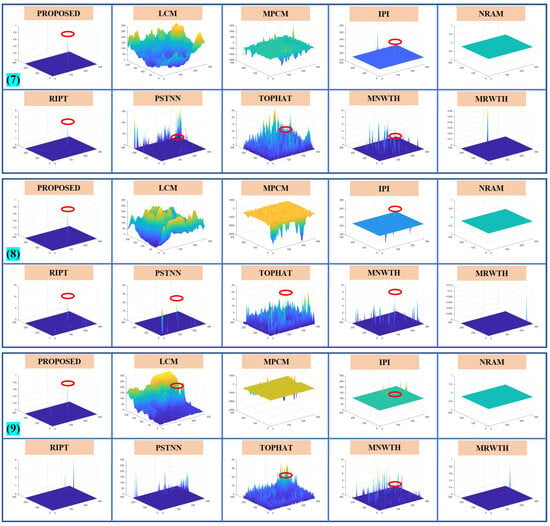
Figure A8.
The 3D map of the proposed algorithm and 9 baseline methods for images (7) to (9).
References
- Zhao, M.; Li, W.; Li, L.; Hu, J.; Ma, P.; Tao, R. Single-Frame Infrared Small-Target Detection: A Survey. IEEE Geosci. Remote Sens. Mag. 2022, 10, 87–119. [Google Scholar] [CrossRef]
- Thanh, N.T.; Sahli, H.; Hao, D.N. Infrared Thermography for Buried Landmine Detection: Inverse Problem Setting. IEEE Trans. Geosci. Remote Sens. 2008, 46, 3987–4004. [Google Scholar] [CrossRef]
- Zhang, T.; Wu, H.; Liu, Y.; Peng, L.; Yang, C.; Peng, Z. Infrared Small Target Detection Based on Non-Convex Optimization with Lp-norm Constraint. Remote Sens. 2019, 11, 559. [Google Scholar] [CrossRef]
- Law, W.C.; Xu, Z.; Yong, K.T.; Liu, X.; Swihart, M.T.; Seshadri, M.; Prasad, P.N. Manganese-Doped near-Infrared Emitting Nanocrystals for in Vivo Biomedical Imaging. Opt. Express 2016, 24, 17553–17561. [Google Scholar] [CrossRef]
- Han, J.; Ma, Y.; Huang, J.; Mei, X.; Ma, J. An Infrared Small Target Detecting Algorithm Based on Human Visual System. IEEE Geosci. Remote Sens. Lett. 2016, 13, 452–456. [Google Scholar] [CrossRef]
- Voicu, L.I.; Patton, R.; Myler, H.R. Detection Performance Prediction on IR Images Assisted by Evolutionary Learning. In Proceedings of the Targets and Backgrounds: Characterization and Representation V, Orlando, FL, USA, 14 July 1999; Volume 3699, pp. 282–292. [Google Scholar] [CrossRef]
- Liu, D.; Li, Z.; Liu, B.; Chen, W.; Liu, T.; Cao, L. Infrared Small Target Detection in Heavy Sky Scene Clutter Based on Sparse Representation. Infrared Phys. Technol. 2017, 85, 13–31. [Google Scholar] [CrossRef]
- Qiang, W.; Hua-Kai, L. An Infrared Small Target Fast Detection Algorithm in the Sky Based on Human Visual System. In Proceedings of the 2018 4th Annual International Conference on Network and Information Systems for Computers (ICNISC), Wuhan, China, 20–22 April 2018; pp. 176–181. [Google Scholar] [CrossRef]
- Deng, H.; Sun, X.; Liu, M.; Ye, C.; Zhou, X. Small Infrared Target Detection Based on Weighted Local Difference Measure. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4204–4214. [Google Scholar] [CrossRef]
- Dai, S.; Li, D. Research on an Infrared Multi-Target Saliency Detection Algorithm under Sky Background Conditions. Sensors 2020, 20, 459. [Google Scholar] [CrossRef]
- Wan, M.; Gu, G.; Cao, E.; Hu, X.; Qian, W.; Ren, K. In-Frame and Inter-Frame Information Based Infrared Moving Small Target Detection under Complex Cloud Backgrounds. Infrared Phys. Technol. 2016, 76, 455–467. [Google Scholar] [CrossRef]
- Xi, Y.; Zhou, Z.; Jiang, Y.; Zhang, L.; Li, Y.; Wang, Z.; Tan, F.; Hou, Q. Infrared Moving Small Target Detection Based on Spatial-Temporal Local Contrast under Slow-Moving Cloud Background. Infrared Phys. Technol. 2023, 134, 104877. [Google Scholar] [CrossRef]
- Ren, X.; Wang, J.; Ma, T.; Yue, C.; Bai, K. Adaptive Background Suppression Method Based on Intelligent Optimization for IR Small Target Detection Under Complex Cloud Backgrounds. IEEE Access 2020, 8, 36930–36947. [Google Scholar] [CrossRef]
- Xu, E.; Wu, A.; Li, J.; Chen, H.; Fan, X.; Huang, Q. Infrared Target Detection Based on Joint Spatio-Temporal Filtering and L1 Norm Regularization. Sensors 2022, 22, 6258. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Qin, H.; Cheng, W.; Wang, C.; Leng, H.; Zhou, H. Small Target Detection in Infrared Image Using Convolutional Neural Networks. In Proceedings of the AOPC 2017: Optical Sensing and Imaging Technology and Applications, Beijing, China, 4–6 June 2017; Volume 10462, pp. 1335–1340. [Google Scholar] [CrossRef]
- Zhao, B.; Wang, C.; Fu, Q.; Han, Z. A Novel Pattern for Infrared Small Target Detection With Generative Adversarial Network. IEEE Trans. Geosci. Remote Sens. 2021, 59, 4481–4492. [Google Scholar] [CrossRef]
- Dai, Y.; Wu, Y.; Zhou, F.; Barnard, K. Attentional Local Contrast Networks for Infrared Small Target Detection. IEEE Trans. Geosci. Remote Sens. 2021, 59, 9813–9824. [Google Scholar] [CrossRef]
- Wang, K.; Du, S.; Liu, C.; Cao, Z. Interior Attention-Aware Network for Infrared Small Target Detection. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–13. [Google Scholar] [CrossRef]
- Wang, K.; Li, S.; Niu, S.; Zhang, K. Detection of Infrared Small Targets Using Feature Fusion Convolutional Network. IEEE Access 2019, 7, 146081–146092. [Google Scholar] [CrossRef]
- Li, B.; Xiao, C.; Wang, L.; Wang, Y.; Lin, Z.; Li, M.; An, W.; Guo, Y. Dense Nested Attention Network for Infrared Small Target Detection. IEEE Trans. Image Process. 2023, 32, 1745–1758. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.; Zhang, R.; Yang, Y.; Bai, H.; Zhang, J.; Guo, J. ISNet: Shape Matters for Infrared Small Target Detection. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022; pp. 867–876. [Google Scholar] [CrossRef]
- Chen, F.; Gao, C.; Liu, F.; Zhao, Y.; Zhou, Y.; Meng, D.; Zuo, W. Local Patch Network With Global Attention for Infrared Small Target Detection. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 3979–3991. [Google Scholar] [CrossRef]
- Chen, Y.; Li, L.; Liu, X.; Su, X. A Multi-Task Framework for Infrared Small Target Detection and Segmentation. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–9. [Google Scholar] [CrossRef]
- Gao, C.; Meng, D.; Yang, Y.; Wang, Y.; Zhou, X.; Hauptmann, A.G. Infrared Patch-Image Model for Small Target Detection in a Single Image. IEEE Trans. Image Process. 2013, 22, 4996–5009. [Google Scholar] [CrossRef]
- Dai, Y.; Wu, Y. Reweighted Infrared Patch-Tensor Model with Both Nonlocal and Local Priors for Single-Frame Small Target Detection. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 3752–3767. [Google Scholar] [CrossRef]
- Chen, C.P.; Li, H.; Wei, Y.; Xia, T.; Tang, Y.Y. A Local Contrast Method for Small Infrared Target Detection. IEEE Trans. Geosci. Remote Sens. 2013, 52, 574–581. [Google Scholar] [CrossRef]
- Wei, Y.; You, X.; Li, H. Multiscale Patch-Based Contrast Measure for Small Infrared Target Detection. Pattern Recognit. 2016, 58, 216–226. [Google Scholar] [CrossRef]
- Peng, L.; Zhang, T.; Huang, S.; Pu, T.; Liu, Y.; Lv, Y.; Zheng, Y.; Peng, Z. Infrared Small-Target Detection Based on Multi-Directional Multi-Scale High-Boost Response. Opt. Rev. 2019, 26, 568–582. [Google Scholar] [CrossRef]
- Guan, X.; Peng, Z.; Huang, S.; Chen, Y. Gaussian Scale-Space Enhanced Local Contrast Measure for Small Infrared Target Detection. IEEE Geosci. Remote Sens. Lett. 2020, 17, 327–331. [Google Scholar] [CrossRef]
- Ye, B.; Peng, J.x. Small Target Detection Method Based on Morphology Top-Hat Operator. J. Image Graph. 2002, 7, 638–642. [Google Scholar]
- Gu, Y.; Wang, C.; Liu, B.; Zhang, Y. A Kernel-Based Nonparametric Regression Method for Clutter Removal in Infrared Small-Target Detection Applications. IEEE Geosci. Remote Sens. Lett. 2010, 7, 469–473. [Google Scholar] [CrossRef]
- Lerallut, R.; Decencière, E.; Meyer, F. Image Filtering Using Morphological Amoebas. Image Vis. Comput. 2007, 25, 395–404. [Google Scholar] [CrossRef]
- Bai, X.; Zhou, F. Analysis of New Top-Hat Transformation and the Application for Infrared Dim Small Target Detection. Pattern Recognit. 2010, 43, 2145–2156. [Google Scholar] [CrossRef]
- Wang, C.; Wang, L. Multidirectional Ring Top-Hat Transformation for Infrared Small Target Detection. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 8077–8088. [Google Scholar] [CrossRef]
- Sun, Y.Q.; Tian, J.W.; Liu, J. Background Suppression Based-on Wavelet Transformation to Detect Infrared Target. In Proceedings of the 2005 International Conference on Machine Learning and Cybernetics, Guangzhou, China, 18–21 August 2005; Volume 8, pp. 4611–4615. [Google Scholar] [CrossRef]
- Dong, X.; Huang, X.; Zheng, Y.; Bai, S.; Xu, W. A Novel Infrared Small Moving Target Detection Method Based on Tracking Interest Points under Complicated Background. Infrared Phys. Technol. 2014, 65, 36–42. [Google Scholar] [CrossRef]
- Han, J.; Liang, K.; Zhou, B.; Zhu, X.; Zhao, J.; Zhao, L. Infrared Small Target Detection Utilizing the Multiscale Relative Local Contrast Measure. IEEE Geosci. Remote Sens. Lett. 2018, 15, 612–616. [Google Scholar] [CrossRef]
- Han, J.; Moradi, S.; Faramarzi, I.; Liu, C.; Zhang, H.; Zhao, Q. A Local Contrast Method for Infrared Small-Target Detection Utilizing a Tri-Layer Window. IEEE Geosci. Remote Sens. Lett. 2020, 17, 1822–1826. [Google Scholar] [CrossRef]
- Han, J.; Moradi, S.; Faramarzi, I.; Zhang, H.; Zhao, Q.; Zhang, X.; Li, N. Infrared Small Target Detection Based on the Weighted Strengthened Local Contrast Measure. IEEE Geosci. Remote Sens. Lett. 2021, 18, 1670–1674. [Google Scholar] [CrossRef]
- Lv, P.; Sun, S.; Lin, C.; Liu, G. A Method for Weak Target Detection Based on Human Visual Contrast Mechanism. IEEE Geosci. Remote Sens. Lett. 2019, 16, 261–265. [Google Scholar] [CrossRef]
- Wu, L.; Ma, Y.; Fan, F.; Wu, M.; Huang, J. A Double-Neighborhood Gradient Method for Infrared Small Target Detection. IEEE Geosci. Remote Sens. Lett. 2021, 18, 1476–1480. [Google Scholar] [CrossRef]
- Cui, H.; Li, L.; Liu, X.; Su, X.; Chen, F. Infrared Small Target Detection Based on Weighted Three-Layer Window Local Contrast. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Nasiri, M.; Chehresa, S. Infrared Small Target Enhancement Based on Variance Difference. Infrared Phys. Technol. 2017, 82, 107–119. [Google Scholar] [CrossRef]
- Chen, L.; Lin, L. Improved Fuzzy C-Means for Infrared Small Target Detection. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Du, P.; Hamdulla, A. Infrared Small Target Detection Using Homogeneity-Weighted Local Contrast Measure. IEEE Geosci. Remote Sens. Lett. 2020, 17, 514–518. [Google Scholar] [CrossRef]
- Du, P.; Hamdulla, A. Infrared Moving Small-Target Detection Using Spatial–Temporal Local Difference Measure. IEEE Geosci. Remote Sens. Lett. 2020, 17, 1817–1821. [Google Scholar] [CrossRef]
- Zhao, B.; Xiao, S.; Lu, H.; Wu, D. Spatial-Temporal Local Contrast for Moving Point Target Detection in Space-Based Infrared Imaging System. Infrared Phys. Technol. 2018, 95, 53–60. [Google Scholar] [CrossRef]
- Dai, Y.; Wu, Y.; Song, Y. Infrared Small Target and Background Separation via Column-Wise Weighted Robust Principal Component Analysis. Infrared Phys. Technol. 2016, 77, 421–430. [Google Scholar] [CrossRef]
- Zhang, L.; Peng, L.; Zhang, T.; Cao, S.; Peng, Z. Infrared Small Target Detection via Non-Convex Rank Approximation Minimization Joint l2,1 Norm. Remote Sens. 2018, 10, 1821. [Google Scholar] [CrossRef]
- Dai, Y.; Wu, Y.; Song, Y.; Guo, J. Non-Negative Infrared Patch-Image Model: Robust Target-Background Separation via Partial Sum Minimization of Singular Values. Infrared Phys. Technol. 2017, 81, 182–194. [Google Scholar] [CrossRef]
- Zhang, L.; Peng, Z. Infrared Small Target Detection Based on Partial Sum of the Tensor Nuclear Norm. Remote Sens. 2019, 11, 382. [Google Scholar] [CrossRef]
- Guan, X.; Zhang, L.; Huang, S.; Peng, Z. Infrared Small Target Detection via Non-Convex Tensor Rank Surrogate Joint Local Contrast Energy. Remote Sens. 2020, 12, 1520. [Google Scholar] [CrossRef]
- Kong, X.; Yang, C.; Cao, S.; Li, C.; Peng, Z. Infrared Small Target Detection via Nonconvex Tensor Fibered Rank Approximation. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–21. [Google Scholar] [CrossRef]
- Yang, L.; Yan, P.; Li, M.; Zhang, J.; Xu, Z. Infrared Small Target Detection Based on a Group Image-Patch Tensor Model. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Liu, H.K.; Zhang, L.; Huang, H. Small Target Detection in Infrared Videos Based on Spatio-Temporal Tensor Model. IEEE Trans. Geosci. Remote Sens. 2020, 58, 8689–8700. [Google Scholar] [CrossRef]
- Yi, H.; Yang, C.; Qie, R.; Liao, J.; Wu, F.; Pu, T.; Peng, Z. Spatial-Temporal Tensor Ring Norm Regularization for Infrared Small Target Detection. IEEE Geosci. Remote Sens. Lett. 2023, 20, 1–5. [Google Scholar] [CrossRef]
- Zhang, G.; Hamdulla, A.; Ma, H. Infrared Small Target Detection With Patch Tensor Collaborative Sparse and Total Variation Constraint. IEEE Geosci. Remote Sens. Lett. 2023, 20, 1–5. [Google Scholar] [CrossRef]
- Hu, Y.; Ma, Y.; Pan, Z.; Liu, Y. Infrared Dim and Small Target Detection from Complex Scenes via Multi-Frame Spatial–Temporal Patch-Tensor Model. Remote Sens. 2022, 14, 2234. [Google Scholar] [CrossRef]
- Aliha, A.; Liu, Y.; Ma, Y.; Hu, Y.; Pan, Z.; Zhou, G. A Spatial–Temporal Block-Matching Patch-Tensor Model for Infrared Small Moving Target Detection in Complex Scenes. Remote Sens. 2023, 15, 4316. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).