Biomass Estimation and Saturation Value Determination Based on Multi-Source Remote Sensing Data
Abstract
1. Introduction
2. Study Area and Data Processing
2.1. Overview of the Study Area
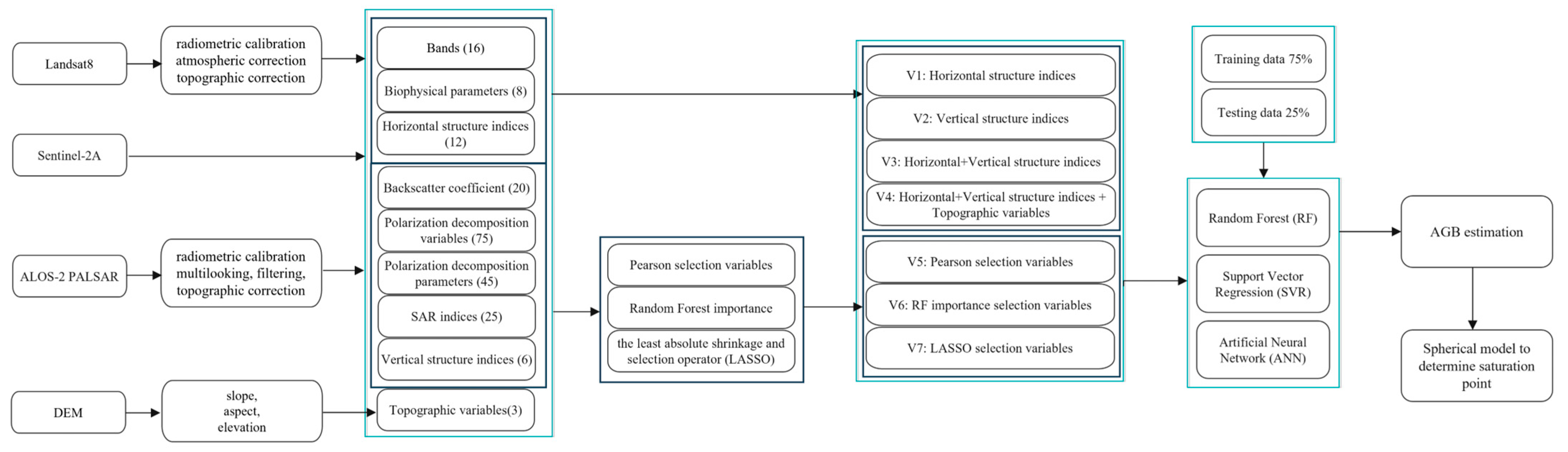
2.2. Remote Sensing Data and Extraction Variables
2.2.1. Optical Data
2.2.2. SAR Data
2.2.3. Topographic Factors
3. Modeling of AGB Estimation
3.1. Variable Selection Methods
3.2. Non-Parametric Model
3.2.1. Random Forest (RF)
3.2.2. Support Vector Regression (SVR)
3.2.3. Artificial Neural Networks (ANN)
3.3. Determination of Biomass Saturation Value Based on Spherical Modeling
4. Results
4.1. Variable Selection
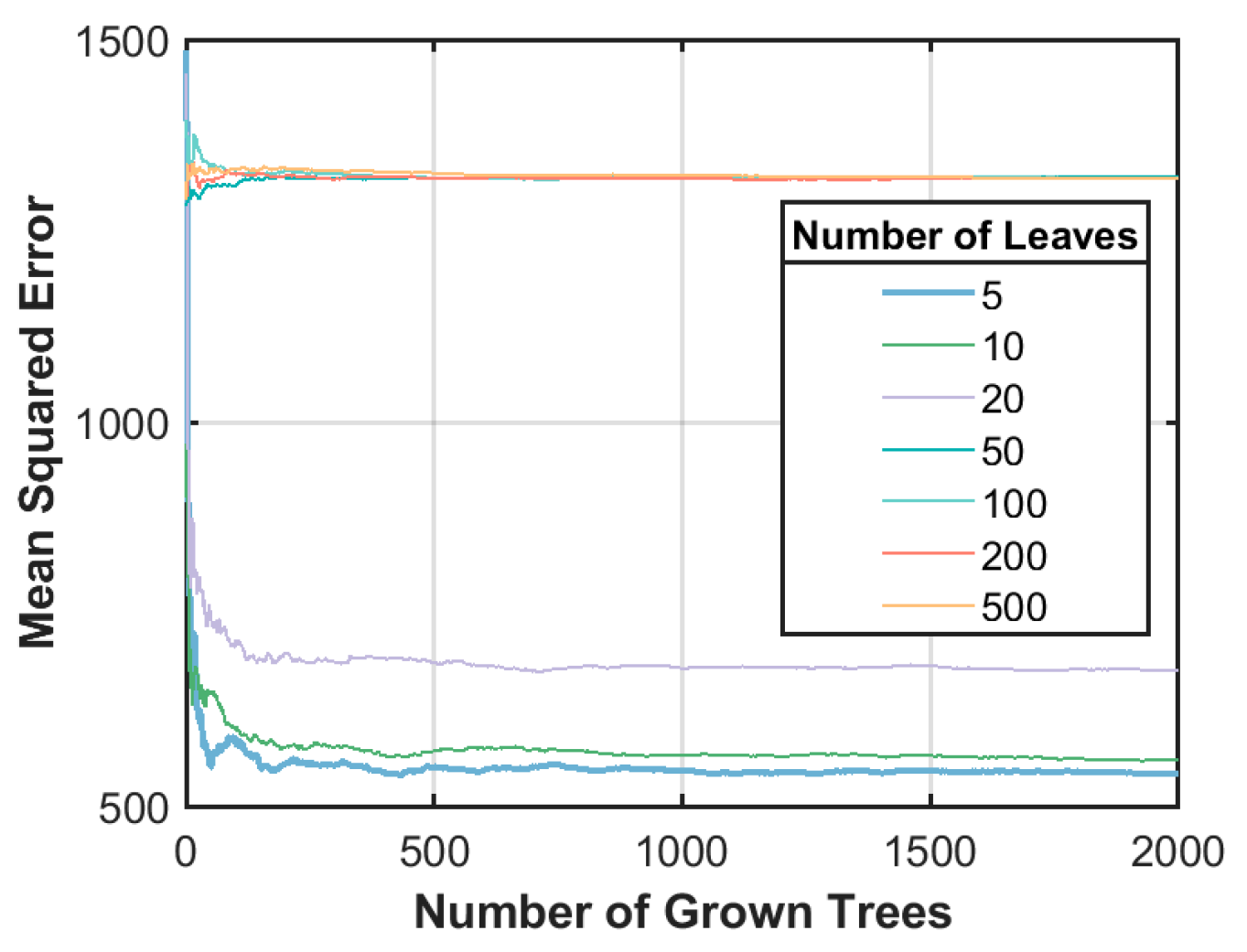
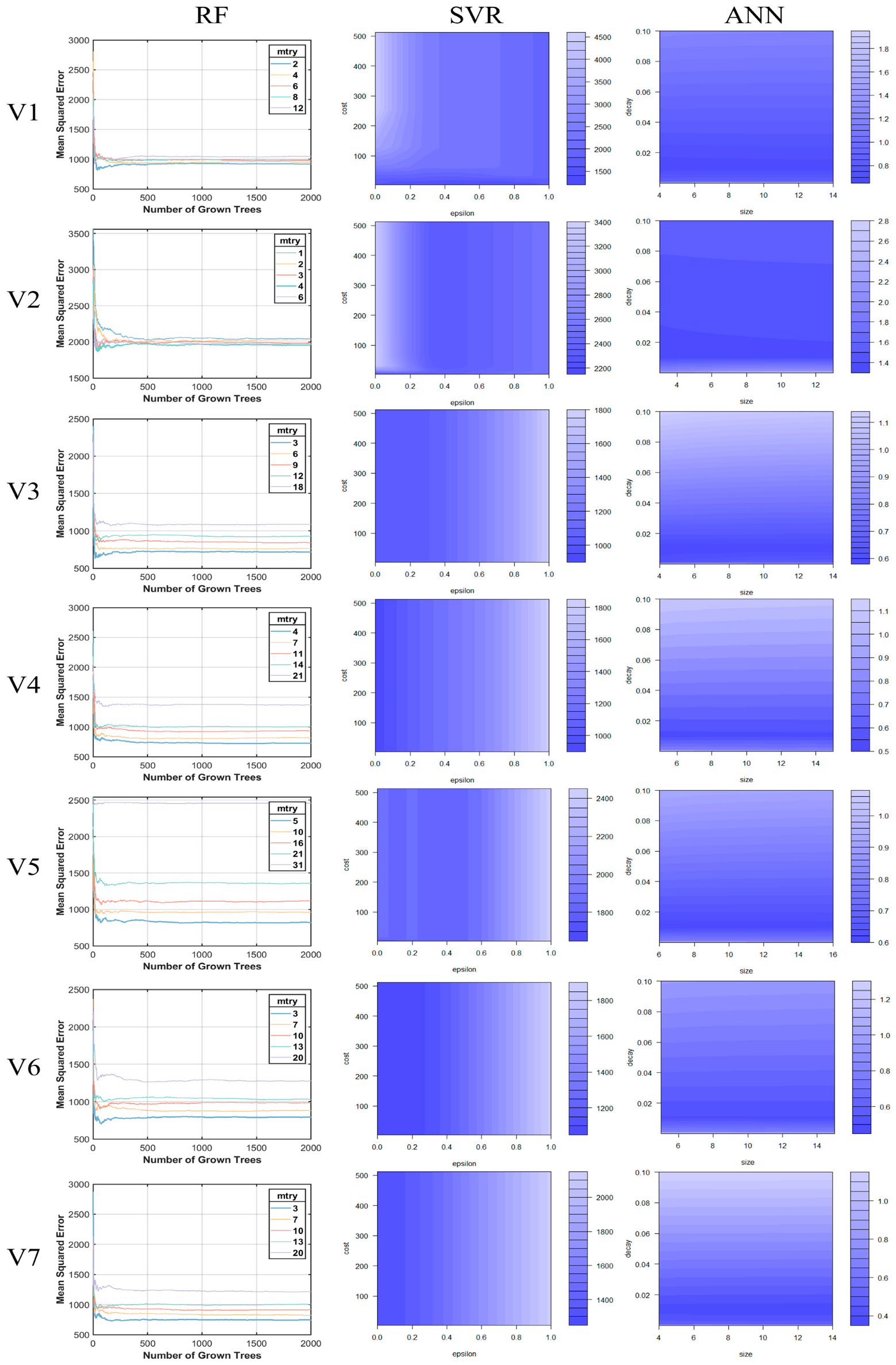
4.2. Optimization of Model Parameters
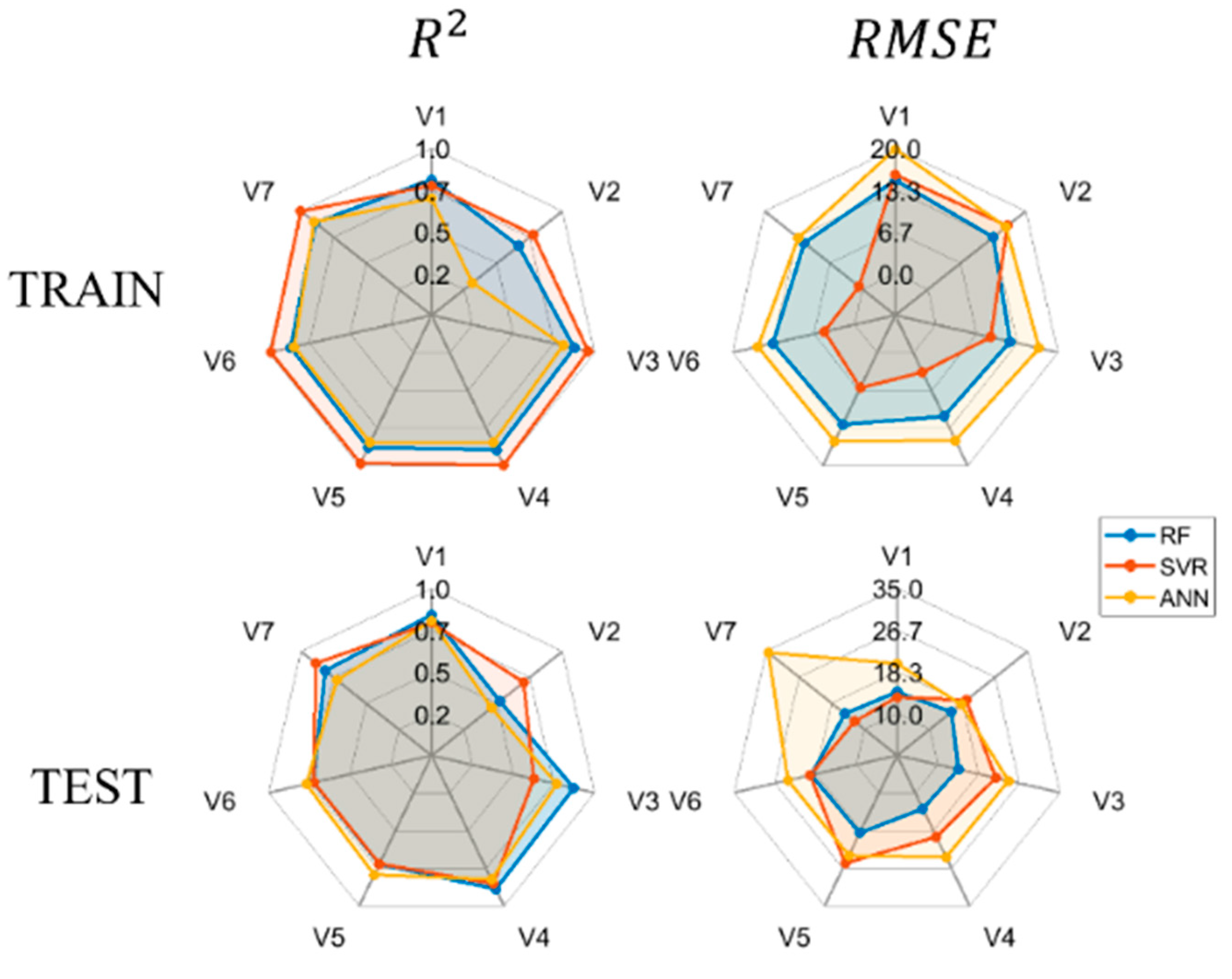
4.3. Estimation of AGB Based on ML Algorithms
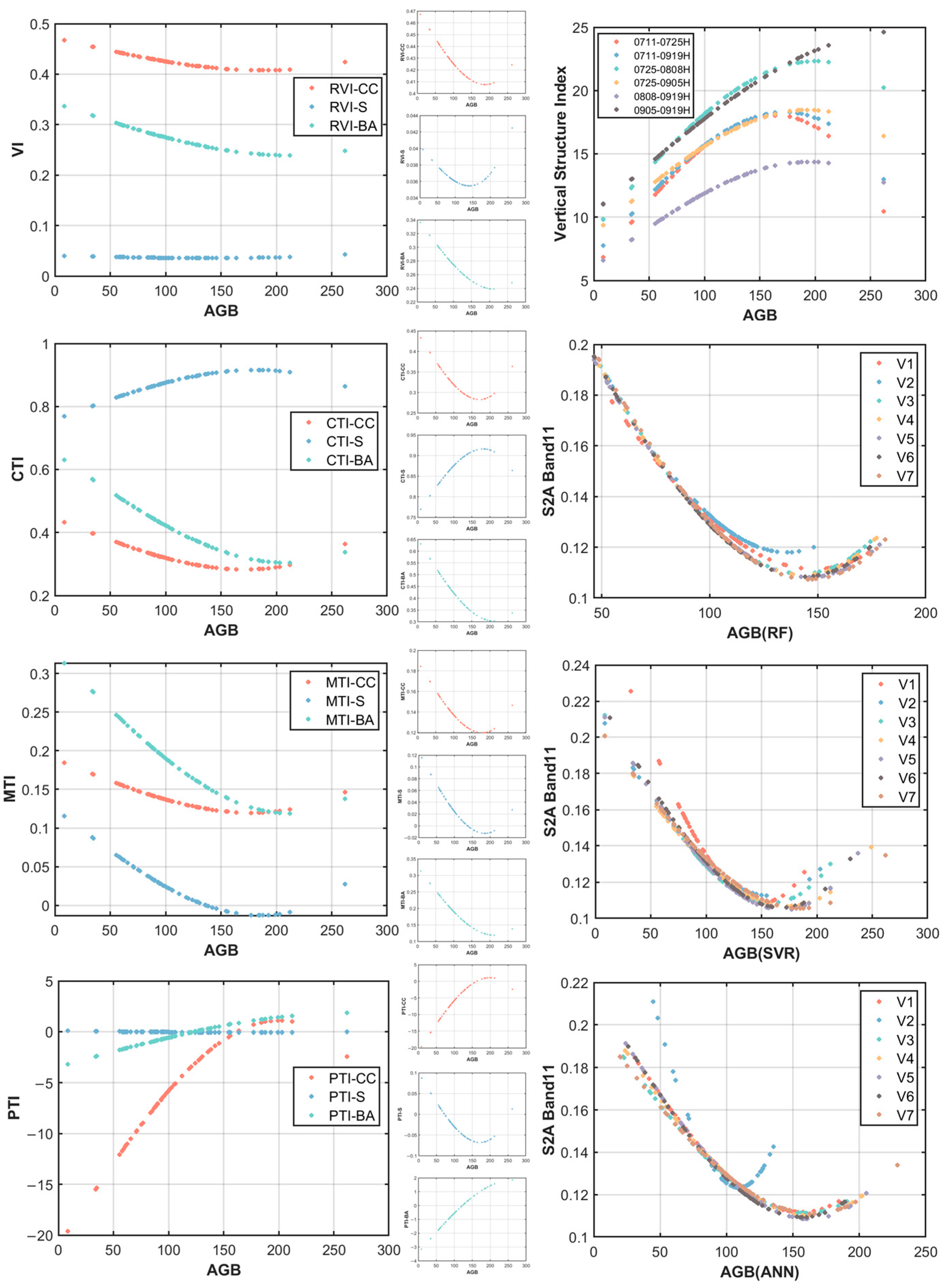
4.4. Determination of the Saturation Value
5. Discussion
5.1. Variable Selection
5.2. Analysis of the Model Results
5.3. Saturation Value Analyze
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Oliveira, C.P.d.; Ferreira, R.L.C.; da Silva, J.A.A.; Lima, R.B.d.; Silva, E.A.; Silva, A.F.d.; Lucena, J.D.S.d.; dos Santos, N.A.T.; Lopes, I.J.C.; Pessoa, M.M.d.L.; et al. Modeling and Spatialization of Biomass and Carbon Stock Using LiDAR Metrics in Tropical Dry Forest, Brazil. Forests 2021, 12, 473. [Google Scholar] [CrossRef]
- Chen, W.; Zheng, Q.; Xiang, H.; Chen, X.; Sakai, T. Forest Canopy Height Estimation Using Polarimetric Interferometric Synthetic Aperture Radar (PolInSAR) Technology Based on Full-Polarized ALOS/PALSAR Data. Remote Sens. 2021, 13, 174. [Google Scholar] [CrossRef]
- Stelmaszczuk-Górska, M.A.; Rodriguez-Veiga, P.; Ackermann, N.; Thiel, C.; Balzter, H.; Schmullius, C. Non-Parametric Retrieval of Aboveground Biomass in Siberian Boreal Forests with ALOS PALSAR Interferometric Coherence and Backscatter Intensity. J. Imaging 2016, 2, 1. [Google Scholar] [CrossRef]
- Urbazaev, M.; Thiel, C.; Migliavacca, M.; Reichstein, M.; Rodriguez-Veiga, P.; Schmullius, C. Improved Multi-Sensor Satellite-Based Aboveground Biomass Estimation by Selecting Temporally Stable Forest Inventory Plots Using NDVI Time Series. Forests 2016, 7, 169. [Google Scholar] [CrossRef]
- Ahmed, R.; Siqueira, P.; Hensley, S. Analyzing the Uncertainty of Biomass Estimates from L-Band Radar Backscatter over the Harvard and Howland Forests. IEEE Trans. Geosci. Remote Sens. 2014, 52, 3568–3586. [Google Scholar] [CrossRef]
- Lee, Y.-S.; Lee, S.; Baek, W.-K.; Jung, H.-S.; Park, S.-H.; Lee, M.-J. Mapping Forest Vertical Structure in Jeju Island from Optical and Radar Satellite Images Using Artificial Neural Network. Remote Sens. 2020, 12, 797. [Google Scholar] [CrossRef]
- Ren, Z.; Zheng, H.; He, X.; Zhang, D.; Yu, X.; Shen, G. Spatial estimation of urban forest structures with Landsat TM data and field measurements. Urban For. Urban Green. 2015, 14, 336–344. [Google Scholar] [CrossRef]
- Dube, T.; Mutanga, O. Investigating the robustness of the new Landsat-8 Operational Land Imager derived texture metrics in estimating plantation forest aboveground biomass in resource constrained areas. ISPRS J. Photogramm. Remote Sens. 2015, 108, 12–32. [Google Scholar] [CrossRef]
- Zhen, Z.; Chen, S.; Yin, T.; Chavanon, E.; Lauret, N.; Guilleux, J.; Henke, M.; Qin, W.; Cao, L.; Li, J.; et al. Using the Negative Soil Adjustment Factor of Soil Adjusted Vegetation Index (SAVI) to Resist Saturation Effects and Estimate Leaf Area Index (LAI) in Dense Vegetation Areas. Sensors 2021, 21, 2115. [Google Scholar] [CrossRef]
- Stratoulias, D.; Nuthammachot, N.; Suepa, T.; Phoungthong, K. Assessing the Spectral Information of Sentinel-1 and Sentinel-2 Satellites for Above-Ground Biomass Retrieval of a Tropical Forest. ISPRS Int. J. Geo-Inf. 2022, 11, 199. [Google Scholar] [CrossRef]
- Liu, Z.; Long, J.; Lin, H.; Xu, X.; Liu, H.; Zhang, T.; Ye, Z.; Yang, P. Combination Strategies of Variables with Various Spatial Resolutions Derived from GF-2 Images for Mapping Forest Stock Volume. Forests 2023, 14, 1175. [Google Scholar] [CrossRef]
- Bastin, J.-F.; Barbier, N.; Couteron, P.; Adams, B.; Shapiro, A.; Bogaert, J.; Cannière, C.D. Aboveground biomass mapping of African forest mosaics using canopy texture analysis: Toward a regional approach. Ecol. Appl. A Publ. Ecol. Soc. Am. 2016, 24, 1984–2001. [Google Scholar] [CrossRef]
- Hlatshwayo, S.T.; Mutanga, O.; Lottering, R.T.; Kiala, Z.; Ismail, R. Mapping forest aboveground biomass in the reforested Buffelsdraai landfill site using texture combinations computed from SPOT-6 pan-sharpened imagery. Int. J. Appl. Earth Obs. Geoinf. 2019, 74, 65–77. [Google Scholar] [CrossRef]
- Cazcarra-Bes, V.; Tello-Alonso, M.; Fischer, R.; Heym, M.; Papathanassiou, K. Monitoring of Forest Structure Dynamics by Means of L-Band SAR Tomography. Remote Sens. 2017, 9, 1229. [Google Scholar] [CrossRef]
- Santoro, M.; Cartus, O.; Carvalhais, N.; Rozendaal, D.M.A.; Avitabile, V.; Araza, A.; de Bruin, S.; Herold, M.; Quegan, S.; Rodríguez-Veiga, P.; et al. The global forest above-ground biomass pool for 2010 estimated from high-resolution satellite observations. Earth Syst. Sci. Data 2021, 13, 3927–3950. [Google Scholar] [CrossRef]
- Bispo, P.d.C.; Rodríguez-Veiga, P.; Zimbres, B.; do Couto de Miranda, S.; Henrique Giusti Cezare, C.; Fleming, S.; Baldacchino, F.; Louis, V.; Rains, D.; Garcia, M.; et al. Woody Aboveground Biomass Mapping of the Brazilian Savanna with a Multi-Sensor and Machine Learning Approach. Remote Sens. 2020, 12, 2685. [Google Scholar] [CrossRef]
- Huang, X.; Ziniti, B.; Torbick, N.; Ducey, M.J. Assessment of Forest above Ground Biomass Estimation Using Multi-Temporal C-band Sentinel-1 and Polarimetric L-band PALSAR-2 Data. Remote Sens. 2018, 10, 1424. [Google Scholar] [CrossRef]
- Kasischke, E.S.; Melack, J.M.; Craig Dobson, M. The use of imaging radars for ecological applications—A review. Remote Sens. Environ. 1997, 59, 141–156. [Google Scholar] [CrossRef]
- Schlund, M.; Davidson, M. Aboveground Forest Biomass Estimation Combining L- and P-Band SAR Acquisitions. Remote Sens. 2018, 10, 1151. [Google Scholar] [CrossRef]
- Hansen, E.; Gobakken, T.; Solberg, S.; Kangas, A.; Ene, L.; Mauya, E.; Næsset, E. Relative Efficiency of ALS and InSAR for Biomass Estimation in a Tanzanian Rainforest. Remote Sens. 2015, 7, 9865–9885. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, X.; Guo, Z. Estimation of tree height and aboveground biomass of coniferous forests in North China using stereo ZY-3, multispectral Sentinel-2, and DEM data. Ecol. Indic. 2021, 126, 107645. [Google Scholar] [CrossRef]
- Alonso, M.T.; Pardini, M.; Papathanassiou, K. Towards Forest Structure Characteristics Retrieval from SAR Tomographic Profiles. In Proceedings of the European Conference on Synthetic Aperture Radar (EUSAR), Berlin, Germany, 3–5 June 2014. [Google Scholar]
- Du, C.; Fan, W.; Ma, Y.; Jin, H.I.; Zhen, Z. The Effect of Synergistic Approaches of Features and Ensemble Learning Algorith on Aboveground Biomass Estimation of Natural Secondary Forests Based on ALS and Landsat 8. Sensors 2021, 21, 5974. [Google Scholar] [CrossRef] [PubMed]
- Fatehi, P.; Damm, A.; Schaepman, M.E.; Kneubühler, M. Estimation of Alpine Forest Structural Variables from Imaging Spectrometer Data. Remote Sens. 2015, 7, 16315–16338. [Google Scholar] [CrossRef]
- Lu, D.; Chen, Q.; Wang, G.; Liu, L.; Li, G.; Moran, E. A survey of remote sensing-based aboveground biomass estimation methods in forest ecosystems. Int. J. Digit. Earth 2014, 9, 63–105. [Google Scholar] [CrossRef]
- Minh, N.P.; Ngoc, T.N.; Nguyen, A.H. An improved adaptive decomposition method for forest parameters estimation using polarimetric SAR interferometry image. Eur. J. Remote Sens. 2019, 52, 359–373. [Google Scholar] [CrossRef]
- Ronoud, G.; Darvish Sefat, A.A.; Fatehi, P. Beech Tree Density Estimation Using Sentinel-2 Data (Case Study: Khyroud Forest). Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, XLII-4/W18, 891–895. [Google Scholar] [CrossRef]
- Mutti, P.R.; da Silva, L.L.; Medeiros, S.D.S.; Dubreuil, V.; Mendes, K.R.; Marques, T.V.; Lucio, P.S.; Santos e Silva, C.M.; Bezerra, B.G. Basin scale rainfall-evapotranspiration dynamics in a tropical semiarid environment during dry and wet years. Int. J. Appl. Earth Obs. Geoinf. 2019, 75, 29–43. [Google Scholar] [CrossRef]
- Akhtar, A.M.; Qazi, W.A.; Ahmad, S.R.; Gilani, H.; Mahmood, S.A.; Rasool, A. Integration of high-resolution optical and SAR satellite remote sensing datasets for aboveground biomass estimation in subtropical pine forest, Pakistan. Environ. Monit. Assess. 2020, 192, 584. [Google Scholar] [CrossRef]
- López-Serrano, P.M.; Cárdenas Domínguez, J.L.; Corral-Rivas, J.J.; Jiménez, E.; López-Sánchez, C.A.; Vega-Nieva, D.J. Modeling of Aboveground Biomass with Landsat 8 OLI and Machine Learning in Temperate Forests. Forests 2019, 11, 11. [Google Scholar] [CrossRef]
- Han, H.; Wan, R.; Li, B. Estimating Forest Aboveground Biomass Using Gaofen-1 Images, Sentinel-1 Images, and Machine Learning Algorithms: A Case Study of the Dabie Mountain Region, China. Remote Sens. 2021, 14, 176. [Google Scholar] [CrossRef]
- Hu, Y.; Xu, X.; Wu, F.; Sun, Z.; Xia, H.; Meng, Q.; Huang, W.; Zhou, H.; Gao, J.; Li, W.; et al. Estimating Forest Stock Volume in Hunan Province, China, by Integrating In Situ Plot Data, Sentinel-2 Images, and Linear and Machine Learning Regression Models. Remote Sens. 2020, 12, 186. [Google Scholar] [CrossRef]
- Souza, G.S.A.d.; Soares, V.P.; Leite, H.G.; Gleriani, J.M.; do Amaral, C.H.; Ferraz, A.S.; Silveira, M.V.d.F.; Santos, J.F.C.d.; Velloso, S.G.S.; Domingues, G.F.; et al. Multi-sensor prediction of Eucalyptus stand volume: A support vector approach. ISPRS J. Photogramm. Remote Sens. 2019, 156, 135–146. [Google Scholar] [CrossRef]
- Benmokhtar, S.; Robin, M.; Maanan, M.; Bazairi, H. Mapping and Quantification of the Dwarf Eelgrass Zostera noltei Using a Random Forest Algorithm on a SPOT 7 Satellite Image. ISPRS Int. J. Geo-Inf. 2021, 10, 313. [Google Scholar] [CrossRef]
- Ghosh, S.M.; Behera, M.D. Aboveground biomass estimation using multi-sensor data synergy and machine learning algorithms in a dense tropical forest. Appl. Geogr. 2018, 96, 29–40. [Google Scholar] [CrossRef]
- Singh, C.; Karan, S.K.; Sardar, P.; Samadder, S.R. Remote sensing-based biomass estimation of dry deciduous tropical forest using machine learning and ensemble analysis. J. Environ. Manag. 2022, 308, 114639. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Long, J.; Zhang, M.; Liu, Z.; Lin, H. Coniferous Plantations Growing Stock Volume Estimation Using Advanced Remote Sensing Algorithms and Various Fused Data. Remote Sens. 2021, 13, 3468. [Google Scholar] [CrossRef]
- Englhart, S.; Keuck, V.; Siegert, F. Aboveground biomass retrieval in tropical forests—The potential of combined X- and L-band SAR data use. Remote Sens. Environ. 2011, 115, 1260–1271. [Google Scholar] [CrossRef]
- Long, J.; Lin, H.; Wang, G.; Sun, H.; Yan, E. Mapping Growing Stem Volume of Chinese Fir Plantation Using a Saturation-based Multivariate Method and Quad-polarimetric SAR Images. Remote Sens. 2019, 11, 1872. [Google Scholar] [CrossRef]
- Lu, Z.; Guanglong, O.; Junfeng, W.; Hui, X. Light Saturation Point Determination and Biomass Remote Sensing Estimation of Pinus kesiya var. langbianensis forest based on spatial regression models. Sci. Silvae Sin. 2020, 56, 38–47. [Google Scholar]
- Zhao, P.; Lu, D.; Wang, G.; Wu, C.; Huang, Y.; Yu, S. Examining Spectral Reflectance Saturation in Landsat Imagery and Corresponding Solutions to Improve Forest Aboveground Biomass Estimation. Remote Sens. 2016, 8, 469. [Google Scholar] [CrossRef]
- Zhang, T.; Lin, H.; Long, J.; Zhang, M.; Liu, Z. Analyzing the Saturation of Growing Stem Volume Based on ZY-3 Stereo and Multispectral Images in Planted Coniferous Forest. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 50–61. [Google Scholar] [CrossRef]
- Li, H.; Lei, Y. Assessment of Forest Vegetation Biomass and Carbon Stocks in China; China Forestry Publishing House: Beijing, China, 2010. [Google Scholar]
- Haijun, W.; Feng, L.; Nan, X. Allometric Equation for Biomass of the Main Carbon Sinks Species in Heilongjiang Province. Prot. For. Sci. Technol. 2016, 21–22+53. [Google Scholar] [CrossRef]
- Puliti, S.; Breidenbach, J.; Schumacher, J.; Hauglin, M.; Klingenberg, T.F.; Astrup, R. Above-ground biomass change estimation using national forest inventory data with Sentinel-2 and Landsat. Remote Sens. Environ. 2021, 265, 112644. [Google Scholar] [CrossRef]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I. Textural Features for Image Classification. IEEE Trans. Syst. Man Cybern. 1973, SMC-3, 610–621. [Google Scholar] [CrossRef]
- Chen, L.; Wang, Y.; Ren, C.; Zhang, B.; Wang, Z. Optimal Combination of Predictors and Algorithms for Forest Above-Ground Biomass Mapping from Sentinel and SRTM Data. Remote Sens. 2019, 11, 414. [Google Scholar] [CrossRef]
- Sa, R.; Fan, W. Estimation of Forest Parameters in Boreal Artificial Coniferous Forests Using Landsat 8 and Sentinel-2A. Remote Sens. 2023, 15, 3605. [Google Scholar] [CrossRef]
- Tanase, M.; Panciera, R.; Lowell, K.; Tian, S.; Hacker, J.; Walker, J. Airborne Multi Temporal L-band Polarimetric SAR Data for Biomass Estimation in Semi-Arid Forests. Remote Sens. Environ. 2014, 145, 93–104. [Google Scholar] [CrossRef]
- Chen, A.; Zebker, H. Reducing Ionospheric Effects in InSAR Data Using Accurate Coregistration. IEEE Trans. Geosci. Remote Sens. 2014, 52, 60–70. [Google Scholar] [CrossRef]
- Latrache, H.; Ouarzeddine, M.; Souissi, B. Improved model-based polarimetric decomposition using the PolInSAR similarity parameter. ISPRS—Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, XLI-B7, 847–850. [Google Scholar] [CrossRef]
- Xie, Q.; Wang, J.; Liao, C.; Shang, J.; Lopez-Sanchez, J.; Fu, H.; Liu, X. On the Use of Neumann Decomposition for Crop Classification Using Multi-Temporal RADARSAT-2 Polarimetric SAR Data. Remote Sens. 2019, 11, 776. [Google Scholar] [CrossRef]
- Cui, Y.; Yamaguchi, Y.; Yang, J.; Park, S.-E.; Kobayashi, H.; Singh, G. Three-Component Power Decomposition for Polarimetric SAR Data Based on Adaptive Volume Scatter Modeling. Remote Sens. 2012, 4, 1559–1572. [Google Scholar] [CrossRef]
- Varghese, A.O.; Suryavanshi, A.; Joshi, A.K. Analysis of different polarimetric target decomposition methods in forest density classification using C band SAR data. Int. J. Remote Sens. 2016, 37, 694–709. [Google Scholar] [CrossRef]
- Huynen, J. Phenomenological Theory of Radar Targets. Ph.D. Thesis, TU Delft, Delft, The Netherlands, 1970. [Google Scholar]
- Pope, K.O.; Rey-Benayas, J.M.; Paris, J.F. Radar remote sensing of forest and wetland ecosystems in the Central American tropics. Remote Sens. Environ. 1994, 48, 205–219. [Google Scholar] [CrossRef]
- Mitchard, E.; Saatchi, S.; White, L.; Abernethy, K.; Jeffery, K.; Lewis, S.; Collins, M.; Lefsky, M.A.; Leal, M.; Woodhouse, I.; et al. Mapping tropical forest biomass with radar and spaceborne LiDAR: Overcoming problems of high biomass and persistent cloud. Biogeosci. Discuss. 2011, 8, 8781–8815. [Google Scholar] [CrossRef]
- Sa, R.; Nei, Y.; Fan, W. Combining Multi-Dimensional SAR Parameters to Improve RVoG Model for Coniferous Forest Height Inversion Using ALOS-2 Data. Remote Sens. 2023, 15, 1272. [Google Scholar] [CrossRef]
- Li, Z.; Chen, Z.; Cheng, Q.; Duan, F.; Sui, R.; Huang, X.; Xu, H. UAV-Based Hyperspectral and Ensemble Machine Learning for Predicting Yield in Winter Wheat. Agronomy 2022, 12, 202. [Google Scholar] [CrossRef]
- Wang, P.; Tan, S.; Zhang, G.; Wang, S.; Wu, X. Remote Sensing Estimation of Forest Aboveground Biomass Based on Lasso-SVR. Forests 2022, 13, 1597. [Google Scholar] [CrossRef]
- Jiang, F.; Kutia, M.; Sarkissian, A.J.; Lin, H.; Long, J.; Sun, H.; Wang, G. Estimating the Growing Stem Volume of Coniferous Plantations Based on Random Forest Using an Optimized Variable Selection Method. Sensors 2020, 20, 7248. [Google Scholar] [CrossRef] [PubMed]
- Lin, W.; Lu, Y.; Li, G.; Jiang, X.; Lu, D. A comparative analysis of modeling approaches and canopy height-based data sources for mapping forest growing stock volume in a northern subtropical ecosystem of China. GIScience Remote Sens. 2022, 59, 568–589. [Google Scholar] [CrossRef]
- Wu, C.; Shen, H.; Wang, K.; Shen, A.; Deng, J.; Gan, M. Landsat Imagery-Based above Ground Biomass Estimation and Change Investigation Related to Human Activities. Sustainability 2016, 8, 159. [Google Scholar] [CrossRef]
- Su, H.; Shen, W.; Wang, J.; Ali, A.; Li, M. Machine learning and geostatistical approaches for estimating aboveground biomass in Chinese subtropical forests. For. Ecosyst. 2020, 7, 64. [Google Scholar] [CrossRef]
- Liu, K.; Wang, J.; Zeng, W.; Song, J. Comparison and Evaluation of Three Methods for Estimating Forest above Ground Biomass Using TM and GLAS Data. Remote Sens. 2017, 9, 341. [Google Scholar] [CrossRef]
- Nasiri, V.; Darvishsefat, A.A.; Arefi, H.; Griess, V.C.; Sadeghi, S.M.; Borz, S.A. Modeling Forest Canopy Cover: A Synergistic Use of Sentinel-2, Aerial Photogrammetry Data, and Machine Learning. Remote Sens. 2022, 14, 1453. [Google Scholar] [CrossRef]
- Chen, Y.; Ma, L.; Yu, D.; Feng, K.; Wang, X.; Song, J. Improving Leaf Area Index Retrieval Using Multi-Sensor Images and Stacking Learning in Subtropical Forests of China. Remote Sens. 2022, 14, 148. [Google Scholar] [CrossRef]
- Halme, E.; Pellikka, P.; Mõttus, M. Utility of hyperspectral compared to multispectral remote sensing data in estimating forest biomass and structure variables in Finnish boreal forest. Int. J. Appl. Earth Obs. Geoinf. 2019, 83, 101942. [Google Scholar] [CrossRef]
- Tuong, T.; Tani, H.; Wang, X.; Thang, N.; Bui, H. Combination of SAR Polarimetric Parameters for Estimating Tropical Forest Aboveground Biomass. Pol. J. Environ. Stud. 2020, 29, 3353–3365. [Google Scholar] [CrossRef]
- Peng, X.; Zhao, A.; Chen, Y.; Chen, Q.; Liu, H.; Wang, J.; Li, H. Comparison of Modeling Algorithms for Forest Canopy Structures Based on UAV-LiDAR: A Case Study in Tropical China. Forests 2020, 11, 1324. [Google Scholar] [CrossRef]
- Meng, S.; Pang, Y.; Zhang, Z.; Jia, W.; Li, Z. Mapping Aboveground Biomass using Texture Indices from Aerial Photos in a Temperate Forest of Northeastern China. Remote Sens. 2016, 8, 230. [Google Scholar] [CrossRef]
- Iizuka, K.; Hayakawa, Y.S.; Ogura, T.; Nakata, Y.; Kosugi, Y.; Yonehara, T. Integration of Multi-Sensor Data to Estimate Plot-Level Stem Volume Using Machine Learning Algorithms–Case Study of Evergreen Conifer Planted Forests in Japan. Remote Sens. 2020, 12, 1649. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, M. Evaluation and Comparison of Different Machine Learning Models for NSAT Retrieval from Various Multispectral Satellite Images. Atmosphere 2022, 13, 1429. [Google Scholar] [CrossRef]
- Ta, N.; Chang, Q.; Zhang, Y. Estimation of Apple Tree Leaf Chlorophyll Content Based on Machine Learning Methods. Remote Sens. 2021, 13, 3902. [Google Scholar] [CrossRef]
- Gao, Y.; Lu, D.; Li, G.; Wang, G.; Chen, Q.; Liu, L.; Li, D. Comparative Analysis of Modeling Algorithms for Forest Aboveground Biomass Estimation in a Subtropical Region. Remote Sens. 2018, 10, 627. [Google Scholar] [CrossRef]
- dos Reis, A.A.; Carvalho, M.C.; de Mello, J.M.; Gomide, L.R.; Ferraz Filho, A.C.; Acerbi Junior, F.W. Spatial prediction of basal area and volume in Eucalyptus stands using Landsat TM data: An assessment of prediction methods. N. Z. J. For. Sci. 2018, 48, 1. [Google Scholar] [CrossRef]
- Dong, L.; Tang, S.; Min, M.; Veroustraete, F.; Cheng, J. Aboveground forest biomass based on OLSR and an ANN model integrating LiDAR and optical data in a mountainous region of China. Int. J. Remote Sens. 2019, 40, 6059–6083. [Google Scholar] [CrossRef]
- Sibanda, M.; Mutanga, O.; Rouget, M.; Kumar, L. Estimating Biomass of Native Grass Grown under Complex Management Treatments Using WorldView-3 Spectral Derivatives. Remote Sens. 2017, 9, 55. [Google Scholar] [CrossRef]
- Jiang, F.; Sun, H.; Chen, E.; Wang, T.; Cao, Y.; Liu, Q. Above-Ground Biomass Estimation for Coniferous Forests in Northern China Using Regression Kriging and Landsat 9 Images. Remote Sens. 2022, 14, 5734. [Google Scholar] [CrossRef]
- Lin, C.; Daoli, P.; Xuejun, W.; Xinyun, C. Estimation of Forest Stock Volume With Spectral and Textural Information from the Sentinel-2A. J. Northeast For. Univ. 2018, 46, 54–58. [Google Scholar] [CrossRef]
- Bolívar-Santamaría, S.; Reu, B. Detection and characterization of agroforestry systems in the Colombian Andes using sentinel-2 imagery. Agrofor. Syst. 2021, 95, 499–514. [Google Scholar] [CrossRef]
- Waqar, M.M.; Sukmawati, R.; Ji, Y.; Sri Sumantyo, J.T. Tropical PeatLand Forest Biomass Estimation Using Polarimetric Parameters Extracted from RadarSAT-2 Images. Land 2020, 9, 193. [Google Scholar] [CrossRef]
- Liang, Y.; Kou, W.; Lai, H.; Wang, J.; Wang, Q.; Xu, W.; Wang, H.; Lu, N. Improved estimation of aboveground biomass in rubber plantations by fusing spectral and textural information from UAV-based RGB imagery. Ecol. Indic. 2022, 142, 109286. [Google Scholar] [CrossRef]
- Ge, J.; Hou, M.; Liang, T.; Feng, Q.; Meng, X.; Liu, J.; Bao, X.; Gao, H. Spatiotemporal dynamics of grassland aboveground biomass and its driving factors in North China over the past 20 years. Sci. Total Environ. 2022, 826, 154226. [Google Scholar] [CrossRef] [PubMed]
- Mao, H.; Meng, J.; Ji, F.; Zhang, Q.; Fang, H. Comparison of Machine Learning Regression Algorithms for Cotton Leaf Area Index Retrieval Using Sentinel-2 Spectral Bands. Appl. Sci. 2019, 9, 1459. [Google Scholar] [CrossRef]
- Sa, R.; Fan, W. Forest Structure Mapping of Boreal Coniferous Forests Using Multi-Source Remote Sensing Data. Remote Sens. 2024, 16, 1844. [Google Scholar] [CrossRef]
- Thapa, R.; Watanabe, M.; Motohka, T.; Shimada, M. Potential of high-resolution ALOS–PALSAR mosaic texture for aboveground forest carbon tracking in tropical region. Remote Sens. Environ. 2015, 160, 122–133. [Google Scholar] [CrossRef]
- Sarker, M.; Nichol, J.; Iz, H.; Ahmad, B.B.; Rahman, A. Forest Biomass Estimation Using Texture Measurements of High-Resolution Dual-Polarization C-Band SAR Data. IEEE Trans. Geosci. Remote Sens. 2013, 51, 3371–3384. [Google Scholar] [CrossRef]
- Zhang, C.; Huang, C.; Li, H.; Liu, Q.; Li, J.; Bridhikitti, A.; Liu, G. Effect of Textural Features in Remote Sensed Data on Rubber Plantation Extraction at Different Levels of Spatial Resolution. Forests 2020, 11, 399. [Google Scholar] [CrossRef]
- Ahmadi, K.; Kalantar, B.; Saeidi, V.; Harandi, E.K.G.; Janizadeh, S.; Ueda, N. Comparison of Machine Learning Methods for Mapping the Stand Characteristics of Temperate Forests Using Multi-Spectral Sentinel-2 Data. Remote Sens. 2020, 12, 3019. [Google Scholar] [CrossRef]
- Sibanda, M.; Mutanga, O.; Rouget, M. Examining the potential of Sentinel-2 MSI spectral resolution in quantifying above ground biomass across different fertilizer treatments. ISPRS J. Photogramm. Remote Sens. 2015, 110, 55–65. [Google Scholar] [CrossRef]
- Astola, H.; Häme, T.; Sirro, L.; Molinier, M.; Kilpi, J. Comparison of Sentinel-2 and Landsat 8 imagery for forest variable prediction in boreal region. Remote Sens. Environ. 2019, 223, 257–273. [Google Scholar] [CrossRef]
- Naik, P.; Dalponte, M.; Bruzzone, L. Prediction of Forest Aboveground Biomass Using Multitemporal Multispectral Remote Sensing Data. Remote Sens. 2021, 13, 1282. [Google Scholar] [CrossRef]
- Li, Y.; Li, C.; Li, M.; Liu, Z. Influence of Variable Selection and Forest Type on Forest Aboveground Biomass Estimation Using Machine Learning Algorithms. Forests 2019, 10, 1073. [Google Scholar] [CrossRef]
- Ou, G.; Li, C.; Lv, Y.; Wei, A.; Xiong, H.; Xu, H.; Wang, G. Improving Aboveground Biomass Estimation of Pinus densata Forests in Yunnan Using Landsat 8 Imagery by Incorporating Age Dummy Variable and Method Comparison. Remote Sens. 2019, 11, 738. [Google Scholar] [CrossRef]
- Li, X.; Ye, Z.; Long, J.; Zheng, H.; Lin, H. Inversion of Coniferous Forest Stock Volume Based on Backscatter and InSAR Coherence Factors of Sentinel-1 Hyper-Temporal Images and Spectral Variables of Landsat 8 OLI. Remote Sens. 2022, 14, 2754. [Google Scholar] [CrossRef]
- Liang, L.; Di, L.; Huang, T.; Wang, J.; Lin, L.; Wang, L.; Yang, M. Estimation of Leaf Nitrogen Content in Wheat Using New Hyperspectral Indices and a Random Forest Regression Algorithm. Remote Sens. 2018, 10, 1940. [Google Scholar] [CrossRef]
- Chen, Y.; Li, L.; Lu, D.; Li, D. Exploring Bamboo Forest Aboveground Biomass Estimation Using Sentinel-2 Data. Remote Sens. 2018, 11, 7. [Google Scholar] [CrossRef]
- Hu, T.; Sun, Y.; Jia, W.; Li, D.; Zou, M.; Zhang, M. Study on the Estimation of Forest Volume Based on Multi-Source Data. Sensors 2021, 21, 7796. [Google Scholar] [CrossRef]
- Hu, Y.; Sun, Z. Assessing the Capacities of Different Remote Sensors in Estimating Forest Stock Volume Based on High Precision Sample Plot Positioning and Random Forest Method. Nat. Environ. Pollut. Technol. 2022, 21, 1113–1123. [Google Scholar] [CrossRef]
- Wang, L.a.; Zhou, X.; Zhu, X.; Dong, Z.; Guo, W. Estimation of biomass in wheat using random forest regression algorithm and remote sensing data. Crop J. 2016, 4, 212–219. [Google Scholar] [CrossRef]
- Zhang, C.; Denka, S.; Cooper, H.; Mishra, D.R. Quantification of sawgrass marsh aboveground biomass in the coastal Everglades using object-based ensemble analysis and Landsat data. Remote Sens. Environ. 2017, 204, 366–379. [Google Scholar] [CrossRef]
- Ku, N.-W.; Popescu, S. A comparison of multiple methods for mapping local-scale mesquite tree aboveground biomass with remotely sensed data. Biomass Bioenergy 2019, 122, 270–279. [Google Scholar] [CrossRef]
- Zandler, H.; Brenning, A.; Samimi, C. Quantifying dwarf shrub biomass in an arid environment: Comparing empirical methods in a high dimensional setting. Remote Sens. Environ. Interdiscip. J. 2015, 158, 140–155. [Google Scholar] [CrossRef]
- Feng, Y.; Lu, D.; Chen, Q.; Keller, M.; Moran, E.; dos-Santos, M.N.; Bolfe, E.L.; Batistella, M. Examining effective use of data sources and modeling algorithms for improving biomass estimation in a moist tropical forest of the Brazilian Amazon. Int. J. Digit. Earth 2017, 10, 996–1016. [Google Scholar] [CrossRef]
- Li, X.; Liu, Z.; Lin, H.; Wang, G.; Sun, H.; Long, J.; Zhang, M. Estimating the Growing Stem Volume of Chinese Pine and Larch Plantations based on Fused Optical Data Using an Improved Variable Screening Method and Stacking Algorithm. Remote Sens. 2020, 12, 871. [Google Scholar] [CrossRef]
- Zhao, P. Aboveground Forest Biomass Estimation Based on Landsat TM and ALOS PALSAR Data. Master’s Thesis, Zhejiang Agriculture Forestry University, Hangzhou, China, 2017. [Google Scholar]
- Chunyu, D. Estimation of Forest Aboveground Biomass and Determination of its Saturation Values Based on Passive and Active Data. Ph.D. Thesis, Northeast Forestry University, Harbin, China, 2023. [Google Scholar]
- Lin, H.; Zhao, W.; Long, J.; Liu, Z.; Yang, P.; Zhang, T.; Ye, Z.; Wang, Q.; Matinfar, H.R. Mapping Forest Growing Stem Volume Using Novel Feature Evaluation Criteria Based on Spectral Saturation in Planted Chinese Fir Forest. Remote Sens. 2023, 15, 402. [Google Scholar] [CrossRef]
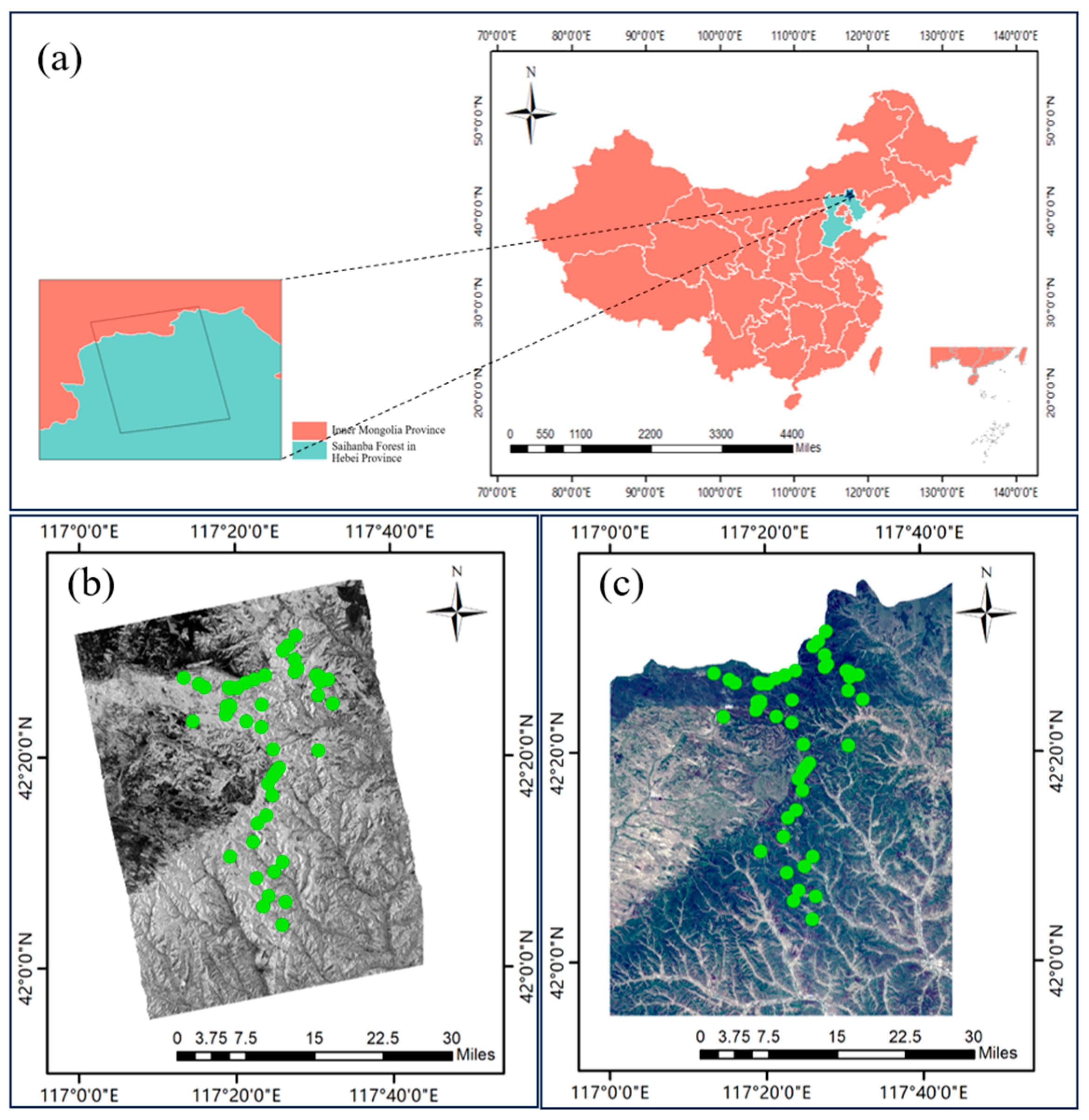
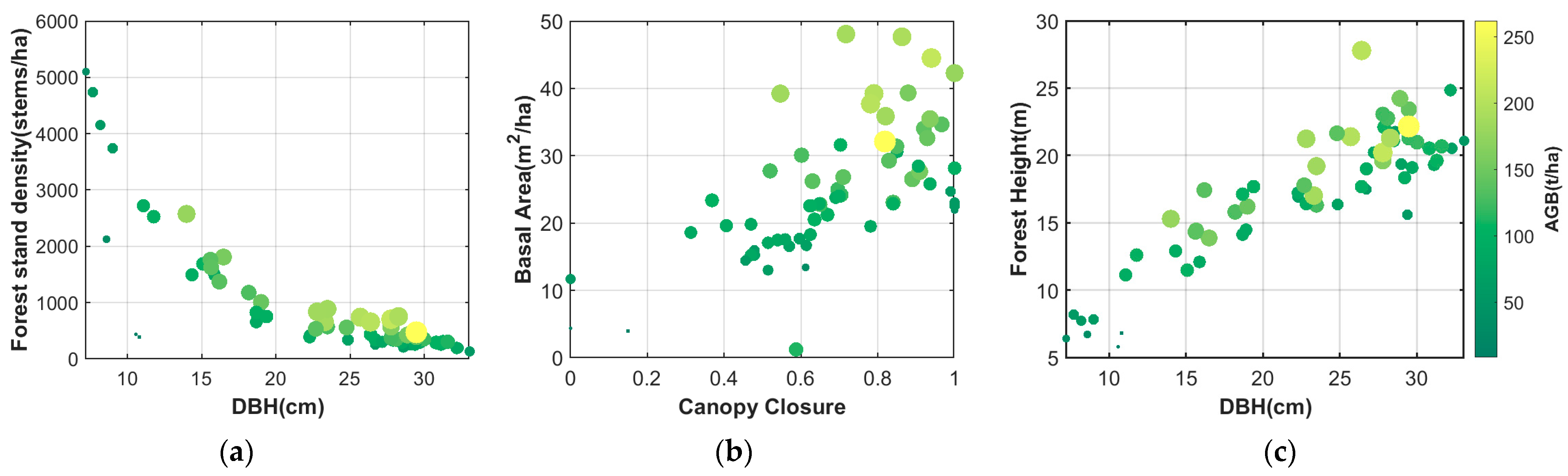


| Parameter | Max | Min | Mean | STD |
|---|---|---|---|---|
| Canopy closure (%) | 1 | 0.15 | 0.7 | 0.196 |
| Mean forest height (m) | 27.8 | 5.81 | 17.3 | 4.88 |
| Mean DBH (cm) | 33.1 | 7.2 | 22.74 | 7.3 |
| Basal area (/ha) | 48 | 1.2 | 24.7 | 9.7 |
| Forest stand density (stems/ha) | 5100 | 133 | 960 | 1083 |
| AGB (t/ha) | 228.64 | 12.27 | 90.6 | 35.75 |
| Tree Species | Academic Name | Allometric Equation |
|---|---|---|
| Larch | Larix gmelinii (Rupr.) Kuzen. | |
| Sphagnum pine | Pinus sylvestris var. mongholica Litv. | |
| Spruce | Picea asperata Mast. |
| Sensor | Time | Spatial Resolution (m) |
|---|---|---|
| Landsat 8 | 16 June 2020 | 30 |
| Sentinel-2A | 21 June 2020 | 10, 20 |
| Variables | Name |
|---|---|
| Band | S2A: B2, B3, B4, B5, B6, B7, B8, B8A, B11, B12; L8: B2, B3, B4, B5, B6, B7 |
| Texture | contrast, dissimilarity, homogeneity, second moment, entropy, mean, variance, correlation |
| Biophysical parameter | fractional vegetation cover (FVC), leaf area index (LAI), chlorophyll content in the leaf (Cab), canopy water content (Cwc) |
| Horizontal structure index | ratio vegetation index (RVI): RVI_CC, RVI_S, RVI_BA; |
| corresponding texture index (CTI): CTI_CC, CTI_S, CTI_BA; | |
| mean texture index (MTI): MTI_CC, MTI_S, MTI_BA; | |
| principal component texture Index (PTI): PTI_CC, PTI_S, PTI_BA |
| Parameter | |
|---|---|
| Data Level | HBQR1.1 |
| Imaging Date | 0711, 0725, 0808, 0905, 0919 |
| Polarization Channel | Full polarization (HH, HV, VH, VV) |
| Variables | Name |
|---|---|
| Backscattering coefficient | HH, HV, VH, VV |
| Polarization decomposition variable | odd scattering (S), double scattering (D), volume scattering (V), M1, M2 |
| Polarization decomposition parameter | nine parameters of the coherence matrix , where the real and imag parts were extracted separately |
| SAR index | canopy structure index (CSI), biomass index (BMI), volume scattering index (VSI), radar forest degradation index (RFDI), radar vegetation index (RVI) |
| Vertical structure index | 0711-0725H, 0725-0808H, 0905-0919H, 0725-0905H, 0808-0919H, 0711-0919H |
| Variables | Pearson Correlation Coefficient | Random Forest Importance | LASSO |
|---|---|---|---|
| Band | S2A: B2, B3, B4, B5, B6, B7, B8, B8A, B11, B12; L8: B5, B6, B7 | S2A: B2, B3, B5, B11, B12; L8: B5 | S2A: B3, B6, B11 |
| Biophysical parameter | L8: Cwc | / | S2: FVC |
| Horizontal structure index | RVI_BA, CTI_CC, CTI_S, CTI_BA, MTI_CC, MTI_S, MTI_BA, PTI_CC, PTI_BA | RVI_BA, CTI_CC, CTI_BA, MTI_BA, PTI_CC, PTI_BA | MTI_BA, PTI_CC, PTI_BA |
| Polarization decomposition variable | / | 0919: VM2 | 0711: FD; 0905: FD |
| Polarization decomposition parameter | 0725: T23_imag; 0808: T13_imag | 0808: T12_imag | 0905: T11, 0905: T23_imag |
| SAR index | / | 0808: CSI | 0725: CSI; 0808: VSI; 0919: VSI; 0919: RVI |
| Vertical structure index | 0711-0725H, 0725-0808H, 0905-0919H, 0725-0905H, 0808-0919H, 0711-0919H | 0711-0725H, 0725-0808H, 0905-0919H, 0725-0905H, 0711-0919H | 0725-0808H; 0905-0919H |
| Optimal Parameter | ML | ||
|---|---|---|---|
| Variables | RF (nTree = 500; nLeaf = 5) | SVR (Kernel = Radial) | ANN |
| V1 | mtry = 2 | C = 4; epsilon = 0.5; gamma = 0.08 | size = 4; decay = 0.01 |
| V2 | mtry = 4 | C = 4; epsilon 0; gamma = 0.17 | size = 3; decay = 0.01 |
| V3 | mtry = 3 | C = 4; epsilon 0; gamma = 0.06 | size = 6; decay = 0.01 |
| V4 | mtry = 4 | C = 4; epsilon 0; gamma = 0.05 | size = 5; decay = 0.01 |
| V5 | mtry = 5 | C = 4; epsilon 0; gamma = 0.03 | size = 6; decay = 0.01 |
| V6 | mtry = 3 | C = 4; epsilon 0; gamma = 0.05 | size = 5; decay = 0.01 |
| V7 | mtry = 3 | C = 4; epsilon 0; gamma = 0.05 | size = 14; decay = 0.01 |
| Variables | ML | Training Set Results | Test Set Results | ||
|---|---|---|---|---|---|
| RMSE | RMSE | ||||
| V1 | RF | 0.8017 | 14.9343 | 0.8332 | 14.3347 |
| SVR | 0.7630 | 15.7717 | 0.7811 | 13.2919 | |
| ANN | 0.6799 | 19.8974 | 0.7925 | 19.9652 | |
| V2 | RF | 0.6439 | 13.3642 | 0.4903 | 15.5579 |
| SVR | 0.7620 | 16.2804 | 0.6843 | 19.3009 | |
| ANN | 0.2669 | 15.9620 | 0.4222 | 17.9815 | |
| V3 | RF | 0.8674 | 12.1673 | 0.8645 | 14.2202 |
| SVR | 0.9585 | 8.9679 | 0.6025 | 21.8577 | |
| ANN | 0.7948 | 16.9127 | 0.7527 | 24.4403 | |
| V4 | RF | 0.8867 | 11.2780 | 0.8799 | 13.4761 |
| SVR | 0.9946 | 3.4059 | 0.8430 | 19.7249 | |
| ANN | 0.8353 | 15.4998 | 0.8113 | 24.2102 | |
| V5 | RF | 0.8706 | 12.6997 | 0.7043 | 18.8707 |
| SVR | 0.9816 | 6.1878 | 0.7003 | 25.5541 | |
| ANN | 0.8366 | 15.6544 | 0.7781 | 23.8184 | |
| V6 | RF | 0.8566 | 13.3741 | 0.7069 | 19.2561 |
| SVR | 0.9871 | 4.9311 | 0.7045 | 19.4594 | |
| ANN | 0.8331 | 15.8408 | 0.7537 | 23.9855 | |
| V7 | RF | 0.8826 | 11.9030 | 0.8029 | 15.0062 |
| SVR | 0.9998 | 0.7376 | 0.8792 | 12.5204 | |
| ANN | 0.8917 | 13.1424 | 0.7065 | 34.5550 | |
| Variables | BS(t/ha) | Variables | BS (t/ha) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| RVI_CC | 0.47 | 0.06 | 188.03 | 0.05 | PTI_S | 0.10 | 0.17 | 171.99 | 0.02 |
| RVI_S | 0.04 | 0.00 | 140.63 | 0.20 | PTI_BA | 3.42 | 5.27 | 263.12 | 0.51 |
| RVI_BA | 0.34 | 0.10 | 212.03 | 0.34 | 0711-0725H | 5.88 | 12.16 | 164.79 | 0.14 |
| CTI_CC | 0.45 | 0.16 | 171.30 | 0.13 | 0711-0919H | 6.91 | 11.38 | 173.00 | 0.15 |
| CTI_S | 0.76 | 0.16 | 181.91 | 0.09 | 0725-0808H | 8.98 | 13.34 | 200.30 | 0.25 |
| CTI_BA | 0.65 | 0.35 | 210.27 | 0.46 | 0725-0905H | 8.71 | 9.76 | 193.59 | 0.19 |
| MTI_CC | 0.19 | 0.07 | 178.29 | 0.16 | 0808-0919H | 6.05 | 8.32 | 195.36 | 0.10 |
| MTI_S | 0.13 | 0.14 | 185.43 | 0.09 | 0905-0919H | 10.37 | 14.32 | 278.03 | 0.18 |
| MTI_BA | 0.33 | 0.21 | 211.58 | 0.49 | S2_B11 | 0.19 | 0.09 | 186.47 | 0.35 |
| PTI_CC | 21.05 | 22.16 | 200.00 | 0.32 |
| Variables | ML | BS (t/ha) | Variables | ML | BS (t/ha) | ||||
|---|---|---|---|---|---|---|---|---|---|
| V1 | RF | 0.25 | 0.14 | 148.16 | V5 | RF | 0.27 | 0.16 | 146.08 |
| SVR | 0.28 | 0.17 | 151.51 | SVR | 0.22 | 0.12 | 169.41 | ||
| ANN | 0.21 | 0.10 | 156.93 | ANN | 0.21 | 0.11 | 162.49 | ||
| V2 | RF | 0.27 | 0.15 | 135.71 | V6 | RF | 0.27 | 0.16 | 143.88 |
| SVR | 0.22 | 0.10 | 157.04 | SVR | 0.22 | 0.12 | 168.35 | ||
| ANN | 0.33 | 0.21 | 109.21 | ANN | 0.22 | 0.11 | 156.66 | ||
| V3 | RF | 0.27 | 0.16 | 142.77 | V7 | RF | 0.27 | 0.17 | 146.17 |
| SVR | 0.22 | 0.11 | 158.58 | SVR | 0.21 | 0.10 | 185.73 | ||
| ANN | 0.20 | 0.09 | 159.94 | ANN | 0.20 | 0.09 | 165.03 | ||
| V4 | RF | 0.27 | 0.16 | 143.33 | |||||
| SVR | 0.21 | 0.10 | 174.11 | ||||||
| ANN | 0.21 | 0.10 | 162.74 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sa, R.; Nie, Y.; Chumachenko, S.; Fan, W. Biomass Estimation and Saturation Value Determination Based on Multi-Source Remote Sensing Data. Remote Sens. 2024, 16, 2250. https://doi.org/10.3390/rs16122250
Sa R, Nie Y, Chumachenko S, Fan W. Biomass Estimation and Saturation Value Determination Based on Multi-Source Remote Sensing Data. Remote Sensing. 2024; 16(12):2250. https://doi.org/10.3390/rs16122250
Chicago/Turabian StyleSa, Rula, Yonghui Nie, Sergey Chumachenko, and Wenyi Fan. 2024. "Biomass Estimation and Saturation Value Determination Based on Multi-Source Remote Sensing Data" Remote Sensing 16, no. 12: 2250. https://doi.org/10.3390/rs16122250
APA StyleSa, R., Nie, Y., Chumachenko, S., & Fan, W. (2024). Biomass Estimation and Saturation Value Determination Based on Multi-Source Remote Sensing Data. Remote Sensing, 16(12), 2250. https://doi.org/10.3390/rs16122250







