From Dawn to Dusk: High-Resolution Tree Shading Model Based on Terrestrial LiDAR Data
Abstract
1. Introduction
2. Materials and Methods
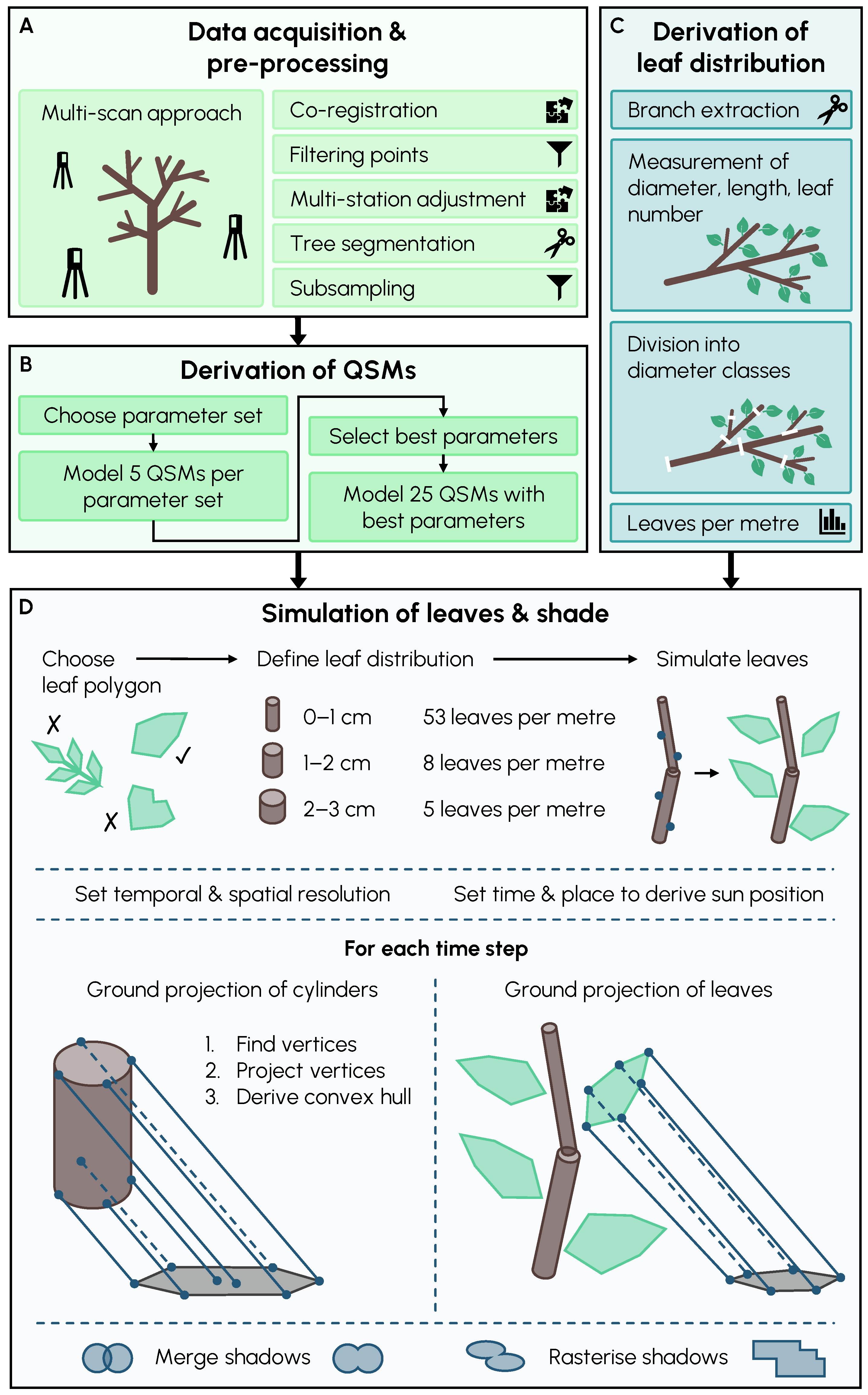
2.1. Simulation Workflow
2.1.1. Data Preparation
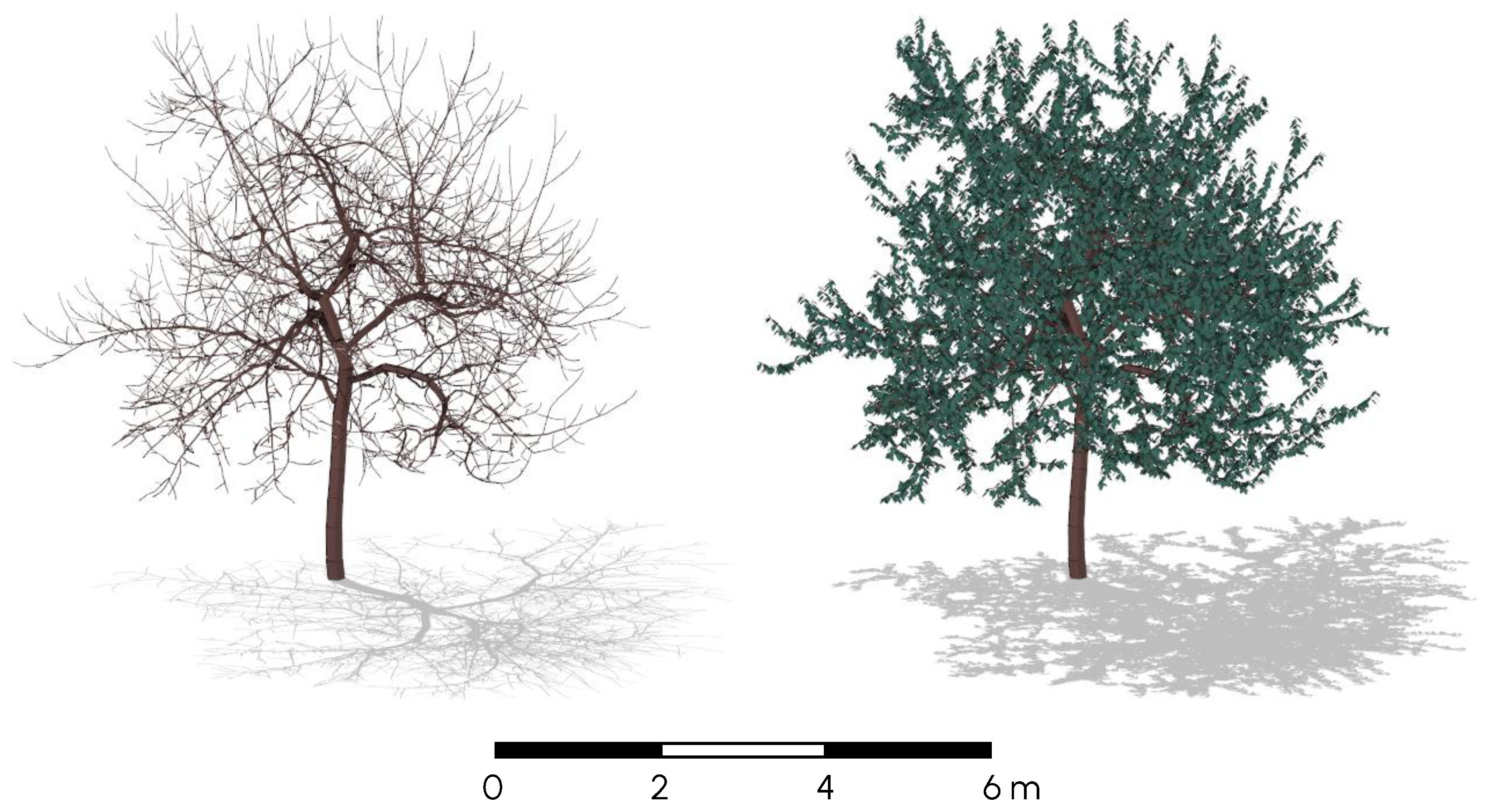
2.1.2. Simulating Leaves and Shade
2.2. Model Validation
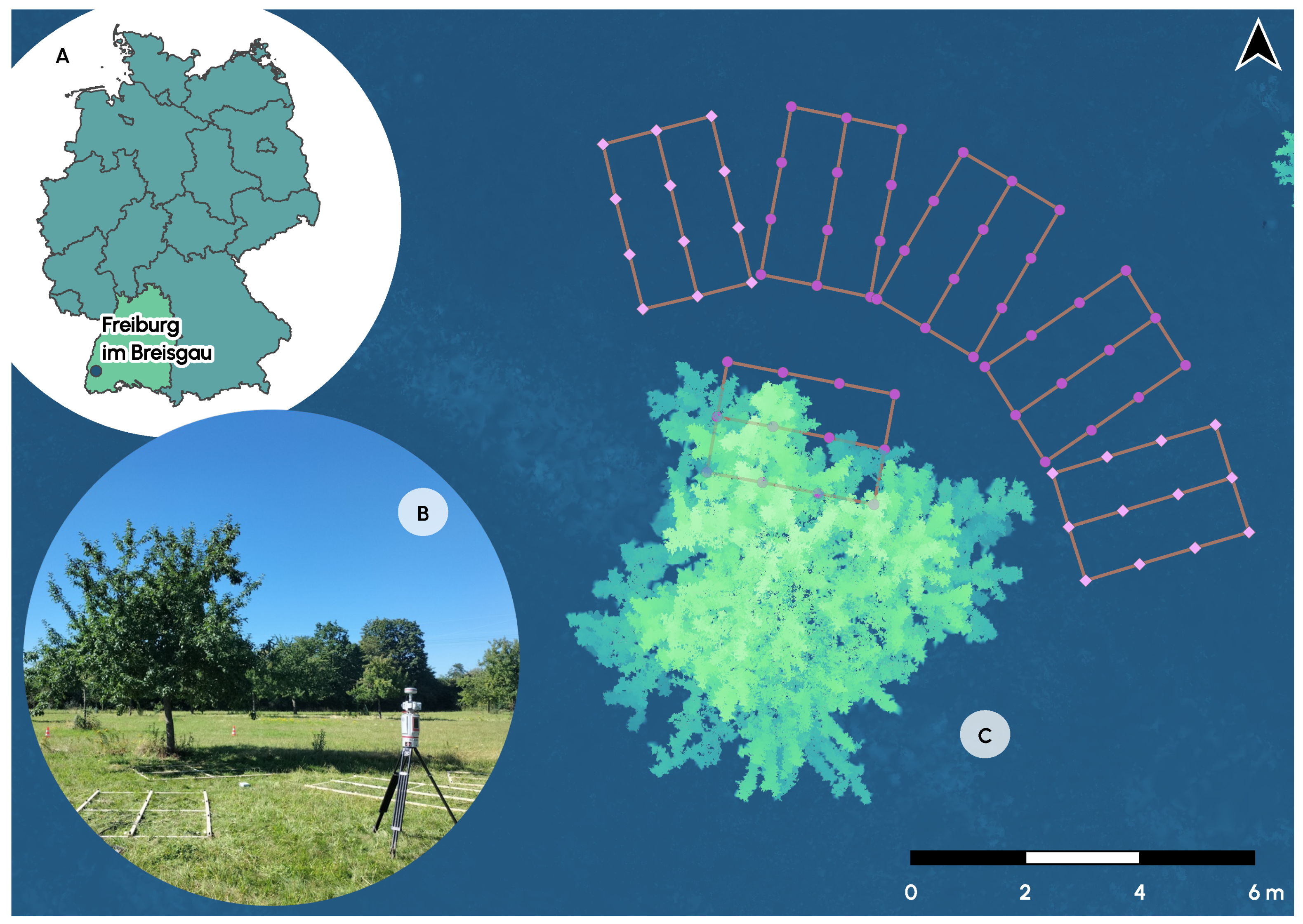
2.2.1. Study Site
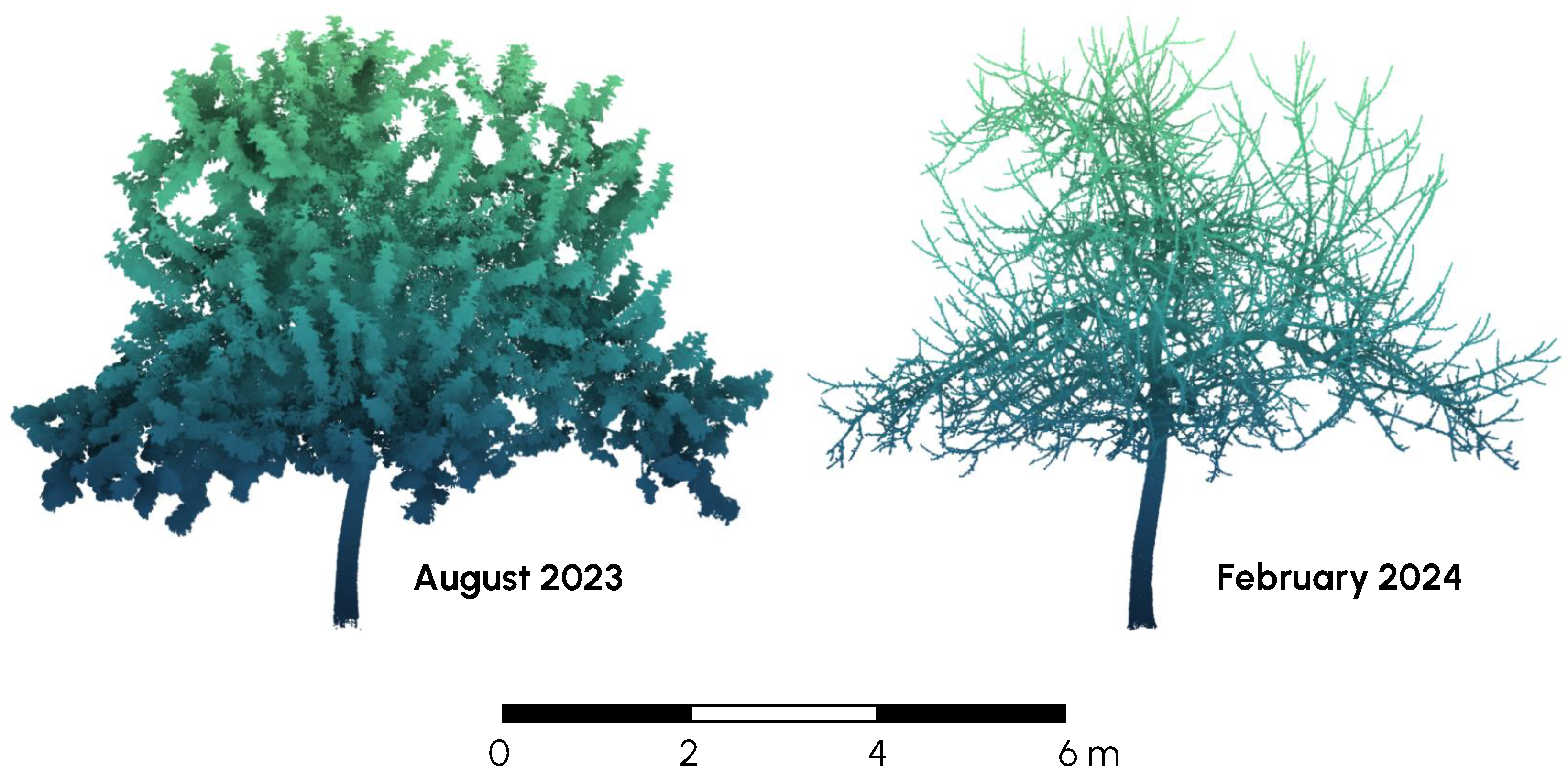
2.2.2. Terrestrial Laser Scanning
2.2.3. Quantitative Structure Models
2.2.4. Simulating Leaves and Shade
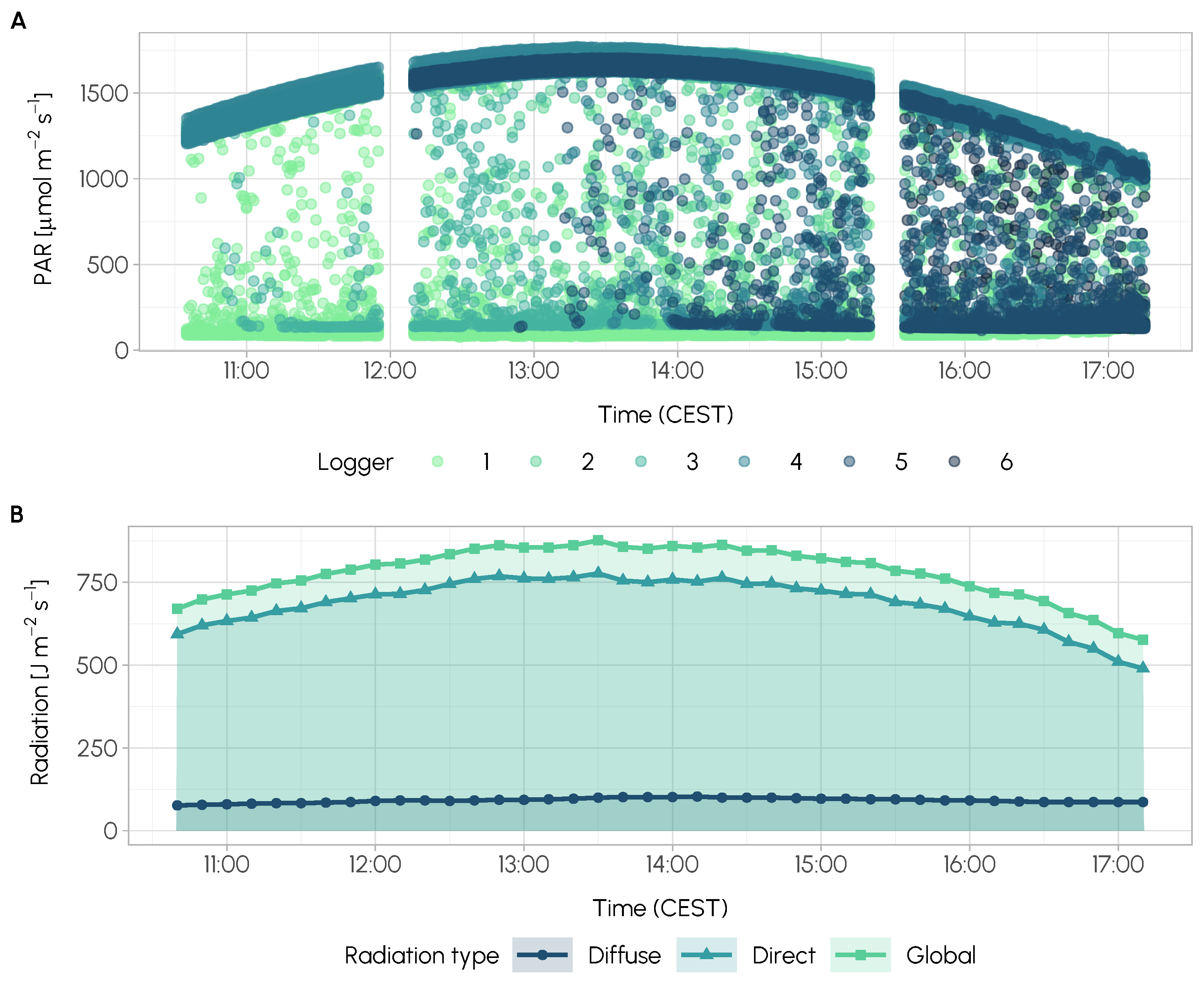
2.2.5. Light Measurements
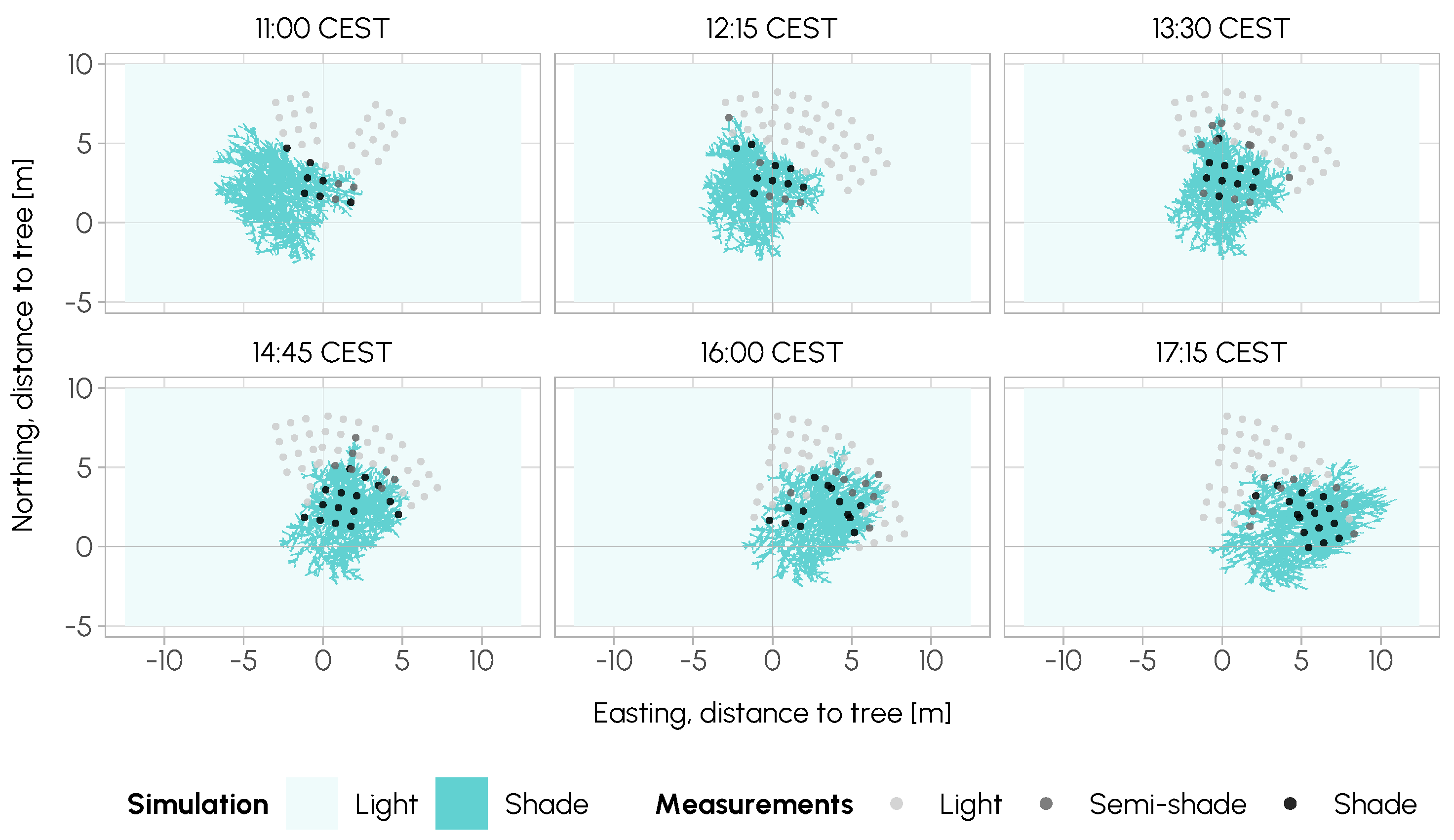
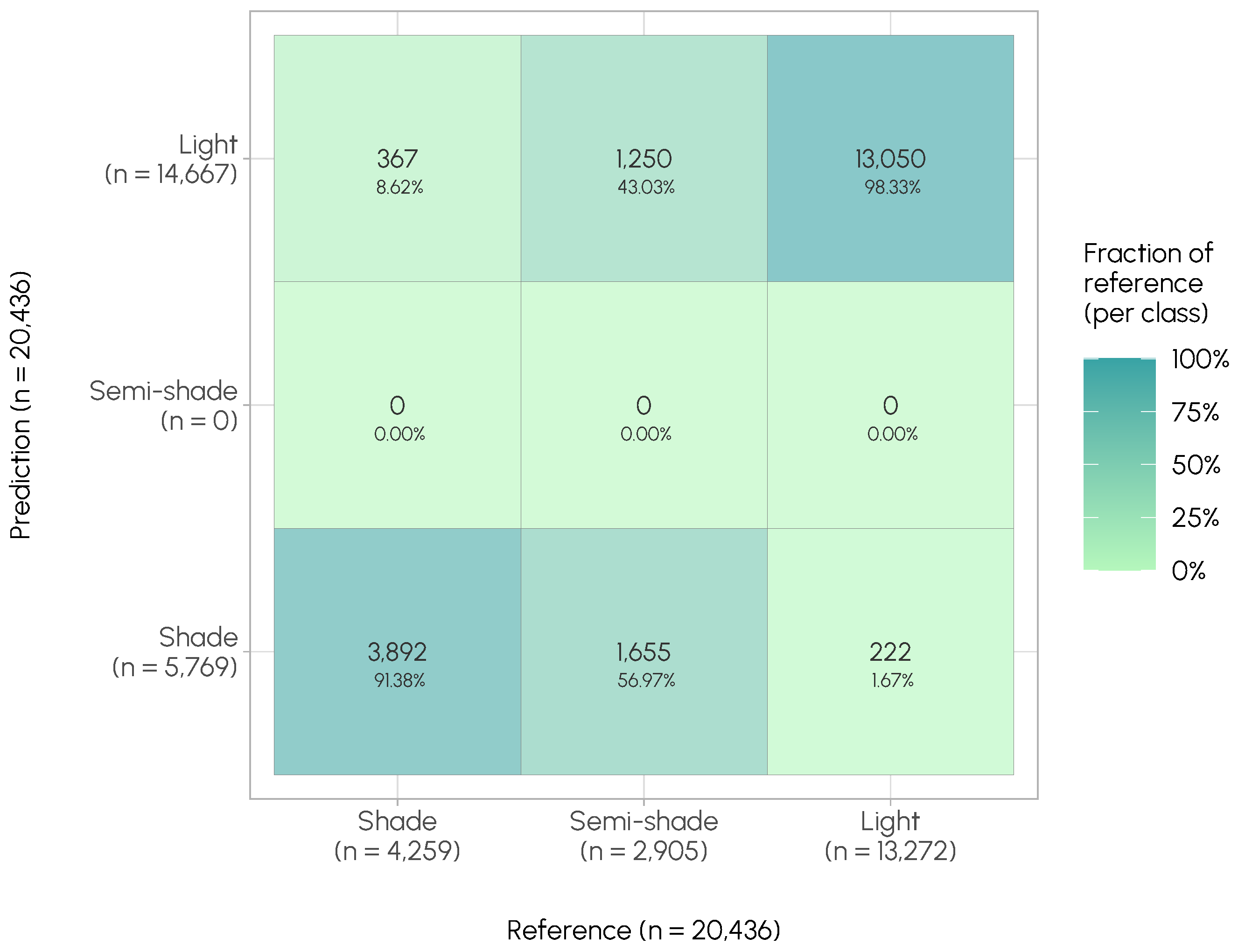
2.2.6. Simulation vs. Measurements
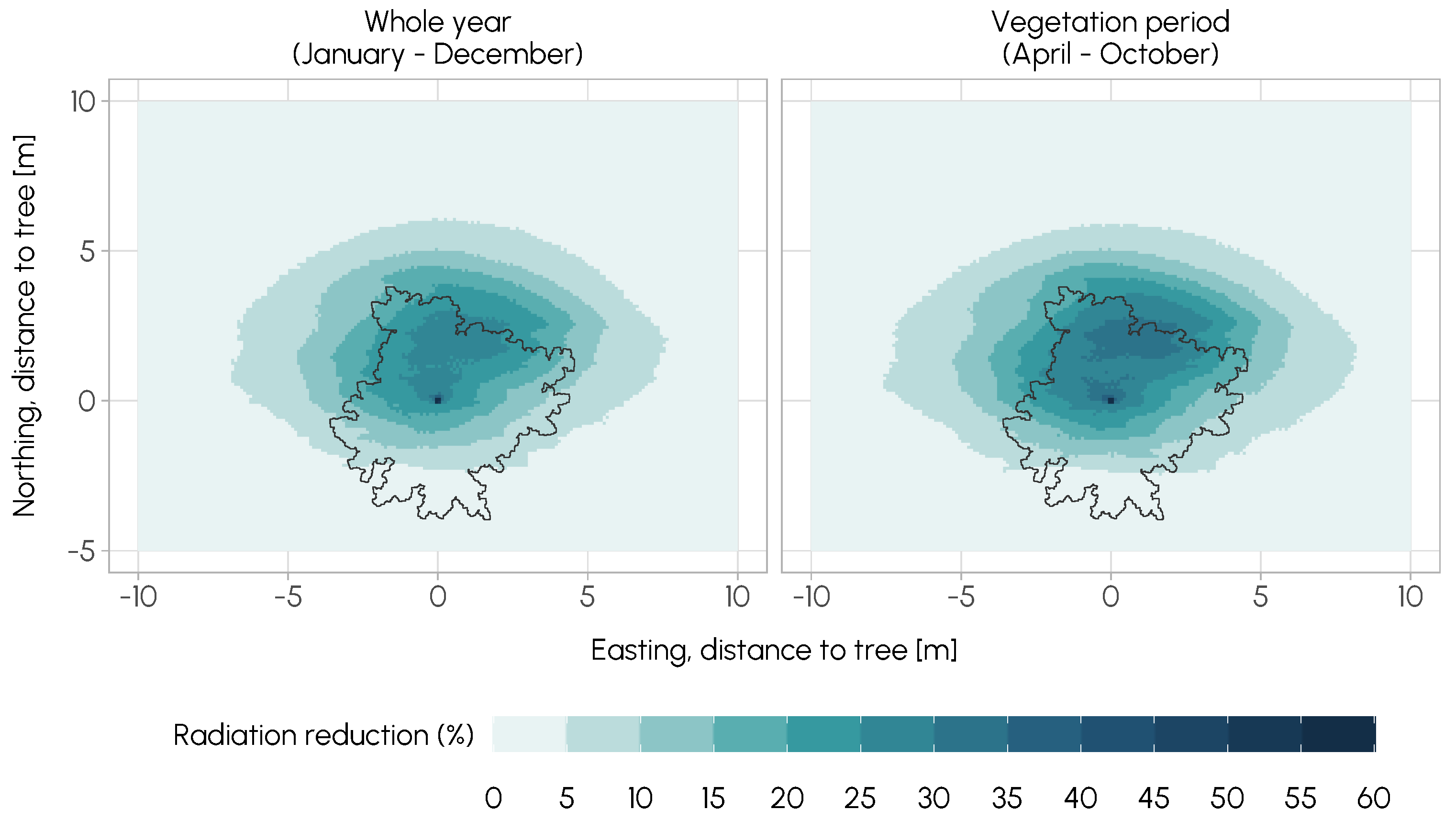
2.3. Example Application
3. Results
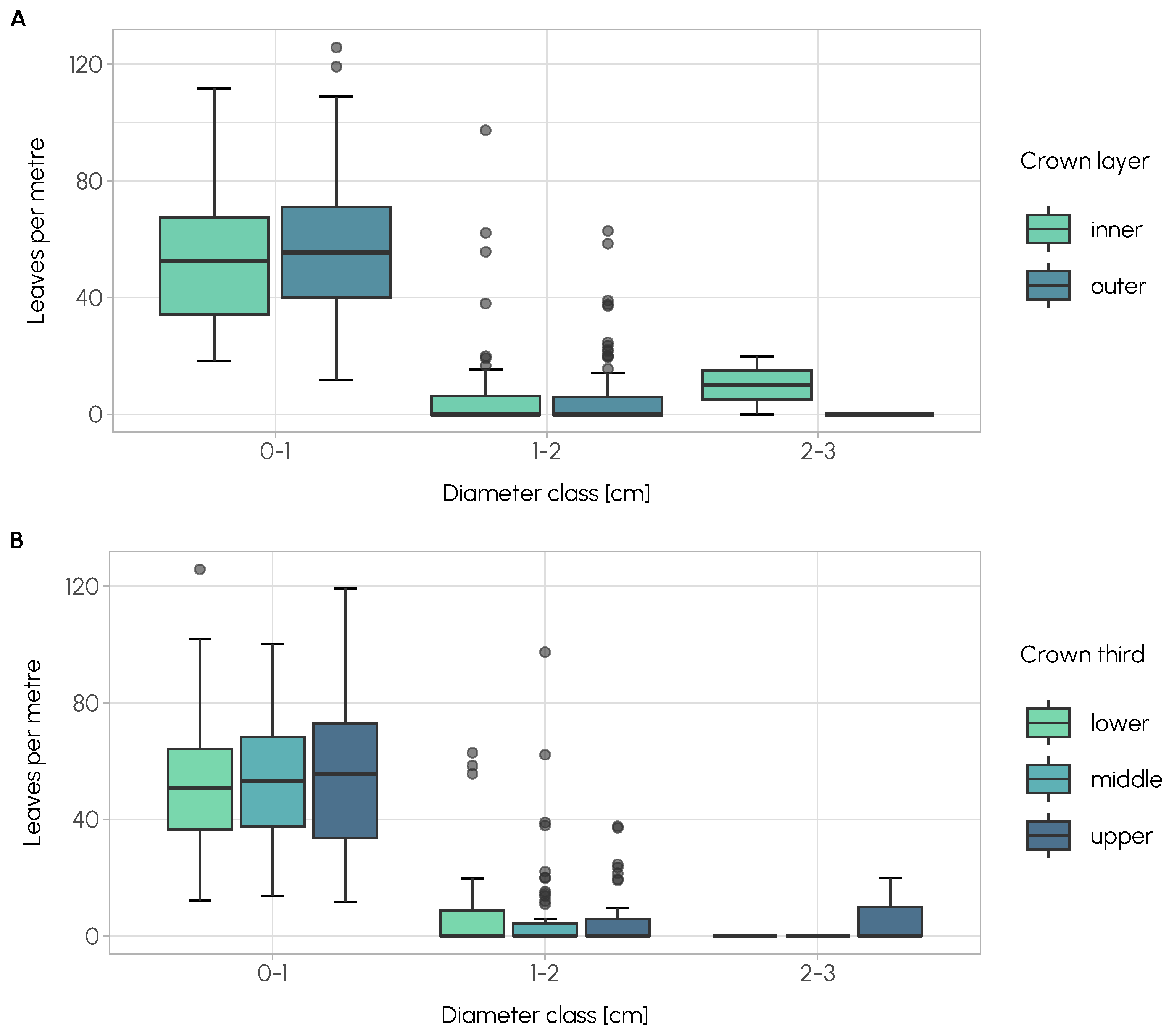
3.1. Leaf Distribution
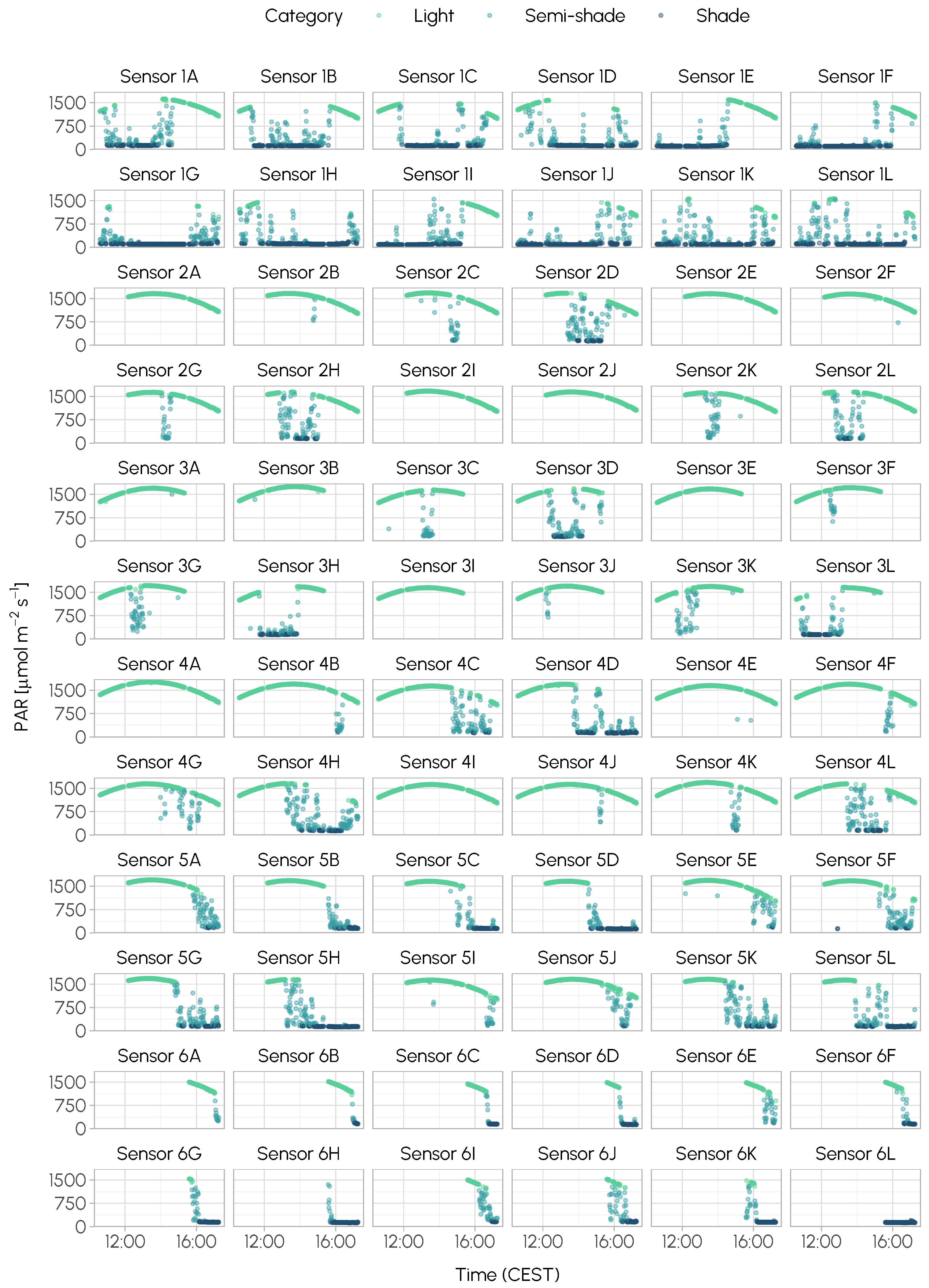
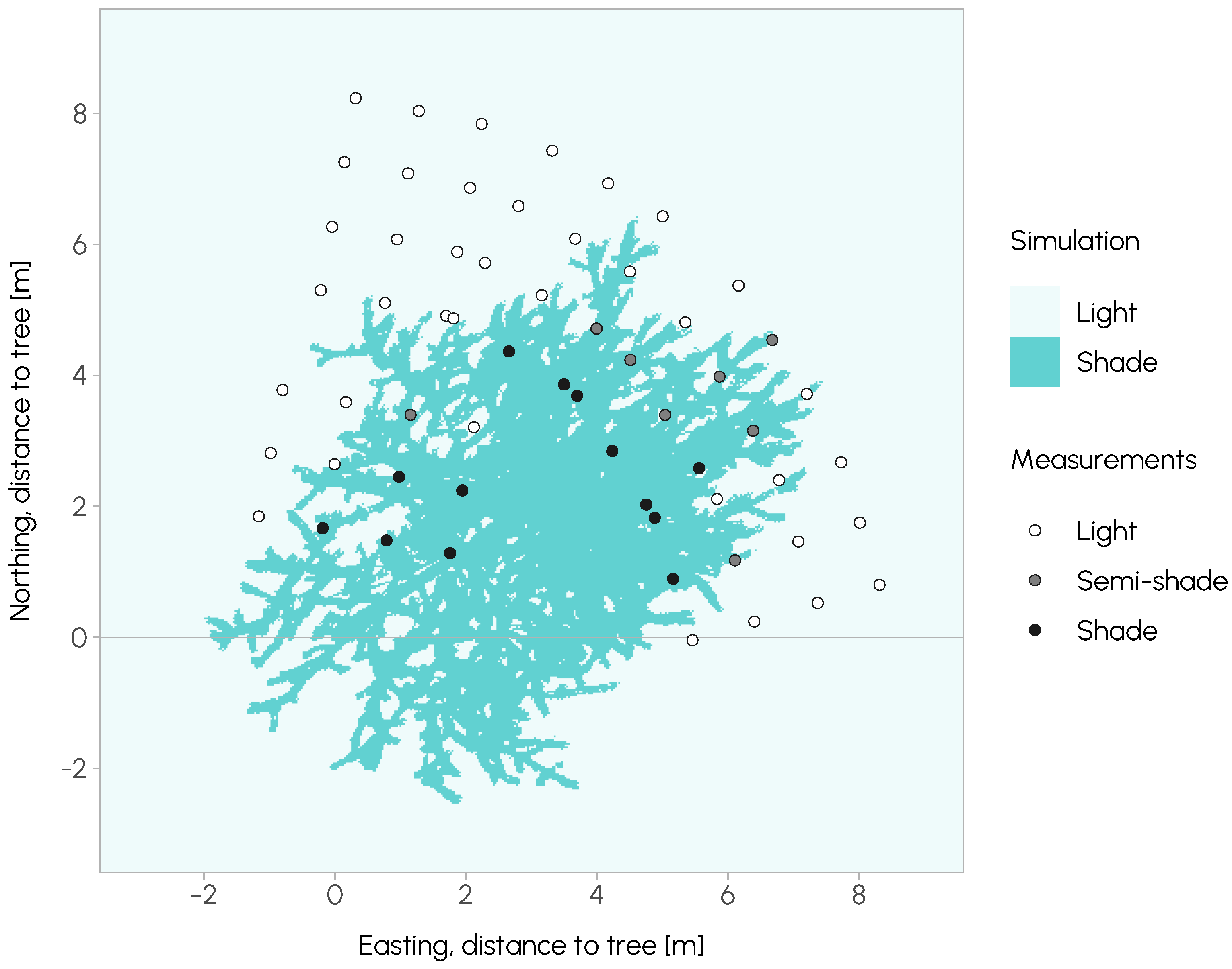
3.2. Simulation vs. Measurements
3.3. Example Application
3.4. Computational Efficiency
4. Discussion
4.1. Simulation Accuracy
4.2. Comparison with Other Approaches
4.3. Example Application
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Additional Tables and Figures
| Simulation Parameter | Value Used for the Validation |
|---|---|
| Tree latitude | 48.0 |
| Tree longitude | 7.8 |
| Spatial resolution | 1 cm |
| Temporal resolution | 1 min |
| Leaf width | 6 cm |
| Leaf length | 10 cm |
| Leaf stem length | 1 cm |
| Leaf axis angle | 45° |
| Leaf density | 0–1 cm → 53.4 leaves/m |
| 1–2 cm → 53.4 leaves/m | |
| 2–3 cm → 7.6 leaves/m | |
| 3–4 cm → 4.6 leaves/m |
Appendix B. Leaf Simulation
- Leaf polygon: In a first step, a 2D leaf polygon must be defined. The leaf base must lie at the coordinates , the leaf axis aligns with the x axis. The leaf polygon must be a simple polygon, i.e., not intersect itself. Currently, three different leaf shapes are implemented, but other manually created polygons can be used as well.
- Leaf distribution: In a next step, the leaf distribution is defined. For each branch diameter class, the lower and upper limits of the diameter classes, the average branch length between the leaves and a scaling factor are required. The scaling factor is later multiplied with the coordinates of the leaf vertices and enables different leaf sizes for each diameter class. The size of the diameter classes can be chosen at will (e.g., 1 mm, 5 mm, 10 mm), as long as each diameter class covers an equally large value range. Additionally, the leaf density and size can vary between different crown sections. For this purpose, the crown can be stratified into different horizontal crown sections (e.g., lower, middle, and upper third of the crown) and/or different crown layers (e.g., inside and outside) to account for differences within the crown with regard to light availability that might influence foliage density along the branches and twigs.
- Leaf starting points: Based on the leaf distribution, the leaf starting points are determined for each cylinder. For cylinders that are longer than the average branch length between leaves, the leaf starting points are distributed evenly along their length. For cylinders smaller than the required length, the cylinder length is divided by the average branch length between leaves, and this fraction is then used to randomly draw from a binomial distribution whether a leaf will be added or not.
- Leaf bases: The leaf base of each leaf is positioned at a small distance from the leaf starting point to simulate leaf stems (petioles). By default, this distance is 1 cm long, but can be adjusted. The leaf stems point in random directions orthogonal to the respective cylinder axis.
- Leaf creation: The leaf polygon is then scaled, rotated, and translated to the desired positions. The polygon is scaled for each different scaling factor specified in the leaf distribution. The leaf polygons are then rotated using rotation matrices so that the leaf axis extends the leaf stem axis. The leaf surfaces are by default angled at 45° to the ground. The leaf angle can be adjusted in the options. Finally, the polygon vertices are moved to their respective leaf bases.
References
- Blackman, G.E.; Black, J.N. Physiological and ecological studies in the analysis of plant environment. Ann. Bot. 1959, 23, 131–145. [Google Scholar] [CrossRef]
- Lupi, C.; Morin, H.; Deslauriers, A.; Rossi, S. Xylem phenology and wood production: Resolving the chicken-or-egg dilemma. Plant Cell Environ. 2010, 33, 1721–1730. [Google Scholar] [CrossRef] [PubMed]
- Kothari, S.; Montgomery, R.A.; Cavender-Bares, J. Physiological responses to light explain competition and facilitation in a tree diversity experiment. J. Ecol. 2021, 109, 2000–2018. [Google Scholar] [CrossRef]
- Leuchner, M.; Hertel, C.; Rötzer, T.; Seifert, T.; Weigt, R.; Werner, H.; Menzel, A. Solar radiation as a driver for growth and competition in forest stands. In Growth and Defence in Plants; Ecological Studies; Matyssek, R., Schnyder, H., Osswald, W.F., Ernst, D., Munch, J.C., Pretzsch, H., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; Volume 220, pp. 175–191. [Google Scholar] [CrossRef]
- Ptushenko, O.S.; Ptushenko, V.V.; Solovchenko, A.E. Spectrum of light as a determinant of plant functioning: A historical perspective. Life 2020, 10, 25. [Google Scholar] [CrossRef] [PubMed]
- Friedel, A.; von Oheimb, G.; Dengler, J.; Härdtle, W. Species diversity and species composition of epiphytic bryophytes and lichens–A comparison of managed and unmanaged beech forests in NE Germany. Feddes Repert. 2006, 117, 172–185. [Google Scholar] [CrossRef]
- Sagar, R.; Singh, A.; Singh, J.S. Differential effect of woody plant canopies on species composition and diversity of ground vegetation: A case study. Trop. Ecol. 2008, 49, 189. [Google Scholar]
- Fu, P.; Rich, P.M. A geometric solar radiation model with applications in agriculture and forestry. Comput. Electron. Agric. 2002, 37, 25–35. [Google Scholar] [CrossRef]
- Zellweger, F.; de Frenne, P.; Lenoir, J.; Rocchini, D.; Coomes, D. Advances in microclimate ecology arising from remote sensing. Trends Ecol. Evol. 2019, 34, 327–341. [Google Scholar] [CrossRef] [PubMed]
- Helbach, J.; Frey, J.; Messier, C.; Mörsdorf, M.; Scherer-Lorenzen, M. Light heterogeneity affects understory plant species richness in temperate forests supporting the heterogeneity-diversity hypothesis. Ecol. Evol. 2022, 12, e8534. [Google Scholar] [CrossRef]
- Way, D.A.; Pearcy, R.W. Sunflecks in trees and forests: From photosynthetic physiology to global change biology. Tree Physiol. 2012, 32, 1066–1081. [Google Scholar] [CrossRef]
- Nair, P.K.R.; Kumar, B.M.; Nair, V.D. Definition and concepts of agroforestry. In An Introduction to Agroforestry; Springer International Publishing: Cham, Switzerland, 2021; pp. 21–28. [Google Scholar] [CrossRef]
- Dufour, L.; Metay, A.; Talbot, G.; Dupraz, C. Assessing light competition for cereal production in temperate agroforestry systems using experimentation and crop modelling. J. Agron. Crop. Sci. 2013, 199, 217–227. [Google Scholar] [CrossRef]
- Ehret, M.; Graß, R.; Wachendorf, M. The effect of shade and shade material on white clover/perennial ryegrass mixtures for temperate agroforestry systems. Agrofor. Syst. 2015, 89, 557–570. [Google Scholar] [CrossRef]
- Lin, C.; McGraw, R.; George, M.; Garrett, H. Shade effects on forage crops with potential in temperate agroforestry practices. Agrofor. Syst. 1998, 44, 109–119. [Google Scholar] [CrossRef]
- Somporn, C.; Kamtuo, A.; Theerakulpisut, P.; Siriamornpun, S. Effect of shading on yield, sugar content, phenolic acids and antioxidant property of coffee beans (Coffea arabica L. cv. Catimor) harvested from north-eastern Thailand. J. Sci. Food Agric. 2012, 92, 1956–1963. [Google Scholar] [CrossRef] [PubMed]
- Kohli, R.K.; Singh, H.P.; Batish, D.R.; Jose, S. Ecological interactions in agroforestry: An overview. In Ecological Basis of Agroforestry; CRC Press: Boca Raton, FL, USA, 2008; pp. 3–14. [Google Scholar]
- Valtorta, S.E.; Leva, P.E.; Gallardo, M.R. Evaluation of different shades to improve dairy cattle well-being in Argentina. Int. J. Biometeorol. 1997, 41, 65–67. [Google Scholar] [CrossRef] [PubMed]
- Mancera, K.F.; Zarza, H.; de Buen, L.L.; García, A.A.C.; Palacios, F.M.; Galindo, F. Integrating links between tree coverage and cattle welfare in silvopastoral systems evaluation. Agron. Sustain. Dev. 2018, 38, 19. [Google Scholar] [CrossRef]
- Pezzopane, J.R.M.; Nicodemo, M.L.F.; Bosi, C.; Garcia, A.R.; Lulu, J. Animal thermal comfort indexes in silvopastoral systems with different tree arrangements. J. Therm. Biol. 2019, 79, 103–111. [Google Scholar] [CrossRef] [PubMed]
- Tsonkova, P.; Mirck, J.; Böhm, C.; Fütz, B. Addressing farmer-perceptions and legal constraints to promote agroforestry in Germany. Agrofor. Syst. 2018, 92, 1091–1103. [Google Scholar] [CrossRef]
- Evans, G.C.; Coombe, D.E. Hemisperical and woodland canopy photography and the light climate. J. Ecol. 1959, 47, 103–113. [Google Scholar] [CrossRef]
- Hale, S.E.; Edwards, C. Comparison of film and digital hemispherical photography across a wide range of canopy densities. Agric. For. Meteorol. 2002, 112, 51–56. [Google Scholar] [CrossRef]
- Ferment, A.; Picard, N.; Gourlet-Fleury, S.; Baraloto, C. A comparison of five indirect methods for characterizing the light environment in a tropical forest. Ann. For. Sci. 2001, 58, 877–891. [Google Scholar] [CrossRef]
- Yan, G.; Hu, R.; Luo, J.; Weiss, M.; Jiang, H.; Mu, X.; Xie, D.; Zhang, W. Review of indirect optical measurements of leaf area index: Recent advances, challenges, and perspectives. Agric. For. Meteorol. 2019, 265, 390–411. [Google Scholar] [CrossRef]
- Engelbrecht, B.M.J.; Herz, H.M. Evaluation of different methods to estimate understorey light conditions in tropical forests. J. Trop. Ecol. 2001, 17, 207–224. [Google Scholar] [CrossRef]
- Reid, R.; Ferguson, I.S. Development and validation of a simple approach to modelling tree shading in agroforestry systems. Agrofor. Syst. 1992, 20, 243–252. [Google Scholar] [CrossRef]
- Dupraz, C.; Liagre, F. Agroforesterie: Des Arbres et des Cultures, 2nd ed.; Éditions France Agricole: Paris, France, 2011. [Google Scholar]
- Talbot, G.; Dupraz, C. Simple models for light competition within agroforestry discontinuous tree stands: Are leaf clumpiness and light interception by woody parts relevant factors? Agrofor. Syst. 2012, 84, 101–116. [Google Scholar] [CrossRef]
- Somarriba, E.; Zamora, R.; Barrantes, J.; Sinclair, F.L.; Quesada, F. ShadeMotion: Tree shade patterns in coffee and cocoa agroforestry systems. Agrofor. Syst. 2023, 97, 31–44. [Google Scholar] [CrossRef]
- Bittner, S.; Gayler, S.; Biernath, C.; Winkler, J.B.; Seifert, S.; Pretzsch, H.; Priesack, E. Evaluation of a ray-tracing canopy light model based on terrestrial laser scans. Can. J. Remote. Sens. 2012, 38, 619–628. [Google Scholar] [CrossRef]
- Li, W.; Guo, Q.; Tao, S.; Su, Y. VBRT: A novel voxel-based radiative transfer model for heterogeneous three-dimensional forest scenes. Remote. Sens. Environ. 2018, 206, 318–335. [Google Scholar] [CrossRef]
- Roupsard, O.; Dauzat, J.; Nouvellon, Y.; Deveau, A.; Feintrenie, L.; Saint-André, L.; Mialet-Serra, I.; Braconnier, S.; Bonnefond, J.M.; Berbigier, P.; et al. Cross-validating sun-shade and 3D models of light absorption by a tree-crop canopy. Agric. For. Meteorol. 2008, 148, 549–564. [Google Scholar] [CrossRef]
- Dassot, M.; Constant, T.; Fournier, M. The use of terrestrial LiDAR technology in forest science: Application fields, benefits and challenges. Ann. For. Sci. 2011, 68, 959–974. [Google Scholar] [CrossRef]
- Calders, K.; Adams, J.; Armston, J.; Bartholomeus, H.; Bauwens, S.; Bentley, L.P.; Chave, J.; Danson, F.M.; Demol, M.; Disney, M.; et al. Terrestrial laser scanning in forest ecology: Expanding the horizon. Remote Sens. Environ. 2020, 251, 112102. [Google Scholar] [CrossRef]
- Schindler, Z.; Morhart, C.; Sheppard, J.P.; Frey, J.; Seifert, T. In a nutshell: Exploring single tree parameters and above-ground carbon sequestration potential of common walnut (Juglans regia L.) in agroforestry systems. Agrofor. Syst. 2023, 97, 1007–1024. [Google Scholar] [CrossRef]
- Schindler, Z.; Seifert, T.; Sheppard, J.P.; Morhart, C. Allometric models for above-ground biomass, carbon and nutrient content of wild cherry (Prunus avium L.) trees in agroforestry systems. Ann. For. Sci. 2023, 80, 28. [Google Scholar] [CrossRef]
- Liang, X.; Kankare, V.; Hyyppä, J.; Wang, Y.; Kukko, A.; Haggrén, H.; Yu, X.; Kaartinen, H.; Jaakkola, A.; Guan, F.; et al. Terrestrial laser scanning in forest inventories. ISPRS J. Photogramm. Remote. Sens. 2016, 115, 63–77. [Google Scholar] [CrossRef]
- Malhi, Y.; Jackson, T.; Bentley, L.P.; Lau, A.; Shenkin, A.; Herold, M.; Calders, K.; Bartholomeus, H.; Disney, M.I. New perspectives on the ecology of tree structure and tree communities through terrestrial laser scanning. Interface Focus 2018, 8, 20170052. [Google Scholar] [CrossRef] [PubMed]
- Lumme, J.; Karjalainen, M.; Kaartinen, H.; Kukko, A.; Hyyppä, J.; Hyyppä, H.; Jaakkola, A.; Kleemola, J. Terrestrial laser scanning of agricultural crops. Int. Arch. Photogramm. Remote. Sens. Spat. Inf. Sci. 2008, XXXVII, 563–566. [Google Scholar]
- Tamás, J.; Riczu, P.; Nagy, G.; Nagy, A.; Jancsó, T.; Nyéki, J.; Szabó, Z. Applicability of 3D laser scanning in precision horticulture. Int. J. Hortic. Sci. 2011, 17, 55–58. [Google Scholar] [CrossRef]
- Wu, D.; Johansen, K.; Phinn, S.; Robson, A. Suitability of airborne and terrestrial laser scanning for mapping tree crop structural metrics for improved orchard management. Remote Sens. 2020, 12, 1647. [Google Scholar] [CrossRef]
- Kunz, M.; Hess, C.; Raumonen, P.; Bienert, A.; Hackenberg, J.; Maas, H.G.; Härdtle, W.; Fichtner, A.; von Oheimb, G. Comparison of wood volume estimates of young trees from terrestrial laser scan data. iForest-Biogeosci. For. 2017, 10, 451–458. [Google Scholar] [CrossRef]
- Raumonen, P.; Åkerblom, M. InverseTampere/TreeQSM, Version 2.4.1; Zenodo: Geneva, Switzerland, 2022. [Google Scholar] [CrossRef]
- Rosskopf, E.; Morhart, C.; Nahm, M. Modelling shadow using 3D tree models in high spatial and temporal resolution. Remote Sens. 2017, 9, 719. [Google Scholar] [CrossRef]
- Bohn Reckziegel, R.; Larysch, E.; Sheppard, J.P.; Kahle, H.P.; Morhart, C. Modelling and comparing shading effects of 3D tree structures with virtual leaves. Remote Sens. 2021, 13, 532. [Google Scholar] [CrossRef]
- Calders, K.; Origo, N.; Burt, A.; Disney, M.; Nightingale, J.; Raumonen, P.; Åkerblom, M.; Malhi, Y.; Lewis, P. Realistic forest stand reconstruction from terrestrial LiDAR for radiative transfer modelling. Remote Sens. 2018, 10, 933. [Google Scholar] [CrossRef]
- Demol, M.; Wilkes, P.; Raumonen, P.; Krishna Moorthy, S.M.; Calders, K.; Gielen, B.; Verbeeck, H. Volumetric overestimation of small branches in 3D reconstructions of Fraxinus excelsior. Silva Fenn. 2022, 56, 10550. [Google Scholar] [CrossRef]
- Morhart, C.; Schindler, Z.; Frey, J.; Sheppard, J.P.; Calders, K.; Disney, M.; Morsdorf, F.; Raumonen, P.; Seifert, T. Limitations of estimating branch volume from terrestrial laser scanning. Eur. J. For. Res. 2024, 143, 687–702. [Google Scholar] [CrossRef]
- Raumonen, P.; Kaasalainen, M.; Åkerblom, M.; Kaasalainen, S.; Kaartinen, H.; Vastaranta, M.; Holopainen, M.; Disney, M.; Lewis, P. Fast automatic precision tree models from terrestrial laser scanner data. Remote Sens. 2013, 5, 491–520. [Google Scholar] [CrossRef]
- Calders, K.; Newnham, G.; Burt, A.; Murphy, S.; Raumonen, P.; Herold, M.; Culvenor, D.; Avitabile, V.; Disney, M.; Armston, J. Nondestructive estimates of above-ground biomass using terrestrial laser scanning. Methods Ecol. Evol. 2015, 6, 198–208. [Google Scholar] [CrossRef]
- Gonzalez de Tanago, J.; Lau, A.; Bartholomeus, H.; Herold, M.; Avitabile, V.; Raumonen, P.; Martius, C.; Goodman, R.C.; Disney, M.; Manuri, S.; et al. Estimation of above-ground biomass of large tropical trees with terrestrial LiDAR. Methods Ecol. Evol. 2018, 9, 223–234. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing. Available online: https://www.R-project.org/ (accessed on 23 May 2024).
- Schindler, Z. qsm2r: Import and Analyze QSMs from TreeQSM in R. Available online: https://github.com/zoeschindler/qsm2r (accessed on 23 May 2024).
- Schindler, Z. qsm2shade: Analyze shade cast of QSMs. Available online: https://github.com/zoeschindler/qsm2shade (accessed on 23 May 2024).
- Hijmans, R.J. Terra: Spatial Data Analysis, R Package Version 1.7-39; R Core Team: Vienna, Austria, 2023. [Google Scholar]
- Peel, M.C.; Finlayson, B.L.; McMahon, T.A. Updated world map of the Köppen-Geiger climate classification. Hydrol. Earth Syst. Sci. 2007, 4, 439–473. [Google Scholar] [CrossRef]
- Deutscher Wetterdienst. Climate Data Center. Available online: https://www.dwd.de/EN/climate_environment/cdc/cdc_en.html (accessed on 17 April 2024).
- Mensah, S.; Glèlè Kakaï, R.; Seifert, T. Patterns of biomass allocation between foliage and woody structure: The effects of tree size and specific functional traits. Ann. For. Res. 2014, 59, 49–60. [Google Scholar] [CrossRef]
- Sheppard, J.; Morhart, C.; Hackenberg, J.; Spiecker, H. Terrestrial laser scanning as a tool for assessing tree growth. iFor. Biogeosci. For. 2017, 10, 172–179. [Google Scholar] [CrossRef]
- Zhu, J.; Shi, Y.; Fang, L.; Liu, X.; Ji, C. Patterns and determinants of wood physical and mechanical properties across major tree species in China. Sci. China Life Sci. 2015, 58, 602–612. [Google Scholar] [CrossRef] [PubMed]
- Kozlowski, T.T.; Pallardy, S.G. Growth Control in Woody Plants; Physiological Ecology Series; Academic Press: San Diego, CA, USA, 1997. [Google Scholar]
- Bienert, A.; Georgi, L.; Kunz, M.; Maas, H.G.; von Oheimb, G. Comparison and combination of mobile and terrestrial laser scanning for natural forest inventories. Forests 2018, 9, 395. [Google Scholar] [CrossRef]
- Brede, B.; Calders, K.; Lau, A.; Raumonen, P.; Bartholomeus, H.M.; Herold, M.; Kooistra, L. Non-destructive tree volume estimation through quantitative structure modelling: Comparing UAV laser scanning with terrestrial LiDAR. Remote Sens. Environ. 2019, 233, 111355. [Google Scholar] [CrossRef]
- Lüttge, U.; Hertel, B. Diurnal and annual rhythms in trees. Trees Struct. Funct. 2009, 23, 683–700. [Google Scholar] [CrossRef]
- Massonnet, C.; Regnard, J.L.; Lauri, P.E.; Costes, E.; Sinoquet, H. Contributions of foliage distribution and leaf functions to light interception, transpiration and photosynthetic capacities in two apple cultivars at branch and tree scales. Tree Physiol. 2008, 28, 665–678. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Meloni, S.; Sinoquet, H. Assessment of the spatial distribution of light transmitted below young trees in an agroforestry system. Ann. For. Sci. 1997, 54, 313–333. [Google Scholar] [CrossRef]
- Van der Zande, D.; Stuckens, J.; Verstraeten, W.W.; Muys, B.; Coppin, P. Assessment of light environment variability in broadleaved forest canopies using terrestrial laser scanning. Remote Sens. 2010, 2, 1564–1574. [Google Scholar] [CrossRef]
- Parkhurst, D.F.; Loucks, O.L. Optimal leaf size in relation to environment. J. Ecol. 1972, 60, 505. [Google Scholar] [CrossRef]
- St. Clair, S.B.; Monson, S.D.; Smith, E.A.; Cahill, D.G.; Calder, W.J. Altered leaf morphology, leaf resource dilution and defense chemistry induction in frost-defoliated aspen (Populus tremuloides). Tree Physiol. 2009, 29, 1259–1268. [Google Scholar] [CrossRef][Green Version]
- Xu, F.; Guo, W.; Xu, W.; Wei, Y.; Wang, R. Leaf morphology correlates with water and light availability: What consequences for simple and compound leaves? Prog. Nat. Sci. 2009, 19, 1789–1798. [Google Scholar] [CrossRef]
- Wright, I.J.; Dong, N.; Maire, V.; Prentice, I.C.; Westoby, M.; Díaz, S.; Gallagher, R.V.; Jacobs, B.F.; Kooyman, R.; Law, E.A.; et al. Global climatic drivers of leaf size. Science 2017, 357, 917–921. [Google Scholar] [CrossRef] [PubMed]
- Baumgarten, F.; Gessler, A.; Vitasse, Y. No risk—No fun: Penalty and recovery from spring frost damage in deciduous temperate trees. Funct. Ecol. 2023, 37, 648–663. [Google Scholar] [CrossRef]
- Hevia, A.; Álvarez-González, J.G.; Majada, J. Comparison of pruning effects on tree growth, productivity and dominance of two major timber conifer species. For. Ecol. Manag. 2016, 374, 82–92. [Google Scholar] [CrossRef]
- Burgess, T.I.; Howard, K.; Steel, E.; Barbour, E.L. To prune or not to prune; pruning induced decay in tropical sandalwood. For. Ecol. Manag. 2018, 430, 204–218. [Google Scholar] [CrossRef]
- Sheppard, J.P.; Bohn Reckziegel, R.; Borrass, L.; Chirwa, P.W.; Cuaranhua, C.J.; Hassler, S.K.; Hoffmeister, S.; Kestel, F.; Maier, R.; Mälicke, M.; et al. Agroforestry: An appropriate and sustainable response to a changing climate in Southern Africa? Sustainability 2020, 12, 6796. [Google Scholar] [CrossRef]
- Laub, M.; Pataczek, L.; Feuerbacher, A.; Zikeli, S.; Högy, P. Contrasting yield responses at varying levels of shade suggest different suitability of crops for dual land-use systems: A meta-analysis. Agron. Sustain. Dev. 2022, 42, 51. [Google Scholar] [CrossRef]
- Rousi, M.; Pusenius, J. Variations in phenology and growth of European white birch (Betula pendula) clones. Tree Physiol. 2005, 25, 201–210. [Google Scholar] [CrossRef] [PubMed]
- Bamba, H.; Korbo, A.; Sanou, H.; Ræbild, A.; Kjær, E.D.; Hansen, J.K. Genetic differentiation in leaf phenology among natural populations of Adansonia digitata L. follows climatic clines. Glob. Ecol. Conserv. 2019, 17, e00544. [Google Scholar] [CrossRef]
- Bohn Reckziegel, R.; Sheppard, J.P.; Kahle, H.P.; Larysch, E.; Spiecker, H.; Seifert, T.; Morhart, C. Virtual pruning of 3D trees as a tool for managing shading effects in agroforestry systems. Agrofor. Syst. 2022, 96, 89–104. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schindler, Z.; Larysch, E.; Frey, J.; Sheppard, J.P.; Obladen, N.; Kröner, K.; Seifert, T.; Morhart, C. From Dawn to Dusk: High-Resolution Tree Shading Model Based on Terrestrial LiDAR Data. Remote Sens. 2024, 16, 2189. https://doi.org/10.3390/rs16122189
Schindler Z, Larysch E, Frey J, Sheppard JP, Obladen N, Kröner K, Seifert T, Morhart C. From Dawn to Dusk: High-Resolution Tree Shading Model Based on Terrestrial LiDAR Data. Remote Sensing. 2024; 16(12):2189. https://doi.org/10.3390/rs16122189
Chicago/Turabian StyleSchindler, Zoe, Elena Larysch, Julian Frey, Jonathan P. Sheppard, Nora Obladen, Katja Kröner, Thomas Seifert, and Christopher Morhart. 2024. "From Dawn to Dusk: High-Resolution Tree Shading Model Based on Terrestrial LiDAR Data" Remote Sensing 16, no. 12: 2189. https://doi.org/10.3390/rs16122189
APA StyleSchindler, Z., Larysch, E., Frey, J., Sheppard, J. P., Obladen, N., Kröner, K., Seifert, T., & Morhart, C. (2024). From Dawn to Dusk: High-Resolution Tree Shading Model Based on Terrestrial LiDAR Data. Remote Sensing, 16(12), 2189. https://doi.org/10.3390/rs16122189








