Resilient Factor Graph-Based GNSS/IMU/Vision/Odo Integrated Navigation Scheme Enhanced by Noise Approximate Gaussian Estimation in Challenging Environments
Abstract
1. Introduction
- (1)
- In using the velocity data output from the odometer as the reference, the approximate Gaussian distribution characteristics of the GNSS/Odometer ground speed residual sequence are analyzed.
- (2)
- Based on the variational Bayesian network and Gaussian mixture model (GMM), an approximate Gaussian estimation algorithm for the measurement data noise model is studied, and a resilient noise model is proposed.
- (3)
- Based on the resilient noise model, the factor graph-based IMU/GNSS/odometer/vision fusion navigation system is implemented, and the superiority of the algorithm is verified through theoretical analyses and road tests.
2. Related Work and Problem Statement
2.1. Multi-Source Fusion Localization Based on Factor Graph
2.2. Adaptive Optimization of Measurement Noise Model
3. Approximate Gaussian Estimation of Measurement Noise Parameters Based on Innovation
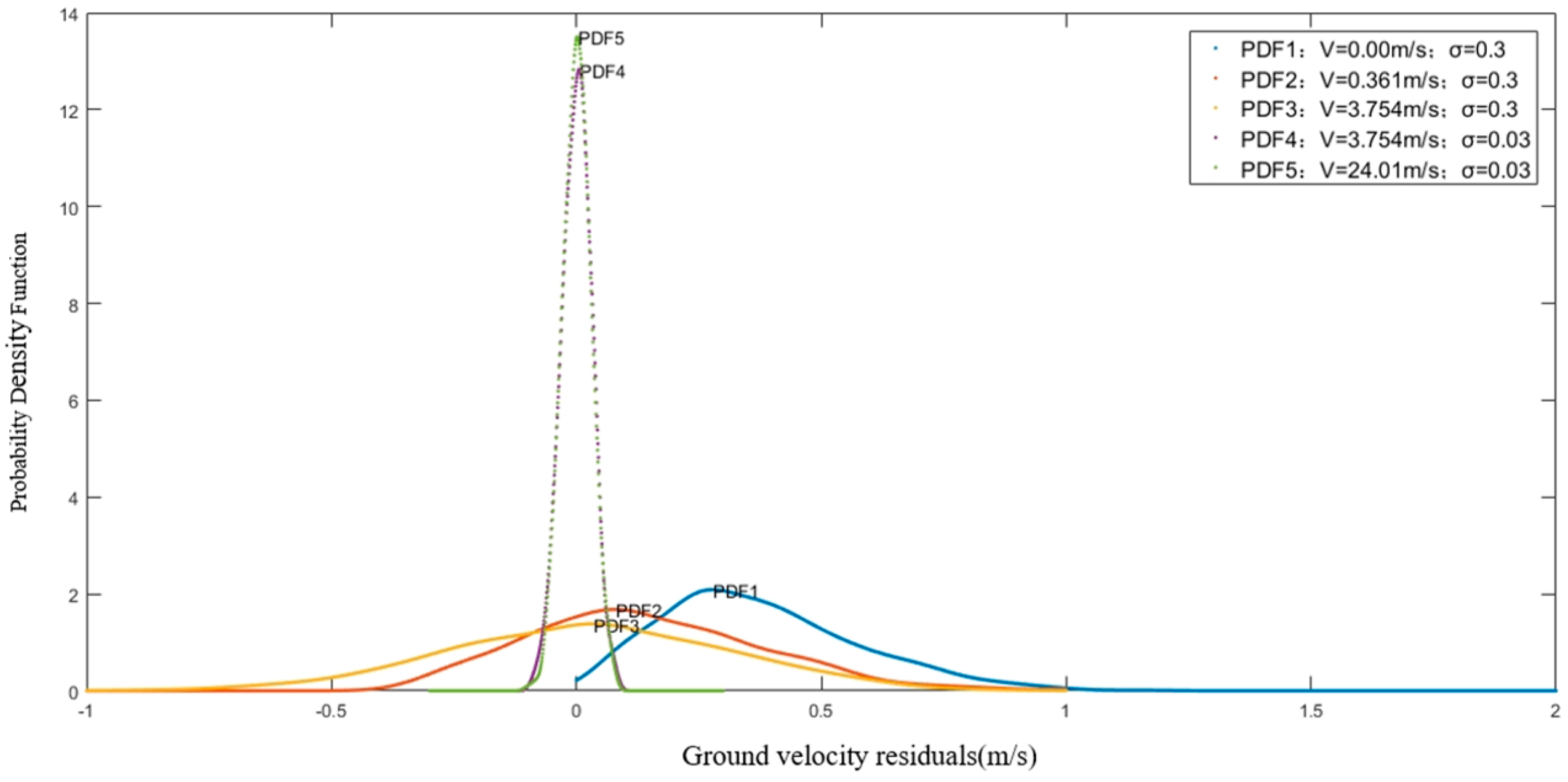
3.1. Approximate Gaussian Distribution Analysis of GNSS/Odometry Velocity Residual Sequences
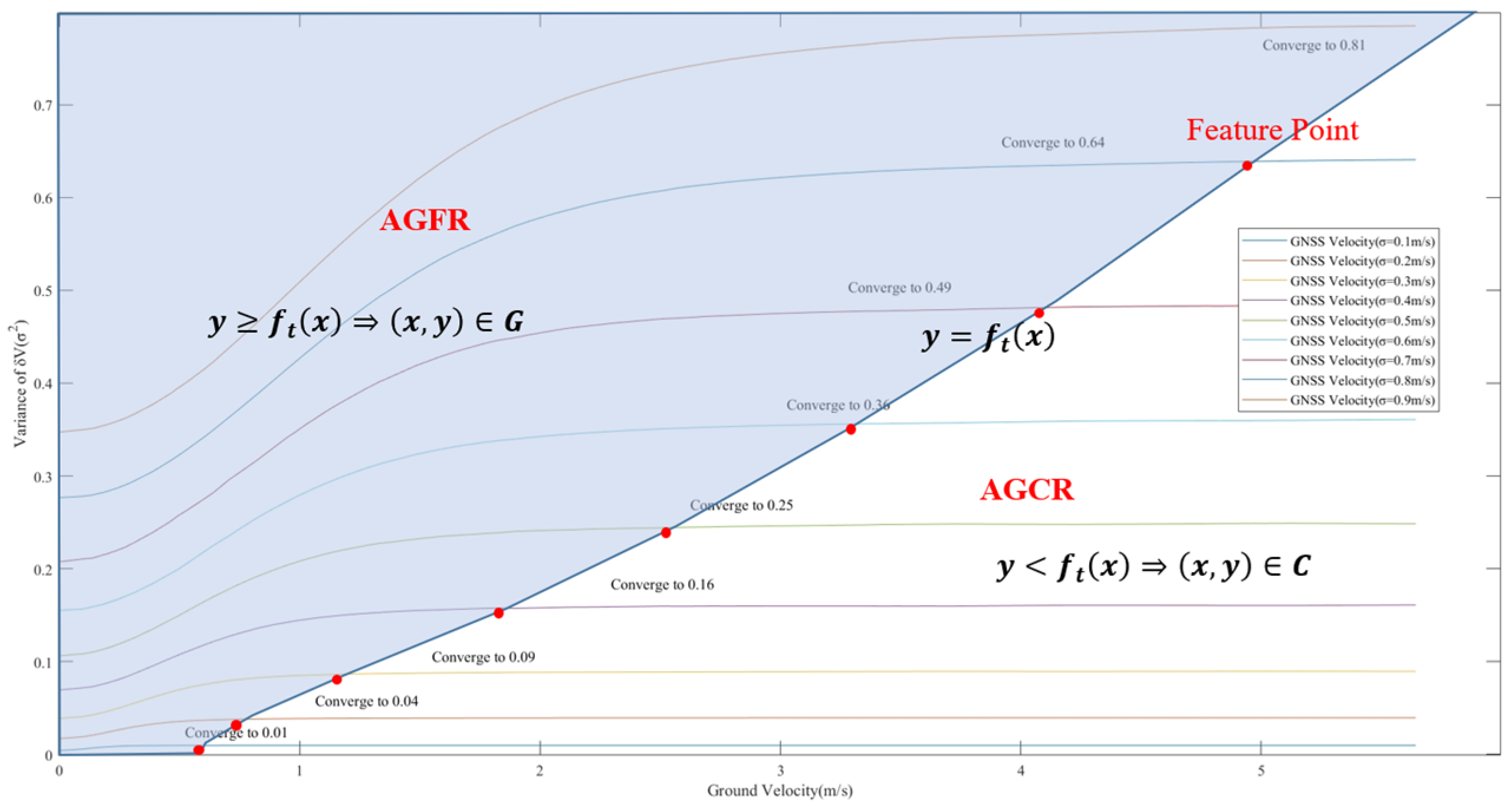
3.2. The Design of Resilient Noise Model Based on the Approximate Gaussian Estimation Algorithm
3.2.1. Variational Bayesian Network Estimation of Noise Parameters Based on Innovation
3.2.2. Noise Parameter Estimation Based on Innovation and Gaussian Mixture Model
| Algorithm 1: GNSS measurement noise parameter estimation algorithm based on GMM |
| Input (Velocity residual sequence , number of Gaussian distributions , convergence threshold ) |
| Output (Parameters for each Gaussian distribution: mean , covariance , and weight coefficient ) |
| Initialize: Initialize the parameters for each Gaussian distribution: (mean , covariance , and weight coefficient ). |
| Iterative Update Steps: |
| while not reached the maximum number of iterations or not converged: |
| E-step (Expectation step): |
| For each data point : |
| Calculate the responsibility of each Gaussian distribution : |
| M-step (Maximization step): |
| For each Gaussian distribution : |
| Update the mean : |
| Update the weight coefficient : |
| Update the covariance : |
| Check for convergence: |
| If the change in parameters is less than the threshold , stop iterating. |
4. IMU/GNSS/Odometer/Vision Fusion Positioning Scheme Based on the Adaptive Factor Graph Optimization Model
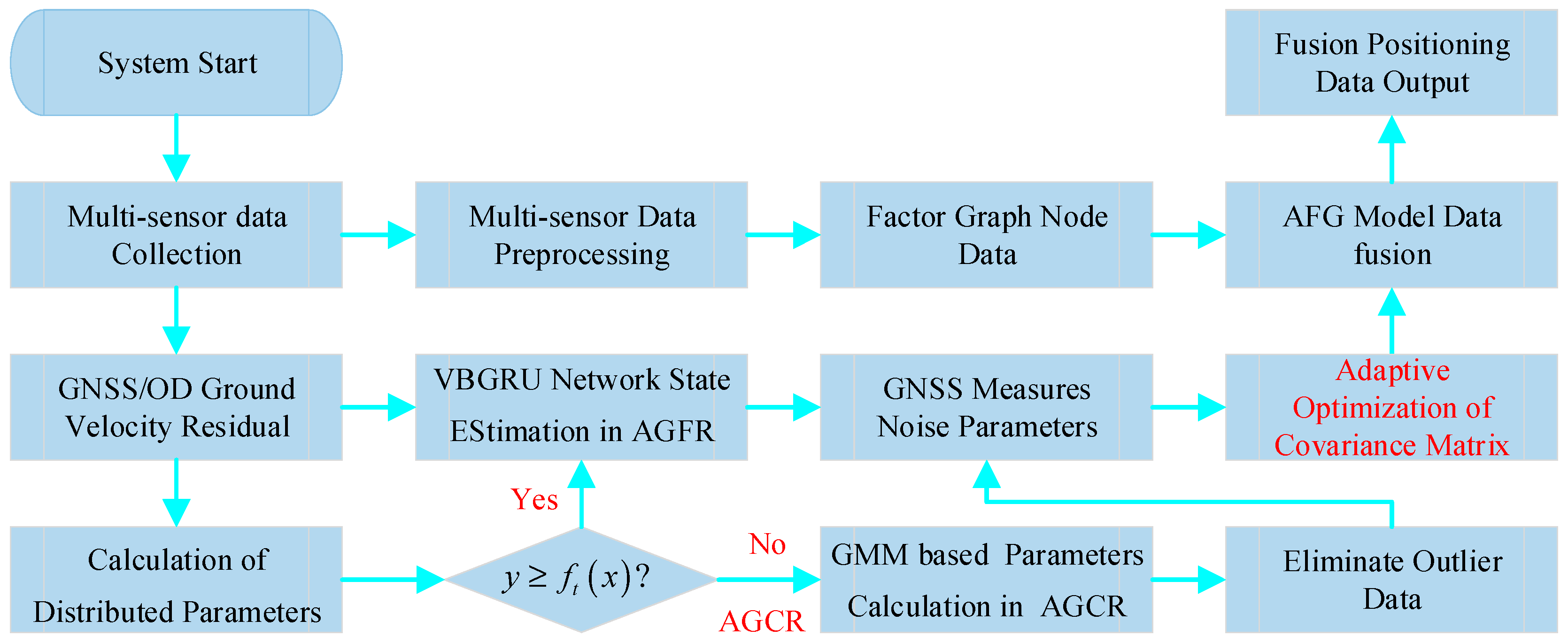
4.1. Adaptive Factor Graph Data Fusion Architecture Design
4.2. INS Factor
4.3. GNSS Factor
4.4. Odometry Factor
4.5. Vision/Map Factor
5. Experimental Verifications
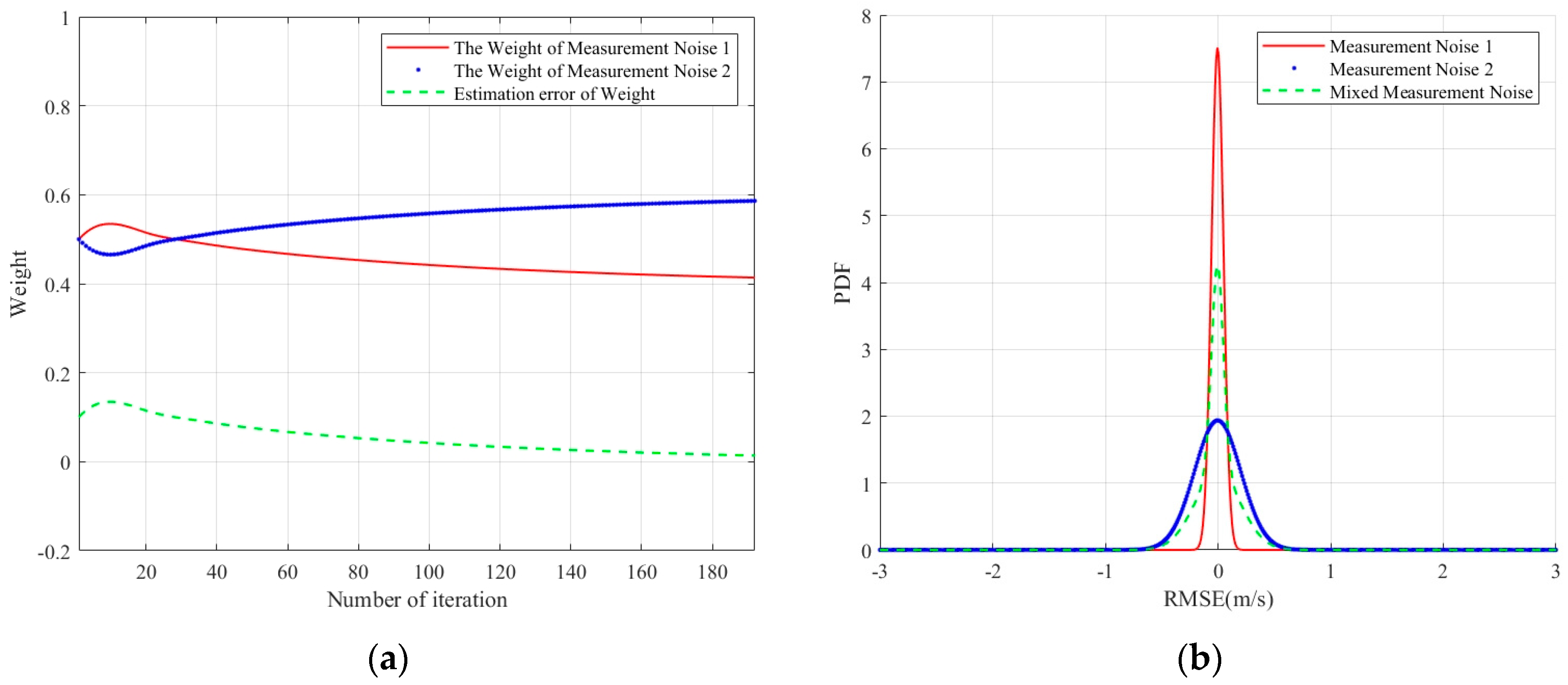
5.1. Simulation Verification of Resilient Noise Model Based on Approximate Gaussian Estimation
5.2. Real-World Road Test
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ali, A.; Chan, B.; Omr, M.; Georgy, J. Coursa Drive: Integrated Navigation Solution for Autonomous Vehicles. In Proceedings of the 32nd International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2019), Miami, FL, USA, 16–20 September 2019; pp. 1220–1233. [Google Scholar]
- Woo, A.; Baris, F.; Melek, W.W. Localization for autonomous driving. In Handbook of Position Location: Theory, Practice, and Advances, 2nd ed.; Wiley: Hoboken, NJ, USA, 2018; pp. 1051–1087. [Google Scholar]
- Chiang, K.W.; Chiu, Y.T.; Srinara, S.; Tsai, M. Performance of LiDAR-SLAM-based PNT with initial poses based on NDT scan matching algorithm. Satell. Navig. 2023, 4, 3. [Google Scholar] [CrossRef]
- Vivacqua, R.P.D.; Bertozzi, M.; Cerri, P.; Martins, F.N.; Vassallo, R.F. Self-localization based on visual lane marking maps: An accurate low-cost approach for autonomous driving. IEEE Trans. Intell. Transp. Syst. 2017, 19, 582–597. [Google Scholar] [CrossRef]
- Liu, W.; Wu, M.; Zhang, X.; Wang, W.; Ke, W.; Zhu, Z. Single-epoch RTK performance assessment of tightly combined BDS-2 and newly complete BDS-3. Satell. Navig. 2021, 2, 6. [Google Scholar] [CrossRef]
- Wang, Z.; Wu, Y.; Niu, Q. Multi-sensor fusion in automated driving: A survey. IEEE Access 2019, 8, 2847–2868. [Google Scholar] [CrossRef]
- Fayyad, J.; Jaradat, M.A.; Gruyer, D.; Najjaran, H. Deep Learning Sensor Fusion for Autonomous Vehicle Perception and Localization: A Review. Sensors 2020, 20, 4220. [Google Scholar] [CrossRef]
- Li, Q.; Queralta, J.P.; Gia, T.N.; Zou, Z.; Westerlund, T. Multi-sensor fusion for navigation and mapping in autonomous vehicles: Accurate localization in urban environments. Unmanned Syst. 2020, 8, 229–237. [Google Scholar] [CrossRef]
- Li, A.; Zhang, Y.; Ji, Y.; Guo, Y.; Zhang, Z. An Post-processing Method of Enhancing Position Accuracy of Strapdown Inertial/Odometer System. Navig. Position. Timing 2021, 8, 75–80. [Google Scholar]
- Li, Z.; Liu, Y.; Zeng, Q.; Liu, J.; Li, F.; Zhang, G. A Vision/Map Attitude Matrix Aided IMU/Odometer Integrated Navigation Method. In Proceedings of the 2022 IEEE International Conference on Unmanned Systems (ICUS), Guangzhou, China, 28–30 October 2022; pp. 254–259. [Google Scholar]
- Rahman, M.T.; Karamat, T.; Givigi, S.; Noureldin, A. Improving multisensor positioning of land vehicles with integrated visual odometry for next-generation self-driving cars. J. Adv. Transp. 2018, 2018, 6513970. [Google Scholar] [CrossRef]
- Meng, Q.; Hsu, L.T. Resilient interactive sensor-independent-update fusion navigation method. IEEE Trans. Intell. Transp. Syst. 2022, 23, 16433–16447. [Google Scholar] [CrossRef]
- Li, X.; Wang, X.; Liao, J.; Li, X.; Li, S.; Lyu, H. Semi-tightly coupled integration of multi-GNSS PPP and S-VINS for precise positioning in GNSS-challenged environments. Satell. Navig. 2021, 2, 1. [Google Scholar] [CrossRef]
- Rosique, F.; Navarro, P.J.; Fernández, C.; Padilla, A. A Systematic Review of Perception System and Simulators for Autonomous Vehicles Research. Sensors 2019, 19, 648. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y. Resilient PNT concept frame. J. Geod. Geoinf. Sci. 2019, 2, 1–7. [Google Scholar]
- Huang, K.; Shi, B.; Li, X.; Li, X.; Huang, S.; Li, Y. Multi-modal sensor fusion for auto driving perception: A survey. arXiv 2022, arXiv:2202.02703. [Google Scholar]
- Aftatah, M.; Lahrech, A.; Abounada, A.; Soulhi, A. GPS/INS/Odometer data fusion for land vehicle localization in GPS denied environment. Mod. Appl. Sci. 2016, 11, 62. [Google Scholar] [CrossRef]
- Meng, Q.; Hsu, L.T. Integrity Monitoring for All-Source Navigation Enhanced by Kalman Filter based Solution Separation. IEEE Sens. J. 2021, 21, 15469–15484. [Google Scholar] [CrossRef]
- Kschischang, F.R.; Frey, B.J.; Loeliger, H.A. Factor graphs and the sum-product algorithm. IEEE Trans. Inf. Theory 2001, 47, 498–519. [Google Scholar] [CrossRef]
- Zeng, Q.; Chen, W.; Liu, J.; Wang, H. An Improved Multi-Sensor Fusion Navigation Algorithm Based on the Factor Graph. Sensors 2017, 17, 641. [Google Scholar] [CrossRef] [PubMed]
- Wen, W.; Kan, Y.C.; Hsu, L.-T. Performance Comparison of GNSS/INS Integrations Based on EKF and Factor Graph Optimization. In Proceedings of the 32nd International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2019), Miami, FL, USA, 16–20 September 2019; pp. 3019–3032. [Google Scholar] [CrossRef]
- Wen, W.; Pfeifer, T.; Bai, X.; Hsu, L.T. It is time for Factor Graph Optimization for GNSS/INS Integration: Comparison between FGO and EKF. arXiv 2004, arXiv:2004.10572. [Google Scholar]
- Zhao, S.; Chen, Y.; Farrell, J.A. High-precision vehicle navigation in urban environments using an MEM’s IMU and single-frequency GPS receiver. IEEE Trans. Intell. Transp. Syst. 2016, 17, 2854–2867. [Google Scholar] [CrossRef]
- Gao, J.; Tang, X.; Zhang, H.; Wu, M. Vehicle INS/GNSS/OD integrated navigation algorithm based on factor graph. Syst. Eng. Electron. 2018, 40, 2547–2553. [Google Scholar] [CrossRef]
- Li, W.; Cui, X.; Lu, M. A robust graph optimization realization of tightly coupled GNSS/INS integrated navigation system for urban vehicles. Tsinghua Sci. Technol. 2018, 23, 724–732. [Google Scholar] [CrossRef]
- Sarkka, S.; Nummenmaa, A. Recursive noise adaptive Kalman filtering by variational Bayesian approximations. IEEE Trans. Autom. Control 2009, 54, 596–600. [Google Scholar] [CrossRef]
- Li, K.; Chang, L.; Hu, B. A variational Bayesian-based unscented Kalman filter with both adaptivity and robustness. IEEE Sens. J. 2016, 16, 6966–6976. [Google Scholar] [CrossRef]
- Hu, M.M.; Jing, Z.L.; Peng, D.D.; Zhou, G.R.; Zheng, Z.M. Variational Bayesian filtering based on Student-t distribution for SINS/GPS integrated navigation. J. ZheJiang Univ. 2018, 52, 1482–1488. [Google Scholar]
- Liu, Y.; Fan, X.; Lv, C.; Wu, J.; Li, L.; Ding, D. An innovative information fusion method with adaptive Kalman filter for integrated INS/GPS navigation of autonomous vehicles. Mech. Syst. Signal Process. 2018, 100, 605–616. [Google Scholar] [CrossRef]
- Yue, Z.; Lian, B.; Tang, C. A GPS/INS Integrated Navigation Method Based on Weighting Adaptive Square-root Cubature Kalman Filter. J. Electron. Inf. Technol. 2018, 40, 565–572. [Google Scholar] [CrossRef]
- Xu, H.; Lian, B.; Liu, S. Multi-source integrated navigation algorithm for iterated maximum posteriori estimation based on sliding-window factor graph. Acta Armamentarii 2019, 40, 807. [Google Scholar]
- Jing, C.; Huang, G.; Li, X.; Zhang, Q.; Yang, H.; Zhang, K.; Liu, G. GNSS/accelerometer integrated deformation monitoring algorithm based on sensors adaptive noise modeling. Measurement 2023, 218, 113179. [Google Scholar] [CrossRef]
- Watson, R.M.; Gross, J.N.; Taylor, C.N.; Leishman, R.C. Uncertainty Model Estimation in an Augmented Data Space for Robust State Estimation. In Proceedings of the 33rd International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2020), Online, 21–25 September 2020; pp. 2686–2695. [Google Scholar] [CrossRef]
- Li, Z.; Zeng, Q.; Liu, Y.; Liu, J. An ROI Optimization Method Based on Dynamic Estimation Adjustment Model. Remote Sens. 2023, 15, 2434. [Google Scholar] [CrossRef]


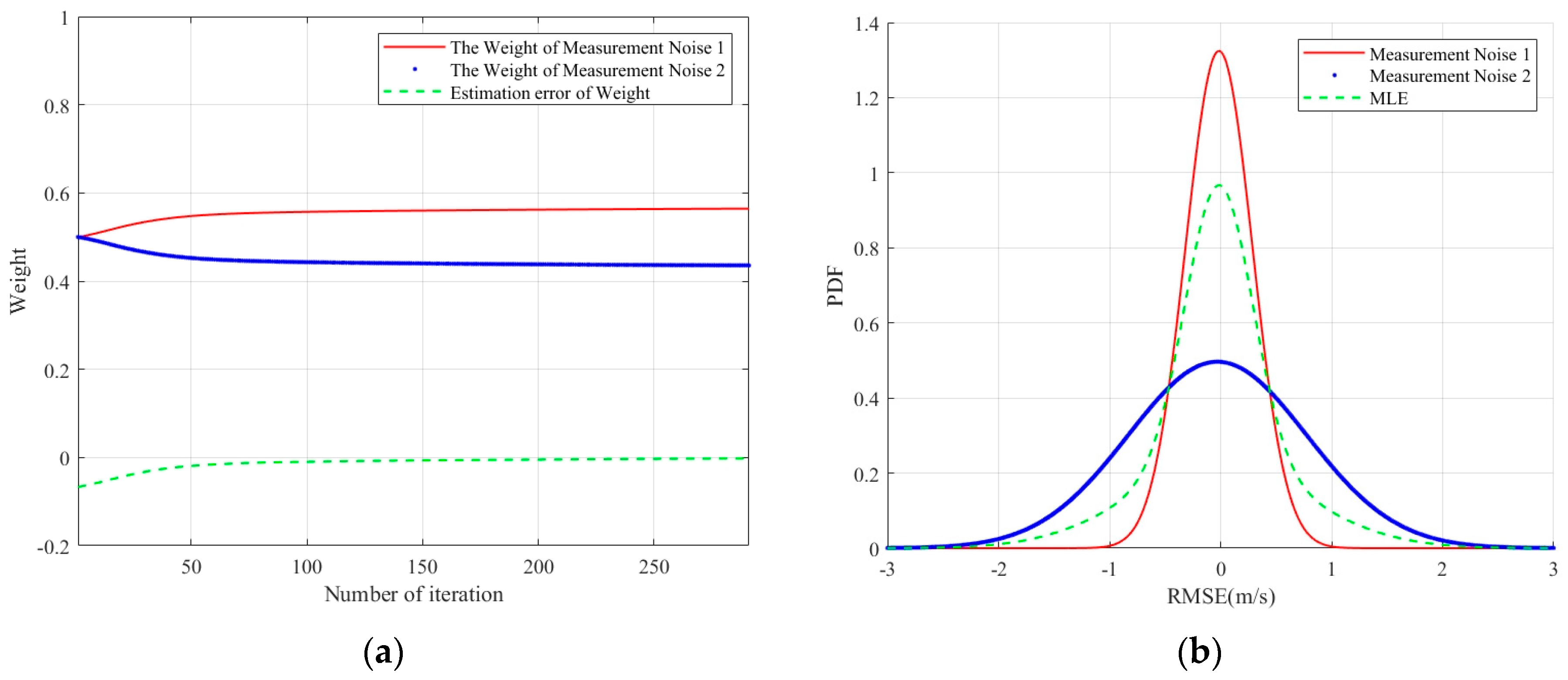
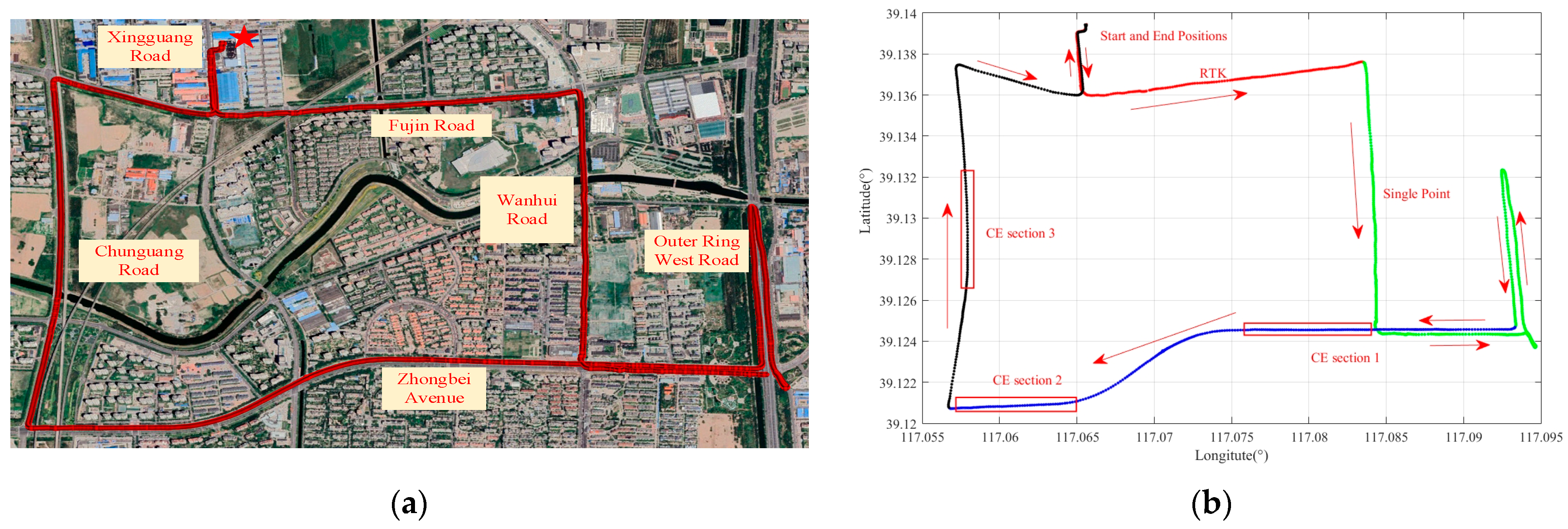



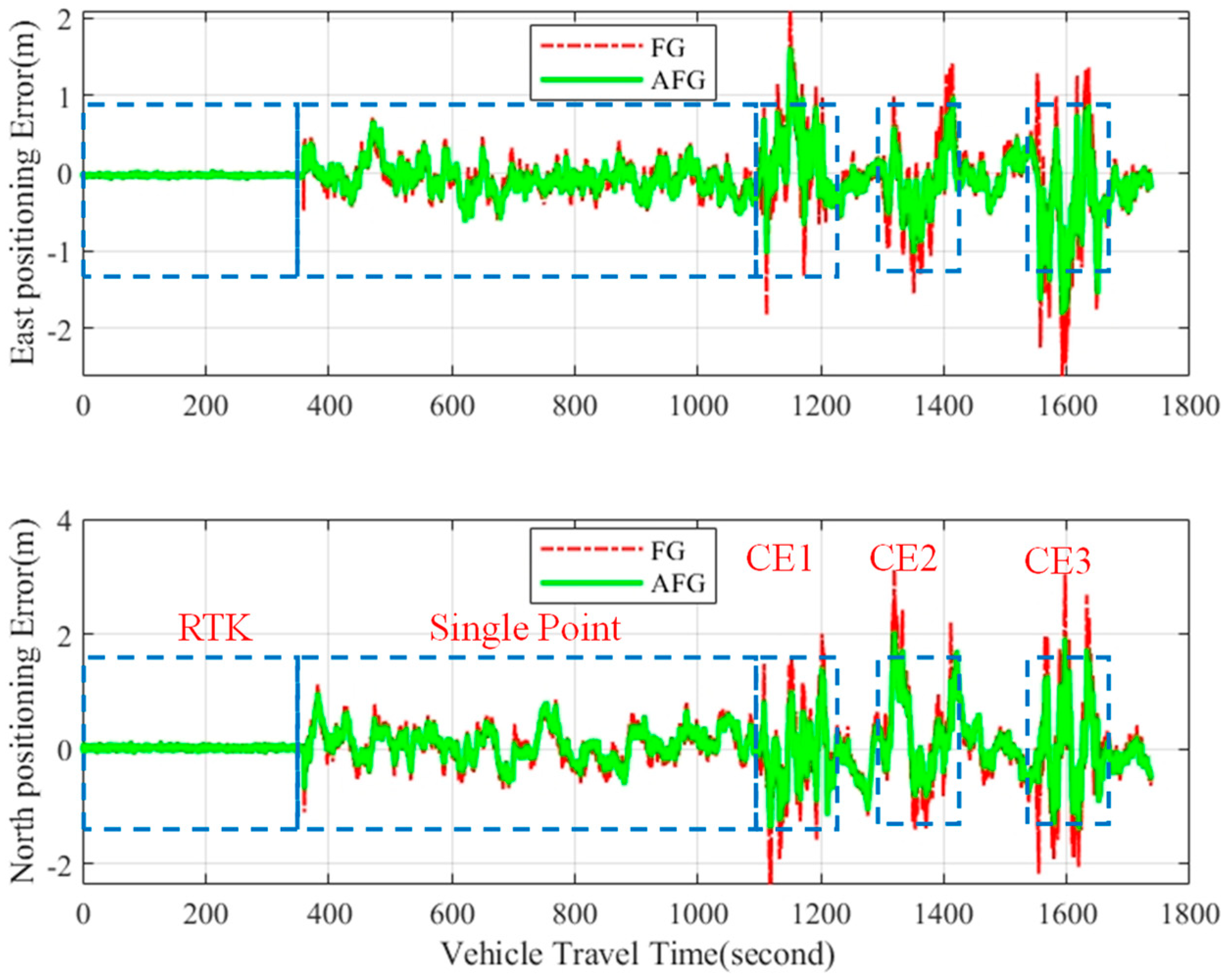
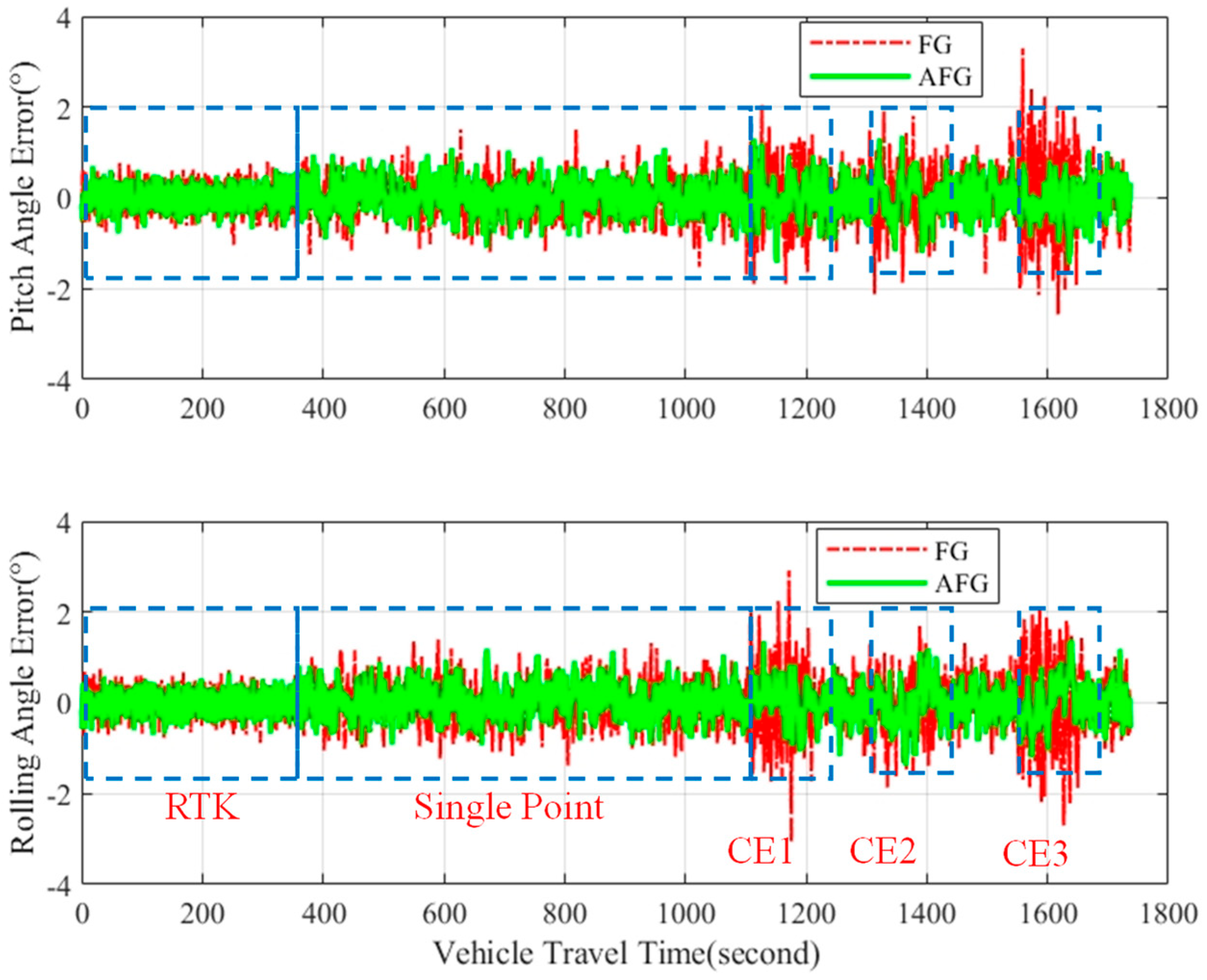

| Mixed Positioning State | RTK | SPP | RTK | CE | SPP | CE | |
|---|---|---|---|---|---|---|---|
| Parameter | Mean | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| RMSE | 0.0500 | 0.2000 | 0.0600 | 0.6000 | 0.3000 | 0.8000 | |
| weight | 0.4000 | 0.6000 | 0.4667 | 0.5333 | 0.3333 | 0.6667 | |
| Positioning State | MLE Estimated Value | GMM Estimated Value | Estimation Error/Truth Value Ratio | |||||
|---|---|---|---|---|---|---|---|---|
| Mean | RMSE | Mean | RMSE | Weight | MLE | GMM | Improvement | |
| RTK SPP | 0.0055 | 0.1560 | −0.0018 | 0.0539 | 0.4153 | - | 7.80% | - |
| −0.0039 | 0.1993 | 0.5847 | 22% | 0.35% | 21.65% ↑ | |||
| RTK CE | −0.0044 | 0.4418 | −0.0041 | 0.0631 | 0.4625 | - | 5.17% | - |
| 0.0024 | 0.0590 | 0.5375 | 26.37% | 0.17% | 26.2% ↑ | |||
| SPP CE | −0.0012 | 0.6665 | 0.0108 | 0.2838 | 0.3354 | - | 5.40% | - |
| −0.0023 | 0.7879 | 0.6746 | 16.60% | 1.51% | 15.09% ↑ | |||
| Device | Manufacturer/Model | Main Parameters | Interface |
|---|---|---|---|
| Reference equipment | SPATIOTEMPORAL/TJYJ/15-S1 | Gyroscope, 0.01°/h; Attitude, 0.03°; Heading, 0.05° | RS422 |
| GNSS | SPATIOTEM-PORAL/SKJW-09 | RTK, 2 cm + 1 ppm (CEP); Speed, 0.05 m/s; Attitude, 0.2° | RS422 |
| INS | SPATIOTEM-PORAL/SKJW-09 | Gyroscope, 30°/h; Accelerometer, 1 mg | RS422 |
| Wheel speed encoder | Kubler/Sendix7058 | Maximum speed, 600 r/min; Resolution 16 bit, 1~65,535 | CAN |
| Stereovision | Smarter Eye/SE1 | Depth of detection, 2~60 m; Baseline, 12 cm; Picture frame rate, 25 fps; HFOV, 40°; Pitch angle, 70~90° | CAN |
| Domain controller | Aixun Hongda/6388H-ZS | 4 generation I7 Celeron processor; 16 G of memory; 512 G solid-state drive | multi-interface |
| Parameter | RTK | SPP | CE-1 | CE-2 | CE-3 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| FG | AFG | FG | AFG | FG | AFG | FG | AFG | FG | AFG | |
| (°) | 0.2282 | 0.2165 | 0.4204 | 0.3551 | 0.7531 | 0.3574 | 0.5446 | 0.4632 | 0.8366 | 0.5264 |
| (°) | 0.2259 | 0.2189 | 0.4151 | 0.3285 | 0.6069 | 0.5327 | 0.5845 | 0.6272 | 0.9315 | 0.6569 |
| (°) | 0.2179 | 0.2078 | 0.9642 | 0.9853 | 5.1604 | 1.7736 | 3.8125 | 1.0995 | 1.5066 | 1.4190 |
| (m/s) | 0.0178 | 0.0173 | 0.0720 | 0.0688 | 0.2059 | 0.1637 | 0.1713 | 0.1561 | 0.2819 | 0.1790 |
| (m/s) | 0.0171 | 0.0169 | 0.0733 | 0.0689 | 0.2253 | 0.1611 | 0.1686 | 0.1397 | 0.3111 | 0.2105 |
| (m) | 0.0178 | 0.0173 | 0.2119 | 0.1978 | 0.6721 | 0.5002 | 0.4745 | 0.3507 | 0.7150 | 0.4324 |
| (m) | 0.0307 | 0.0286 | 0.2857 | 0.2442 | 0.8778 | 0.5849 | 0.6959 | 0.4384 | 1.4027 | 0.8003 |
| Parameter | RTK | SPP | CE-1 | CE-2 | CE-3 |
|---|---|---|---|---|---|
| (°) | 5.13% | 8.40% | 47.23% | 16.78% | 37.08% |
| (°) | 3.10% | 13.97% | 23.76% | 13.22% | 29.48% |
| (°) | 4.64% | 2.19% | 65.63% | 60.91% | 19.08% |
| (m/s) | 2.81% | 4.44% | 20.50% | 14.71% | 27.80% |
| (m/s) | 1.17% | 6.00% | 28.50% | 17.14% | 32.34% |
| (m) | 2.81% | 6.65% | 25.58% | 26.09% | 39.52% |
| (m) | 6.84% | 14.53% | 33.37% | 37.00% | 42.95% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Meng, Q.; Shen, Z.; Wang, L.; Li, L.; Jia, H. Resilient Factor Graph-Based GNSS/IMU/Vision/Odo Integrated Navigation Scheme Enhanced by Noise Approximate Gaussian Estimation in Challenging Environments. Remote Sens. 2024, 16, 2176. https://doi.org/10.3390/rs16122176
Li Z, Meng Q, Shen Z, Wang L, Li L, Jia H. Resilient Factor Graph-Based GNSS/IMU/Vision/Odo Integrated Navigation Scheme Enhanced by Noise Approximate Gaussian Estimation in Challenging Environments. Remote Sensing. 2024; 16(12):2176. https://doi.org/10.3390/rs16122176
Chicago/Turabian StyleLi, Ziyue, Qian Meng, Zuliang Shen, Lihui Wang, Lin Li, and Haonan Jia. 2024. "Resilient Factor Graph-Based GNSS/IMU/Vision/Odo Integrated Navigation Scheme Enhanced by Noise Approximate Gaussian Estimation in Challenging Environments" Remote Sensing 16, no. 12: 2176. https://doi.org/10.3390/rs16122176
APA StyleLi, Z., Meng, Q., Shen, Z., Wang, L., Li, L., & Jia, H. (2024). Resilient Factor Graph-Based GNSS/IMU/Vision/Odo Integrated Navigation Scheme Enhanced by Noise Approximate Gaussian Estimation in Challenging Environments. Remote Sensing, 16(12), 2176. https://doi.org/10.3390/rs16122176






