Hyperspectral Estimation of Chlorophyll Content in Grape Leaves Based on Fractional-Order Differentiation and Random Forest Algorithm
Abstract
1. Introduction
- (1)
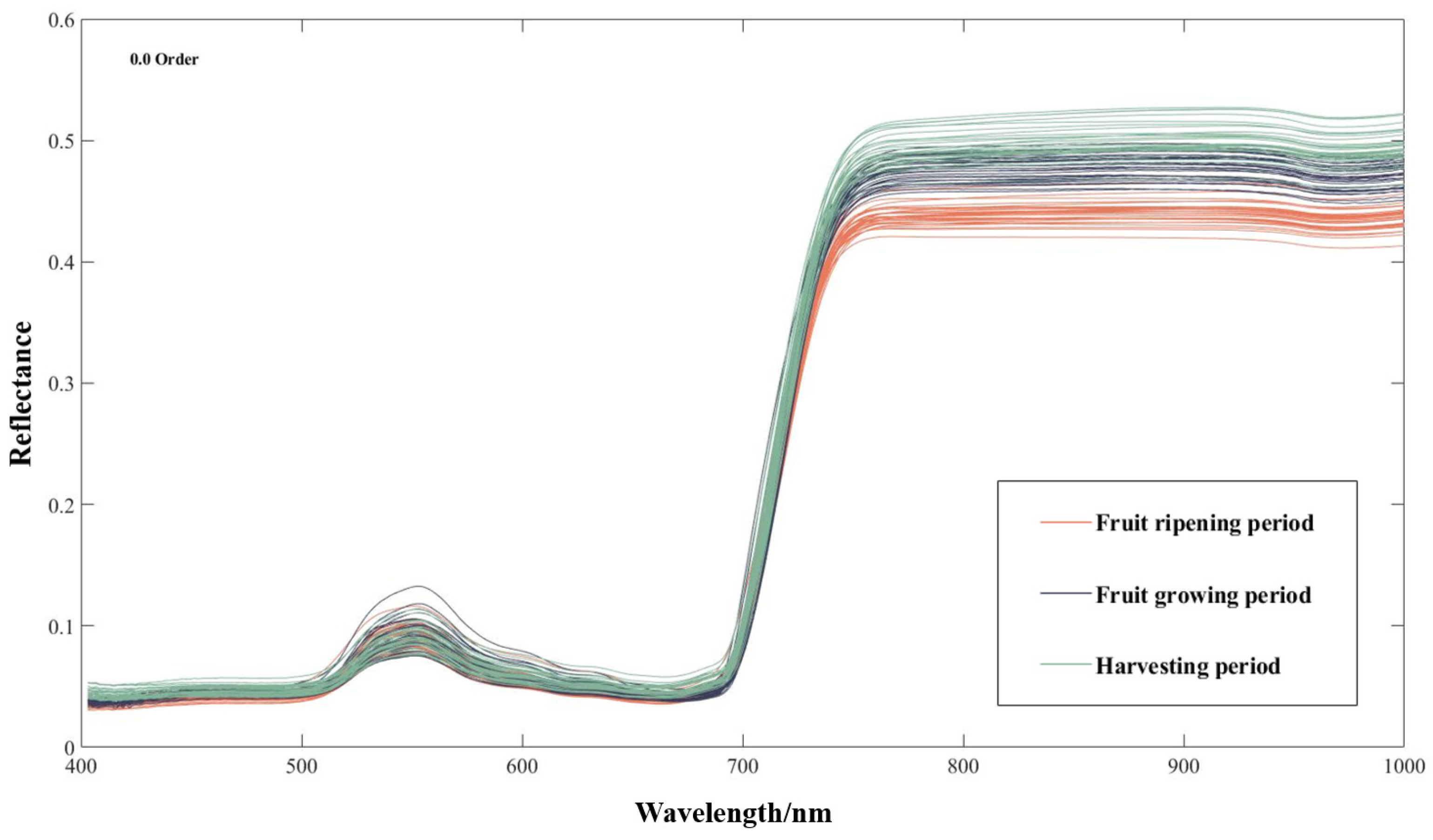
- By comparing the LCC hyperspectral response curves of grapes from different periods and species, the reasons for localized differences in the curves were resolved.
- (2)
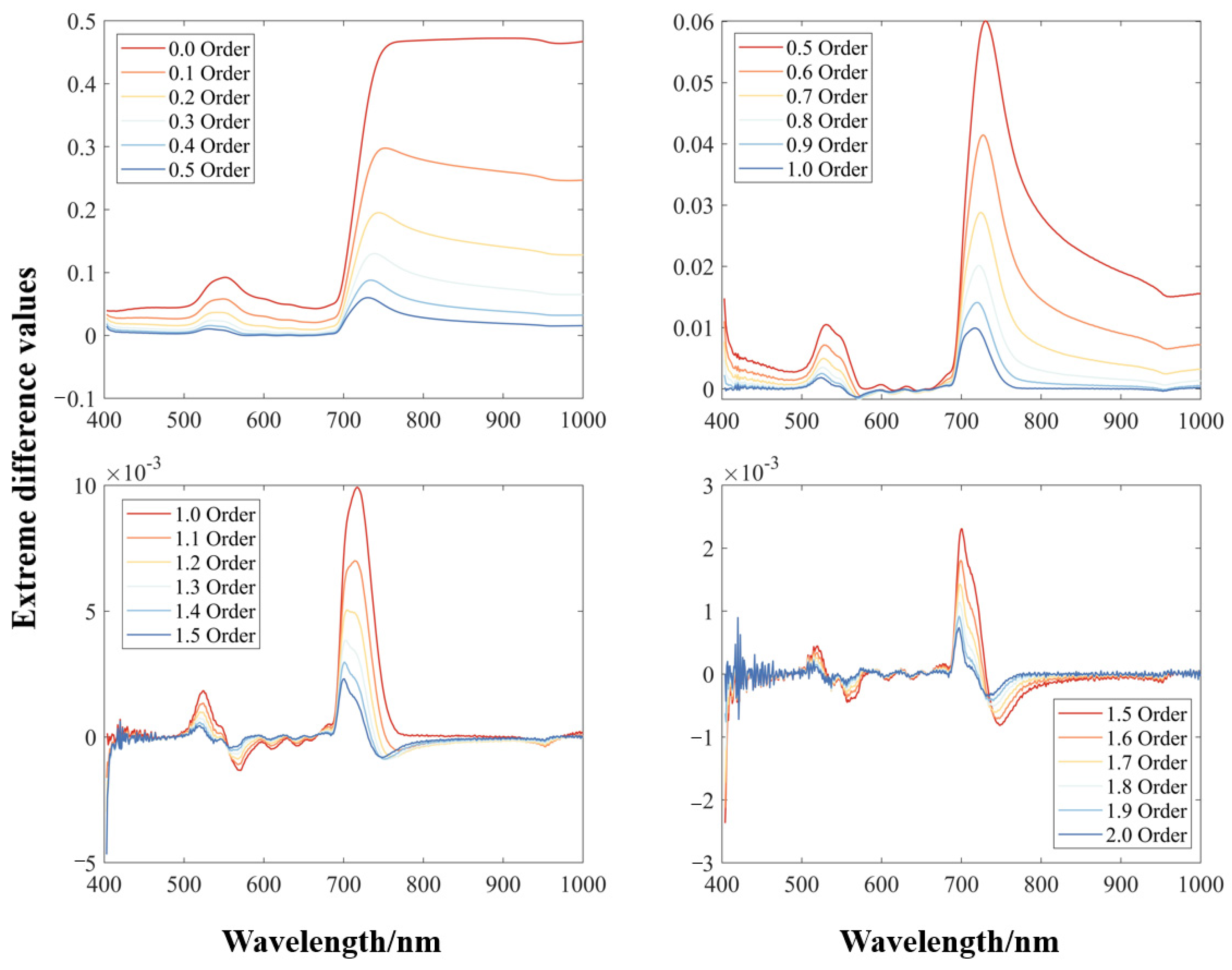
- The raw spectra were processed by FOD at 0.1-order intervals to obtain 0.1–2.0-order differential spectral curves. From the perspective of spectral characterization, it was initially concluded that FOD could better handle hyperspectral data.
- (3)
- We solved the correlation between different orders of spectra and LCC, and screened the characteristic bands to construct vegetation indices for subsequent analysis and modeling.
- (4)
- Using the screened typical vegetation indices as input features, the RFR method was utilized to establish LCC prediction models for grapes in different periods. Three periods were also validated uniformly to analyze whether there is universality for different fertility period FOD enhancing the model effect.
2. Materials and Methods
2.1. Study Site
2.2. Data Acquisition
2.3. Hyperspectral Data Processing
2.4. Models and Evaluation Indicators
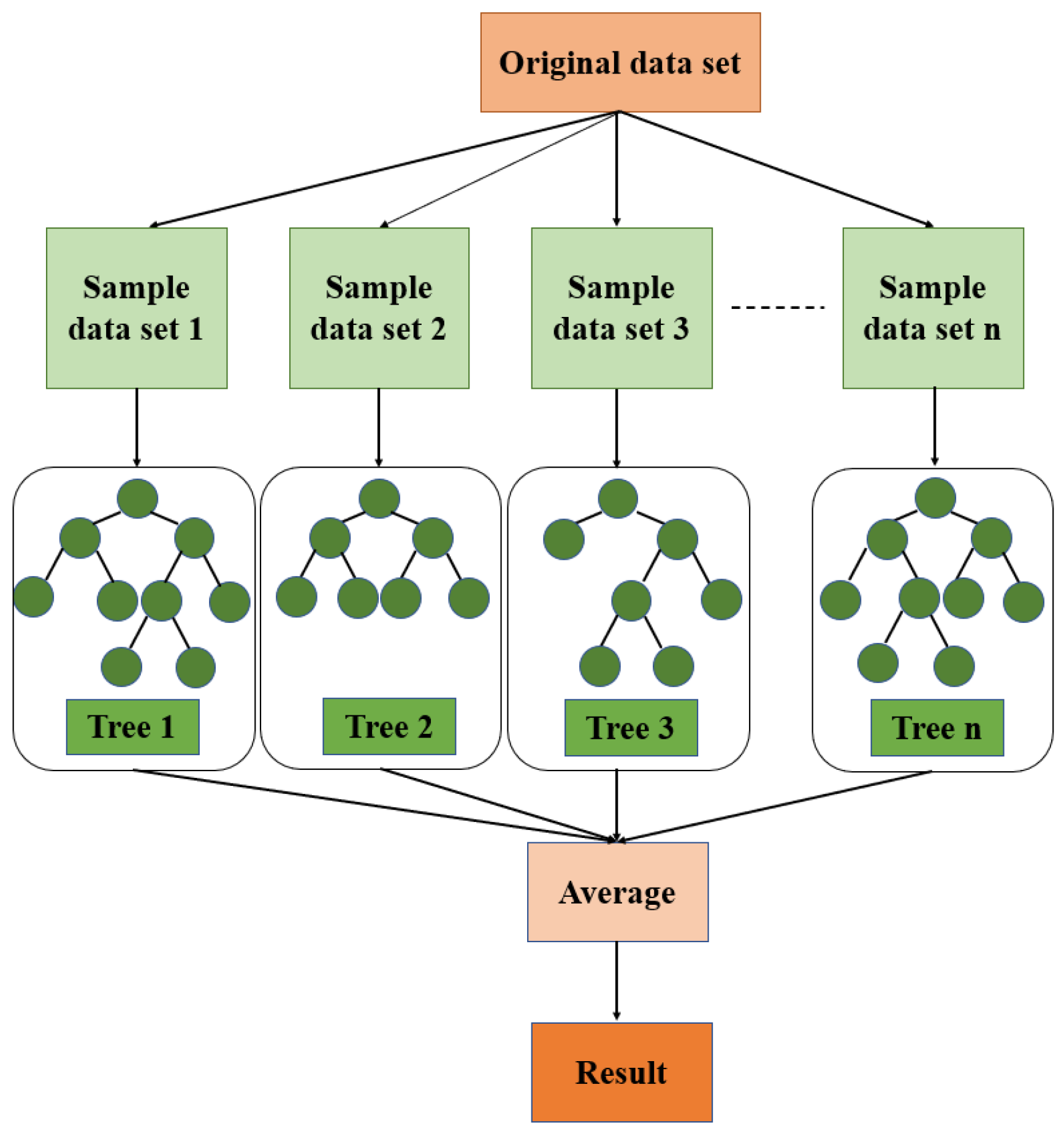
2.4.1. Principles of Random Forest Regression Modeling
2.4.2. Used Metrics
3. Results and Analysis
3.1. Characterization of Spectral Curves of Different Fractional Orders
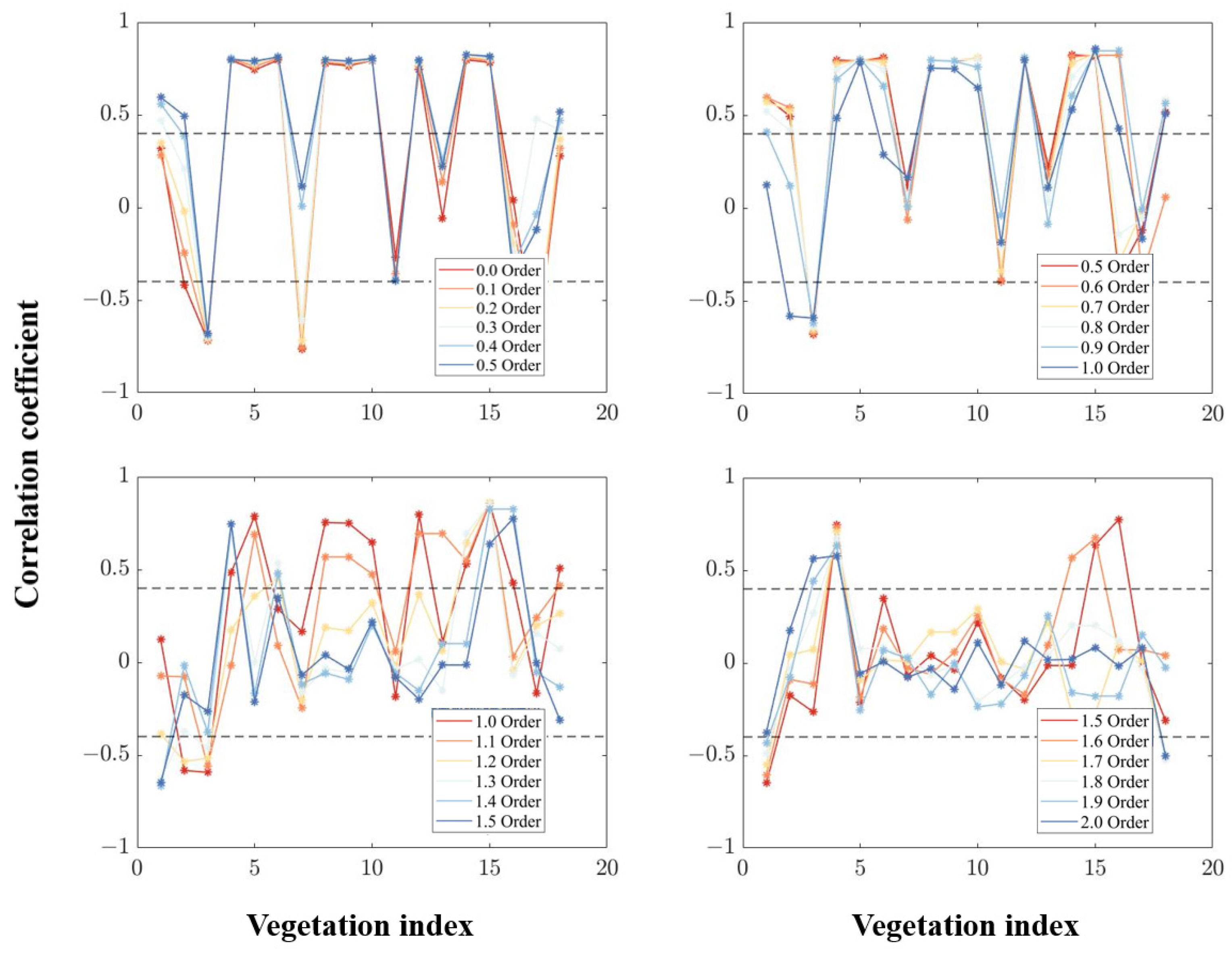
3.2. Trends in Correlation Coefficients
3.2.1. Effect of FOD on Full-Band Correlation Coefficient
3.2.2. Effect of FOD on vegetation indices
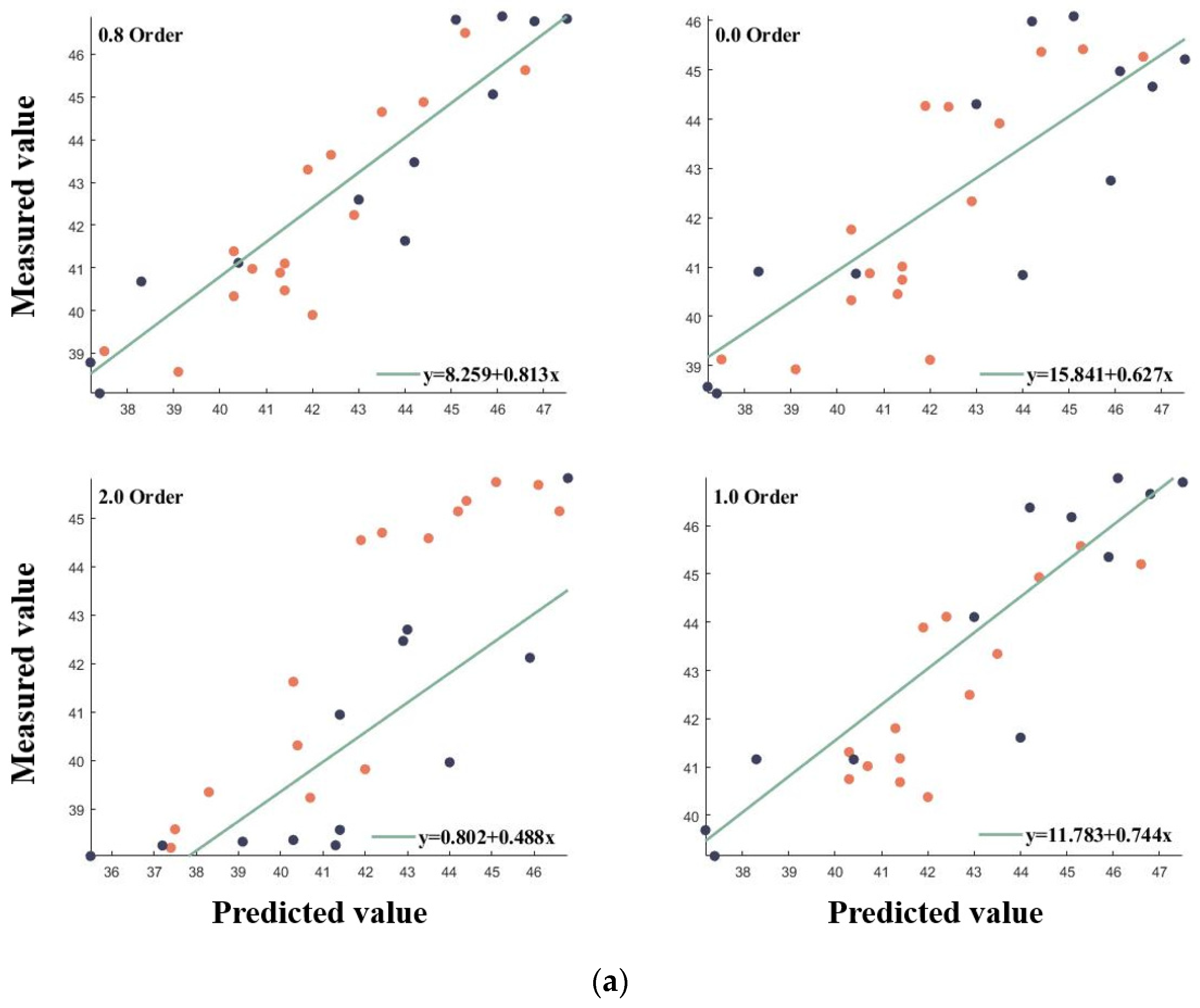
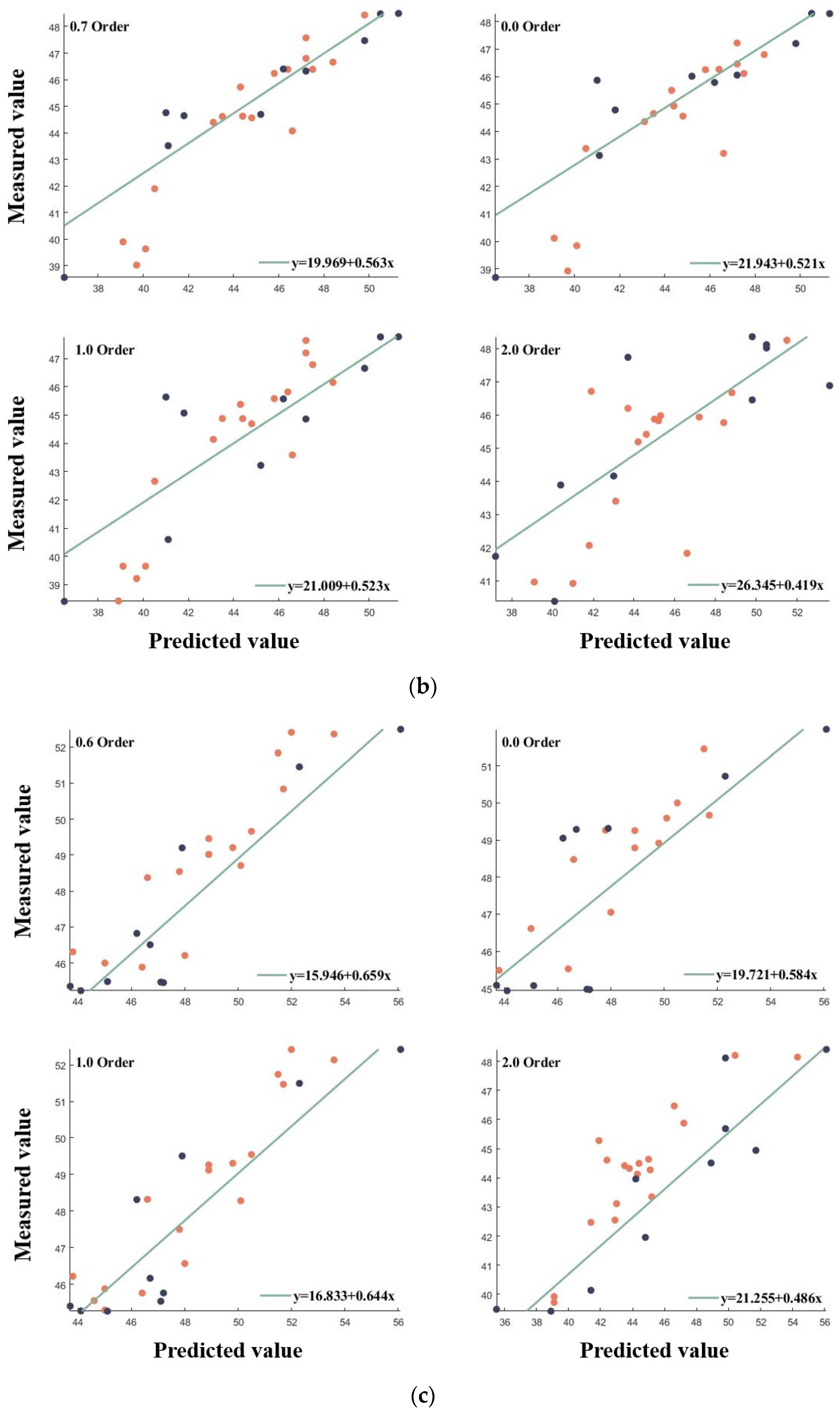
3.3. SPAD Prediction Model for Grapes Based on FOD-RFR
3.3.1. Model for Predicting LCC in Grapes at Different Fertility Stages
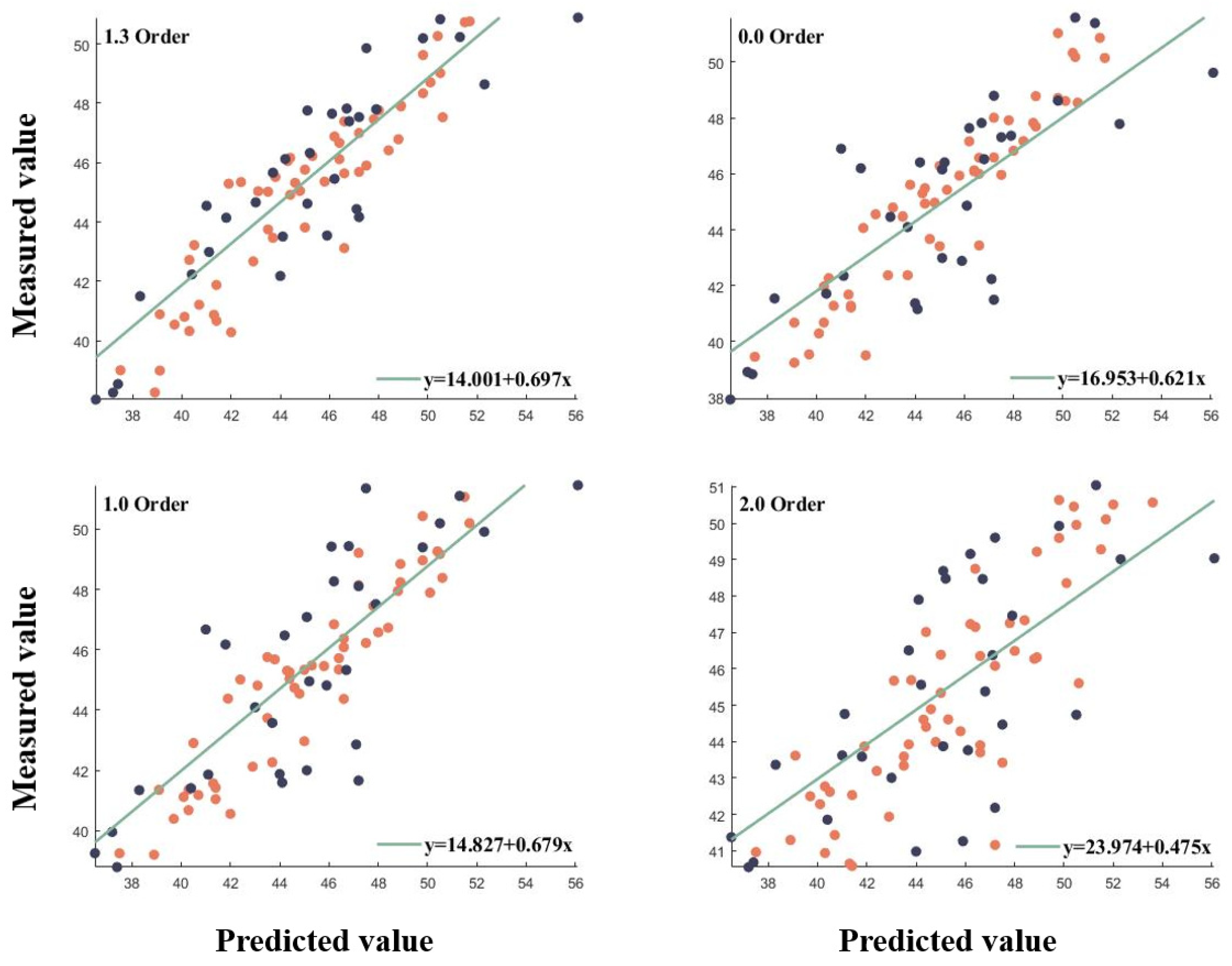
3.3.2. Grape LCC Prediction Model for the Full Life Span
4. Discussion
5. Conclusions
- (1)
- There was better sensitivity between the FOD spectra and grape LCC compared to the raw spectra, with the best correlation improving from 0.797 (order 0) to 0.862 (order 1.2) and the best coefficients of most of the differential spectra improved compared to the raw spectra.
- (2)
- The FOD-RFR chlorophyll prediction models for different fertility stages all had improved accuracy over the integer order, but the optimal order of the models differed for different fertility stages, with 0.8 order for ripening, 0.7 order for berry growth, and 0.6 order for picking. Model accuracy was also improved by applying the model to the full maturity period, with an optimal order of 1.3, where = 0.778, RMSE = 2.1, and NRMSE = 4.7%. This suggests that fractional-order discretization methods can be applied to grape leaf spectral preprocessing, providing theoretical support for improving accurate measurements of grape LCC.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, Z.; Tian, J.; Feng, K.; Gong, X.; Liu, J. Application of a hyperspectral imaging system to quantify leaf-scale chlorophyll, nitrogen and chlorophyll fluorescence parameters in grapevine. Plant Physiol. Biochem. 2021, 166, 723–737. [Google Scholar] [CrossRef]
- Wu, C.; Niu, Z.; Tang, Q.; Huang, W. Estimating chlorophyll content from hyperspectral vegetation indices: Modeling and validation. Agric. For. Meteorol. 2008, 148, 1230–1241. [Google Scholar] [CrossRef]
- Zhang, P.; Dong, T.; Jin, H.; Pei, D.; Pervaiz, T.; Ren, Y.; Jia, H.; Fang, J. Analysis of photosynthetic ability and related physiological traits in nodal leaves of grape. Sci. Hortic. 2022, 304, 111251. [Google Scholar] [CrossRef]
- Rey-Caramés, C.; Aguila, J.T.; Sanz-Garcia, A.; Chica-Olmo, M.; Diago, M.P. Quantifying spatio-temporal variation of leaf chlorophyll and nitrogen contents in vineyards. Biosyst. Eng. 2016, 150, 201–213. [Google Scholar] [CrossRef]
- Yang, X.; Yang, R.; Ye, Y.; Yuan, Z.; Wang, D.; Hua, K. Winter wheat SPAD estimation from UAV hyperspectral data using cluster-regression methods. Int. J. Appl. Earth Obs. Geoinf. 2021, 105, 102618. [Google Scholar] [CrossRef]
- Wojdyło, A.; Nowicka, P.; Tkacz, K.; Turkiewicz, I.P. Fruit tree leaves as unconventional and valuable source of chlorophyll and carotenoid compounds determined by liquid chromatography-photodiode-quadrupole/time of flight-electrospray ionization-mass spectrometry (LC-PDA-qTof-ESI-MS). Food Chem. 2021, 349, 129156. [Google Scholar] [CrossRef]
- Ahmad, N.A.; Muttalib, M.F.A.; Uda, M.N.A.; Arsat, Z.A.; Abdullah, F.; Hashim, M.K.R.; Azizan, F.A.; Jusoh, M.F.; Kamaruzaman, S.R.S.; Nordin, A.A. Measurement of leaf chlorophyll content in Harumanis mango cultivated in a greenhouse using SPAD meter. Mater. Today Proc. 2023; in press. [Google Scholar] [CrossRef]
- Liu, N.; Hokanson, E.W.; Hansen, N.; Townsend, P.A. Multi-year hyperspectral remote sensing of a comprehensive set of crop foliar nutrients in cranberries. ISPRS J. Photogramm. Remote Sens. 2023, 205, 135–146. [Google Scholar] [CrossRef]
- Song, D.; De Silva, K.; Brooks, M.D.; Kamruzzaman, M. Biomass prediction based on hyperspectral images of the Arabidopsis canopy. Comput. Electron. Agric. 2023, 210, 107939. [Google Scholar] [CrossRef]
- Flynn, K.C.; Baath, G.; Lee, T.O.; Gowda, P.; Northup, B. Hyperspectral reflectance and machine learning to monitor legume biomass and nitrogen accumulation. Comput. Electron. Agric. 2023, 211, 107991. [Google Scholar] [CrossRef]
- Lv, S.; Wang, J.; Wang, Z.; Fang, Y.; Wang, S.; Wang, F.; Wang, X.; Qu, G.; Ma, W. Construction of hyperspectral reflectance and spectral index inversion model for the water content of Catalpa bungei leaves. Microchem. J. 2024, 197, 109811. [Google Scholar] [CrossRef]
- Guo, A.; Ye, H.; Huang, W.; Qian, B.; Wang, J.; Lan, Y.; Wang, S. Inversion of maize leaf area index from UAV hyperspectral and multispectral imagery. Comput. Electron. Agric. 2023, 212, 108020. [Google Scholar] [CrossRef]
- Rajewicz, P.A.; Zhang, C.; Atherton, J.; Van Wittenberghe, S.; Riikonen, A.; Magney, T.; Fernandez-Marin, B. Jose Ignacio Garcia Plazaola, Albert Porcar-Castell, The photosynthetic response of spectral chlorophyll fluorescence differs across species and light environments in a boreal forest ecosystem. Agric. For. Meteorol. 2023, 334, 109434. [Google Scholar] [CrossRef]
- Huang, X.; Guan, H.; Bo, L.; Xu, Z.; Mao, X. Hyperspectral proximal sensing of leaf chlorophyll content of spring maize based on a hybrid of physically based modelling and ensemble stacking. Comput. Electron. Agric. 2023, 208, 107745. [Google Scholar] [CrossRef]
- Li, X.; Wei, Z.; Peng, F.; Liu, J.; Han, G. Estimating the distribution of chlorophyll content in CYVCV infected lemon leaf using hyperspectral imaging. Comput. Electron. Agric. 2022, 198, 107036. [Google Scholar] [CrossRef]
- Zhao, R.; An, L.; Tang, W.; Qiao, L.; Wang, N.; Li, M.; Sun, H.; Liu, G. Improving chlorophyll content detection to suit maize dynamic growth effects by deep features of hyperspectral data. Field Crops Res. 2023, 297, 108929. [Google Scholar] [CrossRef]
- Li, L.; Ren, T.; Ma, Y.; Wei, Q.; Wang, S.; Li, X.; Cong, R.; Liu, S.; Lu, J. Evaluating chlorophyll density in winter oilseed rape (Brassica napus L.) using canopy hyperspectral red-edge parameters. Comput. Electron. Agric. 2016, 126, 21–31. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; Miller, J.R.; Morales, A.; Berjón, A.; Agüera, J. Hyperspectral indices and model simulation for chlorophyll estimation in open-canopy tree crops. Remote Sens. Environ. 2004, 90, 463–476. [Google Scholar] [CrossRef]
- Zhang, D.; Zhang, J.; Peng, B.; Wu, T.; Jiao, Z.; Lu, Y.; Li, G.; Fan, X.; Shen, S.; Gu, A.; et al. Hyperspectral model based on genetic algorithm and SA-1DCNN for predicting Chinese cabbage chlorophyll content. Sci. Hortic. 2023, 321, 112334. [Google Scholar] [CrossRef]
- Xiao, B.; Li, S.; Dou, S.; He, H.; Fu, B.; Zhang, T.; Sun, W.; Yang, Y.; Xiong, Y.; Shi, J.; et al. Comparison of leaf chlorophyll content retrieval performance of citrus using FOD and CWT methods with field-based full-spectrum hyperspectral reflectance data. Comput. Electron. Agric. 2024, 217, 108559. [Google Scholar] [CrossRef]
- Sierociuk, D.; Skovranek, T.; Macias, M.; Podlubny, I.; Petras, I.; Dzielinski, A.; Ziubinski, P. Diffusion process modeling by using fractional-order models. Appl. Math. Comput. 2015, 257, 2–11. [Google Scholar] [CrossRef]
- Xu, L.; Shi, S.; Gong, W.; Shi, Z.; Qu, F.; Tang, X.; Chen, B.; Sun, J. Improving leaf chlorophyll content estimation through constrained PROSAIL model from airborne hyperspectral and LiDAR data. Int. J. Appl. Earth Obs. Geoinf. 2022, 115, 103128. [Google Scholar] [CrossRef]
- Kusnierek, K.; Korsaeth, A. Simultaneous identification of spring wheat nitrogen and water status using visible and near infrared spectra and Powered Partial Least Squares Regression. Comput. Electron. Agric. 2015, 117, 200–213. [Google Scholar] [CrossRef]
- Zhang, Y.; Hui, J.; Qin, Q.; Sun, Y.; Zhang, T.; Sun, H.; Li, M. Transfer-learning-based approach for leaf chlorophyll content estimation of winter wheat from hyperspectral data. Remote Sens. Environ. 2021, 267, 112724. [Google Scholar] [CrossRef]
- Lazopoulos, K.A.; Karaoulanis, D.; Lazopoulos, A.K. On fractional modelling of viscoelastic mechanical systems. Mech. Res. Commun. 2016, 78 Pt A, 1–5. [Google Scholar] [CrossRef]
- Zhang, J.; Jing, X.; Song, X.; Zhang, T.; Duan, W.; Su, J. Hyperspectral estimation of wheat stripe rust using fractional order differential equations and Gaussian process methods. Comput. Electron. Agric. 2023, 206, 107671. [Google Scholar] [CrossRef]
- Area, I.; Losada, J.; Nieto, J.J. A note on the fractional logistic equation. Phys. A Stat. Mech. Appl. 2016, 444, 182–187. [Google Scholar] [CrossRef]
- Jin, J.; Wang, Q. Hyperspectral indices developed from the low order fractional derivative spectra can capture leaf dry matter content across a variety of species better. Agric. For. Meteorol. 2022, 322, 109007. [Google Scholar] [CrossRef]
- Song, G.; Wang, Q.; Jin, J. Estimation of leaf photosynthetic capacity parameters using spectral indices developed from fractional-order derivatives. Comput. Electron. Agric. 2023, 212, 108068. [Google Scholar] [CrossRef]
- Ren, K.; Dong, Y.; Huang, W.; Guo, A.; Jing, X. Monitoring of winter wheat stripe rust by collaborating canopy SIF with wavelet energy coefficients. Comput. Electron. Agric. 2023, 215, 108366. [Google Scholar] [CrossRef]
- Abulaiti, Y.; Sawut, M.; Maimaitiaili, B.; Chunyue, M. A possible fractional order derivative and optimized spectral indices for assessing total nitrogen content in cotton. Comput. Electron. Agric. 2020, 171, 105275. [Google Scholar] [CrossRef]
- Zhang, J.; Tian, H.; Wang, D.; Li, H.; Mouazen, A.M. A novel spectral index for estimation of relative chlorophyll content of sugar beet. Comput. Electron. Agric. 2021, 184, 106088. [Google Scholar] [CrossRef]
- Khan, M.; Kumar, P. A level set based fractional order variational model for motion estimation in application-oriented spectrum. Expert Syst. Appl. 2023, 219, 119628. [Google Scholar] [CrossRef]
- Fu, C.; Gan, S.; Xiong, H.; Tian, A. A new method to estimate soil organic matter using the combination model based on short memory fractional order derivative and machine learning model. Infrared Phys. Technol. 2023, 134, 104922. [Google Scholar] [CrossRef]
- Gamini, S.; Kumar, S.S. Homomorphic filtering for the image enhancement based on fractional-order derivative and genetic algorithm. Comput. Electr. Eng. 2023, 106, 108566. [Google Scholar] [CrossRef]
- Li, C.; Chen, A.; Ye, J. Numerical approaches to fractional calculus and fractional ordinary differential equation. J. Comput. Phys. 2011, 230, 3352–3368. [Google Scholar] [CrossRef]
- Kavuran, G. When machine learning meets fractional-order chaotic signals: Detecting dynamical variations. Chaos, Solitons & Fractals 2022, 157, 111908. [Google Scholar] [CrossRef]
- Zhao, C.; Shi, L.; Guan, Y.; Li, X.; Shi, Z. Formal modeling and verification of fractional order linear systems. ISA Trans. 2016, 62, 87–93. [Google Scholar] [CrossRef] [PubMed]
- Cai, W.-L.; Fang, C.; Liu, L.-F.; Sun, F.-Y.; Xin, G.-Z.; Zheng, J.-Y. Pseudotargeted metabolomics-based random forest model for tracking plant species from herbal products. Phytomedicine 2023, 118, 154927. [Google Scholar] [CrossRef] [PubMed]
- Lihou, K.; Wall, R. Predicting the current and future risk of ticks on livestock farms in Britain using random forest models. Vet. Parasitol. 2022, 311, 109806. [Google Scholar] [CrossRef]
- Liu, J.; Jiang, L.; Chen, Y.; Liu, Z.; Yuan, H.; Wen, Y. Study on prediction model of liquid hold up based on random forest algorithm. Chem. Eng. Sci. 2023, 268, 118383. [Google Scholar] [CrossRef]
- Liao, M.; Wen, H.; Yang, L.; Wang, G.; Xiang, X.; Liang, X. Improving the model robustness of flood hazard mapping based on hyperparameter optimization of random forest. Expert Syst. Appl. 2024, 241, 122682. [Google Scholar] [CrossRef]
- da Silva, B.C.; de Mello Prado, R.; Baio, F.H.R.; Campos, C.N.S.; Teodoro, L.P.R.; Teodoro, P.E.; Santana, D.C.; Fernandes, T.F.S.; da Silva Junior, C.A.; de Souza Loureiro, E. New approach for predicting nitrogen and pigments in maize from hyperspectral data and machine learning models. Remote Sens. Appl. Soc. Environ. 2024, 33, 101110. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, Y.; Liu, K.; Lan, S.; Gao, T.; Li, M. Winter wheat yield prediction using integrated Landsat 8 and Sentinel-2 vegetation index time-series data and machine learning algorithms. Comput. Electron. Agric. 2023, 213, 108250. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Merzlyak, M.N.; Zur, Y.; Stark, R.; Gritz, U. Non-Destructive and Remote Sensing Techniques for Estimation of Vegetation Status. Papers in Natural Resources. Paper 273. 2001. Available online: https://digitalcommons.unl.edu/natrespapers/273 (accessed on 31 January 2001).
- Gitelson, A.A. Remote estimation of canopy chlorophyll content in crops. Geophys. Res. Lett. 2005, 32, L08403. [Google Scholar] [CrossRef]
- Kim, M.S.; Daughtry, C.T.; Chapelle, E.W. The use of high spectral resolution bands for estimating absorbed photosynthetically active radiation (A par). In Proceedings of the Sixth Symposium on Physical Measurements and Signatures in Remote Sensing, Val D’Isure, France, 17–21 January 1994; Available online: https://ntrs.nasa.gov/citations/19950010604 (accessed on 1 January 1994).
- Eitel, J.U.H.; Long, D.S.; Gessler, P.E. Using in-situ measurements to evaluate the new RapidEye™ satellite series for prediction of wheat nitrogen status. Int. J. Remote Sens. 2007, 28, 4183–4190. [Google Scholar] [CrossRef]
- Sims, D.A.; Gamon, J.A. Relationships between leaf pigment content and spectral reflectance across a wide range of species, leaf structures and developmental stages. Remote Sens. Environ. 2002, 81, 337–354. [Google Scholar] [CrossRef]
- Dash, J.; Curran, P.J. Evaluation of the MERIS terrestrial chlorophyll index (MTCI). Adv. Space Res. 2007, 39, 100–104. [Google Scholar] [CrossRef]
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef]
- Evangelides, C.; Nobajas, A. Red-Edge Normalised Difference Vegetation Index (NDVI705) from Sentinel-2 imagery to assess post-fire regeneration. Remote Sens. Appl. Soc. Environ. 2020, 17, 100283. [Google Scholar] [CrossRef]
- Peñuelas, J.; Gamon, J.A.; Fredeen, A.L.; Merino, J.; Field, C.B. Reflectance indices associated with physiological changes in nitrogen- and water-limited sunflower leaves. Remote Sens. Environ. 1994, 48, 135–146. [Google Scholar] [CrossRef]
- Pearson, R.L.; Miller, L.D. Remote mapping of standing crop biomass for estimation of the productive of the short grass prairie. Remote Sens. Environ. 1972, 45, 7–12. [Google Scholar] [CrossRef] [PubMed]
- Vogelman, J.E.; Rock, B.N.; Moss, D.M. Red edge spectral measurements form sugar maple leaves. Int. J. Remote Sens. 1993, 14, 1563–1575. [Google Scholar] [CrossRef]
- Jordan, C.F. Derivation of Leaf-Area Index from Quality of Light on the Forest Floor. Ecology 1969, 50, 663–666. [Google Scholar] [CrossRef]
- Haboudane, D.; Miller, J.R.; Tremblay, N.; Zarco-Tejada, P.J.; Dextraze, L. Integrated narrowband vegetation indices for prediction of crop chlorophyll content for application to precision agriculture. Remote Sens. Environ. 2002, 81, 416–426. [Google Scholar] [CrossRef]
- Broge, N.H.; Leblanc, E. Comparing prediction power and stability of broadband and hyperspectral vegetation indices for estimation of green leaf area index and canopy chlorophyll density. Remote Sens. Environ. 2001, 76, 156–172. [Google Scholar] [CrossRef]
- Zheng, T.; Liu, N.; Wu, L.; Li, M.; Sun, H.; Zhang, Q.; Wu, J. Estimation of Chlorophyll Content in Potato Leaves Based on Spectral Red Edge Position. IFAC-Pap. 2018, 51, 602–606. [Google Scholar] [CrossRef]
- Ali, A.; Imran, M. Evaluating the potential of red edge position (REP) of hyperspectral remote sensing data for real time estimation of LAI & chlorophyll content of kinnow mandarin (Citrus reticulata) fruit orchards. Sci. Hortic. 2020, 267, 109326. [Google Scholar] [CrossRef]
- Jiang, G.; Zhou, K.; Wang, J.; Sun, G.; Cui, S.; Chen, T.; Zhou, S.; Bai, Y.; Chen, X. Estimation of rock copper content based on Fractional-order derivative and visible Near-infrared–Shortwave infrared spectroscopy. Ore Geol. Rev. 2022, 150, 105092. [Google Scholar] [CrossRef]
- Zhang, Z.; Ding, J.; Wang, J.; Ge, X. Prediction of soil organic matter in northwestern China using fractional-order derivative spectroscopy and modified normalized difference indices. CATENA 2020, 185, 104257. [Google Scholar] [CrossRef]
- Hong, Y.; Liu, Y.; Chen, Y.; Liu, Y.; Yu, L.; Liu, Y.; Cheng, H. Application of fractional-order derivative in the quantitative estimation of soil organic matter content through visible and near-infrared spectroscopy. Geoderma 2019, 337, 758–769. [Google Scholar] [CrossRef]
- Liu, Y.; Lu, Y.; Chen, D.; Zheng, W.; Ma, Y.; Pan, X. Simultaneous estimation of multiple soil properties under moist conditions using fractional-order derivative of vis-NIR spectra and deep learning. Geoderma 2023, 438, 116653. [Google Scholar] [CrossRef]
- Lao, C.; Chen, J.; Zhang, Z.; Chen, Y.; Ma, Y.; Chen, H.; Gu, X.; Ning, J.; Jin, J.; Li, X. Predicting the contents of soil salt and major water-soluble ions with fractional-order derivative spectral indices and variable selection. Comput. Electron. Agric. 2021, 182, 106031. [Google Scholar] [CrossRef]
- Xu, M.; Liu, R.; Chen, J.M.; Liu, Y.; Shang, R.; Ju, W.; Wu, C.; Huang, W. Retrieving leaf chlorophyll content using a matrix-based vegetation index combination approach. Remote Sens. Environ. 2019, 224, 60–73. [Google Scholar] [CrossRef]
- Qiao, L.; Tang, W.; Gao, D.; Zhao, R.; An, L.; Li, M.; Sun, H.; Song, D. UAV-based chlorophyll content estimation by evaluating vegetation index responses under different crop coverages. Comput. Electron. Agric. 2022, 196, 106775. [Google Scholar] [CrossRef]
- Li, Z.; Bi, S.; Hao, S.; Cui, Y. Aboveground biomass estimation in forests with random forest and Monte Carlo-based uncertainty analysis. Ecol. Indic. 2022, 142, 109246. [Google Scholar] [CrossRef]
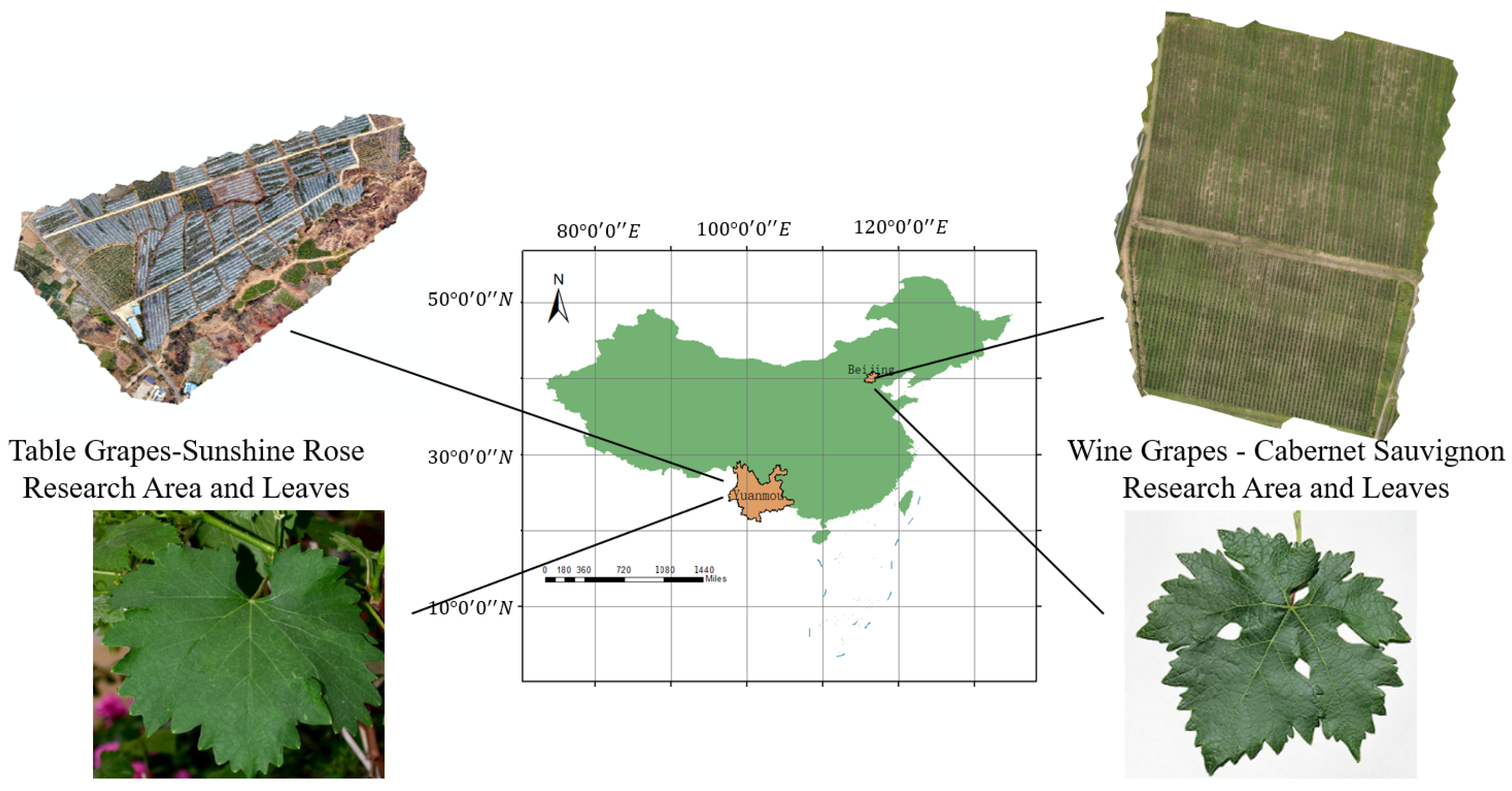
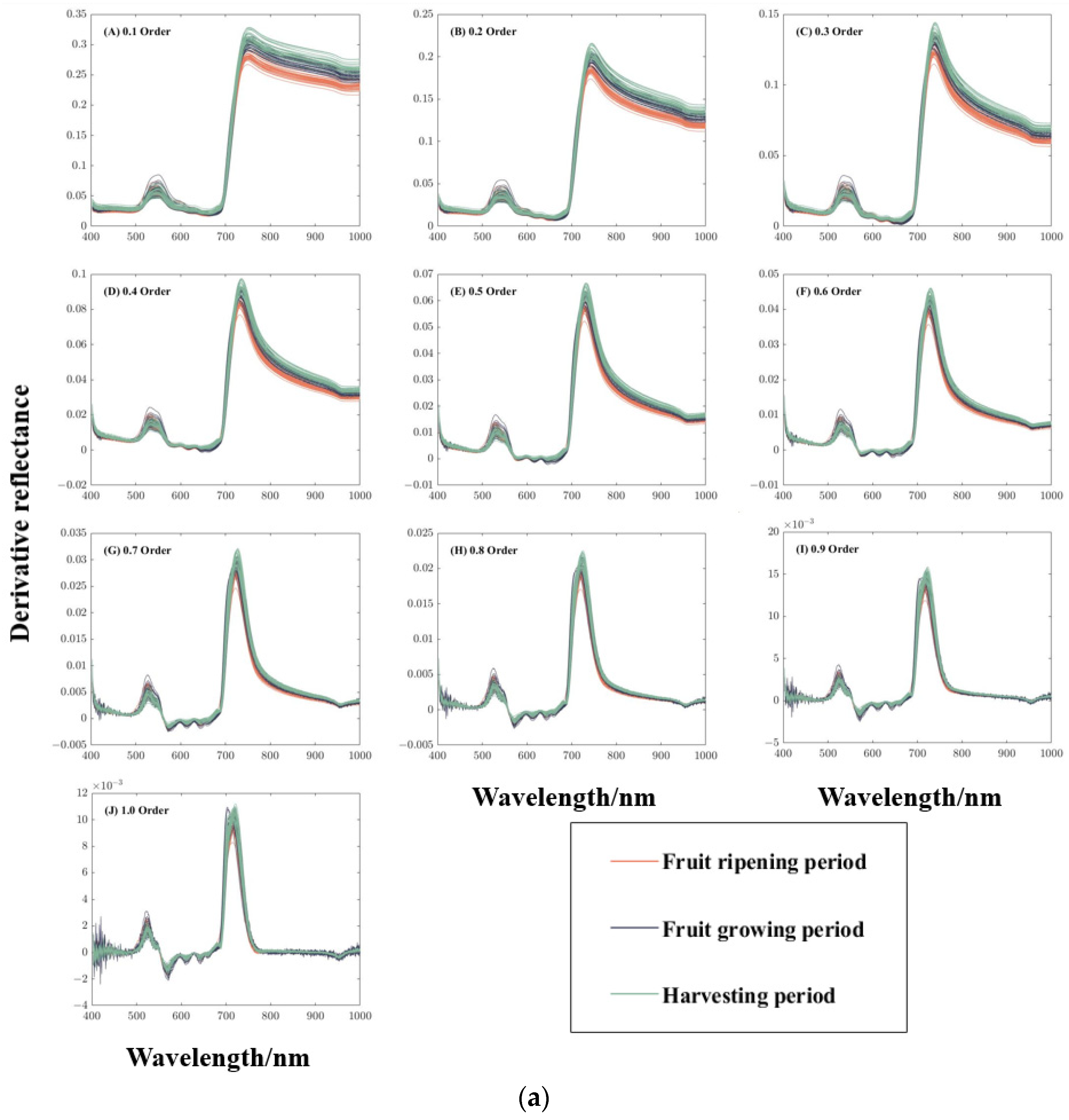
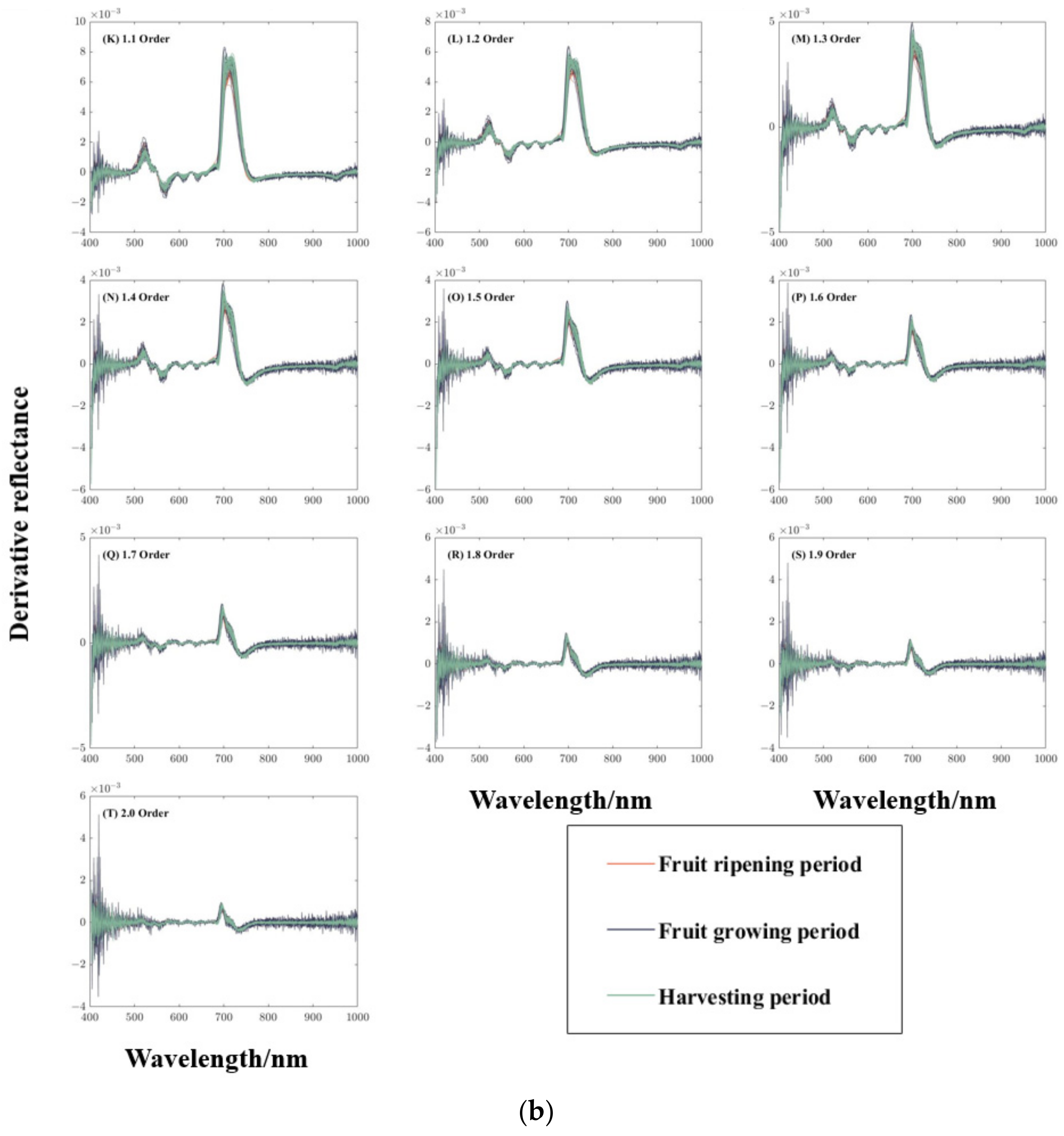
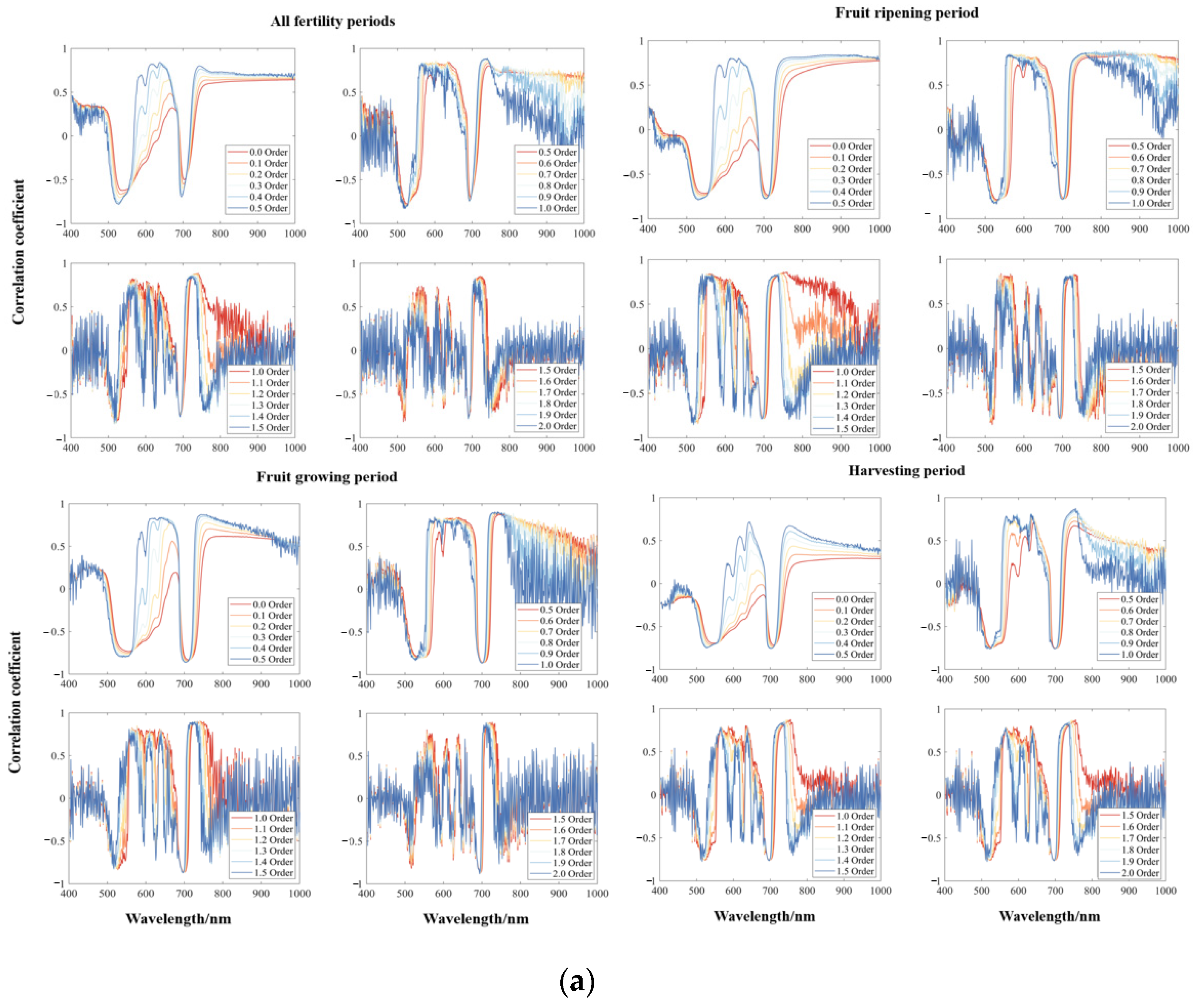
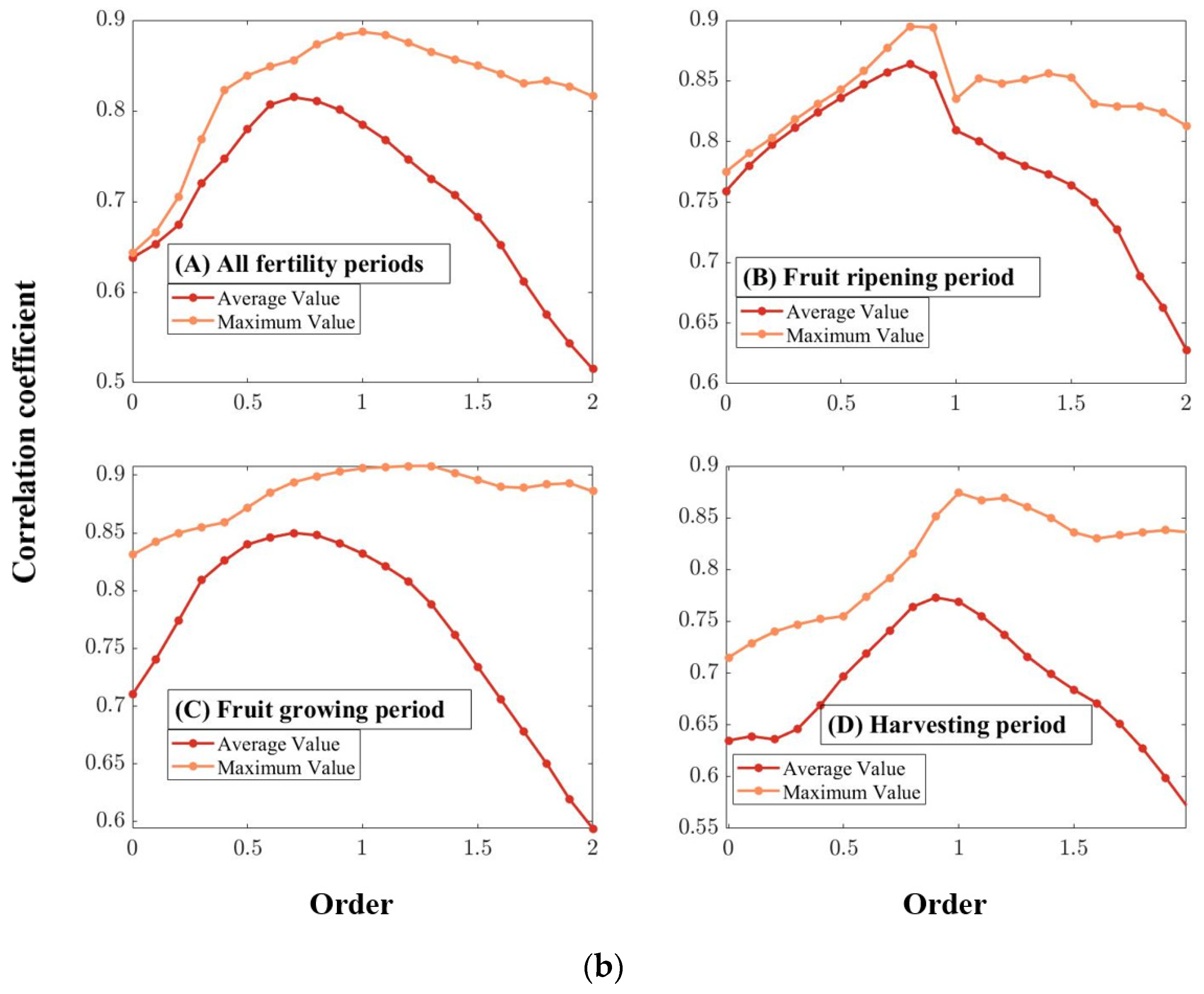
| Site | Time | Variety | Growing Period | Number of Neighborhoods |
|---|---|---|---|---|
| Fangshan District, Beijing | 19 August 2022 | Wine Grapes—Cabernet Sauvignon | Ripening period | 32 |
| Yuanmou County, Chuxiong Yi Autonomous Prefecture, Yunnan Province | 26 August 2023 | Edible Grapes—Sunshine Rose | Growing period | 30 |
| 4 November 2023 | Harvesting period | 29 |
| All Reproductive Periods | Growing Period | Ripening Period | Harvesting Period | |
|---|---|---|---|---|
| Mean value/order | (0.815) 0.7 | (0.848) 0.8 | (0.864) 0.8 | (0.773) 0.9 |
| Max value/order | (0.887) 1.0 | (0.908) 1.2 | (0.895) 0.8 | (0.874) 1.0 |
| VI | Formula | References |
|---|---|---|
| Anthocyanin reflectance index (ARI) | [45] | |
| Green carotenoid index (CAR_green) | [46] | |
| Chlorophyll absorption reflectance index (CARI) | [47] | |
| Green chlorophyll index (CI_green) | [46] | |
| Red edge chlorophyll index (CI) | [46] | |
| Green normalized difference vegetation index (GNDVI) | [45] | |
| Modified chlorophyll absorption reflectance index (MACRI) | [48] | |
| Modified normalized difference (mND_705) | [49] | |
| Modified simple ratio (mSR_705) | [49] | |
| Meris terrestrial chlorophyll index (MTCI) | [50] | |
| Normalized difference vegetation index (NDVI) | [51] | |
| Red edge normalized difference vegetation index () | [52] | |
| Normalized total pigment to chlorophyll index (NPCI) | [53] | |
| Ratio vegetation index 1 () | [54] | |
| Ratio vegetation index 2 () | [55] | |
| Simple ratio (SR) | [56] | |
| Transformed chlorophyll absorption ratio (TCARI) | [57] | |
| Transformed vegetation index (TVI) | [58] |
| Differential Order | 0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1.0 |
| Number | 13 | 12 | 12 | 14 | 12 | 13 | 13 | 13 | 13 | 13 | 12 |
| Correlation coefficient | 0.797 | 0.807 | 0.815 | 0.822 | 0.826 | 0.826 | 0.823 | 0.831 | 0.839 | 0.847 | 0.856 |
| Differential order | 1.1 | 1.2 | 1.3 | 1.4 | 1.5 | 1.6 | 1.7 | 1.8 | 1.9 | 2.0 | |
| Number | 10 | 5 | 6 | 5 | 4 | 4 | 3 | 3 | 3 | 2 | |
| Correlation coefficient | 0.861 | 0.862 | 0.852 | 0.826 | 0.775 | 0.732 | 0.708 | 0.675 | 0.634 | 0.579 |
| (a) | |||||||
| Order | RMSE | NRMSE | Order | RMSE | NRMSE | ||
| Original | 0.695 | 1.975 | 4.6% | 1.1 | 0.752 | 1.783 | 4.1% |
| 0.1 | 0.728 | 1.866 | 4.3% | 1.2 | 0.682 | 2.017 | 4.7% |
| 0.2 | 0.761 | 1.749 | 4.1% | 1.3 | 0.668 | 2.06 | 4.8% |
| 0.3 | 0.777 | 1.716 | 4% | 1.4 | 0.612 | 2.228 | 5.2% |
| 0.4 | 0.824 | 1.498 | 3.5% | 1.5 | 0.691 | 1.987 | 4.6% |
| 0.5 | 0.854 | 1.365 | 3.2% | 1.6 | 0.638 | 2.207 | 5.1% |
| 0.6 | 0.864 | 1.319 | 3.1% | 1.7 | 0.623 | 2.353 | 5.5% |
| 0.7 | 0.869 | 1.295 | 3% | 1.8 | 0.589 | 2.341 | 5.7% |
| 0.8 | 0.883 | 1.224 | 2.8% | 1.9 | 0.528 | 2.347 | 5.7% |
| 0.9 | 0.803 | 1.586 | 3.7% | 2.0 | 0.488 | 2.259 | 5.4% |
| 1.0 | 0.789 | 1.641 | 3.8% | ||||
| (b) | |||||||
| Order | RMSE | NRMSE | Order | RMSE | NRMSE | ||
| Original | 0.699 | 2.534 | 5.6% | 1.1 | 0.637 | 2.799 | 6.2% |
| 0.1 | 0.701 | 2.5 | 5.5% | 1.2 | 0.725 | 2.421 | 5.4% |
| 0.2 | 0.717 | 2.455 | 5.4% | 1.3 | 0.75 | 2.306 | 5.1% |
| 0.3 | 0.693 | 2.555 | 5.7% | 1.4 | 0.702 | 2.521 | 5.6% |
| 0.4 | 0.731 | 2.393 | 5.3% | 1.5 | 0.742 | 2.345 | 5.2% |
| 0.5 | 0.737 | 2.367 | 5.3% | 1.6 | 0.748 | 2.319 | 5.1% |
| 0.6 | 0.735 | 2.375 | 5.3% | 1.7 | 0.713 | 2.472 | 5.5% |
| 0.7 | 0.761 | 2.254 | 5% | 1.8 | 0.752 | 2.296 | 5.1% |
| 0.8 | 0.733 | 2.383 | 5.3% | 1.9 | 0.628 | 2.798 | 6.1% |
| 0.9 | 0.753 | 2.292 | 5.1% | 2.0 | 0.576 | 3.474 | 7.5% |
| 1.0 | 0.644 | 2.752 | 6.1% | ||||
| (c) | |||||||
| Order | RMSE | NRMSE | Order | RMSE | NRMSE | ||
| Original | 0.631 | 2.2 | 4.6% | 1.1 | 0.779 | 1.704 | 3.6% |
| 0.1 | 0.648 | 2.15 | 4.5% | 1.2 | 0.708 | 1.957 | 4.1% |
| 0.2 | 0.699 | 1.988 | 4.2% | 1.3 | 0.619 | 2.238 | 4.7% |
| 0.3 | 0.699 | 1.987 | 4.2% | 1.4 | 0.601 | 2.289 | 4.8% |
| 0.4 | 0.749 | 1.817 | 3.8% | 1.5 | 0.684 | 2.036 | 4.3% |
| 0.5 | 0.785 | 1.679 | 3.5% | 1.6 | 0.648 | 2.15 | 4.5% |
| 0.6 | 0.807 | 1.593 | 3.3% | 1.7 | 0.604 | 3.617 | 7.7% |
| 0.7 | 0.804 | 1.605 | 3.4% | 1.8 | 0.569 | 3.49 | 7.8% |
| 0.8 | 0.781 | 1.697 | 3.6% | 1.9 | 0.587 | 2.544 | 5.8% |
| 0.9 | 0.767 | 1.748 | 3.7% | 2.0 | 0.526 | 4.12 | 8.9% |
| 1.0 | 0.769 | 1.742 | 3.7% | ||||
| Order | RMSE | NRMSE | Order | RMSE | NRMSE | ||
|---|---|---|---|---|---|---|---|
| Original | 0.605 | 2.799 | 6.2% | 1.1 | 0.691 | 2.746 | 5.5% |
| 0.1 | 0.688 | 2.488 | 5.5% | 1.2 | 0.763 | 2.167 | 4.8% |
| 0.2 | 0.706 | 2.412 | 5.4% | 1.3 | 0.778 | 2.1 | 4.7% |
| 0.3 | 0.724 | 2.337 | 5.2% | 1.4 | 0.766 | 2.153 | 4.8% |
| 0.4 | 0.74 | 2.269 | 5% | 1.5 | 0.725 | 2.335 | 5.2% |
| 0.5 | 0.722 | 2.348 | 5.2% | 1.6 | 0.594 | 2.838 | 6.3% |
| 0.6 | 0.702 | 2.426 | 5.4% | 1.7 | 0.55 | 2.987 | 6.6% |
| 0.7 | 0.681 | 2.513 | 5.6% | 1.8 | 0.561 | 2.951 | 6.5% |
| 0.8 | 0.631 | 2.704 | 6% | 1.9 | 0.519 | 3.392 | 7.5% |
| 0.9 | 0.631 | 2.803 | 6% | 2.0 | 0.461 | 3.268 | 7.3% |
| 1.0 | 0.63 | 2.709 | 6% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Xu, X.; Wu, W.; Zhu, Y.; Yang, G.; Yang, X.; Meng, Y.; Jiang, X.; Xue, H. Hyperspectral Estimation of Chlorophyll Content in Grape Leaves Based on Fractional-Order Differentiation and Random Forest Algorithm. Remote Sens. 2024, 16, 2174. https://doi.org/10.3390/rs16122174
Li Y, Xu X, Wu W, Zhu Y, Yang G, Yang X, Meng Y, Jiang X, Xue H. Hyperspectral Estimation of Chlorophyll Content in Grape Leaves Based on Fractional-Order Differentiation and Random Forest Algorithm. Remote Sensing. 2024; 16(12):2174. https://doi.org/10.3390/rs16122174
Chicago/Turabian StyleLi, Yafeng, Xingang Xu, Wenbiao Wu, Yaohui Zhu, Guijun Yang, Xiaodong Yang, Yang Meng, Xiangtai Jiang, and Hanyu Xue. 2024. "Hyperspectral Estimation of Chlorophyll Content in Grape Leaves Based on Fractional-Order Differentiation and Random Forest Algorithm" Remote Sensing 16, no. 12: 2174. https://doi.org/10.3390/rs16122174
APA StyleLi, Y., Xu, X., Wu, W., Zhu, Y., Yang, G., Yang, X., Meng, Y., Jiang, X., & Xue, H. (2024). Hyperspectral Estimation of Chlorophyll Content in Grape Leaves Based on Fractional-Order Differentiation and Random Forest Algorithm. Remote Sensing, 16(12), 2174. https://doi.org/10.3390/rs16122174









