Wind Wave Effects on the Doppler Spectrum of the Ka-Band Spaceborne Doppler Measurement
Abstract
1. Introduction
2. Materials and Methods
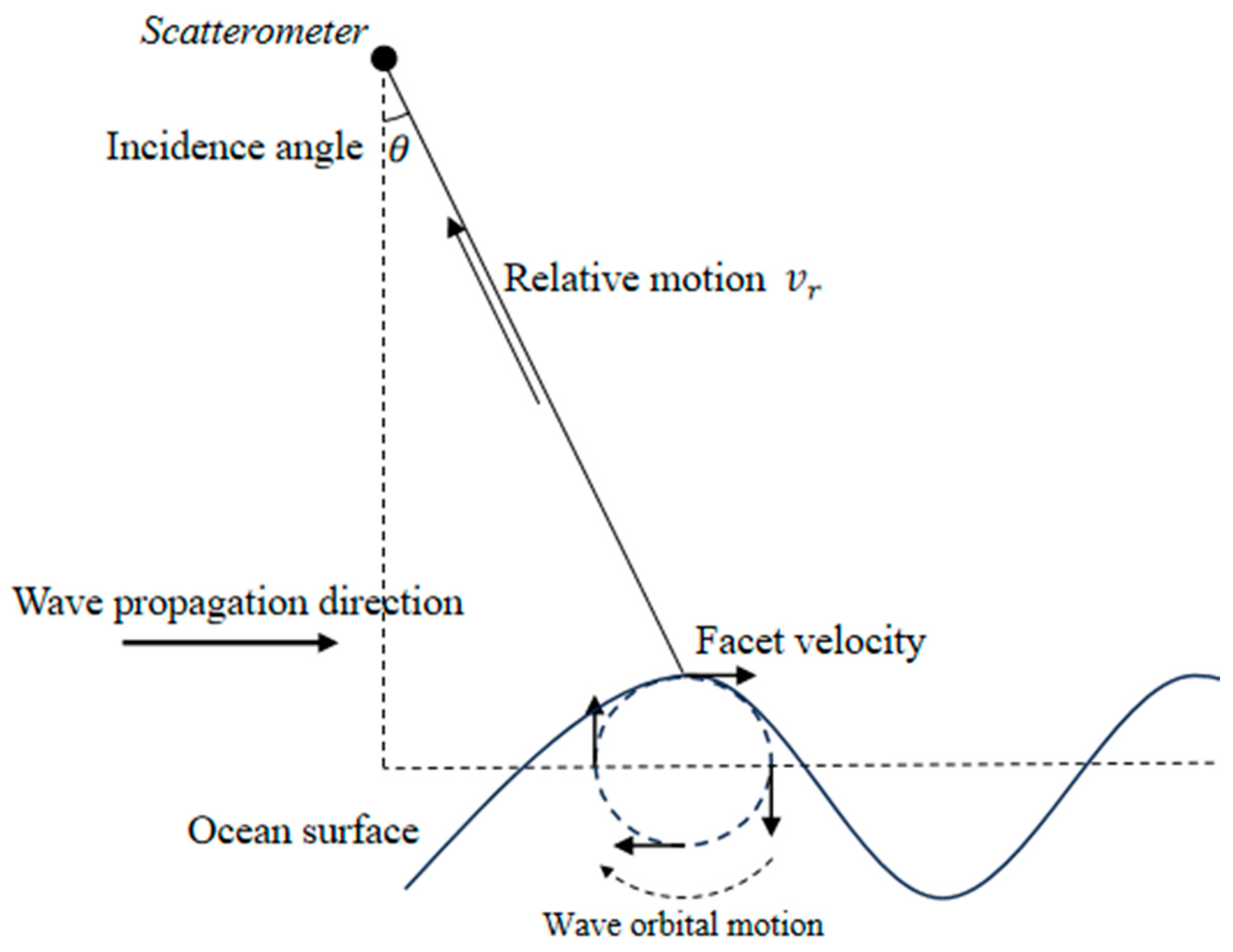
2.1. Measurement Principle
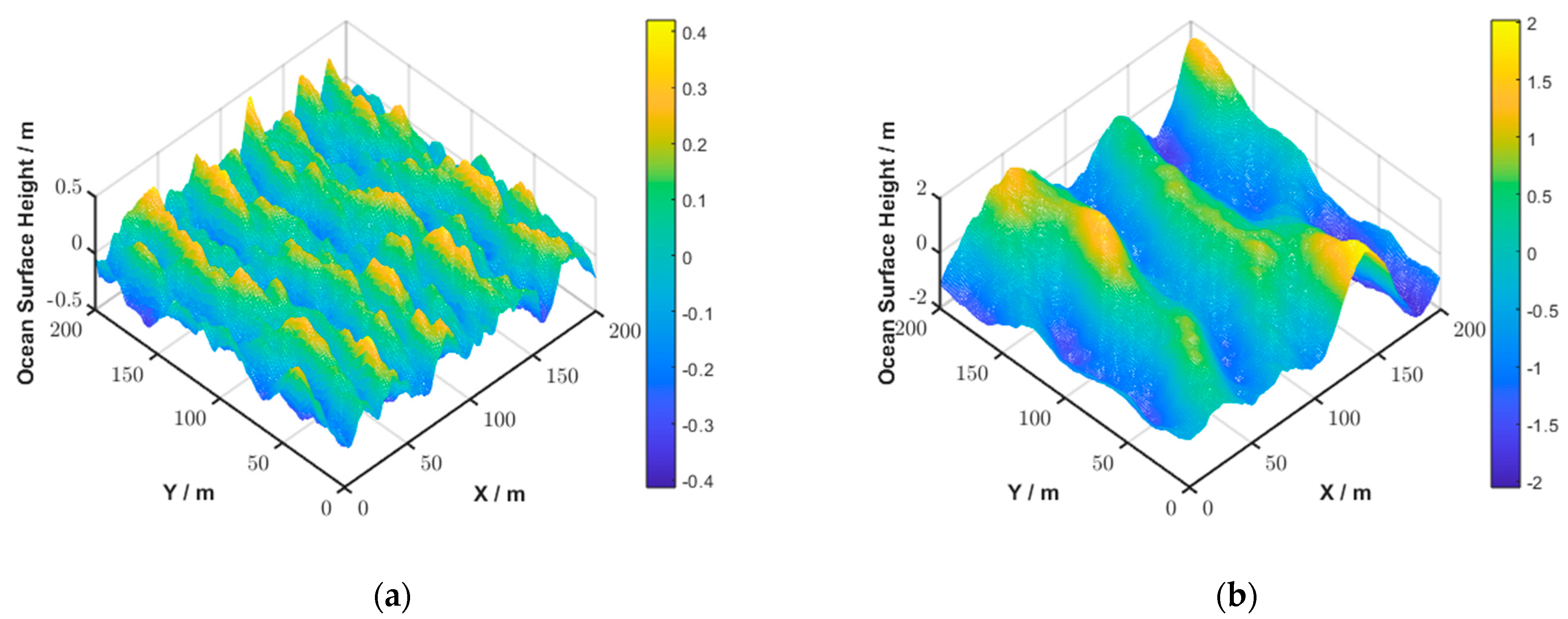
2.2. Dynamic Ocean Surface Generation
2.3. Simulations
3. Results
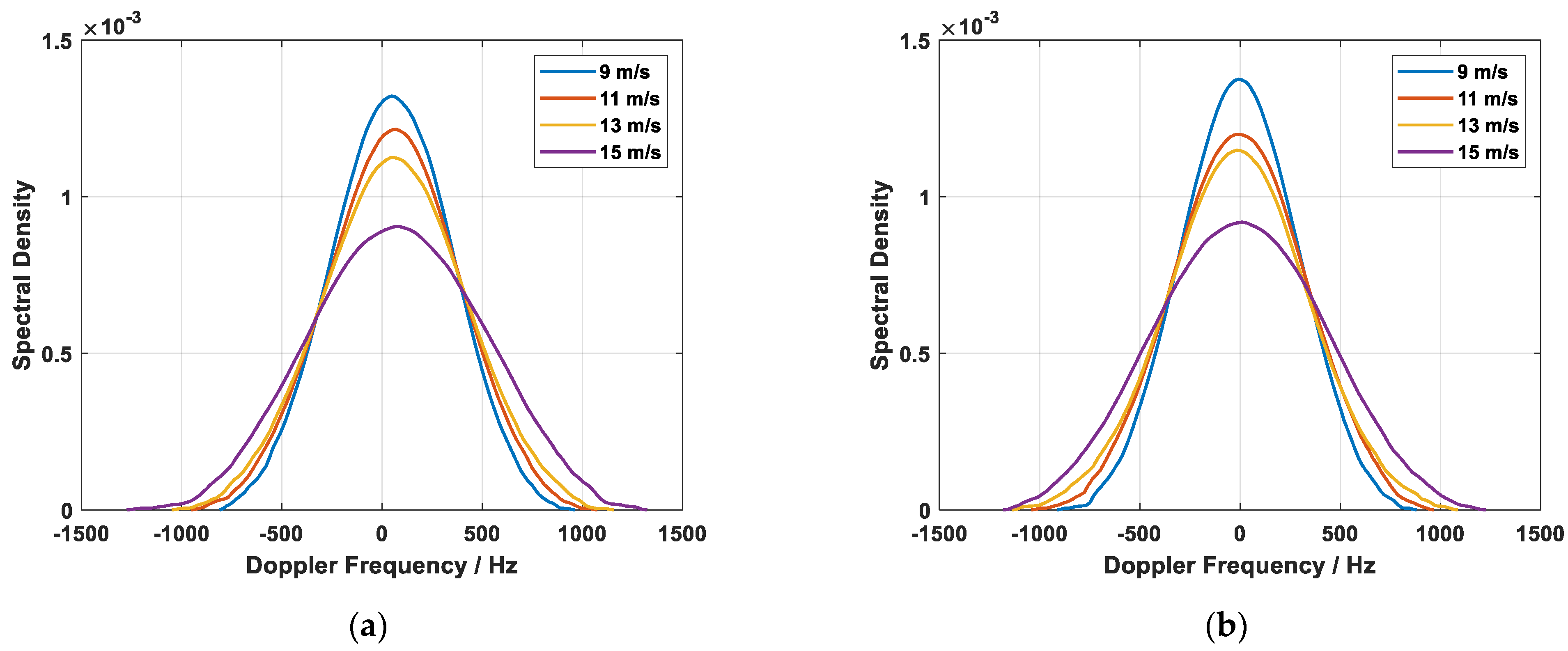
3.1. Doppler Spectrum Variation with Wind Speeds
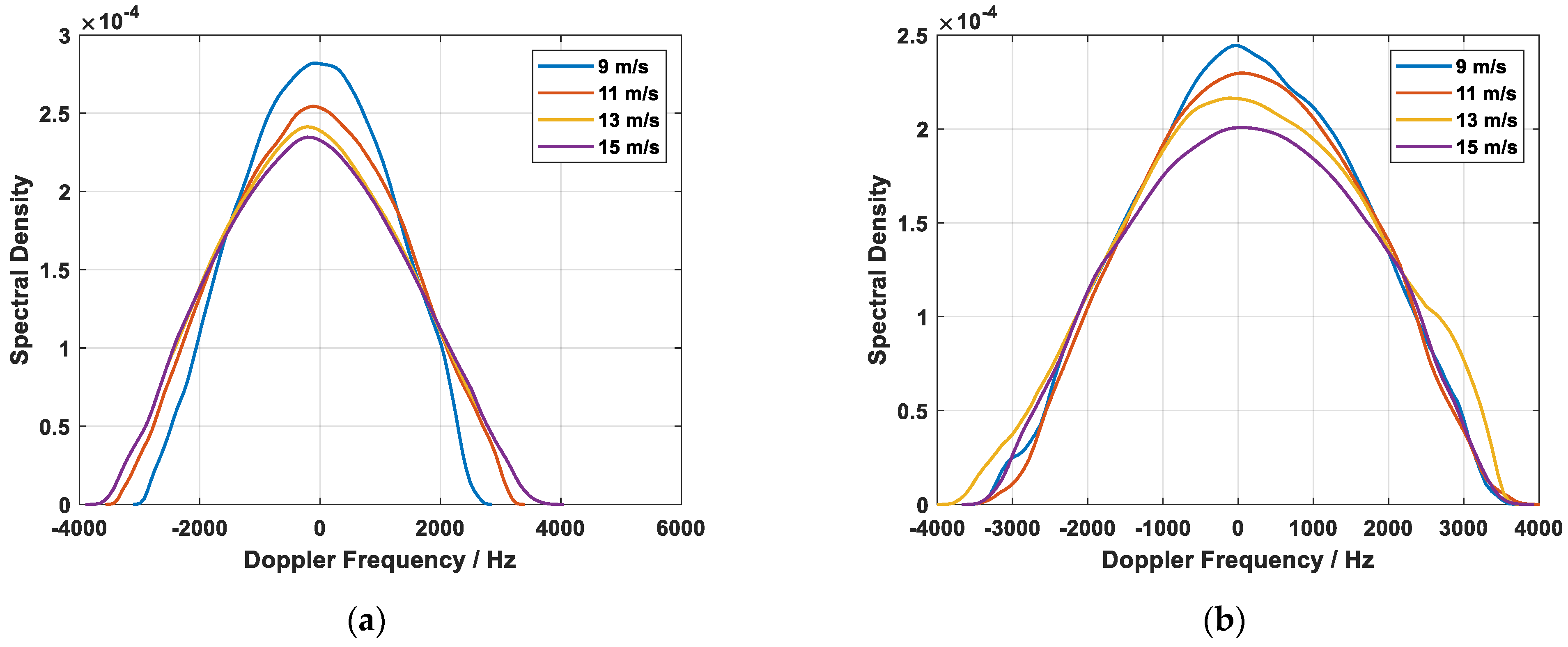
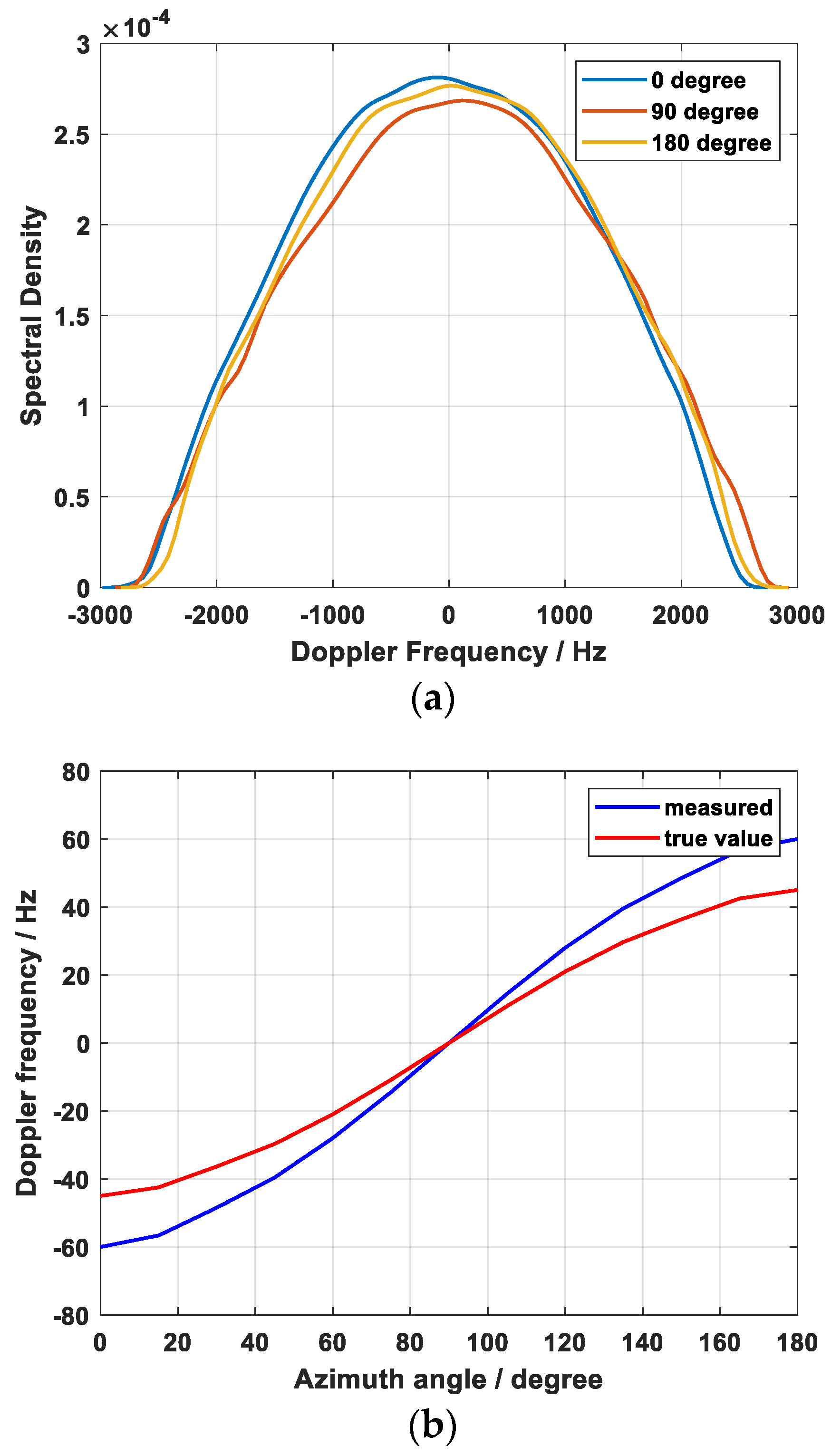
3.2. Doppler Spectrum Variation with Different Azimuth Angles
4. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, R.; Flierl, G.R.; Wunsch, C. A Description of Local and Nonlocal Eddy–Mean Flow Interaction in a Global Eddy-Permitting State Estimate. J. Phys. Oceanogr. 2014, 44, 2336–2352. [Google Scholar] [CrossRef]
- Centurioni, L.R.; Turton, J.; Lumpkin, R.; Braasch, L.; Brassington, G.; Chao, Y.; Charpentier, E.; Chen, Z.; Corlett, G.; Dohan, K.; et al. Global in situ Observations of Essential Climate and Ocean Variables at the Air–Sea Interface. Front. Mar. Sci. 2019, 6, 419. [Google Scholar] [CrossRef]
- Lumpkin, R.; Johnson, G.C. Global ocean surface velocities from drifters: Mean, variance, El Niño–Southern Oscillation response, and seasonal cycle. J. Geophys. Res. Oceans 2013, 118, 2992–3006. [Google Scholar] [CrossRef]
- Wang, S.D.; Shen, Y.M.; Zheng, Y.H. Two-dimensional numerical simulation for transport and fate of oil spills in seas. Ocean Eng. 2005, 32, 1556–1571. [Google Scholar] [CrossRef]
- Klemas, V. Tracking Oil Slicks and Predicting their Trajectories Using Remote Sensors and Models: Case Studies of the Sea Princess and Deepwater Horizon Oil Spills. J. Coast. Res. 2010, 26, 789–797. [Google Scholar] [CrossRef]
- McIntosh, R.E.; Swift, C.T.; Raghavan, R.S.; Baldwin, A.W. Measurement of Ocean Surface Currents from Space with Multifrequency Microwave Radars—A System Analysis. IEEE Trans. Geosci. Remote Sens. 1985, GE-23, 2–12. [Google Scholar] [CrossRef]
- Laws, K.E.; Vesecky, J.F.; Paduan, J.D. Error assessment of HF radar-based ocean current measurements: An error model based on sub-period measurement variance. In Proceedings of the 2011 IEEE/OES 10th Current, Waves and Turbulence Measurements (CWTM), Monterey, CA, USA, 20–23 March 2011; pp. 70–76. [Google Scholar]
- Gould, J.; Sloyan, B.; Visbeck, M. Chapter 3—In Situ Ocean Observations: A Brief History, Present Status, and Future Directions. In International Geophysics; Siedler, G., Griffies, S.M., Gould, J., Church, J.A., Eds.; Academic Press: Cambridge, MA, USA, 2013; Volume 103, pp. 59–81. [Google Scholar]
- Kudryavtsev, V.; Akimov, D.; Johannessen, J.; Chapron, B. On radar imaging of current features: 1. Model and comparison with observations. J. Geophys. Res. Oceans 2005, 110, C07016. [Google Scholar] [CrossRef]
- Johannessen, J.A.; Kudryavtsev, V.; Akimov, D.; Eldevik, T.; Winther, N.; Chapron, B. On radar imaging of current features: 2. Mesoscale eddy and current front detection. J. Geophys. Res. Oceans 2005, 110, C07017. [Google Scholar] [CrossRef]
- Chapron, B.; Collard, F.; Ardhuin, F. Direct measurements of ocean surface velocity from space: Interpretation and validation. J. Geophys. Res. Oceans 2005, 110, C07008. [Google Scholar] [CrossRef]
- Romeiser, R.; Thompson, D.R. Numerical study on the along-track interferometric radar imaging mechanism of oceanic surface currents. IEEE Trans. Geosci. Remote Sens. 2000, 38, 446–458. [Google Scholar] [CrossRef]
- Martin, A.C.H.; Gommenginger, C.; Marquez, J.; Doody, S.; Navarro, V.; Buck, C. Wind-wave-induced velocity in ATI SAR ocean surface currents: First experimental evidence from an airborne campaign. J. Geophys. Res. Oceans 2016, 121, 1640–1653. [Google Scholar] [CrossRef]
- Martin, A.C.H.; Gommenginger, C. Towards wide-swath high-resolution mapping of total ocean surface current vectors from space: Airborne proof-of-concept and validation. Remote Sens. Environ. 2017, 197, 58–71. [Google Scholar] [CrossRef]
- Martin, A.C.H.; Gommenginger, C.P.; Quilfen, Y. Simultaneous ocean surface current and wind vectors retrieval with squinted SAR interferometry: Geophysical inversion and performance assessment. Remote Sens. Environ. 2018, 216, 798–808. [Google Scholar] [CrossRef]
- Trampuz, C.; Gebert, N.; Placidi, S.; Hendriks, I.; Speziali, F.; Navarro, V.; Martin, A.; Gommenginger, C.; Suess, M.; Meta, A. The Airborne Interferometric and Scatterometric radar instrument for Accurate Sea Current and Wind Retrievals. In Proceedings of the EUSAR 2018, 12th European Conference on Synthetic Aperture Radar, Aachen, Germany, 4–7 June 2018; pp. 1–6. [Google Scholar]
- Martin, A.; Macedo, K.; Portabella, M.; Marié, L.; Marquez, J.; McCann, D.; Carrasco, R.; Duarte, R.; Meta, A.; Gommenginger, C.; et al. OSCAR: A new airborne instrument to image ocean-atmosphere dynamics at the sub-mesoscale: Instrument capabilities and the SEASTARex airborne campaign. In Proceedings of the EGU23, the 25th EGU General Assembly, Vienna, Austria, 23–28 April 2023; p. EGU-9940. [Google Scholar]
- Le Traon, P.Y.; Morrow, R. Chapter 3 Ocean Currents and Eddies. In International Geophysics; Fu, L.-L., Cazenave, A., Eds.; Academic Press: Cambridge, MA, USA, 2001; Volume 69, pp. 171–215. [Google Scholar]
- Du, Y.; Dong, X.; Jiang, X.; Zhang, Y.; Zhu, D.; Sun, Q.; Wang, Z.; Niu, X.; Chen, W.; Zhu, C.; et al. Ocean surface current multiscale observation mission (OSCOM): Simultaneous measurement of ocean surface current, vector wind, and temperature. Prog. Oceanogr. 2021, 193, 102531. [Google Scholar] [CrossRef]
- Rodríguez, E.; Bourassa, M.A.; Chelton, D.; Farrar, J.T.; Long, D.G.; Perkovic-Martin, D.; Samelson, R. The Winds and Currents Mission Concept. Front. Mar. Sci. 2019, 6, 438. [Google Scholar] [CrossRef]
- Rodríguez, E.; Wineteer, A.; Perkovic-Martin, D.; Gál, T.; Stiles, B.W.; Niamsuwan, N.; Monje, R.R. Estimating Ocean Vector Winds and Currents Using a Ka-Band Pencil-Beam Doppler Scatterometer. Remote Sens. 2018, 10, 576. [Google Scholar] [CrossRef]
- Ardhuin, F.; Brandt, P.; Gaultier, L.; Donlon, C.; Battaglia, A.; Boy, F.; Casal, T.; Chapron, B.; Collard, F.; Cravatte, S.; et al. SKIM, a Candidate Satellite Mission Exploring Global Ocean Currents and Waves. Front. Mar. Sci. 2019, 6, 209. [Google Scholar] [CrossRef]
- Nouguier, F.; Chapron, B.; Collard, F.; Mouche, A.A.; Rascle, N.; Ardhuin, F.; Wu, X. Sea Surface Kinematics from Near-Nadir Radar Measurements. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6169–6179. [Google Scholar] [CrossRef]
- Gommenginger, C.; Chapron, B.; Hogg, A.; Buckingham, C.; Fox-Kemper, B.; Eriksson, L.; Soulat, F.; Ubelmann, C.; Ocampo-Torres, F.; Nardelli, B.B.; et al. SEASTAR: A Mission to Study Ocean Submesoscale Dynamics and Small-Scale Atmosphere-Ocean Processes in Coastal, Shelf and Polar Seas. Front. Mar. Sci. 2019, 6, 457. [Google Scholar] [CrossRef]
- López-Dekker, P.; Biggs, J.; Chapron, B.; Hooper, A.; Kääb, A.; Masina, S.; Mouginot, J.; Nardelli, B.B.; Pasquero, C.; Prats-Iraola, P.; et al. The Harmony Mission: End of Phase-0 Science Overview. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; pp. 7752–7755. [Google Scholar]
- Chelton, D.; Schlax, M.G.; Freilich, M.H.; Milliff, R.F. Satellite Measurements Reveal Persistent Small-Scale Features in Ocean Winds. Science 2004, 303, 978–983. [Google Scholar] [CrossRef]
- Fabry, P.; Recchia, A.; de Kloe, J.; Stoffelen, A.; Husson, R.; Collard, F.; Chapron, B.; Mouche, A.; Enjolras, V.; Johannessen, J.; et al. Feasibility Study of Sea Surface Currents Measurements with Doppler Scatterometers. In Proceedings of the ESA Living Planet Programme, 12th European Conference on Synthetic Aperture Radar, Edinburgh, UK, 9–13 September 2013. ESA Living Planet Programme. [Google Scholar]
- Miao, Y.; Dong, X.; Bao, Q.; Zhu, D. Perspective of a Ku-Ka Dual-Frequency Scatterometer for Simultaneous Wide-Swath Ocean Surface Wind and Current Measurement. Remote Sens. 2018, 10, 1042. [Google Scholar] [CrossRef]
- Torres, H.; Wineteer, A.; Klein, P.; Lee, T.; Wang, J.; Rodriguez, E.; Menemenlis, D.; Zhang, H. Anticipated Capabilities of the ODYSEA Wind and Current Mission Concept to Estimate Wind Work at the Air–Sea Interface. Remote Sens. 2023, 15, 3337. [Google Scholar] [CrossRef]
- Fayne, J.V.; Smith, L.C.; Liao, T.H.; Pitcher, L.H.; Denbina, M.; Chen, A.C.; Simard, M.; Chen, C.W.; Williams, B.A. Characterizing Near-Nadir and Low Incidence Ka-Band SAR Backscatter from Wet Surfaces and Diverse Land Covers. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 985–1006. [Google Scholar] [CrossRef]
- Nouguier, F.; Chapron, B.; Collard, F.; Ardhuin, F. Synergy of Experimental, Theoretical and Numerical Approaches for a Better Understanding of Skim Near Nadir Ka-Band Doppler Measurements. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 8027–8030. [Google Scholar]
- Ardhuin, F.; Aksenov, Y.; Benetazzo, A.; Bertino, L.; Brandt, P.; Caubet, E.; Chapron, B.; Collard, F.; Cravatte, S.; Delouis, J.M.; et al. Measuring currents, ice drift, and waves from space: The Sea surface KInematics Multiscale monitoring (SKIM) concept. Ocean Sci. 2018, 14, 337–354. [Google Scholar] [CrossRef]
- Elyouncha, A.; Eriksson, L.E.B.; Romeiser, R.; Ulander, L.M.H. Measurements of Sea Surface Currents in the Baltic Sea Region Using Spaceborne Along-Track InSAR. IEEE Trans. Geosci. Remote Sens. 2019, 57, 8584–8599. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, Y.; He, M.; Zhao, C. Doppler Spectra of Microwave Scattering Fields from Nonlinear Oceanic Surface at Moderate- and Low-Grazing Angles. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1104–1116. [Google Scholar] [CrossRef]
- Hansen, M.W.; Kudryavtsev, V.; Chapron, B.; Johannessen, J.A.; Collard, F.; Dagestad, K.F.; Mouche, A.A. Simulation of radar backscatter and Doppler shifts of wave–current interaction in the presence of strong tidal current. Remote Sens. Environ. 2012, 120, 113–122. [Google Scholar] [CrossRef]
- Ryabkova, M.; Karaev, V.; Guo, J.; Titchenko, Y. A Review of Wave Spectrum Models as Applied to the Problem of Radar Probing of the Sea Surface. J. Geophys. Res. Ocean. 2019, 124, 7104–7134. [Google Scholar] [CrossRef]
- Yurovsky, Y.Y.; Kudryavtsev, V.N.; Chapron, B.; Grodsky, S.A. Modulation of Ka-Band Doppler Radar Signals Backscattered from the Sea Surface. IEEE Trans. Geosci. Remote Sens. 2018, 56, 2931–2948. [Google Scholar] [CrossRef]
- Yurovsky, Y.Y.; Kudryavtsev, V.N.; Grodsky, S.A.; Chapron, B.J. Sea Surface Ka-Band Doppler Measurements: Analysis and Model Development. Remote Sens. 2019, 11, 839. [Google Scholar] [CrossRef]
- Chu, X.; He, Y.; Karaev, V.Y. Relationships Between Ku-Band Radar Backscatter and Integrated Wind and Wave Parameters at Low Incidence Angles. IEEE Trans. Geosci. Remote Sens. 2012, 50, 4599–4609. [Google Scholar] [CrossRef]
- Hossan, A.; Jones, W.L. Ku- and Ka-Band Ocean Surface Radar Backscatter Model Functions at Low-Incidence Angles Using Full-Swath GPM DPR Data. Remote Sens. 2021, 13, 1569. [Google Scholar] [CrossRef]
- Abeysekera, S.S. Performance of pulse-pair method of Doppler estimation. IEEE Trans. Aerosp. Electron. Syst. 1998, 34, 520–531. [Google Scholar] [CrossRef]
- Miao, Y.; Dong, X.; Bourassa, M.A.; Zhu, D. Effects of Different Wave Spectra on Wind-Wave Induced Doppler Shift Estimates. In Proceedings of the IGARSS 2020—2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020; pp. 5705–5708. [Google Scholar]
- Thompson, D.R. Calculation of Microwave Doppler Spectra from the Ocean Surface with a Time-Dependent Composite Model. In Radar Scattering from Modulated Wind Waves: Proceedings of the Workshop on Modulation of Short Wind Waves in the Gravity-Capillary Range by Non-Uniform Currents, Bergen aan Zee, The Netherlands, 24–26 May 1988; Komen, G.J., Oost, W.A., Eds.; Springer: Dordrecht, The Netherlands, 1989; pp. 27–40. [Google Scholar]
- Elfouhaily, T.; Chapron, B.; Katsaros, K.; Vandemark, D. A unified directional spectrum for long and short wind-driven waves. J. Geophys. Res. 1997, 102, 15781–15796. [Google Scholar] [CrossRef]
- Thompson, D.R.; Gotwols, B.L.; Keller, W.C. A comparison of Ku -band Doppler measurements at 20° incidence with predictions from a time-dependent scattering model. J. Geophys. Res. 1991, 96, 4947–4955. [Google Scholar] [CrossRef]
- Yan, Q.; Zhang, J.; Fan, C.; Meng, J. Analysis of Ku- and Ka-Band Sea Surface Backscattering Characteristics at Low-Incidence Angles Based on the GPM Dual-Frequency Precipitation Radar Measurements. Remote Sens. 2019, 11, 754. [Google Scholar] [CrossRef]
- Barrick, D. First-order theory and analysis of MF/HF/VHF scatter from the sea. IEEE Trans. Antennas Propag. 1972, 20, 2–10. [Google Scholar] [CrossRef]
- Raney, R.K. Doppler properties of radars in circular orbits. Int. J. Remote Sens. 1986, 7, 1153–1162. [Google Scholar] [CrossRef]
- Panfilova, M.; Ryabkova, M.; Karaev, V.; Skiba, E. Retrieval of the Statistical Characteristics of Wind Waves from the Width and Shift of the Doppler Spectrum of the Backscattered Microwave Signal at Low Incidence Angles. IEEE Trans. Geosci. Remote Sens. 2020, 58, 2225–2231. [Google Scholar] [CrossRef]

| Parameters | Value |
|---|---|
| Carrier Frequency | 35.75 GHz |
| Carrier Wavelength | 0.84 cm |
| Incidence Angle | 6° |
| PRF | 20 kHz |
| Antenna 3 dB beamwidth | 0.15° |
| Satellite Orbital Height | 520 km |
| Platform Velocity | 7000 m/s |
| Ux | 9 m/s | 11 m/s | 13 m/s | 15 m/s |
|---|---|---|---|---|
| 44.4 609 | 46.4 721 | 52.4 813 | 57.4 1289 |
| Ux | 9 m/s | 11 m/s | 13 m/s | 15 m/s |
|---|---|---|---|---|
| −1.3 553 | −1.0 632 | 3.8 780 | 3.3 1226 |
| Ux | 7 m/s | 9 m/s | 11 m/s | 13 m/s | 15 m/s |
|---|---|---|---|---|---|
| −46.3 | −57.5 | −65.1 | −70.7 | −76.6 | |
| wind wave | −28 | −32 | −34 | −40 | −45 |
| −12.4 | −12.4 | −12.4 | −12.4 | −12.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, M.; Zhu, D.; Dong, X. Wind Wave Effects on the Doppler Spectrum of the Ka-Band Spaceborne Doppler Measurement. Remote Sens. 2024, 16, 2083. https://doi.org/10.3390/rs16122083
Yu M, Zhu D, Dong X. Wind Wave Effects on the Doppler Spectrum of the Ka-Band Spaceborne Doppler Measurement. Remote Sensing. 2024; 16(12):2083. https://doi.org/10.3390/rs16122083
Chicago/Turabian StyleYu, Miaomiao, Di Zhu, and Xiaolong Dong. 2024. "Wind Wave Effects on the Doppler Spectrum of the Ka-Band Spaceborne Doppler Measurement" Remote Sensing 16, no. 12: 2083. https://doi.org/10.3390/rs16122083
APA StyleYu, M., Zhu, D., & Dong, X. (2024). Wind Wave Effects on the Doppler Spectrum of the Ka-Band Spaceborne Doppler Measurement. Remote Sensing, 16(12), 2083. https://doi.org/10.3390/rs16122083







