A Low-Cost 3D SLAM System Integration of Autonomous Exploration Based on Fast-ICP Enhanced LiDAR-Inertial Odometry
Abstract
1. Introduction
- We developed a low-cost mobile robot SLAM system, significantly reducing manufacturing costs and enhancing system performance and 3D exploration capabilities through careful design of the robot’s structure and selection of high-performing yet affordably priced sensors and components.
- We successfully deployed an integrated LiDAR and IMU fusion SLAM algorithm framework with 3D autonomous exploration capabilities on the robot and conducted targeted optimizations for this algorithm based on our robot, achieving superior performance on our hardware platform.
- Our research findings have been made available as open-source, providing a high-performance solution for SLAM research under budget constraints and facilitating the wider adoption and application of advanced SLAM technologies.
2. Related Work
2.1. SLAM
2.2. Autonomous Exploration
3. Method
3.1. Cost-Effective Hardware Design
3.2. LiDAR-Inertial Odometry Using Fast-ICP
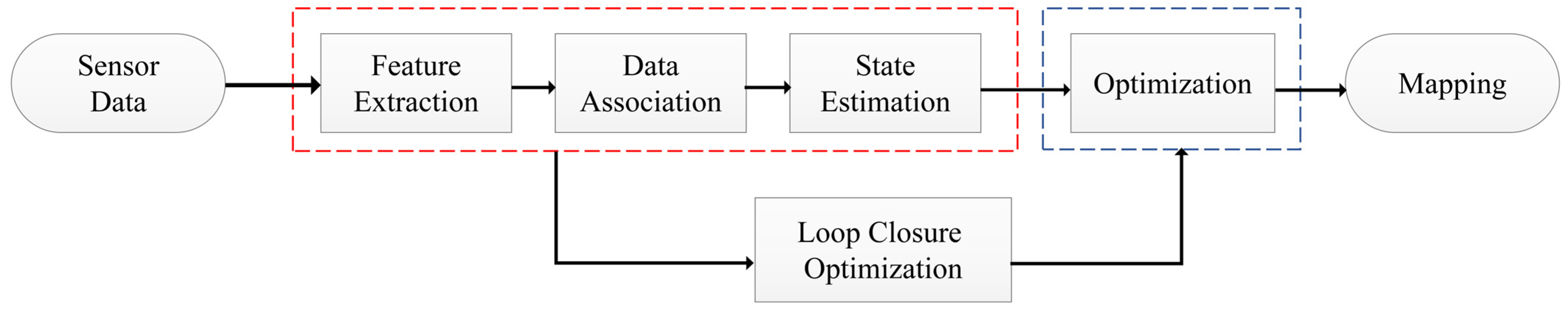
3.2.1. SLAM Framework Design
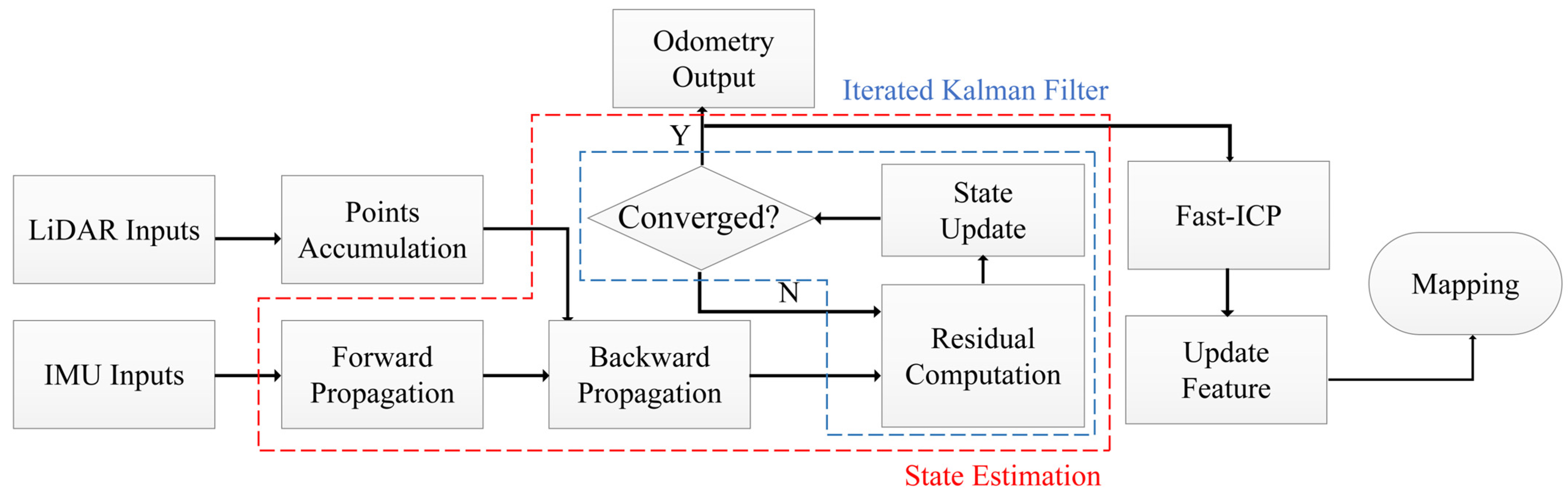
3.2.2. State Estimation Based on State Iterated Kalman Filter
3.2.3. Fast ICP for Improved State Estimation
3.2.4. Map Update
3.3. 3D Auto-Exploration Using RRT
3.3.1. 3D Multi-Goal RRT
3.3.2. NMPC Trajectory Optimizer
4. Experiment
4.1. Dataset Collection
4.2. LiDAR SLAM Experiment
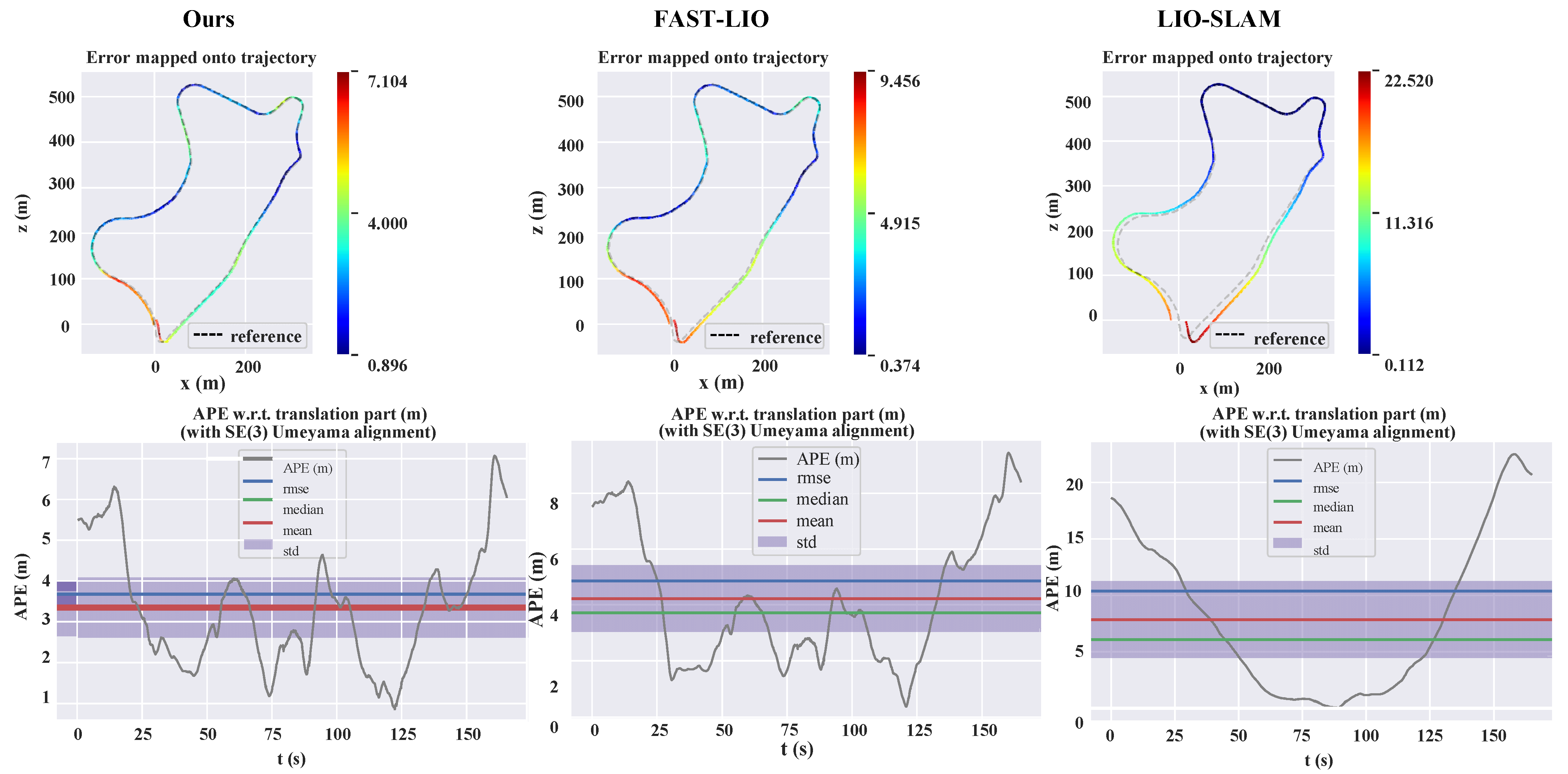
4.2.1. State Location Experiment
4.2.2. Loop Closure Experiment
- Motion 1. Linear movement at 0.7 m/s across a flat surface, completing a circuit and returning to the start.
- Motion 2. Zigzagging motion with the robot swaying left and right, moving in a curved path around the room at an average speed of approximately 0.7 m/s before returning to the starting point.
- Motion 3. Straight-line movement over uneven terrain, completing a circuit and returning to the start, maintaining an average speed of 0.7 m/s.
4.2.3. 3D Reconstruction Experiment
4.3. Auto-Exploration Experiment
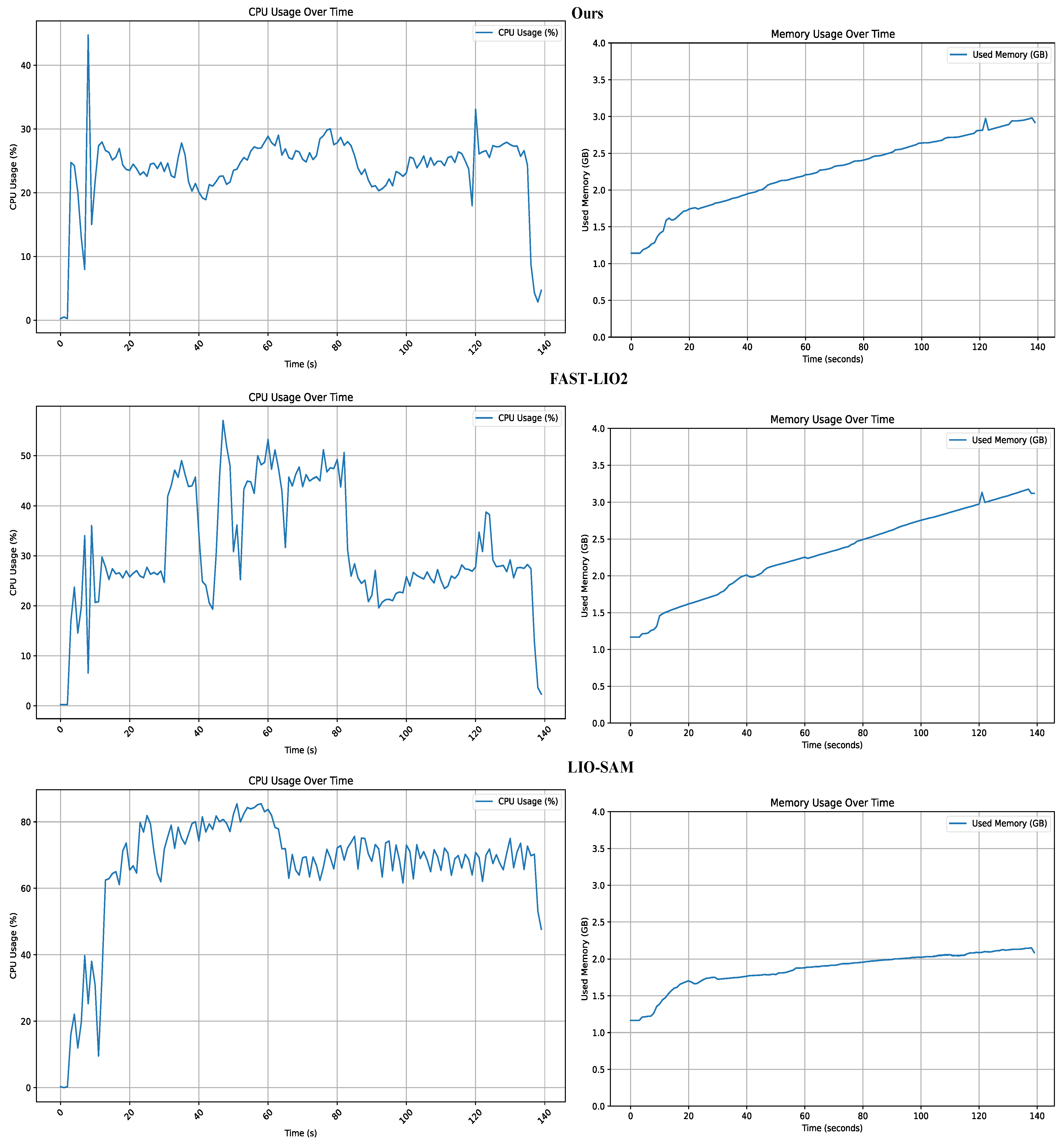
4.4. Analysis of the Resource Occupancy
5. Discussion
- Although the LiDAR-Inertial Odometry framework enhances the efficiency and accuracy of pose estimation, it still heavily relies on the quality of data collected by sensors. Sensor performance degradation in harsh environments could directly affect the system’s precision in localization and mapping.
- While the 3D RRT Exploration algorithm grants the system high-performance autonomous exploration capabilities, its computational complexity substantially escalates in environments with dynamic obstacles, potentially diminishing exploration efficiency and prolonging reaction times. Additionally, we must conduct more experiments to adjust the NMPC weight parameters to make the system’s motion control smoother and easier to port.
- Generating 3D maps offline necessitates extra storage, and activating 3D autonomous exploration and Fast ICP optimization concurrently can result in elevated memory consumption.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Smith, R.C.; Cheeseman, P. On the representation and estimation of spatial uncertainty. Int. J. Robot. Res. 1986, 5, 56–68. [Google Scholar] [CrossRef]
- Durrant-Whyte, H.; Bailey, T. Simultaneous localization and mapping: Part I. IEEE Robot. Autom. Mag. 2006, 13, 99–110. [Google Scholar] [CrossRef]
- Grigorescu, S.; Trasnea, B.; Cocias, T.; Macesanu, G. A survey of deep learning techniques for autonomous driving. J. Field Robot. 2020, 37, 362–386. [Google Scholar] [CrossRef]
- Takleh, T.T.O.; Bakar, N.A.; Rahman, S.A.; Hamzah, R.; Aziz, Z. A brief survey on SLAM methods in autonomous vehicle. Int. J. Eng. Technol. 2018, 7, 38–43. [Google Scholar] [CrossRef]
- Singandhupe, A.; La, H.M. A review of slam techniques and security in autonomous driving. In Proceedings of the 2019 Third IEEE International Conference on Robotic Computing (IRC), Naples, Italy, 25–27 February 2019; pp. 602–607. [Google Scholar]
- Polvi, J.; Taketomi, T.; Yamamoto, G.; Dey, A.; Sandor, C.; Kato, H. SlidAR: A 3D positioning method for SLAM-based handheld augmented reality. Comput. Graph. 2016, 55, 33–43. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, G.; Bao, H. Robust keyframe-based monocular SLAM for augmented reality. In Proceedings of the 2016 IEEE International Symposium on Mixed and Augmented Reality (ISMAR), Merida, Mexico, 19–23 September 2016; pp. 1–10. [Google Scholar]
- Chen, C.-W.; Chen, W.-Z.; Peng, J.-W.; Cheng, B.-X.; Pan, T.-Y.; Kuo, H.-C.; Hu, M.-C. A real-time markerless augmented reality framework based on SLAM technique. In Proceedings of the 2017 14th International Symposium on Pervasive Systems, Algorithms and Networks & 2017 11th International Conference on Frontier of Computer Science and Technology & 2017 Third International Symposium of Creative Computing (ISPAN-FCST-ISCC), Exeter, UK, 21–23 June 2017; pp. 127–132. [Google Scholar]
- Dissanayake, M.G.; Newman, P.; Clark, S.; Durrant-Whyte, H.F.; Csorba, M. A solution to the simultaneous localization and map building (SLAM) problem. IEEE Trans. Robot. Autom. 2001, 17, 229–241. [Google Scholar] [CrossRef]
- Montemerlo, M.; Thrun, S.; Koller, D.; Wegbreit, B. FastSLAM: A factored solution to the simultaneous localization and mapping problem. In Proceedings of the Eighteenth National Conference on Artificial Intelligence, Edmonton, AB, Canada, 28 July 2002–1 August 2002; pp. 593–598. [Google Scholar]
- Thrun, S.; Burgard, W.; Fox, D. A real-time algorithm for mobile robot mapping with applications to multi-robot and 3D mapping. In Proceedings of the 2000 ICRA. Millennium Conference. IEEE International Conference on Robotics and Automation. Symposia Proceedings (Cat. No. 00CH37065), San Francisco, CA, USA, 24–28 April 2000; pp. 321–328. [Google Scholar]
- Davison, A.J.; Reid, I.D.; Molton, N.D.; Stasse, O. MonoSLAM: Real-time single camera SLAM. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 1052–1067. [Google Scholar] [CrossRef] [PubMed]
- Mur-Artal, R.; Montiel, J.M.M.; Tardos, J.D. ORB-SLAM: A versatile and accurate monocular SLAM system. IEEE Trans. Robot. 2015, 31, 1147–1163. [Google Scholar] [CrossRef]
- Engel, J.; Schöps, T.; Cremers, D. LSD-SLAM: Large-scale direct monocular SLAM. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; pp. 834–849. [Google Scholar]
- Mur-Artal, R.; Tardós, J.D. Orb-slam2: An open-source slam system for monocular, stereo, and rgb-d cameras. IEEE Trans. Robot. 2017, 33, 1255–1262. [Google Scholar] [CrossRef]
- Campos, C.; Elvira, R.; Rodríguez, J.J.G.; Montiel, J.M.; Tardós, J.D. Orb-slam3: An accurate open-source library for visual, visual–inertial, and multimap slam. IEEE Trans. Robot. 2021, 37, 1874–1890. [Google Scholar] [CrossRef]
- Chen, W.; Shang, G.; Ji, A.; Zhou, C.; Wang, X.; Xu, C.; Li, Z.; Hu, K. An overview on visual slam: From tradition to semantic. Remote Sens. 2022, 14, 3010. [Google Scholar] [CrossRef]
- Wang, D.; Watkins, C.; Xie, H. MEMS mirrors for LiDAR: A review. Micromachines 2020, 11, 456. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Zhang, F.; Hong, X. Low-cost retina-like robotic lidars based on incommensurable scanning. IEEE ASME Trans. Mechatron. 2021, 27, 58–68. [Google Scholar] [CrossRef]
- Ye, H.; Chen, Y.; Liu, M. Tightly coupled 3d lidar inertial odometry and mapping. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 3144–3150. [Google Scholar]
- Almadhoun, R.; Taha, T.; Seneviratne, L.; Dias, J.; Cai, G. A survey on inspecting structures using robotic systems. Int. J. Adv. Robot. Syst. 2016, 13, 1729881416663664. [Google Scholar] [CrossRef]
- Yamauchi, B. Frontier-based exploration using multiple robots. In Proceedings of the Second International Conference on Autonomous Agents, Minneapolis, MN, USA, 10–13 May 1998; pp. 47–53. [Google Scholar]
- Chickering, D.M. Optimal structure identification with greedy search. J. Mach. Learn. Res. 2002, 3, 507–554. [Google Scholar]
- Mostegel, C.; Wendel, A.; Bischof, H. Active monocular localization: Towards autonomous monocular exploration for multirotor mavs. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 3848–3855. [Google Scholar]
- Placed, J.A.; Castellanos, J.A. A deep reinforcement learning approach for active SLAM. Appl. Sci. 2020, 10, 8386. [Google Scholar] [CrossRef]
- LaValle, S.M. Rapidly-Exploring Random Trees: A New Tool for Path Planning; TR 98-11; Department of Computer Science, Iowa State University: Ames, IA, USA, 1998. [Google Scholar]
- Grisetti, G.; Stachniss, C.; Burgard, W. Improving grid-based slam with rao-blackwellized particle filters by adaptive proposals and selective resampling. In Proceedings of the 2005 IEEE International Conference on Robotics and Automation, Barcelona, Spain, 18–22 April 2005; pp. 2432–2437. [Google Scholar]
- Zhang, J.; Singh, S. LOAM: Lidar odometry and mapping in real-time. In Proceedings of the Robotics: Science and Systems, Berkeley, CA, USA, 12–16 July 2014; pp. 1–9. [Google Scholar]
- Shan, T.; Englot, B. Lego-loam: Lightweight and ground-optimized lidar odometry and mapping on variable terrain. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 4758–4765. [Google Scholar]
- Lin, J.; Zhang, F. Loam livox: A fast, robust, high-precision LiDAR odometry and mapping package for LiDARs of small FoV. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 3126–3131. [Google Scholar]
- Xu, W.; Zhang, F. Fast-lio: A fast, robust lidar-inertial odometry package by tightly-coupled iterated kalman filter. IEEE Robot. Autom. Lett. 2021, 6, 3317–3324. [Google Scholar] [CrossRef]
- Hess, W.; Kohler, D.; Rapp, H.; Andor, D. Real-time loop closure in 2D LIDAR SLAM. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 1271–1278. [Google Scholar]
- Xu, W.; Cai, Y.; He, D.; Lin, J.; Zhang, F. Fast-lio2: Fast direct lidar-inertial odometry. IEEE Trans. Robot. 2022, 38, 2053–2073. [Google Scholar] [CrossRef]
- Shan, T.; Englot, B.; Meyers, D.; Wang, W.; Ratti, C.; Rus, D. Lio-sam: Tightly-coupled lidar inertial odometry via smoothing and mapping. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 24 October 2020–24 January 2021; pp. 5135–5142. [Google Scholar]
- Qin, C.; Ye, H.; Pranata, C.E.; Han, J.; Zhang, S.; Liu, M. Lins: A lidar-inertial state estimator for robust and efficient navigation. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 8899–8906. [Google Scholar]
- Besl, P.J.; McKay, N.D. Method for registration of 3-D shapes. In Proceedings of the Sensor Fusion IV: Control Paradigms and Data Structures, Boston, MA, USA, 12–15 November 1991; pp. 586–606. [Google Scholar]
- Rusinkiewicz, S.; Levoy, M. Efficient variants of the ICP algorithm. In Proceedings of the Proceedings Third International Conference on 3-D Digital Imaging and Modeling, Quebec City, QC, Canada, 28 May–1 June 2001; pp. 145–152. [Google Scholar]
- Pomerleau, F.; Colas, F.; Siegwart, R. A review of point cloud registration algorithms for mobile robotics. Found. Trends Robot. 2015, 4, 1–104. [Google Scholar] [CrossRef]
- Clotet, E.; Palacín, J. Slamicp library: Accelerating obstacle detection in mobile robot navigation via outlier monitoring following icp localization. Sensors 2023, 23, 6841. [Google Scholar] [CrossRef]
- Grisetti, G.; Kümmerle, R.; Stachniss, C.; Burgard, W. A tutorial on graph-based SLAM. IEEE Intell. Transp. Syst. Mag. 2010, 2, 31–43. [Google Scholar] [CrossRef]
- Ristic, B.; Palmer, J.L. Autonomous exploration and mapping with RFS occupancy-grid SLAM. Entropy 2018, 20, 456. [Google Scholar] [CrossRef] [PubMed]
- Bundy, A.; Wallen, L. Breadth-first search. In Catalogue of Artificial Intelligence Tools; Springer: Berlin/Heidelberg, Germany, 1984; p. 13. [Google Scholar]
- Umari, H.; Mukhopadhyay, S. Autonomous robotic exploration based on multiple rapidly-exploring randomized trees. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 1396–1402. [Google Scholar]
- Mukhopadhyay, S.; Umari, H.; Koirala, K. Multi-robot Map Exploration Based on Multiple Rapidly-Exploring Randomized Trees. SN Comput. Sci. 2023, 5, 31. [Google Scholar] [CrossRef]
- Wu, Z.; Meng, Z.; Zhao, W.; Wu, Z. Fast-RRT: A RRT-based optimal path finding method. Appl. Sci. 2021, 11, 11777. [Google Scholar] [CrossRef]
- Kuffner, J.J.; LaValle, S.M. RRT-connect: An efficient approach to single-query path planning. In Proceedings of the 2000 ICRA. Millennium Conference. IEEE International Conference on Robotics and Automation. Symposia Proceedings (Cat. No. 00CH37065), San Francisco, CA, USA, 24–28 April 2000; pp. 995–1001. [Google Scholar]
- Cao, C.; Zhu, H.; Choset, H.; Zhang, J. TARE: A Hierarchical Framework for Efficiently Exploring Complex 3D Environments. In Proceedings of the Robotics: Science and Systems, Virtually, 12–16 July 2021; p. 2. [Google Scholar]
- Huston, J.C.; Graves, B.J.; Johnson, D.B. Three wheeled vehicle dynamics. SAE Trans. 1982, 91, 591–604. [Google Scholar]
- Gfrerrer, A. Geometry and kinematics of the Mecanum wheel. Comput. Aided Geom. Des. 2008, 25, 784–791. [Google Scholar] [CrossRef]
- Raitoharju, M.; Piché, R. On computational complexity reduction methods for Kalman filter extensions. IEEE Aerosp. Electron. Syst. Mag. 2019, 34, 2–19. [Google Scholar] [CrossRef]
- Bentley, J.L. Multidimensional binary search trees used for associative searching. Commun. ACM 1975, 18, 509–517. [Google Scholar] [CrossRef]
- Mayne, D.Q.; Rawlings, J.B.; Rao, C.V.; Scokaert, P.O. Constrained model predictive control: Stability and optimality. Automatica 2000, 36, 789–814. [Google Scholar] [CrossRef]
- Lindqvist, B.; Agha-Mohammadi, A.-A.; Nikolakopoulos, G. Exploration-RRT: A multi-objective path planning and exploration framework for unknown and unstructured environments. In Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27 September–1 October 2021; pp. 3429–3435. [Google Scholar]
- Ma, L.; Xue, J.; Kawabata, K.; Zhu, J.; Ma, C.; Zheng, N. Efficient sampling-based motion planning for on-road autonomous driving. IEEE Trans. Intell. Transp. Syst. 2015, 16, 1961–1976. [Google Scholar] [CrossRef]
- Rusu, R.B.; Cousins, S. 3d is here: Point cloud library (pcl). In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 1–4. [Google Scholar]
- Zhang, S.; Bogus, S.M.; Lippitt, C.D.; Kamat, V.; Lee, S. Implementing remote-sensing methodologies for construction research: An unoccupied airborne system perspective. J. Constr. Eng. Manag. 2022, 148, 03122005. [Google Scholar] [CrossRef]
- Lippitt, C.D.; Zhang, S. The impact of small unmanned airborne platforms on passive optical remote sensing: A conceptual perspective. Int. J. Remote Sens. 2018, 39, 4852–4868. [Google Scholar] [CrossRef]













| Specification | Description |
|---|---|
| Laser Wavelength | 905 nm |
| Detection Range (@ 100 klx) | 40 m @ 10% reflectivity 70 m @ 80% reflectivity |
| Close Proximity Blind Zone 2 | 0.1 m |
| Point Rate | 200,000 points/s (first return) |
| Frame Rate | 10 Hz (typical) |
| IMU | ICM40609 |
| FOV | Horizontal: 360° Vertical: −7°~52° |
| Range Precision 3 (1σ) | ≤2 cm 4 (@ 10 m) ≤3 cm 5 (@ 0.2 m) |
| Angular Precision (1σ) | <0.15° |
| Component | Description | Quantity | Unit Cost ($) | Total Cost ($) |
|---|---|---|---|---|
| Mid-360 | 3D LiDAR sensor with IMU | 1 | 749 | 556.44 |
| Jetson nano 4 GB | SoC, Data Processing Unit | 1 | 129 | 129 |
| STM32F407VET6 | MCU, ROS base plate master control | 2 | 23.5 | 47 |
| carbon plate-A | Body structure, porous rectangles | 1 | 20 | 20 |
| carbon plate-B | LiDAR Support Structure | 1 | 5 | 5 |
| MG513 motor | DC-coded motor, with rubber wheel | 4 | 6.97 | 27.89 |
| Battery | 4000 mAh-30C and 1200 mAh-45C | 45 | ||
| Others | All kinds of wire and copper column | 10 | ||
| Total Cost | 840.33 |
| Model | Robot Type | LiDAR SLAM Dimension | SoC/CPU | Auto Exploration | Cost ($) |
|---|---|---|---|---|---|
| Turtlebot4 | Two-wheeled mobile robot | 2D LiDAR | Raspberry Pi 4B | No | 2191.44 |
| Hiwonder JetAuto Pro | Omnidirectional mobile robot | 2D LiDAR | Jetson nano | 2D | 1399.99 |
| SLAMTEC Hermes | Mobile robot with 2-wheel hub motor | 2D LiDAR | Unknown | No | 3061.17 |
| Unitree Go 2 | Robot dog | 3D LiDAR | 8 core CPU | Unknown | 2588.08 |
| WEILAN AlphaDog C 2022 | Robot dog | 3D LiDAR | ARM 64 bit | Unknown | 5134.41 |
| Ours | Four-wheeled mobile robot | 3D LiDAR | Jetson nano | 3D | 840.33 |
| Name | Version |
|---|---|
| OS | Ubuntu 18.04 |
| SoC | NVIDIA Tegra X1 |
| RAM | 4 GB |
| ROM | 64 GB |
| Accelerator Library | PCL v1.9.1 + Eigen v3.3.4 |
| APE | Translation Error (m) | Rotation Error (Degrees) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Algorithm | Max | Mean | Min | RMSE | Max | Mean | Min | RMSE | |
| Ours | 7.104 | 2.541 | 0.192 | 2.872 | 2.479 | 2.434 | 2.346 | 2.435 | |
| FAST-LIO2 | 9.456 | 2.643 | 0.204 | 2.986 | 2.502 | 2.440 | 2.346 | 2.440 | |
| LIO-SAM | 51.892 | 4.831 | 0.112 | 8.323 | 2.828 | 2.315 | 1.481 | 2.361 | |
| Motion Strategies | Drift (m) | ||
|---|---|---|---|
| X | Y | Z | |
| Linear + Flat | 0.016942 | 0.003476 | 0.157648 |
| Zigzagging + Flat | 0.016289 | 0.004651 | 0.173591 |
| Linear + Uneven | 0.016075 | 0.008972 | 0.210820 |
| Algorithm | Max Drift (m) | Accuracy | ||
|---|---|---|---|---|
| X | Y | Z | ||
| LIO-SAM (LoopClosutre Disable) | 1.226639 | 0.295907 | 1.364643 | 0.54676% |
| FAST-LIO2 | 0.032126 | 0.016737 | 0.278591 | 0.10450% |
| Ours | 0.016075 | 0.008972 | 0.210820 | 0.06235% |
| Algorithm | The Average CPU Usage | The Average Memory Usage |
|---|---|---|
| LIO-SAM | 66.75% | 47.54% |
| FAST-LIO2 | 30.32% | 56.73% |
| Ours | 23.66% | 52.45% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pang, C.; Zhou, L.; Huang, X. A Low-Cost 3D SLAM System Integration of Autonomous Exploration Based on Fast-ICP Enhanced LiDAR-Inertial Odometry. Remote Sens. 2024, 16, 1979. https://doi.org/10.3390/rs16111979
Pang C, Zhou L, Huang X. A Low-Cost 3D SLAM System Integration of Autonomous Exploration Based on Fast-ICP Enhanced LiDAR-Inertial Odometry. Remote Sensing. 2024; 16(11):1979. https://doi.org/10.3390/rs16111979
Chicago/Turabian StylePang, Conglin, Liqing Zhou, and Xianfeng Huang. 2024. "A Low-Cost 3D SLAM System Integration of Autonomous Exploration Based on Fast-ICP Enhanced LiDAR-Inertial Odometry" Remote Sensing 16, no. 11: 1979. https://doi.org/10.3390/rs16111979
APA StylePang, C., Zhou, L., & Huang, X. (2024). A Low-Cost 3D SLAM System Integration of Autonomous Exploration Based on Fast-ICP Enhanced LiDAR-Inertial Odometry. Remote Sensing, 16(11), 1979. https://doi.org/10.3390/rs16111979






