Abstract
Cotton (Gossypium spp.), a crucial cash crop in the United States, requires the constant monitoring of growth parameters for informed decision-making. Recently, forecasting models have gained prominence for predicting canopy indicators, aiding in-season planning and management decisions to optimize cotton production. This study employed unmanned aerial system (UAS) technology to collect canopy cover (CC) data from a 40-hectare cotton field in Driscoll, Texas, in 2020 and 2021. Long short-term memory (LSTM) models, trained using 2020 data, were subsequently applied to forecast the CC values for 2021. These models were compared with real-time auto-regressive integrated moving average (ARIMA) models to assess their effectiveness in predicting the CC values up to 14 days in advance, starting from the 28th day after crop emergence. The results showed that multiple-input multi-step output LSTM models achieved higher accuracy in predicting the in-season CC values during the early growth stages (up to the 56th day), with an average testing RMSE of 3.86, significantly lower than other single-input LSTM models. Conversely, when sufficient testing data are available, single-input stacked-LSTM models demonstrated precision in CC predictions for later stages, achieving an average RMSE of 3.06. These findings highlight the potential of LSTM models for in-season CC forecasting, facilitating effective management strategies in cotton production.
1. Introduction
Artificial intelligence (AI) has emerged as a transformative tool in addressing both food security and environmental sustainability concerns [1,2,3,4,5,6,7,8,9,10,11,12]. Researchers have leveraged AI techniques, such as machine learning (ML) and deep learning (DL), to optimize agricultural practices and mitigate environmental risks. For instance, in aquaponic systems, AI-based IoT monitoring systems enable real-time data collection and analysis, facilitating precise nutrient management for optimal plant growth while minimizing resource usage. Moreover, AI algorithms have been deployed to predict growth stages in crops cultivated in hydroponic setups, enhancing yield and efficiency. In addition to improving agricultural productivity, studies have demonstrated the efficacy of AI-driven approaches in reducing heavy metal toxicity in food products like soybeans and milk, thereby ensuring food safety. Furthermore, AI-powered processing techniques in the dairy sector not only enhance food quality but also contribute to environmental sustainability by reducing the need for chemical preservatives and minimizing waste. This integration of AI into food production and processing systems holds promise for promoting food security while safeguarding the environment.
One of the critical aspects of ensuring food security is effectively monitoring crop growth parameters with the goal of maximizing yield during the cultivation period. Crop growth and development are multifaceted processes influenced by genetics, the environment, management practices, and their interactions. These growth dynamics are quantified through phenotypic measures such as canopy cover (CC), canopy height (CH), and leaf area index (LAI). Traditionally, crop growth forecasts rely on process-based simulation models like the decision support system for agrotechnology (DSSAT) [13] or the Agricultural Production Systems sIMulator (APSIM) [14], despite the need for comprehensive calibration. However, there’s a growing interest in exploring alternative approaches, such as machine learning (ML), particularly utilizing deep learning neural network models like long short-term memory (LSTM) networks [15] and ARIMA-based models. These ML techniques offer potentially viable options for forecasting temporal phenotypic parameters like CC, CH, and LAI, providing a complementary or alternative framework to traditional simulation models.
LSTM networks belong to the category of recurrent neural networks (RNNs) and have the ability to identify and capture long-term dependencies. These networks possess a remarkable ability to effectively acquire new knowledge, to the point that the retention of this information seems to happen effortlessly and lasts for an extended period. Some of the commonly used LSTM models for multi-temporal projections are stacked LSTM [16], vanilla LSTM, bidirectional LSTM [17], and CNN-LSTM [18,19]. The stacked LSTM design is characterized by its use of many linked LSTM layers. In contrast, the bidirectional LSTM model is designed to train two input sequences simultaneously, whereby the first and second sequences are exact replicas of each other. The architecture of this paradigm enables the facilitation of fast learning. It is a kind of neural network that exhibits the capability to capture sequential information in both forward and backward directions, allowing for the retrieval of sequences from either the future to the past or vice versa. This model is characterized by its capacity to handle input sequences in both forward and backward directions, setting it apart from the traditional LSTM models, which are limited to unidirectional input propagation. These models have traditionally been used extensively in forecasting crop outputs [20,21,22], commodity prices [23], and pest and disease incidence [24,25]. In these studies, five LSTM models were used to anticipate the agricultural prices using time-series data from five crops: vanilla LSTM, bidirectional LSTM, stacked LSTM, CNN-LSTM, and convolutional LSTM. The findings revealed the possibility of more accurate price forecasting one month in advance. Similarly, the efficacy of bidirectional LSTMs using multivariate time-series input to anticipate insect damage in rice crops was compared to vanilla and stacked LSTMs.
The acronym ARIMA refers to autoregressive integrated moving average models. The time-series forecasting model discussed is a commonly employed approach that integrates autoregressive (AR) and moving average (MA) components, together with differencing techniques, to achieve stationarity in the time series. ARIMA models have demonstrated efficacy in forecasting future values by using past data sources. Several studies have explored the use of ARIMA-based models to forecast crop growth. In one study [26], historical data on sugarcane productivity from Tamil Nadu was utilized to create ARIMA models for capturing time-series patterns and forecasting. The forecasts’ accuracy was determined by comparing them to actual yield data. The outputs and performance indicators of the models were investigated, providing insights into the usefulness and reliability of the ARIMA approach for sugarcane crop growth forecasting. Elsamie et al. [27] employed an ARIMA dynamic time-series model to capture the temporal changes in Egyptian cotton and predicted key crop parameters.Similarly, the Box–Jenkins ARIMA [28] model was employed to better understand the cotton output in India and discovered that the ARIMA (2, 1, 1) model was appropriate for their data. The study included diagnostic tests to ensure that the model was correct. Using the chosen ARIMA model, the researchers created projections for the years 2015–16 through 2020–21. Policymakers found these estimates beneficial because they provided insight into future grain storage and import and export requirements, allowing them to plan ahead of time.
In recent years, unmanned aerial vehicles (UAVs) equipped with various sensors, collectively referred to as UAS, have been deployed to monitor plant growth at higher spatial and temporal resolutions. Phenotypic traits, such as the CC, CH, and vegetation indices (VIs) obtained from UAS, are utilized in estimating disease severity, crop input status, and crop yield. For instance, Zhao et al. [29] employed UAS-derived vegetation indicators to predict the in-season nitrogen status, while Ballester et al. [30] utilized similar techniques to predict the lint yield on a commercial farm in Australia. These aspects necessitate integration into crop management practices, such as optimizing fertilizer and pesticide usage based on the variables affecting crop growth. Integrating models for predicting canopy attributes can facilitate decision-making in crop management, including irrigation, growth regulators, fertilizers, and harvest-aid treatments. As UAS provides canopy attribute measurements at high temporal and spatial resolutions, ML models such as the long short-term memory (LSTM) or autoregressive integrated moving average (ARIMA) can be employed for the in-season predictions of these attributes as indirect measures of crop growth. Consequently, predicted attributes can be used to make real-time informed crop management decisions [31]. In this study, the use of the LSTM and ARIMA models has been assessed for in-season forecasting of crop growth, with the CC obtained from UAS serving as one of the parameters. Moreover, multiple LSTM models have been compared to classic ARIMA strategies for in-season forecasting of CC.
The main objective of this study is to compare different forecasting models, including variations of the long short-term memory (LSTM) models and the traditional autoregressive integrated moving average (ARIMA) model, to identify the most accurate model for predicting CC values 14 days in advance. An important innovation in this research involves clustering data based on field variability using the K-means algorithm. Subsequently, pairwise cluster distances are computed using the dynamic time warping (DTW) technique, with the clusters exhibiting the smallest DTW distance being used as inputs to multiple-input multi-step output LSTM models. While this approach requires significant computational resources, it provides optimal forecasting accuracy, which is particularly beneficial for predicting cotton crop growth indices during the initial growth phase. For forecasting in later growth stages, single-input LSTM models were utilized due to ample data availability, yielding results comparable to the multiple-input multi-step output LSTM models. By utilizing predicted CC values, in-season management decisions such as irrigation scheduling, application of growth regulators, and harvest-aid chemicals can be planned and optimized, thereby maximizing resource utilization and ensuring a higher yield.
2. Materials and Methods
Before delving into the analysis, a schematic of the framework employed to forecast the CC values in this approach is presented in Figure 1. As depicted in the figure, images are gathered using a UAS for both the years 2020 and 2021. Subsequently, the CC is extracted utilizing Agisoft Metashape 1.7.2 software. Initially, the CC data for 2020 is clustered using the K-means algorithm and then utilized to train the LSTM models. Similarly, the CC data for 2021 serves as the testing dataset after clustering the plots with the K-means algorithm. The model with the lowest testing root mean squared error (RMSE) for forecasting CC values 14 days in advance was selected as the best model.
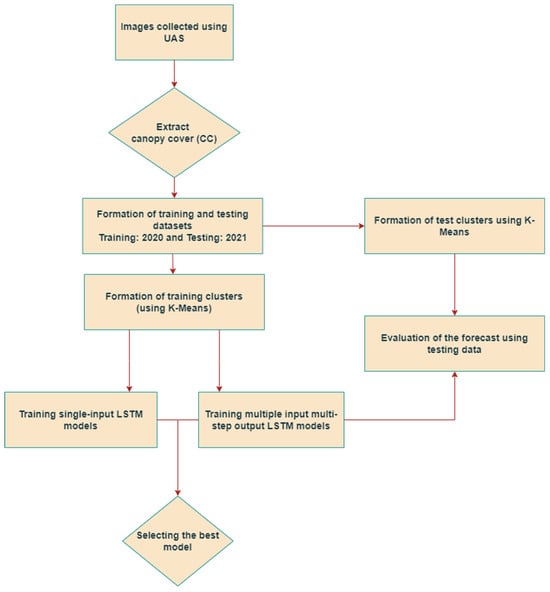
Figure 1.
Flowchart of the analysis for in-season forecasting of CC obtained from unmanned aerial systems (UAS) using LSTM frameworks.
2.1. Data Collection and Feature Extraction
UAS data were collected from an 80.16 hectares commercial field located at Driscoll, Texas (27°40′06.2″N and 97°97°41′22.6″W). The field is divided into two halves and follows a cotton–sorghum rotation (Figure 2).
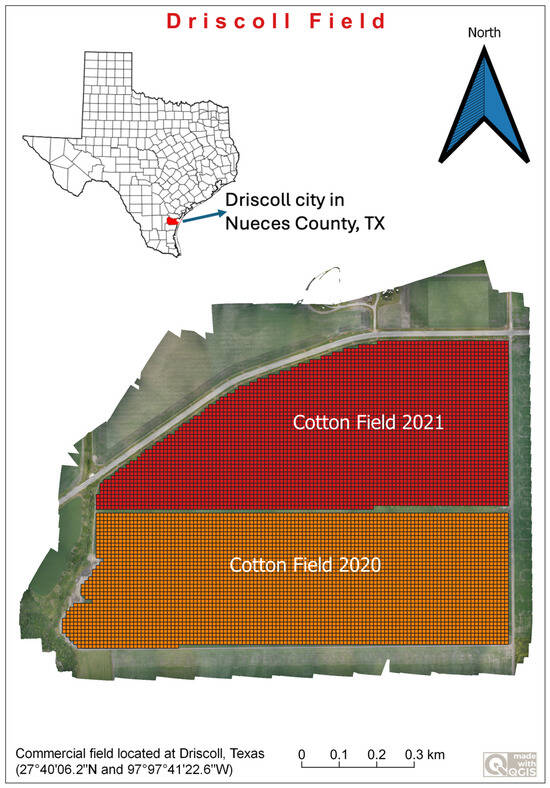
Figure 2.
Data collection site of cotton field.
Data were collected in 2020 and 2021. Table 1 shows the planting date, data collection schedule, defoliation date, and harvest date for both years.

Table 1.
Seeding date, defoliation date, and harvest dates of cotton in 2020 and 2021.
Phantom 4 RTK, which is equipped with a one-inch COSMOS, a red-green-blue (RGB) camera, and a Real-Time Kinematics (RTK) module, was used to collect the UAS data. The procedure for image processing and feature extraction was followed as described by Bhandari et al. [32]. The UAS flights were conducted at irregular intervals, with varying time gaps between each flight, ranging from 10 to 14 days. The collected images were processed using Agisoft Metashape PRO software version 1.8.2 (Agisoft LLC, St. Petersburg, Russia) to generate geospatial data products such as orthomosaics and surface models. The CC was obtained from the orthomosaics by employing the Canopeo algorithm [33], which classifies the image into two classes: canopy and non-canopy. A 10 m by 10 m grid was generated in QGIS software 3.36.2 and overlaid on the classified image to calculate the CC for each grid (Equation (1)). A total of 3500 grids were generated.
Based on the duration from emergence to defoliation application and the goal to forecast two weeks in advance, it was determined to standardize the growth period to test the forecasting frameworks to 116 days. To develop a consistent data framework, irregular temporal datasets obtained during the season were interpolated using the polynomial function, and daily measurements were derived. This approach facilitated the development of equal interval time-series data across years, compensating for non-uniformity in the data collection schedule and differing planting and defoliation timings. The data obtained through the interpolation techniques, as mentioned in the Results section, was then employed as inputs for the LSTM and ARIMA models to forecast the CC values two weeks in advance, beginning from the 28th day after the cotton crop’s germination.
2.2. Formation of Clusters for Analysis
Before fitting the LSTM models to the data, it was imperative to divide the plots into similar clusters for ease of training and validation of the LSTM models. Since the CC data were obtained for 3500 grids for 116 days, it was not possible to train the LSTM models, considering all the time-series sequences, as it would have resulted in millions of training sequences. Having a huge amount of training sequences would have led to a much slower computation time, and due to hardware constraints, it was decided to cluster the grids with similar CC values using the K-means algorithm. As the K-means algorithm is relatively fast and computationally efficient for high-dimensional data due to its linear time complexity, it was used because it helps us provide more control over the granularity of clustering. The continuous time-series data for all the 3500 grids for 2020 and 2021 were grouped into 14 distinct training and testing clusters, respectively, taking the data until the 116th day after emergence (DAP) into consideration. The number of plots which were grouped into each of these 14 clusters for both the years 2020 and 2021 have been shown in Table 2.

Table 2.
Number of cluster-wise cultivation plots generated by K-means algorithm.
2.3. Selection of Appropriate Forecasting Models
2.3.1. Using Data from Individual Cultivation Clusters as LSTM Inputs
Five different LSTM models—two stacked LSTM variants, a bidirectional LSTM, the CNN LSTM, and the encoder–decoder LSTM model—were used to predict the CC values from the 28th day after crop emergence. All these variants of LSTM models were trained on the data clusters obtained for 2020. For 2021, the average RMSE predictions over all the testing clusters were calculated separately, and the best forecasting model was chosen by a majority vote.
2.3.2. Using Data from Similar Pairwise Cultivation Clusters as LSTM Inputs
The datasets created using the information from individual clusters were used as inputs to the multiple-input multi-step output LSTM models to estimate the CC for the next 14 days. For this, the dynamic time warping (DTW) technique was used to find pairwise similar clusters to be given as inputs to the multiple-input multi-step output LSTMs. Here, DTW worked on the principle of utilizing dynamic programming to find the optimal alignment between two clusters, minimizing the total distance while allowing for local variations in the alignment.
To forecast the forthcoming CC values for each cluster, the pairwise DTW distances were computed between the cluster under consideration for the CC prediction and the remaining 13 clusters. For each early season forecast, the clusters exhibiting the minimum DTW distance were selected as inputs for the multiple-input multi-step output LSTM model. However, the training process for this type of LSTM model necessitated significant computational resources due to the pairwise training pairs, despite its potential to enhance the accuracy of the forecasting models. The major drawback of this approach is that for in-season forecasting, data needs to be available for multiple grids to be given as inputs to this type of LSTM model, making it impossible to conduct any forecasting when the CC data from only one grid was available.
2.3.3. Using ARIMA Models for a Comparative Analysis
A comparative study of the LSTM models with the traditional ARIMA-based CC forecasting has been conducted to provide a more accurate estimate.
Contrary to the LSTM models that have been described before, it was imperative to ensure the stationarity of the dataset before using an ARIMA model for analysis. A rising trend component was noted in the values of the CC. Consequently, efforts were undertaken to eliminate non-stationarity from the time-series dataset by implementing six distinct procedures, as seen in Figure 3. The stages were executed in a sequential manner, and the p-value was computed after each step until the time-series data achieved stationarity (p-value < 0.005). The stationarity of the time-series data was verified by the application of the augmented Dickey–Fuller (ADF) test.
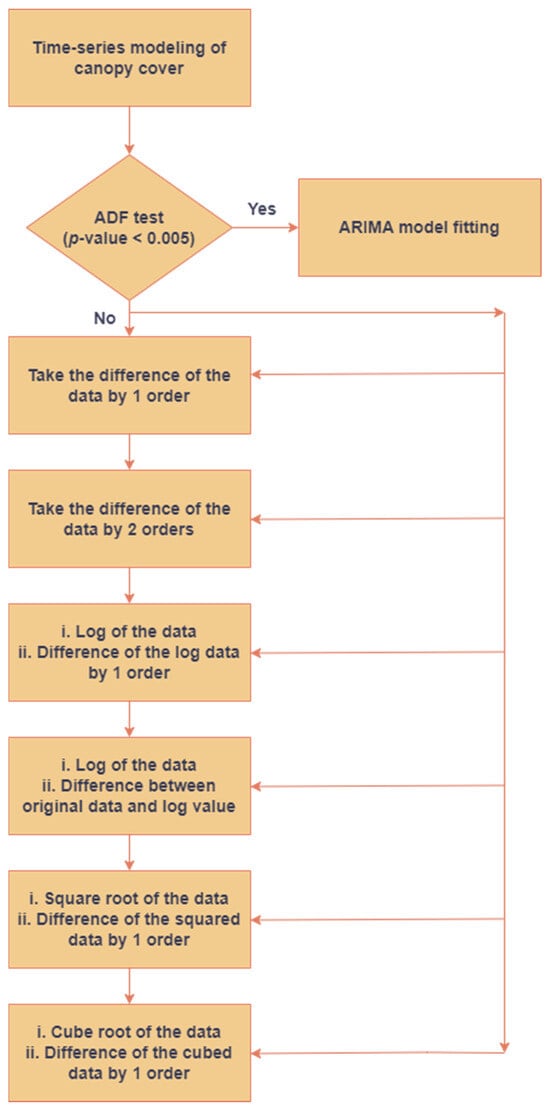
Figure 3.
Pipeline to eliminate non-stationarity from CC before analyzing ARIMA models.
The determination of the order of the ARIMA models was facilitated by the utilization of the partial auto-correlation (PACF) plots and the auto-correlation (ACF) plots, which provided valuable information on the major delays (p and q values) [34,35]. Hence, this methodology was employed in the prediction analysis. If the variables p and q exhibited a geometric fall when plotted together, it was inferred that the process conformed to an ARIMA model with p and q both equal to zero. If the ACF plot showed a geometric decrease and the PACF plot exhibited a complete cessation after p lags, it was inferred that the ARIMA process adhered to a (p, D, 0) distribution, where D represents the degree of differencing applied to the time-series data. In a similar vein, if the ACF plot reached zero after a certain number of lags (q), but the PACF plot exhibited a geometric decrease, it may be inferred that the ARIMA process adhered to a (0, D, q) distribution. The aforementioned methodology was employed to develop the necessary components for conducting a time-series analysis of the canopy’s characteristics. As ARIMA models followed a classical statistical approach that did not require data for training the model, the data for 2021 from all the cultivation plots were averaged to gauge the efficiency of this proposed framework, and the average RMSE estimates have been shown in Table 3.

Table 3.
Comparison of RMSE estimates for different LSTM models.
3. Results
3.1. Analysis of the Dataset
Figure 4 shows the distribution of the CC measurements obtained throughout the growing season for 2020 and 2021 for all the grids. A box plot was used to visualize the data. In general, the trend of CCs showed a slow increase early in the season, followed by a linear growth phase and steady growth. Additionally, the CC values ranged from 0 to 100% in both years, with a similar trend throughout the growing season.
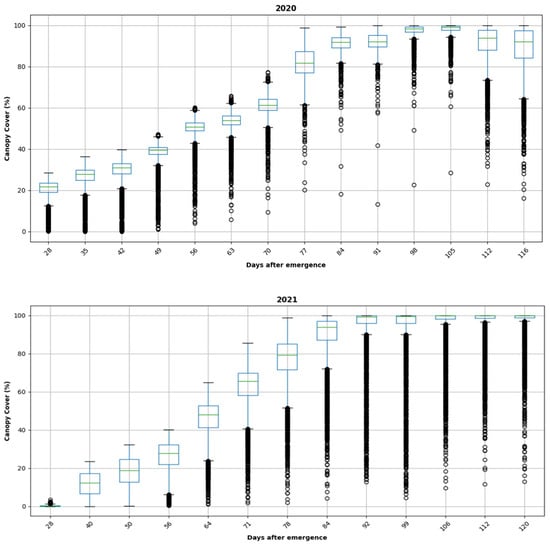
Figure 4.
Box plot of CC data over 3500 distinct plots for 2020 and 2021, respectively (top to bottom).
In Figure 4, the box plot illustrates the CC data recorded using drone imagery. The x-axis represents “Days after emergence”, while the y-axis represents “CC (%)”. Each box plot, corresponding to the years 2020 and 2021, depicts the interquartile range, i.e., the difference between the first and third quartiles for each day after emergence. Additionally, the black dots signify outliers within the dataset.
3.2. Removal of Outliers
Upon examination of the box plot, as depicted in Figure 4, it became evident that a considerable number of outliers are present in the data collected from over 3500 cultivation grids. Consequently, it became imperative to address these outliers before proceeding with the data interpolation for the entire growth period. To accomplish this, we retained the data points falling within the range defined by quartile 1 − (1.5 × interquartile range) and quartile 3 + (1.5 × interquartile range) for analysis. Implementation of the IQR method resulted in the removal of 1101 plots and 1437 grid data points from the 2020 and 2021 cultivation years, respectively. Subsequently, data from the remaining grids were utilized for analysis, ensuring the reliability and accuracy of the subsequent interpretations and conclusions.
3.3. Interpolation of the Dataset
Given that the data were gathered over 14 days at irregular intervals, spanning from emergence to harvest, it was impractical to rely on the data from those specific days for analysis solely. Hence, considering the data’s distribution, as evident from the box plots, the approach was taken to employ a five-degree polynomial interpolation [36] to interpolate the canopy data for both 2020 and 2021. This interpolation process provided enough data for all the plots throughout the 116-day growth period to design the predictive approaches. The distribution of the interpolated canopy data was visualized and is depicted in Figure 5. The interpolated canopy data from emergence to harvest has been shown in different colors to show how the distribution of the data varied over the plots.
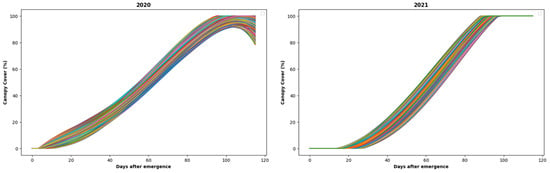
Figure 5.
Interpolated CC data from 28 days to 116 days after emergence for 2020 and 2021.
The analysis of Figure 5 suggests that the CC data for both 2020 and 2021 exhibited a consistent upward trend from emergence to harvest. Consequently, given the observed improvement in the data’s quality post-outlier removal, characterized by this ascending trend, the refined data were utilized as inputs to the LSTM models and the ARIMA approach, which have been elaborated in the subsequent sub-sections.
3.4. Formation of Clusters for Training LSTM Models
Before training the LSTM models, the data recorded for 2020 were clustered using K-means for ease of computation. Utilizing the elbow method, the optimal number of training clusters was determined to be 14, as the sum of squared errors (SSE) reached a plateau. Similarly, to assess the effectiveness of the trained LSTM models, the data for the year 2021 underwent clustering using the K-means algorithm. This process also resulted in choosing 14 as the optimal number of clusters. Subsequently, the selection of the best forecasting model was based on a majority vote, considering the model capable of forecasting future CC values with a minimal root mean square error (RMSE) across the majority of the testing clusters. Figure 6 illustrates the results of the elbow method employed as a metric to ascertain the optimal number of training and testing clusters.
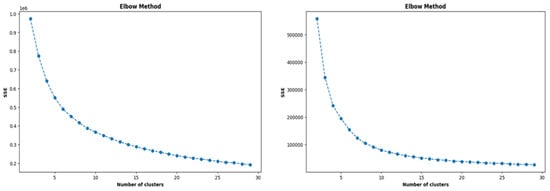
Figure 6.
Number of optimal training and testing clusters obtained from the K-means algorithm for 2020 and 2021 (top to bottom).
However, before proceeding with training the LSTM models, it was imperative to visualize the average interpolated CC data for the newly formed clusters using the K-means algorithm. The average interpolated CC data have been depicted in Figure 7.
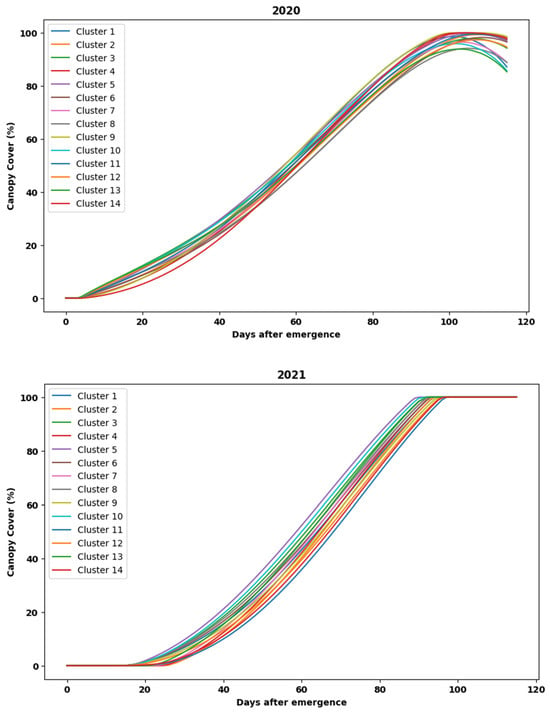
Figure 7.
Average cluster-wise CC (%) data for 2020 and 2021, respectively (top to bottom).
From Figure 7, it can be inferred that the average cluster-wise CC in both 2020 and 2021 showed a steady increase in the indices, and as the line graphs are distinct, with minimal overlap between them, it ascertained the decision of the optimal number of training and testing clusters, which are chosen to be 14 in this case. The number of cultivation plots that were grouped into each distinct cluster is shown in Table 2.
3.5. Training of Single-Input LSTM Models
To train the single-input LSTM models, the mean cultivation data across the clusters for the year 2020 were utilized. Specifically, the training dataset comprised the canopy data for the initial 28 days as inputs, while the corresponding output sequence encompassed the canopy indices from day 29 to day 42. Thereafter, at each step, a real value of the CC was appended to the dataset, and predictions were made for the subsequent 14 days of canopy indices. This iterative process continued until the CC data for the first 98 days served as inputs, and the CC values from day 99 to day 112 were utilized as the corresponding output pair to train the single-input LSTM models. This procedure was repeated for all 14 training clusters, resulting in a total of 42,432 training sequences. Despite varying in length, each sequence maintained a consistent prediction window of 14.
These sequences were employed as inputs for various single-input LSTM models, including stacked LSTMs, the bidirectional LSTM, the CNN LSTM, and encoder–decoder LSTM models. To assess the forecasting performance of these trained LSTMs, the testing dataset for the year 2021 was partitioned into 14 clusters and identified using the K-means algorithm with the elbow method. Then, by taking the average of the testing MSEs across the 14 clusters, the LSTM model, which forecasts the values of the CC, the best has been chosen by a majority vote and has been described in detail below.
3.6. Training of Multiple-Input Multi-Step Output LSTM Models
However, for training the multiple-input multi-step LSTM models, for each cluster, pairwise DTW distances were calculated between the averaged CC data calculated per cluster. As the LSTM model that has been used has two inputs, the pairwise sequences that had the least DTW distances between them were given as inputs for training the LSTM model. For testing the efficiency of the trained LSTM model on the testing dataset, which in this case is the 2021 CC data, the same process of clustering is repeated, and the DTW distances are computed between the clusters. However, no training of the models is carried out. The clusters with the least DTW distances are then given as inputs to the trained model, and the results are computed.
Table 3 displays the evaluation of the LSTM models capable of processing both single-cluster and multi-cluster cultivation data. The first five models in Table 3 are trained on variable-length single-cluster data sequences and generate predictions for a 14-day period. Conversely, the final variant, termed the multiple-input multi-step output LSTM model, is trained on pairwise cluster data using time-series sequences with the shortest DTW distances between them. This training process is highly resource-intensive, demanding significant computational power to calculate the forecasted values. Hence, it is recommended to opt for the LSTMs that handle single-cluster data inputs. Nevertheless, despite its computational demands, the multiple-input multi-step output LSTM model exhibits superior performance, particularly in forecasting the early season growth indices, i.e., a prediction of the CC up to the 56th day after emergence when there is not enough data to be supplied as testing data to the trained LSTM models.
Another noteworthy observation from Table 3 is that a multiple-input multi-step output LSTM model is used as the model to predict the future values of the CC when the data from the 28th day of emergence to the 56th day after emergence are given as inputs. However, due to the resource constraints associated with training the above-stated model, it was decided that the second variant of the single-input LSTM, i.e., a stacked LSTM trained for 100 epochs with a batch size of 32, yielded comparable results at par with the multiple-input multi-step output LSTM models in forecasting the later season growth indices (starting from the 63rd day to the 98th day after emergence). The main reason for doing so is that training a stacked LSTM requires much less computational resources compared to that of a multiple-input multi-step output LSTM model.
3.7. ARIMA Model Analysis
For a more efficient performance comparison of the trained LSTM models, a classical ARIMA approach was used on the 2021 cultivation data. As the ARIMA approach did not require any model training, the cultivation data for all the 2063 plots were averaged, and the RMSE estimates were computed, which have been shown in Table 4. Based on the results from the table, it is evident that the RMSE estimates obtained for forecasting the growth parameters using initial CC data up to the 49th day of emergence were excessively high. Consequently, employing the classical ARIMA approach to forecast the CC values was deemed impractical. This comparison helped in fulfilling the objective, which was to determine the most effective estimator for forecasting future values of the CC, namely from the 28th day of emergence of the cotton crop to the conclusion of the cultivation season.

Table 4.
RMSE estimates of ARIMA-based modeling on 2021 CC data.
4. Discussion
The major goal of this study is to explore the use of ML models for in-season forecasting of crop canopy features. For this, the CC was chosen as a canopy feature as it is significantly important in measuring the canopy leaf area and subsequently for yield estimations [37,38,39] and irrigation scheduling [40]. Our approach is to forecast CC features two weeks in advance with accurate precision so that in-season management decisions can be made. For this, different forecasting models have been used to do a comparative analysis and to choose a model that predicted the indices with the highest accuracy at different phases of the growth cycle.
In order to simplify the analysis and ensure that the forecasting models yielded an unbiased estimate, the CC data recorded for the plots for the year 2020 were used as training data, and the CC data over the year 2021 were used to gauge the efficiency of the trained models. The recorded data for the year 2020 were clustered using the K-means algorithm for ease of training the LSTM models. Similarly, in order to compute the efficiency of the trained models, the CC data for the year 2021 were clustered, and the trained forecasting models were tested. The best forecasting model was decided by a majority vote based on the output of the models, which forecasted the values of CCs up to 14 days in advance with minimal error.
The prediction of CC values from the 28th day to the 63rd day after emergence has been achieved using a multiple-input multi-step output LSTM model. The superiority of the multiple-input multi-step output LSTM model, which utilized similar cluster cultivation data as multiple inputs to the model, over other forecasting methods, has prompted a thorough examination of the data formulation and model architecture that contributed to its enhanced prediction accuracy in predicting the early season growth indices.
Following the data preparation phase, it was crucial to examine the benefits of the resulting curated dataset when utilized as inputs to the multiple-input multi-step output and long short-term memory (LSTM) models. One significant benefit of utilizing these models lies in their ability to effectively capture relationships and dependencies among multiple interdependent input sequences. For instance, when provided with CC data for clusters with low DTW distance as inputs, these models could exploit correlations between different time-series inputs to generate more precise predictions. In this case, the DTW technique was used to measure the similarity between different clusters by stretching or compressing them along the time axis. This alignment allows similar clusters to be matched, even if they are distorted by noise. Given how the data were recorded across all plots, there is a high likelihood of the CC data being influenced by noise. Additionally, another benefit of employing DTW to evaluate the similarity between clusters is that the alignment process remains meaningful, prioritizing the alignment of genuinely similar patterns over accommodating every minor fluctuation in the data [41,42,43].
Similarly, the prediction of CC values, starting from the 63rd day of emergence to the end of the cultivation period, was achieved using a four-layered stacked LSTM model. These models incorporate the CC values for the year 2020 as input variables to train the model, enabling the prediction of CC indices for the year 2021. As anticipated, the root mean square error (RMSE) values for the estimation of CCs exhibited a decline with the inclusion of more actual values into the model. However, the main disadvantage of using single-input LSTM models is that they suffer from a deficiency in capturing the interactions between inputs, resulting in a decrease in predicting accuracy when there is not enough testing data to make predictions. However, it is important to exercise caution to mitigate the risk of overfitting when the input data sequences are not well aligned or curated.
Nonetheless, given the significant computational resources associated with employing a multiple-input multi-step LSTM model, it is recommended to opt for a single-input stacked LSTM architecture, as stated above, for computing growth indices starting from 63 days of cultivation. This approach ensures a more manageable computational load while still achieving a reasonably low RMSE, thus enhancing the precision of forecasting future CC indices.
Another noteworthy insight, observed in Figure 8, is the alignment between all the predicted values for the subsequent 14 days and the actual CC values. Anomalies typically occurred within the predictions around days 6 to 8 while trying to predict the early season growth indices (typically for predicting the future CC values when the real canopy values until days 28 to 35 are given as inputs to the trained LSTM models.) Hence, it suggests the potential application of more advanced time-series forecasting models like the Prophet [44], VARMAX [45], or state-space models [46,47], which can be used to address these prediction anomalies in future analyses.
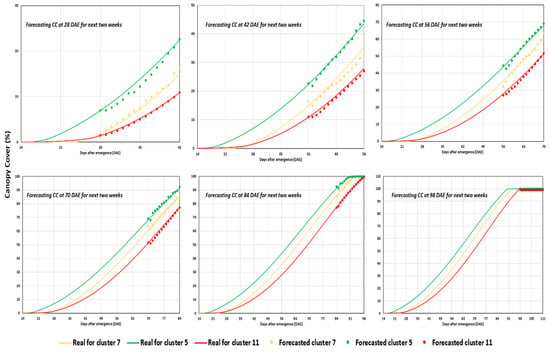
Figure 8.
Bi-weekly prediction of CC from the growth period of four weeks to the end of the cultivation period (14-day prediction) for clusters 11, 5, and 7 (top to bottom).
5. Conclusions and Future Work
Utilizing cultivation data from multiple clusters with a minimal DTW distance for LSTM model training, a four-layered multiple-input multi-step output LSTM model demonstrated superior performance compared to other LSTM models and the traditional ARIMA approach. The RMSE estimates obtained from this model ranged from 4.36 to 2.18 across the entire cultivation period. However, due to computational constraints, this model was only employed for predicting growth indices up to the 56th day of emergence. Subsequently, from the 56th to the 98th day of emergence, when sufficient data became available for LSTM model testing, a stacked LSTM trained for 100 epochs with a batch size of 32 was selected over other LSTM variants due to its cost-effectiveness and relatively low average RMSE. Future research endeavors should incorporate datasets from diverse sites, soils, and climates to develop robust and versatile forecasting models that are capable of accurately predicting canopy features until the harvesting phase. Consequently, robust models are imperative for effectively predicting in-season growth, thereby optimizing management strategies and enhancing yield outcomes.
Author Contributions
Conceptualization, S.B.D., M.B. and K.C.G.; methodology, S.B.D. and U.B.-N.; software, S.B.D. and U.B.-N.; resources, S.K., J.L. and J.L.; data curation, S.B.D., J.L.L.-S., S.K., and K.C.G.; writing, S.B.D. and M.B.; writing—review and editing, M.B., K.N. and U.B.-N.; project administration, M.B., K.N., J.L., L.Z., J.L., P.P., J.L.L.-S., U.B.-N., K.N. and S.K.; funding acquisition, S.K. and M.B. All authors have read and agreed to the published version of the manuscript.
Funding
The authors would like to acknowledge Texas State Support Committee and Cotton Incorporated (project number: 19-846TX) for providing funding to collect data.
Data Availability Statement
The raw code and data may be available upon appropriate request.
Acknowledgments
The authors express their gratitude to all the members of the Digital Agriculture Research and Training Program at Texas A&M AgriLife Research and Extension Center in Corpus Christi for their invaluable assistance and collaboration during the project.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- McDonald, B.L. Food Security; Polity: Cambridge, UK, 2010. [Google Scholar]
- Mahanta, S.; Habib, M.R.; Moore, J.M. Effect of high-voltage atmospheric cold plasma treatment on germination and heavy metal uptake by soybeans (Glycine max). Int. J. Mol. Sci. 2022, 23, 1611. [Google Scholar] [CrossRef] [PubMed]
- Dutta, A.; Dahal, P.; Prajapati, R.; Tamang, P.; Kumar, E.S. IoT based aquaponics monitoring system. In Proceedings of the 1st KEC Conference Proceedings, Lalitpur, Nepal, 27 September 2018; Volume 1, pp. 75–80. [Google Scholar]
- Dhal, S.B.; Jungbluth, K.; Lin, R.; Sabahi, S.P.; Bagavathiannan, M.; Braga-Neto, U.; Kalafatis, S. A machine-learning-based IoT system for optimizing nutrient supply in commercial aquaponic operations. Sensors 2022, 22, 3510. [Google Scholar] [CrossRef] [PubMed]
- Dhal, S.B.; Bagavathiannan, M.; Braga-Neto, U.; Kalafatis, S. Nutrient optimization for plant growth in Aquaponic irrigation using machine learning for small training datasets. Artif. Intell. Agric. 2022, 6, 68–76. [Google Scholar] [CrossRef]
- Dhal, S.B.; Bagavathiannan, M.; Braga-Neto, U.; Kalafatis, S. Can Machine Learning classifiers be used to regulate nutrients using small training datasets for aquaponic irrigation?: A comparative analysis. PLoS ONE 2022, 17, e0269401. [Google Scholar] [CrossRef] [PubMed]
- Arvind, C.S.; Jyothi, R.; Kaushal, K.; Girish, G.; Saurav, R.; Chetankumar, G. Edge computing based smart aquaponics monitoring system using deep learning in IoT environment. In Proceedings of the 2020 IEEE Symposium Series on Computational Intelligence (SSCI), Canberra, ACT, Australia, 1–4 December 2020; pp. 1485–1491. [Google Scholar]
- Dhal, S.B.; Mahanta, S.; Gumero, J.; O’Sullivan, N.; Soetan, M.; Louis, J.; Gadepally, K.C.; Mahanta, S.; Lusher, J.; Kalafatis, S. An IoT-based data-driven real-time monitoring system for control of heavy metals to ensure optimal lettuce growth in hydroponic set-ups. Sensors 2023, 23, 451. [Google Scholar] [CrossRef] [PubMed]
- Habib, M.R.; Mahanta, S.; Jolly, Y.N.; Moore, J.M. Alleviating heavy metal toxicity in milk and water through a synergistic approach of absorption technique and high voltage atmospheric cold plasma and probable rheological changes. Biomolecules 2022, 12, 913. [Google Scholar] [CrossRef] [PubMed]
- Vashisht, P.; Singh, L.; Mahanta, S.; Verma, D.; Sharma, S.; Saini, G.S.; Sharma, A.; Chowdhury, B.; Awasti, N.; Gaurav; et al. Pulsed electric field processing in the dairy sector: A review of applications, quality impact and implementation challenges. Int. J. Food Sci. Technol. 2024, 59, 2122–2135. [Google Scholar] [CrossRef]
- Vashisht, P.; Verma, D.; Charles, A.P.R.; Saini, G.S.; Sharma, S.; Singh, L.; Mahanta, S.; Mahanta, S.; Singh, K.; Gaurav, G. Ozone processing in the dairy sector: A review of applications, quality impact and implementation challenges. ChemRxiv 2023. [Google Scholar] [CrossRef]
- Dhal, S.B.; Mahanta, S.; Gadepally, K.C.; He, S.; Hughes, M.; Moore, J.; Nowka, K.J.; Kalafatis, S. CNN-based real-time prediction of growth stage in soybeans cultivated in hydroponic set-ups. In Proceedings of the SoutheastCon 2023, Orlando, FL, USA, 1–16 April 2023; pp. 193–197. [Google Scholar]
- Jones, J.W.; Hoogenboom, G.; Porter, C.H.; Boote, K.J.; Batchelor, W.D.; Hunt, L.A.; Wilkens, P.W.; Singh, U.; Gijsman, A.J.; Ritchie, J.T. The DSSAT cropping system model. Eur. J. Agron. 2003, 18, 235–265. [Google Scholar] [CrossRef]
- Wang, E.; Robertson, M.J.; Hammer, G.L.; Carberry, P.S.; Holzworth, D.; Meinke, H.; Chapman, S.C.; Hargreaves, J.N.G.; Huth, N.I.; McLean, G. Development of a generic crop model template in the cropping system model APSIM. Eur. J. Agron. 2002, 18, 121–140. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Ullah, M.; Ullah, H.; Khan, S.D.; Cheikh, F.A. Stacked lstm network for human activity recognition using smartphone data. In Proceedings of the 2019 8th European Workshop on Visual Information Processing (EUVIP), Roma, Italy, 28–31 October 2019; pp. 175–180. [Google Scholar]
- Graves, A.; Jaitly, N.; Mohamed, A.R. Hybrid speech recognition with deep bidirectional LSTM. In Proceedings of the 2013 IEEE Workshop on Automatic Speech Recognition and Understanding, Olomouc, Czech Republic, 8–12 December 2013; pp. 273–278. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Xue, J.; Chen, X. Ensemble learning approaches in speech recognition. In Speech and Audio Processing for Coding, Enhancement and Recognition; Springer: New York, NY, USA, 2014; pp. 113–152. [Google Scholar]
- Jiang, Z.; Liu, C.; Hendricks, N.P.; Ganapathysubramanian, B.; Hayes, D.J.; Sarkar, S. Predicting county level corn yields using deep long short term memory models. arXiv 2018, arXiv:1805.12044. [Google Scholar]
- Gavahi, K.; Abbaszadeh, P.; Moradkhani, H. DeepYield: A combined convolutional neural network with long short-term memory for crop yield forecasting. Expert Syst. Appl. 2021, 184, 115511. [Google Scholar] [CrossRef]
- Van Klompenburg, T.; Kassahun, A.; Catal, C. Crop yield prediction using machine learning: A systematic literature review. Comput. Electron. Agric. 2020, 177, 105709. [Google Scholar] [CrossRef]
- Yuan, C.Z.; Ling, S.K. Long short-term memory model based agriculture commodity price prediction application. In Proceedings of the 2020 2nd International Conference on Information Technology and Computer Communications, Kuala Lumpur, Malaysia, 12–14 August 2020; pp. 43–49. [Google Scholar]
- Chen, P.; Xiao, Q.; Zhang, J.; Xie, C.; Wang, B. Occurrence prediction of cotton pests and diseases by bidirectional long short-term memory networks with climate and atmosphere circulation. Comput. Electron. Agric. 2020, 176, 105612. [Google Scholar] [CrossRef]
- Xiao, Q.; Li, W.; Kai, Y.; Chen, P.; Zhang, J.; Wang, B. Occurrence prediction of pests and diseases in cotton on the basis of weather factors by long short term memory network. BMC Bioinform. 2019, 20, 688. [Google Scholar] [CrossRef] [PubMed]
- Suresh, K.K.; Krishna Priya, S.R. Forecasting sugarcane yield of Tamilnadu using ARIMA models. Sugar Tech 2011, 13, 23–26. [Google Scholar] [CrossRef]
- Elsamie, M.A.; Ali, T.; Zhou, D.Y. Using a dynamic time series model (ARIMA) for forecasting of Egyptian cotton crop variables. J. Anim. Plant Sci. 2021, 31, 810–823. [Google Scholar]
- Poyyamozhi, S.; Mohideen, A.K. Forecasting of cotton production in India using ARIMA model. Asia Pac. J. Res. ISSN (Print) 2016, 2320, 5504. [Google Scholar]
- Zhao, D.; Reddy, K.R.; Kakani, V.G.; Read, J.J.; Koti, S. Canopy reflectance in cotton for growth assessment and lint yield prediction. Eur. J. Agron. 2007, 26, 335–344. [Google Scholar] [CrossRef]
- Ballester, C.; Hornbuckle, J.; Brinkhoff, J.; Smith, J.; Quayle, W. Assessment of in-season cotton nitrogen status and lint yield prediction from unmanned aerial system imagery. Remote Sens. 2017, 9, 1149. [Google Scholar] [CrossRef]
- Pylianidis, C.; Osinga, S.; Athanasiadis, I.N. Introducing digital twins to agriculture. Comput. Electron. Agric. 2021, 184, 105942. [Google Scholar] [CrossRef]
- Bhandari, M.; Chang, A.; Jung, J.; Ibrahim, A.M.H.; Rudd, J.C.; Baker, S.; Landivar, J.; Liu, S.; Landivar, J. Unmanned aerial system-based high-throughput phenotyping for plant breeding. Plant Phenome J. 2023, 6, e20058. [Google Scholar] [CrossRef]
- Sullivan, D.G.; Shaw, N.L. Using smartphone technology to assess field crop stands. Agron. J. 2016, 108, 1674–1680. [Google Scholar]
- Hyndman, R. Better acf and pacf plots, but no optimal linear prediction. Electron. J. Stat. [E] 2014, 8, 2296–2300. [Google Scholar]
- Zakria, M.; Muhammad, F. Forecasting the population of Pakistan using ARIMA models. Pak. J. Agric. Sci. 2009, 46, 214–223. [Google Scholar]
- Gasca, M.; Sauer, T. Polynomial interpolation in several variables. Adv. Comput. Math. 2000, 12, 377–410. [Google Scholar] [CrossRef]
- Dhaliwal, J.K.; Panday, D.; Saha, D.; Lee, J.; Jagadamma, S.; Schaeffer, S.; Mengistu, A. Predicting and interpreting cotton yield and its determinants under long-term conservation management practices using machine learning. Comput. Electron. Agric. 2022, 199, 107107. [Google Scholar] [CrossRef]
- Chen, C.; Chen, F. Cotton yield prediction using artificial neural networks. Int. J. Agric. Biol. Eng. 2014, 7, 144–150. [Google Scholar]
- Zhang, C.; Kovacs, J.M.; Kafatos, M. Monitoring cotton yield and growth anomalies using AVHRR NDVI time-series data. Int. J. Remote Sens. 2002, 23, 4653–4665. [Google Scholar]
- Risal, A.; Niu, H.; Landivar-Scott, J.L.; Maeda, M.M.; Bednarz, C.W.; Landivar-Bowles, J.; Duffield, N.; Payton, P.; Pal, P.; Lascano, R.J.; et al. Improving Irrigation Management of Cotton with Small Unmanned Aerial Vehicle (UAV) in Texas High Plains. Water 2024, 16, 1300. [Google Scholar] [CrossRef]
- Wang, K.; Theo, G. Alignment of curves by dynamic time warping. Ann. Stat. 1997, 25, 1251–1276. [Google Scholar] [CrossRef]
- Berndt Donald, J.; Clifford, J. Using dynamic time warping to find patterns in time series. In Proceedings of the 3rd International Conference on Knowledge Discovery and Data Mining, Seattle, WA, USA, 31 July–1 August 1994; pp. 359–370. [Google Scholar]
- Stan, S.; Chan, P. Toward accurate dynamic time warping in linear time and space. Intell. Data Anal. 2007, 11, 561–580. [Google Scholar]
- Gibran, K.; Bushrui, S.B. The Prophet: A New Annotated Edition; Simon and Schuster: New York, NY, USA, 2012. [Google Scholar]
- Casals, J.; García-Hiernaux, A.; Jerez, M. From general state-space to VARMAX models. Math. Comput. Simul. 2012, 82, 924–936. [Google Scholar] [CrossRef]
- Aoki, M. State Space Modeling of Time Series; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Rangapuram, S.S.; Seeger, M.W.; Gasthaus, J.; Stella, L.; Wang, Y.; Januschowski, T. Deep state space models for time series forecasting. In Advances in Neural Information Processing Systems; Curran Associates Inc.: Red Hook, NY, USA, 2018; Volume 31. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).