An Interpolation and Prediction Algorithm for XCO2 Based on Multi-Source Time Series Data
Abstract
1. Introduction
- Due to insufficient satellite data coverage, the acquisition of long-term time series data is limited, thus making the accurate prediction of future CO2 concentrations more challenging.
- Augmenting the existing multisource data with ground semantic information has been incorporated, enhancing the predictive capabilities of the model.
- A daily dataset of seamless XCO2 in the Yangtze River Delta region with a spatial resolution of 0.25°, derived from the fusion of multisource data spanning from 2016 to 2020, has been established.
- The adoption of the TCN-Attention module has improved the quality and efficiency of feature aggregation, enabling the better capture of both local and global spatial features.
- Leveraging the LSTM structure, long-term trends in multisource spatiotemporal data are effectively modeled, facilitating the integration of features across multiple time steps.
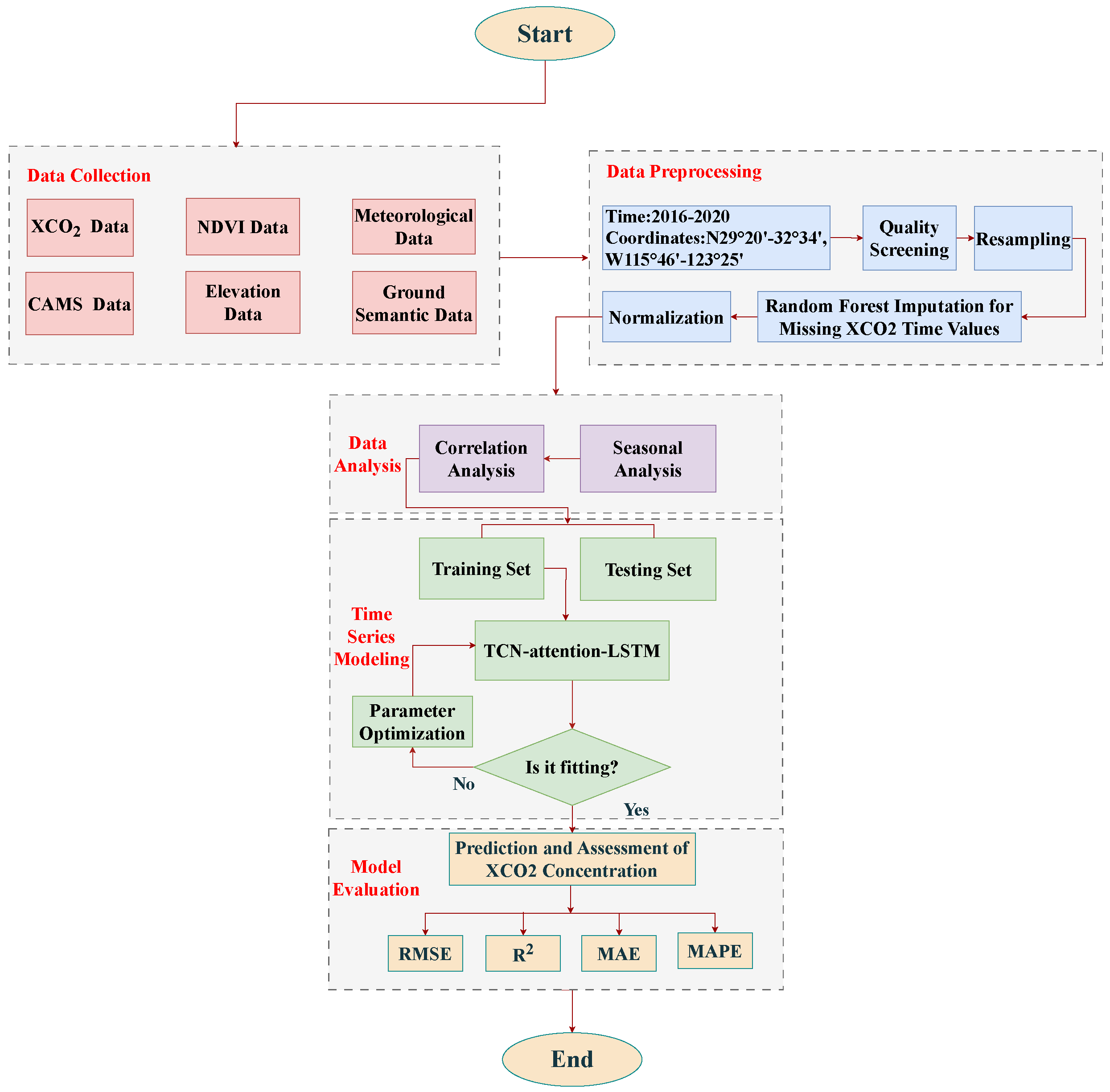
2. Materials and Methods
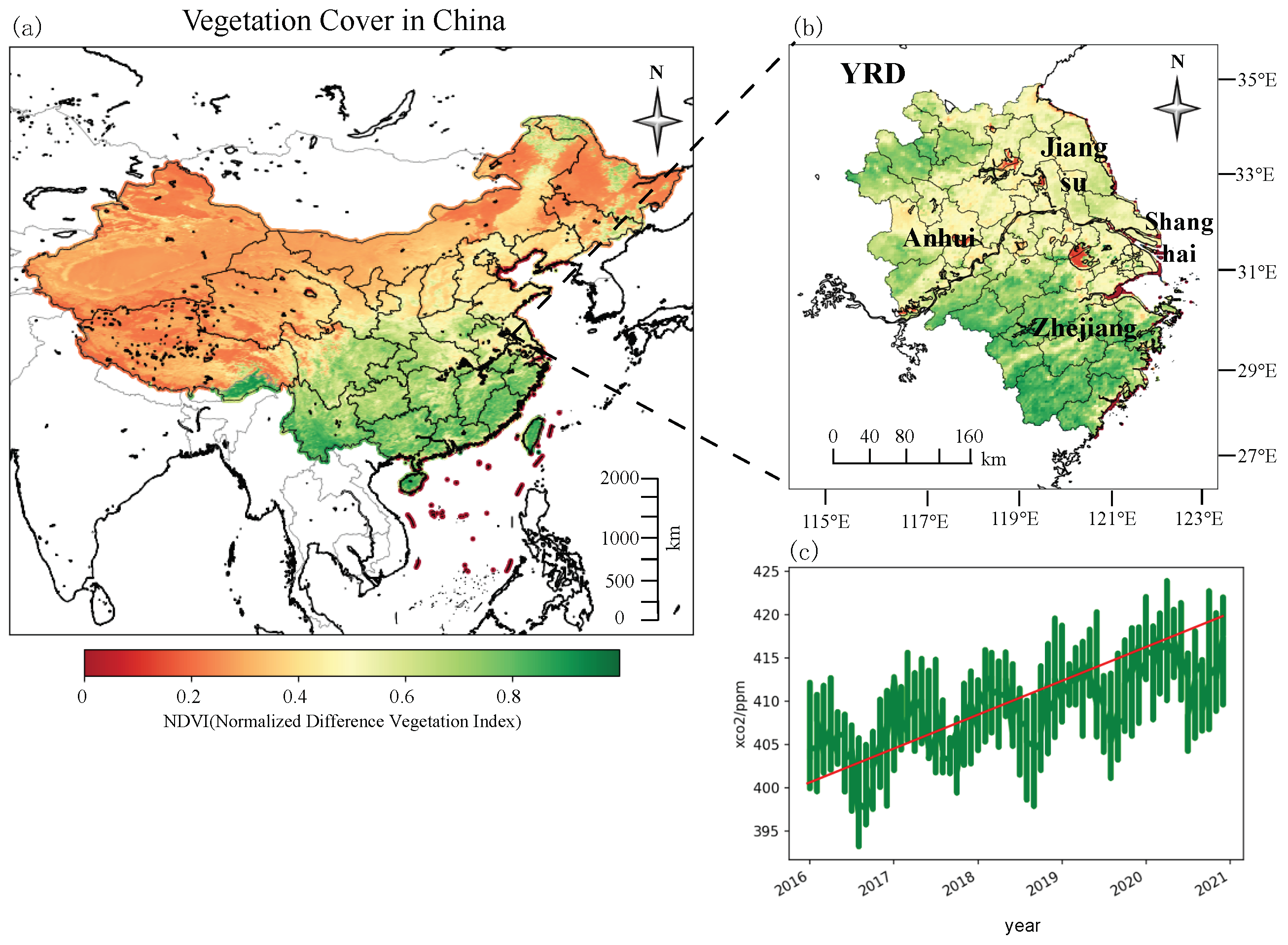
2.1. Study Area
2.2. Multisource Data
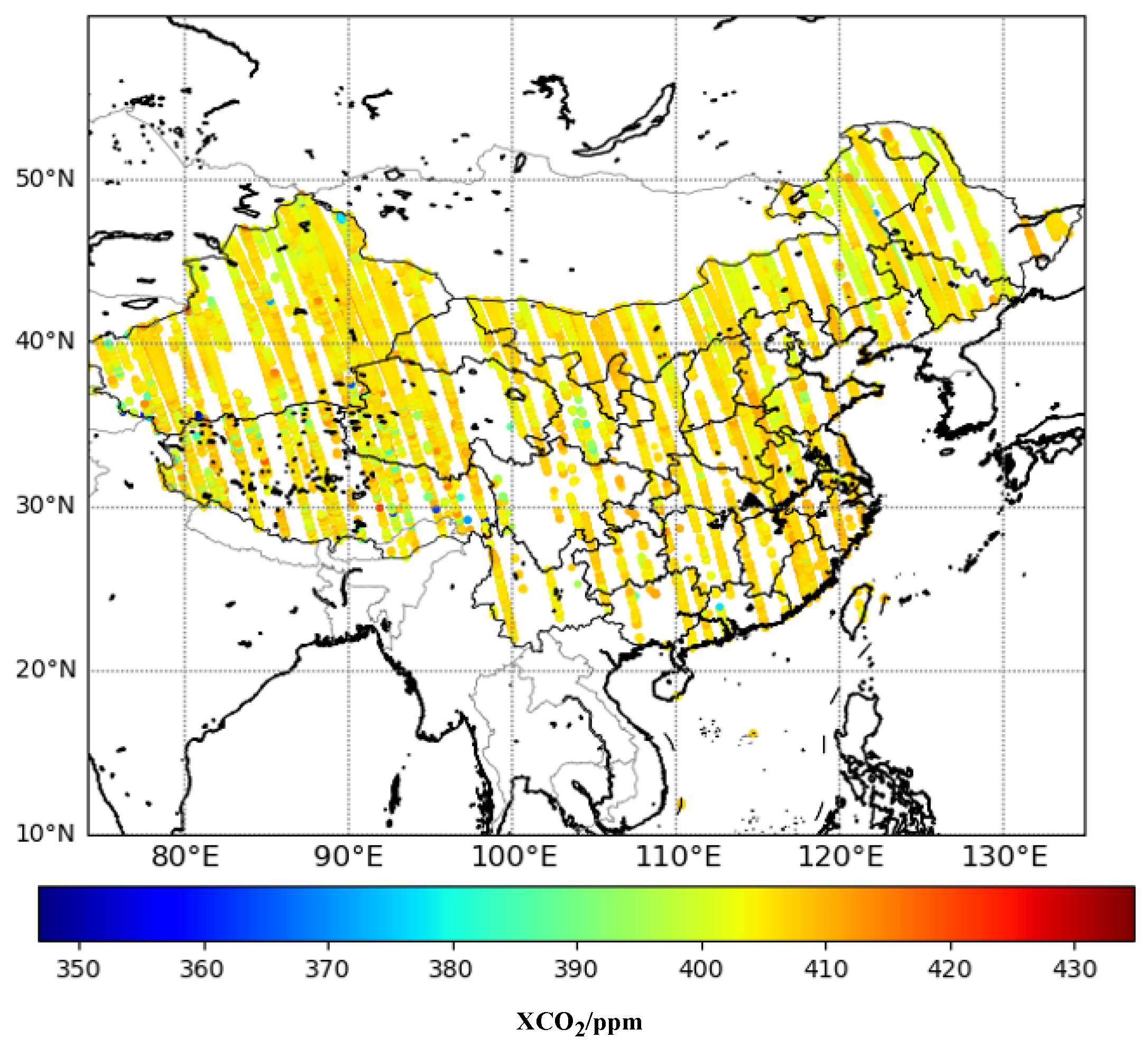
2.2.1. OCO-2 XCO2 Data
2.2.2. CAMS XCO2 Data
2.2.3. Vegetation Data
2.2.4. Meteorological Data
2.2.5. Elevation Data
2.2.6. Land Cover Data
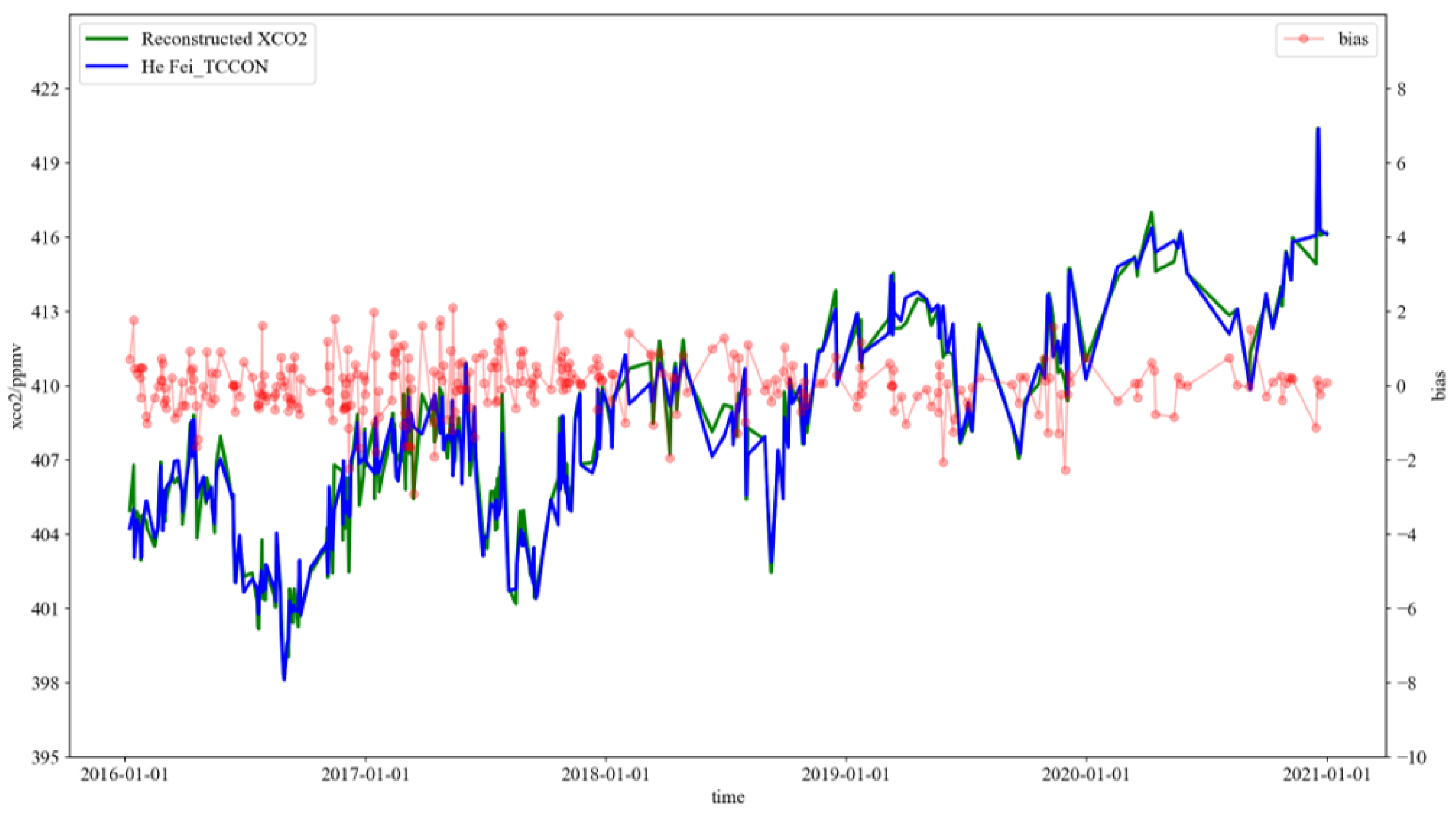
2.2.7. TCCON XCO2 Data
2.2.8. Data Preprocessing
2.3. Data Analysis
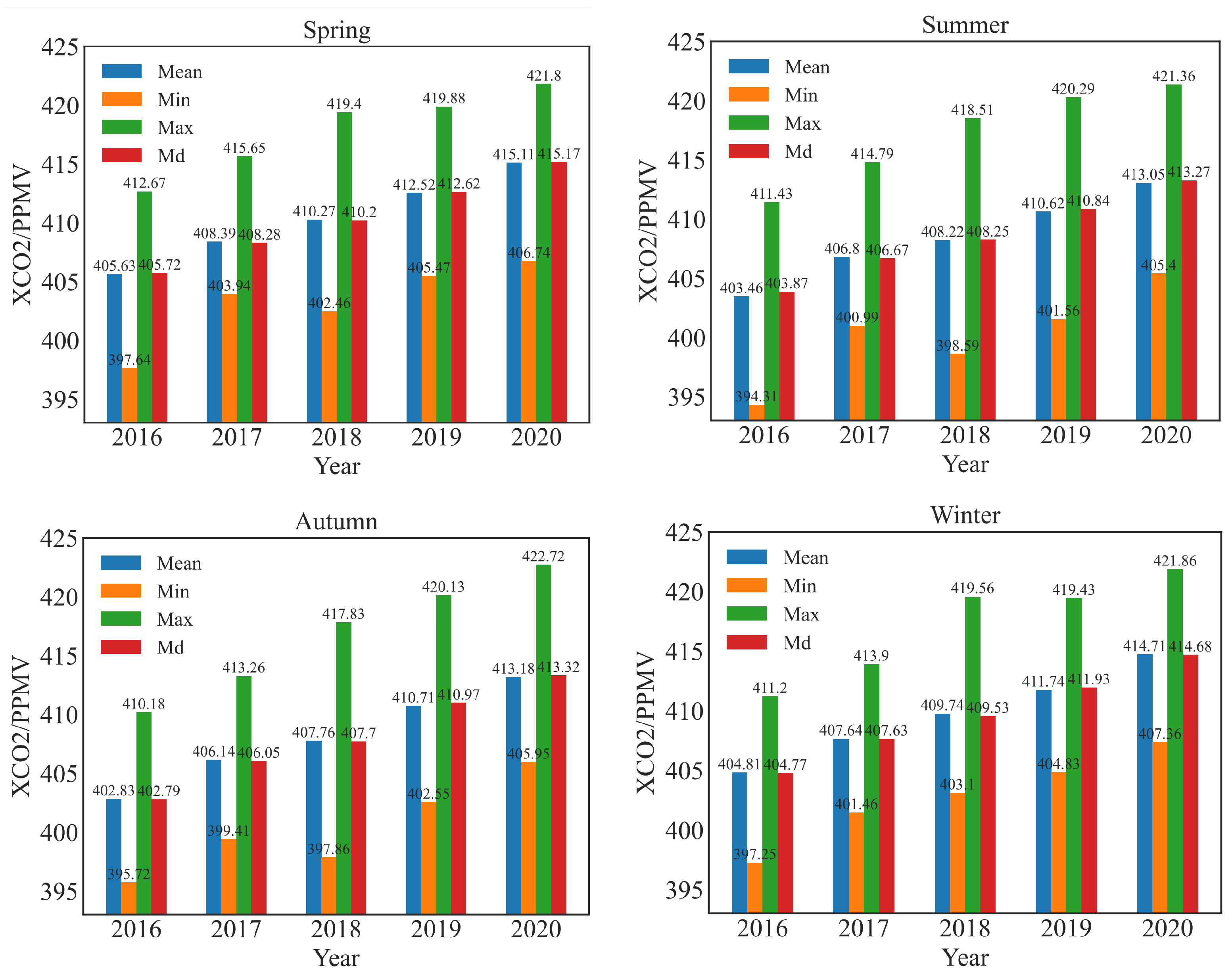
2.3.1. Seasonal Analysis
2.3.2. Statistical Relationship between Variables
2.4. Prediction Models
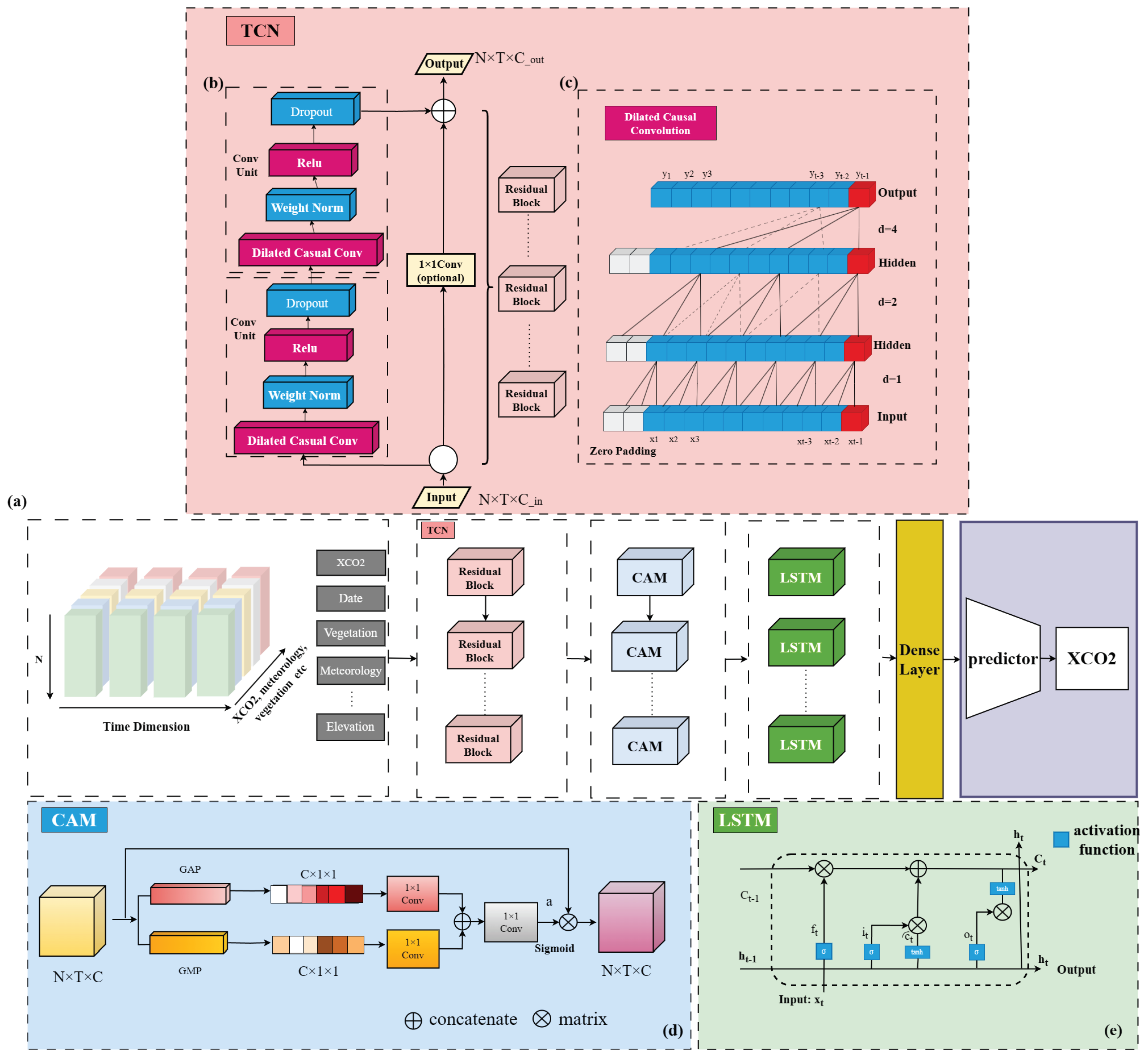
2.4.1. TCN Module
- Causal ConvolutionThe causal convolution imparts a strict temporal constraint on the TCN module with respect to the input XCO2 sequence , , …, , ,.... The output at time t is expressed such that it is only related to the inputs up to and including time t. As illustrated in Figure 8b, its mathematical representation is as follows:Here, is a one-dimensional vector containing n features, and is the variable to be predicted. There exists some relationship between and , denoted by the function f. To ensure that the output tensor and input tensor have the same length, a strategy of zero-padding on the left side of the input tensor is employed. Causal convolution is a unidirectional structure that processes the value at time t and uses only data before time t to ensure the temporal nature of data processing. However, to obtain longer and complete historical information, as the network depth increases, issues such as gradient vanishing, computational complexity, and poor fitting effects may arise. Therefore, dilated convolution is introduced.
- Dilated ConvolutionDilated convolution allows exponentially increasing the receptive field without increasing parameters and model complexity. As shown in Figure 8c, the network structure of dilated convolution is presented. Unlike traditional convolutional neural networks (CNN), dilated convolution permits the input of convolution to have interval sampling controlled by the dilation factor, denoted as d. In the bottom layer, d represents that the input is sampled at each time point, and in the hidden layers, d = 2 means that the input is sampled every 2 time points as one input. For a one-dimensional XCO2 concentration sequence X = (, , …, , xt), the definition of dilated convolution with a filter f on 0, …, k − 1 is given as follows:where S is the input sequence information, d is the dilation factor, k is the filter size, f(i) represents the weight of the convolutional kernel, is the total displacement on the input sequence, and denotes the position in the historical information of the sequence. The dilation factor d = (1, 2, 4) is used, and as d increases, the receptive field of TCN expands, ensuring that the convolutional kernel can flexibly choose the length of historical data information. The receptive field of TCN is expressed as:Here, n is the number of layers, and b is the base of the dilation convolution (dilation factor d = , i = 1, 2, …, n). It can be observed that when the filter size is 3 and the dilation factors are [1, 2, 4], the output yt at time t is determined by the inputs (x1, x2, …, xt), indicating that the receptive field can cover all values in the input sequence.
- Residual blockThe residual structure of TCN is illustrated in Figure 8a. The output of different layers is added to the input data, forming a residual block. After passing through an activation function, the output is obtained. The residual block connection mechanism enhances the network’s feedback and convergence, and helps avoid issues like gradient vanishing and exploding commonly found in traditional neural networks. Each residual unit consists of two one-dimensional dilated causal convolutional layers and a non-linear mapping. Initially, the input data undergoes a one-dimensional dilated causal convolution, followed by weight normalization to address gradient explosion and accelerate network training. Subsequently, a ReLU activation function is applied for non-linear operations. Dropout is added after each dilated convolution to prevent overfitting. Additionally, a 1 × 1 convolution is introduced to return to the original number of channels. Finally, the obtained result is summed with the input to generate the output vectorwhere fi represents the feature vector obtained through convolution at time i, wi denotes the weights of the convolution calculation at time i, Fj represents the convolutional kernel of the j-th layer, bi is the bias vector, weightnorm(x) = , represents the magnitude of the weight w in the Relu(x) = max(0,x) operation, and indicates the unit vector in the same direction as w. ht represents the feature map obtained after the complete convolution of the j-th layer.
2.4.2. Tcn-Cam Module
2.4.3. LSTM Module
2.5. Model Evaluation Metrics
3. Results and Discussion
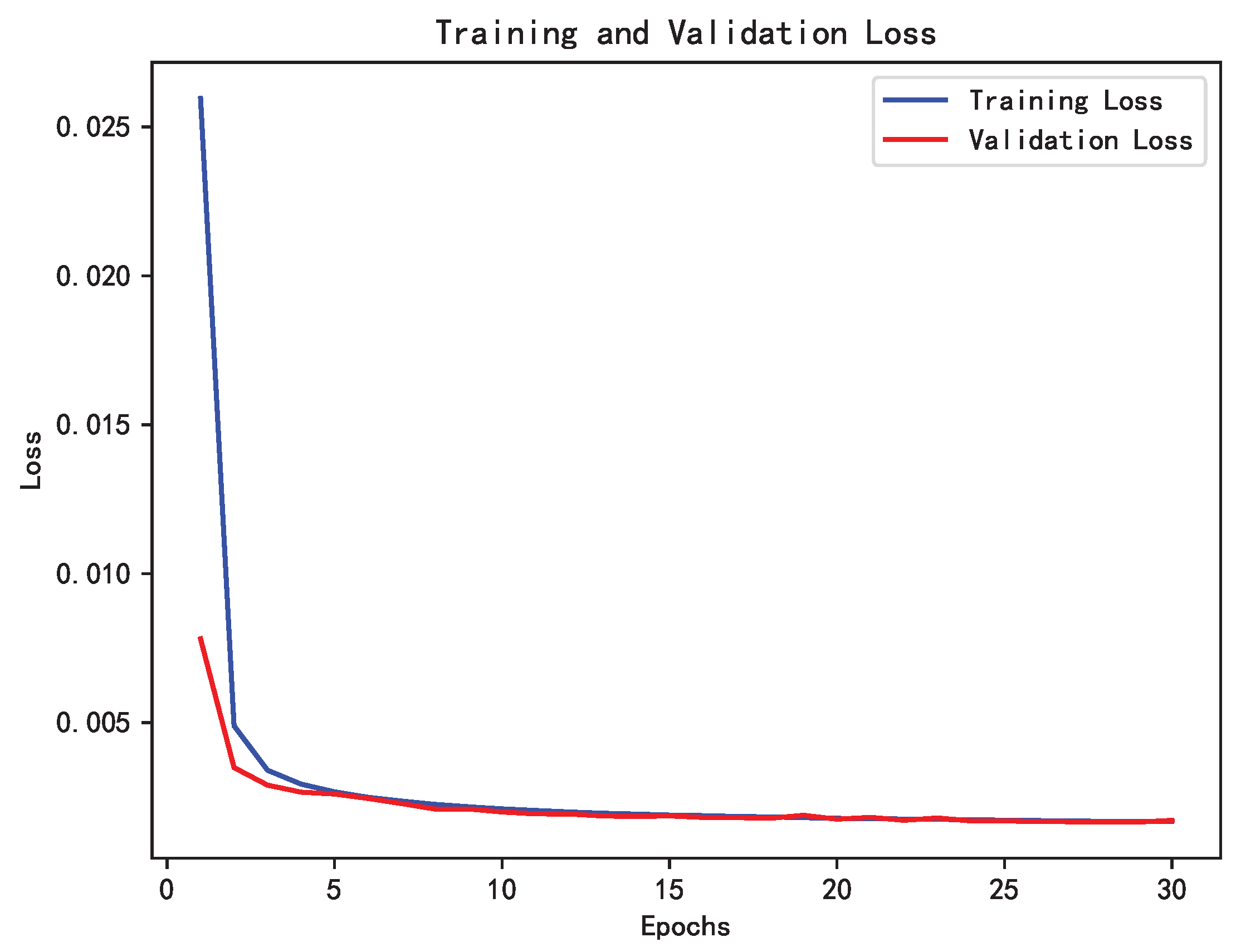
3.1. Experimental Environment
3.2. Sensitivity Analysis
- LSTM, denoted as Model 1;
- TCN, denoted as Model 2;
- TCN-CAM, denoted as Model 3;
- TCN-LSTM, denoted as Model 4;
- CATCN-LSTM, representing the integrated model proposed in this paper.
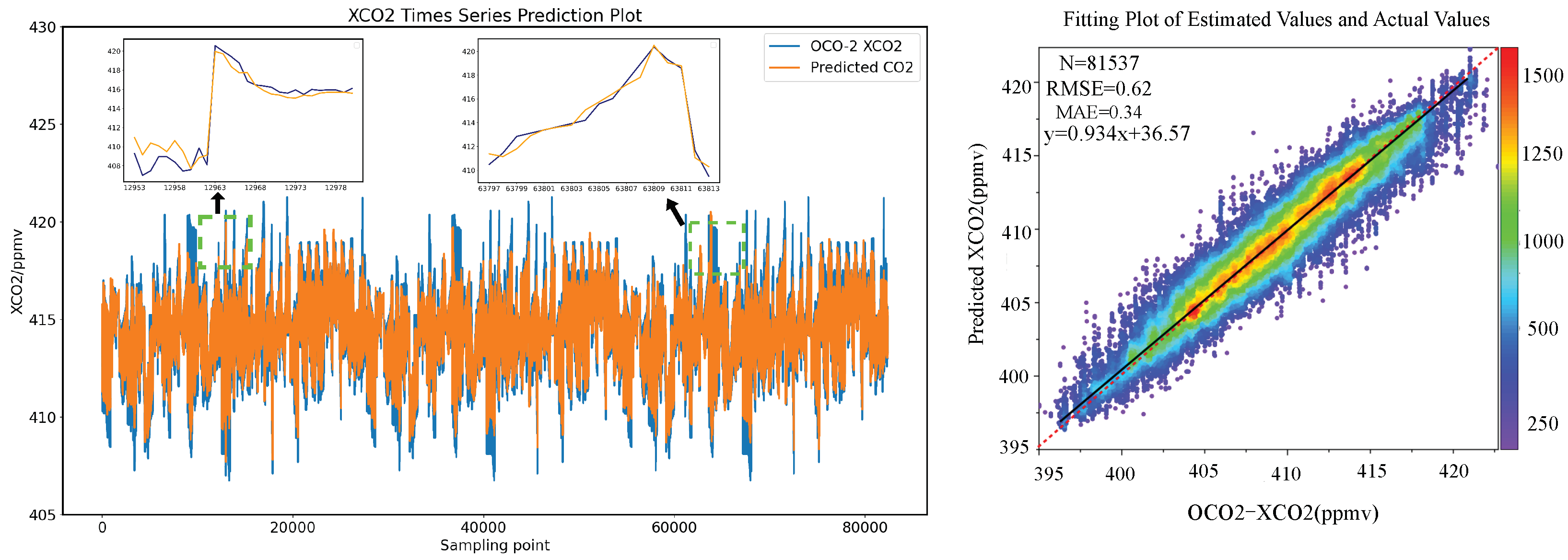
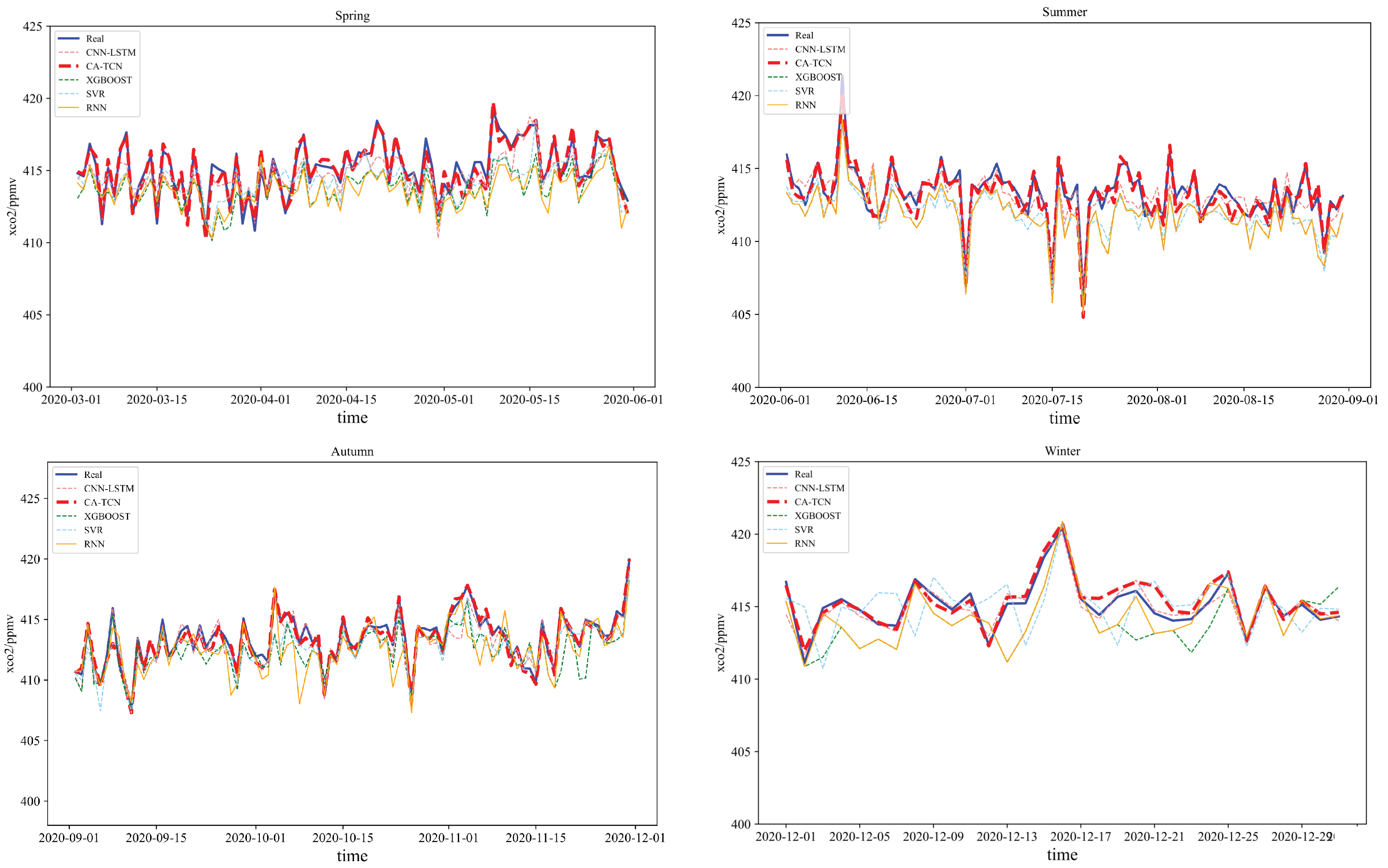
3.3. Comparison of CATCN-LSTM with Other Models
4. Conclusions and Prospect
4.1. Conclusions
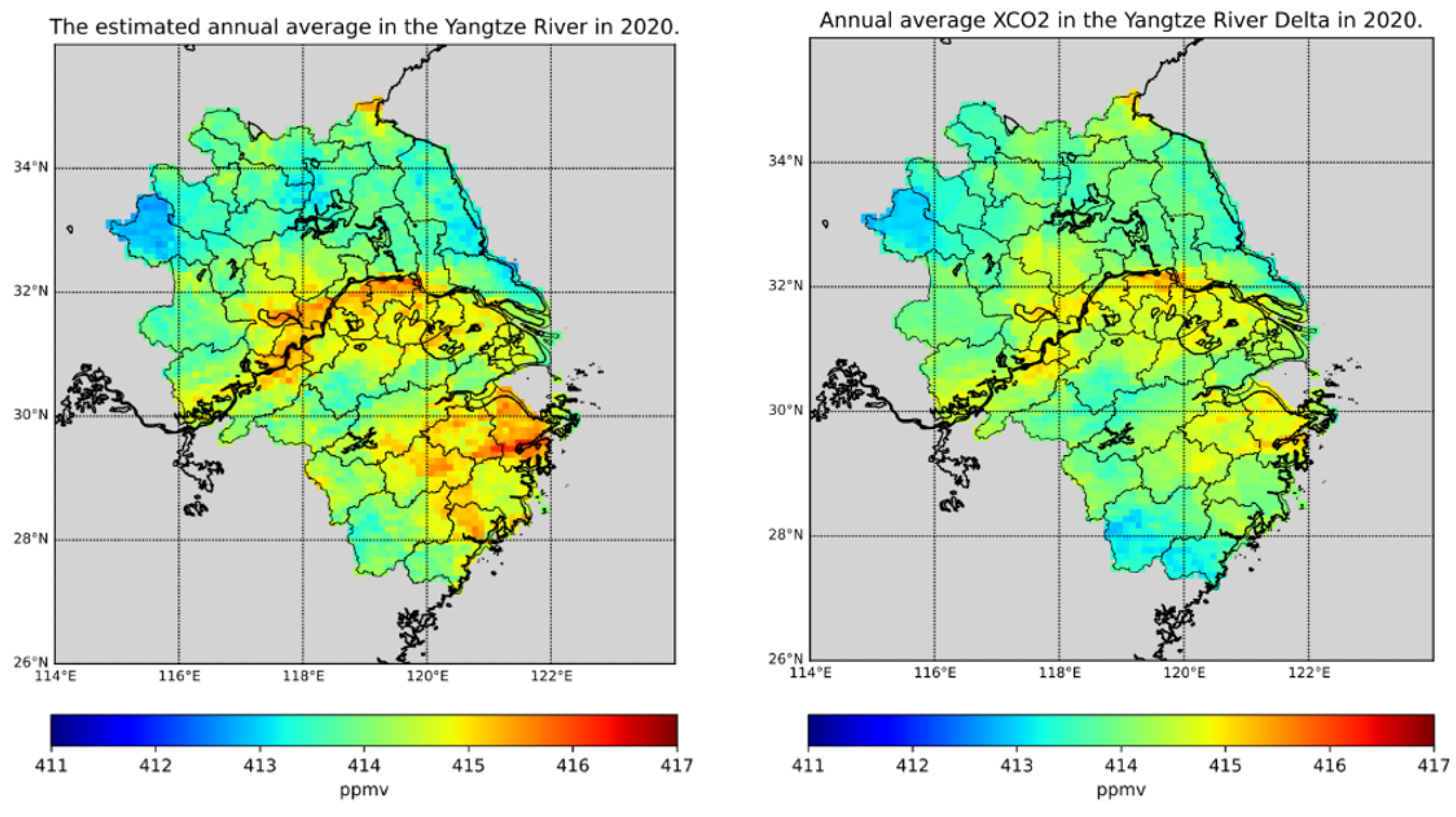
- To address spatiotemporal sparse characteristics of data observed from carbon satellite raw data, this paper employs bilinear interpolation to resample multiple auxiliary datasets with XCO2 data, achieving a daily data granularity of 0.25°. Subsequently, an Extreme Random Forest algorithm is utilized to reconstruct the data from 2016 to 2020. Through ten-fold cross-validation, the model’s robustness is verified, ensuring a high concordance of 92% with ground measurement station data.
- CATCN-LSTM algorithm is proposed for predicting four seasons’ CO2 concentrations in the Yangtze River Delta; it achieved higher predictive accuracy in summer and relatively weaker accuracy in winter. Compared to the LSTM model previously used by Meng and Li [21,22], this model effectively addresses the challenges posed by interdependent features in long sequences and provides a new approach for predicting CO2 concentrations.
4.2. Prospective
- In terms of data, since satellite XCO2 observational data are typically more accurate than reconstructed XCO2 data, future studies can integrate more satellite data to enhance accuracy. For example, satellites like OCO-3 and GOSAT can be integrated, and deep learning techniques can be employed for interpolation when integrating high spatiotemporal resolution XCO2 data. In addition, this study estimates XCO2 data using environmental variables, but did not incorporate anthropogenic factors into the modeling process. Existing research has not adequately addressed this point [43,44,45], and in the future, incorporating social science factors into the model may improve our estimation accuracy.
- In the model aspect, more advanced deep learning architectures or ensemble methods can be explored to further improve the predictive accuracy of CO2 concentrations. Consideration can be given to incorporating technologies like Transformer and spatiotemporal attention mechanisms to better capture the complex spatiotemporal relationships of CO2 concentrations in the atmosphere. Tuning model parameters and conducting sensitivity analyses are recommended to ensure model robustness and stability.
- In terms of ground stations, it is advisable to increase the construction of CO2 ground stations to enhance data reliability and coverage. Real-time monitoring data from ground stations can serve as crucial references for model validation and calibration, thereby increasing the credibility of the model in practical applications.
5. Declaration of Generative AI and AI-Assisted Technologies in the Writing Process
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Brethomé, F.M.; Williams, N.J.; Seipp, C.A.; Kidder, M.K.; Custelcean, R. Direct air capture of CO2 via aqueous-phase absorption and crystalline-phase release using concentrated solar power. Nat. Energy 2018, 3, 553–559. [Google Scholar] [CrossRef]
- Ofipcc, W.G.I. Climate Change 2013: The Physical Science Basis. Contrib. Work. 2013, 43, 866–871. [Google Scholar]
- Zickfeld, K.; Azevedo, D.; Mathesius, S.; Matthews, H.D. Asymmetry in the climate—Carbon cycle response to positive and negative CO2 emissions. Nat. Clim. Change 2021, 11, 613–617. [Google Scholar] [CrossRef]
- Zhenmin, L.; Espinosa, P. Tackling climate change to accelerate sustainable development. Nat. Clim. Change 2019, 9, 494–496. [Google Scholar] [CrossRef]
- Zhao, X.; Ma, X.; Chen, B.; Shang, Y.; Song, M. Challenges toward carbon neutrality in China: Strategies and countermeasures. Resour. Conserv. Recycl. 2022, 176, 105959. [Google Scholar] [CrossRef]
- Jeong, S.; Zhao, C.; Andrews, A.E.; Dlugokencky, E.J.; Sweeney, C.; Bianco, L.; Wilczak, J.M.; Fischer, M.L. Seasonal variations in N2O emissions from central California. Geophys. Res. Lett. 2012, 39, L16805. [Google Scholar] [CrossRef]
- Chiba, T.; Haga, Y.; Inoue, M.; Kiguchi, O.; Nagayoshi, T.; Madokoro, H.; Morino, I. Measuring regional atmospheric CO2 concentrations in the lower troposphere with a non-dispersive infrared analyzer mounted on a UAV, Ogata Village, Akita, Japan. Atmosphere 2019, 10, 487. [Google Scholar] [CrossRef]
- Siabi, Z.; Falahatkar, S.; Alavi, S.J. Spatial distribution of XCO2 using OCO-2 data in growing seasons. J. Environ. Manag. 2019, 244, 110–118. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Jiang, F.; Wang, J.; Ju, W.; Chen, J.M. Terrestrial ecosystem carbon flux estimated using GOSAT and OCO-2 XCO 2 retrievals. Atmos. Chem. Phys. 2019, 19, 12067–12082. [Google Scholar] [CrossRef]
- Hammerling, D.M.; Michalak, A.M.; Kawa, S.R. Mapping of CO2 at high spatiotemporal resolution using satellite observations: Global distributions from OCO-2. J. Geophys. Res. Atmos. 2012, 117, D6. [Google Scholar] [CrossRef]
- Mao, J.; Kawa, S.R. Sensitivity studies for space-based measurement of atmospheric total column carbon dioxide by reflected sunlight. Appl. Opt. 2004, 43, 914–927. [Google Scholar] [CrossRef] [PubMed]
- Liang, A.; Gong, W.; Han, G.; Xiang, C. Comparison of satellite-observed XCO2 from GOSAT, OCO-2, and ground-based TCCON. Remote Sens. 2017, 9, 1033. [Google Scholar] [CrossRef]
- Chen, L.; Zhang, Y.; Zou, M.; Xu, Q.; Tao, J. Overview of atmospheric CO2 remote sensing from space. J. Remote Sens. 2015, 19, 1–11. [Google Scholar]
- Pei, Z.; Han, G.; Ma, X.; Shi, T.; Gong, W. A method for estimating the background column concentration of CO2 using the lagrangian approach. IEEE Trans. Geosci. Remote Sens. 2022, 60, 4108112. [Google Scholar] [CrossRef]
- He, Z.; Lei, L.; Zhang, Y.; Sheng, M.; Wu, C.; Li, L.; Zeng, Z.C.; Welp, L.R. Spatio-temporal mapping of multi-satellite observed column atmospheric CO2 using precision-weighted kriging method. Remote Sens. 2020, 12, 576. [Google Scholar] [CrossRef]
- Jin, C.; Xue, Y.; Jiang, X.; Zhao, L.; Yuan, T.; Sun, Y.; Wu, S.; Wang, X. A long-term global XCO2 dataset: Ensemble of satellite products. Atmos. Res. 2022, 279, 106385. [Google Scholar] [CrossRef]
- He, C.; Ji, M.; Li, T.; Liu, X.; Tang, D.; Zhang, S.; Luo, Y.; Grieneisen, M.L.; Zhou, Z.; Zhan, Y. Deriving full-coverage and fine-scale XCO2 across China based on OCO-2 satellite retrievals and CarbonTracker output. Geophys. Res. Lett. 2022, 49, e2022GL098435. [Google Scholar] [CrossRef]
- Li, J.; Jia, K.; Wei, X.; Xia, M.; Chen, Z.; Yao, Y.; Zhang, X.; Jiang, H.; Yuan, B.; Tao, G.; et al. High-spatiotemporal resolution mapping of spatiotemporally continuous atmospheric CO2 concentrations over the global continent. Int. J. Appl. Earth Obs. Geoinf. 2022, 108, 102743. [Google Scholar] [CrossRef]
- Wang, W.; He, J.; Feng, H.; Jin, Z. High-Coverage Reconstruction of XCO2 Using Multisource Satellite Remote Sensing Data in Beijing–Tianjin–Hebei Region. Int. J. Environ. Res. Public Health 2022, 19, 10853. [Google Scholar] [CrossRef]
- Jingzhi, Z. Research on the Temporal Data Processing and Prediction Model of Atmospheric CO2. Ph.D. Thesis, Anhui University of Science and Technology, Huainan, China, 2020. [Google Scholar]
- Meng, J.; Ding, G.; Liu, L. Research on a prediction method for carbon dioxide concentration based on an optimized LSTM network of spatio-temporal data fusion. IEICE Trans. Inf. Syst. 2021, 104, 1753–1757. [Google Scholar] [CrossRef]
- Li, J.; Zhang, Y.; Gai, R. Estimation of CO2 Column Concentration in Spaceborne Short Wave Infrared Based on Machine Learning. China Environ. Sci. 2023, 43, 1499–1509. [Google Scholar] [CrossRef]
- Voulodimos, A.; Doulamis, N.; Doulamis, A.; Protopapadakis, E. Deep learning for computer vision: A brief review. Comput. Intell. Neurosci. 2018, 2018, 7068349. [Google Scholar] [CrossRef] [PubMed]
- Hu, K.; Jin, J.; Zheng, F.; Weng, L.; Ding, Y. Overview of behavior recognition based on deep learning. Artif. Intell. Rev. 2023, 56, 1833–1865. [Google Scholar] [CrossRef]
- Li, H.; Mu, H.; Zhang, M.; Li, N. Analysis on influence factors of China’s CO2 emissions based on Path–STIRPAT model. Energy Policy 2011, 39, 6906–6911. [Google Scholar] [CrossRef]
- Wu, Y.; Peng, Z.; Ma, Q. A Study on the Factors Influencing Carbon Emission Intensity in the Yangtze River Delta Region. J. Liaoning Tech. Univ. Soc. Sci. Ed. 2023, 25, 28–34. [Google Scholar]
- Nassar, R.; Hill, T.G.; McLinden, C.A.; Wunch, D.; Jones, D.B.; Crisp, D. Quantifying CO2 emissions from individual power plants from space. Geophys. Res. Lett. 2017, 44, 10–045. [Google Scholar] [CrossRef]
- Inness, A.; Ades, M.; Agustí-Panareda, A.; Barré, J.; Benedictow, A.; Blechschmidt, A.M.; Dominguez, J.J.; Engelen, R.; Eskes, H.; Flemming, J.; et al. The CAMS reanalysis of atmospheric composition. Atmos. Chem. Phys. 2019, 19, 3515–3556. [Google Scholar] [CrossRef]
- Agustí-Panareda, A.; Barré, J.; Massart, S.; Inness, A.; Aben, I.; Ades, M.; Baier, B.C.; Balsamo, G.; Borsdorff, T.; Bousserez, N.; et al. The CAMS greenhouse gas reanalysis from 2003 to 2020. Atmos. Chem. Phys. 2023, 23, 3829–3859. [Google Scholar] [CrossRef]
- Yang, W.; Zhao, Y.; Wang, Q.; Guan, B. Climate, CO2, and anthropogenic drivers of accelerated vegetation greening in the Haihe River Basin. Remote Sens. 2022, 14, 268. [Google Scholar] [CrossRef]
- Zhang, Y.; Hu, Z.; Wang, J.; Gao, X.; Yang, C.; Yang, F.; Wu, G. Temporal upscaling of MODIS instantaneous FAPAR improves forest gross primary productivity (GPP) simulation. Int. J. Appl. Earth Obs. Geoinf. 2023, 121, 103360. [Google Scholar] [CrossRef]
- Lian, Y.; Li, H.; Renyang, Q.; Liu, L.; Dong, J.; Liu, X.; Qu, Z.; Lee, L.C.; Chen, L.; Wang, D.; et al. Mapping the net ecosystem exchange of CO2 of global terrestrial systems. Int. J. Appl. Earth Obs. Geoinf. 2023, 116, 103176. [Google Scholar] [CrossRef]
- Liu, B.; Ma, X.; Ma, Y.; Li, H.; Jin, S.; Fan, R.; Gong, W. The relationship between atmospheric boundary layer and temperature inversion layer and their aerosol capture capabilities. Atmos. Res. 2022, 271, 106121. [Google Scholar] [CrossRef]
- Zhang, Z.; Lou, Y.; Zhang, W.; Wang, H.; Zhou, Y.; Bai, J. Assessment of ERA-Interim and ERA5 reanalysis data on atmospheric corrections for InSAR. Int. J. Appl. Earth Obs. Geoinf. 2022, 111, 102822. [Google Scholar] [CrossRef]
- Berrisford, P.; Soci, C.; Bell, B.; Dahlgren, P.; Horányi, A.; Nicolas, J.; Radu, R.; Villaume, S.; Bidlot, J.; Haimberger, L. The ERA5 global reanalysis: Preliminary extension to 1950. Q. J. R. Meteorol. Soc. 2021, 147, 4186–4227. [Google Scholar]
- Toon, G.; Blavier, J.F.; Washenfelder, R.; Wunch, D.; Keppel-Aleks, G.; Wennberg, P.; Connor, B.; Sherlock, V.; Griffith, D.; Deutscher, N.; et al. Total column carbon observing network (TCCON). In Proceedings of the Hyperspectral Imaging and Sensing of the Environment, Vancouver, BC, Canada, 26–30 April 2009; Optica Publishing Group: Washington, DC, USA, 2009; p. JMA3. [Google Scholar]
- Hu, K.; Zhang, Q.; Gong, S.; Zhang, F.; Weng, L.; Jiang, S.; Xia, M. A review of anthropogenic ground-level carbon emissions based on satellite data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 8339–8357. [Google Scholar] [CrossRef]
- Zhang, L.L.; Yue, T.X.; Wilson, J.P.; Zhao, N.; Zhao, Y.P.; Du, Z.P.; Liu, Y. A comparison of satellite observations with the XCO2 surface obtained by fusing TCCON measurements and GEOS-Chem model outputs. Sci. Total Environ. 2017, 601, 1575–1590. [Google Scholar] [CrossRef]
- Ren, W.; Wang, Z.; Xia, M.; Lin, H. MFINet: Multi-Scale Feature Interaction Network for Change Detection of High-Resolution Remote Sensing Images. Remote Sens. 2024, 16, 1269. [Google Scholar] [CrossRef]
- Wunch, D.; Wennberg, P.O.; Osterman, G.; Fisher, B.; Naylor, B.; Roehl, C.M.; O’Dell, C.; Mandrake, L.; Viatte, C.; Kiel, M.; et al. Comparisons of the orbiting carbon observatory-2 (OCO-2) XCO2 measurements with TCCON. Atmos. Meas. Tech. 2017, 10, 2209–2238. [Google Scholar] [CrossRef]
- Wunch, D.; Toon, G.C.; Blavier, J.F.L.; Washenfelder, R.A.; Notholt, J.; Connor, B.J.; Griffith, D.W.; Sherlock, V.; Wennberg, P.O. The total carbon column observing network. Philos. Trans. R. Soc. Math. Phys. Eng. Sci. 2011, 369, 2087–2112. [Google Scholar] [CrossRef]
- Laughner, J.L.; Toon, G.C.; Mendonca, J.; Petri, C.; Roche, S.; Wunch, D.; Blavier, J.F.; Griffith, D.W.; Heikkinen, P.; Keeling, R.F.; et al. The Total Carbon Column Observing Network’s GGG2020 data version. Earth Syst. Sci. Data 2024, 16, 2197–2260. [Google Scholar] [CrossRef]
- Li, T.; Wu, J.; Wang, T. Generating daily high-resolution and full-coverage XCO2 across China from 2015 to 2020 based on OCO-2 and CAMS data. Sci. Total Environ. 2023, 893, 164921. [Google Scholar] [CrossRef]
- Zhang, M.; Liu, G. Mapping contiguous XCO2 by machine learning and analyzing the spatio-temporal variation in China from 2003 to 2019. Sci. Total Environ. 2023, 858, 159588. [Google Scholar] [CrossRef] [PubMed]
- He, S.; Yuan, Y.; Wang, Z.; Luo, L.; Zhang, Z.; Dong, H.; Zhang, C. Machine Learning Model-Based Estimation of XCO2 with High Spatiotemporal Resolution in China. Atmosphere 2023, 14, 436. [Google Scholar] [CrossRef]
- Fichtner, F.; Mandery, N.; Wieland, M.; Groth, S.; Martinis, S.; Riedlinger, T. Time-series analysis of Sentinel-1/2 data for flood detection using a discrete global grid system and seasonal decomposition. Int. J. Appl. Earth Obs. Geoinf. 2023, 119, 103329. [Google Scholar] [CrossRef]
- Qiu, Y.; Zhou, J.; Chen, J.; Chen, X. Spatiotemporal fusion method to simultaneously generate full-length normalized difference vegetation index time series (SSFIT). Int. J. Appl. Earth Obs. Geoinf. 2021, 100, 102333. [Google Scholar] [CrossRef]
- Wang, X.; Li, L.; Gong, K.; Mao, J.; Hu, J.; Li, J.; Liu, Z.; Liao, H.; Qiu, W.; Yu, Y.; et al. Modelling air quality during the EXPLORE-YRD campaign—Part I. Model performance evaluation and impacts of meteorological inputs and grid resolutions. Atmos. Environ. 2021, 246, 118131. [Google Scholar] [CrossRef]
- Li, Q.; Zhang, K.; Li, R.; Yang, L.; Yi, Y.; Liu, Z.; Zhang, X.; Feng, J.; Wang, Q.; Wang, W.; et al. Underestimation of biomass burning contribution to PM2. 5 due to its chemical degradation based on hourly measurements of organic tracers: A case study in the Yangtze River Delta (YRD) region, China. Sci. Total Environ. 2023, 872, 162071. [Google Scholar] [CrossRef]
- Falahatkar, S.; Mousavi, S.M.; Farajzadeh, M. Spatial and temporal distribution of carbon dioxide gas using GOSAT data over IRAN. Environ. Monit. Assess. 2017, 189, 627. [Google Scholar] [CrossRef]
- Shi, Q.; Zhuo, L.; Tao, H.; Yang, J. A fusion model of temporal graph attention network and machine learning for inferring commuting flow from human activity intensity dynamics. Int. J. Appl. Earth Obs. Geoinf. 2024, 126, 103610. [Google Scholar] [CrossRef]
- Guo, X.; Hou, B.; Yang, C.; Ma, S.; Ren, B.; Wang, S.; Jiao, L. Visual explanations with detailed spatial information for remote sensing image classification via channel saliency. Int. J. Appl. Earth Obs. Geoinf. 2023, 118, 103244. [Google Scholar] [CrossRef]
- Yin, H.; Weng, L.; Li, Y.; Xia, M.; Hu, K.; Lin, H.; Qian, M. Attention-guided siamese networks for change detection in high resolution remote sensing images. Int. J. Appl. Earth Obs. Geoinf. 2023, 117, 103206. [Google Scholar] [CrossRef]
- Ren, H.; Xia, M.; Weng, L.; Hu, K.; Lin, H. Dual-Attention-Guided Multiscale Feature Aggregation Network for Remote Sensing Image Change Detection. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 4899–4916. [Google Scholar] [CrossRef]
- Hu, K.; Shen, C.; Wang, T.; Shen, S.; Cai, C.; Huang, H.; Xia, M. Action Recognition Based on Multi-Level Topological Channel Attention of Human Skeleton. Sensors 2023, 23, 9738. [Google Scholar] [CrossRef] [PubMed]
- Hu, K.; Zhang, E.; Xia, M.; Wang, H.; Ye, X.; Lin, H. Cross-dimensional feature attention aggregation network for cloud and snow recognition of high satellite images. Neural Comput. Appl. 2024, 36, 7779–7798. [Google Scholar] [CrossRef]
- Hu, K.; Shen, C.; Wang, T.; Xu, K.; Xia, Q.; Xia, M.; Cai, C. Overview of Temporal Action Detection Based on Deep Learning. Artif. Intell. Rev. 2024, 57, 26. [Google Scholar] [CrossRef]
- Jiang, S.; Lin, H.; Ren, H.; Hu, Z.; Weng, L.; Xia, M. MDANet: A High-Resolution City Change Detection Network Based on Difference and Attention Mechanisms under Multi-Scale Feature Fusion. Remote Sens. 2024, 16, 1387. [Google Scholar] [CrossRef]


| Data | Variables | Spatial Resolution | Temporal Resolution | Source |
|---|---|---|---|---|
| Satellite Data | XCO2 | 1.29 × 2.25 km | 16 day | https://earthdata.nasa.gov/ |
| Reanalysis Data | XCO2 | 0.75° | 3 h | https://ads.atmosphere.copernicus.eu/ |
| Meteorological Data | Relative Humidity (Rh) | |||
| 10-m U Component of Wind (U) | 0.25° | 3 h | https://cds.climate.copernicus.eu/ | |
| 10-m V Component of Wind (V) | ||||
| 2 m Temperature (T2M) | ||||
| Elevation Data | DEM | 90 m × 90 m | - | https://engine-aiearth.aliyun.com/ |
| CLCD | Land, Forest, Grassland, Water Body, Shrubland and so on | 30 m | - | https://engineaiearth.aliyun.com/ |
| Station Data | XCO2 | Point | ∼2 m | https://tccondata.org/ |
| RMSE | SD | Bias | |
|---|---|---|---|
| Li [43] | 1.71 ppm | - | - |
| Zhang [44] | 1.18 ppm | 0.99 ppm | −0.6 |
| He [45] | 1.123 ppm | - | - |
| Ours | 1.01 ppm | 0.75 | 0.4 |
| Lag Order | AC Value | PAC Value | Q Statistic | p Value |
|---|---|---|---|---|
| 1st | 0.938 | 0.938 | 290,163.434 | 0.030 |
| 2nd | 0.888 | 0.069 | 550,369.730 | 0.020 |
| 3rd | 0.843 | 0.022 | 784,843.896 | 0.001 |
| 4th | 0.801 | 0.011 | 996,667.104 | 0.000 |
| 5th | 0.763 | 0.014 | 1,188,779.593 | 0.000 |
| 6th | 0.728 | 0.018 | 1,363,936.930 | 0.000 |
| 7th | 0.697 | 0.014 | 1,524,238.478 | 0.000 |
| 8th | 0.669 | 0.027 | 1,672,195.034 | 0.000 |
| 9th | 0.645 | 0.026 | 1,809,783.745 | 0.000 |
| 10th | 0.624 | 0.022 | 1,938,508.098 | 0.000 |
| Model | MAE | RMSE | MAPE | |
|---|---|---|---|---|
| LSTM | 0.75 | 0.77 | 1.25 | 0.010 |
| TCN | 0.85 | 0.58 | 0.92 | 0.014 |
| TCN-CAM | 0.86 | 0.54 | 0.90 | 0.014 |
| TCN-LSTM | 0.90 | 0.40 | 0.69 | 0.009 |
| CATCN-LSTM | 0.92 | 0.34 | 0.62 | 0.007 |
| Season | Model | MAE | RMSE | MAPE | |
|---|---|---|---|---|---|
| Spring | CATCN-LSTM | 0.917 | 0.403 | 0.681 | 0.0009 |
| CNN-LSTM | 0.878 | 0.595 | 0.901 | 0.0014 | |
| RNN | 0.754 | 0.774 | 1.250 | 0.0018 | |
| SVR | 0.699 | 0.916 | 1.385 | 0.0022 | |
| XGBOOST | 0.602 | 1.027 | 1.594 | 0.0024 | |
| Summer | CATCN-LSTM | 0.941 | 0.344 | 0.559 | 0.0008 |
| CNN-LSTM | 0.863 | 0.588 | 0.926 | 0.0014 | |
| RNN | 0.748 | 0.821 | 1.279 | 0.0023 | |
| SVR | 0.685 | 1.074 | 1.390 | 0.0026 | |
| XGBOOST | 0.620 | 1.255 | 1.624 | 0.0033 | |
| Autumn | CATCN-LSTM | 0.937 | 0.333 | 0.515 | 0.0008 |
| CNN-LSTM | 0.855 | 0.604 | 1.006 | 0.0019 | |
| RNN | 0.721 | 0.871 | 1.483 | 0.0021 | |
| SVR | 0.682 | 0.916 | 1.425 | 0.0022 | |
| XGBOOST | 0.640 | 1.062 | 1.590 | 0.0024 | |
| Winter | CATCN-LSTM | 0.915 | 0.410 | 0.697 | 0.0010 |
| CNN-LSTM | 0.880 | 0.567 | 0.992 | 0.0012 | |
| RNN | 0.734 | 0.821 | 1.304 | 0.0019 | |
| SVR | 0.659 | 0.937 | 1.476 | 0.0022 | |
| XGBOOST | 0.582 | 0.860 | 1.534 | 0.0026 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, K.; Zhang, Q.; Feng, X.; Liu, Z.; Shao, P.; Xia, M.; Ye, X. An Interpolation and Prediction Algorithm for XCO2 Based on Multi-Source Time Series Data. Remote Sens. 2024, 16, 1907. https://doi.org/10.3390/rs16111907
Hu K, Zhang Q, Feng X, Liu Z, Shao P, Xia M, Ye X. An Interpolation and Prediction Algorithm for XCO2 Based on Multi-Source Time Series Data. Remote Sensing. 2024; 16(11):1907. https://doi.org/10.3390/rs16111907
Chicago/Turabian StyleHu, Kai, Qi Zhang, Xinyan Feng, Ziran Liu, Pengfei Shao, Min Xia, and Xiaoling Ye. 2024. "An Interpolation and Prediction Algorithm for XCO2 Based on Multi-Source Time Series Data" Remote Sensing 16, no. 11: 1907. https://doi.org/10.3390/rs16111907
APA StyleHu, K., Zhang, Q., Feng, X., Liu, Z., Shao, P., Xia, M., & Ye, X. (2024). An Interpolation and Prediction Algorithm for XCO2 Based on Multi-Source Time Series Data. Remote Sensing, 16(11), 1907. https://doi.org/10.3390/rs16111907







