Effect of Argo Salinity Drift since 2016 on the Estimation of Regional Steric Sea Level Change Rates
Abstract
1. Introduction
2. Materials and Methods
2.1. Extraction of Linear Rates from SSL Changes
2.2. Evaluation of the Salinity Drift Effect on SSL Linear Rates
3. Results
3.1. Effect of Salinity Drift in Different Depths
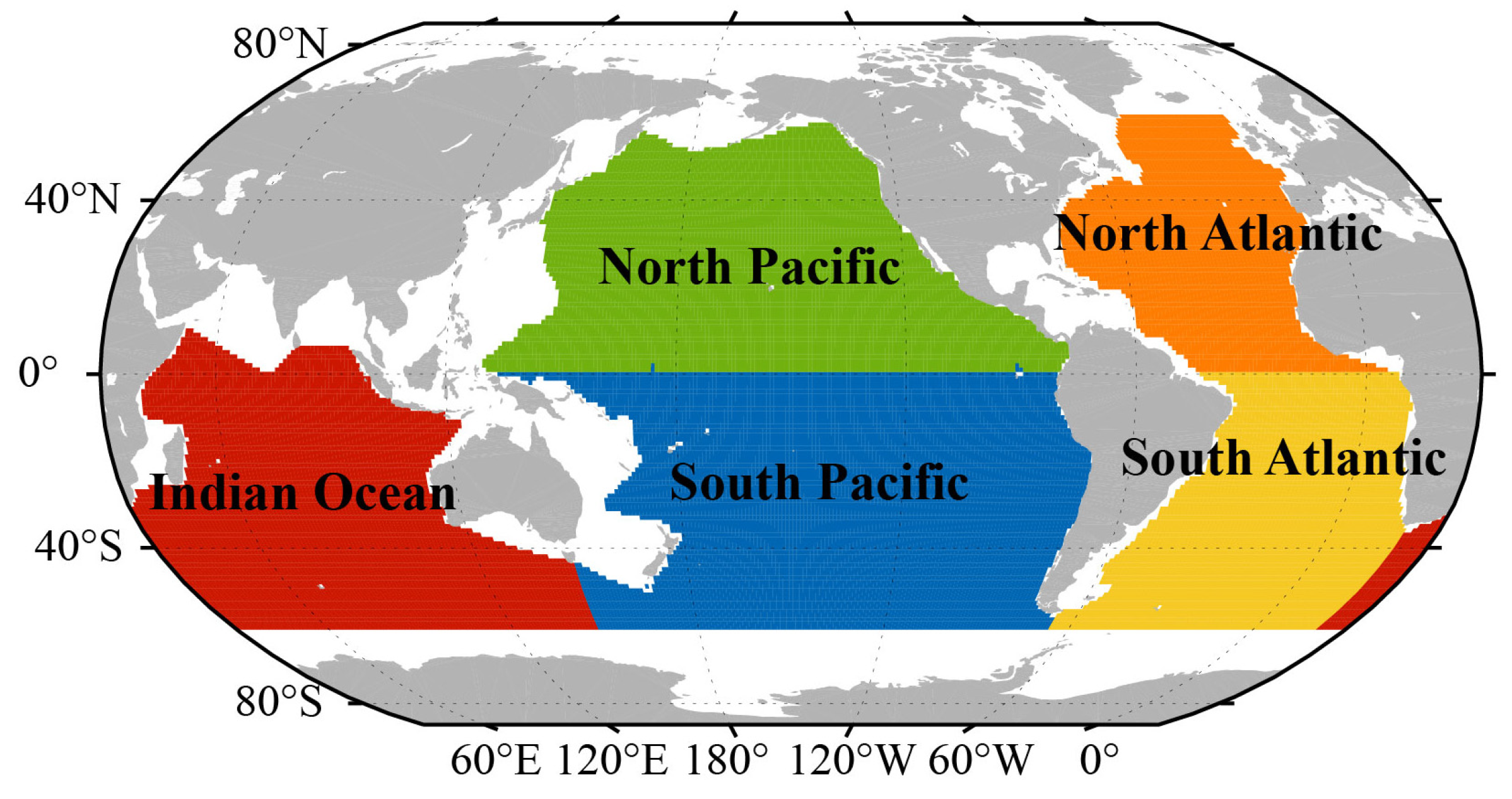
3.2. Effect of Salinity Drift in Different Open Ocean Regions
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yoro, K.O.; Daramola, M.O. Chapter 1—CO2 emission sources, greenhouse gases, and the global warming effect. In Advances in Carbon Capture; Elsevier: Amsterdam, The Netherlands, 2020; pp. 3–28. [Google Scholar] [CrossRef]
- Meyssignac, B.; Boyer, T.; Zhao, Z.; Hakuba, M.Z.; Landerer, F.W.; Stammer, D.; Kohl, A.; Kato, S.; L’Ecuyer, T.; Ablain, M.; et al. Measuring Global Ocean Heat Content to Estimate the Earth Energy Imbalance. Front. Mar. Sci. 2019, 6, 2296–7745. [Google Scholar] [CrossRef]
- Cheng, L.; John, A.; Zeke, H.; Kevin, E.T. How fast are the oceans warming? Science 2019, 363, 128–129. [Google Scholar] [CrossRef]
- Zemp, M.; Huss, M.; Thibert, E.; Eckert, N.; McNabb, R.; Bannwart, J.; Machguth, H.; Nussbaumber, S.U.; Gartner-Roer, I.; Thomson, L.; et al. Global glacier mass changes and their contributions to sea-level rise from 1961 to 2016. Nature 2019, 568, 382–386. [Google Scholar] [CrossRef] [PubMed]
- Avinash, K.; Yadav, J.; Rahul, M. Global warming leading to alarming recession of the Arctic sea-ice cover: Insights from remote sensing observations and model reanalysis. Heliyon 2020, 6, E04355. [Google Scholar] [CrossRef] [PubMed]
- Chao, B.F.; Wu, Y.H.; Li, Y.S. Impact of Artificial Reservoir Water Impoundment on Global Sea Level. Science 2008, 320, 212–214. [Google Scholar] [CrossRef] [PubMed]
- Reager, J.T.; Gardner, A.S.; Famiglietti, J.S.; Wiese, D.N.; Eicker, A.; Lo, M.-H. A decade of sea level rise slowed by climate-driven hydrology. Science 2016, 351, 699–703. [Google Scholar] [CrossRef] [PubMed]
- Yuanyuan, Y.; Min, Z.; Wei, F.; Dapeng, M. Detecting Regional Deep Ocean Warming below 2000 meter Based on Altimetry, GRACE, Argo, and CTD Data. Adv. Atmospheric Sci. 2021, 38, 1778–1790. [Google Scholar] [CrossRef]
- Abraham, J.P.; Baringer, M.; Bindoff, N.L.; Boyer, T.; Cheng, L.J.; Church, J.A.; Conroy, J.L.; Domingues, C.M.; Fasullo, J.T.; Gilson, J.; et al. A review of global ocean temperature observations: Implications for ocean heat content estimates and climate change. Rev. Geophys. 2013, 51, 450–483. [Google Scholar] [CrossRef]
- Roemmich, D.; Owens, W.B. The ARGO project: Global ocean observations for understanding for understanding and prediction of climate variability. Oceanography 2000, 13, 45–50. [Google Scholar] [CrossRef]
- Chen, J.; Tapley, B.; Wilson, C.; Cazenave, A.; Seo, K.-W.; Kim, J.-S. Global ocean mass change from GRACE and GRACE follow-on and altimeter and Argo measurements. Geophys. Res. Lett. 2020, 47, e2020GL090656. [Google Scholar] [CrossRef]
- Barnoud, A.; Pfeffer, J.; Guérou, A.; Frery, M.-L.; Siméon, M.; Cazenave, A.; Chen, J.L.; Llovel, W.; Thierry, V.; Legeais, J.-F.; et al. Contributions of altimetry and Argo to non-closure of the global mean sea level budget since 2016. Geophys. Res. Lett. 2021, 48, e2021GL092824. [Google Scholar] [CrossRef]
- Ponte, R.M.; Sun, Q.; Liu, C.; Liang, X. How salty is the global ocean: Weighing it all or tasting it a sip at a time? Geophys. Res. Lett. 2021, 48, e2021GL092935. [Google Scholar] [CrossRef]
- Roemmich, D.; Gilson, J. The 2004–2008 mean and annual cycle of temperature, salinity, and steric height in the global ocean from the Argo Program. Prog. Oceanogr. 2009, 82, 81–100. [Google Scholar] [CrossRef]
- Li, H.; Xu, F.; Zhou, W.; Wang, D.; Wright, J.S.; Liu, Z.; Lin, Y. Development of a global gridded Argo data set with Barnes successive corrections. J. Geophys. Res. Oceans 2017, 122, 866–889. [Google Scholar] [CrossRef]
- Liao, F.; Hoteit, I. A comparative study of the Argo-era ocean heat content among four different types of data sets. Earth’s Future 2022, 10, e2021EF002532. [Google Scholar] [CrossRef]
- Fourcy, D.; Lorvelec, O. A New Digital Map of Limits of Oceans and Seas Consistent with High-Resolution Global Shorelines. J. Coast. Res. 2013, 29, 471–477. [Google Scholar] [CrossRef]
- Feng, W.; Lemoine, J.-M.; Zhong, M.; Hsu, H.T. Mass-induced sea level variations in the Red Sea from GRACE, steric-corrected altimetry, in-situ bottom pressure records, and hydrographic observations. J. Geodyn. 2014, 78, 1–7. [Google Scholar] [CrossRef]
- Yuanyuan, Y.; Wei, F.; Min, Z.; Dapeng, M.; Yanli, Y. Basin-Scale Sea Level Budget from Satellite Altimetry, Satellite Gravimetry, and Argo Data over 2005 to 2019. Remote Sens. 2022, 14, 4637. [Google Scholar] [CrossRef]
- Geruo, A.; Wahr, J.; Shijie, Z. Computations of the viscoelastic response of a 3-D compressible Earth to surface loading: An application to Glacial Isostatic Adjustment in Antarctica and Canada. Geophys. J. Int. 2013, 192, 557–572. [Google Scholar] [CrossRef]
- Paulson, A.; Shijie, Z.; Wahr, J. Inference of mantle viscosity from GRACE and relative sea level data. Geophys. J. Int. 2007, 171, 497–508. [Google Scholar] [CrossRef]
- Peltier, W.R.; Argus, D.F.; Drummond, R. Space geodesy constrains ice age terminal deglaciation: The global ICE-6G_C (VM5a) model. J. Geophys. Res. Solid Earth 2015, 120, 450–487. [Google Scholar] [CrossRef]
- Peltier, W.R.; Argus, D.F.; Drummond, R. Comment on “An Assessment of the ICE-6G_C (VM5a) Glacial Isostatic Adjustment Model” by Purcell et al. J. Geophys. Res. Solid Earth 2018, 123, 2019–2028. [Google Scholar] [CrossRef]
- Chen, J.; Tapley, B.; Save, H.; Tamisiea, M.E.; Bettadpur, S.; Ries, J. Quantification of ocean mass change using gravity recovery and climate experiment, satellite altimeter, and Argo floats observations. J. Geophys. Res. Solid Earth 2018, 123, 10–212. [Google Scholar] [CrossRef]
- Uebbing, B.; Kusche, J.; Rietbroek, R.; Landerer, F.W. Processing choices affect ocean mass estimates from GRACE. J. Geophys. Res. Oceans 2019, 124, 1029–1044. [Google Scholar] [CrossRef]
- Zhang, L.; Sun, W.K. Progress and prospect of GRACE Mascon product and its application. Rev. Geophys. Planet. Phys. 2022, 53, 35–52. [Google Scholar] [CrossRef]
- Chang, L.; Sun, W.K. Progress and prospect of sea level changes of global and China nearby seas. Rev. Geophys. Planet. Phys. 2021, 52, 266–279. [Google Scholar] [CrossRef]
- Xu, G.; Wu, Y.; Liu, S.; Cheng, S.; Zhang, Y.; Pan, Y.; Wang, L.; Dokuchits, E.Y.; Nkwazema, O.C. How 2022 extreme drought influences the spatiotemporal variations of terrestrial water storage in the Yangtze River Catchment: Insights from GRACE-based drought severity index and in-situ measurements. J. Hydrol. 2023, 626, 130245. [Google Scholar] [CrossRef]
- Ma, W.; Zhou, H.; Dai, M.; Tang, L.; Xu, S.; Luo, Z. Characterizing the drought events in Yangtze River basin via the insight view of its sub-basins water storage variations. J. Hydrol. 2024, 633, 130995. [Google Scholar] [CrossRef]


| Datasets | Time Span | Latitude Coverage | Vertical Stratification | Maximum Depth | Data Source |
|---|---|---|---|---|---|
| SIO | January 2004–March 2024 | 65°S–80°N | 58 layers | 1975 dbar | Argo |
| IPRC | January 2005–April 2020 | 60°S–60°N | 27 layers | 2000 m | Argo |
| BOA | January 2004–June 2023 | 80°S–80°N | 58 layers | 1975 dbar | Argo |
| Data | HSSL | TSSL | SSL | ||
|---|---|---|---|---|---|
| 2005–2015 | 2016–2019 | 2005–2019 | 2005–2019 | 2005–2019 | |
| SIO | 0.06 ± 0.02 | 0 ± 0.04 | −0.01 ± 0.01 | 0.26 ± 0.01 | 0.25 ± 0.02 |
| IPRC | 0.11 ± 0.03 | −0.21 ± 0.18 | −0.07 ± 0.03 | 0.11 ± 0.01 | 0.04 ± 0.03 |
| BOA | 0.09 ± 0.02 | −0.34 ± 0.05 | −0.07 ± 0.02 | 0.25 ± 0.01 | 0.18 ± 0.02 |
| Data | HSSL | TSSL | SSL | ||
|---|---|---|---|---|---|
| 2005–2015 | 2016–2019 | 2005–2019 | 2005–2019 | 2005–2019 | |
| SIO | −0.23 ± 0.14 | −1.49 ± 0.59 | −0.19 ± 0.01 | 1.74 ± 0.24 | 1.55 ± 0.19 |
| IPRC | 0.20 ± 0.19 | −2.58 ± 0.49 | −0.33 ± 0.03 | 1.44 ± 0.22 | 1.11 ± 0.19 |
| BOA | −0.13 ± 0.16 | −3.46 ± 0.66 | −0.53 ± 0.02 | 1.62 ± 0.26 | 1.09 ± 0.18 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, L.; Zhou, H.; Li, J.; Wang, P.; Su, X.; Luo, Z. Effect of Argo Salinity Drift since 2016 on the Estimation of Regional Steric Sea Level Change Rates. Remote Sens. 2024, 16, 1855. https://doi.org/10.3390/rs16111855
Tang L, Zhou H, Li J, Wang P, Su X, Luo Z. Effect of Argo Salinity Drift since 2016 on the Estimation of Regional Steric Sea Level Change Rates. Remote Sensing. 2024; 16(11):1855. https://doi.org/10.3390/rs16111855
Chicago/Turabian StyleTang, Lu, Hao Zhou, Jin Li, Penghui Wang, Xiaoli Su, and Zhicai Luo. 2024. "Effect of Argo Salinity Drift since 2016 on the Estimation of Regional Steric Sea Level Change Rates" Remote Sensing 16, no. 11: 1855. https://doi.org/10.3390/rs16111855
APA StyleTang, L., Zhou, H., Li, J., Wang, P., Su, X., & Luo, Z. (2024). Effect of Argo Salinity Drift since 2016 on the Estimation of Regional Steric Sea Level Change Rates. Remote Sensing, 16(11), 1855. https://doi.org/10.3390/rs16111855











