Long-Term Sea Level Periodicities over the European Seas from Altimetry and Tide Gauge Data
Abstract
1. Introduction
2. Data and Methodology
2.1. Study Area
2.2. Data Description
2.2.1. Sea Level Data
2.2.2. Climate Indices
2.3. Data Analysis Techniques
2.3.1. Hann Lowpass Filter
2.3.2. Temporal Correlation of Smoothed Time Series
2.3.3. Wavelet Analysis
2.3.4. Multiresolution Wavelet Decomposition
3. Results
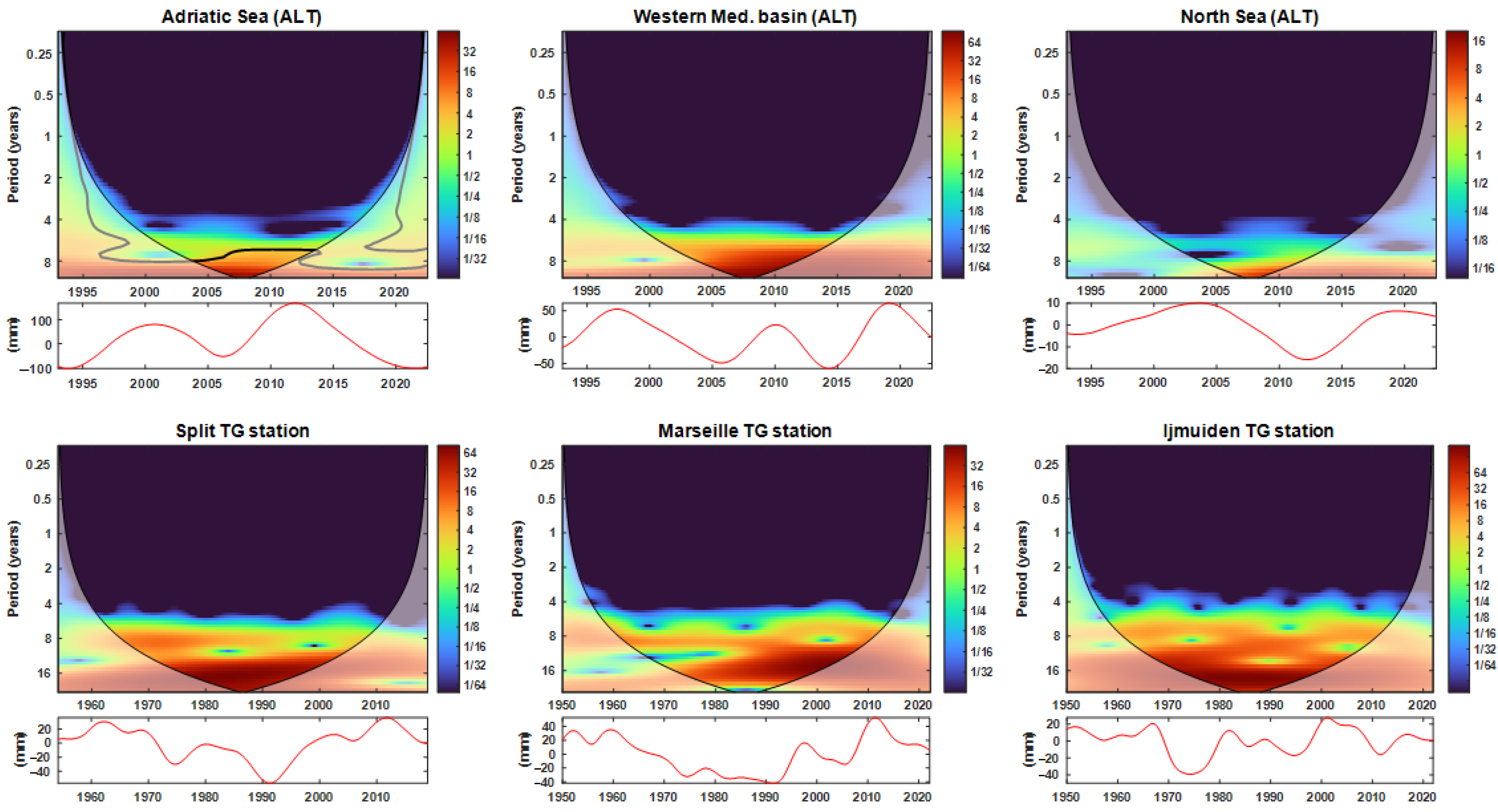
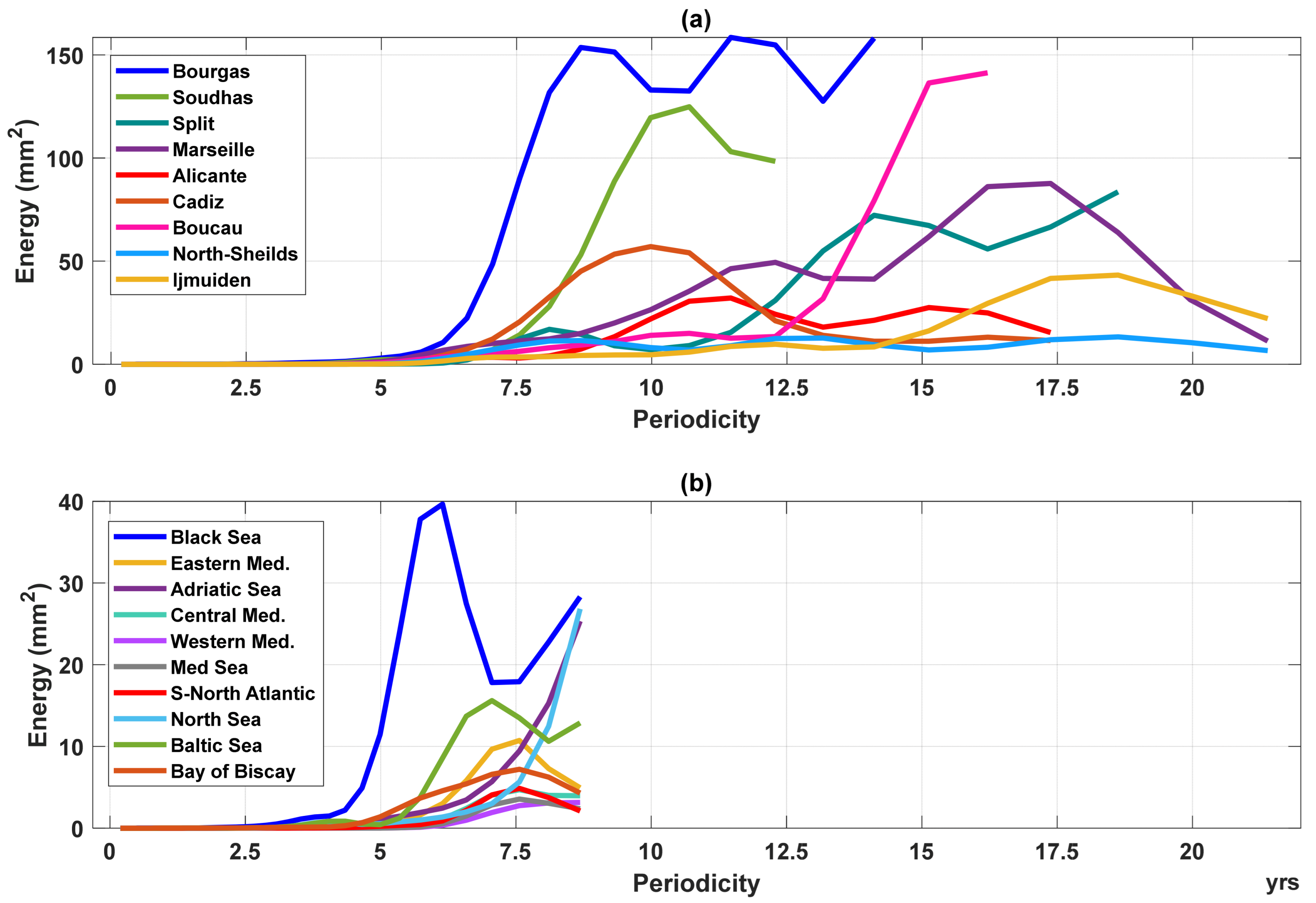
3.1. Unveiling Long-Term Periodicities in Sea Level
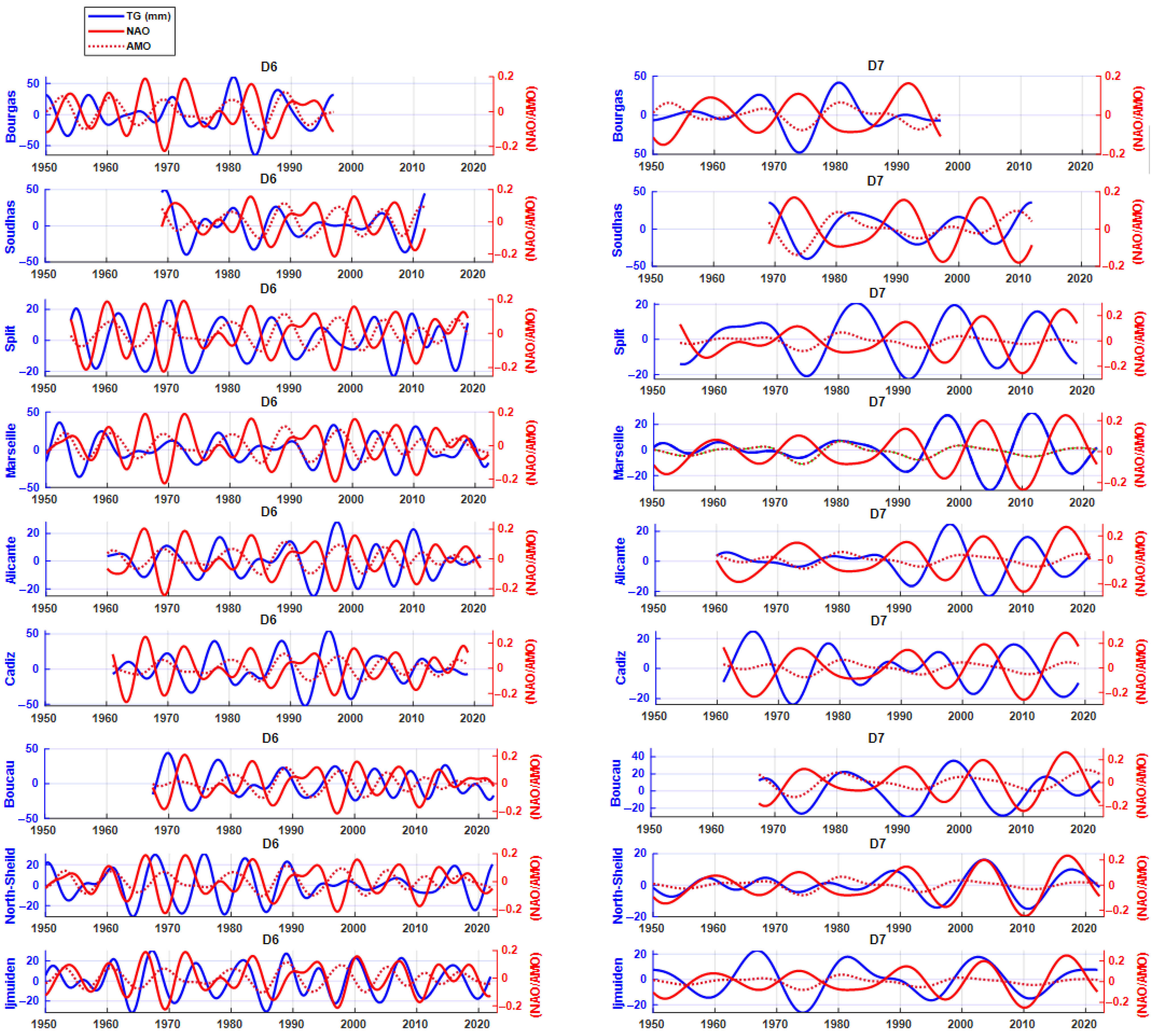
3.2. Multi-Resolution Analysis for Time–Frequency Domain and Connection with Indices
3.3. Time–Frequency Coherence of Sea Level and Atmospheric Indexes
4. Discussion
5. Conclusions
- A multi-scale periodicity was observed using wavelet transform on SL data from the explored TG stations and regions from SL altimetry. This is characterized by two main low-frequency cycles: an 8-year cycle from altimetry data and longer cycles ranging from 8 to 18 years from TG data.
- The wavelet decomposition highlighted a significant correlation of the SL periodicity with the NAO and the AMO. Specifically, the NAO was identified as a critical factor influencing the 8-year cycle in SL, showing a negative correlation along the Mediterranean coast with values up to −0.66 in Alicante, and a positive moderate correlation within the northern European coast (above 47°N of latitude) with values reaching 0.43 in Harlingen station. Conversely, the AMO was more influential in the 16-year cycle, exhibiting a strong positive correlation up to 0.83 in IJmuiden, particularly in the northern studied areas.
- Further examination of the relationship with these climatic indices through Time Dependent Temporal Correlation highlighted significant periods during 1970–2010, 1970–1990, and 1985–2020, in which SL was greatly influenced by the NAO. This was characterized by a high correlation, approaching −0.90 along the Mediterranean Sea. Additionally, a strong positive correlation at the level of a 16-year cycle, reaching 0.90, was predominantly observed in the periods 1960–1990 and 1970–2010 in most TG stations located in the Mediterranean and North Seas, indicating a significant impact of the AMO on SL.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Church, J.A.; White, N.J. Sea-Level Rise from the Late 19th to the Early 21st Century. Surv. Geophys. 2011, 32, 585–602. [Google Scholar] [CrossRef]
- Cazenave, A.; Llovel, W. Contemporary Sea Level Rise. Ann. Rev. Mar. Sci. 2010, 2, 145–173. [Google Scholar] [CrossRef] [PubMed]
- Melet, A.; van de Wal, R.; Amores, A.; Arns, A.; Chaigneau, A.A.; Dinu, I.; Haigh, I.D.; Hermans, T.H.J.; Lionello, P.; Marcos, M.; et al. Sea Level Rise in Europe: Observations and Projections. State Planet. Discuss. 2023, 2023, 1–106. [Google Scholar] [CrossRef]
- Gower, J.; Barale, V. The Rising Concern for Sea Level Rise: Altimeter Record and Geo-Engineering Debate. Remote Sens. 2024, 16, 262. [Google Scholar] [CrossRef]
- Rietbroek, R.; Brunnabend, S.-E.; Kusche, J.; Schröter, J.; Dahle, C. Revisiting the Contemporary Sea-Level Budget on Global and Regional Scales. Proc. Natl. Acad. Sci. USA 2016, 113, 1504–1509. [Google Scholar] [CrossRef] [PubMed]
- Llovel, W.; Balem, K.; Tajouri, S.; Hochet, A. Cause of Substantial Global Mean Sea Level Rise Over 2014–2016. Geophys. Res. Lett. 2023, 50, e2023GL104709. [Google Scholar] [CrossRef]
- Hooijer, A.; Vernimmen, R. Global LiDAR Land Elevation Data Reveal Greatest Sea-Level Rise Vulnerability in the Tropics. Nat. Commun. 2021, 12, 3592. [Google Scholar] [CrossRef]
- Levermann, A.; Clark, P.U.; Marzeion, B.; Milne, G.A.; Pollard, D.; Radic, V.; Robinson, A. The Multimillennial Sea-Level Commitment of Global Warming. Proc. Natl. Acad. Sci. USA 2013, 110, 13745–13750. [Google Scholar] [CrossRef]
- Strauss, B.H.; Kulp, S.A.; Rasmussen, D.J.; Levermann, A. Unprecedented Threats to Cities from Multi-Century Sea Level Rise. Environ. Res. Lett. 2021, 16, 114015. [Google Scholar] [CrossRef]
- Galassi, G.; Spada, G. Linear and Non-Linear Sea-Level Variations in the Adriatic Sea from Tide Gauge Records (1872-2012). Ann. Geophys. 2015, 57, P0658. [Google Scholar] [CrossRef]
- Dara Nur Arifin, A.; Taqyuddin, T. A Phenomenology Approach to Rethinking Coastal Community Vulnerability Toward Sea-Level Rise. Int. J. Soc. Health 2023, 2, 345–353. [Google Scholar] [CrossRef]
- Srinivasan, M.; Tsontos, V. Satellite Altimetry for Ocean and Coastal Applications: A Review. Remote Sens. 2023, 15, 3939. [Google Scholar] [CrossRef]
- Lumban-Gaol, J.; Sumantyo, J.T.S.; Tambunan, E.; Situmorang, D.; Antara, I.M.O.G.; Sinurat, M.E.; Suhita, N.P.A.R.; Osawa, T.; Arhatin, R.E. Sea Level Rise, Land Subsidence, and Flood Disaster Vulnerability Assessment: A Case Study in Medan City, Indonesia. Remote Sens. 2024, 16, 865. [Google Scholar] [CrossRef]
- Fernández-Montblanc, T.; Gómez-Enri, J.; Ciavola, P. The Role of Mean Sea Level Annual Cycle on Extreme Water Levels Along European Coastline. Remote Sens. 2020, 12, 3419. [Google Scholar] [CrossRef]
- Passeri, D.L.; Hagen, S.C.; Medeiros, S.C.; Bilskie, M.V.; Alizad, K.; Wang, D. The Dynamic Effects of Sea Level Rise on Low-gradient Coastal Landscapes: A Review. Earths Future 2015, 3, 159–181. [Google Scholar] [CrossRef]
- Kirwan, M.L.; Megonigal, J.P. Tidal Wetland Stability in the Face of Human Impacts and Sea-Level Rise. Nature 2013, 504, 53–60. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Soto, C.; Cheng, L.; Caesar, L.; Schmidtko, S.; Jewett, E.B.; Cheripka, A.; Rigor, I.; Caballero, A.; Chiba, S.; Báez, J.C.; et al. An Overview of Ocean Climate Change Indicators: Sea Surface Temperature, Ocean Heat Content, Ocean PH, Dissolved Oxygen Concentration, Arctic Sea Ice Extent, Thickness and Volume, Sea Level and Strength of the AMOC (Atlantic Meridional Overturning Circulation). Front. Mar. Sci. 2021, 8, 642372. [Google Scholar] [CrossRef]
- Jevrejeva, S.; Grinsted, A.; Moore, J.C.; Holgate, S. Nonlinear Trends and Multiyear Cycles in Sea Level Records. J. Geophys. Res. Ocean. 2006, 111. [Google Scholar] [CrossRef]
- Agha Karimi, A.; Deng, X.; Andersen, O.B. Sea Level Variation around Australia and Its Relation to Climate Indices. Mar. Geod. 2019, 42, 469–489. [Google Scholar] [CrossRef]
- Tsimplis, M.N.; Calafat, F.M.; Marcos, M.; Jordà, G.; Gomis, D.; Fenoglio-Marc, L.; Struglia, M.V.; Josey, S.A.; Chambers, D.P. The Effect of the NAO on Sea Level and on Mass Changes in the Mediterranean Sea. J. Geophys. Res. Ocean. 2013, 118, 944–952. [Google Scholar] [CrossRef]
- Iglesias, I.; Lorenzo, M.N.; Lázaro, C.; Fernandes, M.J.; Bastos, L. Sea Level Anomaly in the North Atlantic and Seas around Europe: Long-Term Variability and Response to North Atlantic Teleconnection Patterns. Sci. Total Environ. 2017, 609, 861–874. [Google Scholar] [CrossRef] [PubMed]
- Scafetta, N. Multi-Scale Dynamical Analysis (MSDA) of Sea Level Records versus PDO, AMO, and NAO Indexes. Clim. Dyn. 2014, 43, 175–192. [Google Scholar] [CrossRef]
- Ozgenc Aksoy, A. Investigation of Sea Level Trends and the Effect of the North Atlantic Oscillation (NAO) on the Black Sea and the Eastern Mediterranean Sea. Theor. Appl. Clim. 2017, 129, 129–137. [Google Scholar] [CrossRef]
- Jevrejeva, S.; Moore, J.C.; Woodworth, P.L.; Grinsted, A. Influence of Large-Scale Atmospheric Circulation on European Sea Level: Results Based on the Wavelet Transform Method. Tellus A Dyn. Meteorol. Oceanogr. 2005, 57, 183. [Google Scholar] [CrossRef]
- Bonaduce, A.; Pinardi, N.; Oddo, P.; Spada, G.; Larnicol, G. Sea-Level Variability in the Mediterranean Sea from Altimetry and Tide Gauges. Clim. Dyn. 2016, 47, 2851–2866. [Google Scholar] [CrossRef]
- Wakelin, S.L.; Woodworth, P.L.; Flather, R.A.; Williams, J.A. Sea-level Dependence on the NAO over the NW European Continental Shelf. Geophys. Res. Lett. 2003, 30, e2003GL017041. [Google Scholar] [CrossRef]
- Tantet, A.; Dijkstra, H.A. An Interaction Network Perspective on the Relation between Patterns of Sea Surface Temperature Variability and Global Mean Surface Temperature. Earth Syst. Dyn. 2014, 5, 1–14. [Google Scholar] [CrossRef]
- Hansen, J.M.; Aagaard, T.; Kuijpers, A. Sea-Level Forcing by Synchronization of 56- and 74-Year Oscillations with the Moon’s Nodal Tide on the Northwest European Shelf (Eastern North Sea to Central Baltic Sea). J. Coast. Res. 2015, 315, 1041–1056. [Google Scholar] [CrossRef]
- Partal, T. Wavelet Based Periodical Analysis of the Precipitation Data of the Mediterranean Region and Its Relation to Atmospheric Indices. Model. Earth Syst. Environ. 2018, 4, 1309–1318. [Google Scholar] [CrossRef]
- Liang, X.; Lin, Y.; Wu, R.; Li, G.; Khan, N.; Liu, R.; Su, H.; Wei, S.; Zhang, H. Time-Frequency Analysis Framework for Understanding Non-Stationary and Multi-Scale Characteristics of Sea-Level Dynamics. Front. Mar. Sci. 2023, 9, 1070727. [Google Scholar] [CrossRef]
- Holgate, S.J.; Matthews, A.; Woodworth, P.L.; Rickards, L.J.; Tamisiea, M.E.; Bradshaw, E.; Foden, P.R.; Gordon, K.M.; Jevrejeva, S.; Pugh, J. New Data Systems and Products at the Permanent Service for Mean Sea Level. J. Coast. Res. 2013, 29, 493–504. [Google Scholar] [CrossRef]
- Pujol, M.; Schaeffer, P.; Faugère, Y.; Raynal, M.; Dibarboure, G.; Picot, N. Gauging the Improvement of Recent Mean Sea Surface Models: A New Approach for Identifying and Quantifying Their Errors. J. Geophys. Res. Ocean. 2018, 123, 5889–5911. [Google Scholar] [CrossRef]
- Sandwell, D.T.; Harper, H.; Tozer, B.; Smith, W.H.F. Gravity Field Recovery from Geodetic Altimeter Missions. Adv. Space Res. 2021, 68, 1059–1072. [Google Scholar] [CrossRef]
- Seip, K.L.; Grøn, Ø.; Wang, H. The North Atlantic Oscillations: Cycle Times for the NAO, the AMO and the AMOC. Climate 2019, 7, 43. [Google Scholar] [CrossRef]
- Hernández, A.; Sáez, A.; Bao, R.; Raposeiro, P.M.; Trigo, R.M.; Doolittle, S.; Masqué, P.; Rull, V.; Gonçalves, V.; Vázquez-Loureiro, D.; et al. The Influences of the AMO and NAO on the Sedimentary Infill in an Azores Archipelago Lake since ca. 1350 CE. Glob. Planet. Change 2017, 154, 61–74. [Google Scholar] [CrossRef]
- Proakis, J.G.; Manolakis, D.G. Digital Signal Processing: Principles, Algorithms, and Applications; Pearson: London, UK, 2006. [Google Scholar]
- Oppenheim, A.V.; Schafer, R.W. Discrete-Time Signal Processing; Pearson: London, UK, 2010. [Google Scholar]
- Ebisuzaki, W. A Method to Estimate the Statistical Significance of a Correlation When the Data Are Serially Correlated. J. Clim. 1997, 10, 2147–2153. [Google Scholar] [CrossRef]
- Macias-Fauria, M.; Grinsted, A.; Helama, S.; Holopainen, J. Persistence Matters: Estimation of the Statistical Significance of Paleoclimatic Reconstruction Statistics from Autocorrelated Time Series. Dendrochronologia 2012, 30, 179–187. [Google Scholar] [CrossRef]
- Torrence, C.; Compo, G.P. A Practical Guide to Wavelet Analysis. In Bulletin of the American Meteorological Society; American Meteorological Society: Boston, MA, USA, 1998; pp. 61–78. [Google Scholar]
- Kumar, P.; Foufoula-Georgiou, E. Wavelet Analysis for Geophysical Applications. Rev. Geophys. 1997, 35, 385–412. [Google Scholar] [CrossRef]
- Grinsted, A.; Moore, J.C.; Jevrejeva, S. Application of the Cross Wavelet Transform and Wavelet Coherence to Geophysical Time Series. Nonlinear Process Geophys. 2004, 11, 561–566. [Google Scholar] [CrossRef]
- Percival, D.B. Analysis of Geophysical Time Series Using Discrete Wavelet Transforms: An Overview. In Nonlinear Time Series Analysis in the Geosciences; Springer: Berlin/Heidelberg, Germany, 2008; pp. 61–79. [Google Scholar]
- Zhang, K.; Gençay, R.; Ege Yazgan, M. Application of Wavelet Decomposition in Time-Series Forecasting. Econ. Lett. 2017, 158, 41–46. [Google Scholar] [CrossRef]
- Erol, S. Time-Frequency Analyses of Tide-Gauge Sensor Data. Sensors 2011, 11, 3939–3961. [Google Scholar] [CrossRef] [PubMed]
- Percival, D.B.; Walden, A.T. Wavelet Methods for Time SeriesAnalysis; Cambridge University Press: Cambridge, MA, USA, 2000; ISBN 9780511841040. [Google Scholar]
- Akansu, A.N.; Haddad, R.A. Multiresolution Signal Decomposition: Transforms, Subbands, and Wavelets, 2nd ed.; Academic Press: Cambridge, MA, USA; New Jersey Institute of Technology: Newark, NJ, USA, 2001. [Google Scholar]
- Habimana, O. Wavelet Multiresolution Analysis of the Liquidity Effect and Monetary Neutrality. Comput. Econ. 2019, 53, 85–110. [Google Scholar] [CrossRef]
- Baker, R.G.V.; McGowan, S.A. Periodicities in Mean Sea-Level Fluctuations and Climate Change Proxies: Lessons from the Modelling for Coastal Management. Ocean. Coast. Manag. 2014, 98, 187–201. [Google Scholar] [CrossRef]
- de Jonge, V.N.; Essink, K.; Boddeke, R. The Dutch Wadden Sea: A Changed Ecosystem. Hydrobiologia 1993, 265, 45–71. [Google Scholar] [CrossRef]
- Surian, N. Fluvial Changes in the Anthropocene: A European Perspective. In Treatise on Geomorphology; Elsevier: Amsterdam, The Netherlands, 2022; pp. 561–583. [Google Scholar]
- Zampieri, M.; Toreti, A.; Schindler, A.; Scoccimarro, E.; Gualdi, S. Atlantic Multi-Decadal Oscillation Influence on Weather Regimes over Europe and the Mediterranean in Spring and Summer. Glob. Planet. Change 2017, 151, 92–100. [Google Scholar] [CrossRef]
- Ulbrich, U.; Christoph, M. A Shift of the NAO and Increasing Storm Track Activity over Europe Due to Anthropogenic Greenhouse Gas Forcing. Clim. Dyn. 1999, 15, 551–559. [Google Scholar] [CrossRef]
- Eden, C.; Jung, T. North Atlantic Interdecadal Variability: Oceanic Response to the North Atlantic Oscillation (1865–1997). J. Clim. 2001, 14, 676–691. [Google Scholar] [CrossRef]
- Jung, T.; Hilmer, M.; Ruprecht, E.; Kleppek, S.; Gulev, S.K.; Zolina, O. Characteristics of the Recent Eastward Shift of Interannual NAO Variability. J. Clim. 2003, 16, 3371–3382. [Google Scholar] [CrossRef]
- Nakamura, T.; Yamazaki, K.; Iwamoto, K.; Honda, M.; Miyoshi, Y.; Ogawa, Y.; Ukita, J. A Negative Phase Shift of the Winter AO/NAO Due to the Recent Arctic Sea-ice Reduction in Late Autumn. J. Geophys. Res. Atmos. 2015, 120, 3209–3227. [Google Scholar] [CrossRef]
- Zhang, X.; Jin, L.; Chen, C.; Guan, D.; Li, M. Interannual and Interdecadal Variations in the North Atlantic Oscillation Spatial Shift. Chin. Sci. Bull. 2011, 56, 2621–2627. [Google Scholar] [CrossRef]
- García-García, D.; Vigo, I.; Trottini, M. Water Transport among the World Ocean Basins within the Water Cycle. Earth Syst. Dyn. 2020, 11, 1089–1106. [Google Scholar] [CrossRef]
- Boulahia, A.K.; García-García, D.; Vigo, M.I.; Trottini, M.; Sayol, J.-M. The Water Cycle of the Baltic Sea Region from GRACE/GRACE-FO Missions and ERA5 Data. Front. Earth Sci. 2022, 10, 879148. [Google Scholar] [CrossRef]
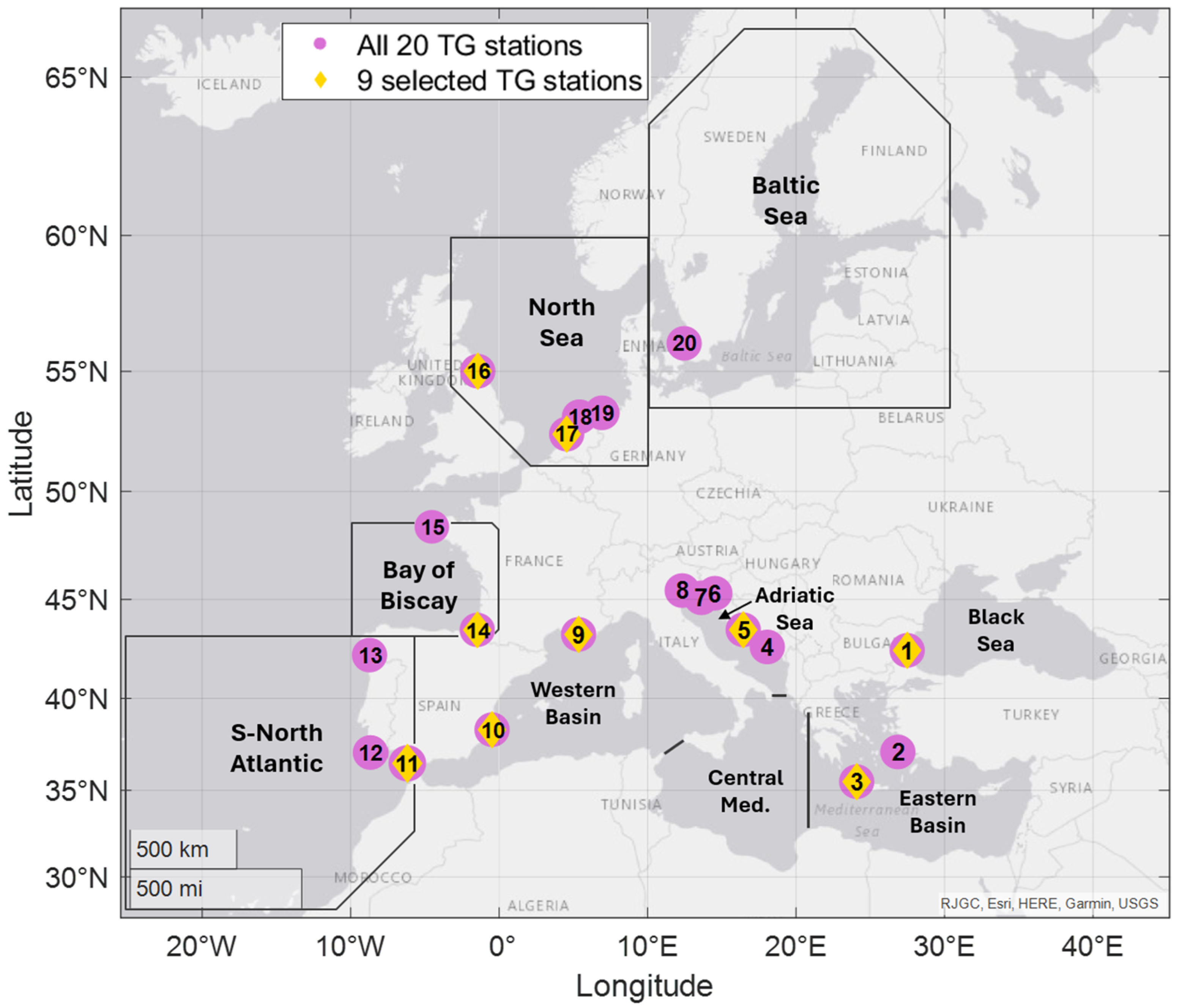
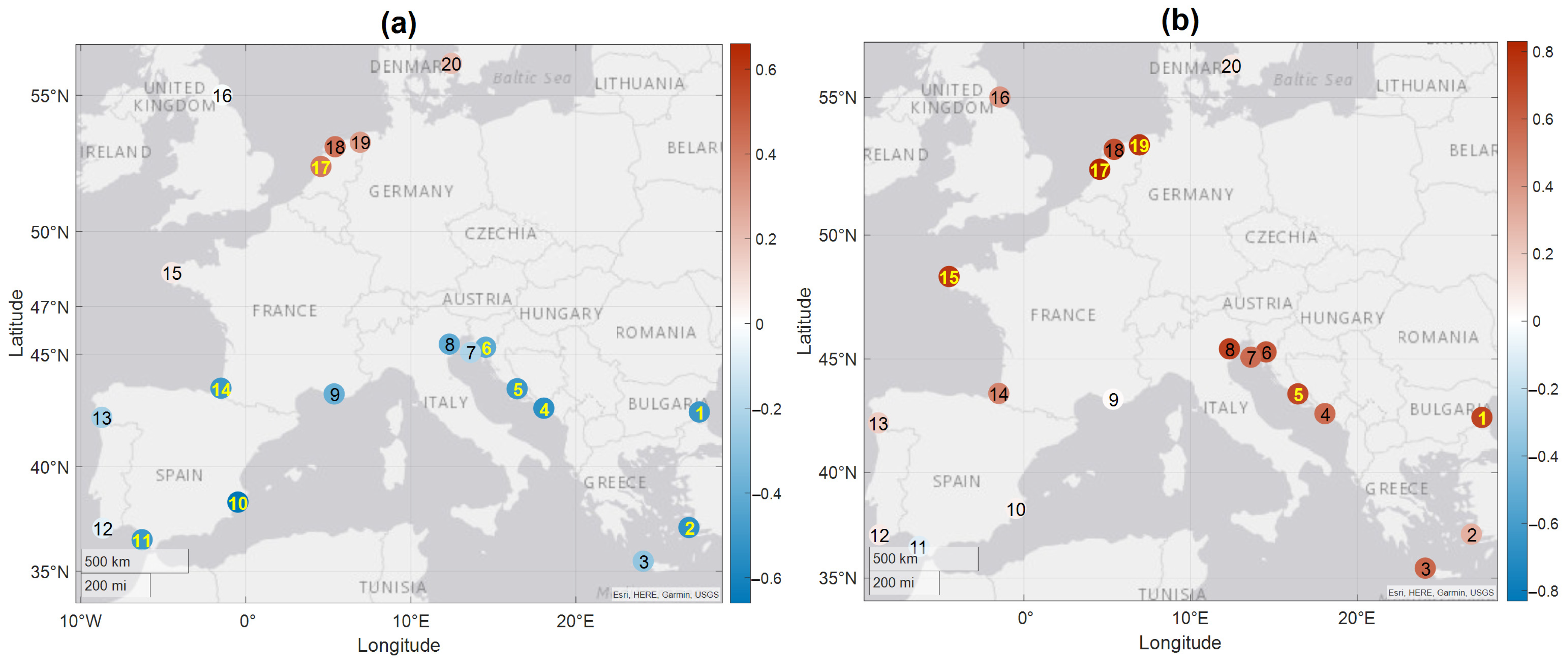
| Region | Station Name (Country) | Longitude | Latitude | Time Span (Length) | Completeness % | Trend ± Error (mm/Year) |
|---|---|---|---|---|---|---|
| Black Sea | 1-Bourgas (Bulgari) | 27.48 | 42.48 | 1950–1996 (46) | 86 | 2.17 ± 0.56 |
| Eastern basin | 2-Leros (Greece) | 26.85 | 37.13 | 1969–2022 (53) | 83 | 1.86 ± 0.29 |
| Eastern basin | 3-Soudhas (Greece) | 24.08 | 35.49 | 1969–2011 (42) | 83 | 0.83 ± 0.45 |
| Adriatic Sea | 4-Dubrovnik (Croatia) | 18.06 | 42.65 | 1956–2018 (62) | 99 | 1.57 ± 0.27 |
| Adriatic Sea | 5-Split (Croatia) | 16.44 | 43.51 | 1954–2018 (64) | 87 | 1.03 ± 0.27 |
| Adriatic Sea | 6-Bakar (Croatia) | 14.53 | 45.3 | 1950–2020 (70) | 88 | 1.03 ± 0.27 |
| Adriatic Sea | 7-Rovinj (Croatia) | 13.62 | 45.08 | 1955–2018 (63) | 98 | 0.77 ± 0.30 |
| Adriatic Sea | 8-Venice (Italy) | 12.33 | 45.43 | 1950–2000 (50) | 94 | 1.23 ± 0.41 |
| Western basin | 9-Marseille (France) | 5.35 | 43.28 | 1950–2022 (72) | 96 | 1.07 ± 0.22 |
| Western basin | 10-Alicante (Spain) | −0.48 | 38.34 | 1960–2020 (60) | 93 | 0.93 ± 0.21 |
| S-North Atlantic | 11-Cádiz (Spain) | −6.29 | 36.54 | 1961–2018 (57) | 97 | 3.58 ± 0.30 |
| S-North Atlantic | 12-Lagos (Portugal) | −8.67 | 37.1 | 1950–1999 (49) | 78 | 0.84 ± 0.38 |
| S-North Atlantic | 13-Vigo (Spain N) | −8.73 | 42.24 | 1950–2018 (68) | 98 | 1.90 ± 0.27 |
| Bay of Biscay | 14-Boucau (France N) | −1.51 | 43.53 | 1967–2022 (55) | 82 | 1.92 ± 0.39 |
| Bay of Biscay | 15-Brest (France N) | −4.49 | 48.38 | 1952–2022 (70) | 90 | 2.07 ± 0.25 |
| North Sea | 16-North-Shield (UK) | −1.44 | 55.01 | 1950–2022 (72) | 92 | 1.60 ± 0.17 |
| North Sea | 17-IJmuiden (Netherland) | 4.55 | 52.46 | 1950–2021 (71) | 100 | 1.90 ± 0.28 |
| North Sea | 18-Harlingen (Netherland) | 5.41 | 53.18 | 1950–2021 (71) | 100 | 1.85 ± 0.37 |
| North Sea | 19-Delfzijl (Netherland) | 6.93 | 53.34 | 1950–2021 (71) | 100 | 2.59 ± 0.37 |
| Baltic Sea | 20-Hornbaek (Danmark) | 12.46 | 56.09 | 1950–2017 (67) | 98 | 1.17 ± 0.34 |
| Regions | Hann-Filtered Data | D6 | ||
|---|---|---|---|---|
| NAO | AMO | NAO | AMO | |
| Black Sea | 0.79 * | −0.62 | 0.92 * | |
| Mediterranean Sea | −0.73 * | |||
| Eastern basin | −0.74 * | |||
| Central basin | −0.59 | |||
| Adriatic Sea | −0.69 * | |||
| Western basin | −0.64 * | |||
| S-North Atlantic | −0.91 * | |||
| Bay of Biscay | −0.71 * | |||
| North Sea | −0.66 * | |||
| Baltic Sea | 0.65 * | |||
| TG Stations | Hann-Filtered Data | D6 | D7 | |||
|---|---|---|---|---|---|---|
| NAO | AMO | NAO | AMO | NAO | AMO | |
| 1-Bourgas | −0.51 * | |||||
| 2-Leros | −0.53 * | −0.67 | ||||
| 3-Soudhas | −0.65 * | 0.54 | 0.58 | |||
| 4-Dubrovnik | −0.74 * | −0.54 * | 0.56 | |||
| 5-Split | −0.77 * | −0.50 * | −0.53 | 0.70 * | ||
| 6-Bakar | −0.66 * | −0.42 * | −0.46 | 0.64 | ||
| 7-Rovinj | −0.71 * | 0.56 | ||||
| 8-Venice | −0.54 | −0.84 * | ||||
| 9-Marseille | −0.64 * | −0.39 | 0.39 | −0.77 * | ||
| 10-Alicante | −0.66 * | −0.66 * | 0.55 * | −0.76 * | ||
| 11-Cádiz | −0.50 * | 0.45 | −0.72 | |||
| 12-Lagos | ||||||
| 13-Vigo | ||||||
| 14-Boucau | −0.50 * | |||||
| 15-Brest | 0.76 * | |||||
| 16-North-Shield | 0.77 * | |||||
| 17-IJmuiden | 0.64 * | 0.41 * | 0.83 * | |||
| 18-Harlingen | 0.43 | 0.22 | ||||
| 19-Delfzijl | 0.30 | 0.22 * | 0.77 * | |||
| 20-Hornbaek | 0.48 * | |||||
| TG Stations | Periods | Hann-Filtered Data | D6 | D7 | ||||
|---|---|---|---|---|---|---|---|---|
| NAO | AMO | NAO | AMO | NAO | AMO | NAO | AMO | |
| 1-Bourgas | 1978–1996 | 1965–1996 | −0.72 * | 0.71 * | 0.81 * | |||
| 1965–1985 | 1965–1985 | −0.93 * | 0.91 * | |||||
| 6-Bakar | 1965–2020 | 1980–2010 | −0.52 * | −0.50 * | 0.70 * | |||
| 1970–2000 | X | −0.92 * | ||||||
| 8-Venice | 1970–2000 | 1970–2000 | −0.90 * | −0.55 * | 0.90 * | |||
| 9-Marseille | 1970–2021 | 1950–1995 | −0.56 * | −0.58 * | −0.83 * | |||
| 10-Alicante | X | 1960–2000 | 0.66 | |||||
| 11-Cadiz | 1961–2010 | 1961–2010 | −0.51 * | −0.67 * | ||||
| 13-Vigo | 1980–2018 | 1970–2010 | −0.34 | |||||
| 1980–2000 | X | −0.91 * | ||||||
| 14-Boucau | 1967–2010 | 1985–2005 | −0.54 * | −0.62 * | ||||
| 15-Brest | X | 1952–1980 | ||||||
| 16-North-Shield | 1980–2021 | X | −0.85 | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zid, F.; Vigo, M.I.; Vargas-Alemañy, J.A.; García-García, D. Long-Term Sea Level Periodicities over the European Seas from Altimetry and Tide Gauge Data. Remote Sens. 2024, 16, 2931. https://doi.org/10.3390/rs16162931
Zid F, Vigo MI, Vargas-Alemañy JA, García-García D. Long-Term Sea Level Periodicities over the European Seas from Altimetry and Tide Gauge Data. Remote Sensing. 2024; 16(16):2931. https://doi.org/10.3390/rs16162931
Chicago/Turabian StyleZid, Ferdous, Maria Isabel Vigo, Juan A. Vargas-Alemañy, and David García-García. 2024. "Long-Term Sea Level Periodicities over the European Seas from Altimetry and Tide Gauge Data" Remote Sensing 16, no. 16: 2931. https://doi.org/10.3390/rs16162931
APA StyleZid, F., Vigo, M. I., Vargas-Alemañy, J. A., & García-García, D. (2024). Long-Term Sea Level Periodicities over the European Seas from Altimetry and Tide Gauge Data. Remote Sensing, 16(16), 2931. https://doi.org/10.3390/rs16162931









