Abstract
In geophysical inversion issues, the Jacobian matrix computation takes the greatest time, and it is the most significant factor limiting the inversion’s calculation speed. We think that the correctness of the inverse problem is determined by the difference between the inversion data and the real data, not the precision of the gradient solution in each iteration. Based on this, we present an approximate computation approach for the Jacobian matrix that may rapidly solve the inverse issue by estimating the gradient information. In this research, the approximate gradient information is solved in each iteration process, and the approximate gradient is utilized for computation; nevertheless, the poor fitting of the evaluation data is correctly evaluated, and the inversion model that fits the criteria is achieved. We employed this approach of estimating the Jacobian matrix to invert the 3D airborne transient electromagnetic method (ATEM) on synthetic data, and it was able to significantly minimize the time necessary for the inversion while maintaining inversion accuracy. When the model mesh is more precise, this technique outperforms the previous way of finding the exact Jacobian matrix in terms of acceleration.
1. Introduction
Geophysical 3D electromagnetic inversion is a common nonlinear, underdetermined inverse issue. Three-dimensional inversion technology has advanced significantly in recent decades, along with advances in mathematical theory and computer science [1]. To solve 3D inversion problems, many researchers have developed a lot of optimization methods such as the Gauss–Newton method [2,3], the conjugate gradient method [4], the quasi-Newton method [5], and others. Because of the size of the 3D inversion issue, modeling and inversion solutions require a long time to complete. In the last two decades, several researchers have attempted to accelerate the inversion solution using various methods. Efficient equation-solving algorithms, represented by several direct solvers [6] and varied inversion procedures [7,8], are gradually gaining popularity. In addition, one of the most important issues limiting the speed of inversion is the computation of the Jacobian matrix, which is a fundamental challenge in several optimization techniques. The Gauss–Newton approach requires directly calculating the Jacobian matrix, and the iterative formula incorporates the second derivative information, which can achieve the local optimum value after a few iterations; however, the Jacobian matrix computation is extremely slow. The only information required for the nonlinear conjugate gradient method and the quasi-Newton method is the objective function’s gradient, which can be calculated by taking the product of the Jacobian matrix and a vector rather than the Jacobian matrix itself. As a result, each iteration has fewer forward operations, but more iterations are required to get the local optimal value. For multi-source electromagnetic methodologies such as ATEM, the Gauss–Newton method, characterized by the explicit computation of the sensitivity matrix, exhibits a faster convergence rate. This is primarily due to the fact that it necessitates approximately equivalent time for both the computation of the Jacobian matrix and the gradient of the objective function within a single iteration, while the Gauss–Newton method requires fewer iterations [9,10].
The disturbance approach, the adjoint forward method, and electromagnetic migration imaging technology are several basic methods for obtaining the Jacobian matrix. Because the perturbation approach requires a significant amount of computation, several researchers have begun to employ the adjoint forward method to construct the Jacobian matrix since the 1990s [11,12,13]. The adjoint forward methods are classified into two groups based on the forward equations used: frequency domain and time domain. Many scholars use the frequency domain adjoint forward method to obtain the Jacobian matrix in electromagnetic method inversion problems based on a finite difference or finite element in the frequency domain [14,15,16,17,18,19,20]. With the extensive application of time-domain electromagnetic simulation methods, time-domain adjoint forward modeling [21,22,23,24] has increasingly become a research hotspot. For certain problems lacking a forward equation, it becomes infeasible to calculate the gradient of the objective function using the adjoint forward method. Consequently, some researchers have turned to electromagnetic migration technology as an alternative approach for solving the Jacobian matrix: Zhdanov and Portniaguine [25] introduced migration imaging technology and completed electromagnetic migration imaging; Newman and Commer [26] calculated the gradient of the objective function using the migration technique’s back propagation field and completed three-dimensional electromagnetic inversion.
In recent years, the direct solution methodology for equations and the Jacobian matrix approximation method have garnered a lot of attention for speeding up the inversion process. The direct solver of equations separates the solution problem into two parts: matrix decomposition and back generation. In the multi-source issue, the source only impacts the right term of the forward equation; therefore, preserving the results of matrix decomposition and the back generation of distinct right terms can significantly increase computing speed [22]. On this basis, the program’s parallel programming may fully utilize the computer’s processing performance while also reducing the program’s computing time. Hu et al. [27] utilized MPI to parallelize magneto-electromagnetic 3D inversion. Liu et al. [28] used OpenMP to create a parallel inversion technique for aircraft electromagnetic data, while Long et al. [29] completed a 3D inversion of CSEM data with the parallel solver Pardiso and MPI. In addition, with the goal of decreasing the time required to calculate the Jacobian matrix, numerous researchers have conducted research on the approximation of the Jacobian matrix. Siripunvaraporn and Egbert [30] used a few recording locations in the research region to compute the Jacobian matrix elements, and then used interpolation to acquire all the Jacobian matrix elements in the whole area, completing two-dimensional magnetotelluranic inversion. Hu et al. [31] completed quasi-three-dimensional MT inversion using the one-dimensional Jacobian matrix rather than the three-dimensional Jacobian matrix. Because the airborne electromagnetic method must be transmitted and received from an aerial vehicle, the transmitter suitable for the flight vehicle is small, as is the transmission power, so the transmitting source’s influence range is limited to the area near the transmitting source. Cox et al. [32] termed it a footprint. Yang et al. [33] employed local grids to speed up the calculation of the Jacobian matrix in airborne electromagnetic technique inversion. Christiansen et al. [34] used the Born approximation forward technique to compute the approximate Jacobian matrix, which expedited the inversion process. Zhang et al. [24] employed the triple grid approach to compute the forward response and Jacobian matrix, respectively, and a rough grid for computing the Jacobian matrix, which significantly increased the inversion calculation efficiency.
This study proposes an approximation approach for obtaining the Jacobian matrix that can significantly reduce the number of forward equations to be solved in the adjoint forward computation while improving calculation performance without sacrificing inversion quality. First, the finite-difference frequency domain simulation of airborne transient electromagnetic response is performed, followed by the calculation of the massive system of equations using the Pardiso direct solver in MKL. The Gauss–Newton technique is used to generate the inversion iterative formula and calculate the exact and approximate Jacobian matrices. The Jacobian matrix is employed in the inversion computation with varying approximation degrees, and the quality of the inversion results as well as the time spent on them are compared. Different levels of random noise are introduced into the synthetic data, and the noisy data are inverted using the approximate Jacobian matrix. The approximate Jacobian matrix approach is proven to be stable.
2. Methods
2.1. Three-Dimensional Modeling
The frequency-domain finite-difference approach is utilized in three-dimensional modeling. The frequency domain curl equation for electromagnetic fields is constructed by combining the constitutive relationship between their physical quantities:
where is the electric field strength, is the magnetic field strength, is the applied current source, is the medium’s conductivity, is the medium’s permeability, is the angular frequency, and is the imaginary number unit; we use the field decomposition method to deal with the field source term. The electric and magnetic field components are classified as primary fields ( and ) and secondary fields ( and ):
Subtracting the background field from the total field yields the curl equation fulfilled by the anomalous field, as shown below:
where denotes the background conductivity. The foregoing equations are integrated to produce the double curl equation fulfilled by the abnormal field [35].
The staggered grid finite difference technique is used for difference approximation, and the electric and magnetic fields are alternately sampled in the grid, with the electric component on the edge and the magnetic component on the plane (see Figure 1).
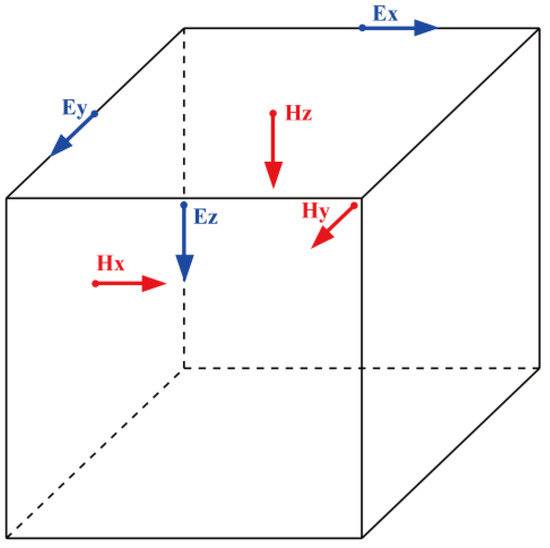
Figure 1.
A staggered grid with sample sites for electric and magnetic components.
For the first type of boundary requirement, edge expansion occurs on the computing region’s periphery. Using the above strategy technique to discretize the double curl equation, where represents the coefficient matrix following the difference and represents the right end containing the source term, the system of equations may be represented as:
The anomalous electric field value is derived by solving large sparse equations using the parallel solver Pardiso from the Intel Math Kernel Library. The overall electric field strength may be calculated by summing the background and anomalous electric fields. The inverse Fourier transform may be used to derive the vertical magnetic field response in the time domain and its time derivative:
We estimated the airborne transient electromagnetic response in the time domain when the emission waveform is a step waveform. In actual applications, the airborne electromagnetic emission system often employs several emission waveforms to increase the quality of the obtained data. Combining the foregoing electromagnetic response with the first derivative of the emission waveform with respect to time yields the electromagnetic response in the time domain for any emission waveform.
The electromagnetic response of the 3D code was compared to the semi-analytical solution of the uniform half space. The design included a uniform half space with a resistivity of 100 Ω·m, a transmitting coil with a radius of 15 m, a transmitting current of 100 A, and both coils situated 30 m above ground. Figure 2 compares the transmitted waveform to the error, and the error for each time channel is less than 4%, demonstrating the validity of the 3D forward program.
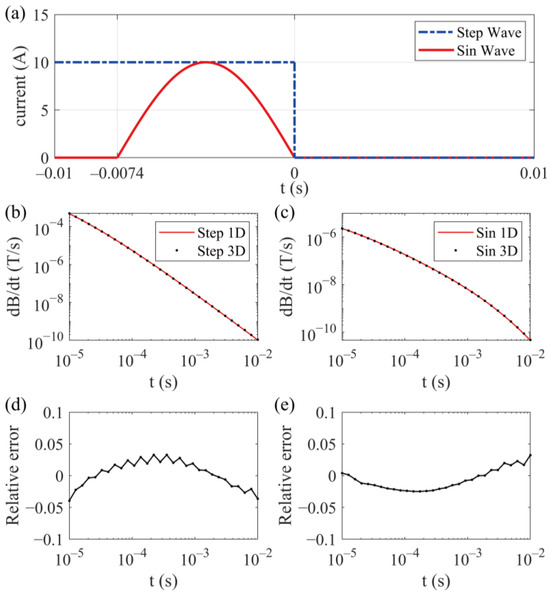
Figure 2.
Comparison of 3D code computation results to analytical solutions. (a) Simulated emission waveform. (b) Step waveform-induced EMF comparison. (c) EMF comparison using sinusoidal waveforms. (d) Error comparison between step waveform 3D code and one-dimensional analytical solution. (e) Comparison of one-dimensional analytical solution error with a sinusoidal waveform 3D code.
In this study, the IP properties of rock ore are described using the Cole–Cole model, which is represented by the following formula:
where signifies zero-frequency resistivity, denotes polarizability, defines the time constant, and represents the frequency correlation coefficient. The IP property of rock ore may be defined by substituting the actual resistivity with the complex resistivity in the Helmholtz equation, as well as the time-domain airborne electromagnetic response that accounts for the excited polarization property of rock ore.
2.2. The Objective Function
In this study, the regularized iterative inversion approach is used for inversion computation, and the goal function below is created, which includes one data-fitting term and two model-weighting components.
The data-fitting term indicates the difference between the measured data and the inversion data, while the model-fitting terms and are utilized to limit the inversion model such that the physical parameter model approaches the predicted model during the iterative process. The matrix formulation of the objective function is as follows:
is the observed data, is the forward operator, is the data-weighting matrix, is the model-weighting matrix, and is the data dissimilarity matrix. Because the data in separate time channels of TEM vary too much, the diagonal elements of use the reciprocal of the absolute values of the observed data to balance the magnitude discrepancies between time channels. uses the Laplace operator to create a smooth inversion model. In this study, given that there is a high connection between distinct IP parameters, reflects the degree of difference between the data, implying that there is a correlation between different parameters throughout the inversion process. For two different physical parameters, and , the specific expressions are as follows:
The nonlinear component is approximated using the Taylor expansion approach, and the model update value at the k+1th iteration is obtained:
where is the Jacobian matrix of the forward operator in the kth iteration, is the data discrepancy evaluation operator in the kth iteration, is the partial derivative matrix of with respect to the model variable, and balances the size of the data-fitting term and the model constraint term. This paper uses Grayver’s technique:
where is the number of iterations, and b and c are artificial constants chosen to balance the absolute scale disparities between the two norms of various constraint terms. In this manner, the regularization factor in each iteration is automatically modified to guarantee that each regularization term contributes to the inversion outcome during the inversion procedure.
2.3. The Approximate Calculation Method of the Jacobian Matrix
The Jacobian matrix technique is a fundamental problem in inversion calculation. Adjoint modeling is a popular approach for calculating the ATEM Jacobian matrix. Starting from the forward equations represented by Equation (8), the partial derivative of model parameter m is taken on both sides of the equation, and the following equation is obtained:
The Jacobian matrix in the frequency domain may be written as the derivative of the magnetic-field component (B) with respect to the model variables ():
depicts the interpolation operator, which maps the electric field component to the magnetic field component. Substituting Equation (21) into (22) yields the following expression:
Because the value of the background field remains constant during the forward operation and its partial derivative with respect to is zero, the formula may be reduced as follows:
Set the intermediate variable G, which is defined as follows:
Set the intermediate variable such that it equals:
The equation shown above is equivalent to
By solving this system of equations, is obtained, and by substituting it into Equation (24), the frequency-domain Jacobian matrix is obtained. In the whole calculation process, solving the equations is the most time-consuming, and it is also the main reason that limits the speed of Jacobian matrix calculation. When the emission source is fixed, G is a fixed matrix, and solving the Jacobian matrix of all the measurement points at one frequency point requires solving 3 × Nx × Ny × Nz equations (Nx, Ny, and Nz denote the number of grid segments in x, y, and z directions, respectively). However, for the ATEM, the emission source changes with the location of the measurement points, assuming that there are Np measurement points. Solving the Jacobian matrix of all measurement points at one frequency point requires solving 3 × Nx × Ny × Nz × Np equations. Solving the Jacobian matrix in this way is extremely time-consuming, so most of the current research aims to solve the transpose matrix of the Jacobian matrix.
Additionally, the expression for becomes:
When the position of the measurement points corresponds with the recording points of the magnetic field component, finding the Jacobian matrix of all the measurement sites at a frequency point requires the solution of Np systems of equations, which are reasonably simple to compute. However, in practice, the position of the measurement points and the position of the magnetic field component recording point in the model grid usually do not coincide, which leads to the magnetic field component of the measurement point position not being displayed and expressed by the and components at the electric-field recording point, so it is necessary to calculate the value of the magnetic-field component recording points near all the measurement points and re-interpolate to the measurement points. When the measurement points are in the same plane, the number of systems of equations to be computed equals Nx × Ny; however, when they are not, the number of systems of equations to be computed increases. Calculating the transposition of the Jacobian matrix requires less computation than directly computing the Jacobian matrix; however, for large-scale operations, the number of equations calculated is related to the model grid, and the computational complexity remains relatively high when performing fine grid division, so it is still unsuitable for large-scale inversion calculation.
The Jacobian matrix in inversion calculates a gradient direction that approximates the local minimum value in each iteration. However, during the iteration process, the gradient information of the objective function is not required to be highly exact; we just need to offer an approximate search direction, and satisfactory inversion results can be produced after multiple iterations (Figure 3). For example, the quasi-Newton method for optimization problems is accelerated by an approximation of the Hessian matrix.
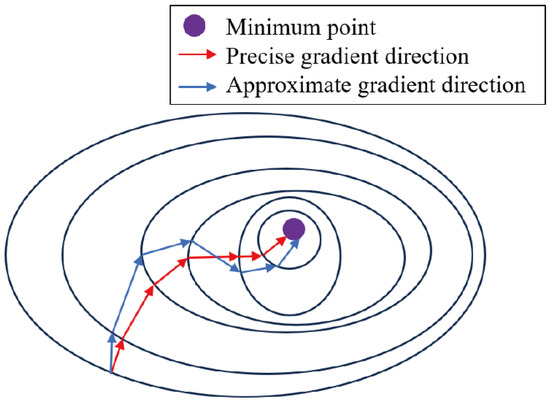
Figure 3.
Schematic diagram of the minimum search using the exact gradient direction versus the approximate gradient direction.
Based on the preceding study, this paper provides a method for approximating the Jacobian matrix, which can significantly minimize the amount of math involved in the inversion. Currently, in the mainstream calculation approach, L is at least an interpolation operator of size (Nx × Ny, 3 × Nx × Ny × Nz). The actual Jacobian matrix must be solved by calculating Nx × Ny equations. However, if we can take a small number of field value calculation points in the vicinity of each measurement point and average them so that the calculation of each frequency point is only related to the measurement point and has nothing to do with the number of grid divisions, the system of equations we calculate can be written as:
The subsurface model is partitioned into hexahedral grids of Nx × Ny × Nz to make the approximation approach easier to understand. For ease of depiction, we simplify the real model by assuming that Np measurement sites are spread in the same plane, as illustrated in Figure 4. In this case, the size of the interpolation operator L in the conventional Jacobian matrix calculation method is (Nx × Ny, 3 × Nx × Ny × Nz), and at least Nx × Ny systems of equations need to be calculated (the blue grid center point in Figure 4). If four field calculation points are selected in the neighborhood of the measurement point, the size of the approximate operator L matrix is (4 × Np, 3 × Nx × Ny × Nz), only 4 × Np equations need to be calculated, and the number of measurement points Np is far less than the number of field calculation points Nx × Ny. If further approximation is carried out, only one field calculation point in the field is selected. The number of equations calculated can be reduced to Np at most (the red points in Figure 4), which greatly reduces the amount of calculation.
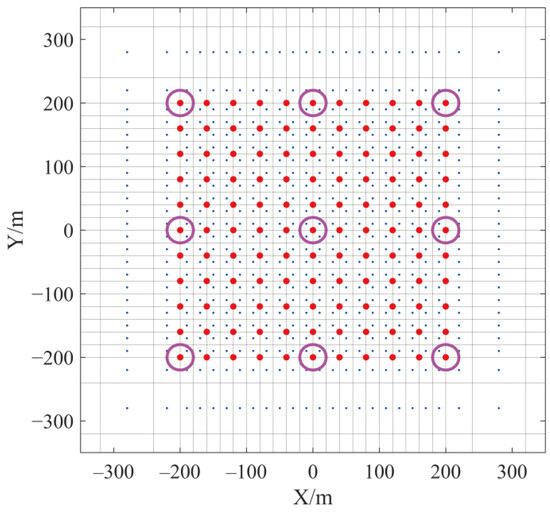
Figure 4.
Calculate the XOY plane of the Jacobian matrix including many measurement points. The red dot represents the measurement point position, whereas the blue dot represents the Hz component position derived in the forward calculation.
We may retrieve the value of the frequency domain Jacobian matrix using the approach described above, and then use the time–frequency transformation in the forward process to obtain the value of the time domain Jacobian matrix.
When calculating the Jacobian matrix, we use the adjoint forward method to obtain the derivative of the induced electromotive force with respect to resistivity; however, in the IP parameter inversion, we require the Jacobian matrix of the induced electromotive force with respect to multiple IP parameters. As a result, using the Cole–Cole model expression and the derivative chain solution rule, we develop the partial derivative expression appropriate for IP parameter inversion [36]:
The adjoint forward approximation approach and the analytical equation of the partial derivative of the Cole–Cole model may be used to swiftly compute the Jacobian matrix for 3D ATEM inversion.
Figure 5 compares the estimated Jacobian matrix computation results with the precise Jacobian matrix. Because of the large scale of the partial derivative matrix, only partial derivatives of resistivity parameters in the first subsurface layer grid (20 grids in the x-direction in the range y = 0–20 m) for 30 time channels in a single set of observations (observations at x = 0 m and y = 0 m in Figure 4) are shown. Figure 5a,b exhibit the precise and approximate Jacobian matrix computation results, respectively. The absolute size of the elements in the Jacobian matrix has increased dramatically since the approximation, but the distribution rule remains stable. Figure 5c shows the Jacobian matrix elements from the tenth time channel for comparison. Figure 5d depicts the relative inaccuracy of the approximate Jacobian matrix and the actual Jacobian matrix. The components of the approximate Jacobian matrix deviate significantly from the precise value; however, as long as the Jacobian matrix is comparable to the actual value in the subterranean distribution, gradient information may be determined very accurately.
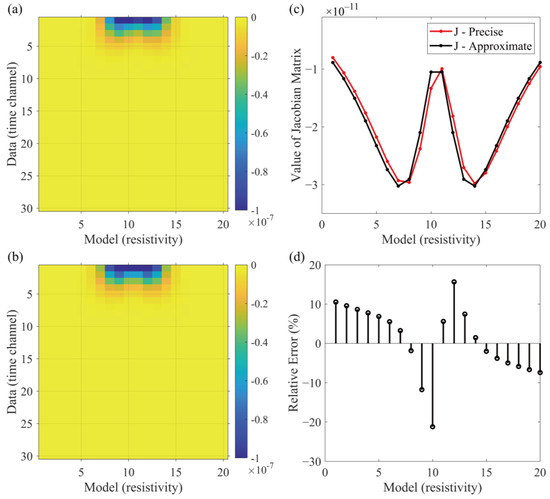
Figure 5.
Comparison of partial elements between an accurate Jacobian matrix and an approximate Jacobian matrix. (a) The partial values of an accurate Jacobian matrix; (b) the partial values of an approximate Jacobian matrix; (c) a comparison of partial derivatives of the tenth time channel with regard to several model variables is performed; (d) the relative error of the partial derivatives.
2.4. Parallelization of Programs
Each frequency is calculated independently throughout the calculating process, which provides a natural parallel advantage. To speed the inversion computation, this work uses the message passing interface (MPI) to perform the program’s multi-process parallel calculation on a personal computer. The subprocess is in charge of forward-calculating various frequency points, computing the Jacobian matrix, and performing time–frequency transformations. The master process collects the subprocess’s computation results, synthesizes large-scale equations, and computes the matrix. In this study, parallel programming and inversion computation are performed on a personal computer (an Intel (R) CoreTM i7-8700 processor), which significantly enhances the program’s calculation performance.
3. Inversion Example
We created 28 × 28 × 18 hexahedral grids to test the efficacy of the suggested approximation approach (see Figure 6). The transmitting coil had a radius of 15 m and a sending current of 100 A, and both the transmitting and receiving coils were 30 m in the air, with a total of 121 measurement sites, shown as red dots at z = 30 m in Figure 6. The computation area was split into 20 grids with equal intervals in the x and y directions, with each grid measuring 20 m. In the z direction, the grid size steadily grew from the surface to the deep; the initial grid size was 20 m, and each subsequent grid size was 1.1 times the previous grid size. The border and air region were made up of eight extended grids on the x, y, and z axes. In the synthetic model, an oblique low-resistance polarized body was buried in uniform half-space, progressively deepening from the negative to positive direction of X and Y. The surrounding rock had a resistivity of 200 Ω·m, a polarizability of 0.01, a time constant of 0.0001, and a frequency correlation coefficient of 0.01. The target body had a resistivity of 50 Ω·m, a polarization of 0.5, a time constant of 0.005, and a frequency correlation coefficient of 0.5. Our original model for the inversion was a uniform half-space with 100 Ω·m resistivity, 0.1 polarizability, 0.001 time constant, and a 0.1 frequency correlation coefficient.
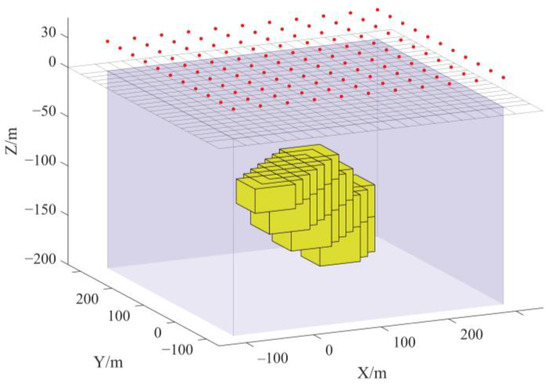
Figure 6.
Schematic diagram of the model. The red points are the locations of the sampling points, and the internal oblique body is the low-resistance polarization target body.
To see how the approximate Jacobian matrix calculation approach suggested in this research affects the accuracy of inversion findings, a few field value calculation locations in the region were utilized to compute the form of the equation. When computing equations such as , a few field value calculation sites in the neighborhood were employed to see how the approximate Jacobian matrix calculation approach provided in this research affects the accuracy of inversion findings:
Table 1 displays the 2-norm of cross-gradient values between the inversion and true models derived with four approximation degrees. J represents the calculation results obtained by the exact Jacobian matrix; J represents the calculation results at n field value calculation points in the vicinity of the sampling point, and the average of them is used as the value at the sampling point of the approximate Jacobian matrix to participate in the following calculation. They have approximately the same cross-gradient 2-norm as the actual model, and the precise and approximate Jacobian computation methods provide similar results.

Table 1.
The inversion produces varying degrees of Jacobian approximation cross-gradient 2-norm with the genuine model.
Figure 7 shows the inversion results achieved by the two Jacobian calculation techniques. The approximate Jacobian calculation method employs the most approximate way, which is to use the value of just one field value calculation point in the neighborhood rather than the value of its sampling point. The results show that there is no significant difference between the inversion results obtained by the exact Jacobian matrix calculation method and the approximate Jacobian matrix calculation method, which can better recover the resistivity information of underground media, and the recovery results of the polarizability and frequency correlation coefficient are also improved. The target body’s form may also be defined by its relative size, and the time constant’s sensitivity to the electromagnetic reaction is minimal. When the correct Jacobian matrix is used in the inversion computation, the change between each iteration calculation is insufficient, and the recovery impact is low. Although the change in computation in the iterative process is still small, another local minimum point is discovered throughout the process of determining the local minimum value, which can enhance the inversion result to some extent.
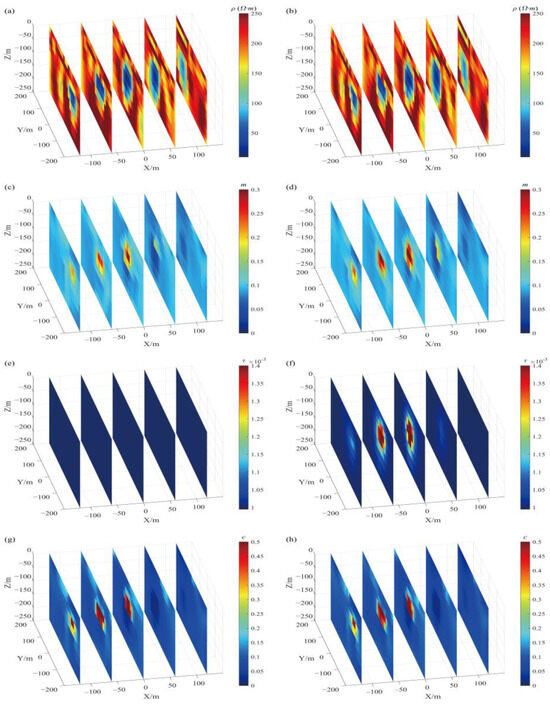
Figure 7.
Comparison of the inversion results of four IP parameters with the precise Jacobian matrix (a,c,e,g) and the approximate Jacobian matrix (b,d,f,h).
To analyze the accelerating impact of the number of processes on inversion, this study calculates the problem with various numbers of processes. Figure 8 depicts the time required for each iteration with varying numbers of processes, as well as the speedup ratio. The computation time lowers as the number of processes rises, but it remains restricted by the computer’s capability. The CPU usage rate reached 100% during the computation, and the impact of increasing the number of processes on calculation performance is unclear. The computation speed of the computer employed in this work can be up to 4.15 times faster than serial computing.
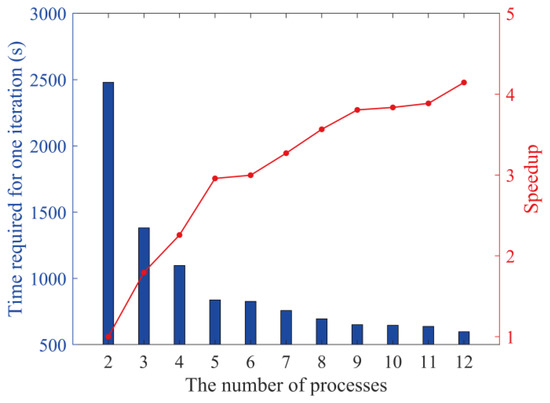
Figure 8.
The relationship between the number of processes and computational speed.
In addition, we utilized 12 computation processes and recorded the time spent on inversion calculations at various degrees of Jacobian approximation. Figure 9 depicts the time consumed and speedup ratio for each iteration of the various approximate Jacobian computation methods. The graphic clearly shows how the Jacobian approximation approach may significantly reduce the time necessary for each iteration of the inversion. When the highest approximation ratio is used for computation, the speed is 2.88 times that of the actual Jacobian matrix calculation technique.
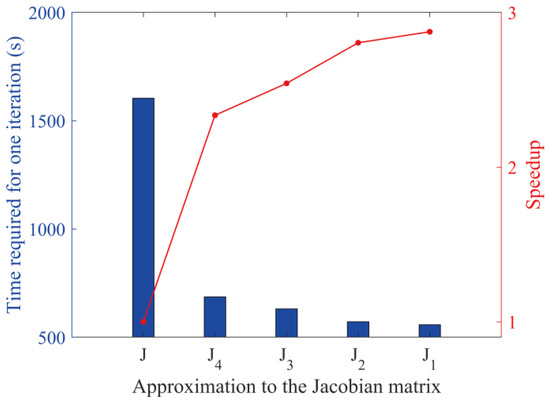
Figure 9.
The effect of various approximation degrees of Jacobian matrix computation algorithms on calculation speed.
The approximate Jacobian matrix was chosen, resulting in an estimated gradient direction. Figure 10 shows the fluctuation of the data-fitting error with the number of iterations when various Jacobian approximation methods are used in the computation. The approximation method used in this paper has little effect on the model’s gradient search direction, so the change in error with the number of iterations in the local minimum search process is similar, and the number of iterations is not increased as a result of the gradient direction approximation.
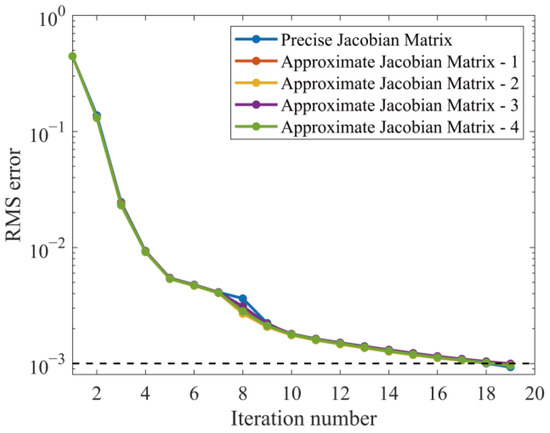
Figure 10.
The relationship between data fitting error and the number of iterations when different approximate Jacobian matrices are used in the calculation.
Combining the above two groups of analyses on the time of each iteration and the total number of iterations, it is possible to demonstrate that the method of approximating the Jacobian matrix in this paper can reduce the time required for each iteration without increasing the number of iterations, significantly improving the calculation speed of the entire inversion process.
To further validate the stability of the suggested technique, various amounts of random noise were applied to the synthetic data, and the approximate Jacobian matrix computation method described in this work was employed for calculation. Figure 11 shows the XOY inversion slices at z = −130 m with the addition of 1%, 3%, and 5% random noise.
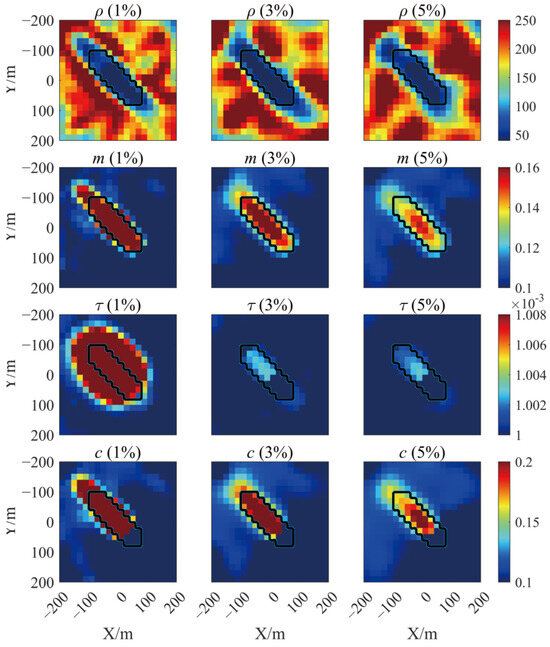
Figure 11.
The XOY slice at z = −130 m shows the inversion results for four IP settings with varying noise levels.
Even after adding various degrees of random noise, the inversion results may still determine the target body’s position and approximate form. Figure 10’s XOY section shows that the target body stretches from the negative direction of the X and Y axes to the positive direction of X and Y. The inversion results of resistivity, polarizability, and frequency correlation coefficient with noise can accurately describe the lateral electrical changes of the underground medium and delineate the precise position of the low-resistance polarization body, but the inversion results of the time constant are poor. The absolute magnitude of the time constants acquired by inversion varies depending on the noise level, but the relative magnitude may still be used to estimate the position of the polarimetric body. The results of the inversion with noise reveal that approximating the Jacobian matrix has no effect on the inversion algorithm’s stability.
4. Results
In this research, the issue of huge quantities of Jacobian matrix calculations in inversion is investigated and improved. The approximate Jacobian matrix calculation method and parallel computing technologies are utilized to speed up the inversion computation of ATEM data. The approximate Jacobian matrix approach can minimize the number of adjoint forward equations while also providing three times or more speedup in large-scale fine inversion. The approximate Jacobian matrix was used in the inversion computation of time-domain aviation electromagnetic data, and multi-parameter three-dimensional inversion results were produced. In comparison to the fine Jacobian matrix findings, the inversion computation time was significantly increased without sacrificing inversion quality. We also ran computations on noisy data to demonstrate that the approximate Jacobian matrix calculation approach has no effect on the inversion algorithm’s stability.
Three-dimensional inversion is a computationally intensive, ill-posed problem, and there are currently two main approaches to reducing inversion time: reducing the amount of calculation required during the inversion iteration and speeding up the calculation by using faster algorithms or better hardware. The approximate Jacobian matrix calculation technique obtains an estimated gradient direction to carry out inversion iteration while decreasing the quantity of work. The approximation approach presented in this study may also be applied to the inversion process based on various forward-modeling methodologies, as well as parallel computing technology and a fast and accurate forward algorithm, to encourage the development of large-scale 3D inversion.
Author Contributions
Conceptualization, D.L.; methodology, H.R.; software, H.R.; validation, D.L.; formal analysis, D.L.; investigation, H.R.; resources, D.L.; data curation, C.F.; writing—original draft preparation, D.L.; writing—review and editing, D.L.; visualization, R.W.; supervision, Z.W.; project administration, Z.W.; funding acquisition, R.W. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the National Natural Science Foundation of China (42374170), the Beijing Science and Technology Plan “Deep Earth Exploration Technology Breakthrough” special project of China (Z181100005718001).
Data Availability Statement
Data associated with this research are available and can be obtained by contacting the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Yin, C.-C.; Ren, X.-Y.; Liu, Y.-H.; Qi, Y.-F.; Qiu, C.-K.; Cai, J. Review on airborne electromagnetic inverse theory and applications. Geophysics 2015, 80, W17–W31. [Google Scholar]
- Salzo, S.; Villa, S. Convergence analysis of a proximal Gauss-Newton method. Comput. Optim. Appl. 2012, 53, 557–589. [Google Scholar] [CrossRef]
- Wilson, G.A.; Raiche, A.P.; Sugeng, F. 2.5D inversion of airborne electromagnetic data. Explor. Geophys. 2006, 37, 363–371. [Google Scholar] [CrossRef]
- Zhdanov, M.; Tolstaya, E. Minimum support nonlinear parametrization in the solution of a 3D magnetotelluric inverse problem. Inverse Probl. 2004, 20, 937. [Google Scholar] [CrossRef]
- Liu, D.C.; Nocedal, J. On the limited memory BFGS method for large scale optimization. Math. Program. 1989, 45, 503–528. [Google Scholar] [CrossRef]
- Schenk, O.; Gärtner, K.; Fichtner, W.; Stricker, A. PARDISO: A high-performance serial and parallel sparse linear solver in semiconductor device simulation. Future Gener. Comput. Syst. 2001, 18, 69–78. [Google Scholar] [CrossRef]
- Liu, Y.; Farquharson, C.G.; Yin, C.; Baranwal, V.C. Wavelet-based 3-D inversion for frequency-domain airborne EM data. Geophys. J. Int. 2017, 213, 1–15. [Google Scholar] [CrossRef]
- Xie, J.; Cai, H.; Hu, X.; Long, Z.; Xu, S.; Fu, C.; Wang, Z.; Di, Q. 3-D Magnetotelluric Inversion and Application Using the Edge-Based Finite Element With Hexahedral Mesh. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–11. [Google Scholar] [CrossRef]
- Egbert, G.D.; Kelbert, A. Computational recipes for electromagnetic inverse problems. Geophys. J. Int. 2012, 189, 251–267. [Google Scholar] [CrossRef]
- Yin, C.; Liu, Y.; Xiong, B. Status and prospect of 3D inversions in EM geophysics. Sci. China Earth Sci. 2020, 63, 452–455. [Google Scholar] [CrossRef]
- Gregory, A.N.; Paul, T.B. Solution accelerators for large-scale three-dimensional electromagnetic inverse problems. Inverse Probl. 2004, 20, S151. [Google Scholar]
- Newman, G.A.; Alumbaugh, D.L. Three-dimensional massively parallel electromagnetic inversion—I. Theory. Geophys. J. Int. 1997, 128, 345–354. [Google Scholar] [CrossRef]
- Newman, G.A.; Alumbaugh, D.L. Three-dimensional magnetotelluric inversion using non-linear conjugate gradients. Geophys. J. Int. 2000, 140, 410–424. [Google Scholar] [CrossRef]
- Cai, H.; Long, Z.; Lin, W.; Li, J.; Lin, P.; Hu, X. 3D multinary inversion of controlled-source electromagnetic data based on the finite-element method with unstructured mesh. Geophysics 2021, 86, E77–E92. [Google Scholar] [CrossRef]
- Commer, M.; Newman, G.A. New advances in three-dimensional controlled-source electromagnetic inversion. Geophys. J. Int. 2008, 172, 513–535. [Google Scholar] [CrossRef]
- Liu, Y.; Yin, C. 3D inversion for multipulse airborne transient electromagnetic data. Geophysics 2016, 81, E401–E408. [Google Scholar] [CrossRef]
- Mackie, R.L.; Madden, T.R. Three-dimensional magnetotelluric inversion using conjugate gradients. Geophys. J. Int. 1993, 115, 215–229. [Google Scholar] [CrossRef]
- Zhang, B.; Yin, C.; Liu, Y.; Ren, X.; Baranwal, V.C.; Xiong, B. 3D inversion of large-scale frequency-domain airborne electromagnetic data using unstructured local mesh. Geophysics 2021, 86, E333–E342. [Google Scholar] [CrossRef]
- Domenzain, D.; Liu, L.; Vela, I.Y.; Christiansen, A.V. 3D DC inversion, visualization, and processing of dense time-lapse data in fine domains applied to remediation monitoring. Geophysics 2023, 88, E147–E158. [Google Scholar] [CrossRef]
- Rodi, W.; Mackie, R.L. Nonlinear conjugate gradients algorithm for 2-D magnetotelluric inversion. Geophysics 2001, 66, 174–187. [Google Scholar] [CrossRef]
- Hui, Z.J.; Yin, C.C.; Liu, Y.H.; Zhang, B.; Ren, X.Y.; Wang, C. 3D inversions of time-domain marine EM data based on unstructured finite-element method. Chin. J. Geophys. 2020, 63, 3167–3179. (In Chinese) [Google Scholar]
- Oldenburg, D.W.; Haber, E.; Shekhtman, R. Three dimensional inversion of multisource time domain electromagnetic data. Geophysics 2012, 78, E47–E57. [Google Scholar] [CrossRef]
- Ren, X.; Yin, C.; Macnae, J.; Liu, Y.; Zhang, B. 3D time-domain airborne electromagnetic inversion based on secondary field finite-volume method. Geophysics 2018, 83, E219–E228. [Google Scholar] [CrossRef]
- Zhang, B.; Engebretsen, K.W.; Fiandaca, G.; Cai, H.; Auken, E. 3D inversion of time-domain electromagnetic data using finite elements and a triple mesh formulation. Geophysics 2021, 86, E257–E267. [Google Scholar] [CrossRef]
- Zhdanov, M.S.; Portniaguine, O. Time-domain electromagnetic migration in the solution of inverse problems. Geophys. J. Int. 1997, 131, 293–309. [Google Scholar] [CrossRef]
- Newman, G.A.; Commer, M. New advances in three dimensional transient electromagnetic inversion. Geophys. J. Int. 2005, 160, 5–32. [Google Scholar] [CrossRef]
- Hu, X.; Li, Y.; Yang, W.-C.; Wei, W.-B.; Gao, R.; Bo, H.; Peng, R.-H. Three-dimensional magnetotelluic parallel inversion algorithm using data space method. Chin. J. Geophys. 2012, 55, 3969–3978. (In Chinese) [Google Scholar]
- Liu, Y.-H.; Yin, C.-C.; Ren, X.-Y.; Qiu, C.-K. 3D parallel inversion of time-domain airborne EM data. Appl. Geophys. 2016, 13, 701–711. [Google Scholar] [CrossRef]
- Long, Z.; Cai, H.; Hu, X.; Li, G.; Shao, O. Parallelized 3-D CSEM Inversion with Secondary Field Formulation and Hexahedral Mesh. IEEE Trans. Geosci. Remote Sens. 2020, 58, 6812–6822. [Google Scholar] [CrossRef]
- Siripunvaraporn, W.; Egbert, G. An efficient data-subspace inversion method for 2-D magnetotelluric data. Geophysics 2000, 65, 791–803. [Google Scholar] [CrossRef]
- Hu, Z.; Hu, X.-Y.; He, Z.-X. Pseudo-Three-Dimensional magnetotelluric inversion using nonlinear conjugate gradients. Chin. J. Geophys. 2006, 49, 1226–1234. (In Chinese) [Google Scholar]
- Cox, L.H.; Wilson, G.A.; Zhdanov, M.S. 3D inversion of airborne electromagnetic data using a moving footprint. Explor. Geophys. 2010, 41, 250–259. [Google Scholar] [CrossRef]
- Yang, D.; Oldenburg, D.W.; Haber, E. 3-D inversion of airborne electromagnetic data parallelized and accelerated by local mesh and adaptive soundings. Geophys. J. Int. 2014, 196, 1492–1507. [Google Scholar] [CrossRef]
- Christiansen, A.V.; Auken, E.; Kirkegaard, C.; Schamper, C.; Vignoli, G. An efficient hybrid scheme for fast and accurate inversion of airborne transient electromagnetic data. Explor. Geophys. 2016, 47, 323–330. [Google Scholar] [CrossRef]
- Newman, G.A.; Alumbaugh, D.L. Frequency-domain modelling of airborne electromagnetic responses using staggered finite differences. Geophys. Prospect. 1995, 43, 1021–1042. [Google Scholar] [CrossRef]
- Lei, D.; Ren, H.; Fu, C.; Wang, Z.; Zhen, Q. Computation of Analytical Derivatives for Airborne TEM Inversion Using a Cole-Cole Parameterization Based on the Current Waveform of the Transmitter. Sensors 2023, 23, 439–455. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).