Abstract
Precision point positioning (PPP) utilizing the Global Navigation Satellite System (GNSS) is a traditional and widely employed technology. Its performance is susceptible to observation discontinuities and unfavorable geometric configurations. Consequently, the integration of the Inertial Navigation System (INS) and GNSS makes full use of their respective advantages and effectively mitigates the limitations of GNSS positioning. However, the GNSS/INS integration faces significant challenges in complex and harsh urban environments. In recent years, the geometry between the user and the satellite has been effectively improved with the advent of lower-orbits and faster-speed Low Earth Orbit (LEO) satellites. This enhancement provides more observation data, opening up new possibilities and opportunities for high-precision positioning. Meanwhile, in contrast to the traditional extended Kalman filter (EKF) approach, the performance of the LEO-enhanced GNSS/INS tightly coupled integration (TCI) can be significantly improved by employing the factor graph optimization (FGO) method with multiple iterations to achieve stable estimation. In this study, LEO data and the FGO method were employed to enhance the GNSS/INS TCI. To validate the effectiveness of the method, vehicle data and simulated LEO observations were subjected to thorough analysis. The results suggest that the integration of LEO data significantly enhances the positioning accuracy and convergence speed of the GNSS/INS TCI. In contrast to the FGO GNSS/INS TCI without LEO enhancement, the average enhancement effect of the LEO is 22.16%, 7.58%, and 10.13% in the north, east, and vertical directions, respectively. Furthermore, the average root mean square error (RMSE) of the LEO-enhanced FGO GNSS/INS TCI is 0.63 m, 1.21 m, and 0.85 m in the north, east, and vertical directions, respectively, representing an average improvement of 41.91%, 13.66%, and 2.52% over the traditional EKF method. Meanwhile, the simulation results demonstrate that LEO data and the FGO method effectively enhance the positioning and convergence performance of GNSS/INS TCI in GNSS-challenged environments (tall buildings, viaducts, underground tunnels, and wooded areas).
1. Introduction
Autonomous navigation and positioning technologies are crucial in various fields, including autonomous vehicles and unmanned aerial vehicles [1,2]. The Global Navigation Satellite System (GNSS) is the primary method of positioning and provides high-precision positioning services with all-weather, real-time, and global coverage. However, high-precision positioning is still challenging in complex and harsh environments [3,4]. GNSS signals can be affected by external interference, leading to signal loss and resulting in low-quality observation data and an insufficient number of satellites. This can make it difficult to provide accurate and reliable positioning services by relying solely on GNSS navigation [5,6]. The Inertial Navigation System (INS) is an autonomous navigation system that provides carrier position, velocity, and attitude information without external signal interference. However, the INS error accumulates with time, affecting the positioning accuracy. Therefore, to make full use of the respective advantages of GNSS and INS, they are usually integrated, which can effectively overcome the deficiencies of a single navigation system positioning and provide users with high-precision positioning services [7,8].
In recent decades, there has been extensive research and application focusing on GNSS/INS integration techniques. Currently, tightly coupled integration (TCI) based on extended Kalman filtering (EKF) is a widely used scheme in the field of integrated navigation [9,10,11,12,13,14]. In 2007, Godha et al. evaluated the performance of a GPS/INS TCI of low-cost MEMS IMUs under weak observing conditions and showed that sub-meter and meter positional accuracy can be provided in suburban and densely populated urban areas, respectively [15]. In 2009, Roesler et al. proposed a PPP/INS tightly combined Kalman filter to obtain three-dimensional (3D) positioning accuracy of less than 15 cm using airborne data [16]. In 2023, Lai et al. established the BDS-3 PPP-B2b/INS TCI model and showed that decimeter-level positioning accuracy can be obtained in urban environments [17].
Although the GNSS/INS TCI can effectively improve the single GNSS positioning accuracy, it remains heavily reliant on GNSS. In complex and harsh urban environments (tall buildings, viaducts, underground tunnels, woods, etc.), GNSS signals are highly susceptible to blocking or even interruption [17,18,19]. At this time, the positioning accuracy of the GNSS/INS TCI is severely affected and cannot provide long-term high-precision positioning services. To address this challenge, this paper considers two aspects to improve the performance of GNSS/INS TCI: (1) The introduction of Low Orbit Satellite (LEO) observations can compensate for the lack of observations due to the loss of GNSS signals in complex environments; (2) In complex urban environments, GNSS measurements exhibit non-Gaussian distribution and high time-dependency. The traditional EKF GNSS/INS TCI is inadequate in providing optimal positioning performance [20]. Therefore, the factor graph optimization (FGO) method is employed to establish the GNSS/INS TCI model, which enhances positioning accuracy and robustness.
LEO satellites can effectively complement and enhance global positioning, navigation, and timing (PNT) services, as they are characterized by greater speed and strong signal power. They have received significant attention due to their potential benefits [21,22,23,24,25,26,27,28]. In 2022, Liu et al. designed the LEO constellation to enhance the Beidou Navigation Satellite System (BDS), and simulation experiments showed that the LEO constellation improved the positioning accuracy of BDS from the decimeter level to less than 5 cm and the convergence time was reduced to within 3.5 min [29]. In 2023, Teng et al. designed and optimized two LEO navigation enhancement constellations and selected nine stations for simulation experiments, which showed that the two LEO enhancement positioning accuracies were improved by 5.7–71.9% and 24.2–69.5%, respectively [30]. In 2024, Zhang et al. used simulated LEO data to validate the performance of LEO-enhanced GPS/INS and showed that the addition of LEO significantly improves the positioning accuracy of single GPS and GPS/INS integration [31]. Xu et al. investigated LEO-enhanced multi-GNSS precision point positioning (PPP) using real dual-frequency navigation signals from the CENTISPACETM ESAT1 satellite and the results showed that the LEO signals significantly improved high-precision positioning [32]. Therefore, the introduction of LEO into the GNSS/INS TCI can effectively improve the impact of GNSS observation anomalies in harsh environments.
The FGO method utilizes all the historical information for multiple iterations thus achieving stable estimation. It has significant advantages in dealing with nonlinear problems in complex environments. Therefore, the FGO method, which is widely used in the field of robotics, has also been applied to GNSS [33] and GNSS/INS integrated positioning [34]. In 2019, Wen et al. employed an FGO method to implement GNSS/INS TCI and conducted two sets of experiments in urban canyon environments for demonstration. The GNSS/INS positioning accuracy was significantly improved compared to the traditional EKF GNSS/INS TCI [35]. In 2020, Chang et al. proposed the FGO GNSS/IMU/ODO/LiDAR-SLAM navigation system and conducted vehicle experiments in open areas and tunnels. The results show that the maximum root mean square (RMS) of position drift error for this system is reduced by 62.8%, 72.3%, and 52.1% during GNSS outages in north, east and vertical directions, respectively, compared to the conventional GNSS/INS/ODO integration [36]. In 2021, Tang et al. developed a pre-integrated model that includes the Earth’s rotation in the GNSS/INS integration and the experimental results showed that the accuracy of the FGO GNSS/INS integration can be improved to that of the EKF GNSS/INS [37]. Wen et al. proposed an FGO model for GNSS and real-time kinematic (RTK) positioning. Compared to the filtered approach, the model was evaluated on a dataset of an urban canyon environment in Hong Kong and significantly improved the GNSS and GNSS-RTK positioning accuracy [38].
In conclusion, GNSS/INS integrated navigation research is mainly based on the traditional Kalman filter method. However, there are fewer studies on GNSS/INS based on the FGO method. Additionally, there are more studies on LEO-enhanced GNSS precision positioning, while there are limited studies on LEO-enhanced GNSS/INS integrated navigation. Therefore, the innovation of this study is to establish a LEO-enhanced GNSS/INS TCI model with the FGO method, which has the following characteristics based on previous studies: (1) The GNSS/INS TCI typically uses the EKF method and this paper develops a GNSS/INS TCI model using the FGO method; (2) The introduction of LEO observations realizes the EKF and FGO GNSS/LEO/INS models. This innovation is expected to improve the positioning accuracy and robustness of the integrated navigation system.
In this study, an LEO-enhanced FGO GNSS/INS TCI model is proposed, which can better deal with vehicle navigation in complex and harsh environments. At the same time, the addition of LEO provides more opportunities and can provide certain reference values for the future development of the integrated navigation field. The rest of the paper is organized as follows: Section 2 presents the model and framework of the EKF and FGO GNSS/LEO/INS TCI algorithm. Section 3 presents the experimental scheme and analysis, where the TCI algorithm is validated using on-board data and simulated LEO data. Additionally, a weak observation environment is simulated to test the applicability of the FGO GNSS/LEO/INS TCI in complex environments. The discussion of the experimental validation results is presented in Section 4, followed by conclusions in Section 5.
2. Methodology Model
This paper evaluates two TCI models, namely, LEO-enhanced EKF GNSS/INS and LEO-enhanced FGO GNSS/INS. The evaluation is based on the dual-frequency ionospheric-free pseudo-range, carrier-phase, and Doppler observations from GNSS and LEO, as well as INS-predicted observations as the initial observations. The following section describes the two algorithmic models.
2.1. LEO-Enhanced EKF GNSS/INS TCI
The core concept of the EKF involves expanding nonlinear functions into Taylor series and neglecting terms of second order and higher. This enables the derivation of an approximate linearized model, followed by the application of the Kalman filter to accomplish state estimation.
The Kalman filter state equation for the LEO-enhanced EKF GNSS/INS TCI is expressed as:
where represents the system state vector, represents the system state transition matrix, represents the system noise driving matrix, and represents the system noise vector that follows a Gaussian normal distribution with a mean value of zero.
The observation equation for the LEO-enhanced GNSS/INS TCI can be expressed as:
where denotes the observation innovation vector, denotes the matrix of design coefficients for the k epoch, and denotes the observation noise, which follows a Gaussian normal distribution; denotes the a priori variance of the observation noise.
2.1.1. LEO-Enhanced GNSS/INS TCI Algorithm Structure
The LEO-enhanced EKF GNSS/INS TCI framework is shown in Figure 1. If there is no available GNSS or LEO observation data for the current INS epoch, the navigation information of the INS mechanization and the variance of the Kalman filter time update will be directly output. If there is available observation data, the LEO-enhanced GNSS/INS tightly coupled integration will be conducted.
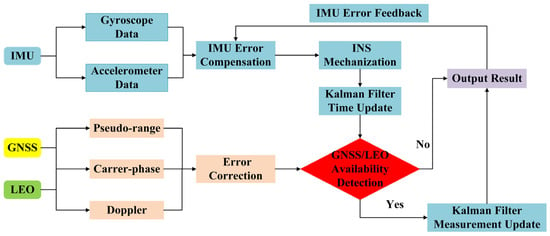
Figure 1.
Schematic diagram of LEO-enhanced GNSS/INS TCI structure based on EKF.
2.1.2. Observation Function of the LEO-Enhanced GNSS/INS TCI
The observation innovation vector for the GNSS/LEO/INS TCI can be obtained from the difference between the dual-frequency observations of GNSS/LEO and the observations predicted by INS, which can be expressed as:
To obtain INS predictions, INS mechanization is arranged to update the position and velocity of the receiver. However, INS data are based on the IMU center and GNSS/LEO data are based on the GNSS receiver antenna phase center. Therefore, a lever-arm correction is required. The lever-arm corrected linearized function can be expressed as [18,31]:
where denotes the differential form of observation innovation vector; b, n, i, and e denote the body frame, the navigation frame, the inertial frame, and the Earth-centered Earth-fixed frame, respectively; denotes the GNSS lever-arm error in the b-frame; denotes the LEO lever-arm error in the b-frame; and denote the wavelength and ambiguity of the ionospheric-free carrier; denotes the angular rate error of the gyroscope output; (k = n and b, j = e and n) denotes the rotation matrix from the j-frame to the k-frame; denotes the tropospheric wet delay projection function.
- where
Thus, the design coefficient matrix for the LEO-enhanced GNSS/INS TCI can be obtained from Equations (3) and (4), and it can be expressed as:
where
with
where denotes the direction cosine of the satellite-receiver vector; denotes the angular rate of the gyroscope output of the b-frame relative to the i-frame in the n-frame; and denote the rotational angular velocity of the n-frame relative to the e-frame and the e-frame relative to i-frame in the n-frame, respectively.
2.1.3. State Function of the LEO-Enhanced GNSS/INS TCI
The state vector of the LEO-enhanced GNSS/INS TCI can be expressed as:
where denotes the three-dimensional position correction in the n-frame; denotes the three-dimensional velocity correction in the n-frame; denotes the attitude correction; and denotes the bias error correction of accelerometer and gyroscope; and denotes the scale factor error correction of accelerometer and gyroscope; and denote the receiver clock offset and clock drift in the GNSS system, respectively; and denote the receiver clock offset and clock drift in the LEO system; denotes residual of the wet tropospheric delay; and denotes ionospheric-free ambiguity correction in the GNSS and LEO.
The state transfer matrix of the LEO-enhanced GNSS/INS TCI is expressed as:
with:
where and represent position-dependent state coefficient; , , , , and represent velocity-dependent state coefficient; , , and represent attitude-dependent state coefficient; , , , and represent the state coefficients related to the INS bias errors and scale factor errors; and represent the state coefficients related to the receiver clock offset and clock drift; represents the state coefficient related to tropospheric zenith wet delay; represents the state coefficient related to ambiguity; represents the sampling interval; represents specific force from the accelerometer; the remaining parameters can be referred to in Equation (12).
When GNSS or LEO data are available, the state parameters and the corresponding covariance matrix are updated using the Kalman filter measurement update, which can be expressed as:
where and denote the estimated state vector at k epoch and k−1 epoch, respectively; denotes the predicted variance-covariance matrix; and denotes the estimated variance-covariance matrix; denotes the gain matrix at k epoch; denotes the dynamic noise covariance matrix.
2.2. LEO-Enhanced FGO GNSS/INS TCI
The factor graph is a bilateral graph model that combines variables and factor nodes. It can be used to solve the problem of fusing heterogeneous sensors with different frequencies. Figure 2 illustrates the LEO-enhanced GNSS/INS framework, which includes all historical observation information and states. This is one of the main differences between the LEO-enhanced EKF GNSS/INS. The study uses the INS factor and the ambiguity factor to associate the front and back epoch state nodes. Marginalization is then employed to limit the computational complexity of the sliding-window optimizer by converting the INS factor and the GNSS/LEO factor corresponding to the marginalized states into a priori factors. For further information on marginalization, please check the references [37,39].
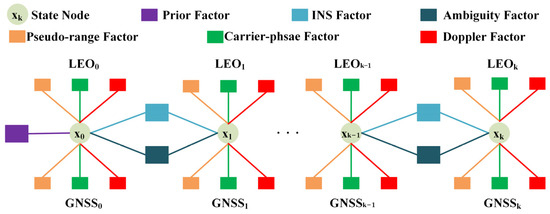
Figure 2.
Schematic diagram of LEO-enhanced GNSS/INS TCI structure based on FGO.
2.2.1. FGO Theory
The objective of utilizing LEO-enhanced FGO GNSS/INS TCI is to determine the optimal a posteriori state based on the initial measurements. Information fusion for integrated navigation has high nonlinearity and can be solved by optimization methods such as g2o/Ceres/GTSAM. Ceres is an open source C++ library for modeling and solving large, complex optimization problems. It focuses on solving nonlinear least squares problems and the framework is easy to use with lower computation time. Therefore, in this paper, we use the Ceres Solver as a nonlinear optimization solver.
As GNSS measurements, LEO measurements, and INS information are independent of each other, this paper presents the LEO-enhanced GNSS/INS integration as a maximum a posteriori (MAP) problem [40]. It can be expressed as:
where denotes the optimal estimate of the system state variation; denotes the raw GNSS or LEO measurements of the k epoch; i denotes the index of the measurements performed at k (e.g., one epoch may have multiple pseudo-range, carrier-phase, and Doppler measurements); denotes the system state of the k epoch; and denotes all the a priori information, i.e., the measurements provided by the INS.
The above problem is transformed into a nonlinear optimization problem in the LEO-enhanced FGO GNSS/INS TCI, where all sensor measurements are considered as factors associated with a particular state . According to the reference [35], the MAP problem can be expressed as:
where is the factor associated with the measurements, which can be derived from the GNSS, LEO, and INS measurements; is the observation function associated with zj; denotes the state set from the first epoch to the current epoch. When the observation noise conforms to a Gaussian distribution, the negative logarithm of the probability distribution is proportional to the measurement-associated error function. Therefore, it can be converted to:
2.2.2. INS Factor
The INS utilizes a three-axis accelerometer and a three-axis gyroscope to provide acceleration and angular velocity observations. The linearized model can be expressed as follows:
where denotes the state of the k epoch. The measurement functions for acceleration and angular velocity in INS are as follows:
where denotes the time difference from k epoch to k−1 epoch; denotes measurements of the three-axis accelerometers; denotes measurements of the three-axis gyroscopes; denotes the pitch; denotes the roll; and denotes the heading.
Further, the error function of the INS acceleration and angular velocity measurements can be expressed as:
where and are the covariance matrices associated with the acceleration and gyroscope measurements, respectively.
2.2.3. GNSS and LEO Factors
The LEO-enhanced GNSS/INS TCI involves the pseudo-range, carrier-phase, and Doppler factors. The GNSS dual-frequency pseudo-range, carrier-phase, and Doppler combination model can be expressed as follows:
where indices s and r denote satellite and receiver is the geometric distance between the phase center of the receiver antenna and the satellite; c is the speed of light in a vacuum; and denote the receiver clock offset and the satellite clock offset, respectively; is the tropospheric delay; denotes other corrections such as relativity effects, Earth rotation effects, antenna phase center offset (PCO) and variance (PCV). In Doppler data processing, only the receiver clock variation and satellite clock variation are considered as sources of error due to their significant variation. Other error terms are negligible and therefore excluded. Finally, , , and are pseudo-range, carrier-phase and Doppler observation noise, and unmodeled multipath errors.
Thus, the error functions for the GNSS pseudo-range, carrier-phase, and Doppler measurements can be obtained as follows:
The observation quality of each satellite is different due to the differences in signal-to-noise ratio, satellite elevation, and observation environment. In this study, the satellite elevation-dependent weight model is used to estimate the a priori variance () of GNSS observations [18]:
where denotes the satellite elevation and denotes the precision of the observation.
Similarly, the pseudo-range factor, carrier-phase factor, and Doppler factor of LEO can be obtained. In this paper, the GNSS factor, INS factor, and LEO factor are proposed. Therefore, the optimal state set X = {x1, x2, x3, …, xk, …} can be solved as:
3. Experiment Evaluations
To evaluate the performance of the method, a set of actual and simulation experiments are arranged. This section specifically describes the experiment data, processing strategy, and experiment analysis.
3.1. Experiment Data and Scheme
To evaluate the performance of the LEO-enhanced GNSS/INS TCI, a test vehicle equipped with a GNSS receiver and a tactical-grade IMU (POS320) was placed in a typical complex urban environment (tall buildings, trees, etc.) in Beijing, China, on 17 December 2020. The experimental trajectory is shown in Figure 3. In all figures in the paper, LEO-enhanced GNSS/INS is denoted as GNSS/INS/LEO.
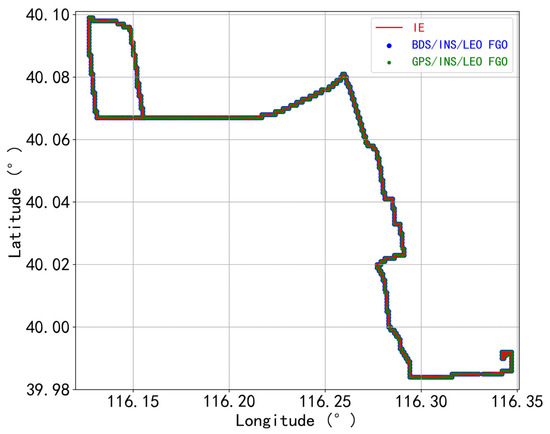
Figure 3.
The trajectory of the land vehicle experiment in Beijing, China.
In the test, the sampling rates of GNSS, LEO, and IMU data were 1 Hz, 1 Hz, and 200 Hz, respectively, and the detailed information on the IMU sensor is shown in Table 1. Since there are no available LEO navigation satellites operated in orbit, we simulated two commonly used low-orbit constellations, namely, the inclined orbit constellation and the polar orbit constellation, with a total of 160 satellites providing global coverage. The orbital altitude of the LEO satellites is 970 km. There are 70 satellites in six polar orbits with an orbital inclination of 90° and 90 satellites in 10 inclined orbits with an orbital inclination of 60° [31]. The simulated LEO observations mainly include the satellite clock error, tidal error, Earth rotation, relativistic effect, tropospheric delay, phase winding, and other simulated errors. In this case, the Saastamoinen model is used for the tropospheric delay, the satellite PCV and PCO corrections are set to 0, the noise in the pseudo-range observations is set to 0.5 m, the noise in the carrier-phase is set to 0.003 m, and the multipath effect is not considered. The signal frequency of the LEO simulated data are the same as the GPS L1 and L2 frequencies, i.e., LEO L1: 1575.42 MHz, LEO L2: 1227.60 MHz.

Table 1.
Technical parameters of the POS320.
The number of available GNSS and LEO satellites and the corresponding PDOP are shown in Figure 4. GPS availability is low, with less than four satellites or no satellites available in some periods; BDS is slightly better but suffers from the same phenomenon as GPS. Comparatively, LEO can increase the number of available satellites to some extent. The statistics show that the average number of available satellites for GPS, GPS/LEO, BDS, and BDS/LEO are 6.5, 13.4, 12.8, and 19.6, respectively, and the corresponding PDOP are 4.3, 1.9, 4.1, and 2.1, respectively. However, in certain epochs, the addition of LEO satellites does not significantly augment the numbers of available satellites for GPS/LEO and BDS/LEO, even less than 4. Consequently, the PDOP values associated with these epochs is worse. In conclusion, LEO increases the number of available satellites and improves the geometry. When using LEO satellites, the smaller the corresponding PDOP, the better the satellite distribution, and the higher the theoretical positioning accuracy.
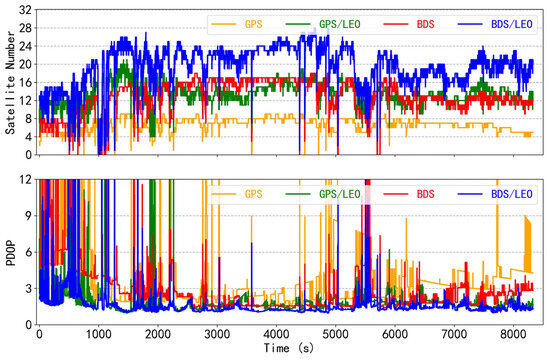
Figure 4.
Time series of the number of available satellites and PDOP for the GPS, GPS/LEO, BDS, and BDS/LEO.
In the experiment, the reference station was set up nearby in an open environment as far as possible to avoid the surrounding signal reflectors. The GNSS RTK/INS tight combination algorithm provided by NovAtel Inertial Explorer 8.7 (IE 8.7) commercial software generates the positioning reference values. To ensure time alignment for integrated navigation, GPST is used uniformly for GNSS, LEO, and INS. The offset between the GNSS antenna and the center of the IMU is measured during the experiments to ensure spatial alignment. Please refer to Table 2 for a detailed processing strategy.

Table 2.
LEO-enhanced GNSS/INS TCI models and strategies.
To verify the performance of the method, we carried out the experimental program as follows:
- The paper analyzed the positioning performance of EKF GNSS/INS and LEO-enhanced EKF GNSS/INS TCI. The purpose was to verify the improvement of LEO-enhanced EKF GNSS/INS TCI.
- Meanwhile, the paper analyzed the positioning performance of FGO GNSS/INS and LEO-enhanced FGO GNSS/INS TCI. The purpose was to verify the improvement of LEO-enhanced FGO GNSS/INS TCI.
- Comparison of the LEO-enhanced EKF and FGO GNSS/INS TCI positioning performance.
- Weak GNSS conditions were simulated to validate the performance of the LEO-enhanced FGO GNSS/INS in complex urban environments.
3.2. LEO-Enhanced EKF and FGO GNSS/INS TCI
This section analyzes the positioning performance of the LEO-enhanced EKF GNSS/INS TCI and the LEO-enhanced FGO GNSS/INS TCI. To ensure reliable and accurate positioning results, the statistics of the RMSE value of the positioning error exclude the first 1000 epochs, as the PPP/INS tight integration requires a certain convergence period.
3.2.1. LEO-Enhanced EKF GNSS/INS TCI
The variation of the position errors of the EKF GPS/INS TCI, the LEO-enhanced EKF GPS/INS TCI, the EKF BDS/INS TCI, and the LEO-enhanced EKF BDS/INS TCI with respect to the reference value in the n-frame is shown in Figure 5. It can be seen that the position errors of the GPS/INS TCI and the BDS/INS TCI were worse in comparison to the results with the inclusion of the LEO, which is mainly influenced by the availability of the GPS and BDS satellites significantly. Figure 6 shows the RMSE of the corresponding position error. Comparing the results of LEO-enhanced GPS/INS and LEO-enhanced BDS/INS TCI with those without LEO enhancement, the RMSE of the LEO-enhanced GPS/INS TCI improved from 1.23 m, 1.31 m, and 0.71 m to 1.08 m, 1.18 m, and 0.63 m, in the north, east, and vertical directions, respectively, providing improvements of 11.69%, 9.72%, and 10.46%; the RMSE of the LEO-enhanced BDS/INS TCI improved from 1.85 m, 1.75 m, and 2.14 m to 1.08 m, 1.18 m, and 0.63 m, in the north, east, and vertical directions, respectively, providing improvements of 3.82%, 11.12%, and 21.25%. Obviously, the positioning accuracy and convergence performance of GPS and BDS are significantly improved after obtaining LEO satellite augmentation.
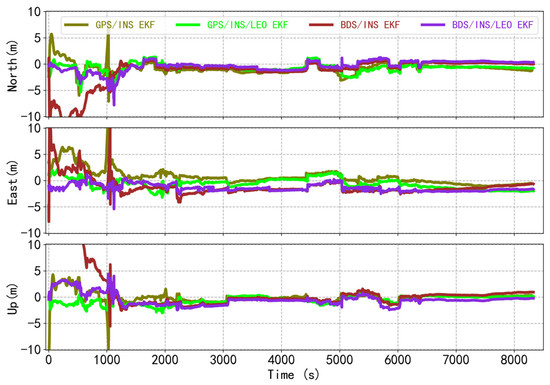
Figure 5.
The position differences for the GPS/INS, LEO-enhanced GPS/INS, BDS/INS, and LEO-enhanced BDS/INS tightly coupled integration based on EKF.
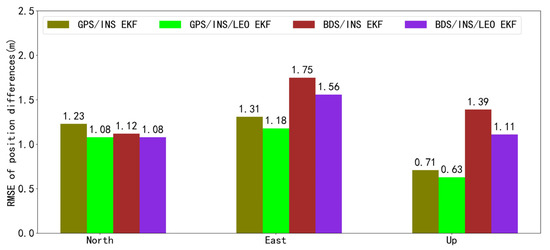
Figure 6.
RMSE of position differences for the GPS/INS, LEO-enhanced GPS/INS, BDS/INS, and LEO-enhanced BDS/INS tightly coupled integration based on EKF.
3.2.2. LEO-Enhanced FGO GNSS/INS TCI
The variation of the position errors of the FGO GPS/INS TCI, the LEO-enhanced FGO GPS/INS TCI, the FGO BDS/INS TCI, and the LEO-enhanced FGO BDS/INS TCI with respect to the reference value in the n-frame is shown in Figure 7. Consistent with the conclusions of the EKF tight integration, the position errors of the GNSS/INS TCI also show worse results relative to the inclusion of the LEO. Figure 8 shows the RMSE of the corresponding position error. Comparing the result of the LEO-enhanced GPS/INS and the LEO-enhanced BDS/INS TCI with those without LEO enhancement, the RMSE of the LEO-enhanced GPS/INS TCI improved from 0.97 m, 0.93 m, and 0.71 m to 0.69 m, 0.89 m, and 0.62 m, in the north, east, and vertical directions, respectively, providing improvements of 29.05%, 3.78%, and 12.98%; the RMSE of the LEO-enhanced BDS/INS TCI improved from 0.67 m, 1.71 m, and 1.16 m to 0.57 m, 1.52 m, and 1.07 m, in the north, east, and vertical directions, respectively, providing improvements of 15.28%, 11.38%, and 7.27%. Obviously, for the FGO GNSS/INS TCI, the performance of the integrated navigation positioning is also significantly improved after obtaining LEO augmentation.
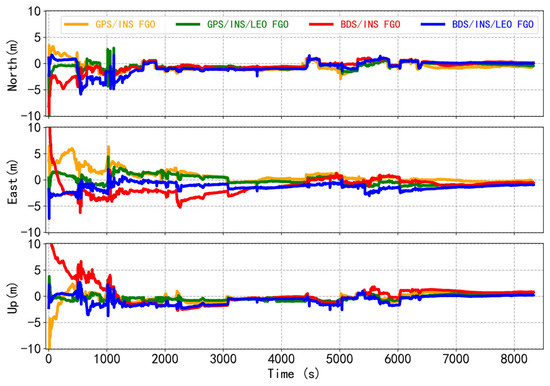
Figure 7.
The position differences of the GPS/INS, LEO-enhanced GPS/INS, BDS/INS, and LEO-enhanced BDS/INS tightly coupled integration based on FGO.
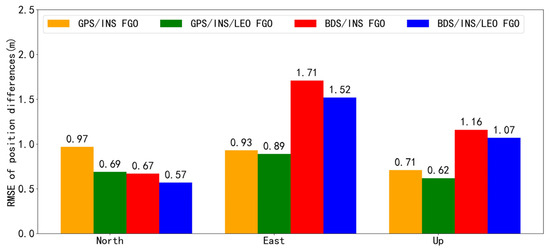
Figure 8.
RMSE of position differences for the GPS/INS, LEO-enhanced GPS/INS, BDS/INS, and LEO-enhanced BDS/INS tightly coupled integration based on FGO.
In order to further demonstrate the positioning performance of the LEO-enhanced GNSS/INS TCI, the paper calculates the cumulative probability distribution of the error. In general, the cumulative distribution function (CDF) is used to estimate the probability distribution of the positioning error. Based on the CDF of the position offsets for the FGO GPS/INS, LEO-enhanced GPS/INS, BDS/INS, and LEO-enhanced BDS/INS shown in Figure 9, the percentages for those epochs with position offsets within 0.5 m in the north direction were 26.6% and 99.8%, respectively, for the GPS/INS and LEO-enhanced GPS/LEO; such percentages in the east direction were 90.0%, and 99.7%, and they were 71.6%, and 99.9% in the vertical direction. The percentages for those epochs with position offsets within 1 m in the north direction were 99.1% and 99.8%, respectively, for the BDS/INS and LEO-enhanced BDS/LEO; such percentages in the east direction were 65.7%, and 89.4%, and they were 94.9% and 99.1% in the vertical direction. Given the above CDF trends, the LEO-enhanced GNSS/INS TCI offer better stability and higher accuracy than without LEO.
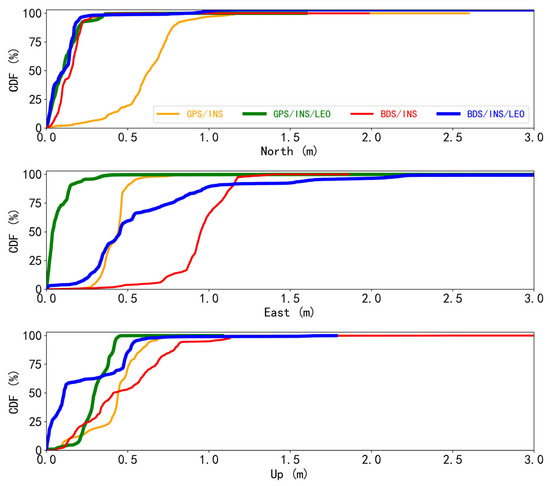
Figure 9.
Cumulative distribution function of position difference for the GPS/INS, LEO-enhanced GPS/INS, BDS/INS, and LEO-enhanced BDS/INS tightly coupled integration based on FGO.
3.2.3. The Performance Comparison between EKF and FGO Method
Table 3 demonstrates the EKF and FGO GPS/INS, LEO-enhanced GPS/INS, BDS/INS, and LEO-enhanced BDS/INS TCI position error RMSE statistics. Comparing the EKF and FGO methods, the raw data are consistent in their assumptions and provide the same a priori information and elevation angle weighting method. In addition, the data pre-processing and parameter settings of the experiments are consistent and the raw observations are reasonably used for the solution. Compared to the EKF GNSS/INS TCI with those without LEO augmentation, the average enhancement effect of the LEO scheme in the north, east, and vertical directions was 7.76%, 10.42%, and 15.87%. Compared to the FGO GNSS/INS TCI with those without LEO augmentation, the average augmentation effect of the LEO scheme in the north, east, and vertical directions was 22.16%, 7.58%, and 10.13%, respectively. In general, whether it is EKF tight integration or FGO tight integration, LEO can play a significant role in its positioning performance.

Table 3.
RMSE of position differences for GPS/INS, LEO-enhanced GPS/INS, BDS/INS, and LEO-enhanced BDS/INS tightly coupled integration between EKF and FGO (unit: m).
According to Table 3, comparing the EKF tight integrations, the FGO GPS/INS position error RMSE improved by 20.80% and 29.32% in the north and east directions, respectively, while there was no improvement in the vertical direction; and the LEO-enhanced FGO GPS/INS position error RMSE improved by 36.37%, 24.67%, and 2.37% in the north, east, and vertical directions, respectively. Additionally, the FGO BDS/INS position error RMSE improved by 40.34%, 2.36%, and 17.35% in the north, east, and vertical directions, respectively; and the LEO-enhanced BDS/INS position error RMSE improved by 47.45%, 2.64%, and 2.67% in the north, east, and vertical directions, respectively. Obviously, the positioning accuracy of FGO TCI is superior to EKF TCI. The 3D positioning errors of FGO GPS/INS, LEO-enhanced GPS/INS, BDS/INS, and LEO-enhanced BDS/INS TCI were 1.52 m, 1.28 m, 2.17 m, and 1.94 m, respectively, which were improved by 21.24%, 25.58%, 34.83%, and 11.42% compared with the EKF scheme. According to Figure 5 and Figure 7, the FGO integration scheme has better stability and higher accuracy than the EKF integration scheme. However, when relatively good positioning accuracy was obtained based on EKF, the positioning accuracy improvement based on FGO was not so significant.
Therefore, the study in this section shows that LEO provides more observation data and improves the geometric distribution of GNSS satellites, which has a significant improvement on the positioning performance of the GNSS/INS TCI. The addition of LEO has led to a certain improvement in the stability, continuity, and accuracy of the EKF and FGO GNSS/INS TCI. With the completion of the future LEO constellation, the positioning accuracy of the GNSS/INS navigation will be further improved, taking into account the advantages of the FGO, which is of great significance for the improvement of automatic navigation vehicle technology in the future.
3.3. LEO-Enhanced FGO GNSS/INS TCI Performance under GNSS with the Low-Observability Environment
The above results demonstrate that the FGO TCI performance is superior to the traditional EKF TCI to a certain extent and that LEO satellites are very effective in enhancing the performance of the GNSS/INS TCI. In this section, the performance of the FGO TCI is further evaluated under the low observability of GNSS satellites, i.e., in complex and harsh urban environments.
3.3.1. LEO-Enhanced FGO GNSS/INS TCI Position Performance
In complex and harsh urban environments, GNSS pseudo-range, carrier-phase, and Doppler observations can be easily affected by errors such as multipath, leading to decreased positioning accuracy, especially with fewer observation satellites. To verify this problem, partial loss of GNSS is simulated with the raw GNSS observation data. Figure 10 illustrates the sequence of the number of satellites after the simulation, and the average number of available satellites for GPS, GPS/LEO, BDS, and BDS/LEO are 4.7, 12.2, 6.0, and 13.5, respectively, which shows that the number of available satellites for GNSS decreases compared to Figure 4.
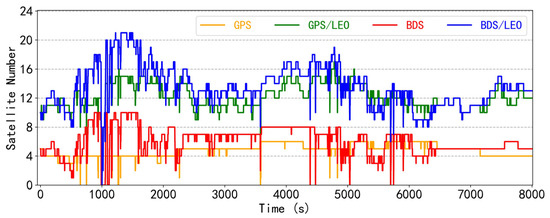
Figure 10.
Time series of the number of available satellites for the FGO GPS, GPS/LEO, BDS, and BDS/LEO under the low-observability environment.
To process the simulated data and analyze the improvement effect of LEO satellites on the performance of FGO integration under weak GNSS conditions, four integrations of FGO GPS/INS, LEO-enhanced GPS/INS, BDS/INS, and LEO-enhanced BDS/INS were used. Figure 11 shows the four TCI position results, where LEO significantly improved the GNSS/INS positioning performance under weak GNSS conditions. Through the study, it is believed that when the position deviation of 10 consecutive epochs is less than 3 m, it can be considered convergence. It is evident that the convergence speed of the LEO-enhanced GNSS/INS TCI has significantly improved. Additionally, the positioning offsets in the north, east, and vertical directions exhibit less fluctuation and tend to remain stable. Meanwhile, there is a significant re-convergence process for GPS/INS TCI and BDS/INS TCI in the 4800–6000 epochs, while the LEO-enhanced GNSS/INS TCI is almost recoverable due to the increase in the number of LEO satellites. Therefore, as shown by the variation of differences in Figure 11 and the RMSE statistics in Figure 12, the LEO-enhanced GNSS/INS has a significantly higher positioning accuracy and possesses a more excellent stability in weak GNSS observation conditions.
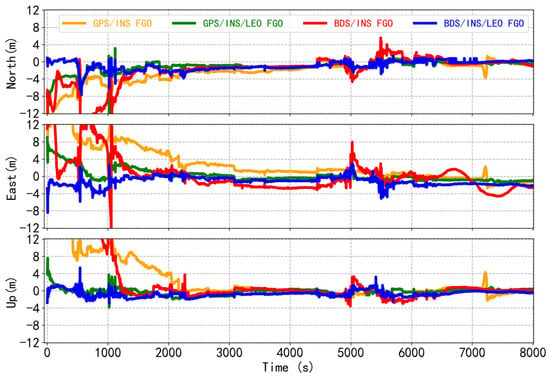
Figure 11.
The position differences of the FGO GPS/INS, LEO-enhanced GPS/INS, BDS/INS, and LEO-enhanced BDS/INS tightly coupled integration under the low-observability environment.
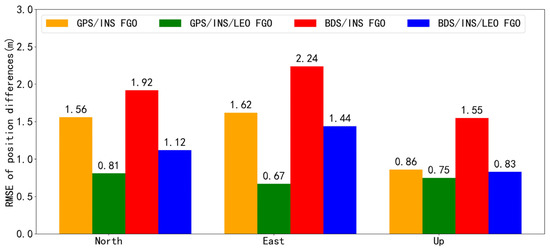
Figure 12.
RMSE of position differences for the FGO GPS/INS, LEO-enhanced GPS/INS, BDS/INS, and LEO-enhanced BDS/INS tightly coupled integration under the low-observability environment.
According to the RMSE of the positions presented in Figure 11, it can be concluded that the LEO-enhanced GNSS/INS TCI provided higher positioning accuracy. The RMSEs of the LEO-enhanced GPS/INS in the north, east, and vertical directions were 0.81 m, 0.67 m, and 0.75 m, respectively, and the enhancement effect of LEO was 48.67%, 58.90%, and 13.12%, respectively. The RMSEs of the LEO-enhanced BDS/INS in the north, east, and vertical directions were 1.12 m, 1.44 m, and 0.83 m, respectively, and the LEO enhancement effect was 41.85%, 35.68%, and 46.28%, respectively. It is important to note that the introduction of LEO satellites has a clear constraint on the impact of low GNSS satellite observability. Compared to Figure 7 and Figure 11, the improvement in convergence speed and positioning accuracy of LEO-enhanced FGO GNSS/INS TCI was more obvious under low GNSS satellite observation. Therefore, with the completion of future LEO constellations, vehicle navigation in harsh environments can be improved to provide user-satisfying and stable positioning results even when the GNSS signals are severely interfered with. This is important for vehicle, airborne, and other combinations of navigation to provide more stable and broader applications.
3.3.2. LEO-Enhanced FGO GNSS/INS TCI Convergence Performance
To evaluate the effect of LEO on the convergence performance of the FGO GNSS/INS TCI, the raw data were randomly divided into four sets of observations in the 2000 epoch interval, and the four sets of data were processed using GNSS/INS and LEO-enhanced GNSS/INS TCI. The position solution achieved for GPS/INS, LEO-enhanced GPS/INS, BDS/INS, and LEO-enhanced BDS/INS are shown in Figure 13. For four sets of random data, this paper considers that convergence is reached when the error is less than 3 m for 10 consecutive epochs. The addition of LEO data can significantly improve the convergence time of GPS/INS and BDS/INS. Regrettably, the vertical convergence of the second dataset in the LEO-enhanced BDS/INS mode is slightly slower. Additionally, to measure the positioning accuracy after convergence, this paper statistically calculates the corresponding RMSEs by selecting the smoothed intervals following convergence of the LEO-enhanced GNSS/INS modes, as depicted in Figure 14. It can be seen that the U-direction of the second set of data and the N-direction of the third set of data in LEO-enhanced GPS/INS TCI have slightly poorer positioning accuracies. Similarly, the N-direction of the first set of data and the U-direction of the second set of data in the LEO-enhanced BDS/INS TCI have slightly poorer positioning accuracies. Even so, it still meets the needs of users for positioning accuracy in complex environments.
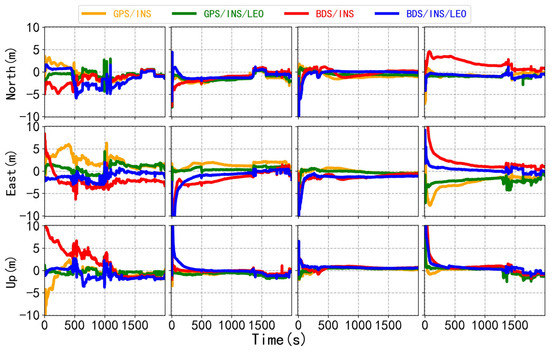
Figure 13.
Convergence performance of the GPS/INS, LEO-enhanced GPS/INS, BDS/INS, and LEO-enhanced BDS/INS tightly coupled integration based on FGO.
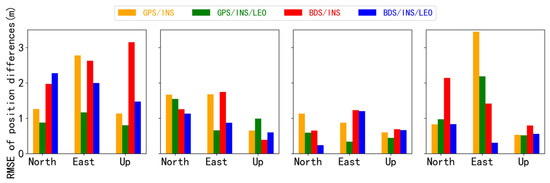
Figure 14.
RMSE of position differences for the four tightly coupled integrations based on FGO.
Table 4 shows the 3D positioning errors for FGO GPS/INS TCI, LEO-enhanced GPS/INS TCI, BDS/INS TCI, and LEO-enhanced BDS/INS TCI. It is evident that the addition of LEO significantly improved the 3D positioning accuracy of the GNSS/INS TCI. The results in this section indicate that the LEO-enhanced FGO GNSS/INS TCI significantly improved convergence speed and positioning accuracy. Therefore, the LEO-enhanced FGO integrated navigation method can enhance vehicle navigation performance in harsh environments and enable more stable and wide-ranging applications.

Table 4.
3D positioning errors for FGO GPS/INS, LEO-enhanced GPS/INS, BDS/INS, and LEO-enhanced BDS/INS tightly coupled integration (unit: m).
4. Discussion
The field experiments and simulations above have demonstrated the significant contribution of LEO and FGO methods to improve vehicle positioning accuracy in harsh environments. The low orbit, greater speed, and strong signals of LEO satellites can improve the geometry between the user and the satellite and provide more observations that can be used for parameter estimation. Consequently, this enhancement significantly improves the positioning performance of the GNSS/INS TCI. The references [27,29,31,41,42] presented show relatively consistent results.
In addition, compared to the traditional EKF tight integration method, the FGO tight integration method demonstrates superior positioning performance in LEO-enhanced GNSS/INS. Due to the involvement of multiple sensor fusions and a complex dynamic environment, nonlinear problems are unavoidable. The FGO method conducts multiple iterations based on all historical and current measurements to achieve stable estimation, providing a clear advantage in dealing with nonlinear problems. Meanwhile, FGO can utilize historical information of sensors and model constraint relationships between observed data and state variables at different moments [19,35]. This approach effectively enhances robustness to outliers. Therefore, the LEO and FGO methods can effectively enhance the accuracy and robustness of integrated navigation, providing a more reliable solution for positioning requirements in complex environments.
5. Conclusions
The continuity, reliability, and robustness of traditional extended Kalman filter-based GNSS/INS integration in complex and harsh urban environments are susceptible to GNSS anomalies. To solve this problem, this paper proposes a LEO-enhanced factor graph optimization method for GNSS/INS tight integration.
The study validates the algorithmic model using a set of vehicle data and simulated LEO data and the validation results show that: (1) Compared with the traditional GNSS/INS TCI method, the FGO method using multiple iterations can achieve stable estimation. This can effectively enhance the positioning performance of the GNSS/INS integration in complex and harsh urban environments. The average position RMSE of the FGO GNSS/INS TCI are 0.82 m, 1.32 m, and 0.94 m with an improvement of 30.57%, 15.84%, and 8.68% in the north, east, and vertical directions, respectively, compared with those of the EKF GNSS/INS TCI. The average position RMSE of the LEO-enhanced FGO GNSS/INS TCI are 0.63 m, 1.21 m, and 0.85 m with an improvement of 41.91%, 13.66%, and 2.52% in the north, east, and vertical directions, respectively, compared with those of the LEO-enhanced EKF GNSS/INS TCI; (2) LEO can improve satellite geometry and provide more observation data. In the case of GNSS anomalies, LEO effectively improves the positioning performance of GNSS/INS TCI. For the EKF GNSS/INS TCI, the average enhancement effect of LEO is 7.76%, 10.42%, and 15.87% in the north, east, and vertical directions, respectively. Meanwhile, for the FGO GNSS/INS TCI, the average enhancement effect of LEO is 22.16%, 7.58%, and 10.13% in the north, east, and vertical directions, respectively.
The LEO-enhanced FGO GNSS/INS TCI significantly improves positioning accuracy and convergence performance in complex and harsh urban environments. This method is highly significant for dynamic positioning demand systems, as it effectively copes with the challenges of positioning in complex urban environments and achieves significant performance improvement. The next step is to conduct LEO-enhanced FGO GNSS/INS positioning performance experiments under various complex scenarios. Additionally, observation data such as vision and 5G can be included to enable richer multi-source FGO combination algorithms. This is highly significant in the field of high-precision positioning, including autonomous driving, unmanned aerial vehicles, and intelligent transportation.
Author Contributions
Conceptualization, S.Z., R.T. and Z.G.; methodology, S.Z., R.T. and Z.G.; software, S.Z., R.T. and Z.G.; investigation, S.Z. and R.T.; data curation, S.Z., R.T. and Z.G.; writing—original draft preparation, S.Z.; writing—review and editing, S.Z., R.T., D.Z., S.W. and X.L.; visualization, S.Z.; funding acquisition, R.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the program of the National Natural Science Foundation of China (Grant Nos. 41974032 and 42274019), Rui Tu.
Data Availability Statement
The data generated or analyzed during this study are available from the corresponding author on reasonable request. The data are not publicly available due to privacy reason.
Acknowledgments
The authors would like to thank the anonymous reviewers who gave valuable suggestions that helped to improve the quality of the manuscript.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Elamin, A.; Abdelaziz, N.; El-Rabbany, A. A GNSS/INS/LiDAR Integration Scheme for UAV-Based Navigation in GNSS-Challenging Environments. Sensors 2022, 22, 9908. [Google Scholar] [CrossRef] [PubMed]
- Eling, C.; Klingbeil, L.; Kuhlmann, H. Real-time single-frequency GPS/MEMS-IMU attitude determination of lightweight UAVs. Sensors 2015, 15, 26212–26235. [Google Scholar] [CrossRef] [PubMed]
- Gao, Z.; Zhang, H.; Ge, M.; Niu, X.; Shen, W.; Wickert, J.; Schuh, H. Tightly coupled integration of ionosphere-constrained precise point positioning and inertial navigation systems. Sensors 2015, 15, 5783–5802. [Google Scholar] [CrossRef] [PubMed]
- Hsu, L.-T.; Huang, F.; Ng, H.-F.; Zhang, G.; Zhong, Y.; Bai, X.; Wen, W. Hong Kong UrbanNav: An Open-Source Multisensory Dataset for Benchmarking Urban Navigation Algorithms. NAVIGATION J. Inst. Navig. 2023, 70, navi.602. [Google Scholar] [CrossRef]
- Han, H.; Xu, T.; Wang, J. Tightly Coupled Integration of GPS Ambiguity Fixed Precise Point Positioning and MEMS-INS through a Troposphere-Constrained Adaptive Kalman Filter. Sensors 2016, 16, 1057. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Zhang, X.; Niu, X.; Wang, J.; Pei, L.; Yu, F.; Zhang, H.; Yang, C.; Gao, Z.; Zhang, Q.; et al. Progress and Achievements of Multi-sensor Fusion Navigation in China during 2019–2023. J. Geod. Geoinf. Sci. 2023, 6, 102–114. [Google Scholar]
- Li, S.; Wang, S.; Zhou, Y.; Shen, Z.; Li, X. Tightly Coupled Integration of GNSS, INS, and LiDAR for Vehicle Navigation in Urban Environments. IEEE Internet Things J. 2022, 9, 24721–24735. [Google Scholar] [CrossRef]
- Ibrahim, A.; Abosekeen, A.; Azouz, A.; Noureldin, A. Enhanced Autonomous Vehicle Positioning Using a Loosely Coupled INS/GNSS-Based Invariant-EKF Integration. Sensors 2023, 23, 6097. [Google Scholar] [CrossRef] [PubMed]
- Chiang, K.W.; Duong, T.T.; Liao, J.K. The performance analysis of a real-time integrated INS/GPS vehicle navigation system with abnormal GPS measurement elimination. Sensors 2013, 13, 10599–10622. [Google Scholar] [CrossRef] [PubMed]
- Liu, D.; Wang, H.; Xia, Q.; Jiang, C. A Low-Cost Method of Improving the GNSS/SINS Integrated Navigation System Using Multiple Receivers. Electronics 2020, 9, 1079. [Google Scholar] [CrossRef]
- Zhao, L.; Blunt, P.; Yang, L.; Ince, S. Performance Analysis of Real-Time GPS/Galileo Precise Point Positioning Integrated with Inertial Navigation System. Sensors 2023, 23, 2396. [Google Scholar] [CrossRef] [PubMed]
- Yao, Y.; Xu, X.; Zhu, C.; Chan, C.-Y. A hybrid fusion algorithm for GPS/INS integration during GPS outages. Measurement 2017, 103, 42–51. [Google Scholar] [CrossRef]
- Abd Rabbou, M.; El-Rabbany, A. Tightly coupled integration of GPS precise point positioning and MEMS-based inertial systems. GPS Solut. 2014, 19, 601–609. [Google Scholar] [CrossRef]
- Zhang, X.; Zhu, F.; Tao, X.; Duan, R. New optimal smoothing scheme for improving relative and absolute accuracy of tightly coupled GNSS/SINS integration. GPS Solut. 2017, 21, 861–872. [Google Scholar] [CrossRef]
- Godha, S.; Cannon, M.E. GPS/MEMS INS integrated system for navigation in urban areas. GPS Solut. 2007, 11, 193–203. [Google Scholar] [CrossRef]
- Roesler, G.; Martell, H. Tightly Coupled Processing of Precise Point Position (PPP) and INS Data. In Proceedings of the Institute of Navigation, Savannah, GA, USA, 22–25 September 2009. [Google Scholar]
- Lai, L.; Meng, X.; Zhao, D.; Li, X.; Guo, W.; Li, L. PPP/INS Tight Integration with BDS-3 PPP-B2b Service in the Urban Environment. Sensors 2023, 23, 2652. [Google Scholar] [CrossRef] [PubMed]
- Gao, Z.; Zhang, H.; Ge, M.; Niu, X.; Shen, W.; Wickert, J.; Schuh, H. Tightly coupled integration of multi-GNSS PPP and MEMS inertial measurement unit data. GPS Solut. 2016, 21, 377–391. [Google Scholar] [CrossRef]
- Wen, W.; Pfeifer, T.; Bai, X.; Hsu, L.T. Factor graph optimization for GNSS/INS integration: A comparison with the extended Kalman filter. Navigation 2021, 68, 315–331. [Google Scholar] [CrossRef]
- Han, H.; Wang, J.; Du, M. GPS/BDS/INS tightly coupled integration accuracy improvement using an improved adaptive interacting multiple model with classified measurement update. Chin. J. Aeronaut. 2018, 31, 556–566. [Google Scholar] [CrossRef]
- Prol, F.S.; Ferre, R.M.; Saleem, Z.; Valisuo, P.; Pinell, C.; Lohan, E.S.; Elsanhoury, M.; Elmusrati, M.; Islam, S.; Celikbilek, K.; et al. Position, Navigation, and Timing (PNT) Through Low Earth Orbit (LEO) Satellites: A Survey on Current Status, Challenges, and Opportunities. IEEE Access 2022, 10, 83971–84002. [Google Scholar] [CrossRef]
- Ge, H.; Li, B.; Jia, S.; Nie, L.; Wu, T.; Yang, Z.; Shang, J.; Zheng, Y.; Ge, M. LEO Enhanced Global Navigation Satellite System (LeGNSS): Progress, opportunities, and challenges. Geo-Spat. Inf. Sci. 2021, 25, 1–13. [Google Scholar] [CrossRef]
- Zheng, Y.; Ge, H.; Li, B. The convergence mechanism of Low Earth Orbit enhanced GNSS (LeGNSS) Precise Point Positioning (PPP). Geo-Spat. Inf. Sci. 2023, 1–16. [Google Scholar] [CrossRef]
- Shi, Y.; Xu, T.; Li, M.; Wei, K.; Wang, S.; Wang, D. Real-Time Precise Orbit Determination of Low Earth Orbit Satellites Based on GPS and BDS-3 PPP B2b Service. Remote Sens. 2024, 16, 833. [Google Scholar] [CrossRef]
- Ge, H.; Li, B.; Ge, M.; Zang, N.; Nie, L.; Shen, Y.; Schuh, H. Initial Assessment of Precise Point Positioning with LEO Enhanced Global Navigation Satellite Systems (LeGNSS). Remote Sens. 2018, 10, 984. [Google Scholar] [CrossRef]
- Li, X.; Li, X.; Ma, F.; Yuan, Y.; Zhang, K.; Zhou, F.; Zhang, X. Improved PPP Ambiguity Resolution with the Assistance of Multiple LEO Constellations and Signals. Remote Sens. 2019, 11, 408. [Google Scholar] [CrossRef]
- Ke, M.; Lv, J.; Chang, J.; Dai, W.; Zhu, M. Integrating GPS and LEO to accelerate convergence time of precise point positioning. In Proceedings of the 2015 International Conference on Wireless Communications & Signal Processing (WCSP), Nanjing, China, 15–17 October 2015; pp. 1–5. [Google Scholar]
- Zhao, Q.; Pan, S.; Gao, C.; Gao, W.; Xia, Y. BDS/GPS/LEO triple-frequency uncombined precise point positioning and its performance in harsh environments. Measurement 2020, 151, 107216. [Google Scholar] [CrossRef]
- Liu, J.; Hao, J.; Yang, Y.; Xu, Z.; Liu, W.; Wu, R. Design optimisation of low earth orbit constellation based on BeiDou Satellite Navigation System precise point positioning. IET Radar Sonar Navig. 2022, 16, 1241–1252. [Google Scholar] [CrossRef]
- Teng, Y.; Jia, X.; Peng, G. LEO navigation augmentation constellation design and precise point positioning performance analysis based on BDS-3. Adv. Space Res. 2023, 72, 1944–1960. [Google Scholar] [CrossRef]
- Zhang, S.; Tu, R.; Gao, Z.; Zhang, P.; Wang, S.; Lu, X. Low-Earth-Orbit Satellites and Robust Theory-Augmented GPS/Inertial-Navigation-System Tight Integration for Vehicle-Borne Positioning. Electronics 2024, 13, 508. [Google Scholar] [CrossRef]
- Xu, S.; Yang, Q.; Du, X.; Xu, X.; Zhao, Q.; Yang, L.; Qin, Y.; Guo, J. Multi-GNSS Precise Point Positioning enhanced by the real navigation signals from CENTISPACETM LEO mission. Adv. Space Res. 2024, 73, 4175–4186. [Google Scholar] [CrossRef]
- Watson, R.M.; Gross, J.N. Evaluation of Kinematic Precise Point Positioning Convergence with an Incremental Graph Optimizer. In Proceedings of the IEEE/ION Position, Location and Navigation Symposium (PLANS), Monterey, CA, USA, 23–26 April 2018; pp. 589–596. [Google Scholar]
- Li, W.; Cui, X.; Lu, M. A Robust Graph Optimization Realization of Tightly Coupled GNSS/INS Integrated Navigation System for Urban Vehicles. Tsinghua Sci. Technol. 2018, 23, 724–732. [Google Scholar] [CrossRef]
- Wen, W.; Bai, X.; Kan, Y.C.; Hsu, L.-T. Tightly Coupled GNSS/INS Integration via Factor Graph and Aided by Fish-Eye Camera. IEEE Trans. Veh. Technol. 2019, 68, 10651–10662. [Google Scholar] [CrossRef]
- Chang, L.; Niu, X.; Liu, T. GNSS/IMU/ODO/LiDAR-SLAM Integrated Navigation System Using IMU/ODO Pre-Integration. Sensors 2020, 20, 4702. [Google Scholar] [CrossRef] [PubMed]
- Tang, H.; Niu, X.; Zhang, T.; Fan, J.; Liu, J. Exploring the Accuracy Potential of IMU Preintegration in Factor Graph Optimization. arXiv 2021, arXiv:2109.03010v2. [Google Scholar]
- Wen, W.; Hsu, L.T. Towards Robust GNSS Positioning and Real-time Kinematic Using Factor Graph Optimization. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 5884–5890. [Google Scholar]
- Engel, J.; Koltun, V.; Cremers, D. Direct Sparse Odometry. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 611–625. [Google Scholar] [CrossRef] [PubMed]
- Barfoot, T.D. State Estimation for Robotics; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar]
- Li, X.; Ma, F.; Li, X.; Lv, H.; Bian, L.; Jiang, Z.; Zhang, X. LEO constellation-augmented multi-GNSS for rapid PPP convergence. J. Geod. 2018, 93, 749–764. [Google Scholar] [CrossRef]
- Hong, J.; Tu, R.; Zhang, P.; Zhang, R.; Han, J.; Fan, L.; Wang, S.; Lu, X. GNSS rapid precise point positioning enhanced by low Earth orbit satellites. Satell. Navig. 2023, 4, 11. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).