InSAR-DEM Block Adjustment Model for Upcoming BIOMASS Mission: Considering Atmospheric Effects
Abstract
1. Introduction
2. Methodology
2.1. InSAR-DEM Block Adjustment Based on Function Model
2.2. Atmospheric Effects Correction Based on Correlation Analysis
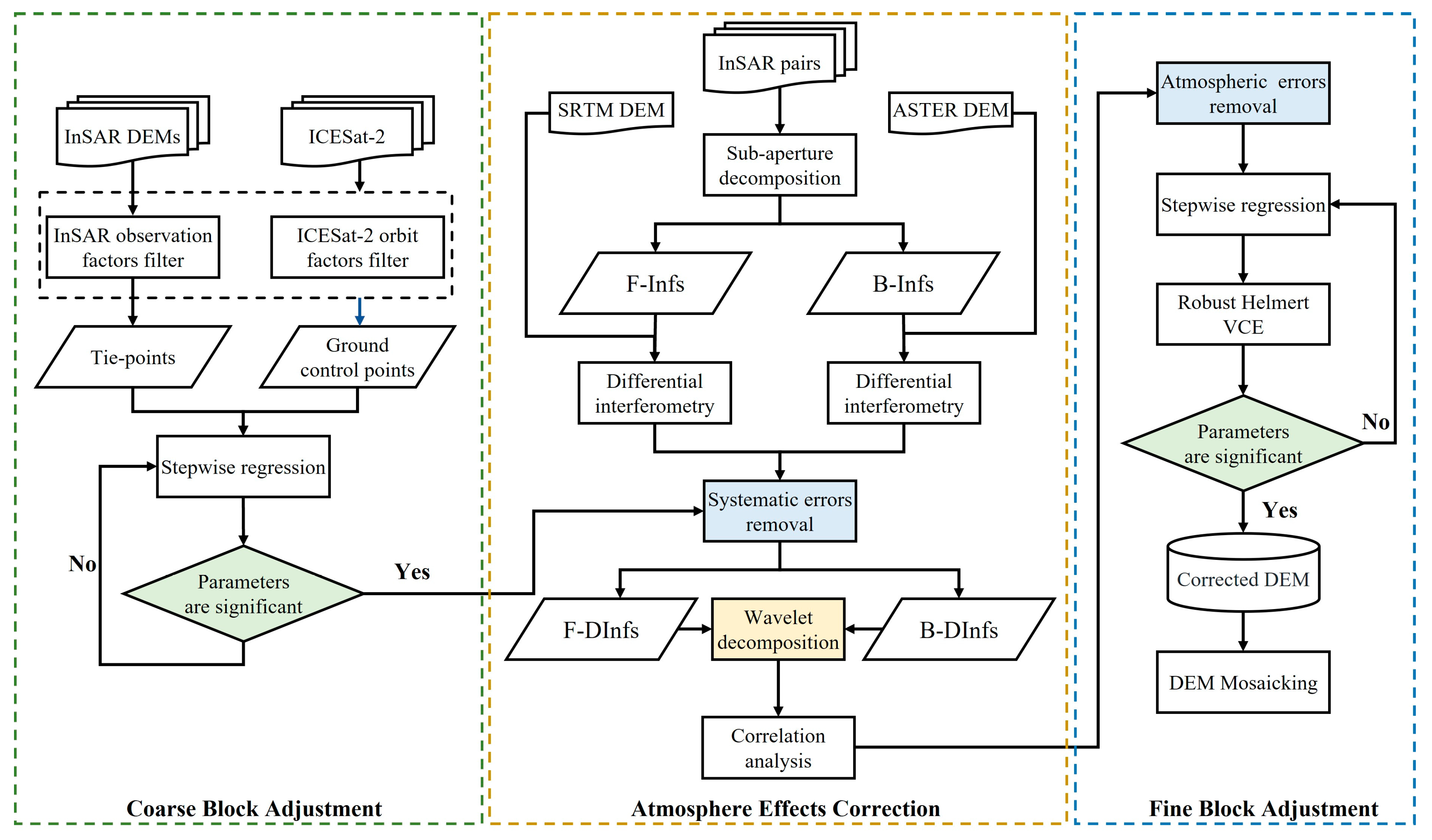
2.3. InSAR-DEM Block Adjustment Model Considering Atmospheric Effects
- (1)
- Coarse Block Adjustment
- (2)
- Atmosphere Effects Correction
- (3)
- Fine Block Adjustment
3. Test Sites and Data Sets
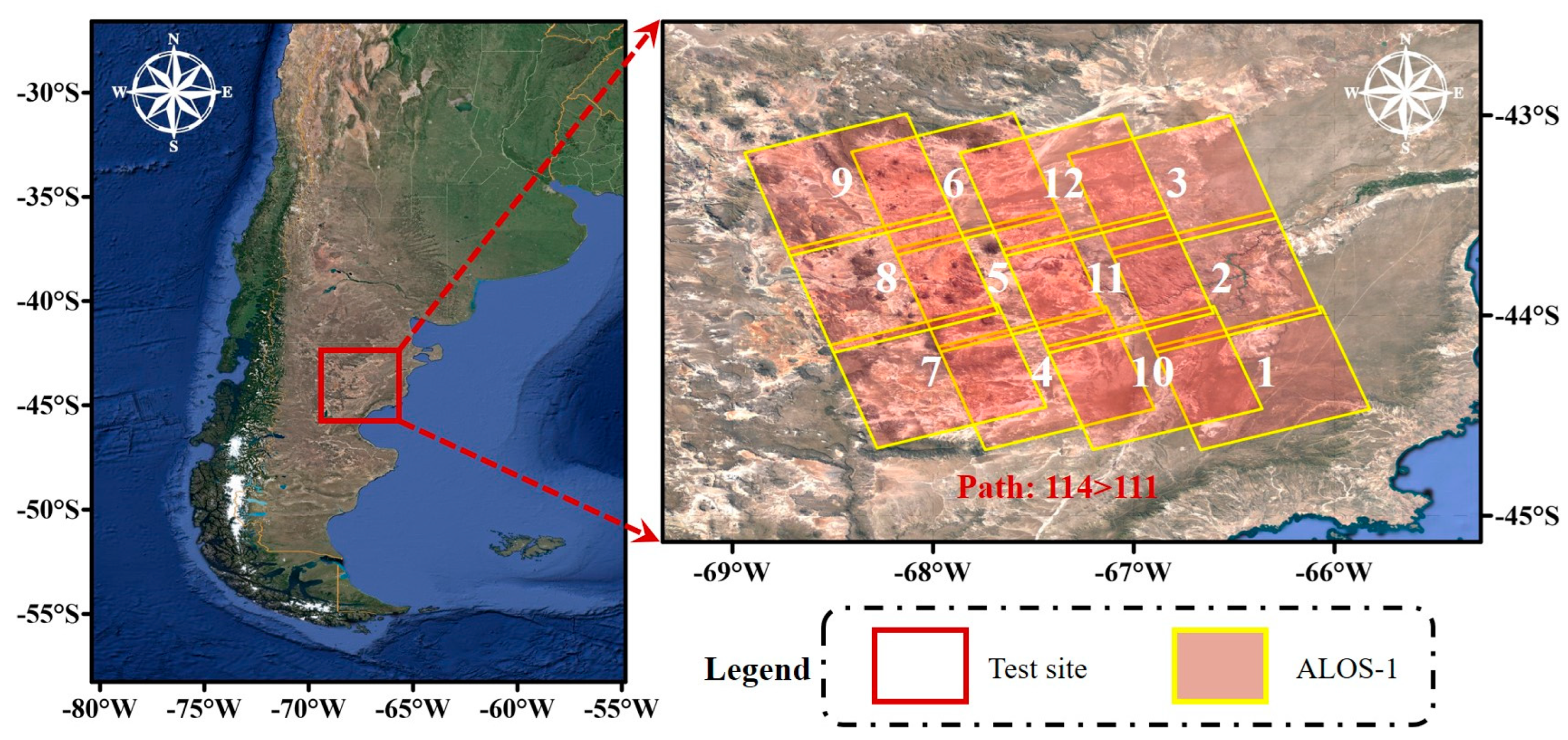
3.1. Test Sites
3.1.1. Inland Test Site
3.1.2. Coastal Test Site
3.2. Data Sets
3.2.1. ALOS-1 PALSAR
3.2.2. ICESat-2 ATL08 Product (Version 5)
3.2.3. Global Digital Elevation Products
4. Results and Analysis
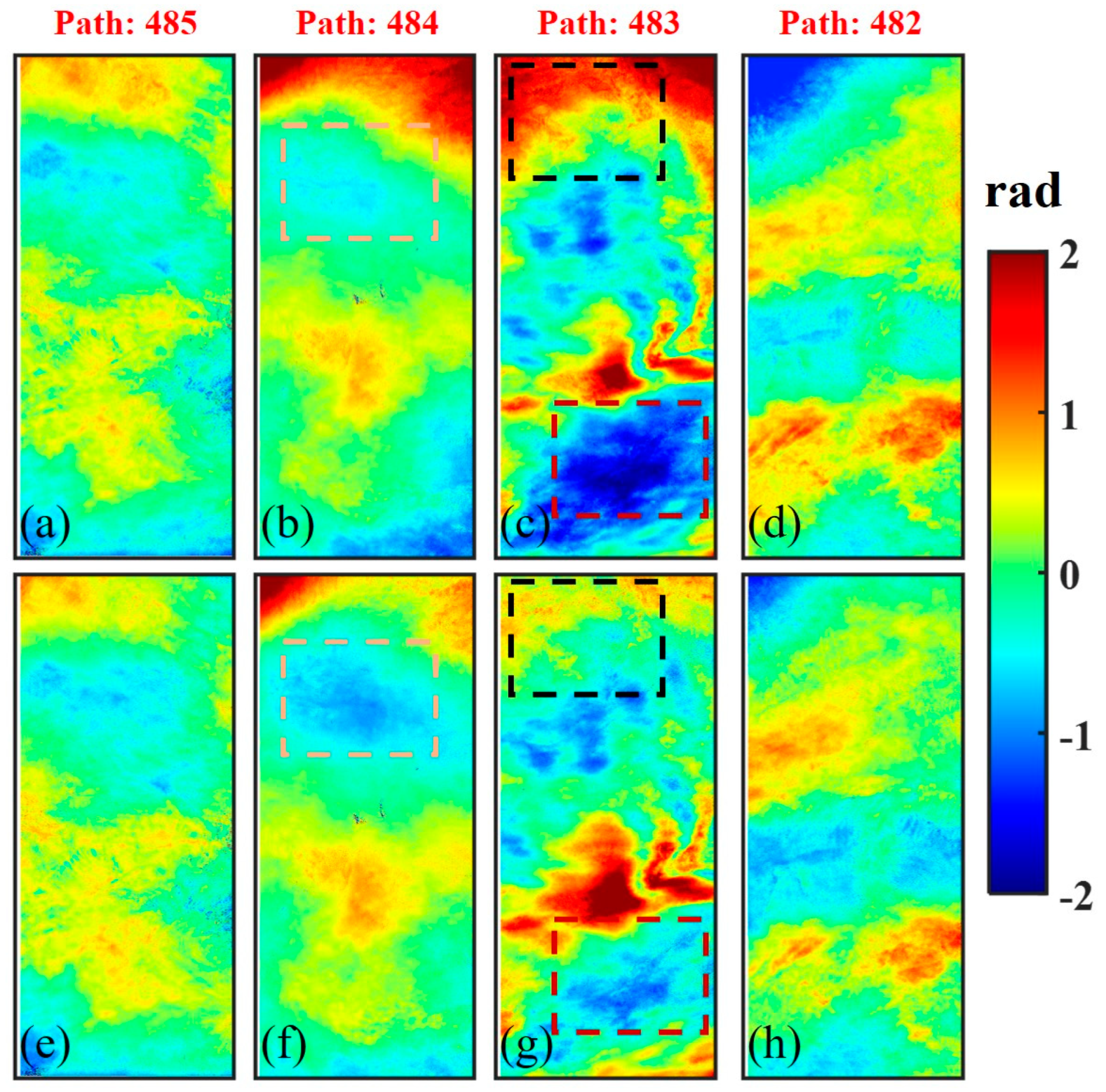
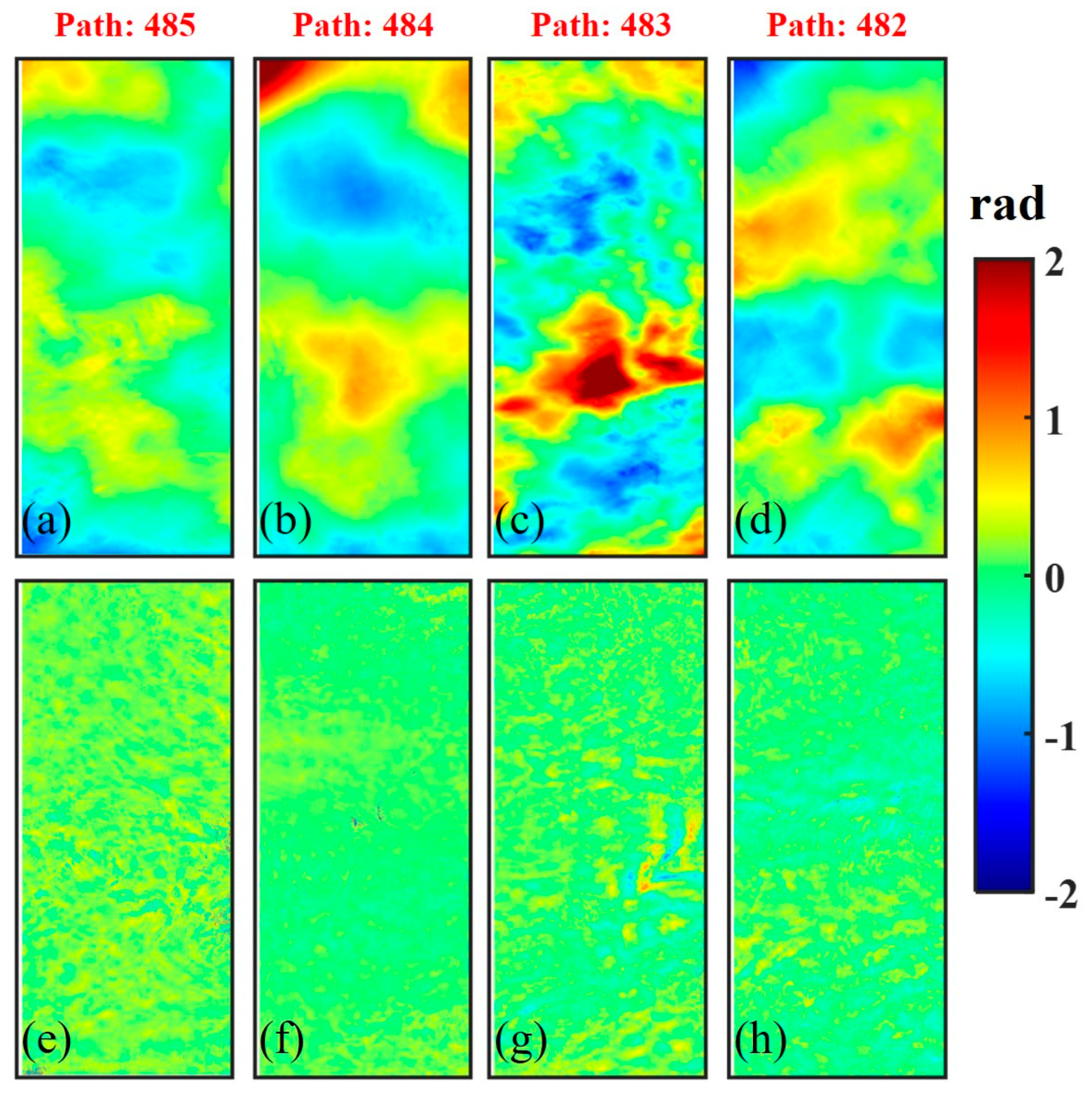
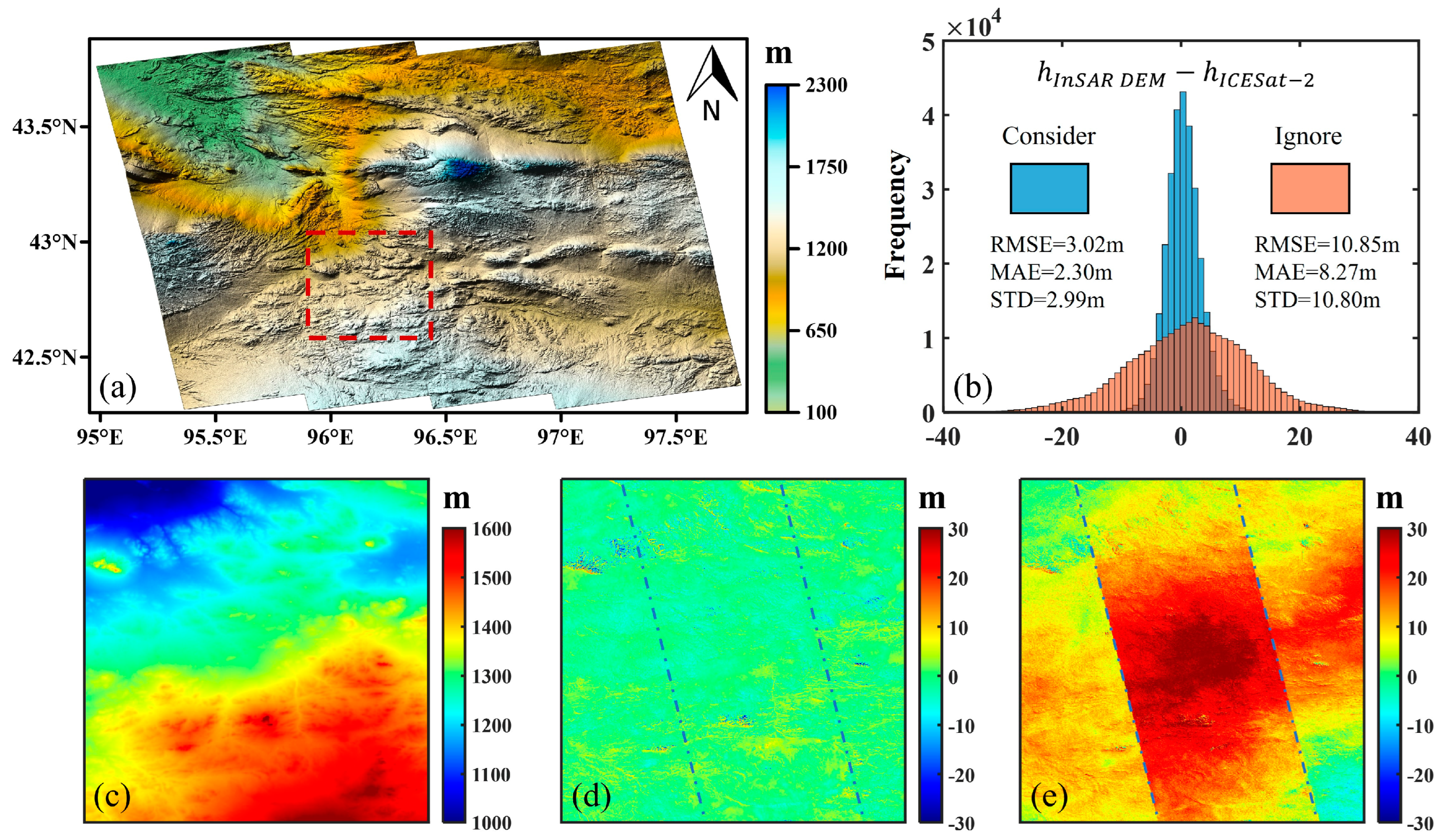
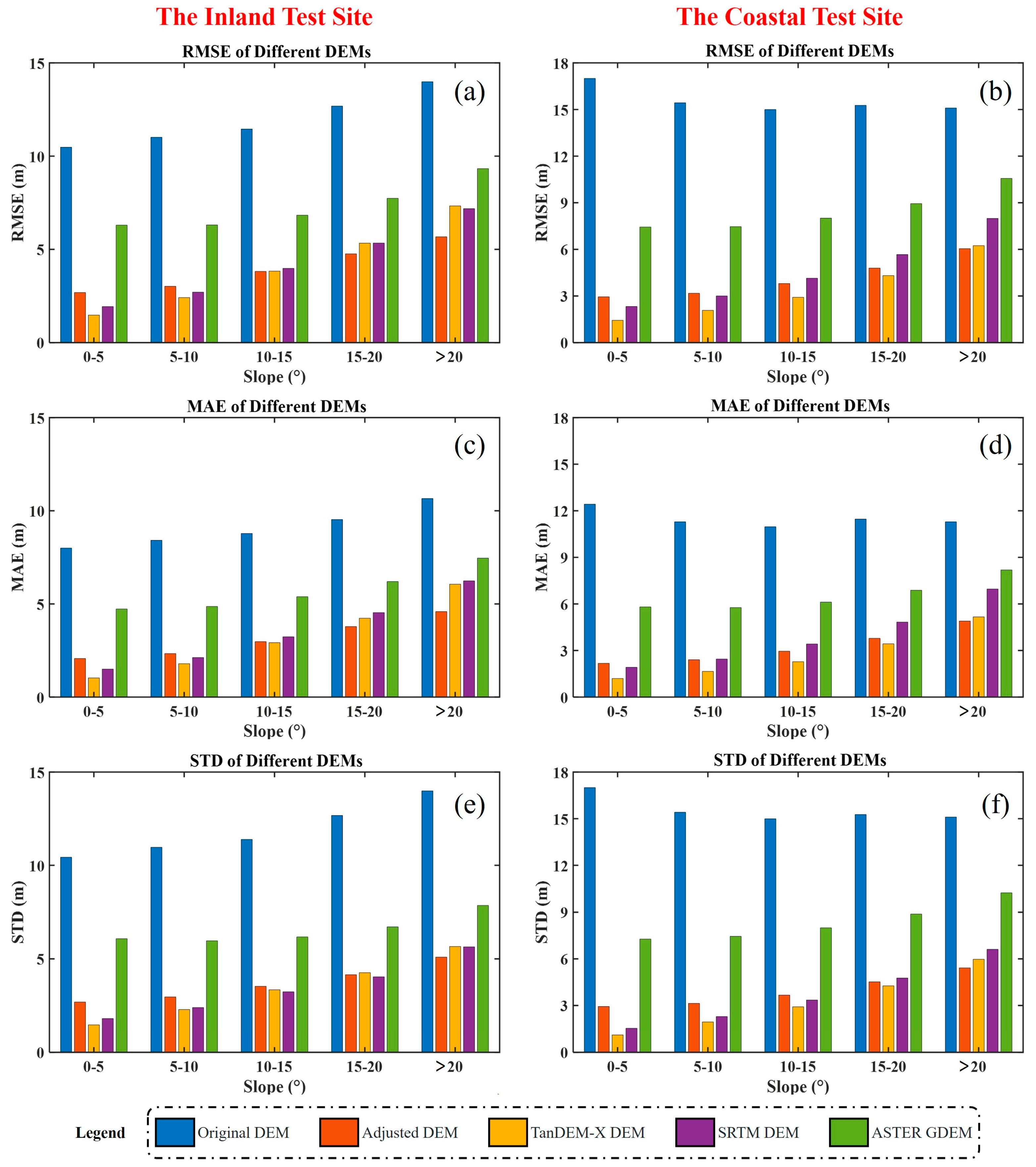
4.1. Inland Test Site
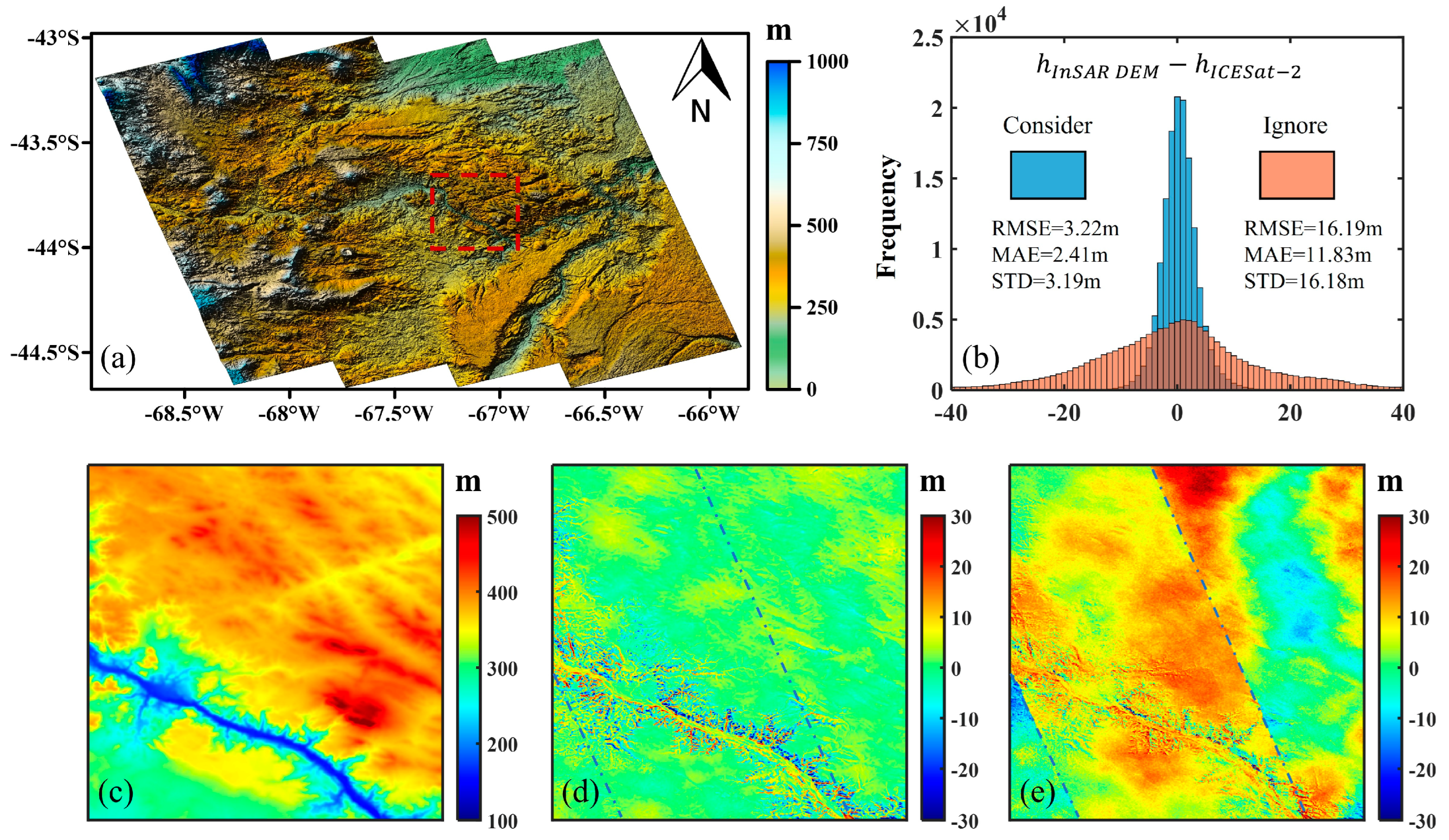
4.2. Coastal Test Site
5. Discussion
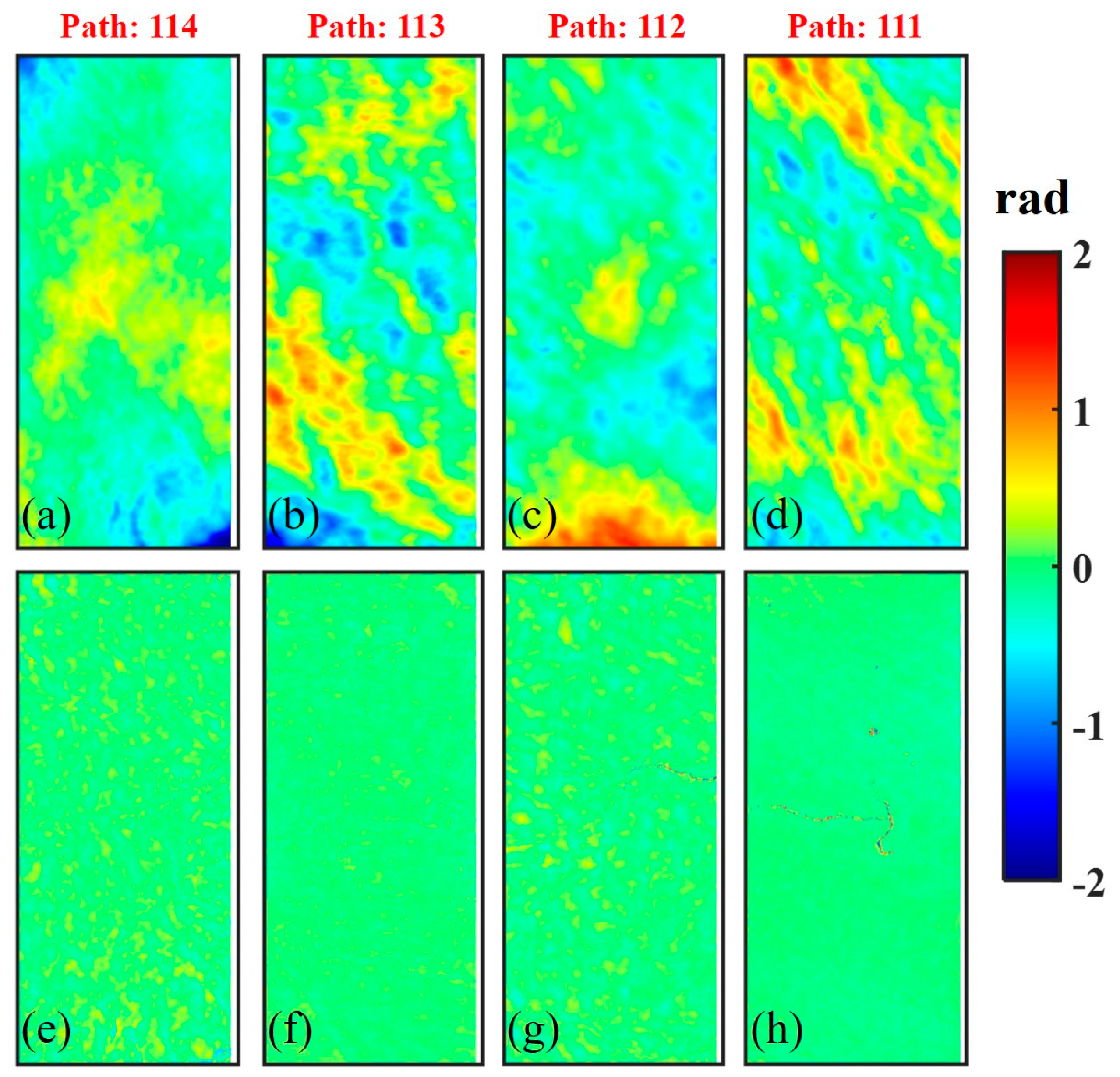
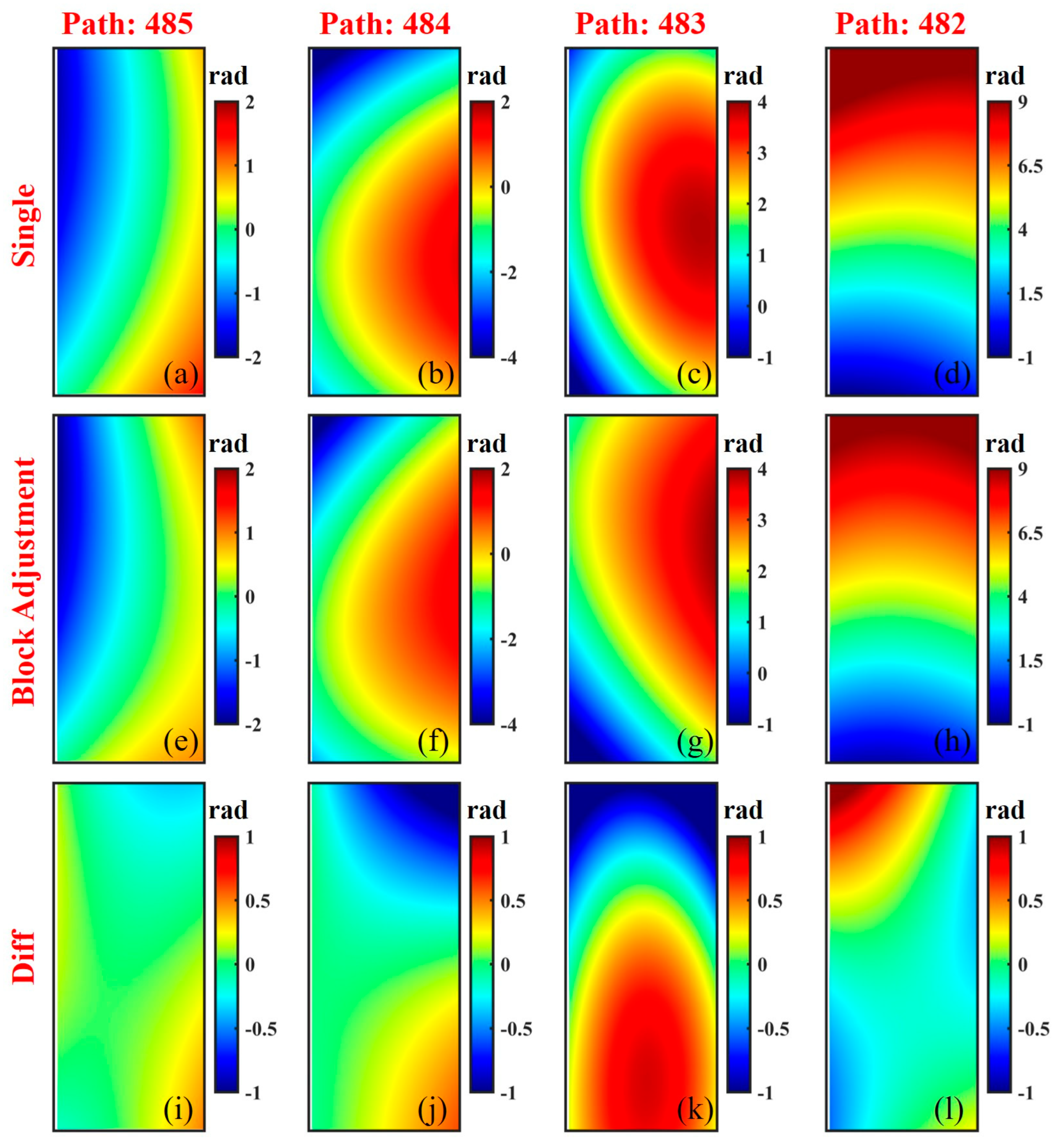
5.1. The Impact of Atmospheric Effects on the Estimation of Block Adjustment
- (1)
- Height matching between InSAR-DEM and GCPs, as well as between TPs
- (2)
- The long-wavelength signals of atmospheric effects are mixed with systematic errors
5.2. The Impact of Slope on DEM Calibration
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rizzoli, P.; Martone, M.; Gonzalez, C.; Wecklich, C.; Borla Tridon, D.; Bräutigam, B.; Bachmann, M.; Schulze, D.; Fritz, T.; Huber, M.; et al. Generation and Performance Assessment of the Global TanDEM-X Digital Elevation Model. ISPRS J. Photogramm. Remote Sens. 2017, 132, 119–139. [Google Scholar] [CrossRef]
- Rodriguez, E.; Morris, C.; Belz, J.; Chapin, E.; Martin, J.; Daffer, W.; Hensley, S. An Assessment of the SRTM Topographic Products. 2005. Available online: https://www.researchgate.net/publication/235704654_An_assessment_of_the_SRTM_topographic_products_Technical_Report_JPL_D-31639 (accessed on 12 May 2024).
- Le Toan, T.; Quegan, S.; Davidson, M.W.J.; Balzter, H.; Paillou, P.; Papathanassiou, K.; Plummer, S.; Rocca, F.; Saatchi, S.; Shugart, H.; et al. The BIOMASS Mission: Mapping Global Forest Biomass to Better Understand the Terrestrial Carbon Cycle. Remote Sens. Environ. 2011, 115, 2850–2860. [Google Scholar] [CrossRef]
- Fatoyinbo, T.; Armston, J.; Simard, M.; Saatchi, S.; Denbina, M.; Lavalle, M.; Hofton, M.; Tang, H.; Marselis, S.; Pinto, N.; et al. The NASA AfriSAR Campaign: Airborne SAR and Lidar Measurements of Tropical Forest Structure and Biomass in Support of Current and Future Space Missions. Remote Sens. Environ. 2021, 264, 112533. [Google Scholar] [CrossRef]
- Quegan, S.; Chave, J.; Dall, J.; Le Toan, T.; Papathanassiou, K.; Rocca, F.; Saatchi, S.; Scipal, K.; Shugart, H.; Ulander, L.; et al. The Science and Measurement Concepts Underlying the BIOMASS Mission. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 5542–5545. [Google Scholar]
- Banda, F.; Giudici, D.; Le Toan, T.; d’Alessandro, M.M.; Papathanassiou, K.; Quegan, S.; Riembauer, G.; Scipal, K.; Soja, M.; Tebaldini, S.; et al. The BIOMASS Level 2 Prototype Processor: Design and Experimental Results of Above-Ground Biomass Estimation. Remote Sens. 2020, 12, 985. [Google Scholar] [CrossRef]
- Quegan, S.; Lomas, M.; Papathanassiou, K.P.; Kim, J.-S.; Tebaldini, S.; Giudici, D.; Scagliola, M.; Guccione, P.; Dall, J.; Dubois-Fenandez, P.; et al. Calibration Challenges for the Biomass P-Band SAR Instrument. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 8575–8578. [Google Scholar]
- Ferretti, A.; Prati, C.; Rocca, F. Permanent Scatterers in SAR Interferometry. IEEE Trans. Geosci. Remote Sens. 2001, 39, 8–20. [Google Scholar] [CrossRef]
- Wessel, B.; Gruber, A.; Huber, M.; Roth, A. TanDEM-X: Block Adjustment of Interferometric Height Models. In Proceedings of the ISPRS Hannover Workshop 2009 “High-Resolution Earth Imaging for Geospatioal Information”, International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Hannover, Germany, 2–5 June 2009; pp. 1–6. Available online: https://elib.dlr.de/62358/ (accessed on 12 May 2024).
- Wessel, B.; Gruber, A.; Gonzalez, J.H.; Bachmann, M.; Wendleder, A. TanDEM-X: DEM Calibration Concept. In Proceedings of the IGARSS 2008—2008 IEEE International Geoscience and Remote Sensing Symposium, Boston, MA, USA, 7–11 July 2008; Volume 3, pp. III-111–III-114. [Google Scholar]
- Gruber, A.; Wessel, B.; Huber, M.; Roth, A. Operational TanDEM-X DEM Calibration and First Validation Results. ISPRS J. Photogramm. Remote Sens. 2012, 73, 39–49. [Google Scholar] [CrossRef]
- Schutz, B.E.; Zwally, H.J.; Shuman, C.A.; Hancock, D.; DiMarzio, J.P. Overview of the ICESat Mission. Geophys. Res. Lett. 2005, 32, 2005GL024009. [Google Scholar] [CrossRef]
- Markus, T.; Neumann, T.; Martino, A.; Abdalati, W.; Brunt, K.; Csatho, B.; Farrell, S.; Fricker, H.; Gardner, A.; Harding, D.; et al. The Ice, Cloud, and Land Elevation Satellite-2 (ICESat-2): Science Requirements, Concept, and Implementation. Remote Sens. Environ. 2017, 190, 260–273. [Google Scholar] [CrossRef]
- Huber, M.; Wessel, B.; Kosmann, D.; Felbier, A.; Schwieger, V.; Habermeyer, M.; Wendleder, A.; Roth, A. Ensuring Globally the TanDEM-X Height Accuracy: Analysis of the Reference Data Sets ICESat, SRTM and KGPS-Tracks. In Proceedings of the 2009 IEEE International Geoscience and Remote Sensing Symposium, Cape Town, South Africa, 12–17 July 2009; IEEE: Piscataway, NJ, USA, 2009; pp. II-769–II-772. [Google Scholar]
- Hueso Gonzalez, J.; Bachmann, M.; Scheiber, R.; Krieger, G. Definition of ICESat Selection Criteria for Their Use as Height References for TanDEM-X. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2750–2757. [Google Scholar] [CrossRef]
- Wang, R.; Lv, X.; Zhang, L. A Novel Three-Dimensional Block Adjustment Method for Spaceborne InSAR-DEM Based on General Models. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 3973–3987. [Google Scholar] [CrossRef]
- Wang, R.; Lv, X.; Chai, H.; Zhang, L. A Three-Dimensional Block Adjustment Method for Spaceborne InSAR Based on the Range-Doppler-Phase Model. Remote Sens. 2023, 15, 1046. [Google Scholar] [CrossRef]
- Huber, S.; de Almeida, F.Q.; Villano, M.; Younis, M.; Krieger, G.; Moreira, A. Tandem-L: A Technical Perspective on Future Spaceborne SAR Sensors for Earth Observation. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4792–4807. [Google Scholar] [CrossRef]
- Xiao, R.; Yu, C.; Li, Z.; He, X. Statistical Assessment Metrics for InSAR Atmospheric Correction: Applications to Generic Atmospheric Correction Online Service for InSAR (GACOS) in Eastern China. Int. J. Appl. Earth Obs. Geoinf. 2021, 96, 102289. [Google Scholar] [CrossRef]
- Dou, F.; Lv, X.; Chai, H. Mitigating Atmospheric Effects in InSAR Stacking Based on Ensemble Forecasting with a Numerical Weather Prediction Model. Remote Sens. 2021, 13, 4670. [Google Scholar] [CrossRef]
- Jung, H.-S.; Won, J.-S.; Kim, S.-W. An Improvement of the Performance of Multiple-Aperture SAR Interferometry (MAI). IEEE Trans. Geosci. Remote Sens. 2009, 47, 2859–2869. [Google Scholar] [CrossRef]
- Yang, Y.; Xu, T.; Song, L. Robust Estimation of Variance Components with Application in Global Positioning System Network Adjustment. J. Surv. Eng. 2005, 131, 107–112. [Google Scholar] [CrossRef]
- Gonzalez, J.H.; Bachmann, M.; Krieger, G.; Fiedler, H. Development of the TanDEM-X Calibration Concept: Analysis of Systematic Errors. IEEE Trans. Geosci. Remote Sens. 2010, 48, 716–726. [Google Scholar] [CrossRef]
- Liu, Z.; Fu, H.; Zhu, J.; Zhou, C.; Zuo, T. Using Dual-Polarization Interferograms to Correct Atmospheric Effects for InSAR Topographic Mapping. Remote Sens. 2018, 10, 1310. [Google Scholar] [CrossRef]
- Fu, H.Q.; Zhu, J.J.; Wang, C.C.; Zhao, R.; Xie, Q.H. Atmospheric Effect Correction for InSAR With Wavelet Decomposition-Based Correlation Analysis Between Multipolarization Interferograms. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5614–5625. [Google Scholar] [CrossRef]
- Hanssen, R.F. Radar Interferometry: Data Interpretation and Error Analysis; Kluwer: Norwell, MA, USA, 2001. [Google Scholar]
- Abrams, M.; Crippen, R.; Fujisada, H. ASTER Global Digital Elevation Model (GDEM) and ASTER Global Water Body Dataset (ASTWBD). Remote Sens. 2020, 12, 1156. [Google Scholar] [CrossRef]
- Shirzaei, M.; Walter, T.R. Estimating the Effect of Satellite Orbital Error Using Wavelet-Based Robust Regression Applied to InSAR Deformation Data. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4600–4605. [Google Scholar] [CrossRef]
- Liao, H.; Meyer, F.J.; Scheuchl, B.; Mouginot, J.; Joughin, I.; Rignot, E. Ionospheric Correction of InSAR Data for Accurate Ice Velocity Measurement at Polar Regions. Remote Sens. Environ. 2018, 209, 166–180. [Google Scholar] [CrossRef]
- Rosenqvist, A.; Shimada, M.; Ito, N.; Watanabe, M. ALOS PALSAR: A Pathfinder Mission for Global-Scale Monitoring of the Environment. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3307–3316. [Google Scholar] [CrossRef]
- Li, Y.; Fu, H.; Zhu, J.; Wu, K.; Yang, P.; Wang, L.; Gao, S. A Method for SRTM DEM Elevation Error Correction in Forested Areas Using ICESat-2 Data and Vegetation Classification Data. Remote Sens. 2022, 14, 3380. [Google Scholar] [CrossRef]
- Neuenschwander, A.; Guenther, E.; White, J.C.; Duncanson, L.; Montesano, P. Validation of ICESat-2 Terrain and Canopy Heights in Boreal Forests. Remote Sens. Environ. 2020, 251, 112110. [Google Scholar] [CrossRef]



| Data Sources | Chip Grid | Selection Criteria | |
|---|---|---|---|
| GCPs | ICESat-2 ATL08 Version 5 | 5 km × 5 km | 1. Strong beam 2. Cloud cover less than 20% 3. Not located in the geometric distortion area of SAR images 4. InSAR coherence greater than 0.5 |
| TPs | InSAR DEMs | 3 km × 3 km | 1. Slope less than 30° 2. Not located in the geometric distortion area of SAR images 3. InSAR coherence greater than 0.5 |
| Test Sites | Time | Number * | Path * | (m) | Pixel Spacing (m) | Orbit | |
|---|---|---|---|---|---|---|---|
| Inland | 25 July 2010 | 1–3 | 482 | 557.5 | 92 | 3.16 × 9.37 | ASC |
| 11 August 2010 | 4–6 | 483 | 435.6 | 46 | 3.16 × 9.37 | ASC | |
| 28 August 2010 | 7–9 | 484 | 317.3 | 46 | 3.16 × 9.37 | ASC | |
| 14 September 2010 | 10–12 | 485 | 465.3 | 46 | 3.16 × 9.37 | ASC | |
| Coastal | 4 June 2010 | 1–3 | 111 | 131.4 | 46 | 3.26 × 9.37 | ASC |
| 8 July 2010 | 4–6 | 113 | 160.9 | 46 | 3.26 × 9.37 | ASC | |
| 25 July 2010 | 7–9 | 114 | 537.5 | 46 | 3.26 × 9.37 | ASC | |
| 6 August 2010 | 10–12 | 112 | 489.3 | 46 | 3.26 × 9.37 | ASC |
| Dataset | Horizontal Datum | Vertical Datum | Time (Year) | Resolution (m) | Absolute Vertical Accuracy (m) | Technique |
|---|---|---|---|---|---|---|
| TanDEM-X DEM | WGS84 | WGS84 | 2016 | 30 | 10 | InSAR |
| SRTM DEM V003 | WGS84 | EGM96 | 2013 | 30 | 16 | InSAR |
| ASTER GDEM V2 | WGS84 | EGM96 | 2011 | 30 | 17 | Optical stereophotogrammetry |
| Test Sites | 0~5° | 5~10° | 10~15° | 15~20° | >20° |
|---|---|---|---|---|---|
| Inland | 151,680 | 102,129 | 27,047 | 6448 | 2403 |
| Coastal | 71,292 | 50,441 | 15,840 | 3641 | 1064 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, K.; Fu, H.; Zhu, J.; Hu, H.; Li, Y.; Liu, Z.; Wan, A.; Wang, F. InSAR-DEM Block Adjustment Model for Upcoming BIOMASS Mission: Considering Atmospheric Effects. Remote Sens. 2024, 16, 1764. https://doi.org/10.3390/rs16101764
Wu K, Fu H, Zhu J, Hu H, Li Y, Liu Z, Wan A, Wang F. InSAR-DEM Block Adjustment Model for Upcoming BIOMASS Mission: Considering Atmospheric Effects. Remote Sensing. 2024; 16(10):1764. https://doi.org/10.3390/rs16101764
Chicago/Turabian StyleWu, Kefu, Haiqiang Fu, Jianjun Zhu, Huacan Hu, Yi Li, Zhiwei Liu, Afang Wan, and Feng Wang. 2024. "InSAR-DEM Block Adjustment Model for Upcoming BIOMASS Mission: Considering Atmospheric Effects" Remote Sensing 16, no. 10: 1764. https://doi.org/10.3390/rs16101764
APA StyleWu, K., Fu, H., Zhu, J., Hu, H., Li, Y., Liu, Z., Wan, A., & Wang, F. (2024). InSAR-DEM Block Adjustment Model for Upcoming BIOMASS Mission: Considering Atmospheric Effects. Remote Sensing, 16(10), 1764. https://doi.org/10.3390/rs16101764







