Abstract
Coastal sediment grain size is an important factor in determining coastal morphodynamics. In this study, we explore a novel approach for retrieving the median sediment grain size (D50) of gravel-dominated beaches using Synthetic Aperture Radar (SAR) spaceborne imagery. We assessed this by using thirty-six Sentinel-1 (C-band SAR) satellite images acquired in May and June 2022 and 2023, and three NovaSAR (S-band SAR) satellite images acquired in May and June 2022, for three different training sites and one test site across England (the UK). The results from the Sentinel-1 C-band data show strong positive correlations (R2) between the D50 and the backscatter coefficients for 15/18 of the resultant models. The models were subsequently used to derive predictions of D50 for the test site, with the models which exhibited the strongest correlations resulting in Mean Absolute Errors (MAEs) in the range 2.26–5.47 mm. No correlation (R2 = 0.04) was found between the backscatter coefficients from the S-band NovaSAR data and D50. These results highlight the potential to derive near-real time estimates of coastal sediment grain size for gravel beaches to better inform coastal erosion and monitoring programs.
1. Introduction
Sediment grain size is an important element in understanding coastal dynamics and for effective beach management and protection, as grain size is a crucial factor that determines both beach morphology and shoreline changes [1]. As such, the monitoring of sediment grain size is essential in providing insights into sediment transportation and coastal morphodynamics [2]. Currently, quantifying the size of sediment grains on beaches is primarily performed using conventional in situ surveying methods (e.g., manually counting or sieving sediments), which are expensive and time-consuming, especially when there is a need to survey large or remote regions [1,3]. Additionally, due to the dynamic nature of coastal regions, it may be necessary to carry out frequent surveys, which further increases the associated time and costs. For this reason, in recent years, there has been increased interest in developing the use of remote sensing techniques to monitor coastal environments (e.g., [1,4,5]). Considering that more than 99% of beaches are not monitored, the use of remote sensing could offer significant promise in supporting the monitoring and protection of coastal areas and local communities from the ever increasing threat of sea level rise and changes due to climate change [6].
Previous studies that have used remote sensing techniques to characterise sediment grain size and their properties in inter-tidal areas largely focused on using data derived from the visible range of the electromagnetic spectrum (e.g., [4,7,8,9]). For example, Yu et al. [4] initially found low correlations between the reflectance from multi-temporal Landsat data and grain size, but incorporated the use of a support vector machine (SVM) to find a coarsening trend in grain size, which agreed with the field measurements. However, a major limitation of optical satellite approaches is the requirement for near cloud-free conditions, which can be problematic for monitoring a large proportion of coastal areas across the world. Deronde et al. [8] used HyMap data to classify median grain size classes to an accuracy of 88% based on their reflectance in the visible to near-infrared range. Although the issue of cloud cover can be somewhat overcome through the acquisition of data from an airborne platform (e.g., such as in the case of HyMap), such surveys can be costly.
Satellite Synthetic Aperture Radar (SAR) data have been fundamental for retrieving environmental data for a wide array of geoscience applications. This trend has been underpinned by both the increased availability of free-to-use datasets, such as the Sentinel-1 data provided by the European Space Agency (ESA), and the growing number and capability of commercially-operated SAR satellites. Examples of the extensive range of applications of SAR data include the mapping of crop types (e.g., [10]), monitoring geohazards (e.g., volcano monitoring (e.g, [11]) and landslides mapping (e.g., [12])), and flood mapping (e.g., [13]).
SAR data have also been used to map grain sizes in some sedimentary environments. For instance, Gaber et al. [14] used fully-polarimetric SAR to map and characterise the grain sizes of sediment in desert environments into three main categories: gravel, gravel/sand and sand. Their results showed that a supervised classification based on RADARSAT-2 (C-band) data produced the best overall accuracy of 96.43%. However, despite these promising results, there is a paucity of research on the application of SAR data to characterise sediment specifically in coastal regions. Previous studies which have used SAR data to map coastal sediments focused mostly on studying smaller coastal sediments on intertidal flats. In coastal environments, there are other factors, besides grain size, which may influence the SAR backscatter coefficient. In a study investigating the ability of Sentinel-1 SAR to map intertidal flats in Baie Des Veys (France), Deroin [15] found that dielectric properties (moisture and salinity) influenced the backscatter response. It was found that due to these tidal flats having a high moisture content and a shallow gradient, volume scattering was minimal, and backscatter response was low over most of the intertidal areas [15]. Conversely, whilst tidal level will inevitably alter the moisture content of the beach, a different study found no significant relationship between the tidal level and the backscattering coefficient following a comparison of multiple SAR images [16]. Brakenhoff [17] found that if the beach elevation is greater than 0.5 m above the high tide level, then the water table will be too low to influence the surface sediment moisture. Therefore, the knowledge of the tidal level, at the time in which the SAR imagery was acquired, and the beach elevation is important to negate the impact of moisture from tides. Surface roughness also has a strong influence on radar backscatter, which has been instrumental in mapping intertidal environments [15,18,19,20]. In the Westerschelde estuary (the Netherlands), a strong correlation was found between the D50 and SAR backscatter, which was attributed to the roughness of the flats [18,19]. This was because surface roughness increased with the decreasing mud content, and thus increasing grain size, of the flats [18]. Similarly, the extraction of roughness parameters from sand ripples on intertidal flats in the German Bight, which was then related to ERS C-band SAR imagery, allowed for a crude sediment classification of a small test area [21]. Additionally, the use of backscatter from L-, C- and X-band SAR data to map areas of sediments, macrophytes and mussels, along the coast of the German Wadden Sea, appears to match what is observed from field measurements [20]. Whilst these studies typically focus on the smaller sediments (i.e., sandy/muddy sediments), very few studies have investigated the use of SAR on gravel beaches (gravel is defined as coarser grain sizes of above 2 mm in diameter, in accordance with the Wentworth scale [22]), which are found in many coastal areas. In this regard, a strong positive correlation was found between the D50 on several beaches across Japan and the backscattering coefficient using ALOS L-band SAR data [16], which included beaches with coarser sediments. However, this was included as part of a wider study on shoreline detection and therefore, there was limited investigation into this relationship and its significance. Moreover, most previous studies sought to characterise sediments into broad categories and did not estimate the actual absolute sediment grain size [14]. Accordingly, this study aims to address this by being the first to specifically explore the possibility of directly estimating coastal sediment size on gravel beaches from SAR satellite imagery. The objectives of this study are (i) to compare ground-based measurements of grain size from different coastal sites across the UK (Aldeburgh Beach, Suffolk; Chesil Beach, Dorset; Thorpeness Beach, Suffolk) with satellite SAR backscatter observations to extract potential correlations between these two datasets; (ii) to subsequently use such correlations to predict the D50 over an independent test site (Weybourne Beach, Norfolk).
2. Materials and Methods
2.1. Study Area
In order to assess the ability to estimate sediment grain size using satellite SAR, we selected four locations from three different coastal regions across England (the UK), encompassing a total of 34 km of coastline. These sites are located in Norfolk (location 1 in Figure 1) on the east coast, Suffolk (locations 2 and 3 in Figure 1) also on the east coast and in Dorset (location 4 in Figure 1) on the south coast. Thorpeness Beach, Aldeburgh Beach and Chesil Beach were used as training sites, and Weybourne Beach was used as the testing site.
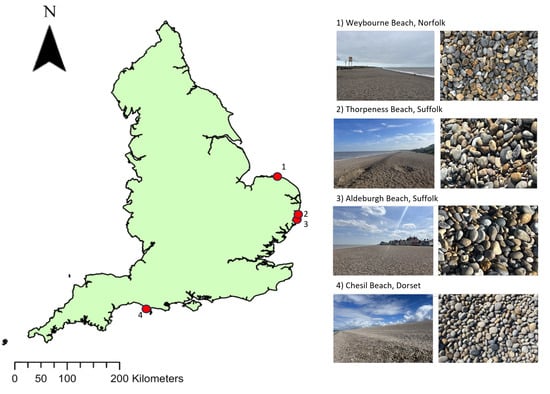
Figure 1.
A map of England showing the locations of the study sites.
These particular beach locations consist of coarse sediments with D50 values greater than 2 mm. Classified according to the Wentworth grain scale [22], the sediment size at Chesil Beach ranges from granular pebbles (2–4 mm) in the northwest of Chesil Beach at West Bay, to coarse pebbles/cobbles (55–65 mm) in Portland, located to the southeast of Chesil Beach. Having such a range in grain sizes across the same beach, where environmental and tidal conditions are mostly uniform, facilitates a robust analysis of the relationship between grain size and SAR backscatter. Aldeburgh and Thorpeness Beach are situated on the Suffolk coast, a coastline which mostly consists of sand and gravel sediments [23]. The backshore of Aldeburgh Beach consists of a berm ridge, with the area above the high-water mark (HWM), in which we studied to avoid influence of moisture, consisting almost entirely of gravel sediment [23]. Thorpeness Beach also has a similar structure to Aldeburgh Beach, with gravel located at the backshore above the HWM. Sediments measured as part of this study were in the range of 23.2–38.2 mm and 24.8–39.3 mm at Aldeburgh Beach and Thorpeness Beach, respectively. Weybourne Beach, also situated on the East coast of England, was selected as an independent site on which to test grain size prediction capabilities based on the established relationship between the D50 values and the associated backscatter found at the training sites. Weybourne Beach also consists of gravel sediments, with measured D50 values of 27.5–36 mm. The selected beaches have different orientations, with Weybourne Beach orientated to the north, Aldeburgh and Thorpeness Beach orientated to the east, and Chesil Beach orientated to the southwest.
2.2. Ground Truth Data
2.2.1. Grain Size Measurements
We collected ground truth validation data at each of the four locations. To achieve this, multiple cross-section transects from the backshore to the breaker zone, perpendicular to the waterline, were taken 150 m apart along each beach. In the case of Chesil Beach, the site was separated into five different areas—Portland, the beach area next to Chesil Beach Visitors’ Centre, Abbotsbury, West Bexington, and West Bay—due to the length of this beach and varying sediment grain size. Along each of the transects, we measured the grain size and took precise coordinate and elevation data.
To obtain grain sizes of the beaches during field campaigns, we used Wolman’s [24] pebble count for sediment sampling and selection. This involved selecting and measuring sediments at random along each of the transects from the dry areas of the beach, i.e., above the waterline at the time of survey. This was to mitigate the impact of moisture content on the corresponding SAR backscatter. Sediments were measured in situ to ensure that no pebbles were removed from the beach, using digital calipers with a resolution of 0.1 mm and accuracy of ±0.2 mm.
We then calculated the median diameter (D50) of the sediment for each transect cross-section. The median was used, as it is less susceptible to outliers, i.e., very large or very small pebbles, which are not representative of the beach composition as a whole. Due to this, the D50 value is a metric that has been used previously in multiple studies to describe coastal sediment grain size (e.g., [1,16,25]).
To enable comparisons of the backscatter values from areas with different sediment sizes, regardless of the beach they were measured from, we split the D50 values into categories. These categories are areas with a D50 value of 0–9 mm, 10–19 mm, 20–29 mm, 30–39 mm, 50–59 mm and 60–69 mm. There were no measured areas which had a D50 value of 40–49 mm.
2.2.2. Beach Elevation Measurements
Along each transect where the grain sizes were measured, we also recorded longitude, latitude, and elevation measurements. This was to georeference the location of the transects to the SAR image for the precise extraction of the corresponding SAR backscatter coefficients. These measurements were made using a Leica GS10 GNSS receiver (Sourced from the University of Nottingham, Nottingham, UK). We mounted the receiver onto a 2 m pole with a rounded base in order to prevent sinking into the sediment. The Real Time Kinematic (RTK) system was used to receive GNSS corrections from a nearby base station or local network. This was achieved by receiving these RTK corrections over the 3G network and resulted in an improved positional accuracy to within 2 cm. The elevation was recorded as the height above the Ordnance Survey Newlyn Datum, which is approximately the height above mean sea level in metres.
2.3. SAR Data Processing
We correlated the measurements of D50 for the three test locations (Thorpeness Beach, Aldeburgh Beach and Chesil Beach) with data from two SAR satellites operating at different frequencies:
Sentinel-1 Level-1 Ground Range Detected (GRD) 20 × 22 m spatial resolution [26]. Level-1 Interferometric Wide (IW) Swath GRD products. We used both the Vertical–Vertical (VV) and the Vertical–Horizontal (VH) polarisations. Sentinel-1 has an associated frequency of 5.404 GHz and a wavelength of 5.5 cm (C-band) [27].
NovaSAR Level-1 Ground Range Detected (GRD) stripmap at 6 m spatial resolution. Only the VV polarisation was used because NovaSAR does not have an imaging mode configured to collect data in the VH polarisation. NovaSAR has an associated frequency of 3.2 GHz and a wavelength of 9.4 cm (S-band) [28].
Sentinel-1 is commonly used in SAR applications due to the data being openly and freely available. We also used NovaSAR data to test the capabilities of S-band SAR, which is a relatively underused band, but considered to have similar capabilities of C-band SAR [29]. Due to the planned launch of NASA’s NISAR in 2024, which incorporates an S-band sensor, new capabilities of this band are being widely explored (e.g., [30,31]). Therefore, we wanted to compare the abilities of each of the sensors for this application, irrespective of the differences in the image acquisition.
We adopted tailored processing steps to extract the backscatter coefficient in terms of sigma naught () for each of the SAR products. The Sentinel-1 data were pre-processed in Google Earth Engine [32]. This was to allow for time series analysis in future research. The NovaSAR data were pre-processed using the ESA SentiNel Application Platform (SNAP) (Version 8.0), using the NovaSAR-1 Product Reader SNAP plugin.
The Sentinel-1 data were imported into Google Earth Engine [32]. The Sentinel-1 data in Google Earth Engine is already pre-processed upon importing, which involves applying an orbit file, removing GRD border noise (which involves the removal of low-intensity noise that invalidates the data on the edge of the scenes), removing thermal noise, applying a radiometric calibration (which involves computing backscatter intensity value), and applying a terrain correction using the SRTM 30 meter DEM [33]. We then exported the processed data in a GeoTIFF file format for analysis in QGIS (Version 3.24.1).
We processed the NovaSAR-1 data by converting the amplitude to dB units, calibrating the image, applying a single produce speckle filter, applying a terrain correction with the Range-Doppler Terrain Correction using the bilinear interpolation DEM re-sampling method and WSG84 map projection, and then finally exporting the processed image to a GeoTIFF file format for analysis in QGIS.
The timings of the field surveys were planned to coincide with the satellite overpasses. For Sentinel-1, the data acquired and field surveys took place in May and June in 2022 and 2023. The NovaSAR data were acquired in May and June 2022 to also coincide with field surveys at the three test locations. However, due to tasking issues, it was not possible to acquire NovaSAR data for Weybourne Beach in 2022, or for any of the locations during the 2023 field campaign. (Details on the timing of SAR acquisitions and corresponding field survey dates for each site are provided in Table A1).
The SAR data were imported into QGIS along with the longitude, latitude and elevation data collected during the field campaigns. We then extracted the backscatter over the transect area from each SAR image and, for each individual transect, calculated the mean average backscatter to compare this to the corresponding measured D50 values. We separated the SAR data into the backscatter from Sentinel-1 in ascending and descending, VV and VH polarisation, and backscatter from NovaSAR in order to investigate the various effects of factors such as band, polarisation, and orbit pass on the ability to predict grain size.
3. Results
3.1. Variations in SAR Backscatter
We correlated the backscatter coefficient (in dB) from Sentinel-1 data for each polarisation (VV and VH), orbit pass (ascending and descending), against the measured D50 values from the ground surveys for each time period (2022, 2023, and 2022–2023 combined) (Figure 2, Figure 3, Figure 4 and Figure 5). For each orbit pass and time period, we also correlated the backscatter coefficient in VH against the backscatter coefficient in VV (Figure 6 and Figure 7).
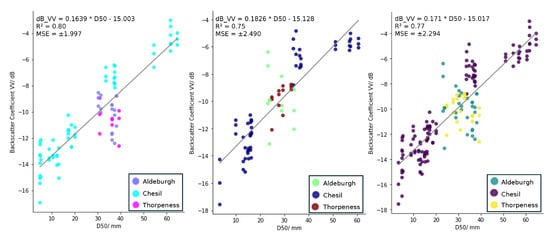
Figure 2.
The Sentinel-1 backscatter coefficient (dB) in the VV polarisation and ascending orbit plotted against the D50 (mm) values for 2022 (left), 2023 (middle), and the 2022 and 2023 data combined (right).
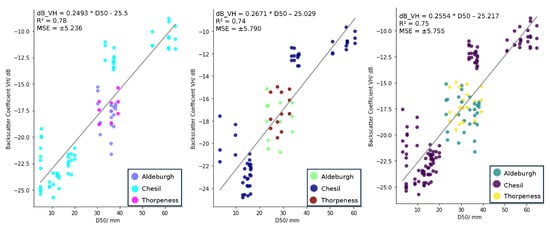
Figure 3.
The Sentinel-1 backscatter coefficient (dB) in the VH polarisation and ascending orbit plotted against the D50 (mm) values for 2022 (left), 2023 (middle), and the 2022 and 2023 data combined (right).
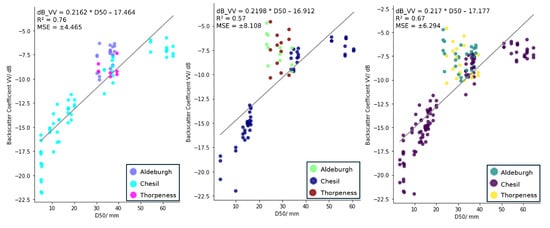
Figure 4.
The Sentinel-1 backscatter coefficient (dB) in the VV polarisation and descending orbit plotted against the D50 (mm) values for 2022 (left), 2023 (middle), and the 2022 and 2023 data combined (right).
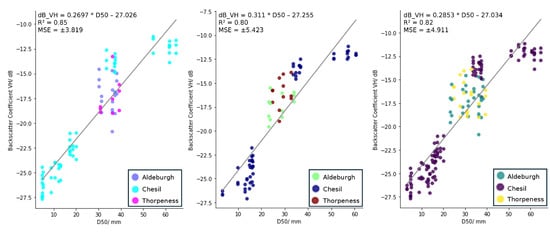
Figure 5.
The Sentinel-1 backscatter coefficient (dB) in the VH polarisation and descending orbit plotted against the D50 (mm) values for 2022 (left), 2023 (middle), and the 2022 and 2023 data combined (right).
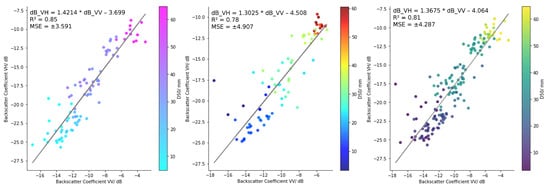
Figure 6.
The Sentinel-1 backscatter coefficient (dB) in the VH polarisation plotted against the Sentinel-1 backscatter coefficient (dB) in the VV polarisation from the ascending orbit for 2022 (left), 2023 (middle), and the 2022 and 2023 data combined (right), coloured according to the D50 (mm) values.
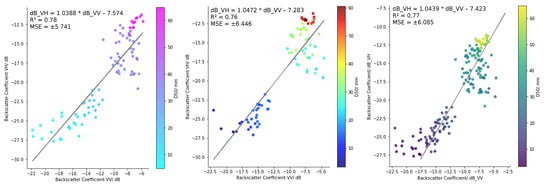
Figure 7.
The Sentinel-1 backscatter coefficient (dB) in the VH polarisation plotted against the Sentinel-1 backscatter coefficient (dB) in the VV polarisation from the descending orbit for 2022 (left), 2023 (middle), and the 2022 and 2023 data combined (right), coloured according to the D50 (mm) values.
Overall, the results show a positive linear relationship between D50 and the backscatter coefficient from Sentinel-1 for all years, in both the ascending and descending orbit passes and in both the VV and VH polarisations. The results also show a positive linear relationship between the Sentinel-1 VH backscatter coefficient and the VV backscatter coefficient for all years and both orbit passes.The equation of the linear regression model, the value and the Mean Squared Error (MSE) are plotted on each of the graphs in Figure 2, Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7.
We found no correlation (R2 = 0.04) between the backscatter coefficient from NovaSAR data and D50, even at Chesil Beach, where sediment is graded (Figure 8). We also tested the correlation between the backscatter coefficient and D75 (the third quartile of the sediment grain size) to determine whether the NovaSAR backscatter would be more correlated with a greater metric. However, although there was a slight improvement in the value (where = 0.1), overall, there was also no correlation between the backscatter coefficient from NovaSAR data and D75.
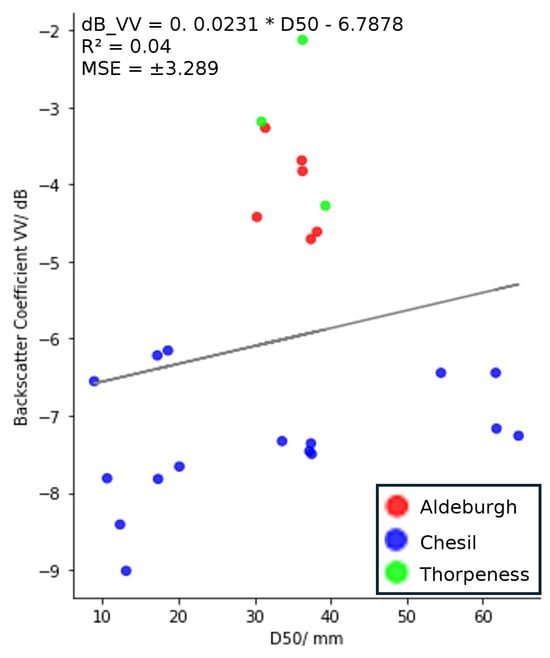
Figure 8.
The NovaSAR backscatter coefficient (dB) in the VV polarisation plotted against the D50 (mm) values for 2022 data.
3.2. Average Backscatter and D50
Our results show a general trend of increasing mean backscatter with increasing median sediment size (D50) for all categories of sediment (areas with a D50 of 0–9 mm, 10–19 mm, 20–29 mm, 30–39 mm, 50–59 mm and 60–69 mm). There were some exceptions where the mean backscatter was higher for some smaller D50 sizes in the ascending orbit in the VH polarisation. For the 2022, 2023, and 2022–2023 combined data, the average dB for the range where the D50 was within 0–9 mm was 0.2 dB, 2.7 dB, and 0.3 dB, respectively, higher than the average dB for areas where the D50 was within 10–19 mm. In the descending orbit, for both VV and VH polarisations and for 2022, 2023, and for the 2022–2023 data combined, the average backscatter coefficient was higher by approximately 0.7 dB for beach areas where the D50 was within the 50–59 mm range than within the 60–69 mm range. The average backscatter was also greater in the VV polarisation in the descending orbit in areas where D50 was within the 20–29 mm range compared to in the 30–39 mm range, in 2023 and the 2022–2023 data combined. The one-sigma standard deviation, displayed as the vertical lines in Figure 9 and Figure 10, shows large standard deviations in the 30–39 mm and the 0–9 mm ranges in the ascending orbit, and in the 20–29 range for the years 2023 and the combined 2022–2023 data in the VH polarisation in the descending orbit mode.

Figure 9.
The mean average Sentinel-1 backscatter coefficient (dB) in the ascending orbit for VV (left) and VH (right) polarisations, and their associated standard deviations, plotted for each category of the D50 (mm) values.
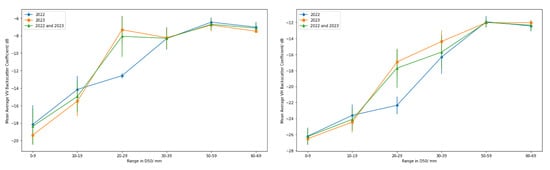
Figure 10.
The mean average Sentinel-1 backscatter coefficient (dB) in the descending orbit for VV (left) and VH (right) polarisations, and their associated standard deviations, plotted for each category of the D50 (mm) values.
3.3. Predicting Grain Size
We derived linear regression models from the data displayed in Figure 2, Figure 3, Figure 4 and Figure 5 to derive estimates of D50 values at the independent test site, Weybourne Beach (location 1 in Figure 1). The use of linear regression models was chosen due to them having a greater value than other models that we tested. We also did not want to include multiple variables and instead wanted to test the ability to predict grain size from the backscatter coefficient alone without the incorporation of other data, such as slope, which may not be available at all sites. The linear regression equations in Figure 2, Figure 3, Figure 4 and Figure 5 are displayed as the backscatter coefficient in terms of D50, so therefore these equations were rearranged so that the Sentinel-1 backscatter from the corresponding polarisation and orbit pass could be inputted into the equation to derive a value of D50. Table 1 displays the values, the Mean Absolute Error (MAE), in terms of deviation of the outputted prediction of the D50 value from the actual D50 value using the Leave One Out (LOO) statistical test, and the MAE of the predicted D50 value from the measured D50 value at the test site at Weybourne Beach.

Table 1.
Evaluation of the performance of each linear regression model comparing the value, Mean Absolute Error (MAE) using the Leave One Out (LOO) analysis, and the MAE at the test site (Weybourne Beach). The table is ordered from the model with the highest value to the lowest value for the models using a single input of VV or VH backscatter.
The highest value was from the resultant model which was derived from VH Sentinel-1 backscatter in the descending orbit and D50 values from 2022 data. This model also had the lowest MAE for the LOO statistical test of 5.17 mm. However, the model which was derived using the VV Sentinel-1 backscatter and D50 values from the 2023 data had the lowest MAE of 2.26 mm at the test beach, Weybourne Beach.
In order to investigate potential synergistic advantages, we also tested the ability to predict grain size using a combination of the VV and VH backscatter coefficients for each orbit pass and year. This was achieved through the development of Multiple Linear Regression (MLR) models, by using the corresponding backscatter coefficients for the VV and VH polarisations as explanatory variables to predict the associated grain size (i.e., the response variable) based on the relationships in Figure 6 and Figure 7. The equations of these MLR models are displayed in Table 2. The MLR models resulted in greater values, which are also displayed in Table 2, than the values of the relationship between the VH and VV polarisations alone. The results from this analysis show that the maximum MAE from the LOO analysis was 6.04 mm, with a minimum MAE of 4.98 mm, while the maximum MAE for the Weybourne Beach test site was 4.25 mm and the minimum MAE was 3.03 mm. Overall, the models which combine the VV and VH backscatter data resulted in the best prediction capabilities as a whole.

Table 2.
Equations of the multiple linear regression (MLR) models along with an evaluation of the performance of each model, comparing the value, Mean Absolute Error (MAE) using the Leave One Out (LOO) analysis, and the MAE at the test site (Weybourne Beach). The table is ordered from the model with the highest value to the lowest value for the models which use inputs of both the VV and VH backscatter.
Additionally, we computed a correlation coefficient matrix to determine the relationship between the values and the MAE values. We found a strong positive correlation (0.71) between the values and the MAE from the LOO test and moderate positive correlations (0.47 and 0.43 respectively) between the values and the MAE at Weybourne Beach and the MAE from the LOO test and MAE at Weybourne Beach.
Overall, for all of the models, the predictions over the test beach at Weybourne Beach had a MAE of ≤6.95 mm. However, if we just use the models which have values , the MAE over Weybourne Beach is reduced to ≤5.57 mm.
4. Discussion
4.1. Sediment Grain Size and Sentinel-1 C-Band SAR
Overall, we found a strong positive correlation between the mean backscatter coefficients from Sentinel-1 C-band SAR and D50 values for a range of gravel-dominated beaches across England (the UK). We also found a general trend of increasing Sentinel-1 average backscatter with increasing D50 in both, VV and VH, polarisations. Previous studies have also found similar results. Wu et al. [16] found a strong, positive correlation between D50 values and the backscatter coefficient from the PLASAR-2 L-band SAR sensor. They noted that there was a higher backscatter from beach areas which consist of beach materials with a larger median diameter than those which are composed of smaller pebbles [16]. Van der Wal et al. [18], also found a positive correlation between D50 and the backscatter coefficient. This study looked at smaller sediments (muddy to sandy sediments of ≤2 mm) but attributed these results to the surface roughness and the dielectric properties of the intertidal flat area in which they studied. From these correlations, we were able to derive 18 linear regression models from the relationships between the D50 values and the Sentinel-1 backscatter coefficients found in Figure 2, Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7 and use these to predict the D50 values at an independent test site.
4.1.1. Effects of Polarisation
For all beach areas, backscatter values were greater in the VV polarisation compared to the VH polarisation for the same D50 values (e.g., for an area with a D50 value of 64.7 mm, the backscatter coefficient was −4.5 dB in the VV polarisation, compared to −11.7 dB in the VH polarisation in the ascending orbit; for areas with smaller sediments, i.e., with a D50 value of 4.9 mm, the backscatter coefficient was −15.4 dB in the VV, compared to −24.7 dB in the VH, also in the ascending orbit). Nevertheless, the backscatter response increased in both the VV and VH polarisations with increasing D50 values. We suggest that this could be attributed to the roughness of the beach increasing with an increasing grain size. Although the study did not focus specifically on coastal sediments, it has been found that an increase in grain size causes an increase in surface roughness [34]. Moreover, previous work focusing on coastal sediments, albeit smaller sediments than in this study, attributed the relationship between increasing backscatter from ERS C-band SAR satellite imagery and grain size to increasing roughness [18]. Other studies which analysed grain sizes from backscatter using acoustic multi-beam echosounders also attributed roughness as an important factor related to grain size which influences the backscatter return (e.g., [35,36]).
Upon plotting the backscatter coefficients from the VH polarisation against the backscatter coefficients from VV polarisation, the R2 values suggest a very strong correlation, with R2 ≥ 0.76 for all years and both ascending and descending orbit passes. This suggests that the changes in surface properties have a similar effect on both polarisations (with the backscatter coefficient decreasing as grain size decreases), and that the scattering mechanisms in both polarisations are similar. We hypothesise that the most likely dominant scattering mechanism is volume scattering for bigger grains, due to the relatively large amount of return scatter to the signal, as beach areas with larger grains present are hypothesised as having a rougher surface. Additionally, beach areas with grain sizes of the same or larger spatial magnitude of the Sentinel-1 wavelength have the ability to interact with the SAR signal and return a larger amount of backscatter. As the grain size decreases, we suggest that the dominant scattering mechanism becomes specular reflection due to the decrease in surface roughness, coupled with the grain size being below the wavelength of C-band SAR. This is supported by a lower return backscatter in both the VV and VH polarisations for smaller grains.
4.1.2. Effects of Orbit Pass
At Chesil Beach, the backscatter values were greater in the ascending than in the descending orbit pass. The backscatter was, on average, 2.23 dB greater in the VV polarisation in the ascending orbit pass, compared to the VV polarisation in the descending orbit pass, and 1.68 dB greater in the VH polarisation in the ascending orbit pass, compared to the VH polarisation in the descending orbit pass. However, at Aldeburgh and Thorpeness Beaches, backscatter values were greater in the descending orbit pass than the ascending. At Aldeburgh Beach, the backscatter coefficient was, on average, 2.39 dB greater in the descending orbit pass in the VV polarisation and 0.72 dB greater in the descending orbit pass in the VH polarisation. Thorpeness Beach displayed similar differences between the orbit passes to Aldeburgh Beach with backscatter values, on average, 2.04 dB greater in the descending orbit pass in the VV polarisation and 0.51 dB greater in the descending orbit pass in the VH polarisation compared to the backscatter values in the ascending orbit pass. We suggest that this is due to the orientation of these two beaches being orientated towards the SAR sensor in the descending orbit pass, resulting in a greater amount of backscatter being received by the sensor. As the differences between the ascending and descending backscatter values are smaller in the VH polarisation, compared to the VV polarisation, this give some explanation as to why the two models with the highest R2 values consist of backscatter from the VH polarisation; as the models combine beaches, one of which has a greater response in the ascending orbit mode (Chesil), while the others have a greater response in the descending orbit mode (Aldeburgh and Thorpeness), when this difference is minimised, the points have a greater fit, and thus, a greater R2 value. Therefore, it is important to consider the orientation of the beach relative to the sensor. Based off the backscatter coefficients from Aldeburgh Beach and Thorpeness Beach, we observe that there is less of an effect on the backscatter coefficients in the VH polarisation compared to the VV polarisation when the beach is orientated towards the sensor.
4.1.3. Limits of Grain Size Derivation
Upon categorising the beach areas based on their D50 values (0–9 mm, 10–19 mm, 20–29 mm, 30–39 mm, 50–59 mm and 60–69 mm) and comparing the mean average backscatter coefficient values for each of these categories, we observed a general trend of increasing average backscatter coefficient values for increasing D50 values. For each category of increasing D50, the average backscatter coefficient was higher (less negative) than the previous category in most cases, except for the 10–19 mm category, where the 0–9 mm category had slightly higher average backscatter in the VH ascending data, the 20–29 mm category, which displayed a slightly higher average backscatter than the 30–39 mm category in the descending orbit for just 2023 and 2022–2023 combined data, and in the descending orbit mode for both polarisations and all years, where the 50–59 mm category also displayed a slightly higher average backscatter than the 60–69 mm category. For the descending orbit, only slight variations in dB were observed between the 50–59 mm and the 60–69 mm categories and between the 0–9 mm and 10–19 mm categories, which are both the biggest and smallest categories of grain sizes analysed in this study. This was also the case for the smallest (0–9 mm) category in the ascending orbit for VH, where this had a slightly higher average backscatter than the 10–19 mm category. Therefore, we suggest that these are the upper and lower limits of the grain sizes we can distinguish between using C-band SAR data. We suggest that, especially for the smallest grain sizes (0–9 mm), the increase in mean backscatter was greater due to noise as opposed to grain size, overall concluding that the model, which utilises C-band SAR, would not be able to distinguish between areas of beaches with D50 values outside the range of 10–50 mm. This is supported by the fact that in the plots which display the backscatter coefficient plotted against D50 (Figure 2, Figure 3, Figure 4 and Figure 5) the linear relationship begins to flatten at the start and end of most of the graphs. This flattening is also more prominent in graphs that show backscatter coefficients from the descending orbit pass. This could be because the grain sizes on the upper end of the D50 values (50–69 mm) begin to exceed the wavelength of C-band SAR. However, the biggest D50 values are still below the wavelength of NovaSAR, and therefore, as will be discussed in further detail below, have not caused variations in dB for this sensor. In terms of the average backscatter being greater in the 20–29 mm category compared to the 30–39 mm category in the VV polarisation in the descending orbit for only the 2023 and 2022–2023 data, we attribute this to a greater backscatter coefficient from Aldeburgh and Thorpeness Beach in the VV polarisations and descending orbit in 2023, which therefore affected the 2022–2023 combined data as displayed in Figure 4. The VV descending 2023 and VV descending 2022 and 2023 models are the only two models with R2 values of <0.7, due to this higher amount of backscatter from Aldeburgh and Thorpeness Beach in the VV polarisation and descending orbit in 2023.
4.2. Sediment Grain Size and NovaSAR S-Band SAR
Upon plotting D50 against the backscattering coefficient in VV polarisation for NovaSAR data, the results show that there was no correlation (R2 = 0.04) between the D50 and the mean backscatter coefficient (Figure 8). We initially anticipated that the NovaSAR S-band SAR would be unlikely to be able to determine the sediment grain size at the study sites. This is due to the longer wavelength of NovaSAR (94 mm) [28], which is larger than the largest D50 found at any of the study sites (64.7 mm). Therefore, it was expected that there will be fewer interactions between the S-band radar signal and the sediment, as generally the strongest backscatter returns are from objects of the same or larger spatial magnitude as the sensor’s wavelength. Although the R2 value did increase, we also found no correlation between a larger metric, D75, and the backscatter coefficient of NovaSAR (R2 = 0.1). Therefore, we conclude that for the range of grain sizes (8.9–64.7 mm) studied using NovaSAR data processed according to the processing methodology outlined, the grain size does not affect the backscatter coefficient.
4.3. Potential to Predict D50 from Sentinel-1 Backscatter
We tested the ability to predict the D50 from Sentinel-1 backscatter by predicting the D50 over our test site at Weybourne Beach using the resultant regression models from the analysis above. The best overall predictions for D50 values in both polarisations and orbits result from inputting both the VV and VH backscatter coefficients into the MLR models derived from the relationships in Figure 6 and Figure 7. For all of these models, the R2 values were ≥0.79 and the MAE was ≤4.25 mm when using these models to predict the D50 values over the test site. The lowest MAE from predictions using the MLR models was 3.03 mm.
The descending orbit mode in the VH polarisation resulted in the highest R2 values across all years, with R2 values of 0.85, 0.82 and 0.80 for 2022, 2022–2023 data combined, and 2023 data, respectively. These models resulted in MAEs between the predicted and measured D50 values over the test area of 5.47 mm, 4.66 mm and 3.56 mm, respectively.
We computed the correlations between the R2 values, the MAE using the Leave One Out (LOO) statistical test, and the MAE from the test site across all the models. There was a strong (0.80) correlation between the R2 values and the MAE values from the LOO statistical test and a moderate correlation (0.49) between the R2 values and the MAE from the test site at Weybourne Beach. This shows when the model has a higher R2 value, this is more likely to result in a lower MAE in the LOO statistical test and is less so related to a lower MAE over the test area. This is likely because the LOO test utilises the data which have already been used to calibrate a model (takes out a data point from the already established model), compared to the test area, in which these data are independent from the model and so are not involved in the calibration.
Overall, for all of the resultant models, the MAE between the predicted D50 and the actual D50 at Weybourne Beach was ≤7.41 mm. When only the models with an R2 value ≥ 0.75 were considered, the MAE decreased to ≤5.57 mm. The model with the lowest MAE (2.26 mm) over the test site was the model derived using backscatter from the VV polarisation in the ascending orbit pass. Overall, we anticipate that this methodology will be able to be used to derive the D50 values of multiple gravel beaches remotely and frequently, irrespective of cloud cover and illumination conditions. Bearing in mind there is a paucity of frequent grain size records for many coastal areas, deriving D50 values within this level of accuracy will provide a greater understanding of coastal sediments than currently exists.
5. Conclusions
In this paper, we have presented a novel approach to derive estimates of median sediment grain size (D50) on gravel beaches to within 2.26 mm from Sentinel-1 satellite C-band SAR data. We established strong positive linear relationships between D50 values and the backscatter coefficients from VV and VH polarisations in the ascending and descending orbit passes for data collected in May and June 2022 and 2023. There was also a strong positive linear relationship between the VV backscatter coefficients and VH backscatter coefficients. We observed a greater backscatter response in the VV polarisation compared to VH polarisation and differences between the backscatter response in the different orbit passes (ascending and descending) and suggested some reasons for these variations. We conclude that C-band SAR is preferable to the use of S-band SAR for the ranges of D50 values studied (3.3–64.7 mm) due to the smaller wavelength of C-band SAR compared to S-band SAR. However, we suggest that the upper limit of grain sizes, which can be differentiated against using C-band SAR, is within the range of 50–69 mm, with grains greater than this suspected to have a similar backscatter to those within this range. We suggest that further research could focus on the use of X-band SAR and the combination of all three bands (X, C and S) to give the best potential to derive grain sizes of multiple sizes. We also suggest studying a greater range of grain sizes from a multitude of different gravel beaches. These grains should include those within the wavelength ranges of NovaSAR to determine whether these larger grains display a response which is similar to what is observed with the Sentinel-1 data. Expanding the study to multiple beaches will also enable further understanding of the effects of beach orientation on the backscatter response.
Author Contributions
Conceptualisation—S.M. (Sophie Mann), S.G., A.C. and S.M. (Stuart Marsh); Data curation—S.M. (Sophie Mann) and A.N.; Formal analysis—S.M. (Sophie Mann), A.N., E.H. and S.G.; Funding acquisition—S.M. (Stuart Marsh); Investigation—S.M. (Sophie Mann); Methodology—S.M. (Sophie Mann), A.N. and S.G.; Project administration—S.M. (Sophie Mann) and S.M. (Stuart Marsh); Resources—L.B., A.C. and S.M. (Stuart Marsh); Software—S.M. (Sophie Mann) and A.N.; Supervision—A.N., E.H., S.G., L.B. and S.M. (Stuart Marsh); Validation—S.M. (Sophie Mann); Visualisation—S.M. (Sophie Mann), A.N. and E.H.; Writing—original draft—S.M. (Sophie Mann); Writing—review and editing—S.M. (Sophie Mann), A.N., E.H., S.G., L.B., A.C. and S.M. (Stuart Marsh). All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Engineering and Physical Sciences Research Council Centre for Doctoral Training (CDT) in Geospatial Systems. Grant Number: EP/S023577/1.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Sentinel-1 data: available for download from the Copernicus Open Access Hub, https://scihub.copernicus.eu/ (accessed on 16 January 2024) or through Google Earth Engine [32]. NovaSAR-1 data: provided by Surrey Satellite Technology (SSTL) and Airbus Defence and Space to the UK Hydrographic Office. Requests for data should be made to Airbus Defence and Space. Specific orbit pass and acquisition dates and time of the satellite imagery used in this study can be found in Table A1. For sediment grain size data, please contact corresponding author, S. Mann, for data access. Email: lgysjma@nottingham.ac.uk.
Acknowledgments
The authors would like to extend their thanks to the Engineering and Physical Sciences Research Council (EPSRC) for funding this research. We would also like to express our gratitude to Cristina Vrinceanu, Stephen Dugdale, Frazer Christie, Iain Woodhouse, amongst others, for their helpful suggestions and insights regarding the project, and to Sean Ince for his support with the field equipment. Thanks also goes to the United Kingdom Hydrographic Office (UKHO), SSTL and Airbus Defence and Space for providing tasking and access to NovaSAR data and to the European Space Agency (ESA) for providing access to the Sentinel-1 data used in this research. A. Novellino, E. Hussain and L. Bateson published with the permission from the Director of the British Geological Survey.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A

Table A1.
Satellite acquisition and field data collection dates.
Table A1.
Satellite acquisition and field data collection dates.
| Site | Satellite | Orbit Pass | Acquisition Date and Time | Field Survey Date |
|---|---|---|---|---|
| Aldeburgh Beach | Sentinel-1 | Ascending | 30 April 2022 17:41 | 13 May 2022 |
| Aldeburgh Beach | Sentinel-1 | Ascending | 24 May 2022 17:41 | 13 May 2022 |
| Aldeburgh Beach | Sentinel-1 | Ascending | 5 May 2022 17:41 | 13 May 2022 |
| Aldeburgh Beach | Sentinel 1 | Descending | 2 May 2022 06:14 | 13 May 2022 |
| Aldeburgh Beach | Sentinel-1 | Descending | 14 May 2022 06:14 | 13 May 2022 |
| Aldeburgh Beach | Sentinel-1 | Descending | 26 May 2022 06:15 | 13 May 2022 |
| Aldeburgh Beach | NovaSAR | Descending | 26 May 2022 09:33 | 13 May 2022 |
| Chesil Beach | Sentinel-1 | Ascending | 10 May 2022 17:57 | 23–25 May 2022 |
| Chesil Beach | Sentinel-1 | Ascending | 22 May 2022 17:57 | 23–25 May 2022 |
| Chesil Beach | Sentinel-1 | Ascending | 3 June 2022 17:57 | 23–25 May 2022 |
| Chesil Beach | Sentinel-1 | Descending | 7 May 2022 06:23 | 23–25 May 2022 |
| Chesil Beach | Sentinel-1 | Descending | 19 May 2022 06:23 | 23–25 May 2022 |
| Chesil Beach | Sentinel-1 | Descending | 31 May 2022 06:23 | 23–25 May 2022 |
| Chesil Beach | NovaSAR | Ascending | 31 May 2022 10:15 | 23–25 May 2022 |
| Thorpeness Beach | Sentinel-1 | Ascending | 30 April 2022 17:41 | 13 May 2022 |
| Thorpeness Beach | Sentinel-1 | Ascending | 24 May 2022 17:41 | 13 May 2022 |
| Thorpeness Beach | Sentinel-1 | Ascending | 5 May 2022 17:41 | 13 May 2022 |
| Thorpeness Beach | Sentinel 1 | Descending | 2 May 2022 06:14 | 13 May 2022 |
| Thorpeness Beach | Sentinel-1 | Descending | 14 May 2022 06:14 | 13 May 2022 |
| Thorpeness Beach | Sentinel-1 | Descending | 26 May 2022 06:15 | 13 May 2022 |
| Thorpeness Beach | NovaSAR | Descending | 26 May 2022 09:33 | 13 May 2022 |
| Weybourne Beach | Sentinel-1 | Ascending | 30 April 2022 17:41 | 31 May 2022 |
| Weybourne Beach | Sentinel-1 | Ascending | 24 May 2022 17:41 | 31 May 2022 |
| Weybourne Beach | Sentinel-1 | Ascending | 5 June 2022 17:42 | 31 May 2022 |
| Weybourne Beach | Sentinel-1 | Descending | 2 May 2022 06:14 | 31 May 2022 |
| Weybourne Beach | Sentinel-1 | Descending | 14 May 2022 06:14 | 31 May 2022 |
| Weybourne Beach | Sentinel-1 | Descending | 26 May 2022 06:14 | 31 May 2022 |
| Aldeburgh Beach | Sentinel-1 | Ascending | 7 May 2023 17:41 | 22 May 2023 |
| Aldeburgh Beach | Sentinel-1 | Ascending | 19 May 2023 17:41 | 22 May 2023 |
| Aldeburgh Beach | Sentinel-1 | Ascending | 31 May 2023 17:41 | 22 May 2023 |
| Aldeburgh Beach | Sentinel-1 | Descending | 9 May 2023 06:15 | 22 May 2023 |
| Aldeburgh Beach | Sentinel-1 | Descending | 21 May 2023 06:15 | 22 May 2023 |
| Aldeburgh Beach | Sentinel-1 | Descending | 2 June 2023 06:15 | 22 May 2023 |
| Chesil Beach | Sentinel-1 | Ascending | 5 May 2023 17:57 | 15–19 May 2023 |
| Chesil Beach | Sentinel-1 | Ascending | 17 May 2023 17:57 | 15–19 May 2023 |
| Chesil Beach | Sentinel-1 | Ascending | 29 May 23 17:57 | 15–19 May 2023 |
| Chesil Beach | Sentinel-1 | Descending | 2 May 2023 06:23 | 15–19 May 2023 |
| Chesil Beach | Sentinel-1 | Descending | 14 May 2023 06:23 | 15–19 May 2023 |
| Chesil Beach | Sentinel-1 | Descending | 26 May 2023 06:23 | 15–19 May 2023 |
| Thorpeness Beach | Sentinel-1 | Ascending | 7 May 2023 17:41 | 22 May 2023 |
| Thorpeness Beach | Sentinel-1 | Ascending | 19 May 2023 17:41 | 22 May 2023 |
| Thorpeness Beach | Sentinel-1 | Ascending | 31 May 2023 17:41 | 22 May 2023 |
| Thorpeness Beach | Sentinel-1 | Descending | 9 May 2023 06:15 | 22 May 2023 |
| Thorpeness Beach | Sentinel-1 | Descending | 21 May 2023 06:15 | 22 May 2023 |
| Thorpeness Beach | Sentinel-1 | Descending | 2 June 2023 06:15 | 22 May 2023 |
| Weybourne Beach | Sentinel-1 | Ascending | 7 May 2023 17:42 | 24 May 2023 |
| Weybourne Beach | Sentinel-1 | Ascending | 19 May 2023 17:42 | 24 May 2023 |
| Weybourne Beach | Sentinel-1 | Ascending | 31 May 2023 17:42 | 24 May 2023 |
| Weybourne Beach | Sentinel-1 | Descending | 9 May 2023 06:14 | 24 May 2023 |
| Weybourne Beach | Sentinel-1 | Descending | 21 May 2023 06:14 | 24 May 2023 |
| Weybourne Beach | Sentinel-1 | Descending | 2 June 2023 06:14 | 24 May 2023 |
References
- Cabezas-Rabadán, C.; Pardo-Pascual, J.E.; Palomar-Vázquez, J. Characterizing the relationship between the sediment grain size and the shoreline variability defined from sentinel-2 derived shorelines. Remote Sens. 2021, 13, 2829. [Google Scholar] [CrossRef]
- Bio, A.; Bastos, L.; Granja, H.; Pinho, J.L.S.; Gonçalves, J.A.; Henriques, R.; Madeira, S.; Magalhães, A.; Rodrigues, D. Methods for coastal monitoring and erosion risk assessment: Two Portuguese case studies. Rev. Gestão Costeira Integr. J. Integr. Coast. Zone Manag. 2015, 15, 47–63. [Google Scholar] [CrossRef]
- Chardon, V.; Schmitt, L.; Piégay, H.; Lague, D. Use of terrestrial photosieving and airborne topographic LiDAR to assess bed grain size in large rivers: A study on the Rhine River. Earth Surf. Process. Landforms 2020, 45, 2314–2330. [Google Scholar] [CrossRef]
- Yu, X.; Zhan, C.; Liu, Y.; Bi, J.; Li, G.; Cui, B.; Wang, L.; Liu, X.; Wang, Q. Retrieval of Remotely Sensed Sediment Grain Size Evolution Characteristics along the Southwest Coast of Laizhou Bay Based on Support Vector Machine Learning. J. Mar. Sci. Eng. 2022, 10, 968. [Google Scholar] [CrossRef]
- McAllister, E.; Payo, A.; Novellino, A.; Dolphin, T.; Medina-Lopez, E. Multispectral satellite imagery and machine learning for the extraction of shoreline indicators. Coast. Eng. 2022, 174, 104102. [Google Scholar] [CrossRef]
- Vitousek, S.; Buscombe, D.; Vos, K.; Barnard, P.L.; Ritchie, A.C.; Warrick, J.A. The future of coastal monitoring through satellite remote sensing. Camb. Prism. Coast. Futur. 2023, 1, 10. [Google Scholar] [CrossRef]
- Bartholdy, J.; Folving, S. Sediment classification and surface type mapping in the Danish Wadden Sea by remote sensing. Neth. J. Sea Res. 1986, 20, 337–345. [Google Scholar] [CrossRef]
- Deronde, B.; Kempeneers, P.; Forster, R.M. Imaging spectroscopy as a tool to study sediment characteristics on a tidal sandbank in the Westerschelde. Estuar. Coast. Shelf Sci. 2006, 69, 580–590. [Google Scholar] [CrossRef]
- Rainey, M.P.; Tyler, A.N.; Gilvear, D.J.; Bryant, R.G.; McDonald, P. Mapping intertidal estuarine sediment grain size distributions through airborne remote sensing. Remote Sens. Environ. 2003, 86, 480–490. [Google Scholar] [CrossRef]
- Blickensdörfer, L.; Schwieder, M.; Pflugmacher, D.; Nendel, C.; Erasmi, S.; Hostert, P. Mapping of crop types and crop sequences with combined time series of Sentinel-1, Sentinel-2 and Landsat 8 data for Germany. Remote Sens. Environ. 2022, 269, 112831. [Google Scholar] [CrossRef]
- Meyer, F.J.; McAlpin, D.B.; Gong, W.; Ajadi, O.; Arko, S.; Webley, P.W.; Dehn, J. Integrating SAR and derived products into operational volcano monitoring and decision support systems. ISPRS J. Photogramm. Remote Sens. 2015, 100, 106–117. [Google Scholar] [CrossRef]
- Novellino, A.; Pennington, C.; Leeming, K.; Taylor, S.; Alvarez, I.G.; McAllister, E.; Arnhardt, C.; Winson, A. Mapping landslides from space: A review. Landslides 2024, 21, 1041–1052. [Google Scholar] [CrossRef]
- Grimaldi, S.; Xu, J.; Li, Y.; Pauwels, V.R.; Walker, J.P. Flood mapping under vegetation using single SAR acquisitions. Remote Sens. Environ. 2020, 237, 111582. [Google Scholar] [CrossRef]
- Gaber, A.; Soliman, F.; Koch, M.; El-Baz, F. Using full-polarimetric SAR data to characterize the surface sediments in desert areas: A case study in El-Gallaba Plain, Egypt. Remote Sens. Environ. 2015, 162, 11–28. [Google Scholar] [CrossRef]
- Deroin, J.P. Potential of Sentinel 1 Satellites for Mapping Tidal Flats. Case Study of the Baie Des Veys (Normandy, France). In Proceedings of the IGARSS 2020—2020 IEEE International Geoscience and Remote Sens, Symposium, Virtual, 26 September 2020; pp. 5733–5736. [Google Scholar]
- Wu, L.; Tajima, Y.; Yamanaka, Y.; Shimozono, T.; Sato, S. Study on characteristics of SAR imagery around the coast for shoreline detection. Coast. Eng. J. 2019, 61, 152–170. [Google Scholar] [CrossRef]
- Brakenhoff, L.B.; Smit, Y.; Donker, J.J.; Ruessink, G. Tide-induced variability in beach surface moisture: Observations and modelling. Earth Surf. Process. Landf. 2019, 44, 317–330. [Google Scholar] [CrossRef]
- Van Der Wal, D.; Herman, P.M.; Wielemaker-van Den Dool, A. Characterisation of surface roughness and sediment texture of intertidal flats using ERS SAR imagery. Remote Sens. Environ. 2005, 98, 96–109. [Google Scholar] [CrossRef]
- Van Der Wal, D.; Herman, P.M. Regression-based synergy of optical, shortwave infrared and microwave remote sensing for monitoring the grain-size of intertidal sediments. Remote Sens. Environ. 2007, 111, 89–106. [Google Scholar] [CrossRef]
- Gade, M.; Melchionna, S.; Stelzer, K.; Kohlus, J. Multi-frequency SAR data help improving the monitoring of intertidal flats on the German North Sea coast. Estuar. Coast. Shelf Sci. 2014, 140, 32–42. [Google Scholar] [CrossRef]
- Gade, M.; Alpers, W.; Melsheimer, C.; Tanck, G. Classification of sediments on exposed tidal flats in the German Bight using multi-frequency radar data. Remote Sens. Environ. 2008, 112, 1603–1613. [Google Scholar] [CrossRef]
- Wentworth, C.K. A scale of grade and class terms for clastic sediments. J. Geol. 1922, 30, 377–392. [Google Scholar] [CrossRef]
- Neal, A.; Pontee, N.I.; Pye, K.; Richards, J. Internal structure of mixed-sand-and-gravel beach deposits revealed using ground-penetrating radar. Sedimentology 2002, 49, 789–804. [Google Scholar] [CrossRef]
- Wolman, M.G. A method of sampling coarse river-bed material. EOS Trans. Am. Geophys. Union 1954, 35, 951–956. [Google Scholar]
- Narra, P.; Coelho, C.; Fonseca, J. Sediment grain size variation along a cross-shore profile–representative d 50. J. Coast. Conserv. 2015, 19, 307–320. [Google Scholar] [CrossRef]
- IW GRD Resolutions. Available online: https://sentinel.esa.int/web/sentinel/technical-guides/sentinel-1-sar/products-algorithms/level-1-algorithms/ground-range-detected/iw (accessed on 24 April 2024).
- Novellino, A.; Mansour, M.; Wang, L. Measuring Soil Moisture with Spaceborne Synthetic Aperture Radar Data; Open Report; British Geological Survey: Nottingham, UK, 2020; 45p. [Google Scholar]
- NovaSAR-1 User Guide. Available online: https://research.csiro.au/cceo/novasar/novasar-introduction/novasar-1-user-guide/ (accessed on 3 April 2024).
- Natale, A.; Guida, R.; Bird, R.; Whittaker, P.; Cohen, M.; Hall, D. Demonstration and analysis of the applications of S-band SAR. In Proceedings of the 2011 3rd International Asia-Pacific Conference on Synthetic Aperture Radar (APSAR), Seoul, Republic of Korea, 26 September 2011; pp. 1–4. [Google Scholar]
- Iervolino, P.; Guida, R.; Whittaker, P. NovaSAR-S and maritime surveillance. In Proceedings of the 2013 IEEE International Geoscience and Remote Sens. Symposium-IGARSS, Melbourne, Australia, 21 July 2013; pp. 1282–1285. [Google Scholar]
- Saini, O.; Bhardwaj, A.; Chatterjee, R.S. Analysis of Back-Scattering Coefficient of NovaSAR-1 S-Band SAR datasets for different Land Covers. In Proceedings of the National Seminar on Recent Advances in Geospatial Technology & Applications, Dehradun, India, 2 March 2020. [Google Scholar]
- Gorelic, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Sentinel-1 Algorithms. Available online: https://developers.google.com/earth-engine/guides/sentinel1 (accessed on 3 April 2024).
- Kabeya, K.K.; Legge, T.F.H. Relationship between grain size and some surface roughness parameters of rock joints. Int. J. Rock Mech. Min. Sci. 1997, 34, 146. [Google Scholar] [CrossRef]
- Ferrini, V.L.; Flood, R.D. The effects of fine-scale surface roughness and grain size on 300 kHz multibeam backscatter intensity in sandy marine sedimentary environments. Mar. Geol. 2006, 228, 153–172. [Google Scholar] [CrossRef]
- Runya, R.M.; McGonigle, C.; Quinn, R.; Howe, J.; Collier, J.; Fox, C.; Dooley, J.; O’loughlin, R.; Calvert, J.; Scott, L.; et al. Examining the links between multi-frequency multibeam backscatter data and sediment grain size. Remote Sens. 2021, 13, 1539. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).