TFCD-Net: Target and False Alarm Collaborative Detection Network for Infrared Imagery
Abstract
1. Introduction
- We propose a framework that effectively models both targets with TSB and false alarm sources with FEBs. This approach aims to address the challenges posed by complex and cluttered backgrounds while maintaining interpretability.
- We introduce a dedicated FEB to estimate potential false alarm sources. By integrating multiple FEBs into the framework, false alarm sources are estimated and eliminated on multiple scales and in a blockwise manner. This block not only enhances the accuracy of our method, but also can serve as a preprocess module to suppress false alarm sources for other ISTD algorithms.
- Extensive experiments on public datasets validated the effectiveness of our model compared to other state-of-the-art approaches. In addition to accurately detecting targets, our model can produce multi-scale false alarm source estimation results. These estimations are not just incidental outcomes; they can be used to generate false alarm source datasets that can contribute to further studies in the field.
2. Related Works
2.1. Image-Structure-Based ISTD
2.2. Deep Learning-Based ISTD
3. Proposed Method
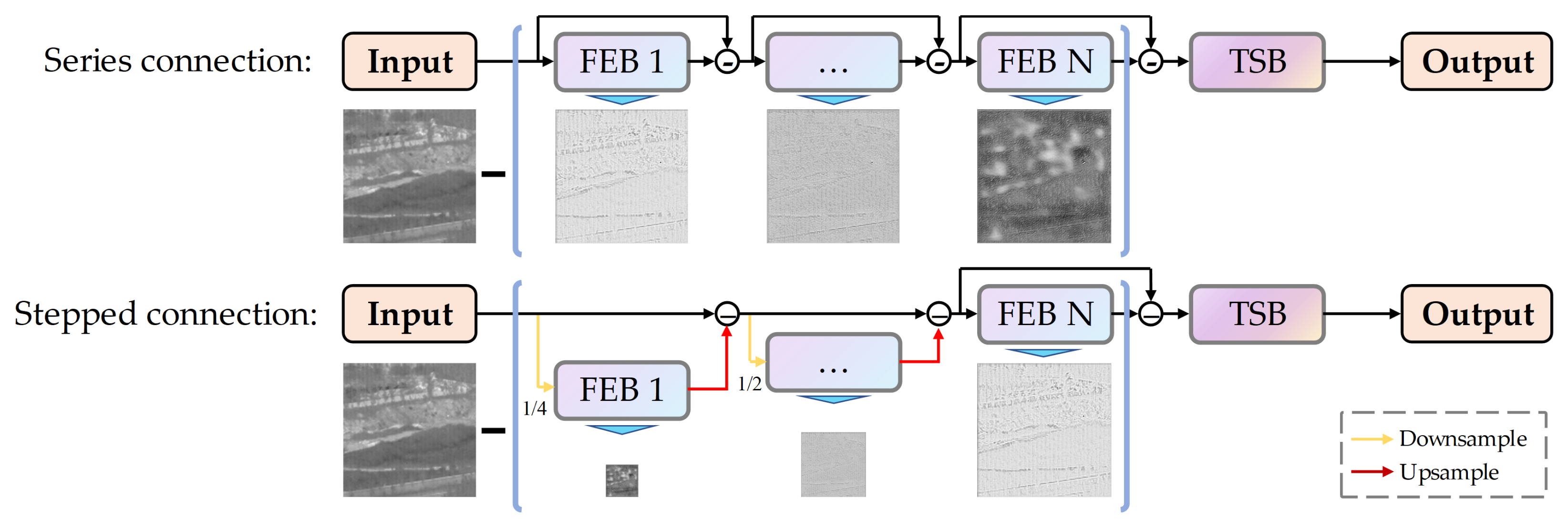
3.1. Overall Framework
3.2. False Alarm Source Estimation Block
3.3. Loss Function
4. Experiments
4.1. Settings
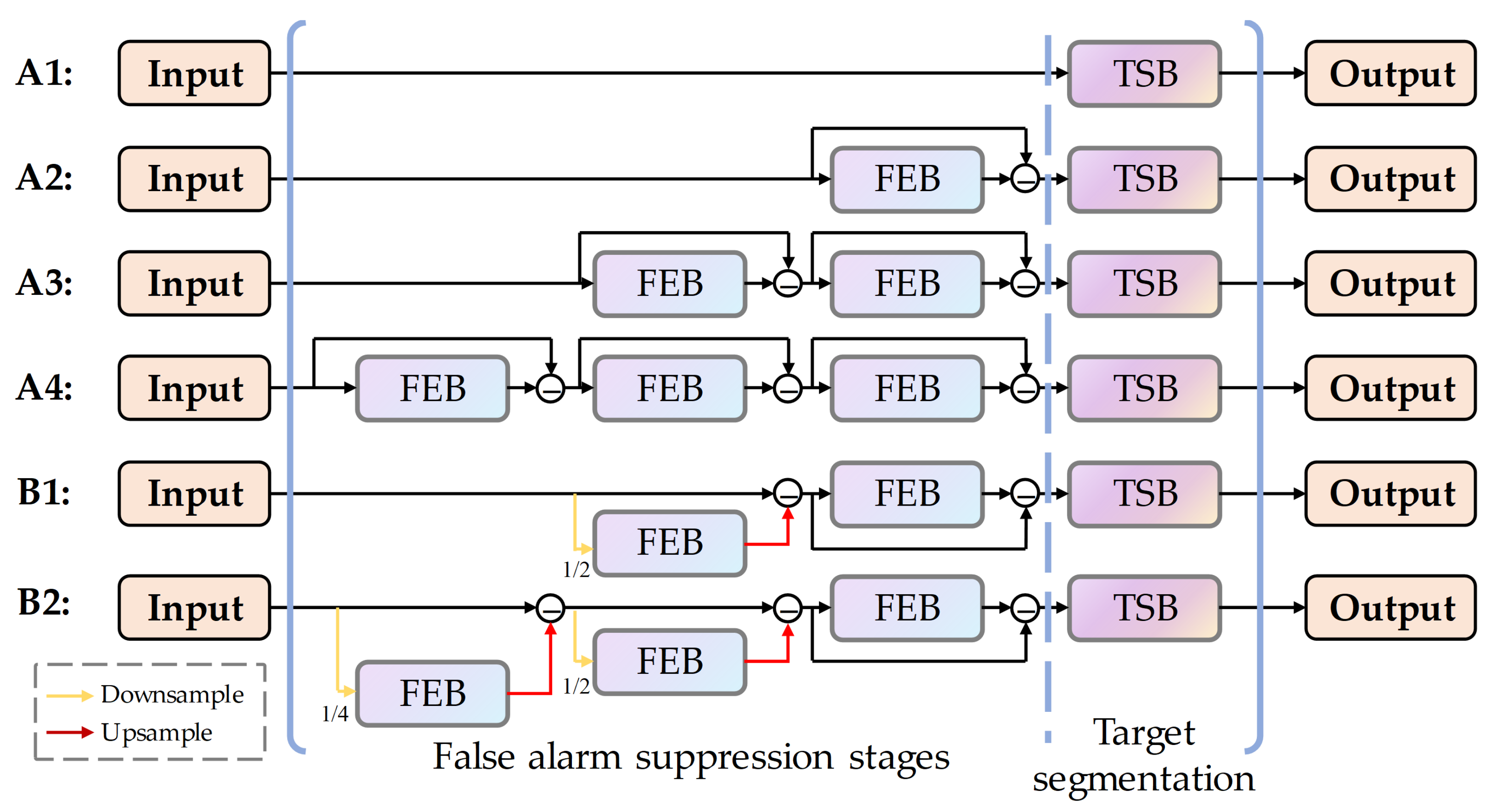
4.2. Ablation Experiments
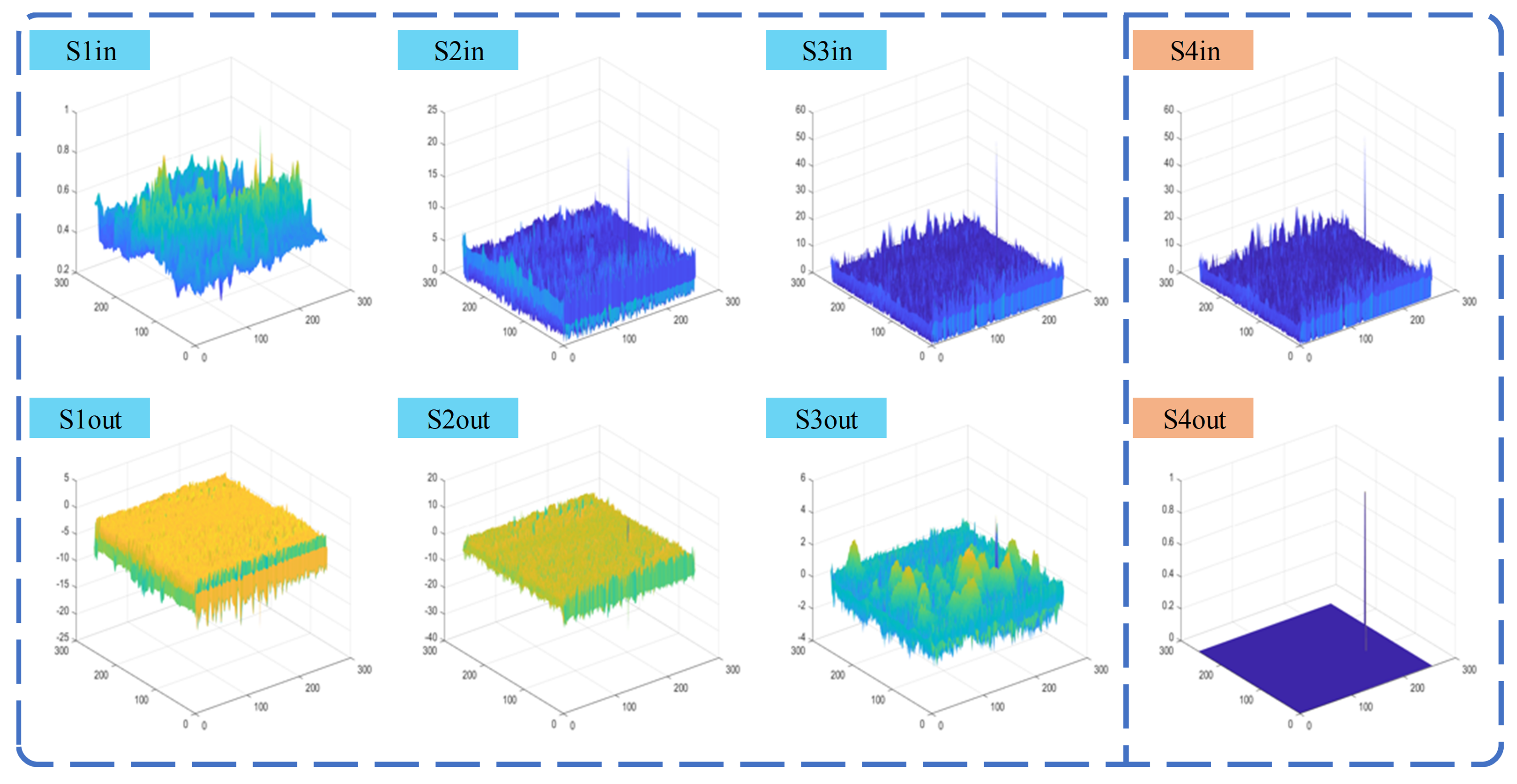
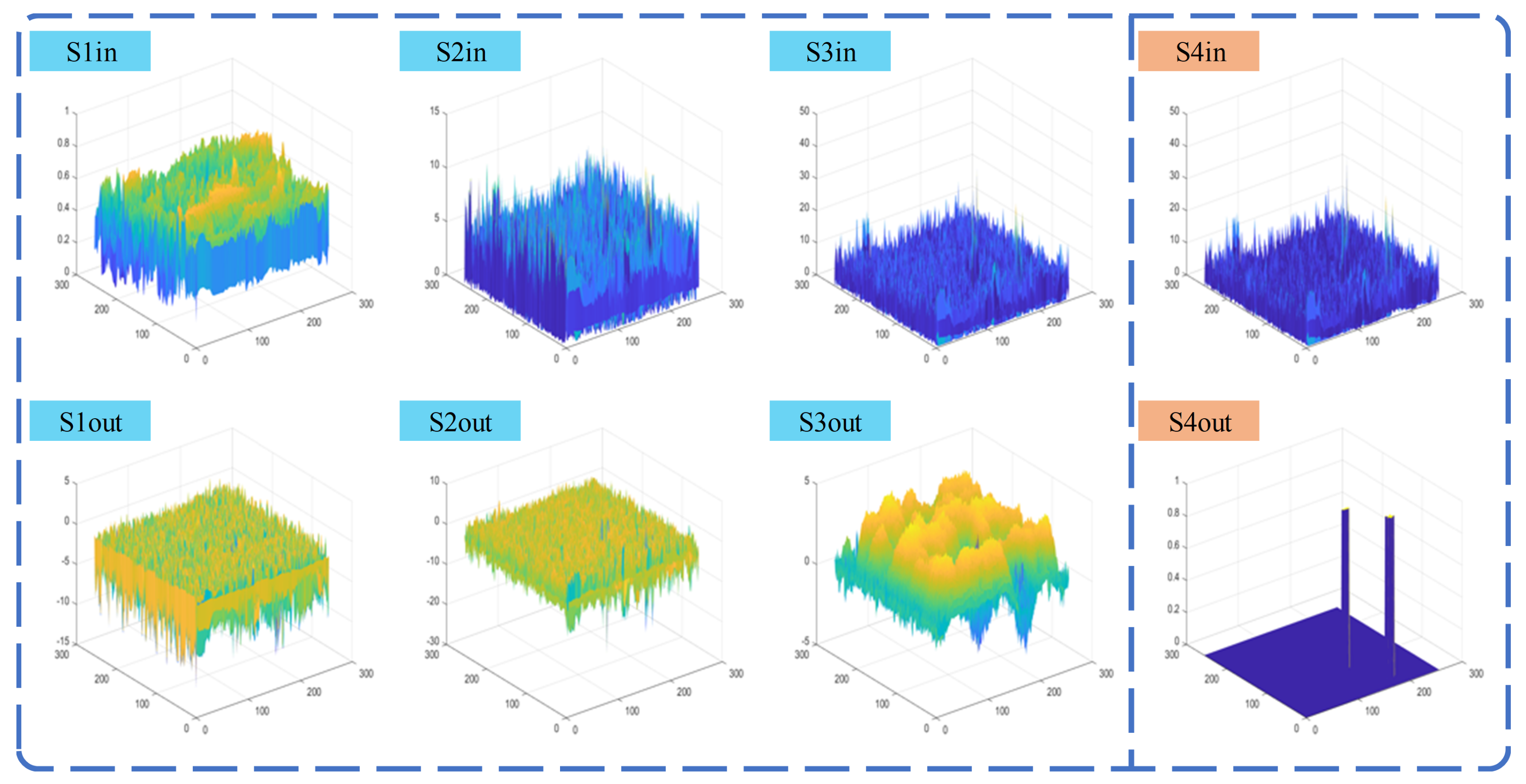
4.3. False Alarm Source Estimation Capability
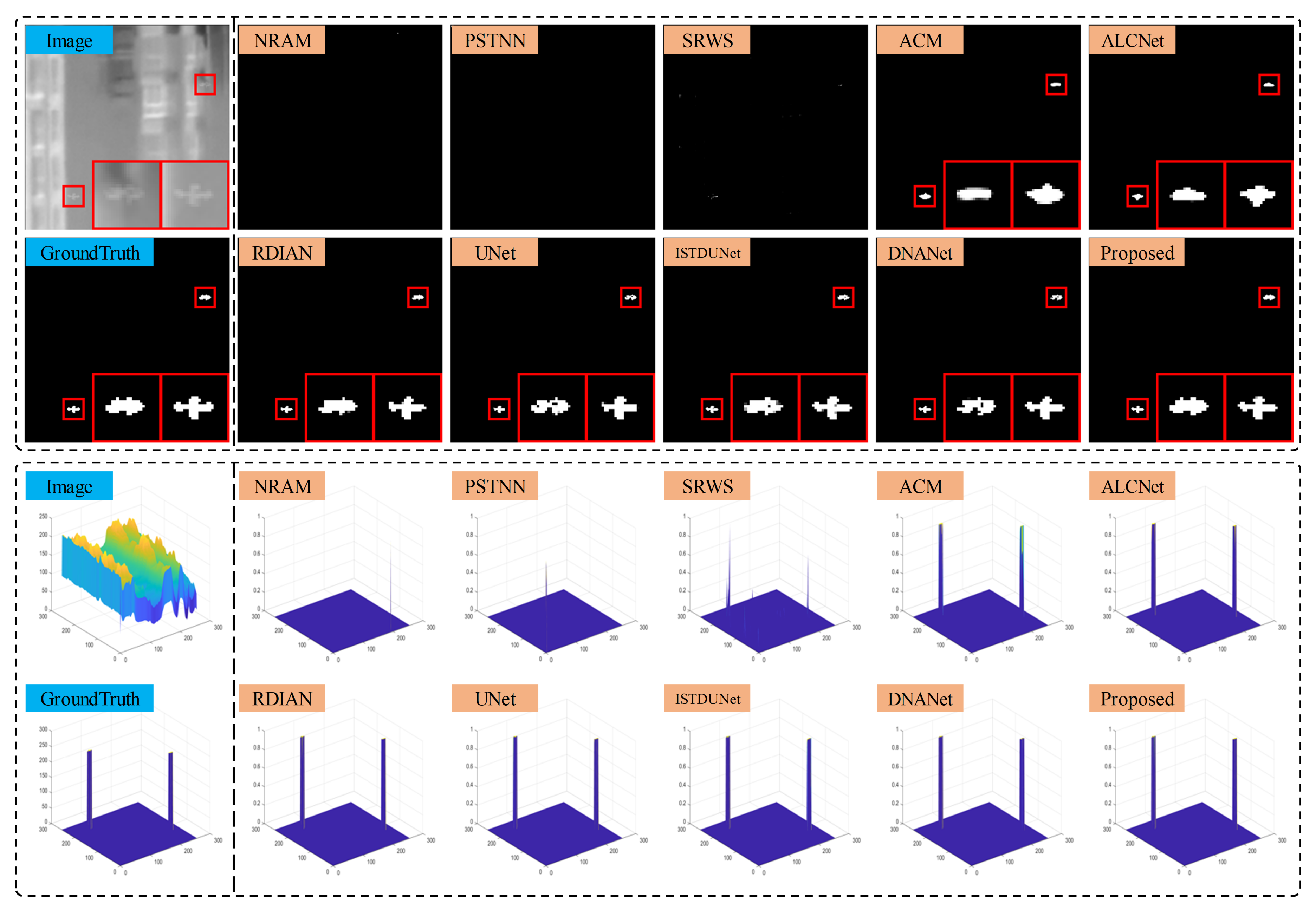
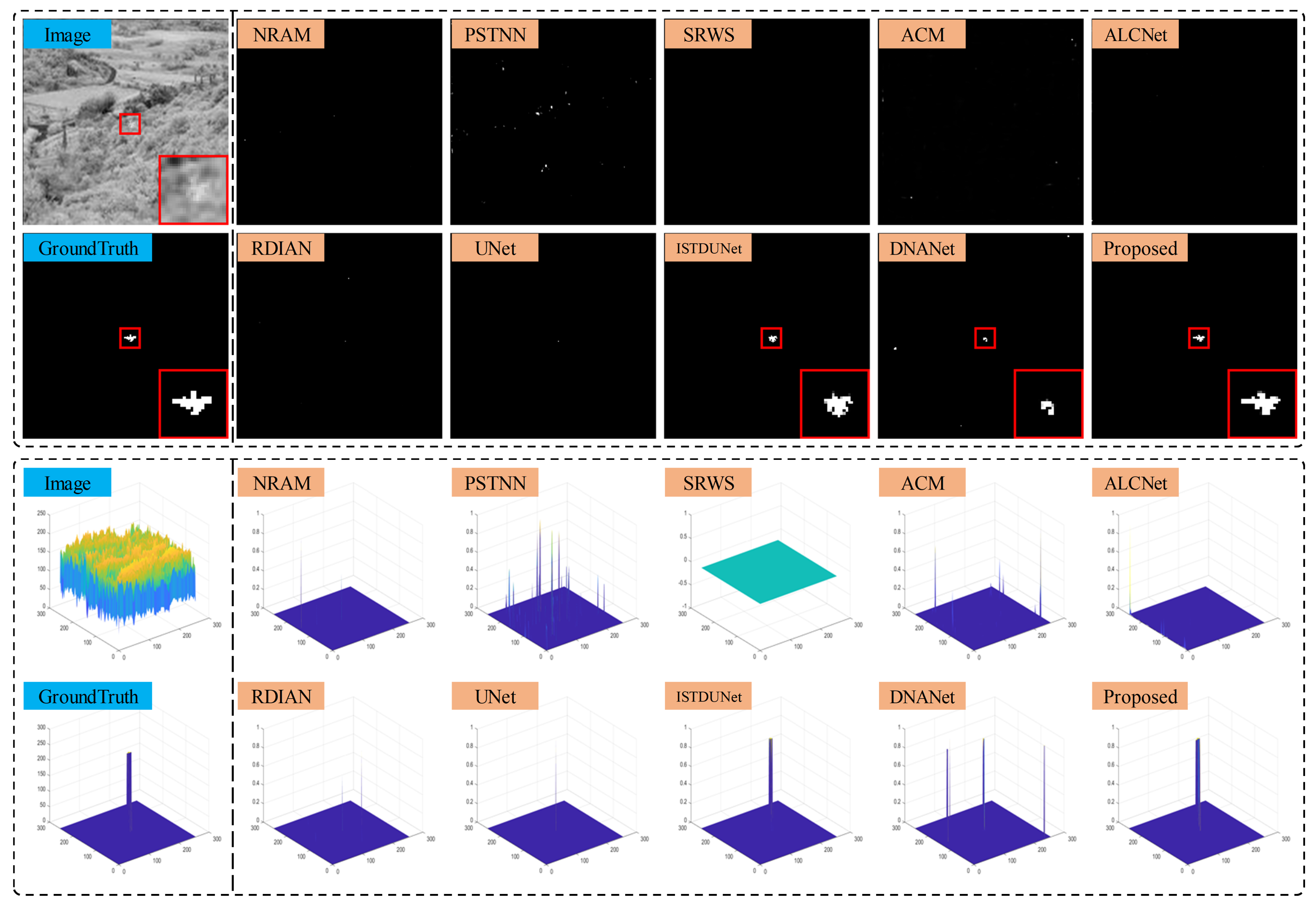
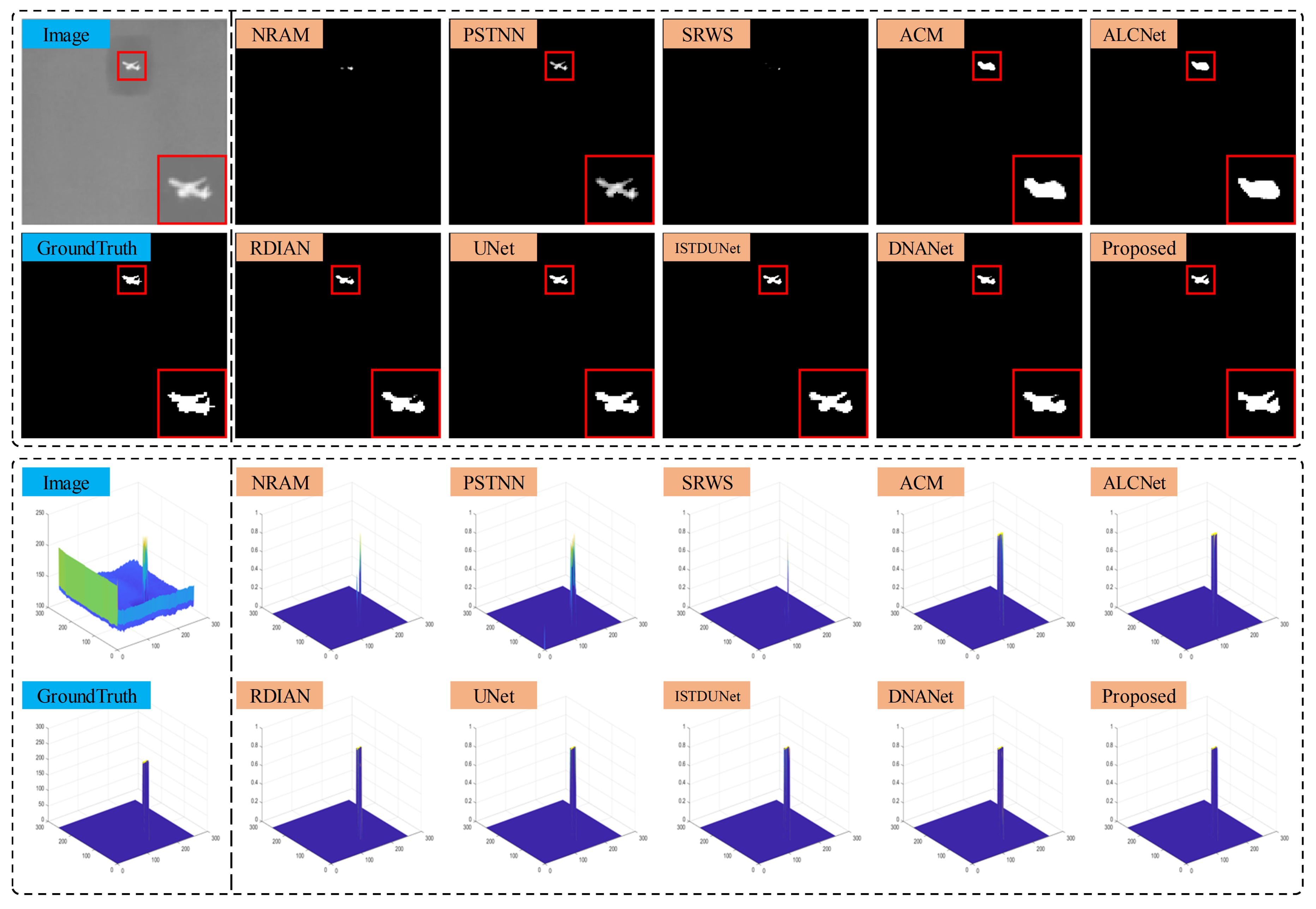
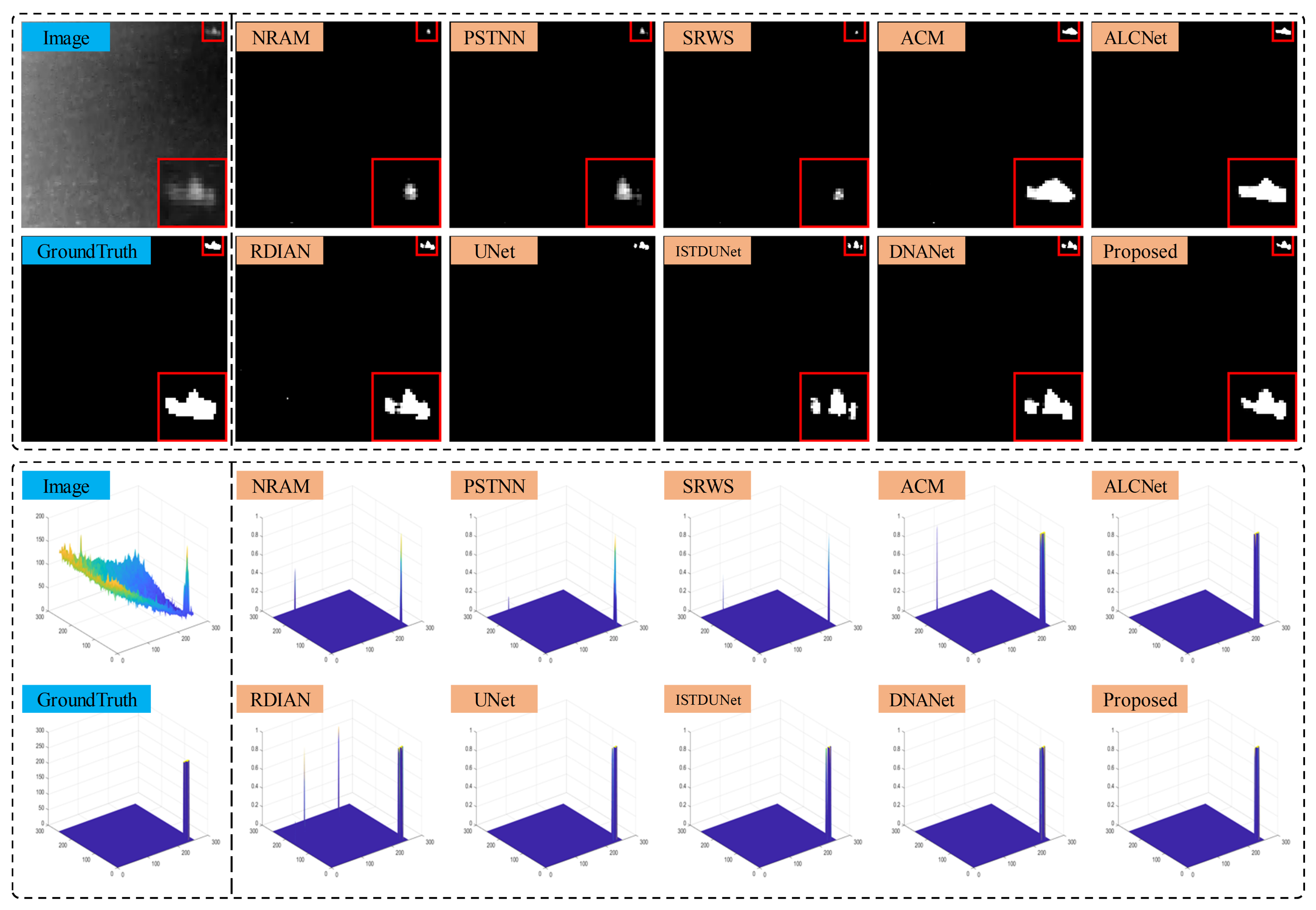
4.4. Comparative Experiments
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Prasad, D.K.; Rajan, D.; Rachmawati, L.; Rajabally, E.; Quek, C. Video Processing From Electro-Optical Sensors for Object Detection and Tracking in a Maritime Environment: A Survey. IEEE Trans. Intell. Transp. Syst. 2017, 18, 1993–2016. [Google Scholar] [CrossRef]
- Kim, S.; Lee, J. Scale invariant small target detection by optimizing signal-to-clutter ratio in heterogeneous background for infrared search and track. Pattern Recognit. 2012, 45, 393–406. [Google Scholar] [CrossRef]
- Filizzola, C.; Corrado, R.; Marchese, F.; Mazzeo, G.; Paciello, R.; Pergola, N.; Tramutoli, V. RST-FIRES, an exportable algorithm for early-fire detection and monitoring: Description, implementation, and field validation in the case of the MSG-SEVIRI sensor. Remote Sens. Environ. 2016, 186, 196–216. [Google Scholar] [CrossRef]
- Thanh, N.T.; Sahli, H.; Hao, D.N. Infrared Thermography for Buried Landmine Detection: Inverse Problem Setting. IEEE Trans. Geosci. Remote Sens. 2008, 46, 3987–4004. [Google Scholar] [CrossRef]
- Kou, R.K.; Wang, C.P.; Peng, Z.M.; Zhao, Z.H.; Chen, Y.H.; Han, J.H.; Huang, F.Y.; Yu, Y.; Fu, Q. Infrared small target segmentation networks: A survey. Pattern Recognit. 2023, 143, 25. [Google Scholar] [CrossRef]
- Rawat, S.S.; Verma, S.K.; Kumar, Y. Review on recent development in infrared small target detection algorithms. In Proceedings of the International Conference on Computational Intelligence and Data Science (ICCIDS), Chennai, India, 20–22 February 2020; Volume 167, pp. 2496–2505. [Google Scholar] [CrossRef]
- Zhang, T.F.; Li, L.; Cao, S.Y.; Pu, T.; Peng, Z.M. Attention-Guided Pyramid Context Networks for Detecting Infrared Small Target under Complex Background. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 4250–4261. [Google Scholar] [CrossRef]
- Deshpande, S.D.; Er, M.H.; Venkateswarlu, R.; Chan, P. Max-mean and max-median filters for detection of small targets. In Signal and Data Processing of Small Targets 1999; Drummond, O.E., Ed.; International Society for Optics and Photonics (SPIE): Bellingham, WA, USA, 1999; Volume 3809, pp. 74–83. [Google Scholar] [CrossRef]
- Liu, Y.H.; Peng, Z.M.; Huang, S.Q.; Wang, Z.R.; Pu, T. River detection using LBP and morphology in infrared image. In Proceedings of the 9th International Symposium on Advanced Optical Manufacturing and Testing Technologies (AOMATT)—Optoelectronic Materials and Devices for Sensing and Imaging, Chengdu, China, 26–29 June 2018; Volume 10843. [Google Scholar] [CrossRef]
- Xiao, S.Y.; Peng, Z.M.; Li, F.S. Infrared Cirrus Detection Using Non-Convex Rank Surrogates for Spatial-Temporal Tensor. Remote Sens. 2023, 15, 2334. [Google Scholar] [CrossRef]
- Kong, X.; Yang, C.P.; Cao, S.Y.; Li, C.H.; Peng, Z.M. Infrared Small Target Detection via Nonconvex Tensor Fibered Rank Approximation. IEEE Trans. Geosci. Remote Sens. 2022, 60, 21. [Google Scholar] [CrossRef]
- Marvasti, F.S.; Mosavi, M.R.; Nasiri, M. Flying small target detection in IR images based on adaptive toggle operator. IET Comput. Vis. 2018, 12, 0327. [Google Scholar] [CrossRef]
- Hu, Y.X.; Ma, Y.P.; Pan, Z.X.; Liu, Y.H. Infrared Dim and Small Target Detection from Complex Scenes via Multi-Frame Spatial-Temporal Patch-Tensor Model. Remote Sens. 2022, 14, 2234. [Google Scholar] [CrossRef]
- Wang, Y.; Cao, L.H.; Su, K.K.; Dai, D.; Li, N.; Wu, D. Infrared Moving Small Target Detection Based on Space-Time Combination in Complex Scenes. Remote Sens. 2023, 15, 5380. [Google Scholar] [CrossRef]
- Ding, L.H.; Xu, X.; Cao, Y.; Zhai, G.T.; Yang, F.; Qian, L. Detection and tracking of infrared small target by jointly using SSD and pipeline filter. Digit. Signal Process. 2021, 110, 9. [Google Scholar] [CrossRef]
- Tom, V.T.; Peli, T.; Leung, M.; Bondaryk, J.E. Morphology-based algorithm for point target detection in infrared backgrounds. In Signal and Data Processing of Small Targets 1993; Drummond, O.E., Ed.; International Society for Optics and Photonics (SPIE): Bellingham, WA, USA, 1993; Volume 1954, pp. 2–11. [Google Scholar] [CrossRef]
- Deng, L.Z.; Zhu, H.; Zhou, Q.; Li, Y.S. Adaptive top-hat filter based on quantum genetic algorithm for infrared small target detection. Multimed. Tools Appl. 2018, 77, 10539–10551. [Google Scholar] [CrossRef]
- Bai, X.Z.; Zhou, F.G. Analysis of new top-hat transformation and the application for infrared dim small target detection. Pattern Recognit. 2010, 43, 2145–2156. [Google Scholar] [CrossRef]
- Kim, S.; Yang, Y.; Lee, J.; Park, Y. Small Target Detection Utilizing Robust Methods of the Human Visual System for IRST. J. Infrared Millim. Terahertz Waves 2009, 30, 994–1011. [Google Scholar] [CrossRef]
- Wei, Y.; You, X.; Li, H. Multiscale patch-based contrast measure for small infrared target detection. Pattern Recognit. 2016, 58, 216–226. [Google Scholar] [CrossRef]
- Qi, S.X.; Xu, G.J.; Mou, Z.Y.; Huang, D.Y.; Zheng, X.L. A fast-saliency method for real-time infrared small target detection. Infrared Phys. Technol. 2016, 77, 440–450. [Google Scholar] [CrossRef]
- Chen, C.L.P.; Li, H.; Wei, Y.T.; Xia, T.; Tang, Y.Y. A Local Contrast Method for Small Infrared Target Detection. IEEE Trans. Geosci. Remote Sens. 2014, 52, 574–581. [Google Scholar] [CrossRef]
- Han, J.H.; Moradi, S.; Faramarzi, I.; Zhang, H.H.; Zhao, Q.; Zhang, X.J.; Li, N. Infrared Small Target Detection Based on the Weighted Strengthened Local Contrast Measure. IEEE Geosci. Remote Sens. Lett. 2021, 18, 1670–1674. [Google Scholar] [CrossRef]
- Lu, R.T.; Yang, X.G.; Li, W.P.; Fan, J.W.; Li, D.L.; Jing, X. Robust Infrared Small Target Detection via Multidirectional Derivative-Based Weighted Contrast Measure. IEEE Geosci. Remote Sens. Lett. 2022, 19, 5. [Google Scholar] [CrossRef]
- Gao, C.Q.; Meng, D.Y.; Yang, Y.; Wang, Y.T.; Zhou, X.F.; Hauptmann, A.G. Infrared Patch-Image Model for Small Target Detection in a Single Image. IEEE Trans. Image Process. 2013, 22, 4996–5009. [Google Scholar] [CrossRef]
- Dai, Y.; Wu, Y.; Song, Y.; Guo, J. Non-negative infrared patch-image model: Robust target-background separation via partial sum minimization of singular values. Infrared Phys. Technol. 2017, 81, 182–194. [Google Scholar] [CrossRef]
- Sun, Y.; Yang, J.; An, W. Infrared small target detection based on reweighted infrared patch-image model and total variation regularization. In Image and Signal Processing for Remote Sensing XXV; Bruzzone, L., Bovolo, F., Eds.; International Society for Optics and Photonics (SPIE): Bellingham, WA, USA, 2019; Volume 11155, p. 111551F. [Google Scholar] [CrossRef]
- Zhu, H.; Ni, H.; Liu, S.; Xu, G.; Deng, L. TNLRS: Target-Aware Non-Local Low-Rank Modeling With Saliency Filtering Regularization for Infrared Small Target Detection. IEEE Trans. Image Process. 2020, 29, 9546–9558. [Google Scholar] [CrossRef] [PubMed]
- Bi, Y.G.; Bai, X.Z.; Jin, T.; Guo, S. Multiple Feature Analysis for Infrared Small Target Detection. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1333–1337. [Google Scholar] [CrossRef]
- Cao, S.Y.; Deng, J.K.; Luo, J.H.; Li, Z.; Hu, J.S.; Peng, Z.M. Local Convergence Index-Based Infrared Small Target Detection against Complex Scenes. Remote Sens. 2023, 15, 1464. [Google Scholar] [CrossRef]
- Li, S.S.; Li, Y.J.; Li, Y.; Li, M.J.; Xu, X.R. YOLO-FIRI: Improved YOLOv5 for Infrared Image Object Detection. IEEE Access 2021, 9, 141861–141875. [Google Scholar] [CrossRef]
- Ma, J.Y.; Tang, L.F.; Xu, M.L.; Zhang, H.; Xiao, G.B. STDFusionNet: An Infrared and Visible Image Fusion Network Based on Salient Target Detection. IEEE Trans. Instrum. Meas. 2021, 70, 13. [Google Scholar] [CrossRef]
- Ryu, J.; Kim, S. Heterogeneous Gray-Temperature Fusion-Based Deep Learning Architecture for Far Infrared Small Target Detection. J. Sens. 2019, 2019, 4658068. [Google Scholar] [CrossRef]
- McIntosh, B.; Venkataramanan, S.; Mahalanobis, A. Infrared Target Detection in Cluttered Environments by Maximization of a Target to Clutter Ratio (TCR) Metric Using a Convolutional Neural Network. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 485–496. [Google Scholar] [CrossRef]
- Dai, Y.M.; Wu, Y.Q.; Zhou, F.; Barnard, K. Asymmetric Contextual Modulation for Infrared Small Target Detection. In Proceedings of the IEEE Winter Conference on Applications of Computer Vision (WACV), Waikoloa, HI, USA, 3–8 January 2021; pp. 949–958. [Google Scholar] [CrossRef]
- Huang, L.; Dai, S.; Huang, T.; Huang, X.; Wang, H. Infrared small target segmentation with multiscale feature representation. Infrared Phys. Technol. 2021, 116, 103755. [Google Scholar] [CrossRef]
- Zhao, B.; Wang, C.; Fu, Q.; Han, Z. A Novel Pattern for Infrared Small Target Detection With Generative Adversarial Network. IEEE Trans. Geosci. Remote Sens. 2021, 59, 4481–4492. [Google Scholar] [CrossRef]
- Chen, F.; Gao, C.; Liu, F.; Zhao, Y.; Zhou, Y.; Meng, D.; Zuo, W. Local Patch Network With Global Attention for Infrared Small Target Detection. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 3979–3991. [Google Scholar] [CrossRef]
- Kou, R.; Wang, C.; Yu, Y.; Peng, Z.; Yang, M.; Huang, F.; Fu, Q. LW-IRSTNet: Lightweight Infrared Small Target Segmentation Network and Application Deployment. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–13. [Google Scholar] [CrossRef]
- Sun, H.; Bai, J.X.; Yang, F.; Bai, X.Z. Receptive-Field and Direction Induced Attention Network for Infrared Dim Small Target Detection With a Large-Scale Dataset IRDST. IEEE Trans. Geosci. Remote Sens. 2023, 61, 13. [Google Scholar] [CrossRef]
- Hou, Q.Y.; Wang, Z.P.; Tan, F.J.; Zhao, Y.; Zheng, H.L.; Zhang, W. RISTDnet: Robust Infrared Small Target Detection Network. IEEE Geosci. Remote Sens. Lett. 2022, 19, 5. [Google Scholar] [CrossRef]
- Wang, H.; Zhou, L.P.; Wang, L. Miss Detection vs. False Alarm: Adversarial Learning for Small Object Segmentation in Infrared Images. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 8508–8517. [Google Scholar] [CrossRef]
- Dai, Y.M.; Wu, Y.Q.; Zhou, F.; Barnard, K. Attentional Local Contrast Networks for Infrared Small Target Detection. IEEE Trans. Geosci. Remote Sens. 2021, 59, 9813–9824. [Google Scholar] [CrossRef]
- Li, B.Y.; Xiao, C.; Wang, L.G.; Wang, Y.Q.; Lin, Z.P.; Li, M.; An, W.; Guo, Y.L. Dense Nested Attention Network for Infrared Small Target Detection. IEEE Trans. Image Process. 2023, 32, 1745–1758. [Google Scholar] [CrossRef] [PubMed]
- Hou, Q.Y.; Zhang, L.W.; Tan, F.J.; Xi, Y.Y.; Zheng, H.L.; Li, N. ISTDU-Net: Infrared Small-Target Detection U-Net. IEEE Geosci. Remote Sens. Lett. 2022, 19, 5. [Google Scholar] [CrossRef]
- Zhang, L.D.; Peng, L.B.; Zhang, T.F.; Cao, S.Y.; Peng, Z.M. Infrared Small Target Detection via Non-Convex Rank Approximation Minimization Joint l(2,1) Norm. Remote Sens. 2018, 10, 1821. [Google Scholar] [CrossRef]
- Zhang, L.D.; Peng, Z.M. Infrared Small Target Detection Based on Partial Sum of the Tensor Nuclear Norm. Remote Sens. 2019, 11, 382. [Google Scholar] [CrossRef]
- Zhang, T.F.; Peng, Z.M.; Wu, H.; He, Y.M.; Li, C.H.; Yang, C.P. Infrared small target detection via self-regularized weighted sparse model. Neurocomputing 2021, 420, 124–148. [Google Scholar] [CrossRef]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You Only Look Once: Unified, Real-Time Object Detection. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 779–788. [Google Scholar] [CrossRef]
- Liu, W.; Anguelov, D.; Erhan, D.; Szegedy, C.; Reed, S.; Fu, C.Y.; Berg, A.C. SSD: Single Shot MultiBox Detector. In Computer Vision—ECCV 2016, PT I; Leibe, B., Matas, J., Sebe, N., Welling, M., Eds.; Springer International Publishing AG: Cham, Switzerland, 2016; Volume 9905, pp. 21–37. [Google Scholar] [CrossRef]
- Long, J.; Shelhamer, E.; Darrell, T. Fully Convolutional Networks for Semantic Segmentation. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 3431–3440. [Google Scholar] [CrossRef]
- Girshick, R. Fast R-CNN. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1440–1448. [Google Scholar] [CrossRef]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 1137–1149. [Google Scholar] [CrossRef] [PubMed]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the 18th International Conference on Medical Image Computing and Computer-Assisted Intervention (MICCAI), Munich, Germany, 5–9 October 2015; Volume 9351, pp. 234–241. [Google Scholar] [CrossRef]
- He, K.M.; Zhang, X.Y.; Ren, S.Q.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef]
- Nair, V.; Hinton, G.E. Rectified linear units improve restricted boltzmann machines. In Proceedings of the 27th International Conference on International Conference on Machine Learning, Madison, WI, USA, 21–24 June 2010; pp. 807–814. [Google Scholar]
- Zhang, K.; Zuo, W.M.; Chen, Y.J.; Meng, D.Y.; Zhang, L. Beyond a Gaussian Denoiser: Residual Learning of Deep CNN for Image Denoising. IEEE Trans. Image Process. 2017, 26, 3142–3155. [Google Scholar] [CrossRef] [PubMed]
- Tripathi, P.C.; Bag, S. CNN-DMRI: A Convolutional Neural Network for Denoising of Magnetic Resonance Images. Pattern Recognit. Lett. 2020, 135, 57–63. [Google Scholar] [CrossRef]
- Rahman, M.A.; Wang, Y. Optimizing Intersection-Over-Union in Deep Neural Networks for Image Segmentation. In Advances in Visual Computing; Springer: Cham, Switzerland, 2016; pp. 234–244. [Google Scholar]
- Chang, C.I. An Effective Evaluation Tool for Hyperspectral Target Detection: 3D Receiver Operating Characteristic Curve Analysis. IEEE Trans. Geosci. Remote Sens. 2021, 59, 5131–5153. [Google Scholar] [CrossRef]
- Luo, Y.; Li, X.; Chen, S.; Xia, C.; Zhao, L. IMNN-LWEC: A Novel Infrared Small Target Detection Based on Spatial–Temporal Tensor Model. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–22. [Google Scholar] [CrossRef]










| Structure | NUAA-SIRST | NUDT-SIRST | ||||
|---|---|---|---|---|---|---|
| A1 | 65.49 | 92.02 | 88.9 | 78.23 | 90.79 | 41.09 |
| A2 | 67.13 | 94.3 | 108.94 | 91.19 | 97.04 | 18.67 |
| A3 | 68.65 | 94.30 | 103.52 | 92.66 | 97.46 | 16.63 |
| A4 | 66.95 | 93.92 | 104.45 | 92.43 | 97.88 | 17.61 |
| B1 | 62.06 | 91.63 | 120.15 | 75.11 | 93.76 | 68.85 |
| B2 | 58.86 | 95.06 | 148.97 | 54.34 | 84.34 | 149.49 |
| Method | ||||
|---|---|---|---|---|
| NRAM | 11.4 | 58.52 | 23.45 | 20.47 |
| PSTNN | 21.69 | 68.04 | 216.64 | 35.65 |
| SRWS | 8.69 | 66.35 | 9.27 | 15.99 |
| ACM | 67.65 | 95.77 | 138.66 | 80.71 |
| ALCNet | 69.93 | 94.92 | 118.31 | 82.31 |
| RDIAN | 86.93 | 97.25 | 34.19 | 93.01 |
| UNet | 89.84 | 96.4 | 19.89 | 94.65 |
| ISTDUNet | 89.73 | 97.88 | 29.76 | 94.58 |
| DNANet | 91.63 | 97.46 | 22.74 | 95.63 |
| Proposed | 92.66 | 97.99 | 17.01 | 96.19 |
| Method | ||||
|---|---|---|---|---|
| NRAM | 26.17 | 81.75 | 10.27 | 41.49 |
| PSTNN | 41.69 | 84.79 | 56.51 | 58.84 |
| SRWS | 12.36 | 84.79 | 4.00 | 22.00 |
| ACM | 63.49 | 92.78 | 113.08 | 77.67 |
| ALCNet | 64.52 | 93.54 | 117.79 | 78.43 |
| RDIAN | 70.46 | 93.54 | 95.89 | 82.67 |
| UNet | 68.28 | 93.16 | 98.39 | 81.15 |
| ISTDUNet | 66.66 | 92.78 | 104.24 | 79.99 |
| DNANet | 69.23 | 93.16 | 104.38 | 81.86 |
| Proposed | 69.38 | 93.16 | 91.82 | 81.92 |
| Method | ||||||||
|---|---|---|---|---|---|---|---|---|
| NRAM | 0.6067 | 0.1209 | 0.0050 | 0.7276 | 0.6118 | 24.0264 | 0.1159 | 0.7226 |
| PSTNN | 0.7556 | 0.2860 | 0.0053 | 1.0416 | 0.7609 | 53.7055 | 0.2807 | 1.0362 |
| SRWS | 0.6210 | 0.1019 | 0.0050 | 0.7229 | 0.6261 | 20.2999 | 0.0969 | 0.7179 |
| ACM | 0.9406 | 0.8161 | 0.0051 | 1.7566 | 0.9457 | 158.6904 | 0.8109 | 1.7515 |
| ALCNet | 0.9233 | 0.8261 | 0.0051 | 1.7494 | 0.9285 | 161.3891 | 0.8210 | 1.7443 |
| RDIAN | 0.9713 | 0.9331 | 0.0050 | 1.9045 | 0.9764 | 185.3606 | 0.9281 | 1.8994 |
| UNet | 0.9691 | 0.9255 | 0.0050 | 1.8946 | 0.9741 | 184.3357 | 0.9205 | 1.8896 |
| ISTDUNet | 0.9778 | 0.9369 | 0.0050 | 1.9148 | 0.9828 | 186.2700 | 0.9319 | 1.9097 |
| DNANet | 0.9757 | 0.9483 | 0.0050 | 1.9240 | 0.9807 | 188.8106 | 0.9433 | 1.9190 |
| Proposed | 0.9782 | 0.9504 | 0.0050 | 1.9287 | 0.9833 | 189.3753 | 0.9454 | 1.9237 |
| Method | ||||||||
|---|---|---|---|---|---|---|---|---|
| NRAM | 0.7335 | 0.2656 | 0.0050 | 0.9990 | 0.7385 | 52.8825 | 0.2605 | 0.9940 |
| PSTNN | 0.8406 | 0.4227 | 0.0051 | 1.2632 | 0.8457 | 82.9856 | 0.4176 | 1.2581 |
| SRWS | 0.6709 | 0.1429 | 0.0050 | 0.8139 | 0.6759 | 28.5292 | 0.1379 | 0.8089 |
| ACM | 0.9146 | 0.7524 | 0.0051 | 1.6670 | 0.9197 | 147.1186 | 0.7473 | 1.6619 |
| ALCNet | 0.9053 | 0.7717 | 0.0051 | 1.6770 | 0.9104 | 150.7933 | 0.7666 | 1.6719 |
| RDIAN | 0.9227 | 0.8171 | 0.0051 | 1.7398 | 0.9278 | 160.3318 | 0.8120 | 1.7347 |
| UNet | 0.9092 | 0.7951 | 0.0051 | 1.7043 | 0.9143 | 155.9492 | 0.7900 | 1.6992 |
| ISTDUNet | 0.9125 | 0.7829 | 0.0051 | 1.6955 | 0.9176 | 153.3739 | 0.7778 | 1.6904 |
| DNANet | 0.9178 | 0.8191 | 0.0051 | 1.7369 | 0.9229 | 160.4584 | 0.8140 | 1.7318 |
| Proposed | 0.9098 | 0.8056 | 0.0051 | 1.7154 | 0.9151 | 154.0000 | 0.8003 | 1.7102 |
| Method | Params () | Inference (ms) | Training on NUAA (s/epoch) | Training on NUDT (s/epoch) |
|---|---|---|---|---|
| ACM | 0.3978 | 3.905 | 1.5274 | 4.5036 |
| ALCNet | 0.4270 | 3.894 | 1.4335 | 4.7769 |
| RDIAN | 0.2166 | 2.757 | 2.6016 | 8.2245 |
| UNet | 34.5259 | 2.116 | 4.1787 | 13.0852 |
| ISTDUNet | 2.7519 | 13.489 | 6.4446 | 18.6608 |
| DNANet | 4.6966 | 15.819 | 8.4540 | 26.3606 |
| Proposed | 1.4501 | 4.203 | 3.9463 | 12.4757 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, S.; Li, Z.; Deng, J.; Huang, Y.; Peng, Z. TFCD-Net: Target and False Alarm Collaborative Detection Network for Infrared Imagery. Remote Sens. 2024, 16, 1758. https://doi.org/10.3390/rs16101758
Cao S, Li Z, Deng J, Huang Y, Peng Z. TFCD-Net: Target and False Alarm Collaborative Detection Network for Infrared Imagery. Remote Sensing. 2024; 16(10):1758. https://doi.org/10.3390/rs16101758
Chicago/Turabian StyleCao, Siying, Zhi Li, Jiakun Deng, Yi’an Huang, and Zhenming Peng. 2024. "TFCD-Net: Target and False Alarm Collaborative Detection Network for Infrared Imagery" Remote Sensing 16, no. 10: 1758. https://doi.org/10.3390/rs16101758
APA StyleCao, S., Li, Z., Deng, J., Huang, Y., & Peng, Z. (2024). TFCD-Net: Target and False Alarm Collaborative Detection Network for Infrared Imagery. Remote Sensing, 16(10), 1758. https://doi.org/10.3390/rs16101758







