Enhancing Semi-Supervised Few-Shot Hyperspectral Image Classification via Progressive Sample Selection
Abstract
1. Introduction
- We identified the key challenges in FS HSI classification and performed a comprehensive analysis of the spatial–spectral consistency presented in HSI data. We thus designed an efficient pseudo-label selection strategy that fully utilizes this property and incorporates the feature distribution of abundant unlabeled samples.
- In addition to the proposed pseudo-labeling model, we propose an AL approach for expert annotation selection based on the temporal spatial–spectral confidence difference to mitigate the randomness of initial FS training samples, thereby expanding the utilization of unlabeled samples.
- The extensive experimental results demonstrate that our base model manages to achieve state-of-the-art performance without any bells and whistles, even when provided with extremely limited labeled samples. Furthermore, the incorporation of the AL approach enhances performance at the cost of limited expert annotations.
2. Related Work
2.1. Semi-Supervised Learning Methods
2.2. Active Learning Methods
3. Proposed Method
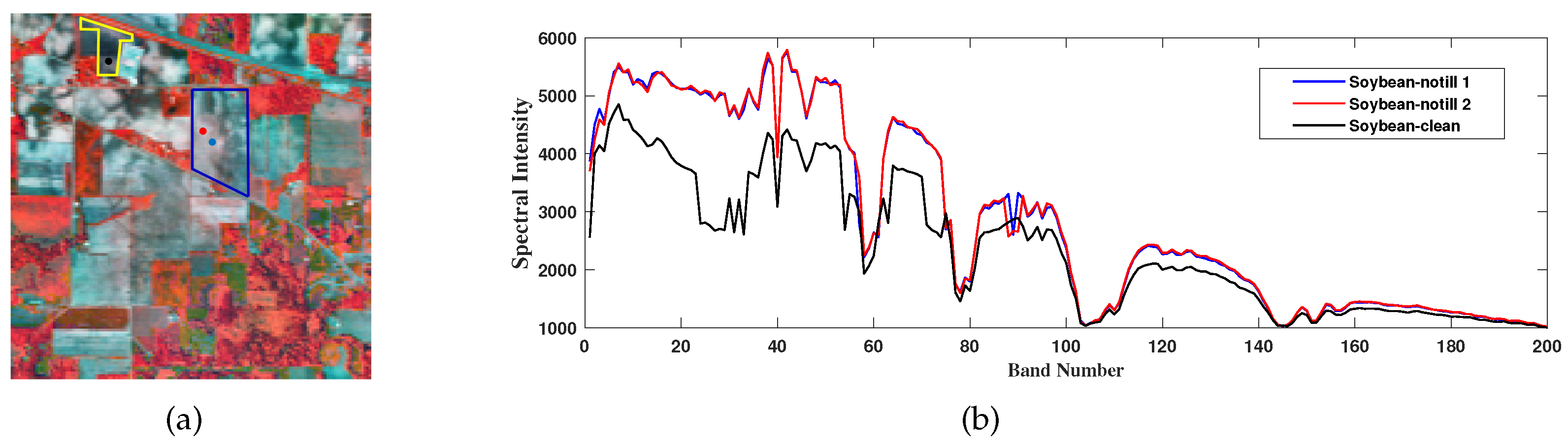
3.1. Generic Pseudo-Labeling FS HSI Classification and Limitations
3.2. Progressive Pseudo-Label Selection Guided by Spatial–Spectral Consistency
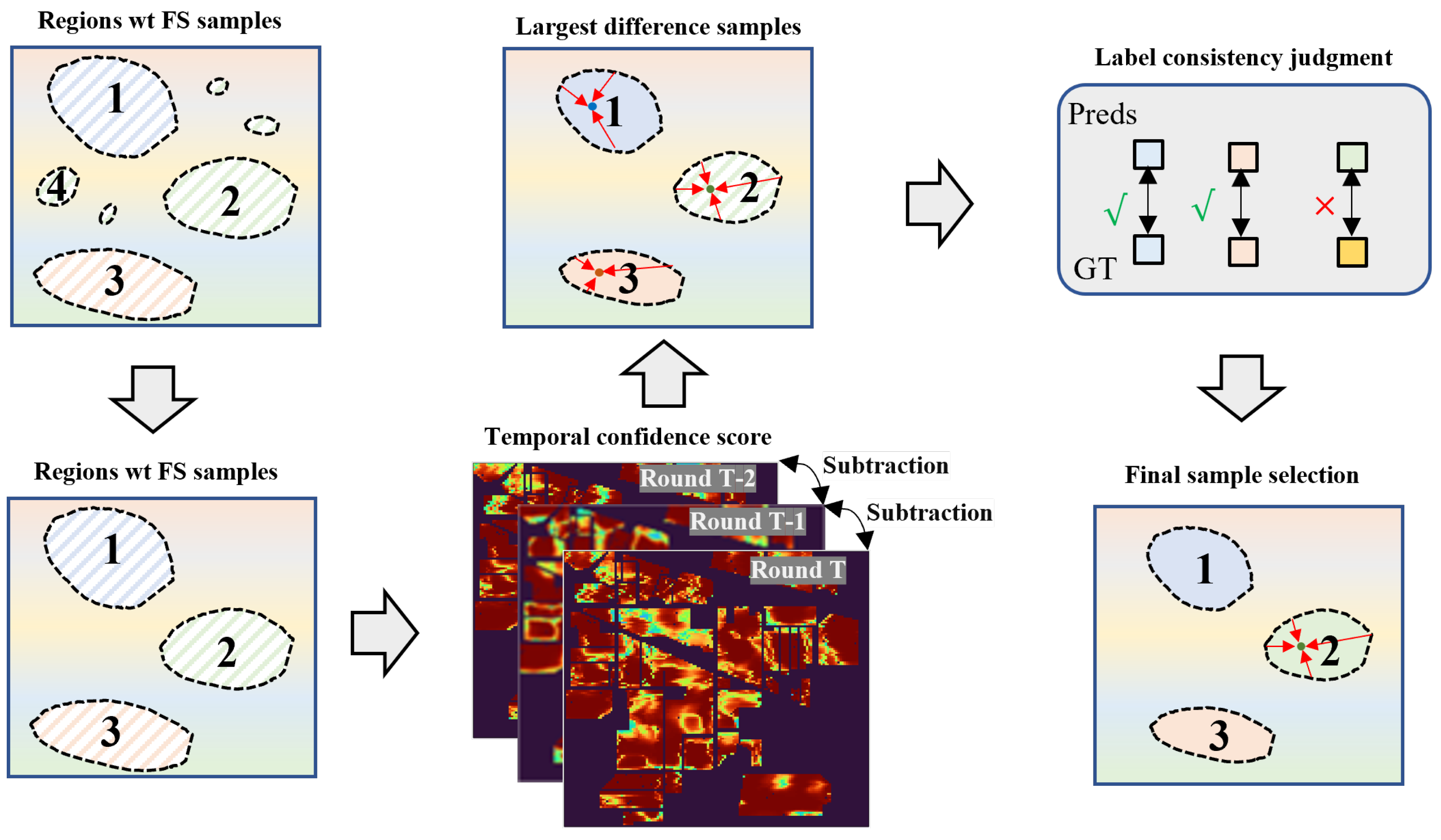
3.3. Incorporation of Active Learning
| Algorithm 1 Expanding reliable training set via progressive sample selection |
| Input: FS-labeled set ; unlabeled set ; max training rounds R; confidence threshold ; connected region sample size threshold ; initialized model ; |
| Output: Model |
| 1: Training initialized model with |
| 2: for to R do |
| 3: Get confidence score and label of via Equations (2) and (3) |
| 4: Generate two maps and via Equations (4) and (5) |
| 5: Obtain connected regions of by eight-neighborhood method |
| 6: Select regions that contain FS training samples as Equation (6) |
| 7: Merge pseudo-labeled samples as for next iteration as Equation (7) |
| 8: Density-weighted selection is adopted for remaining regions via Equation (8) |
| 9: Get predicted label for samples in via Equations (9) and (10) |
| 10: Augment for next round as Equation (11) Re-train using as training set |
| 11: end for |
3.4. Hybrid Classification Framework
3.4.1. Conv Block
3.4.2. Encoder Block
3.4.3. Inference
4. Experimental Analysis
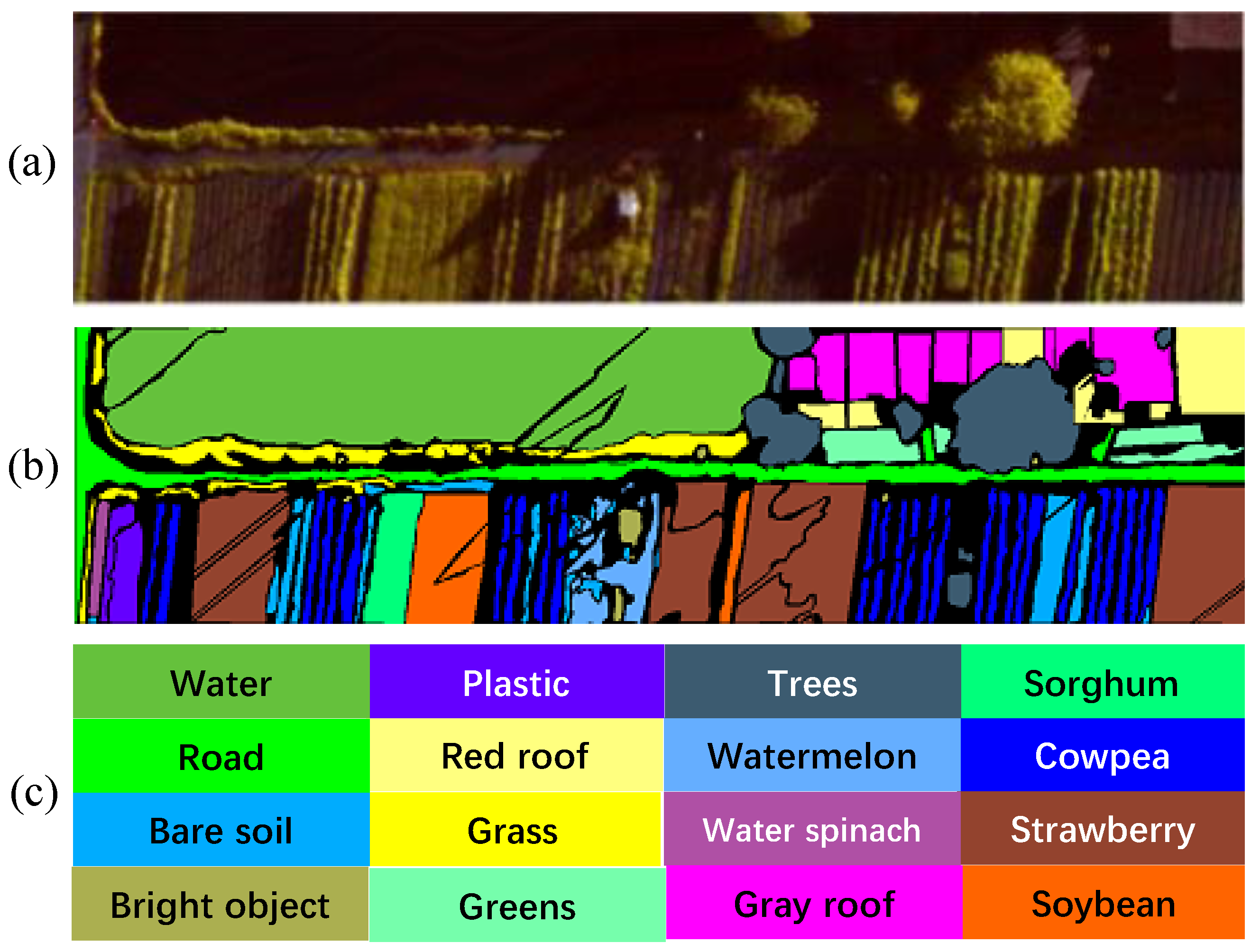
4.1. Datasets
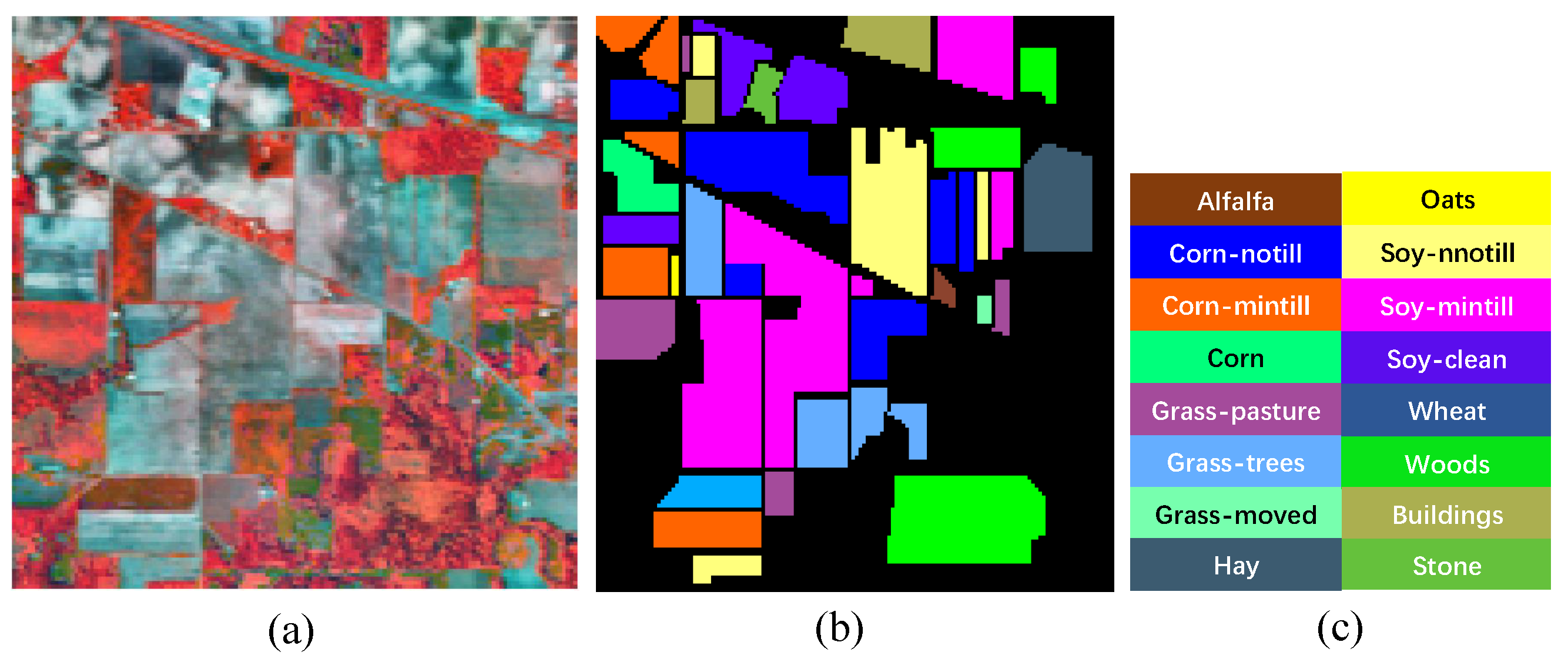
4.1.1. IP Dataset
4.1.2. PU Dataset
4.1.3. HC Dataset
4.1.4. HH Dataset
4.2. Evaluation Metrics
4.3. Implementation Details
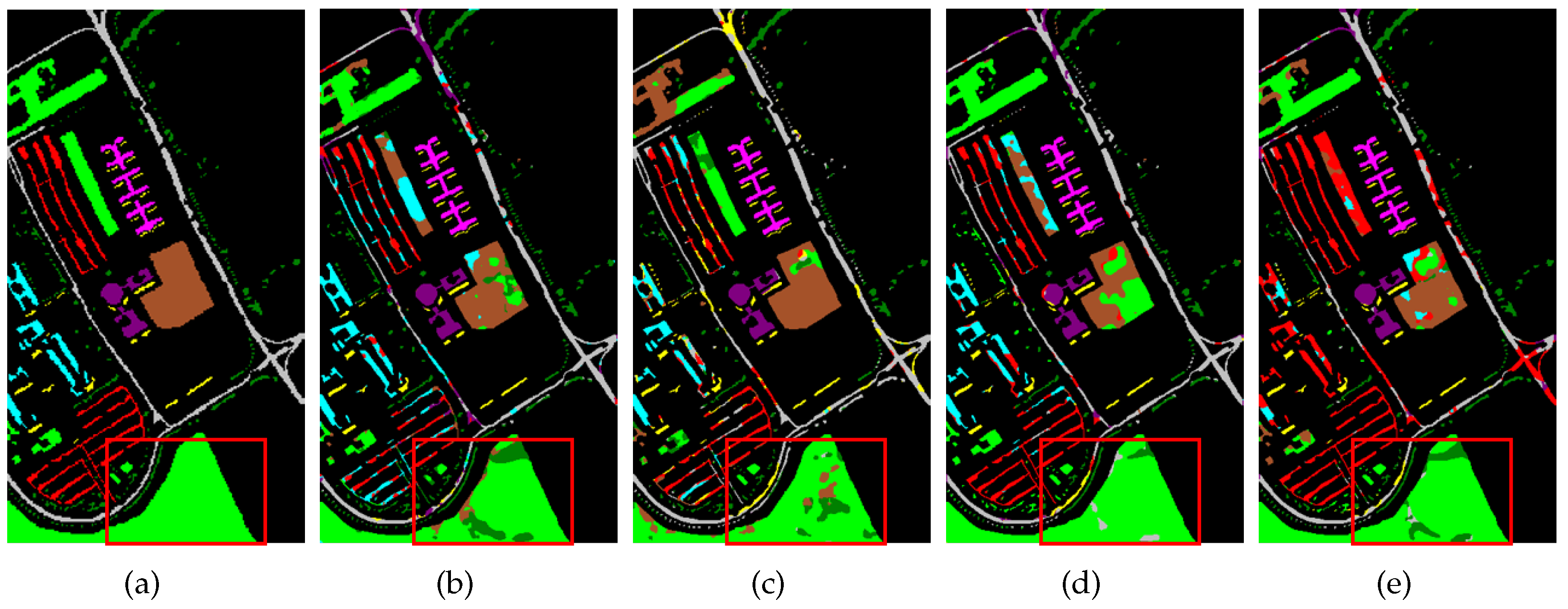
4.4. Results and Analysis
4.4.1. IP Dataset Result
4.4.2. PU Dataset Result
4.4.3. HC Dataset Result
4.4.4. HH Dataset Result
4.5. Hyperparameter Sensitivity
4.5.1. Convergence Analysis
4.5.2. Confidence Threshold
4.5.3. Connected Region Size Threshold
4.6. Ablation Study
4.6.1. Pseudo-Label Selection Strategy
4.6.2. AL Strategy
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Roy, S.K.; Krishna, G.; Dubey, S.R.; Chaudhuri, B.B. HybridSN: Exploring 3-D–2-D CNN Feature Hierarchy for Hyperspectral Image Classification. IEEE Geosci. Remote Sens. Lett. 2020, 17, 277–281. [Google Scholar] [CrossRef]
- Santara, A.; Mani, K.; Hatwar, P.; Singh, A.; Garg, A.; Padia, K.; Mitra, P. BASS Net: Band-Adaptive Spectral-Spatial Feature Learning Neural Network for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5293–5301. [Google Scholar] [CrossRef]
- Hong, D.; Han, Z.; Yao, J.; Gao, L.; Zhang, B.; Plaza, A.; Chanussot, J. SpectralFormer: Rethinking Hyperspectral Image Classification With Transformers. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5518615. [Google Scholar] [CrossRef]
- Sun, H.; Zheng, X.; Lu, X.; Wu, S. Spectral–Spatial Attention Network for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2020, 58, 3232–3245. [Google Scholar] [CrossRef]
- Sun, H.; Zheng, X.; Lu, X. A Supervised Segmentation Network for Hyperspectral Image Classification. IEEE Trans. Image Process. 2021, 30, 2810–2825. [Google Scholar] [CrossRef]
- Nalepa, J.; Myller, M.; Kawulok, M. Hyperspectral Data Augmentation. arXiv 2019, arXiv:1903.05580. [Google Scholar]
- Li, W.; Chen, C.; Zhang, M.; Li, H.; Du, Q. Data Augmentation for Hyperspectral Image Classification with Deep CNN. IEEE Geosci. Remote Sens. Lett. 2019, 16, 593–597. [Google Scholar] [CrossRef]
- Haut, J.M.; Paoletti, M.E.; Plaza, J.; Plaza, A.; Li, J. Hyperspectral Image Classification Using Random Occlusion Data Augmentation. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1751–1755. [Google Scholar] [CrossRef]
- Li, W.; Wu, G.; Zhang, F.; Du, Q. Hyperspectral Image Classification Using Deep Pixel-Pair Features. IEEE Trans. Geosci. Remote Sens. 2017, 55, 844–853. [Google Scholar] [CrossRef]
- Zhang, C.; Yue, J.; Qin, Q. Global Prototypical Network for Few-Shot Hyperspectral Image Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 4748–4759. [Google Scholar] [CrossRef]
- Li, Z.; Liu, M.; Chen, Y.; Xu, Y.; Li, W.; Du, Q. Deep Cross-Domain Few-Shot Learning for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5501618. [Google Scholar] [CrossRef]
- Zhao, L.; Luo, W.; Liao, Q.; Chen, S.; Wu, J. Hyperspectral Image Classification with Contrastive Self-Supervised Learning Under Limited Labeled Samples. IEEE Geosci. Remote Sens. Lett. 2022, 19, 6008205. [Google Scholar] [CrossRef]
- Feng, J.; Zhao, N.; Shang, R.; Zhang, X.; Jiao, L. Self-Supervised Divide-and-Conquer Generative Adversarial Network for Classification of Hyperspectral Images. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5536517. [Google Scholar] [CrossRef]
- Li, X.; Cao, Z.; Zhao, L.; Jiang, J. ALPN: Active-Learning-Based Prototypical Network for Few-Shot Hyperspectral Imagery Classification. IEEE Geosci. Remote. Sens. Lett. 2022, 19, 5508305. [Google Scholar] [CrossRef]
- Ding, C.; Zheng, M.; Chen, F.; Zhang, Y.; Zhuang, X.; Fan, E.; Wen, D.; Zhang, L.; Wei, W.; Zhang, Y. Hyperspectral Image Classification Promotion Using Clustering Inspired Active Learning. Remote Sens. 2022, 14, 596. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, L.; Zhao, R.; Shi, Z. A Bayesian Meta-Learning-Based Method for Few-Shot Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5500613. [Google Scholar] [CrossRef]
- Tang, H.; Li, Y.; Han, X.; Huang, Q.; Xie, W. A Spatial–Spectral Prototypical Network for Hyperspectral Remote Sensing Image. IEee Geosci. Remote Sens. Lett. 2020, 17, 167–171. [Google Scholar] [CrossRef]
- Seydgar, M.; Rahnamayan, S.; Ghamisi, P.; Bidgoli, A.A. Semisupervised Hyperspectral Image Classification Using a Probabilistic Pseudo-Label Generation Framework. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5535218. [Google Scholar] [CrossRef]
- Yao, W.; Lian, C.; Bruzzone, L. ClusterCNN: Clustering-Based Feature Learning for Hyperspectral Image Classification. IEEE Geosci. Remote Sens. Lett. 2021, 18, 1991–1995. [Google Scholar] [CrossRef]
- Zhang, L.; Xu, J.; Zhang, J.; Gong, Y. Information enhancement for travelogues via a hybrid clustering model. In Proceedings of the 2018 Digital Image Computing: Techniques and Applications (DICTA), Canberra, ACT, Australia, 10–13 December 2018; pp. 1–8. [Google Scholar]
- Zhong, S.; Zhou, T.; Wan, S.; Yang, J.; Gong, C. Dynamic Spectral–Spatial Poisson Learning for Hyperspectral Image Classification With Extremely Scarce Labels. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5517615. [Google Scholar] [CrossRef]
- Tuia, D.; Ratle, F.; Pacifici, F.; Kanevski, M.F.; Emery, W.J. Active Learning Methods for Remote Sensing Image Classification. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2218–2232. [Google Scholar] [CrossRef]
- Li, J.; Bioucas-Dias, J.M.; Plaza, A. Supervised hyperspectral image segmentation using active learning. In Proceedings of the 2010 2nd Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing, Reykjavik, Iceland, 14–16 June 2010; pp. 1–4. [Google Scholar] [CrossRef]
- Tuia, D.; Volpi, M.; Copa, L.; Kanevski, M.; Munoz-Mari, J. A Survey of Active Learning Algorithms for Supervised Remote Sensing Image Classification. IEEE J. Sel. Top. Signal Process. 2011, 5, 606–617. [Google Scholar] [CrossRef]
- Roy, S.K.; Mondal, R.; Paoletti, M.E.; Haut, J.M.; Plaza, A. Morphological Convolutional Neural Networks for Hyperspectral Image Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 8689–8702. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, H.; Shen, Q. Spectral–Spatial Classification of Hyperspectral Imagery with 3D Convolutional Neural Network. Remote Sens. 2017, 9, 67. [Google Scholar] [CrossRef]
- Zhou, F.; Hang, R.; Liu, Q.; Yuan, X. Hyperspectral image classification using spectral-spatial LSTMs. Neurocomputing 2019, 328, 39–47. [Google Scholar] [CrossRef]
- Tan, K.; Zhou, S.; Du, Q. Semisupervised Discriminant Analysis for Hyperspectral Imagery With Block-Sparse Graph. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1765–1769. [Google Scholar] [CrossRef]
- Krishnapuram, B.; Carin, L.; Figueiredo, M.A.T.; Hartemink, A.J. Sparse multinomial logistic regression: Fast algorithms and generalization bounds. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 957–968. [Google Scholar] [CrossRef] [PubMed]
- Gong, Z.; Tong, L.; Zhou, J.; Qian, B.; Duan, L.; Xiao, C. Superpixel Spectral–Spatial Feature Fusion Graph Convolution Network for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5536216. [Google Scholar] [CrossRef]
- Zhang, H.; Zou, J.; Zhang, L. EMS-GCN: An End-to-End Mixhop Superpixel-Based Graph Convolutional Network for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5526116. [Google Scholar] [CrossRef]
- Wang, W.; Liu, F.; Liao, W.; Xiao, L. Cross-Modal Graph Knowledge Representation and Distillation Learning for Land Cover Classification. IEee Trans. Geosci. Remote Sens. 2023, 61, 5520318. [Google Scholar] [CrossRef]
- Liu, Q.; Xiao, L.; Yang, J.; Wei, Z. CNN-Enhanced Graph Convolutional Network with Pixel- and Superpixel-Level Feature Fusion for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2021, 59, 8657–8671. [Google Scholar] [CrossRef]
- Ding, C.; Li, Y.; Wen, Y.; Zheng, M.; Zhang, L.; Wei, W.; Zhang, Y. Boosting few-shot hyperspectral image classification using pseudo-label learning. Remote Sens. 2021, 13, 3539. [Google Scholar] [CrossRef]
- Cui, B.; Cui, J.; Lu, Y.; Guo, N.; Gong, M. A sparse representation-based sample pseudo-labeling method for hyperspectral image classification. Remote Sens. 2020, 12, 664. [Google Scholar] [CrossRef]
- Yue, J.; Fang, L.; Rahmani, H.; Ghamisi, P. Self-Supervised Learning with Adaptive Distillation for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5501813. [Google Scholar] [CrossRef]
- Tong, X.; Yin, J.; Han, B.; Qv, H. Few-Shot Learning With Attention-Weighted Graph Convolutional Networks For Hyperspectral Image Classification. In Proceedings of the 2020 IEEE International Conference on Image Processing (ICIP), Abu Dhabi, United Arab Emirates, 25–28 October 2020; pp. 1686–1690. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, L.; Wei, W.; Zhang, Y. Deep Self-Supervised Learning for Few-Shot Hyperspectral Image Classification. In Proceedings of the IGARSS 2020—2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September 2020–2 October 2020; pp. 501–504. [Google Scholar] [CrossRef]
- Liu, S.; Luo, H.; Tu, Y.; He, Z.; Li, J. Wide Contextual Residual Network with Active Learning for Remote Sensing Image Classification. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 7145–7148. [Google Scholar] [CrossRef]
- Yang, J.; Qin, J.; Qian, J.; Li, A.; Wang, L. AL-MRIS: An Active Learning-Based Multipath Residual Involution Siamese Network for Few-Shot Hyperspectral Image Classification. Remote Sens. 2024, 16, 990. [Google Scholar] [CrossRef]
- Wang, J.; Li, L.; Liu, Y.; Hu, J.; Xiao, X.; Liu, B. AI-TFNet: Active Inference Transfer Convolutional Fusion Network for Hyperspectral Image Classification. Remote Sens. 2023, 15, 1292. [Google Scholar] [CrossRef]
- Liu, C.; He, L.; Li, Z.; Li, J. Feature-Driven Active Learning for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2018, 56, 341–354. [Google Scholar] [CrossRef]
- Sun, L.; Zhao, G.; Zheng, Y.; Wu, Z. Spectral–Spatial Feature Tokenization Transformer for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5522214. [Google Scholar] [CrossRef]
- Song, W.; Li, S.; Fang, L.; Lu, T. Hyperspectral Image Classification with Deep Feature Fusion Network. IEEE Trans. Geosci. Remote Sens. 2018, 56, 3173–3184. [Google Scholar] [CrossRef]
- Xue, Z.; Zhou, Y.; Du, P. S3Net: Spectral–Spatial Siamese Network for Few-Shot Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5531219. [Google Scholar] [CrossRef]
- Zeng, J.; Xue, Z.; Zhang, L.; Lan, Q.; Zhang, M. Multistage Relation Network with Dual-Metric for Few-Shot Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5510017. [Google Scholar] [CrossRef]
- Zheng, Z.; Zhong, Y.; Ma, A.; Zhang, L. FPGA: Fast Patch-Free Global Learning Framework for Fully End-to-End Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2020, 58, 5612–5626. [Google Scholar] [CrossRef]
- Zhong, S.; Chen, S.; Chang, C.I.; Zhang, Y. Fusion of Spectral–Spatial Classifiers for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2021, 59, 5008–5027. [Google Scholar] [CrossRef]
- Zheng, C.; Wang, N.; Cui, J. Hyperspectral Image Classification with Small Training Sample Size Using Superpixel-Guided Training Sample Enlargement. IEEE Trans. Geosci. Remote Sens. 2019, 57, 7307–7316. [Google Scholar] [CrossRef]
- Hu, L.; He, W.; Zhang, L.; Zhang, H. Cross-Domain Meta-Learning Under Dual-Adjustment Mode for Few-Shot Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5526416. [Google Scholar] [CrossRef]
- Zhong, Z.; Li, J.; Luo, Z.; Chapman, M. Spectral–Spatial Residual Network for Hyperspectral Image Classification: A 3-D Deep Learning Framework. IEEE Trans. Geosci. Remote Sens. 2018, 56, 847–858. [Google Scholar] [CrossRef]
- Roy, S.K.; Manna, S.; Song, T.; Bruzzone, L. Attention-Based Adaptive Spectral–Spatial Kernel ResNet for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2021, 59, 7831–7843. [Google Scholar] [CrossRef]


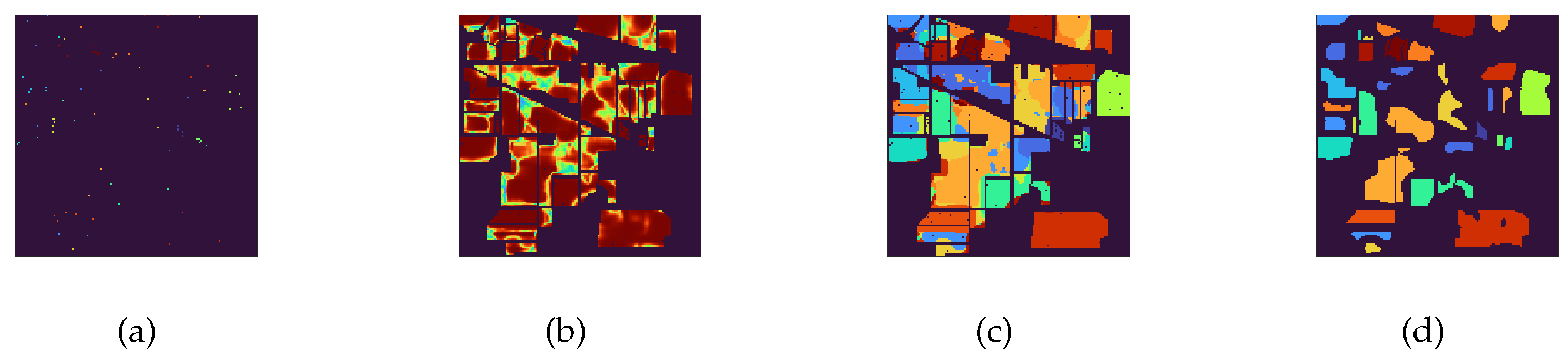










| Class | SSFTT | S3Net | DM-MRN | FPGA | FSS | STSE-DWLR | DSSPL | Ours: rPL | Ours: rPL-AL |
|---|---|---|---|---|---|---|---|---|---|
| 1 | |||||||||
| 2 | |||||||||
| 3 | |||||||||
| 4 | |||||||||
| 5 | |||||||||
| 6 | |||||||||
| 7 | |||||||||
| 8 | |||||||||
| 9 | |||||||||
| 10 | |||||||||
| 11 | |||||||||
| 12 | |||||||||
| 13 | |||||||||
| 14 | |||||||||
| 15 | |||||||||
| 16 | |||||||||
| OA | |||||||||
| AA | |||||||||
| Kappa |
| Class | SSFTT | S3Net | DM-MRN | FPGA | FSS | STSE-DWLR | DSSPL | Ours: rPL | Ours: rPL-AL |
|---|---|---|---|---|---|---|---|---|---|
| 1 | |||||||||
| 2 | |||||||||
| 3 | |||||||||
| 4 | |||||||||
| 5 | |||||||||
| 6 | |||||||||
| 7 | |||||||||
| 8 | |||||||||
| 9 | |||||||||
| OA | |||||||||
| AA | |||||||||
| Kappa |
| Class | SSFTT | S3Net | DM-MRN | MDMC | FPGA | SSRN | A2S2K-ResNet | Ours: rPL | Ours: rPL-AL |
|---|---|---|---|---|---|---|---|---|---|
| 1 | |||||||||
| 2 | |||||||||
| 3 | |||||||||
| 4 | |||||||||
| 5 | |||||||||
| 6 | |||||||||
| 7 | |||||||||
| 8 | |||||||||
| 9 | |||||||||
| 10 | |||||||||
| 11 | |||||||||
| 12 | |||||||||
| 13 | |||||||||
| 14 | |||||||||
| 15 | |||||||||
| 16 | |||||||||
| OA | |||||||||
| AA | |||||||||
| Kappa |
| Class | SSFTT | S3Net | DM-MRN | MDMC | FPGA | SSRN | A2S2K-ResNet | Ours: rPL | Ours: rPL-AL |
|---|---|---|---|---|---|---|---|---|---|
| 1 | |||||||||
| 2 | |||||||||
| 3 | |||||||||
| 4 | |||||||||
| 5 | |||||||||
| 6 | |||||||||
| 7 | |||||||||
| 8 | |||||||||
| 9 | |||||||||
| 10 | |||||||||
| 11 | |||||||||
| 12 | |||||||||
| 13 | |||||||||
| 14 | |||||||||
| 15 | |||||||||
| 16 | |||||||||
| 17 | |||||||||
| 18 | |||||||||
| 19 | |||||||||
| 20 | |||||||||
| 21 | |||||||||
| 22 | |||||||||
| OA | |||||||||
| AA | |||||||||
| Kappa |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, J.; Zhang, J.; Huang, H.; Zhang, J. Enhancing Semi-Supervised Few-Shot Hyperspectral Image Classification via Progressive Sample Selection. Remote Sens. 2024, 16, 1747. https://doi.org/10.3390/rs16101747
Zhao J, Zhang J, Huang H, Zhang J. Enhancing Semi-Supervised Few-Shot Hyperspectral Image Classification via Progressive Sample Selection. Remote Sensing. 2024; 16(10):1747. https://doi.org/10.3390/rs16101747
Chicago/Turabian StyleZhao, Jiaguo, Junjie Zhang, Huaxi Huang, and Jian Zhang. 2024. "Enhancing Semi-Supervised Few-Shot Hyperspectral Image Classification via Progressive Sample Selection" Remote Sensing 16, no. 10: 1747. https://doi.org/10.3390/rs16101747
APA StyleZhao, J., Zhang, J., Huang, H., & Zhang, J. (2024). Enhancing Semi-Supervised Few-Shot Hyperspectral Image Classification via Progressive Sample Selection. Remote Sensing, 16(10), 1747. https://doi.org/10.3390/rs16101747






