Physics-Informed Deep Learning Inversion with Application to Noisy Magnetotelluric Measurements
Abstract
:1. Introduction
2. Problem Statement
3. Methods
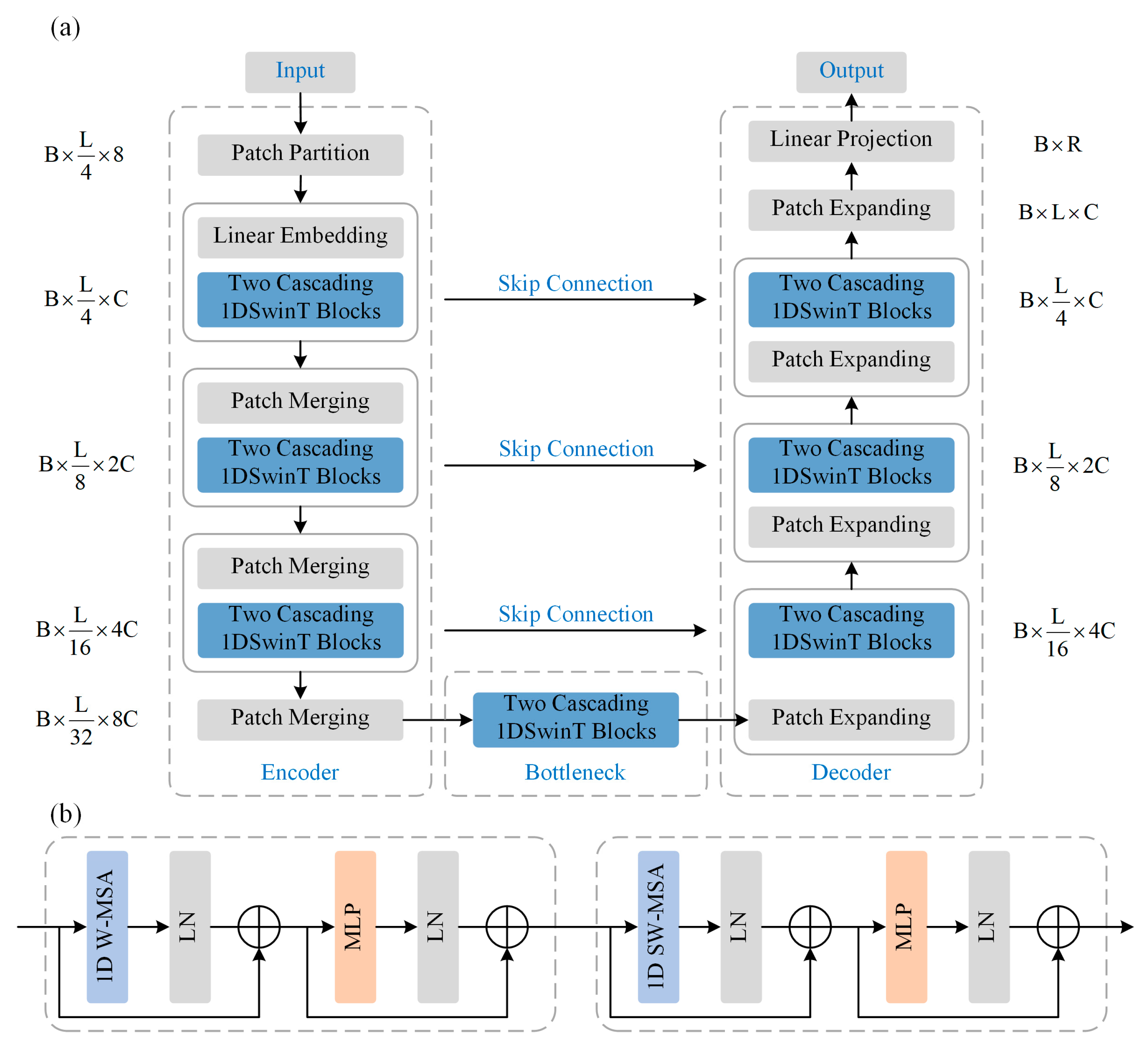
3.1. Neural Network Architecture
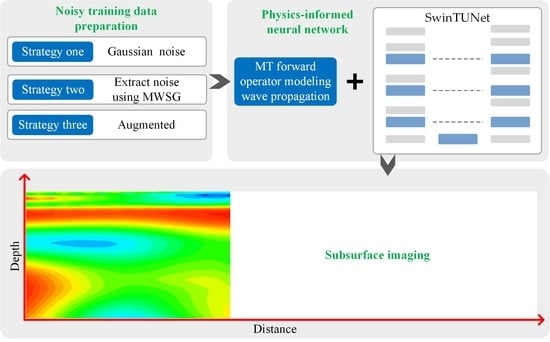
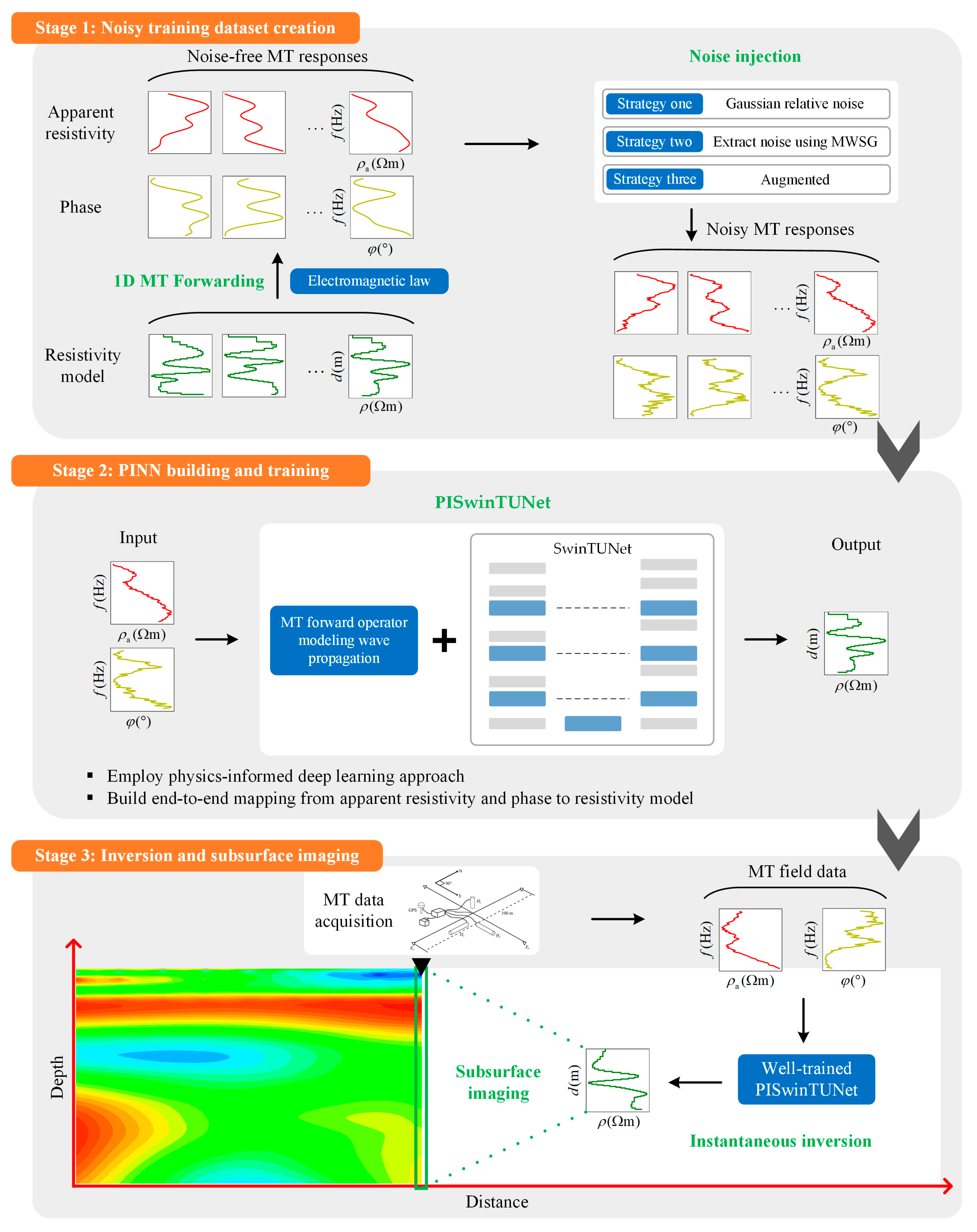
3.2. Noisy Injection Strategies
3.2.1. Strategy One
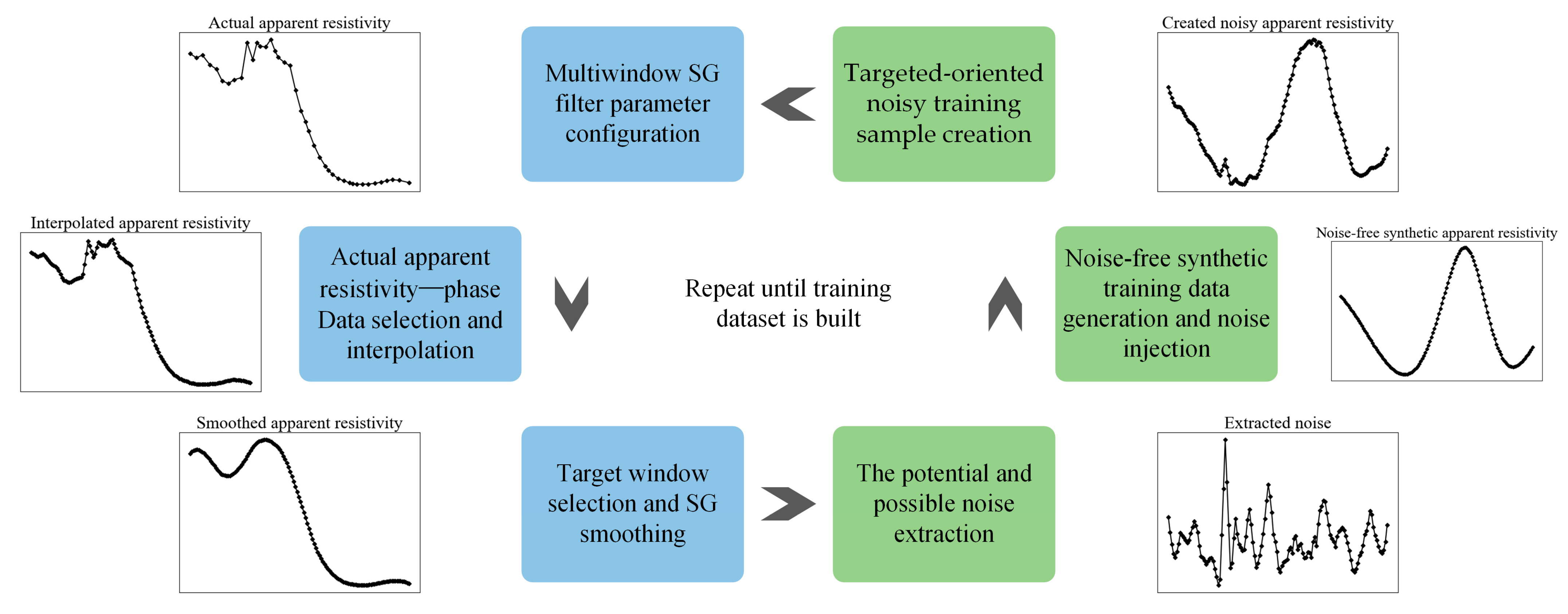
3.2.2. Strategy Two
- Set the polynomial order as 3 and predefine the multiple window set encompassing windows with different sizes (the window size has to be odd; [39,40]). The window set can be formulated as:where represents the ith window with a size of . Following Liu et al. [41], the largest window size is set to 65 (), and thus, the corresponding window number is 31.
- Randomly select an from the MT field dataset and convert it to using linear interpolation.
- Randomly select a target window from the window set and apply the SG filter to smooth . Express the smoothed as .
- Extract the potential and possible noise from and following:where and denote the extracted noises from the actual apparent resistivity and phase data, respectively.
- Generate a noise-free synthetic training sample following the data preparation method described in the following Section 3.3, and obtain the noisy training input data by adding the extracted noises and in the apparent resistivity and phase data following:where and denote the noisy apparent resistivity and phase data, respectively.
- Repeat steps 2 to 5 until the noisy training dataset is built.
3.2.3. Strategy Three
3.3. DL Inversion Scheme
4. Results
4.1. Synthetic Example with Familiar Noise
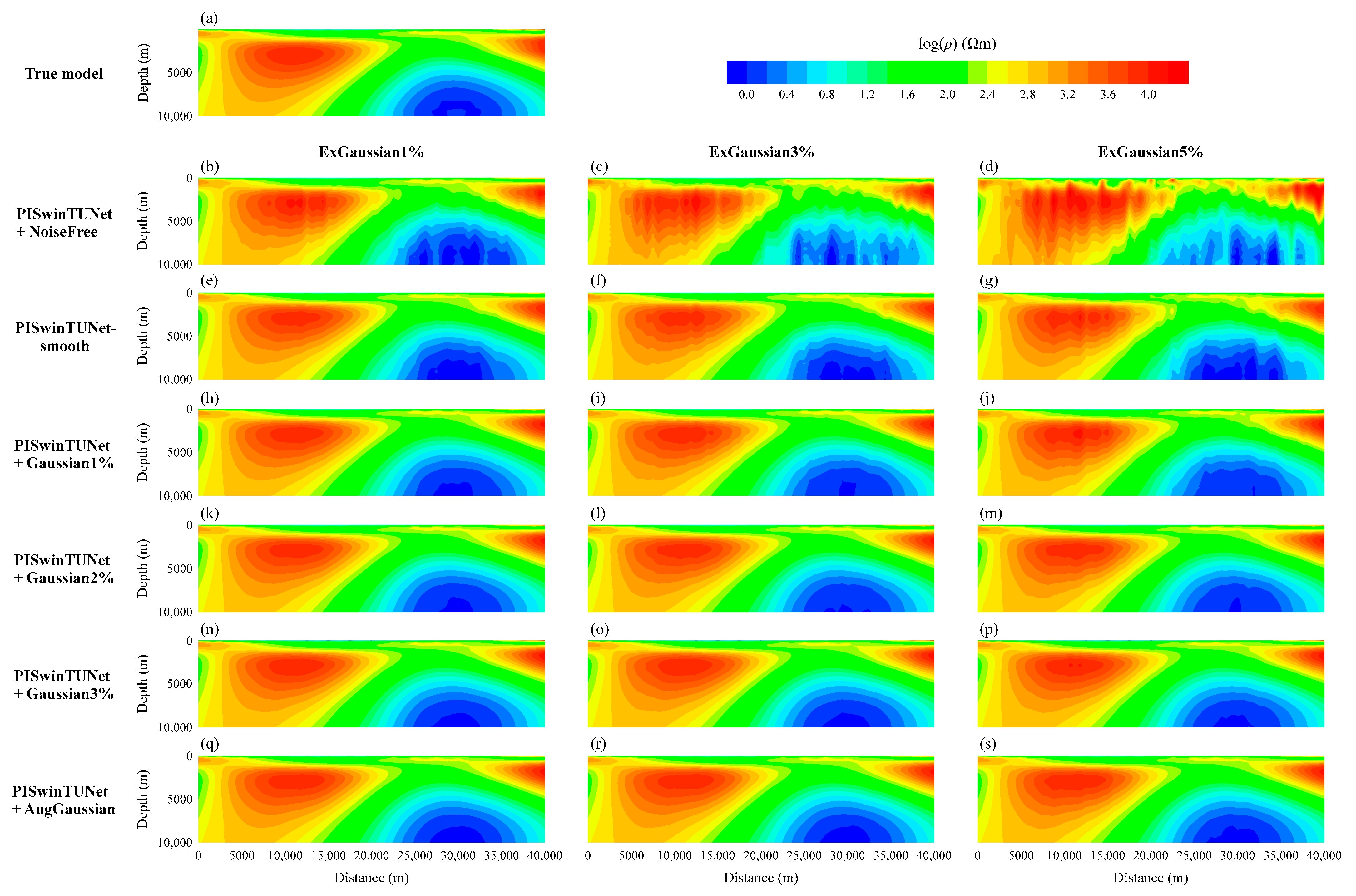
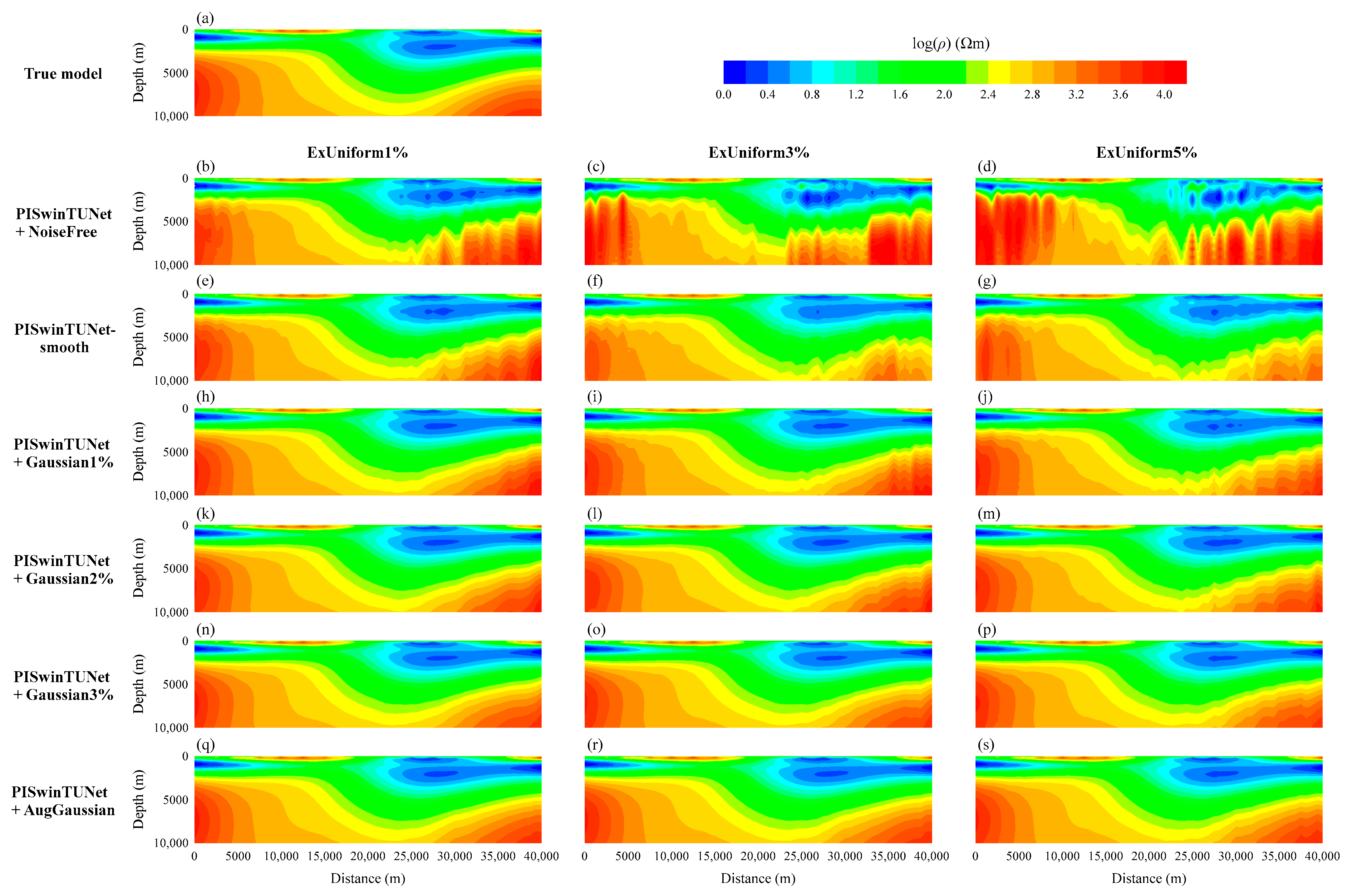
4.2. Synthetic Example with Unfamiliar Noise
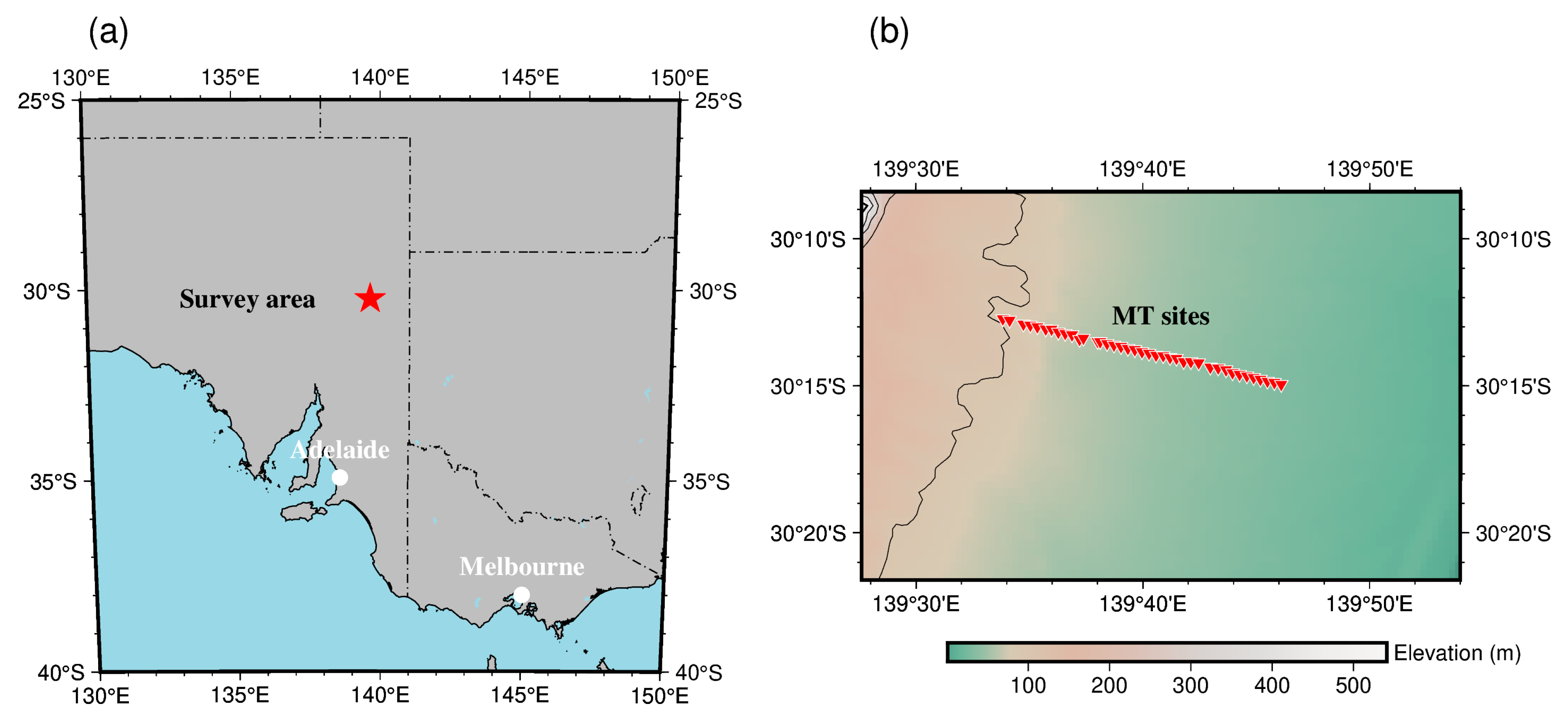
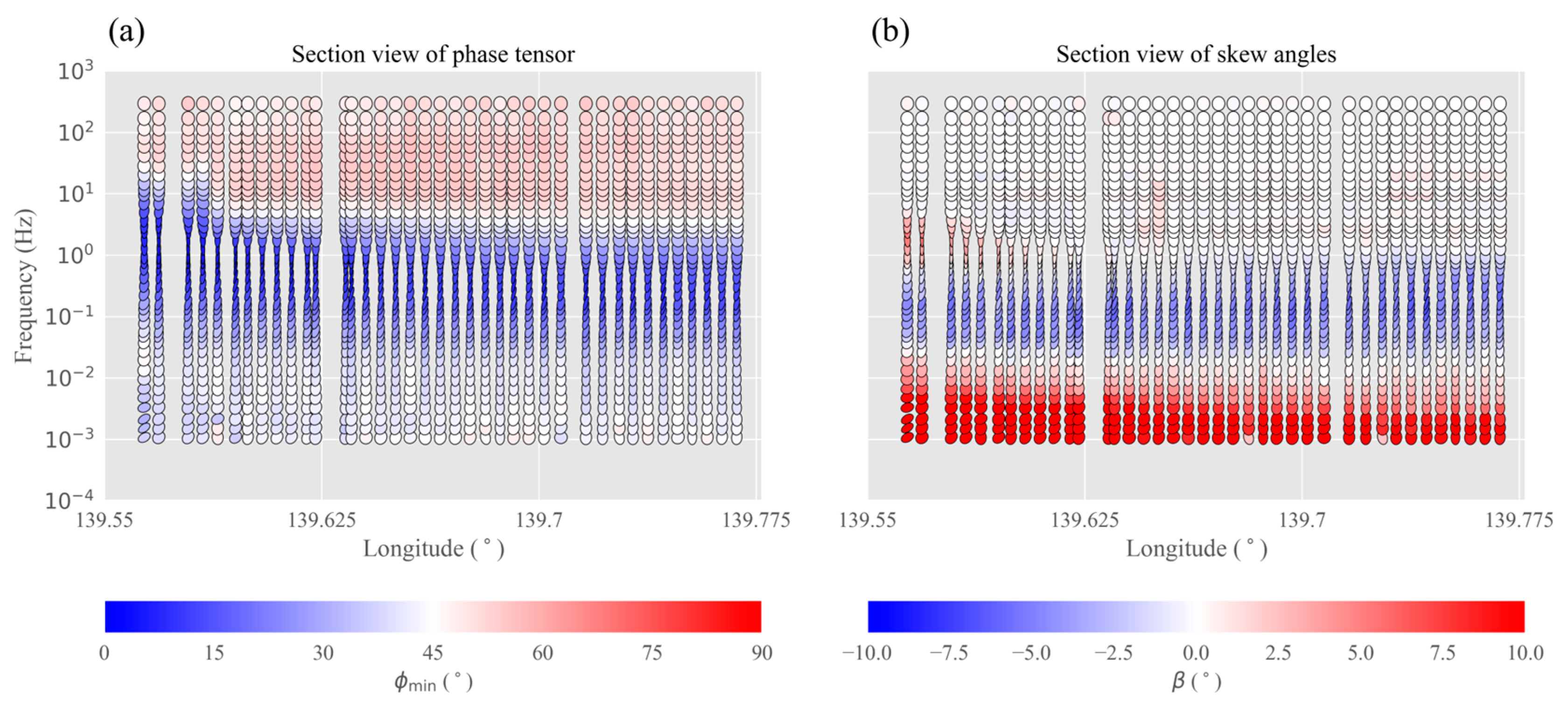
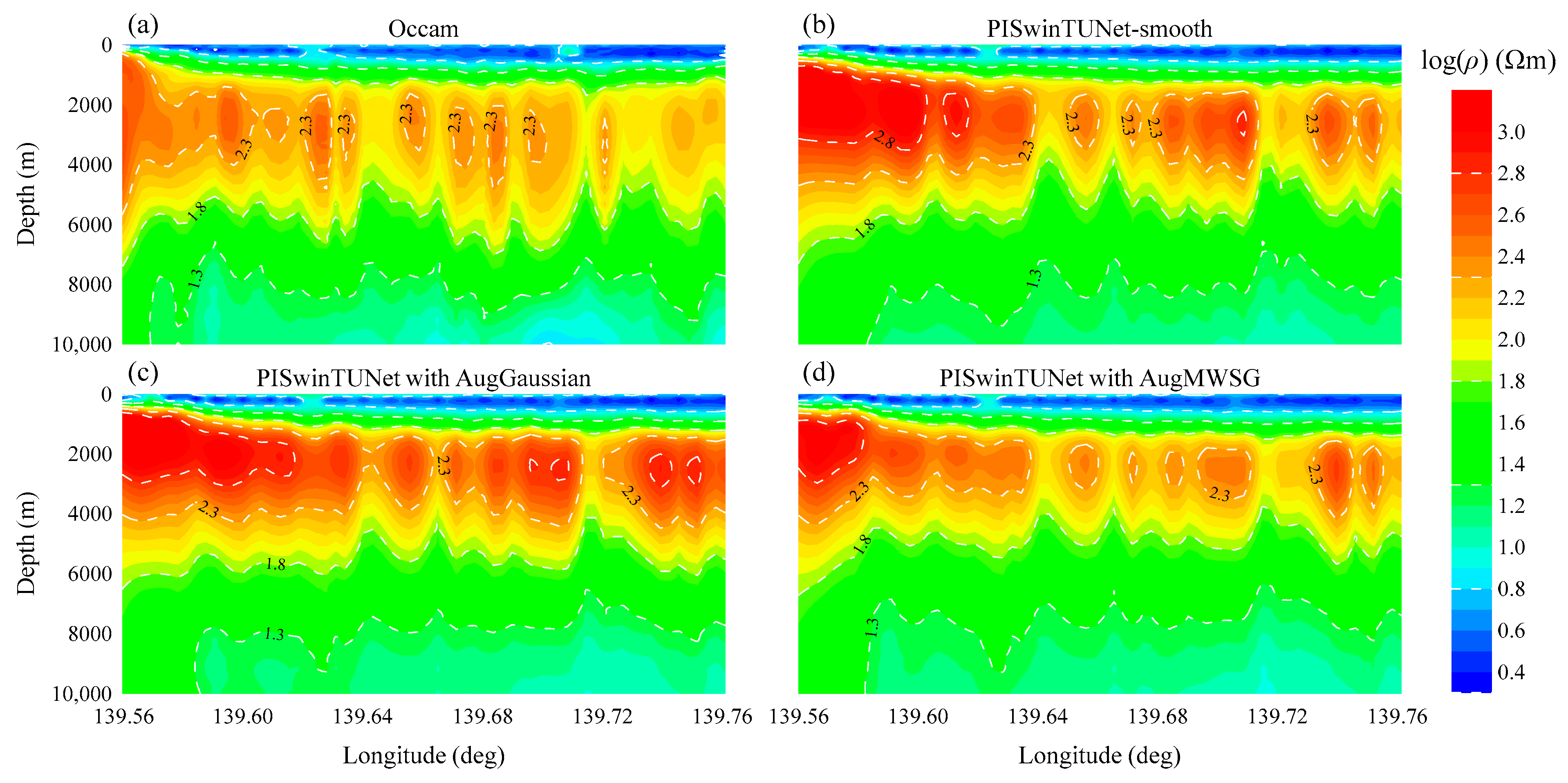
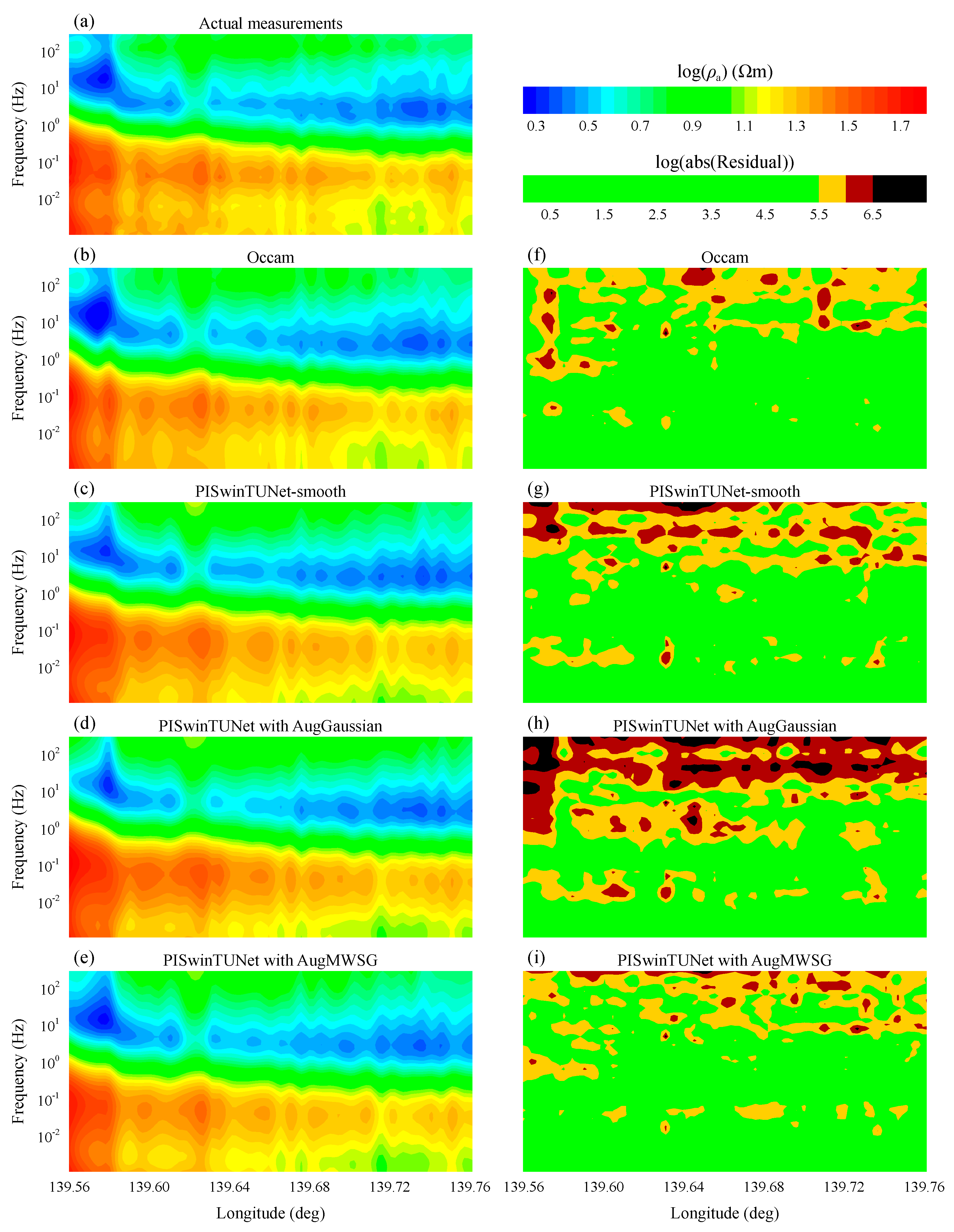
4.3. Field Example
5. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tikhonov, A.N. Determination of the electrical characteristics of the deep strata of the earth’s crust. Dolk. Acad. Nauk. SSSR 1950, 73, 295–311. [Google Scholar]
- Cagniard, L. Basic Theory of the Magnetotelluric Method of Geophysical Prospecting. Geophysics 1953, 18, 605–635. [Google Scholar] [CrossRef]
- Grayver, A.V.; Streich, R.; Ritter, O. Three-dimensional parallel distributed inversion of CSEM data using a direct forward solver. Geophys. J. Int. 2013, 193, 1432–1446. [Google Scholar] [CrossRef]
- Liu, Y.; Yin, C.C. 3D inversion for multipulse airborne transient electromagnetic data. Geophysics 2016, 81, E401–E408. [Google Scholar] [CrossRef]
- Constable, S.C.; Parker, R.L.; Constable, C.G. Occam’s inversion: A practical algorithm for generating smooth models from electromagnetic sounding data. Geophysics 1987, 52, 289–300. [Google Scholar] [CrossRef]
- Siripunvaraporn, W.; Egbert, G. An efficient data-subspace inversion method for 2-D magnetotelluric data. Geophysics 2000, 65, 791–803. [Google Scholar] [CrossRef]
- Newman, G.A.; Alumbaugh, D.L. Three-dimensional magnetotelluric inversion using non-linear conjugate gradients. Geophys. J. Int. 2002, 140, 410–424. [Google Scholar] [CrossRef]
- Kelbert, A.; Egbert, G.D.; Schultz, A. Non-linear conjugate gradient inversion for global EM induction: Resolution studies. Geophys. J. Int. 2008, 173, 365–381. [Google Scholar] [CrossRef]
- Xiang, E.; Guo, R.; Dosso, S.E.; Liu, J.; Dong, H.; Ren, Z. Efficient Hierarchical Trans-Dimensional Bayesian Inversion of Magnetotelluric Data. Geophys. J. Int. 2018, 213, 1751–1767. [Google Scholar] [CrossRef]
- Luo, H.M.; Wang, J.Y.; Zhu, P.M.; Shi, X.M.; He, G.M.; Chen, A.P.; Wei, M. Quantum genetic algorithm and its application in magnetotelluric data inversion. Chin. J. Geophys. 2009, 52, 260–267. [Google Scholar]
- Araya-Polo, M.; Jennings, J.; Adler, A.; Dahlke, T. Deep-learning tomography. Lead. Edge 2018, 37, 58–66. [Google Scholar] [CrossRef]
- Das, V.; Pollack, A.; Wollner, U.; Mukerji, T. Convolutional neural network for seismic impedance inversion. Geophysics 2019, 84, R869–R880. [Google Scholar] [CrossRef]
- Bai, P.; Vignoli, G.; Viezzoli, A.; Nevalainen, J.; Vacca, G. (Quasi-) Real-Time Inversion of Airborne Time-Domain Electromagnetic Data via Artificial Neural Network. Remote Sens. 2020, 12, 3440. [Google Scholar] [CrossRef]
- Wu, S.H.; Huang, Q.H.; Zhao, L. Convolutional neural network inversion of airborne transient electromagnetic data. Geophys. Prospect. 2021, 69, 1761–1772. [Google Scholar] [CrossRef]
- Puzyrev, V. Deep learning electromagnetic inversion with convolutional neural networks. Geophys. J. Int. 2019, 218, 817–832. [Google Scholar] [CrossRef]
- Moghadas, D. One-dimensional deep learning inversion of electromagnetic induction data using convolutional neural network. Geophys. J. Int. 2020, 222, 247–259. [Google Scholar] [CrossRef]
- Ling, W.; Pan, K.; Ren, Z.; Xiao, W.; He, D.; Hu, S.; Liu, Z.; Tang, J. One-Dimensional Magnetotelluric Parallel Inversion Using a ResNet1D-8 Residual Neural Network. Comput. Geosci. 2023, 180, 105454. [Google Scholar] [CrossRef]
- Wang, H.; Liu, W.; Xi, Z.Z. Nonlinear inversion for magnetotelluric sounding based on deep belief network. J. Cent. South Univ. 2019, 26, 2482–2494. [Google Scholar] [CrossRef]
- Liao, X.; Shi, Z.; Zhang, Z.; Yan, Q.; Liu, P. 2D Inversion of Magnetotelluric Data Using Deep Learning Technology. Acta Geophys. 2022, 70, 1047–1060. [Google Scholar] [CrossRef]
- Zhang, J.; Li, J.; Chen, X.; Li, Y.; Huang, G.; Chen, Y. Robust Deep Learning Seismic Inversion with a Priori Initial Model Constraint. Geophys. J. Int. 2021, 225, 2001–2019. [Google Scholar] [CrossRef]
- Sun, J.; Niu, Z.; Innanen, K.A.; Li, J.; Trad, D.O. A theory-guided deep-learning formulation and optimization of seismic waveform inversion. Geophysics 2020, 85, R87–R99. [Google Scholar] [CrossRef]
- Liu, B.; Pang, Y.; Jiang, P.; Liu, Z.; Liu, B.; Zhang, Y.; Cai, Y.; Liu, J. Physics-Driven Deep Learning Inversion for Direct Current Resistivity Survey Data. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5906611. [Google Scholar] [CrossRef]
- Liu, W.; Wang, H.; Xi, Z.; Zhang, R.; Huang, X. Physics-Driven Deep Learning Inversion with Application to Magnetotelluric. Remote Sens. 2022, 14, 3218. [Google Scholar] [CrossRef]
- Jin, Y.; Shen, Q.; Wu, X.; Chen, J.; Huang, Y. A Physics-Driven Deep-Learning Network for Solving Nonlinear Inverse Problems. Petrophys.-SPWLA J. Form. Eval. Reserv. Descr. 2020, 61, 86–98. [Google Scholar] [CrossRef]
- Matsuoka, K. Noise Injection into Inputs in Back-Propagation Learning. IEEE Trans. Syst. Man. Cyb. 1992, 22, 436–440. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Regularization for Deep Learning. 2016, pp. 216–261. Available online: https://www.deeplearningbook.org/contents/regularization.html (accessed on 28 July 2023).
- Liu, W.; Lü, Q.; Yang, L.; Lin, P.; Wang, Z. Application of Sample-Compressed Neural Network and Adaptive-Clustering Algorithm for Magnetotelluric Inverse Modeling. IEEE Geosci. Remote Sens. Lett. 2021, 18, 1540–1544. [Google Scholar] [CrossRef]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin Transformer: Hierarchical Vision Transformer Using Shifted Windows. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Online, 10–17 October 2021. [Google Scholar]
- Liu, Z.; Hu, H.; Lin, Y.; Yao, Z.; Xie, Z.; Wei, Y.; Ning, J.; Cao, Y.; Zhang, Z.; Dong, L.; et al. Swin Transformer V2: Scaling Up Capacity and Resolution. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022. [Google Scholar]
- Bai, D.; Lu, G.; Zhu, Z.; Zhu, X.; Tao, C.; Fang, J.; Li, Y. Prediction Interval Estimation of Landslide Displacement Using Bootstrap, Variational Mode Decomposition, and Long and Short-Term Time-Series Network. Remote Sens. 2022, 14, 5808. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. arXiv 2017, arXiv:1706.03762. [Google Scholar]
- Hendrycks, D.; Gimpel, K. Gaussian Error Linear Units (GELUs). arXiv 2016, arXiv:1606.08415. [Google Scholar]
- Bai, D.; Lu, G.; Zhu, Z.; Zhu, X.; Tao, C.; Fang, J. Using Electrical Resistivity Tomography to Monitor the Evolution of Landslides’ Safety Factors under Rainfall: A Feasibility Study Based on Numerical Simulation. Remote Sens. 2022, 14, 3592. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016. [Google Scholar]
- Bai, D.; Lu, G.; Zhu, Z.; Tang, J.; Fang, J.; Wen, A. Using time series analysis and dual-stage attention-based recurrent neural network to predict landslide displacement. Environ. Earth Sci. 2022, 81, 509. [Google Scholar] [CrossRef]
- Sheng, Z.; Xie, S.Q.; Pan, C.Y. Probability Theory and Mathematical Statistic, 4th ed.; Higher Education Press: Beijing, China, 2008. [Google Scholar]
- Savitzky, A.; Golay, M.J.E. Smoothing and Differentiation of Data by Simplified Least Squares Procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Chen, J.; Jönsson, P.; Tamura, M.; Gu, Z.; Matsushita, B.; Eklundh, L. A Simple Method for Reconstructing a High-Quality NDVI Time-Series Data Set Based on the Savitzky–Golay Filter. Remote Sens. Environ. 2004, 91, 332–344. [Google Scholar] [CrossRef]
- Luo, J.; Ying, K.; He, P.; Bai, J. Properties of Savitzky–Golay Digital Differentiators. Digit. Signal Process. 2005, 15, 122–136. [Google Scholar] [CrossRef]
- Gorry, P.A. General Least-Squares Smoothing and Differentiation by the Convolution (Savitzky-Golay) Method. Anal. Chem. 1990, 62, 570–573. [Google Scholar] [CrossRef]
- Liu, W.; Wang, H.; Xi, Z.; Zhang, R. Smooth Deep Learning Magnetotelluric Inversion Based on Physics-Informed Swin Transformer and Multiwindow Savitzky–Golay Filter. IEEE Trans. Geosci. Remote Sens. 2023, 61, 4505214. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Krieger, L.; Peacock, J.R. MTpy: A Python Toolbox for Magnetotellurics. Comput. Geosci. 2014, 72, 167–175. [Google Scholar] [CrossRef]
- Caldwell, T.G.; Bibby, H.M.; Brown, C. The magnetotelluric phase tensor. Geophys. J. Int. 2004, 158, 457–469. [Google Scholar] [CrossRef]


| Hyperparameter | Configuration |
|---|---|
| Total epoch | 200 |
| Batch size | 128 |
| Optimizer | Adam with default parameters [42] |
| Learning rate | The initial value is 0.01, and in case the validating loss demonstrates no reduction or remains the same for five consecutive epochs, it will be decreased by a factor of 0.8 |
| Early stopping | The training procedure will be terminated if the validation loss demonstrates no reduction or remains constant over a span of 50 consecutive epochs |
| Inversion Data | Inversion Method (PISwinTUNet+) | Inversion Misfit | |||||
|---|---|---|---|---|---|---|---|
| 1% Gaussian Noise | 3% Gaussian Noise | 5% Gaussian Noise | |||||
| Model Misfit | Data Misfit | Model Misfit | Data Misfit | Model Misfit | Data Misfit | ||
| Synthetic example in Figure 6 | NoiseFree | 0.1439 | 0.0406 | 0.2526 | 0.1307 | 0.4187 | 0.2753 |
| Smoothing technique [38] | 0.0717 | 0.0207 | 0.0960 | 0.0349 | 0.1628 | 0.0630 | |
| Gaussian1% | 0.0355 | 0.0099 | 0.0463 | 0.0195 | 0.0892 | 0.0324 | |
| Gaussian2% | 0.0393 | 0.0078 | 0.0470 | 0.0101 | 0.0676 | 0.0139 | |
| Gaussian3% | 0.0393 | 0.0080 | 0.0417 | 0.0095 | 0.0505 | 0.0121 | |
| AugGaussian | 0.0418 | 0.0062 | 0.0414 | 0.0082 | 0.0435 | 0.0104 | |
| Test set consisting of 20,000 samples | NoiseFree | 0.2740 | 0.1647 | 0.4766 | 0.3619 | 0.6227 | 0.5414 |
| Smoothing technique [38] | 0.1657 | 0.0653 | 0.1934 | 0.1153 | 0.2370 | 0.1670 | |
| Gaussian1% | 0.0407 | 0.0130 | 0.0805 | 0.0253 | 0.1191 | 0.0438 | |
| Gaussian2% | 0.0335 | 0.0117 | 0.0463 | 0.0154 | 0.0670 | 0.0215 | |
| Gaussian3% | 0.0337 | 0.0124 | 0.0409 | 0.0143 | 0.0536 | 0.0177 | |
| AugGaussian | 0.0256 | 0.0088 | 0.0309 | 0.0109 | 0.0406 | 0.0143 | |
| Inversion Data | Inversion Method (PISwinTUNet+) | Inversion Misfit | |||||
|---|---|---|---|---|---|---|---|
| 1% Uniform Noise | 3% Uniform Noise | 5% Uniform Noise | |||||
| Model Misfit | Data Misfit | Model Misfit | Data Misfit | Model Misfit | Data Misfit | ||
| Synthetic example in Figure 7 | NoiseFree | 0.1260 | 0.0515 | 0.2415 | 0.1425 | 0.3749 | 0.2678 |
| Smoothing technique [38] | 0.0591 | 0.0175 | 0.1139 | 0.0330 | 0.1112 | 0.0497 | |
| Gaussian1% | 0.0419 | 0.0090 | 0.0474 | 0.0126 | 0.0521 | 0.0195 | |
| Gaussian2% | 0.0345 | 0.0088 | 0.0381 | 0.0091 | 0.0407 | 0.0124 | |
| Gaussian3% | 0.0317 | 0.0099 | 0.0342 | 0.0101 | 0.0338 | 0.0107 | |
| AugGaussian | 0.0290 | 0.0059 | 0.0294 | 0.0059 | 0.0298 | 0.0070 | |
| Test set consisting of 20,000 samples | NoiseFree | 0.2062 | 0.1122 | 0.3655 | 0.2438 | 0.4723 | 0.3600 |
| Smoothing technique [38] | 0.1639 | 0.0567 | 0.1738 | 0.0837 | 0.1917 | 0.1136 | |
| Gaussian1% | 0.0344 | 0.0118 | 0.0541 | 0.0164 | 0.0782 | 0.0240 | |
| Gaussian2% | 0.0319 | 0.0114 | 0.0366 | 0.0127 | 0.0449 | 0.0151 | |
| Gaussian3% | 0.0329 | 0.0123 | 0.0351 | 0.0129 | 0.0396 | 0.0143 | |
| AugGaussian | 0.0251 | 0.0087 | 0.0270 | 0.0093 | 0.0303 | 0.0106 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, W.; Wang, H.; Xi, Z.; Wang, L. Physics-Informed Deep Learning Inversion with Application to Noisy Magnetotelluric Measurements. Remote Sens. 2024, 16, 62. https://doi.org/10.3390/rs16010062
Liu W, Wang H, Xi Z, Wang L. Physics-Informed Deep Learning Inversion with Application to Noisy Magnetotelluric Measurements. Remote Sensing. 2024; 16(1):62. https://doi.org/10.3390/rs16010062
Chicago/Turabian StyleLiu, Wei, He Wang, Zhenzhu Xi, and Liang Wang. 2024. "Physics-Informed Deep Learning Inversion with Application to Noisy Magnetotelluric Measurements" Remote Sensing 16, no. 1: 62. https://doi.org/10.3390/rs16010062
APA StyleLiu, W., Wang, H., Xi, Z., & Wang, L. (2024). Physics-Informed Deep Learning Inversion with Application to Noisy Magnetotelluric Measurements. Remote Sensing, 16(1), 62. https://doi.org/10.3390/rs16010062